Triple Frequency Impedance Matching by Frequency Transformation

ABSTRACT

The purpose of this article is to bring to the attention of students and teachers of circuit theory, as well as of practising design engineers, a recently reported technique for impedance matching at multiple frequencies. This will be done through a specific example, namely that of design of a lumped network for matching a given load resistance R_L to a given source resistance R_S at three given frequencies ω₁, ω₂, and ω₃. The method is based on application of the frequency transformation technique, commonly used in analog filter design, to a basic single frequency matching network. By comparison with the existing approach of assuming a network configuration and solving a set of simultaneous equations, as reported in a recent paper, the new method is shown to have the advantages of design by synthesis, elegance, and simplicity. Further, by virtue of the synthesis approach, the method allows a number of alternative networks to be designed, so that the best one can be selected on the basis of a predetermined criterion.

Keywords:

• Frequency transformation
• Network design
• Impedance matching
• Multiple frequency matching

1. INTRODUCTION

Modern multiband mobile communication has created the need for microwave systems which can handle several frequencies by the same hardware, without the necessity for switching. This in turn requires networks which can match a given load to a given source at multiple frequencies. Most of the work reported in the literature on this subject has focussed on dual band matching, using distributed networks [1–5]. Triple frequency matching has also been reported [6] using such networks. Distributed network systems become bulky, particularly when the operating frequencies are not very high, and lumped or hybrid systems have therefore been developed for compact devices [7,8].

Most of the network topologies used so far have been based on design by analysis, i.e. by assuming a possible network configuration from heuristic considerations and experience, analysing it, and then solving a set of simultaneous equations to derive the component values. The purpose of this article is to bring to the attention of students and teachers of circuit theory as well as of practising design engineers a recently proposed method [9,10] for the same purpose, which is based on the frequency transformation technique, as commonly used in analog filter design [11]. This will be done through a specific example, namely that of designing a network for matching a load resistance R_L to a given source resistance R_S at three given frequencies ω₁, ω₂, and ω₃. The reason for this specific choice is to compare the method with the existing approach for the same design, as reported in a recent paper [8]. It is shown that the new method is characterized by design by synthesis, elegance, and simplicity. The circuit configuration evolves automatically, and by virtue of the synthesis approach, a number of alternative circuits can be easily found, from which the best one can be selected in accordance with a predetermined criterion.

First, for ready reference, we give a brief review of the general theory, and then discuss the design of the triple frequency transformer.

2. GENERAL THEORY

2.1 Basic L-Network for Impedance Matching

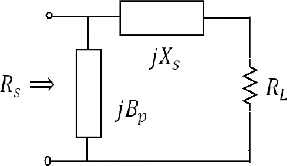
We first consider the general L-network shown in Figure 1 (called network D2 in [10]), where X_s is a reactance and B_p is a susceptance. For matching, we require the relation(1)

Figure 1: The basic L-network for impedance matching.

to be satisfied at the frequency or frequencies of interest. Simplifying Eq. (1(1) ) and equating the real and imaginary parts on both sides give the following equations:(2a) and(2b) Eq. (2b) shows that B_p and X_s should be of the same sign. Also, combining Eqs. (2a) and (2b) to eliminate B_p, we get(3) Eq. (3(2b) ) shows that the configuration is applicable only if R_s > R_L. This is no restriction, however, because for the other case, i.e. R_s < R_L, the positions of the source and the load are to be interchanged. Eq. (3(2b) ) gives(4) and correspondingly,(5) As mentioned earlier, B_p and X_s should both be either positive or negative.

As discussed in the comprehensive network theoretic formulation of the technique by Dutta Roy [10], one could have a parallel development with the L-network having the shunt arm B_p across R_L and the series arm X_s in series with the source (this is called network D1 in [10]). As mentioned later in this article, this alternative is important in deriving other alternative equivalent circuits for matching.

2.2 Single Frequency Matching

For matching at a single frequency ω₀, one choice is to have an inductor L₁ for X_s and a capacitor C₂ for B_p, while the other choice is to have C₁ for X_s and L₂ for B_p. Using the first choice, the element values are: L₁ = R₁/ω₀ and C₂ = G₂/ω₀.

2.3 Application of Frequency Transformation

Frequency transformation is a well-known technique in analog filter design [11] by which a normalized low-pass filter with cut-off at 1 radian/sec can be transformed to any other kind of filter, be it high-pass, band-pass, band-stop, or multiband-pass, with the same tolerances as in the prototype. Basically, it transforms the frequency of 1 radian/sec to the cut-off frequencies of the desired filter. In more general terms, the performance at 1 radian/sec is reproduced in the transformed filter at the desired frequencies. There is no reason why performance cannot be impedance matching, as demonstrated in [9,10] and this article.

Let S denote the complex frequency variable in the single frequency matching network and let ω₀ be normalized to 1 radian/sec. Then the problem reduces to that of transforming S = ±j1 to the multiple frequencies s = ±jω_k, where, in general, k = 1 … N, s being the complex frequency variable in the transformed network. As is well known [12,13], the transformation function is an LC immittance (impedance or admittance) function of the form(6) where the limits of the summation are determined by the number of frequencies at which matching is required. For example, if N = 2, then the first two terms in Eq. (6(5) ) suffice. Alternatively, one can use only the first term in the summation, which, in fact, is of the same form as the reciprocal of the first two terms. For N = 3, as is the case in the example to follow, either of the first two terms and one term in the summation serve the purpose. In general, for N odd and ≥3, either of the first two terms is to be taken along with the summation with i ranging from 1 to (N − 1)/2. For N even and ≥4, there are two choices, viz. (1) take the first two terms and the summation with i ranging from 1 to (N − 2)/2 or (2) take only the summation with i ranging from 1 to (N/2). In addition, as already mentioned, there are two choices for the basic single frequency matching network. Clearly, with the flexibility in choosing the basic network and the transformation function, one can generate a number of matching networks having the same performance. Some more alternative networks can be generated by synthesizing each of the reactance and susceptance functions by the other Foster or Cauer or mixed canonic forms. From this multiplicity of networks, one can choose the best one using some appropriate criterion like the total inductance or capacitance or the spread in the values of the components.

3. TRIPLE FREQUENCY MATCHING NETWORK

We shall now illustrate the simplicity, elegance, and flexibility of the frequency transformation technique by designing a triple frequency matching network. The basic network is shown in Figure 2(a), where the fact that ω₀ has been normalized to 1 radian/sec has been taken into account. One appropriate transformation for this case is(7) The impedance of L₁ ( = R₁) thus transforms into(8) The right-hand side of Eq. (8(7) ) represents a series connection of a capacitance C_se = 1/(k₀ R₁) and a parallel L_sC_s circuit with L_s = k₁ R₁/q₁ and C_s = 1/(k₁ R₁), as shown in Figure 2(b).

Similarly, the admittance of C₂ ( = G₂) transforms to the circuit shown in the shunt arm of Figure 2(b) with the following element values: L_pe = 1/(k₀ G₂), C_p = k₁ G₂/q₁, and L_p = 1/(k₁ G₂).

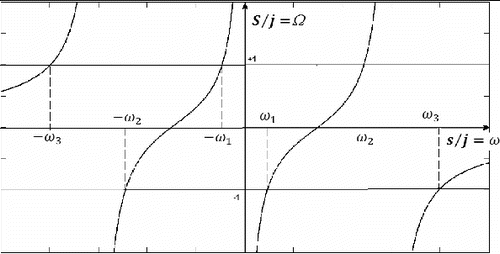
Now the only task that remains to be done is to find the values of k₀, k₁, and q₁. For this purpose, put S = j1 and s = jω in Eq. (8(7) ); after simplification, we get the following equation in ω:(9) The roots of this equation should give ω₁, ω₂, and ω₃, but not all with positive signs. To find which one(s) would be positive, we sketch the reactance function of Eq. (8(7) ) as shown in Figure 3 and find the frequencies at which S/j = 1. Clearly, the roots of Eq. (9(8) ) are −ω₁, ω₂, and −ω₃. Figure 3 also shows that had we taken S/j = −1 in Eq. (8(7) ), the resulting cubic equation would have the roots ω₁, −ω₂, and ω₃. Returning to Eq. (9(8) ), we see that the left-hand side should be equal to(10)

Figure 2: Triple frequency impedance transformer: (a) basic single frequency matching circuit and (b) triple frequency matching circuit with element values given in the text.

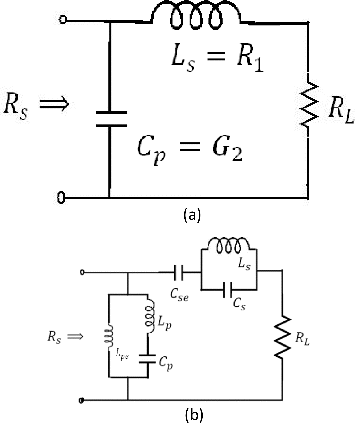
Figure 3: Reactance sketch of Eq. (8(7) ).

Comparing the right-hand side of Eq. (10(9) ) with the left-hand side of Eq. (9(8) ), we get the following three equations:(11) Solving these equations, we finally get(12) The circuit of Figure 2(b) was previously derived by Lin, Chen, and Zhao [8] following the conventional approach, i.e. by assuming the circuit, analysing it, and then setting up and solving the equations obtained at the three frequencies. As a numerical example, they considered the following specifications: R_L = 25 Ω, R_S = 50 Ω, and {ω₁, ω₂, ω₃} = {0.225, 0.425, 0.625} GHz. Calculations from Eq. (12(11) ) and the expressions for the element values given under Eq. (8(7) ) give: C_se = 23.5 pF, L_s = 2.78 nH, C_s = 41.31 pF, L_pe = 29.38 nH, C_p = 2.22 pF, and L_p = 51.64 nH. These are exactly the same as those obtained in [8]. Simulation and experimental results given in [8] validate the design.

4. ALTERNATIVE CIRCUITS FOR TRIPLE FREQUENCY MATCHING

As mentioned in the previous section, several alternative circuits for the triple frequency impedance matching can now be obtained. Figure 2(b) network, as it is, has the shunt arm in Foster 2 form (henceforth abbreviated as F2) and the series arm in Foster 1 form (henceforth abbreviated as F1). The shunt arm can also be realized in F1 and the series arm can also be realized as F2. Accordingly, we have four alternative circuits, viz. (F2, F1), (F2, F2), (F1, F2), and (F1, F1). Note that for a three-element network, Cauer forms will reduce to either F1 or F2.

Second, using an inductance for B_p and a capacitance for X_s in the basic network of Figure 1, and then applying the transformation of Eq. (7(6) ), one obtains a different circuit which also allows four different circuits to be generated.

Third, if the basic network is chosen as D1 of [10], in which there is a shunt arm B_p across R_L and a series arm X_s in series with R_S, then as in the case of D2 discussed so far, another eight networks can be generated, thus making a total of 16 alternative circuits for the same impedance matching purpose.

As mentioned in Section 2.2, an alternative transformation for triple frequency impedance matching is(13) The values of the constants have been worked out in [10] along with a possible circuit by transforming the basic network D1, in which the series arm is F1 and the shunt arm is F2. Following the same procedure as in the case of Eq. (7(6) ), another 16 different circuits can be generated, thus making a grand total of 32 alternative circuits for any specified triple frequency impedance matching problem.

All these circuits can now be compared in terms of total inductance, total capacitance, maximum inductance, maximum capacitance, inductance spread, and capacitance spread, as done in [10] for a dual frequency impedance matching circuit, and the best one can be chosen in accordance with a predetermined criterion.

5. CONCLUSIONS

As discussed and demonstrated in this article, application of frequency transformation on the basic single frequency impedance matching network eases the problem of designing multiple frequency matching networks. It gives multiple solutions and facilitates the choice of the most suitable network in a given situation.

ACKNOWLEDGEMENTS

This work was supported by the Indian National Science Academy through the Honorary Scientist scheme. The author thanks Shoubhik Dutta Roy and Yashwant V Joshi for their help in the preparation of this article. Thanks are also due to the reviewer for constructive comments.

Additional information

Notes on contributors

S.C. Dutta Roy

S.C. Dutta Roy received his Bachelor's, Master's, and Doctorate degrees from the University of Calcutta, Calcutta, India, in 1956, 1959, and 1965, respectively. He was a lecturer at the University of Kalyani, West Bengal, India, for five years before taking up an assistant professor's position at the University of Minnesota, Minneapolis, Minnesota, USA. He returned to India in 1968 and spent more than four decades at the Indian Institute of Technology Delhi (IITD) as an associate professor, professor, head of the department, and dean of undergraduate studies. On sabbatical leave from IITD, he spent a year at the University of Leeds, UK, and another year at the Iowa State University, Ames, Iowa, USA, as a visiting professor. Upon superannuation from IITD, he continued there first as an emeritus fellow, then as a senior scientist of the Indian National Science Academy (INSA), and finally as an honorary scientist of the INSA. Currently, he continues working from home as an INSA honorary scientist.

Professor Dutta Roy's research interests are in circuits, systems, and signal processing. He has published more than 260 research papers in IEEE, IEE, and other reputed journals and transactions, and has mentored 30 PhD students. He holds one US and three Indian patents and is the creator of five highly popular full-length video courses, four of which are available on YouTube for free downloading. His research has been recognized by a fellowship of the IEEE and of all the National Academies of Science and Engineering of India, and a distinguished fellowship of the Institution of Electronics and Telecommunication Engineers, New Delhi, India, and several national awards, including the most prestigious Shanti Swarup Bhatnagar Prize.

E-mail: [email protected]