Integration of GPS with a WiFi high accuracy ranging functionality

Abstract

High accuracy seamless positioning is required to support a vast number of applications in varying operational environments. Over the last few years, the global positioning system (GPS) has become the de facto technology for positioning applications. However, its performance is limited in indoor and dense urban environments due to multipath as well as signal attenuation and blockage. A number of techniques integrating GPS with other positioning technologies have been developed to address the limitations of standalone GPS in these difficult environments. While most of the developed techniques cover the outages of GPS in such environments, they do not provide acceptable performance, in terms of positioning accuracy, especially for some mission-critical (e.g. safety) applications. This paper proposes a tightly coupled (i.e. in the measurement domain) GPS/WiFi integration method which, in addition to addressing GPS outages, improves the overall positioning accuracy to the meter-level, thus satisfying the requirements of a number of location based services and intelligent transport systems applications. The performance of the proposed GPS/WiFi integration method is assessed for a number of scenarios in a simulation environment for an identified dense urban area in London, UK.

Keywords:

• GPS integration
• time estimation
• WiFi
• Improved FOCUSS for Arrival Time Estimation (IFATE)
• Time Difference of Arrival (TDOA)
• WLAN IEEE802.11g

1. Introduction

The need for positioning and navigation services in all environments has attracted significant research in recent years. This is to support the requirements of the vast number of existing and emerging applications such as pedestrian navigation, safety and security operations, asset tracking, location based services (LBS), and intelligent transport systems (ITS) (1–3). The use of the global positioning system (GPS) has significantly increased over the last few years which stimulated the improvement and development of other global navigation satellite systems (GNSS). However, the use of GNSS in indoor and dense urban environments is limited due to multipath and signal attenuation and blockage. Research is on-going to enable GNSS operations in such environments by the use of high sensitivity receivers, Pseudolites and GPS re-radiators. However, achieving affordable real-time high accuracy remains a challenge (4).

The limitations of GPS in indoor and dense urban areas have attracted research and development of bespoke and overlaid positioning systems. Bespoke systems refer to terrestrial systems solely developed to provide positioning services. They are generally based on infrared, ultrasound, ultra wideband (UWB), vision, and magnetic signals (5). Examples of such systems include Active Badge, CRICKET, Sonitor, and Ubisense (5–8). While most of these systems can support centimeter (cm)-level (95%) position accuracy, their use is limited by their high cost and small coverage areas. Overlaid positioning systems on the other hand, exploit existing wireless network infrastructure (i.e. signals of opportunity) to support positioning. Such wireless networks include cellular, wireless local area networks (WLAN) or WiFi (in this paper, WLAN and WiFi are used as synonymous), Bluetooth, Zigbee, and UWB. Existing methods that exploit signals of opportunity are typically based on proximity detection with Cell-ID measurements, feature matching with received signal strength (RSS) measurements (i.e. RSS fingerprinting), and trilateration/multilateration with RSS and time of flight (TOF) ranging measurements (9). Proximity detection with Cell-ID is easy to implement but provides poor accuracy depending on the cell radius. RSS fingerprinting requires significant effort to build and maintain the associated databases (9, 10). The performance of trilateration/multilateration depends on the quality of the ranging measurements. RSS ranges are obtained by applying a propagation model relating the signal power loss to the distance travelled. Achieving high accuracy RSS ranging requires the use of site-specific and highly complex propagation models (11). This is due to the sensitivity of RSS measurements to variations within the surrounding environment. TOF ranges are obtained by scaling TOF measurements by the propagation speed. However, the high propagation speed of RF signals imposes stringent requirements on the extraction of TOF measurements. These requirements are the need to provide precise time synchronization between wireless nodes and estimate the signal propagation time with high accuracy and precision.

In order to address the limitations of GPS in indoor and dense urban areas, and achieve seamless positioning in all environments, a number of integration techniques with terrestrial systems have been developed. Such systems include inertial navigation systems (INS), map-matching, and overlaid systems. INS is based on the concept of dead reckoning (DR), which estimates the user position based on the displacement (distance and angle) from an initial position (12). The performance of a GPS/INS integrated system depends on the INS grade, the maximum GPS signal outage period, and the GPS/INS integration method. GPS/INS integrated systems are typically suitable for short GPS signal outage durations. For longer outage durations such as in indoor and dense urban environments, the performance of the integrated system is weakened due to the accumulative nature of INS errors. GPS/map-matching integration for vehicle navigation suffers from similar limitations due to ambiguities in road junctions.

Most of the current GPS/overlaid integrated systems are based on WiFi and cellular networks, and has been applied in three forms: assisted GPS (AGPS), position domain integration (loosely coupled), and measurement domain integration (tightly coupled).

AGPS improves the performance of GPS receivers by providing them with aiding data (e.g. ephemeris and ionospheric correction parameters) as well as initial position and time estimates. While most of the AGPS systems are based on cellular networks (e.g. GSM) (13), WiFi-based AGPS systems have also been developed (14, 15). Although AGPS improves the GPS receiver sensitivity and reduces the time to first fix, it does not address GPS outages in indoor and dense urban areas.

Loosely coupled GPS/overlaid systems integration has been widely implemented to address GPS outages such as the Skyhook positioning platform (16). This is mainly by extracting Cell-ID and RSS measurements (17–19). For example, in Ref. (20), a proximity detection method using WiFi Cell-ID in conjunction with GPS is proposed to support knowledge-based logistics systems in dense urban areas. In Refs. (3, 21), integrated GPS/DR/WiFi RSS fingerprinting techniques are implemented in a loosely coupled mode to improve performance over GPS/DR systems. In Ref. (22), a loosely coupled GPS/WiFi integrated system using WiFi RSS ranging is applied while in Ref. (17) the same integration technique is applied with WiFi RSS fingerprinting, achieving a position accuracy of about 13 m (95%). However, there are two main limitations associated with loosely coupled GPS/overlaid systems integration. Firstly, it is not always possible to obtain a GPS position in indoor and dense urban areas and hence, the integrated solution will often be based on the overlaid system. Secondly, the applied overlaid positioning measurements (i.e. RSS and Cell-ID) typically do not provide a sufficient level of accuracy. Cell-ID positioning accuracy depends on the cell radius (∼50 m for WiFi and ∼150 m for cellular networks in urban areas). RSS measurements based positioning has accuracies of about 6 m (95%) in indoor environments and about 40 m (95%) in urban areas when used in fingerprinting mode and significantly worse performance when used in RSS ranging mode (9, 19). This is mainly due to the variability of RSS readings from different receivers (23), people movements, and the effects of device orientation (24).

Tightly coupled GPS/overlaid systems integration requires the extraction of RSS or TOF ranging measurements. Integration of WiFi RSS ranging with GPS is typically limited by the poor RSS ranging accuracy. A 5m RSS ranging accuracy was achieved in Ref. (25) within an area of only 20 m radius centered around the WiFi access point. Integration of GPS pseudoranges with TOF ranges from overlaid systems is proposed in Refs. (26–28). In Ref. (26), integration of GPS with cellular system time difference of arrival (TDOA) measurements achieved an accuracy of 44 m root mean square error when using 3 TDOA and 2 GPS pseudorange measurements. In Ref. (27), an integrated GPS/round-trip time of flight (RTOF) WLAN solution was proposed, with a target position accuracy of at least 10 m. However, the extraction of the WLAN RTOF measurements for this solution is based on the work in Refs. (29, 30), where achieving a meter-level ranging accuracy requires averaging over 100s of observations. This greatly limits the application of this method in a dynamic platform.

In order to address some of the above limitations, this paper proposes a GPS/WiFi tightly coupled integrated system with the aim of achieving real-time meter-level position accuracy with high availability in dense urban areas. The motivation of the present work is to meet the requirements of a number of safety critical and emergency LBS and ITS applications, such as collision warning and lane-level navigation. Unlike other systems in the literature, the proposed system is intended not to only address GPS outages, but to also improve the overall position accuracy. This is achieved through real-time high quality WiFi-based ranging data and improved system geometry. The work exploits the improved FOCUSS (FOCal Underdetermined System Solver) for arrival time estimation (IFATE) algorithm developed by the authors, which enables the extraction of WiFi real-time high-accuracy (sub-meter) ranging (31–33). The advantages of the proposed integrated system for indoor and dense urban areas include: (1) increased overall number of measurements, and improved coverage for GPS outages, especially when less than four GPS satellites are visible; (2) enhanced position accuracy due to the high quality of the WiFi ranging functionality; (3) better vertical geometry and hence position accuracy due to the additional WiFi reference nodes; (4) improved initial position accuracy resulting in reduced convergence time of the position estimation process as a result of the WiFi relatively short communications range; (5) ability to combine the WiFi-based initial solution with a 3D city model and GPS ephemeris data. The system can therefore eliminate GPS satellites blocked by surrounding buildings and reduce the effects of GPS multipath; and (6) accurate seamless positioning in all environments.

The paper is organized as follows: Section 2 provides a brief introduction to the IFATE algorithm and its application to WiFi, while Section 3 presents its performance using both simulated and real data. Section 4 discusses the applied integration algorithm of WiFi with GPS. The performance of the integrated system is evaluated in Section 5 and the paper concludes in Section 6.

2 IFATE algorithm

The use of TOF ranging has the potential to achieve meter-level positioning accuracy but is limited by the precise time synchronization and time estimation requirements (nanosecond (ns)-level in the case of RF signals). While the time synchronization requirement can be addressed by the use of RTOF, TDOA, or Differential TDOA (DTDOA) (34, 35), the time estimation, especially in the case of overlaid systems, remains an issue. The time estimation process refers to the estimation of the arrival time of the direct path transmitted ranging signal. The most common time estimation technique is based on transmitting a known signal and performing cross correlation at the receiver with a locally stored version of the transmitted signal (34). However, in limited bandwidth systems, dense multipath components widen and shift the peak of the cross-correlation function, leading to errors in the estimation of the arrival time of the direct path. On the other hand, super-resolution estimation techniques have the ability to address the limitations of the cross-correlation technique, especially in dense multipath environments. Super-resolution techniques include multiple signal classification (MUSIC) (36), estimation of signal parameters via rotational invariant techniques (ESPRIT) (37), and super-resolution pseudorandom noise correlation method (SPM) (38). Although these techniques can significantly improve the time estimation accuracy, they require averaging over several observations and are thus not real-time. They also require prior estimation of the number of multipath components, suffer from high signal to noise ratio (SNR) and high computational requirements (2).

The authors developed the IFATE algorithm which addresses the limitations associated with the super-resolution techniques, while achieving the same level of performance. IFATE is an iterative time estimation algorithm that provides super-resolution estimation under low SNR conditions. It is based on the FOCUSS sparse estimation algorithm and addresses the bandwidth, dense multipath, and noise limitations. Oversampling is applied at the receiver to improve the resolution of the estimated time without the need to average over multiple measurements. This enables real-time applications and reduces the time variability effect of the propagation channel. A number of measures are introduced within IFATE to reduce its computational complexity compared to existing super-resolution time estimation techniques (31–33).

IFATE is applied to a WiFi TDOA setup, where WiFi-enabled reference nodes estimate the arrival time of the ranging signal transmitted by standard WiFi mobile nodes. The long sequence of the WLAN IEEE802.11g standard frame preamble is selected as the ranging signal (39). The use of the frame preamble long sequence has three advantages: (1) it avoids involving the mobile user in the positioning process (for security applications); (2) it minimizes the effect of the ranging process on the data throughput since no specific ranging signals are transmitted; and (3) the long sequence provides good auto-correlation characteristics with two distinctive correlation peaks which are used to estimate the quality of the received signal. In order to achieve sub-meter ranging accuracy, IFATE applies a sampling rate of 1 giga sample per second (GSPS) which translates into about 30 cm ranging resolution. This sampling rate is only applied at the reference nodes. A number of measures were considered to minimize the drawbacks associated with the required high sampling rate as part of the reference node architecture (33).

3 IFATE performance evaluation

This section investigates the performance of IFATE in a simulation environment as well as using real-data collected within an indoor laboratory environment. Sections 3.1 and 3.2 discuss the setup and results of the simulation and of the hardware tests, respectively.

3.1 Simulation evaluation

The simulation test environment was developed using MATLAB. The baseband frame preamble of the WLAN IEEE802.11g standard was generated with a sampling rate of 1 GSPS (39). The propagation channel was simulated using the Medbo and Schramm (40) indoor line of sight (LOS) multipath model and additive white Gaussian noise. The effects of frequency mismatch at the receiver were included. The transmitter-receiver separation was assumed to be random with a uniform distribution between 1 and 300 m (the assumed maximum WiFi coverage range). In addition to IFATE, the cross-correlation and super-resolution SPM techniques were applied to the received signal (33, 38). Figure 1 presents the performance of IFATE against the SPM and cross-correlation techniques in terms of the estimated absolute range error (i.e. time estimation error) and the processing time for SNR values ranging from 0 to 50 dB. The results in Figure 1 are the average of 500 runs for each SNR value.

Figure 1 Performance of IFATE against SPM and cross-correlation in terms of: (a) absolute range error in meters and (b) processing time in seconds (33).

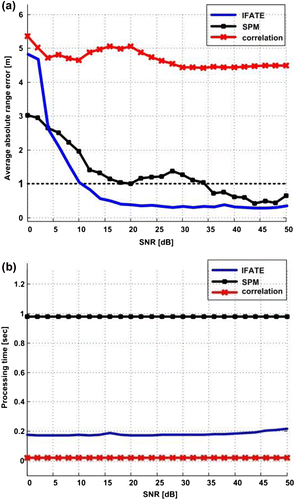
In terms of the average range error, it can be seen from Figure 1(a) that IFATE is superior to existing algorithms for SNR values greater than 5 dB. Although, the SPM algorithm can detect overlapped multipath components, it achieves sub-meter ranging accuracy only at SNR values higher than 35 dB which agrees with the findings in Ref. (38). On the other hand, cross-correlation suffers from a range estimation error that is independent of the SNR value as shown in Figure 1(a). This is due to the shift of the correlation peak as a result of the effects of limited bandwidth and dense multipath. In Figure 1(b), it is evident that cross-correlation has superior performance in terms of computational complexity. On the other hand, IFATE is significantly faster than SPM, which requires averaging over a set of measurements to improve the rank of the correlation matrix and applies eigen decomposition (a computationally intensive process) to the received signal correlation matrix.

3.2 Hardware evaluation

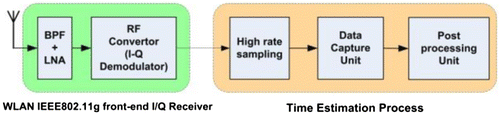
The performance of IFATE was also evaluated in an indoor laboratory environment. A WiFi-enabled reference node was developed (see Figure 2) (33). It consists of a band pass filter (BPF), low noise amplifier (LNA), and an RF down-convertor which outputs the baseband I/Q (In-phase/Quadrature) received signal. The time estimation process comprises of a high rate sampling, data capture, and post processing units.

Figure 2 Structure of the implemented WiFi-enabled reference node (33).

The TP-LINK TL-WN422G USB WLAN IEEE802.11b/g transceiver was used as the mobile WiFi node. The MAXIM MAX2830EVKIT performed the WLAN IEEE802.11g I/Q front-end receiver functionality within the reference node. The Agilent DSO5014A digital storage oscilloscope (DSO) was used to perform both the high rate sampling at 1 GSPS and data capture functionalities (33). The captured data was then post processed offline using MATLAB. The tests captured the effects of people movement and interference from Bluetooth and other WiFi devices.

In Ref. (33), the authors showed, on the basis of real data collected in a controlled multipath test, the ability of IFATE to detect closely spaced multipath components with inter-delay of ∼10 ns. Furthermore, IFATE was tested using a wireless TDOA configuration depicted in Figure 3.

Figure 3 Wireless TDOA indoor test configurations (33).

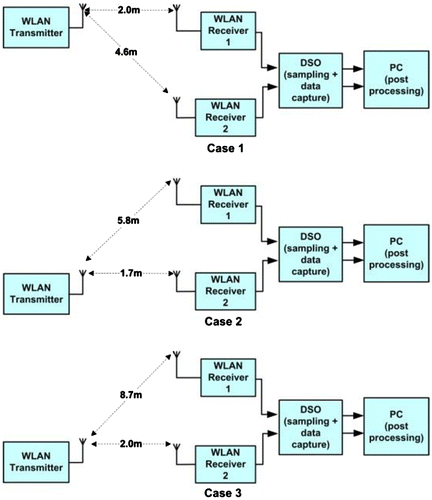
In this TDOA configuration, the TP-LINK mobile node was used as the WLAN transmitter which continuously transmits the ranging signal. TDOA measurements were then collected using two synchronized reference nodes. This is achieved, as shown in Figure 3, by the use of two WLAN receivers connected by cables to the DSO which has the ability to synchronously sample and collect data from its input channels. The post processing stage applies frequency mismatch correction, tests the signal quality, and then performs the IFATE time estimation process (33). The short separation between the transmitter and receivers in these tests is due to the physical constraints within the laboratory environment. The collected TDOA measurements had a mean error of −0.45 ns and standard deviation of 2.53 ns (33). These results demonstrated IFATE’s ability to support sub-meter ranging accuracy. However, they included synchronization errors within the DSO and delay variations between the two WLAN receivers.

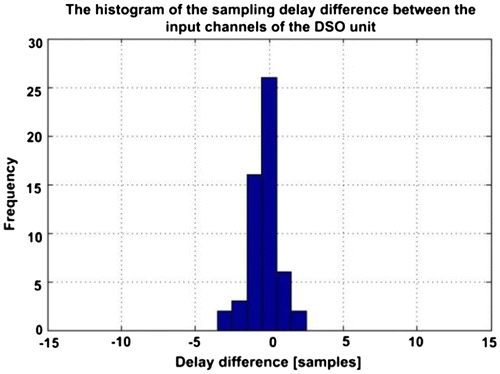
The performance of IFATE is further investigated in this paper by identifying and isolating the DSO synchronization error. The ability of the DSO to synchronously sample and collect data was tested by using a triangular signal as the common source to all of its input channels, with a sampling rate of 1 GSPS. The synchronization error represents the delay between the peaks of the sampled triangular signals from each channel. The DSO synchronization error distribution is shown in Figure 4 with a mean of −0.33 ns and a standard deviation of 1.3 ns.

Figure 4 Distribution of the synchronization error of the digital storage oscilloscope.

By removing the DSO synchronization error from the IFATE TDOA results, the measurements mean error becomes −0.12 ns (−0.04 m) and the standard deviation becomes 2.17 ns (0.65 m). The following section presents the WiFi/GPS integration method, which uses the corrected WiFi TDOA measurements presented in this section.

4 GPS/WiFi integration

The tightly coupled integration of the GPS and WiFi measurements in this paper uses an epoch-by-epoch weighted least squares (WLS) method. The performance is characterized by the achieved positioning accuracy and the dilution of precision (DOP). The DOP is a parameter that relates the range measurement error to the user position error (41). It depends on the user/reference nodes geometry, where reference nodes include both WiFi reference nodes and GPS satellites. This section presents the position estimation and DOP calculation methods for standalone GPS, standalone WiFi TDOA, and the GPS/WiFi TDOA integrated solutions.

4.1 Global positioning system

In the case of GPS, measurements (i.e. pseudorange observations) from at least four satellites are required to compute the user 3D position and correct for the receiver clock error (). The GPS observation euquations for m measurements are (42):(1)

where is the pseudorange measurement, are the coordinates of the ith GPS satellite, c the speed of light, the user GPS clock error and the measurement errors including noise. Equation (1) is then linearized using first order Taylor series with respect to an initial solution , leading to:(2)

Where:

In matrix form, Equation (2) becomes:(3)

where

where , is the user effective range error (UERE), I is the identity matrix, and is the transpose operator. In the case of m > 4, Equation (3) can be solved using least squares (LS) (42):(4)

This is provided that the inverse of exists. The LS estimates are added to the initial solution in order to iteratively obtain the user position. The position error is the Euclidean distance between the final LS solution and the true position.

Different variants of the DOP parameter are used to characterize the performance of the position/time solution. These are the geometric DOP (GDOP), position DOP (PDOP), horizontal DOP (HDOP), vertical DOP (VDOP), and time DOP (TDOP) and are calculated based on a local coordinates frame. The different DOP parameters are computed from the covariance matrix of the LS solution .(5) (6)

where D₁, D₂, D₃, and D₄ are the diagonal elements of the matrix. The above LS estimation and DOP calculation is based on the assumption that GPS pseudorange errors are independent and identically distributed with the same variance. However, GPS pseudorange errors can have different variances for example due to being a function of the satellite elevation (i.e. where and the variance of the ith GPS pseudo range measurement error). In this case, the user position is computed using the weighted LS (WLS) as:(7)

where the weighting matrix . In this case, the WDOP is applied instead of the GDOP which is defined as (41, 43). The use of WDOP provides a better measure of the position error than the GDOP, especially when low-elevation satellites are used (43, 44). In order to provide a fair comparison between the WDOP in the case of WLS and DOP in the case of LS, the weighting matrix is normalized by to be where (44). The position covariance matrix then becomes and hence, WDOP is:(8)

4.2 WiFi TDOA

For WiFi TDOA-based positioning, at least three measurements from four WiFi reference nodes are required to compute the user 3D position . TDOA measurements are obtained by differencing two time of arrival (TOA) pseudorange measurements in order to remove the user clock error, similar to the case of differential GPS (42). Equations (9) and (10) present the respective WiFi TOA pseudorange and WiFi TDOA observation equations for n reference nodes.(9) (10)

for where are the coordinates of the ith WiFi reference node, the TOA pseudorange measurement, the user WiFi clock error, the pseudorange measurement error with , the TDOA measurement, and is the TDOA measurement error. By following the same process as for GPS, the linearized WiFi pseudorange observation equation in matrix form becomes:(11)

where

and in the case of independent and identically distributed WiFi range errors with the same variance. All parameters in Equation (11) are defined in Equations (2) and (3) for the GPS case. The TDOA observation equations can then be obtained from Equation (11) by applying a TOA-to-TDOA transformation matrix S (45):(12)

where S is an (n−1 × n) matrix (each row of S contains a 1, −1 and n − 2 zero elements) and . The TOA-to-TDOA transformation can be performed by sequential differencing, referenced differencing or a hybrid of the two. In the case of sequential differencing and for n TOA measurements, TDOA_ij = TOA_i–TOA_j where i = j + 1 for j = 1, 2, …, n−1 and . In referenced differencing, one TOA measurement is used as a reference and TDOA measurements are then obtained by differencing the rest of the TOA measurements with respect to the reference measurement (i.e. TDOA_ij = TOA_i–TOA_j where i is constant and j = 1, 2, …, n with ). These methods provide the same level of positioning performance provided that the quality of the measurements from the reference nodes is the same. It can be observed that the last column of has only zero elements, reducing Equation (12) to (45):(13)

where

The TDOA LS solution is then given by:(14)

However, results in Ref. (46) suggest that the WLS is more suited for TDOA measurements (similar to GPS-only based positioning) and is computed as:(15)

where when the pseudorange measurements have independent and identical error distributions with the same variance. The position covariance matrix is , and hence, the Weighted PDOP (WPDOP) for the TDOA WLS is:(16)

For the case where the pseudorange measurements are independent but with different error variances, the weighting matrix for the TDOA WLS becomes , where and hence, the covariance matrix becomes(17)

The WPDOP is then given by:(18)

Similar to the GPS case (Equation (8)), to provide a fair comparison of the DOP values for different scenarios, the measurement weighting matrix R is normalized by a common weight (e.g. ). Therefore,(19)

4.3 GPS/WiFi TDOA Integration

The epoch-by-epoch WLS solution for the tightly coupled GPS/WiFi integration is performed in this paper by joining the GPS and WiFi pseudorange observation equations into a single set of equations. The paper introduces the integration matrix (Q) which contains the TOA-to-TDOA transformation matrix S from Equation (12).

For the case of m GPS and n WiFi pseudorange measurements (i.e. n−1 TDOA WiFi measurements) with a total of k = m + n pseudorange measurements, the linearized observation equations in matrix form are:(20)

where , , ,

The integration matrix (Q) is formed based on the observation equations above as , where 0 is a matrix of zero elements and is the TOA-to-TDOA transformation matrix in Equation (12). Applying Q to Equation (20) leads to the linearized observation equation:(21)

The WLS is applied to Equation (21), since the GPS and WiFi measurements have different error variances, leading to:(22) where. In order to compare the observed DOP between the GPS-only and the GPS/WiFi cases, the weighting matrix is normalized by the GPS pseudorange error variance (i.e. ). Hence, the position covariance matrix becomes:(23)

and(24)

The computation of the PDOP, HDOP and VDOP follows from WDOP similar to Equation (6), where in this case, are the diagonal elements of the matrix. The implementation of the GPS/WiFi integration method presented in this section is discussed in the next section.

5 Experiment and analysis

5.1 Test setup

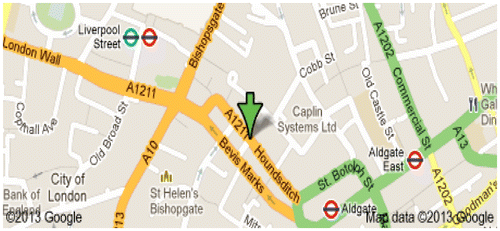
As previously discussed, the motivation behind the proposed tight coupling GPS/WiFi integration in this paper is to address GPS outages and improve the position accuracy in difficult environments. Hence, a representative environment in the city of London, UK (Houndsditch) was selected for testing (Figure 5). The evaluation of the integrated system was performed in a simulation environment using MATLAB. A simplified 3D city model was developed for the test environment. The user was assumed to be stationary on the Houndsditch Street located at Lat/Lon of 51.514506^o/–0.077379^o and at a height of 67.27 m. The user was equipped with a GPS receiver and a WLAN IEEE802.11g transceiver with collocated antennas.

Figure 5 The selected test area to demonstrate the integrated GPS/WiFi performance.

The GPS range measurements are simulated based on the user known position and the GPS almanac data of week 694. The GPS pseudorange errors are assumed to be independent and identically distributed with the same variance. The use of the same variance for different GPS pseudorange measurements is justified because only high-elevation (>30°) satellites are visible and used in the integrated solution. It was demonstrated in Ref. (44) that the impact of the elevation angle above 30° on the pseudorange errors is negligible. Blocked satellites are identified based on the user position, known heights of the surrounding buildings and the GPS almanac data.

A maximum number of four WiFi-enabled reference nodes were placed on the buildings around Houndsditch within the 3D city model. The WiFi reference nodes are assumed to be perfectly synchronized and capable of implementing the IFATE algorithm presented in sections 2 and 3. This stringent synchronization requirement can be alleviated by using DTDOA measurements (35). Although the extraction processes of TDOA and DTDOA measurements are different, the mathematical representation of both types of measurements is the same. Hence, the position estimation methods in Section 4 are applicable to both. The simulated WiFi measurements have the same statistics observed from the indoor laboratory experiment in section 3 after removing the DSO synchronization errors. These statistics represent a conservative case since the ranging performance is expected to be better in dense urban areas than in the laboratory (in terms of the multipath severity and density). The locations of the four WiFi reference nodes (RN) are listed in Table 1.

Table 1. Coordinates of the WiFi reference nodes used in the test scenarios.

Reference node ID	Latitude (°)	Longitude (°)	Height (m)
RN1	51.51436	−0.076811	73.77
RN2	51.51479	−0.07804	71.77
RN3	51.514941	−0.077484	79.77
RN4	51.515056	−0.077771	71.77

To investigate the performance of GPS in dense urban areas and to demonstrate the advantages of GPS/WiFi integration, four test scenarios were identified: (1) standalone GPS in an open area, (2) standalone GPS in a built-up area, (3) integrated GPS/WiFi with 3 WiFi RNs in the built-up area, and (4) integrated GPS/WiFi with 4 WiFi RNs in the built-up area. The open and built-up areas were implemented in the simulation by simply removing and adding the surrounding buildings in the 3D city model. The user position error, HDOP and VDOP for each test scenario were evaluated for a 24 h period at 5 min intervals with 100 simulation runs at each interval.

5.2 Results and discussion

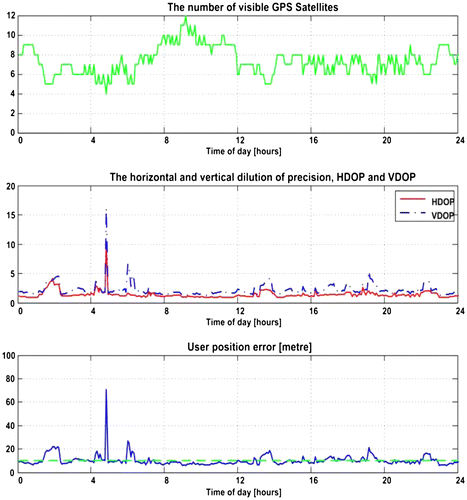
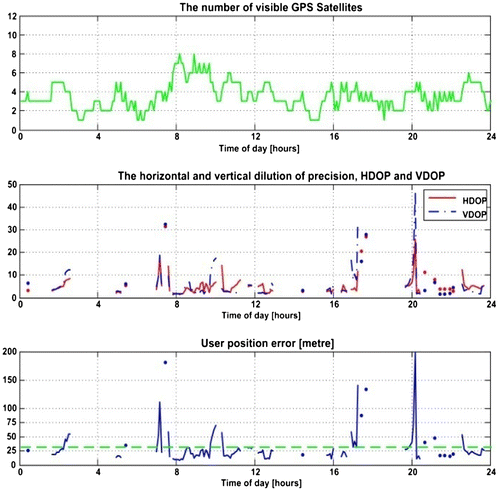
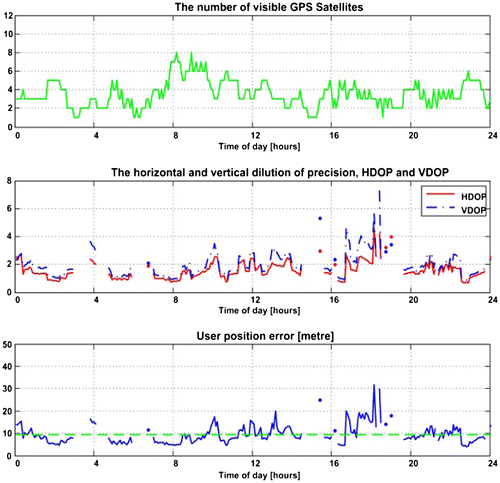
Figures67 present the results of the standalone GPS performance for the 1st and 2nd test scenarios, respectively.

Figure 6 Standalone GPS performance in the open area (1st test scenario).

Figure 7 Standalone GPS performance in the built-up area (2nd test scenario).

The effects of the surrounding buildings on GPS performance are evident from these two figures; the number of visible satellites drops from 4-to-12 satellites (open area) to 1-to-8 (built-up area). This results in a reduced measurement availability (i.e. measurements from at least four satellites with good geometry) from 100 to 42.28%, an increase in the average HDOP (from 1.41 to 5.43), average VDOP (from 2.18 to 5.75), and average position error (from 10.3 to 30.9 m).

Figure 8 depicts the performance of the 3rd test scenario where GPS measurements are integrated with measurements from 3 WiFi RNs (RN1, RN2, and RN3), leading to the addition of two TDOA measurements. In comparison to the 2nd test scenario, the measurement availability increases to 80.28%. Furthermore, the average position error improves to 9.54 m and the average HDOP and VDOP to 1.56 and 1.97, respectively.

Figure 8 GPS/WiFi integrated solution with 3 WiFi reference nodes (3rd test scenario).

Figure 9 depicts the performance of the 4th test scenario where 4 WiFi RNs are used in the GPS/WiFi integrated solution. This test scenario presents superior performance compared to the other test scenarios, with an average position error of 2.41 m, a 100% measurement availability and average HDOP and VDOP of 0.17 and 0.63, respectively. This level of accuracy is sufficient to meet the requirements of a wide variety of LBS and ITS applications in dense urban areas, currently limited by the performance of existing positioning systems.

Figure 9 GPS/WiFi integrated solution with 4 WiFi reference nodes (4th test scenario).

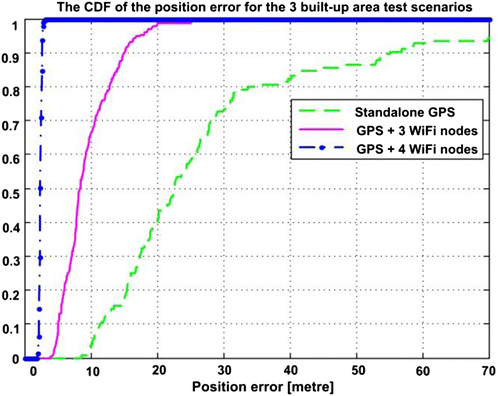
Figure 10 provides a comparison of the three built-up area test scenarios (i.e. 2nd, 3rd, and 4th test scenarios) in terms of the cumulative distribution function (CDF) of the obtained position error. The improved performance of the GPS/WiFi tight coupling is evident, with 2.75 m (95%) position accuracy with 4 WiFi RNs (4th test scenario). In comparison, the 2nd (standalone GPS) and 3rd (GPS with 3 WiFi RNs) test scenarios achieve position accuracies of 70 m (95%) and 16.8 m (95%), respectively.

Figure 10 CDF of the position error for the built-up area test scenarios.

6 Conclusions

This paper proposed a tightly coupled integration (i.e. in the measurement domain) of GPS with a high accuracy WiFi ranging system. The motivation of this integration is to address GPS outages in indoor and dense urban areas, and to improve the positioning accuracy for these environments. The integration is performed using an epoch-by-epoch weighted least squares method. The extraction of real-time high accuracy (sub-meter) WiFi ranging measurements is performed using the IFATE algorithm, developed by the authors. The performance of the integration method is performed in MATLAB by building a simplified 3D city model for a given dense urban area in London, UK. The statistics of real WiFi ranging data observed in a laboratory environment are used in the simulation platform. The achieved positioning accuracy of the integrated system is 2.75 m (95%) with 100% measurement availability when using 4 WiFi reference nodes. This is significantly better than the 70 m (95%) position error with 42.28% measurement availability obtained using standalone GPS in the same operational environment. The performance of the integrated system has the potential to address the requirements of a number of LBS and ITS applications. Future work will include additional positioning systems, such as GLONASS and INS and implement more sophisticated integration algorithms (e.g. Kalman and Particle filters).

Notes on contributors

Khalid Nur is a research associate at the centre for transport studies (CTS) within the Department of Civil and Environmental Engineering at Imperial College London. His research interest is in the development of high accuracy and cost effective positioning capabilities for difficult environments. He holds a BSc degree in Electrical and Electronic Engineering from the University of Khartoum (Sudan), an MSc in Communications and Signal Processing from Newcastle University (UK) and a PhD in Wireless Positioning Systems from Imperial College London (UK).

Shaojun Feng is a research fellow at the CTS within the Department of Civil and Environmental Engineering at Imperial College London. He leads the navigation research team within the Imperial College Engineering Geomatics Group (ICEGG). He is a fellow of the Royal Institute of Navigation (RIN) and Member of the US Institute of Navigation.

Cong Ling is a senior lecturer in the Electrical and Electronic Engineering Department at Imperial College London. His research interests are coding, signal processing and security, especially lattices. Dr Ling is an Associate Editor of IEEE Transactions on Communications. He has also served as an Associate Editor of IEEE Transactions on Vehicular Technology.

Washington Ochieng is the head of the CTS and holds the chair in Positioning and Navigation Systems in the Department of Civil and Environmental Engineering at Imperial College London. He is also the director of the ICEGG. He is a chartered engineer, fellow of the Royal Institute of Navigation and the Institution of Civil Engineers, and member of the US Institute of Navigation.