Numerical weather modeling-based slant tropospheric delay estimation and its enhancement by GNSS data

Abstract

Unmitigated tropospheric delay is one of the major error sources in precise point positioning (PPP). Precise Slant Tropospheric Delay (STD) estimation could help to provide cleaner observables for PPP, and improve its convergence, accuracy, and stability.STD is difficult to model accurately due to the rapid spatial and temporal variation of the water vapor in the troposphere. In the traditional approach, the STD is mapped from the zenith direction, which assumes a spherically symmetric local tropospheric profile and has limitations. In this paper, a new approach of directly estimating the STD from high resolution numerical weather modeling (NWM) products is introduced. This approach benefits from the best available meteorological information to improve real time STD estimation, with the RMS residual lower than 3.5 cm above 15° elevation, and 2 cm above 30°. Therefore, the new method can provide sufficient accuracy to improve PPP convergence time. To improve the performance of the new method in highly variable tropospheric conditions, a correction scheme is proposed which combines NWM information with multi-GNSS observations from a network of local continuously operating reference stations. It is demonstrated through a case study that this correction scheme is quite effective in reducing the STD estimation residuals and PPP convergence time.

Keywords:

• slant troposphere delay
• numerical weather modeling (NWM)
• precise point positioning (PPP)
• multi GNSS

1. Introduction

Mitigating various GNSS errors is one of the key steps in precise point positioning (PPP). The satellite related errors, such as orbit and clock errors, and also the satellite-based fractional-cycle biases (FCB) can be removed by applying external products, which are typically generated from a global network of reference stations (1, 2). Some receiver related errors, such as phase center variations, tidal effects, ocean loading, and carrier phase wind-up can be removed by modeling and calibration. The signal propagation errors, i.e. the ionospheric and the tropospheric delays, are treated differently. Using dual frequency measurements, the first order ionospheric delay is mitigated by applying the ionosphere-free linear combination of the code and carrier phase observations. The tropospheric delay is further split into the hydrostatic (dry) delay and the non-hydrostatic (wet) delay. The dry hydrostatic tropospheric delay is modeled using a priori information. The troposphere wet delay is estimated as one of the unknowns, for example, in an Extended Kalman Filter formulation, together with other unknowns, such as the receiver coordinates, and the carrier phase integer ambiguities. This procedure typically takes 20 min for the solution to converge to centimeter level accuracy (3).

This disadvantageous long convergence time is mainly due to the un-mitigated or un-modeled residual error left in the observations (4). Due to limitations in the modeling and accuracy, the residual tropospheric delay often remains, and in some cases (such as extreme weather events), it may even become the dominating error source affecting PPP convergence time and positioning accuracy. Precise tropospheric delay estimation helps to de-correlate the tropospheric delay residuals from other error residuals resulting in cleaner observations, and thus benefiting PPP solutions in terms of accuracy, efficiency, and stability.

This paper introduces a new tropospheric delay estimation scheme. It is based on direct STD estimation using NWM products, and is enhanced by multi-GNSS observations from a local continuously operating reference stations (CORS) network. Section 2 introduces the background information and reviews the traditional tropospheric delay estimation methods. Section 3 presents the NWM-based tropospheric delay estimation algorithm and quantifies its performance. Exploiting multi-GNSS observations from a local CORS network, a correction scheme is presented and tested in Section 4. The paper is concluded in Section 5.

2 Background

Slant tropospheric delay (STD), the tropospheric delay in the path of a particular satellite, accounts for the delays due to both slowed propagation in the compressed air and geometric propagation bending. It can reach a magnitude of 25 m at low elevation angles (5). STD is affected by atmospheric conditions along the slant path, which has rapid variations both spatially and temporally, and is difficult to model precisely.

The conventional STD estimation follows a two-step procedure: first modeling the receiver zenith total delay (ZTD); and second applying a “mapping function” to map the ZTD to the individual satellite elevation angle ϵ, as shown in Equation (1).(1)

Traditionally the ZTD is modeled as the sum of the zenith hydrostatic delay (ZHD) and the zenith wet (or non-hydrostatic) delay (ZWD). The ZHD accounts for 80–90% of the ZTD, and is caused by a mixture of dry air and water vapor in the hydrostatic equilibrium. If surface pressure measurements are provided, it can be predicted with a total error below 5 mm (6). This accuracy is sufficient for most PPP applications. The ZWD is mainly caused by the water vapor in the atmosphere, and is more difficult to model due to the complex dynamic fluctuations of the evaporation and condensation processes. Most popular ZWD models are highly correlated, with an estimation accuracy of not better than a few centimeters (6). The Hopfield and the Saastamoinen models (7–9) are well-established ZTD models and are adopted in many applications. They are based on the input of the onsite surface meteorological measurements, and when these measurements are not available (which is quite common to most applications), standard surface parameters can be used instead, with the cost of degraded accuracy. Unlike the Hopfield and Saastamoinen models, the minimum operational performance standard (MOPS) model, an empirical tropospheric delay defined by RTCA (10), is not only based on the values of the surface meteorological data, but also considers their seasonal average, variation, and lapse rates, using a small lookup tables sorted according to latitude belts with a 15° resolution. In the MOPS model, the target ZTD residual error is specified as 12 cm. Storm van Leeuwen et al. showed that this specification is met in the mid-latitude areas, although a latitude dependent bias was also found for lower latitude stations, which mainly comes from modeling limitations (11). The MOPS model has been adopted for wide area differential GPS systems, such as WAAS, EGNOS, and MSAS (12).

Hydrostatic and wet mapping functions project the corresponding zenith delay to the elevation angle of an observation. The accuracy of the mapping function directly impacts the STD estimation accuracy, especially for low elevation angles. Most modern mapping functions are variants from the Marini’s continued fraction (13), which use three-term coefficients to describe the variation of the mapping ratio at a certain elevation angle ϵ, as shown in Equation (2).(2)

Different mapping functions mainly differ in the way the Marini coefficients are determined. Among them, the Niell mapping function is the most widely adopted empirical mapping function. It is based on global profiles of the atmosphere, and proposes to interpolate the Marini coefficients from lookup tables which depend on latitude with 15° resolution. The wet coefficients are linearly interpolated from the tabulated values on latitude boundaries directly, while the hydrostatic coefficients on latitude boundaries are tabulated as their annual fluctuation average and amplitude.

Starting from the early 2000s, NWM was introduced into the tropospheric delay estimation, and the improvements are mainly made in two areas: firstly more accurate zenith delay estimation, e.g. NOAATrop (14) and TropoGrid (5, 15) model, which use the NWM parameters to replace the conventional surface meteorological measurements or standard parameters; and secondly through better mapping functions that are closer to reality by having the Marini coefficients fitted from NWM ray tracing. Well-known mapping functions, such as isobaric mapping function (IMF) (16), global mapping function (GMF) (17), vienna mapping function (VMF), (18, 19) and its updates VMF1 (20, 21), are all developed based upon NWM products.

However, the above traditional tropospheric delay estimation methods, including the ones using NWM, cannot truly reflect the sophisticated weather changes in real time. Empirical zenith models or mapping functions are based on seasonal averaged parameters which may be quite different from the actual values in a real situation. NWM-based zenith models or mapping functions are limited by their real time availability. If they are computed on the basis of a single site, significant central processing resources are required, if serving a large number of users. Alternatively, if they are generated on a grid basis, there is a trade-off between the modeling accuracy and computation load. A higher resolution grid can provide better accuracy, but also suffers from a high computation load, as the parameter fitting procedure on each grid point is time and resource consuming. The highest resolution of the troposphere parameter grid seen in the literature is 1° by 1° (5), equivalent to ∼100 km spacing on the equator, which is still quite large for the actual troposphere variation in many weather events. Another important limitation of the traditional tropospheric delay estimation is that most of the mapping functions are only expressed as a function of elevation. Thus they are independent of azimuth, which implies an assumption that the atmosphere around the receiver site is spherically symmetric. This assumption may not be valid when the weather is rapidly changing, especially in the event of a weather front passing the user location. The asymmetry of the troposphere profile dramatically degrades the tropospheric delay estimation accuracy, and influences the PPP performance. An approach (22-24) to consider the troposphere profile asymmetry is to add the troposphere gradient terms to Equation (1) as(3) where MF_grad is a mapping function for the gradient component, G_N and G_E are the gradient terms on the north-south and east-west directions, respectively, ϕ is the azimuth. The gradient terms are then solved as extra unknowns in the PPP solution. Although they can absorb the troposphere profile asymmetry to a certain extent, this absorption is limited by its linear-plan modeling, and cannot fully describe the complicated azimuth dependent STD variation. As these two gradient terms are solved together with coordinates, they will also absorb some other non-tropospheric variations, and introduce biases to the final positioning solution.

3 NWM-based direct STD estimation

3.1 Overview

With the advent of a variety of new meteorological measurements and powerful processing techniques, numerical weather modeling (NWM) products have matured in recent decades, and can produce more accurate weather predictions. The products are also available for larger areas and with higher resolution. NWM uses a series of mathematical models to generate either short-term weather forecasts or longer-term climate predictions. It assimilates various observations collected from a dense meteorological sensor network, including ground meteorological stations, radiosonde weather balloons, remote sensing weather satellites and commercial aircraft. Benefiting from these weather sensors and increased power of the supercomputers, NWM can provide the best achievable analysis or prediction on the real physical conditions of the atmosphere, which contain the necessary information for GNSS tropospheric delay estimation.

Inspired by the high quality of NWM and rich information on real atmospheric conditions, NWM-based direct STD estimation has been proposed (25, 26). This proposed technique avoids estimating STD from the traditional approach of zenith modeling combined with a mapping function, and computes the STD directly from the atmosphere conditions, which are provided in the NWM. This means the local atmosphere profile is not assumed to be spherically symmetric, and the azimuth-dependent delay can be estimated with detailed variations and close to reality. Importantly, this method can provide good accuracy at low elevation angles where the traditional methods often struggle. In terms of the positioning domain, the troposphere delay is spatially de-correlated and modeled individually on each observation, and so there are smaller noise residuals left in the observables. Thus, both the PPP convergence time and solution accuracy can be improved.

In this section, the NWM product used in this paper is first introduced, followed by the STD estimation algorithm which is based on direct ray-tracing in the NWM, and finally performance validation is undertaken and preliminary test results discussed.

3.2 NWM product

The quality of the NWM products has a direct impact on the performance of the proposed STD estimation method. Nowadays there are a number of global and regional NWM products developed in different countries worldwide. Table 1 lists some well-known global NWM products. The NWM product used in this paper is the unified model (UM) produced by UK Met Office (UKMO). The technique developed in this paper using the UM can also be applied to other NWM products.

Table 1. Global numerical weather modeling products.

Product Name	Country	Development Agency
Unified Model (UM)	UK	UK Met Office
Integrated Forecast System (IFS), also known as ECMWF	European	European Centre for Medium-Range Weather Forecasts
Global Forecast System (GFS)	US	NOAA
Global Weather Forecast Model(GME)	Germany	German Weather Service
ARPEGE	France	French Weather Service
Global Environmental Multiscale Model(GEM)	Canada	Meteorological Service of Canada

The UM product contains a set of NWM models. It provides a global, regional and a local (UK) models that differ in not only the coverage, but also resolution. A higher resolution model provides more detailed atmosphere information, but the lager data size slows the STD estimation process. For this reason, the UK local model, which has 4 km horizontal resolution, is not used in this paper.

The UM regional model is also referred to as the North Atlantic European (NAE) model, which indicates its coverage. It is a 4-dimensional data-set. Horizontally the data is provided in a 600 by 360 grid with a regular spacing of 0.11 degree (∼12.3 km), both in latitude and longitude, over the coverage area, as shown in Figure 1. Vertically, the data is provided on 15 geopotential layers ranging from 1000 mbar (close to earth surface) to 30 mbar (∼25 km above surface) pressure levels. Temporally, the 3D grid data are updated at an interval of 6 h. The UM global model has globally distributed 1024 × 769 horizontal grid points, with 0.56° × 0.38° resolution (∼40 km spacing in the equator). It has 35 vertical geopotential layers ranging from 1000 mbar up to 0.01 mbar (∼80 km above the surface). Its temporal resolution is the same as the NAE model.

Figure 1 UK Met Office UM NAE model coverage.

The NAE model provides more atmosphere detail than the global model in the lower part (below the 30 mbar pressure level) of the troposphere, where most of the water vapor is distributed and also where the troposphere condition variation is more dynamic. However, the global model provides information for the upper part of the troposphere. Tests in Refs. (27, 28) have shown that the signal delay in the upper troposphere is in the level of decimeters, which is not negligible for a precise STD estimation. Therefore, the UM NAE model and the global model are combined in the proposed algorithm to give the best achievable accuracy. The ray tracing technique (introduced in the next Section) switches to the global model, when it is outside the region where the regional model is defined. It is worth noting that if using the global model alone the STD estimation performance will degrade, but not significantly (29). Therefore, the proposed technique is not limited to a certain regional area, and can be applied worldwide.

Both the NAE and global models contain two fields, the analysis field and the forecast field. The analysis field works in the post-processing mode, provides atmosphere physical conditions at a certain epoch in the past, using the measurements taken before and after the target epoch. The forecast field works in the operational mode, and could be available in real time. It uses recent measurements to predict the atmosphere physical conditions at the current epoch or some epochs in the future up to 48 h. Clearly, the information contained in the analysis field is closer to reality than the information in the forecast field; and the advantage of the forecast field is its real time applicability. However, it has been shown in tests (28) that the difference in the STD estimation is small, which means that the NWM-based STD estimation can be used in real time applications.

3.3 Ray tracing based estimation strategy

The troposphere delay comes from the slowing and bending of the signal in the atmosphere. A denser propagation medium leads to as lower propagation, and a higher gradient of the medium density leads to more bending of the propagation path. Therefore, the slowing and bending factor relates to the medium’s refractive index n (30, 31). This refractive index is determined by the atmospheric composition and density, which depends on the atmosphere pressure, temperature, and humidity. The atmospheric refractive index n is very slightly larger than 1. Therefore, an alternative expression, refractivity N, is defined as , and is more frequently used in literature.

NWM products provide a number of physical conditions on each of its 3D grid points. In these parameters, pressure P, temperature T, relative humidity RH, and height H can be used as inputs to compute the refractivity N, which has been assessed in a microphysical model for the radio signal transmission in Ref. (32) as(4) where are constants, P_d and e are partial pressures for dry air and water vapor, respectively, and are compressibility factor densities of dry air and water vapor, respectively. A detailed analysis of P_d, e, and as functions of [RH, P, T, H] can be found in Refs. (6, 32–34)). The determination of the refractivity set of constants is still an ongoing research topic. Here the “best average” values given in Ref. (29) are used.

In order to estimate the STD along the signal path, the ray tracing algorithm is applied. In this algorithm, the whole troposphere is considered as composed of a series of thin layers. Within each of the thin layers, the given physical parameters [RH, P, T], and therefore the derived refractivity N, are assumed to be constant. To keep this assumption close to reality, the depth of these homogeneous thin layers is set as a smaller value in the variable and dense air which is in the lower troposphere, and a larger value in the stable and sparse air which is in the upper troposphere, as shown in Table 2.

Table 2. Relationship between the height and depth of the homogeneous thin layers in ray-tracing.

Height (km)	0–2	2–6	6–16	16–36	36–80
Depth (m)	10	20	50	100	500

Based on the homogeneous nature of the thin layer, the propagation path within each thin layer is also assumed to be a straight line. Therefore, the atmosphere non-dispersive delay in each thin layer can be computed as,(5) where S is the distance the signal travels in the thin layer. The signal bending is assumed to happen at the pierce points between the thin layers, and the bending angle can be computed from the refractivities of the adjacent thin layers, by Snell’s law. Ray tracing is then performed to derive the coordinates of the pierce points on the signal propagation path from receiver to the satellite. The slant total delay, denoted by , can be estimated as the sum of the delays in each thin layer, i.e.(6)

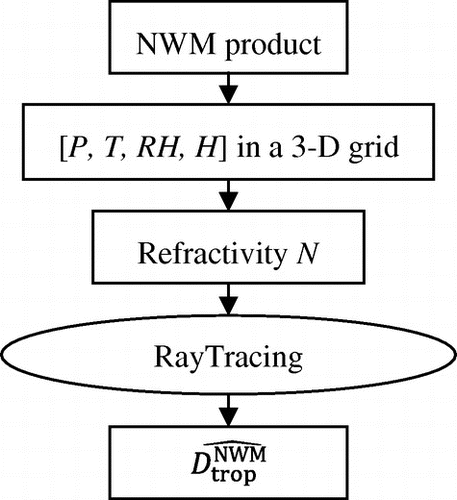
The above NWM-based STD estimation procedure is summarized as a schematic diagram in Figure 2 with detailed description in Ref. (25).

Figure 2 Flowchart of STD estimation from NWM product.

3.4 Performance validation

Unlike the traditional zenith tropospheric delay estimation, which could be evaluated by the radiosonde data, it is hard to find a highly accurate “truth” data to evaluate the accuracy of the STD estimation. In the authors’ tests, the ambiguity fixed PPP solutions at a UK national CORS station KEYW (52°52′44″N, 1°4′41″W) were used to evaluate the NWM-based STD estimation. This evaluation procedure is reviewed as follows.

The carrier phase observation equation is given by(7) where is the carrier phase observable in meters, is the geometric distance between the receiver and satellite, is the wavelength of the observation frequency, N is the integer ambiguity, c is the speed of light, and are the clock offset for the satellite and receiver, respectively, D_ion and D_trop are the ionosphere and troposphere delay, respectively, and is all other noises, including multipath, thermal noise, etc.

By re-ordering Equation (7), an estimation of the troposphere delay term D_trop, noted as , can be defined as(8)

Unlike the true slant troposphere delay D_trop, is a measureable value. Using precise satellite orbit and clock products (such as the products provided by the IGS), and the precisely measured station coordinates, and can be precisely determined to centimeter level. N and can be accurately obtained from the ambiguity fixed PPP solutions. As the station coordinates are given as known values, this ambiguity fixing procedure is easier and more reliable than in the traditional PPP. The ionosphere delay term can be determined to the first order, via the dual frequency geometry-free combination. The higher order ionosphere delay and disturbance, which are at the level of centimeters (32), are absorbed in the noise term . Therefore, is a value measureable from the right hand side of Equation (8). It can be considered as a noise contaminated slant troposphere delay, and could represent the latter if the noise level is kept at a low level.

The noise term can neither be separated from nor measured. Therefore, to keep close to the truth as much as possible, a feasible approach is to select the evaluation receiver site and equipment that are of a high standard. The selected evaluation site, KEYW, is operated by the UK government’s mapping and surveying agency, the ordnance survey. As one of the national CORS stations, it is located at a carefully selected site, and also equipped with high grade antenna to minimize the impact of multipath. Because, the UK is in the mid-latitude region, the influence from the higher order ionosphere effect and disturbance is also small at this station. Therefore, it is reasonable to assume that at this station the PPP processing noise term is less than 2 cm for observations above 15° elevation. This noise also decreases as the satellite elevation increases.

The STD measurement contaminated with low noise can be used to evaluate the NWM-based STD estimation, which is an independent estimation approach as described earlier. Noting the estimation noise by , the NWM-based STD estimation can be considered as,(9)

Therefore, the difference between and , named as the NWM-based STD estimation residual , is given by(10)

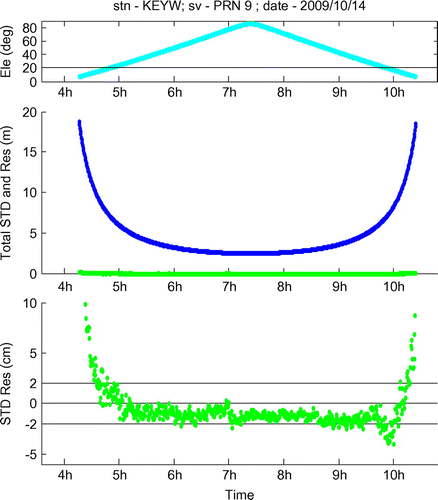
The two noise terms and are independent and is a random noise with zero mean. Therefore, can be considered as the sum of these two noise sources. As an example, Figure 3 shows the size of the total STD (blue line) and also the NWM-based STD estimation residual . It can be seen that the STD is about 3 m when the satellite elevation is close to the zenith, and can reach 20 meters when the elevation is close to the cut off angle (7°). This increase is due to the longer signal ray path in the troposphere when the elevation is low. Compared to the size of , the residual is really close to zero (green line) as shown the middle sub-figure. The zoomed-in view in the bottom sub-figure shows that in this case the residual is well-controlled within ± 2 cm for most of the epochs when the elevation is lower than 20°. As this residual consists of the NWM estimation noise and the PPP processing noise, it means the NWM-based estimation is within ±2 cm of the truth. As shown in the figure, this residual will increase when the satellite elevation is low, which is not only because the PPP processing noise will rise due to the increased multipath, but also because the NWM estimation noise will rise due to the amplified uncertainty in the longer ray path in the troposphere.

Figure 3 An example of slant troposphere delay (STD) and its NWM-based estimation residual against time.

To validate this NWM-based estimation performance over a longer time period, a statistical analysis of the estimation residual was carried out. A whole month (October 2009) of 30-s-interval GNSS observations collected at the KEYW station was processed using the ambiguity fixed PPP method, to generate the STD measurements on each observation, which were then used to evaluate the NWM-based STD estimations at the same observation. The NWM-based STD estimation residual was calculated from Equation (10). There were 671,770 samples collected successfully in total (some epochs were left out due gaps in the archived raw data, either NWM or GNSS observations). As shown in the example above, the size of depends on the observation elevation. In the statistical analysis, they were grouped into a series of 5° elevation bins. Figure 4 shows the root mean square (RMS) values of the against elevation, where green bars are based on the analysis NWM field, and red bars are based on the forecast NWM field. It can be seen that for the estimation residual from the analysis field, the RMS value is lower than 3.5 cm when the elevation is above 15°, and lower than 2 cm when the elevation is above 30°. Considering the earlier assumption that the PPP processing noise is less than 2 cm for elevation angles larger than 15°, it can be concluded that the extra noise introduced by the NWM-based estimation is quite small. Thus, the NWM-based STD estimation is good enough to be used as a priori information for the PPP procedure, replacing the traditional PPP troposphere delay estimation method, i.e. model the dry delay and solve the wet delay as an unknown. In this new approach, the PPP engine is able to estimate the STD to a good accuracy at the beginning of the PPP solution. This accuracy is comparable to the converged STD accuracy in the traditional PPP approach. Having this improved troposphere estimation means the observables of PPP from epoch to epoch are cleaner, and will lead to a reduced PPP convergence time.

Figure 4 RMS of NWM-based STD estimation residual against observation elevation. (left (green) column – analysis field, right (red) column – forecast field).

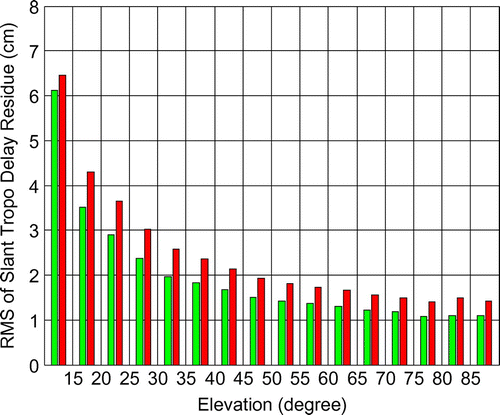
Also, shown in Figure 4 is the comparison between the NWM analysis field based estimation and the forecast field based estimation. As explained earlier, the analysis field is closer to reality than the forecast field. This leads to a poorer STD estimation from the forecast field compared to the estimation from the analysis field. This is confirmed in Figure 4 which shows that in general, the RMS estimation residual from the forecast field is larger than the RMS residual from the analysis field, for any elevation bin. However, the difference is small and typically less than 0.5 cm. This small difference indicates that the forecast field is good enough to be used in the NWM-based STD estimation, which makes this STD estimation technique practical for real time applications.

In the above validation procedure, a question may be raised as to why , inversely computed from the carrier phase observation equation by the Equation (8), is used to represent STD, rather than the traditional PPP solved STD, i.e. . The main reason is that the traditional measurement assumes a circular symmetric troposphere profile around the receiver, which leaves the azimuth dependent STD variation in the PPP noise term . Therefore, it is not appropriate to use this measurement to evaluate the NWM-based STD estimation, which highlights the azimuth dependent variation.

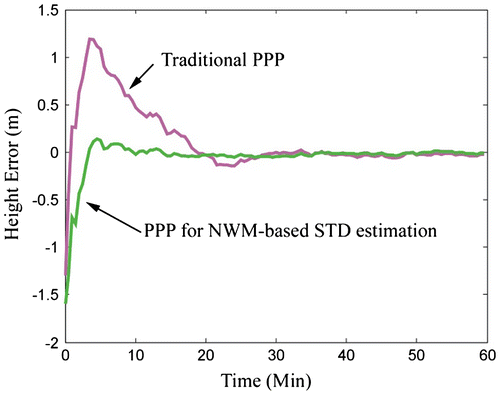
The STD estimation improvement of the NWM-based method can be reflected on the PPP performance. Tests have been carried on the PPP software POINT. The NWM-based STD estimation is applied directly to the raw measurements, as a correction to the troposphere delay. The zenith wet troposphere delay is then removed from the PPP unknown variable list, as from the above statistical analysis, the NWM-based estimation is close enough to the truth, and the residual left is small enough to be considered as part of thermal noise. An example of PPP performance is shown in Figure 5, for a case which contains clear the azimuth dependent variation. In this figure, the PPP solved receiver height is shown against time, as the PPP height solution usually has larger error than horizontal solution, and can be used as an indication to the PPP convergence time. It can be seen that the NWM-based method has much smaller height variation and much quicker convergence time than the traditional method. This improved performance is benefited from two improvements: 1) the real time information is well-approximated in the NWM data-set, so the STD estimation is more accurate than the traditional approach which uses empirical models; 2) the troposphere delay estimation is made on the STD directly, thus the azimuth dependent tropospheric delay discrepancies have been removed from the individual measurements, as a result the convergence task is carried out on the observations with smaller biased noise.

Figure 5 PPP convergence performance comparison.

4 Multi-GNSS enhancement to the NWM-based STD estimation

4.1 Problem

Although shown in the above Figure 4, statistically the real-time applicable forecast field-based STD estimation could achieve a similar accuracy as the analysis field-based estimation, it also has a limitation. In the procedure to produce the forecast field, a number of candidate data-sets are simulated from different weather scenarios and condition assumptions. The final published forecast field is the candidate data-set which has the largest probability to happen. Therefore, if a low probability weather event occurs, for example, a rain storm which is often accompanied by dramatic changes in pressure and humidity, the forecast field has difficulty in predicting the weather conditions accurately. Furthermore, the accurate forecasts last for a shorter period than normal, and the 6 h interval update rate of the forecast product is not fast enough to capture the changing conditions. As a result, the forecast field-based STD estimation accuracy decreases and eventually degrades the PPP performance.

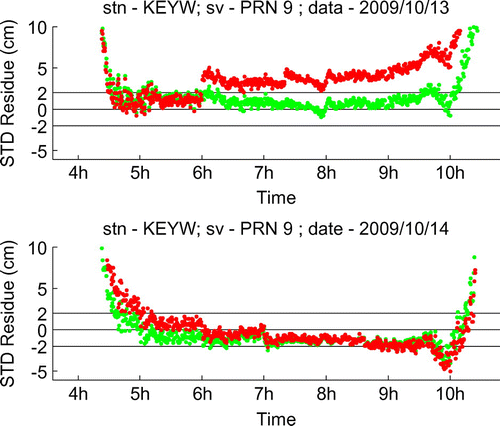
Figure 6 shows two examples of the NWM-based STD estimation residual. These two examples are based on the observations to the same satellite (PRN9) at the KEYW station, on two consecutive days. The lower subfigure shows a “quiet” example of troposphere condition variation. It can be seen that the forecast field-based estimation (red) matches quite well with the analysis field-based estimation (green). The upper subfigure shows an active example of troposphere condition variation. In this subfigure, a mis-match can be found between the forecast and analysis fields-based estimations. This mis-match starts from 6:00 on that day, which is the epoch on which a new forecast data-set is applied. Clearly the newly applied forecast data-set is somewhat different from reality, probably because of the fast-changing troposphere condition. This discrepancy leads to a larger estimation residual comparing to the analysis field.

Figure 6 Examples of NWM-based STD estimation residual. (green – from analysis field; red – from forecast field).

As the rapidly-changing tropospheric conditions is a large scale event in the area local to the receiver, it not only affects a single observation, but also most (if not all) of the observations simultaneously. This can be seen in Figure 7, which shows the epoch-wise RMS of the STD estimation residuals of all observable satellites from the KEYW station. The same time periods as in Figure 6 are selected. It can be seen that there is a clear rise in the forecast field-based estimation residual RMS on the troposphere condition variation active day, between 06:00 and 12:00, which suggests that there is only one forecast data-set having discrepancy with reality, due to the very active tropospheric variation.

Figure 7 Examples of epoch-wise STD residual RMS. (greed – from analysis field; red – from forecast field).

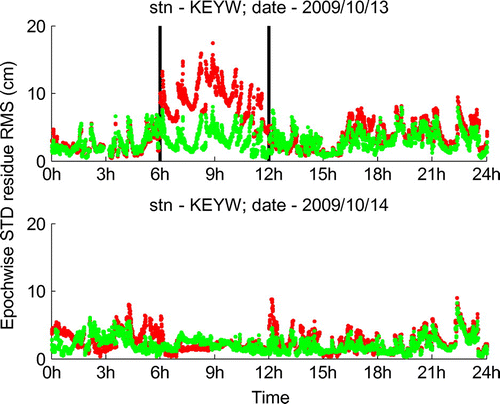
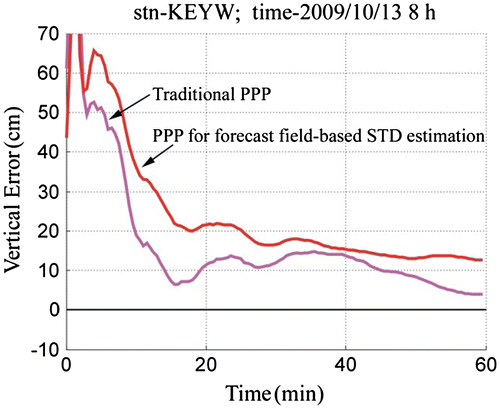
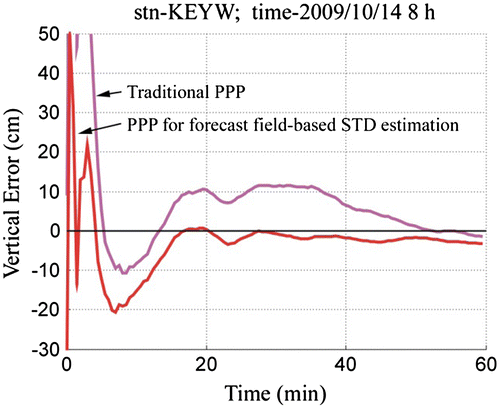
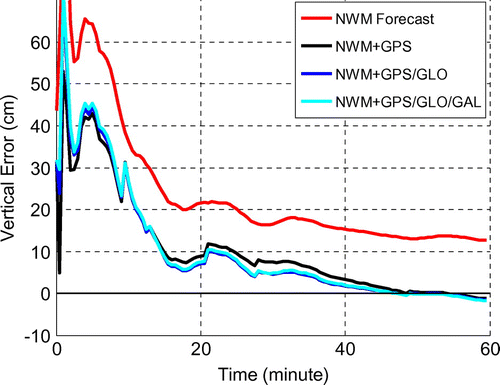
The increase of the estimation residuals during the period with the bad forecast, in Figure 7 is around 10 cm. The degraded STD estimation on all observables will therefore affect the NWM-based PPP performance. Figure 8 shows the vertical error from a one-hour PPP test in the above identified bad STD prediction period (from 08:00 to 09:00). It can be seen that due to the degraded STD estimation, the convergence performance of the forecast field-based PPP solution is even worse than the traditional PPP solution. In the forecast field-based solution, the vertical error is not able to converge to the 10 cm accuracy threshold within the testing hour, while the traditional PPP converges to that accuracy in about 45 min. In contrast, Figure 9 shows what the normal performance should like, during a good STD prediction hour. In this case, it takes the traditional PPP about 35 min to converge to better than 10 cm vertical accuracy, while to reach the same threshold it only takes the forecast field-based PPP less than 15 min.

Figure 8 Example of PPP convergence performances on a troposphere condition active variation hour.

Figure 9 Another Example of PPP convergence performances on a troposphere condition quiet variation hour.

4.2 Integrated STD estimation strategy

To enhance the estimation performance in the very active troposphere variation period, another external resource is introduced, the observations from the CORS network. The CORS network was originally established for the operation of network-RTK service. Although traditional PPP does not require a CORS network as dense as that required for traditional network RTK, the established CORS network can be used to benefit the above NWM-based STD estimation. Similar to the NWM forecast field, the CORS observations also can be provided in real time. However, unlike the NWM product, they can be available with a much higher data rate, and can therefore provide a much better match with reality than the NWM forecast field. Therefore, it can be used to improve the accuracy of the STD estimation based, especially during the time periods when the troposphere variation is very active.

During the periods of most active troposphere variation period, the NWM forecast field may not provide satisfied prediction accuracy, which means that the NWM estimation noise will rise. From Equation (10), this increased noise may dominate the NWM-based STD estimation residual , and increase the amplitude of this measureable value. To reduce the increased NWM estimation noise, a 3D delay correction grid is proposed here. It aims to reflect and correct the discrepancy between the NWM prediction and reality. This correction grid is proposed as a discrepancy delay density grid. That is, for the signal piercing though this grid, the correction to its STD estimation can be calculated from the values given at the relevant correction grid nodes, and also the length of the signal trace in the grid. Using to denote the correction term, the NWM estimation noise is then given as,(11) where is the reduced estimation noise after the correction. The STD estimation in Equation (9) is then revised, consisting of both the original NWM-based estimation and the new correction from the discrepancy delay density grid, and is denoted by as,(12)

Therefore, the revised STD estimation algorithm integrates of the NWM forecast and CORS observations. Updating Equations (10–12), the measureable residual of this integrated estimation, denoted by , is given as,(13)

As and are independent random noises, the reduced NWM estimation noise and after the correction will help to reduce the size of the integrated estimation residual.

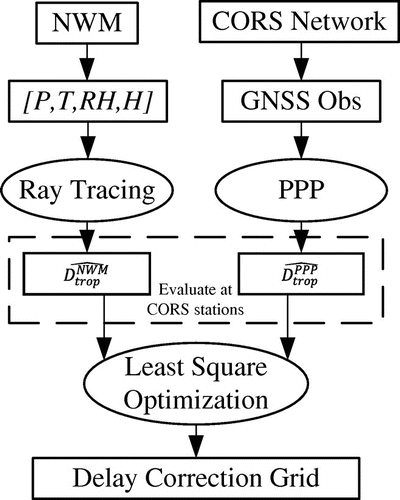
The flowchart of the correction grid generation procedure is shown in Figure 10. As described earlier that, can be measured at the CORS stations, by differentiating the STD computation from the CORS observations using PPP () and the STD estimation from the NWM (). The residuals () collected at the same epoch, and from all of the CORS stations network-wide, can be evaluated in a least square-procedure, to find an optimized correction grid, which minimize the sum of the squares of all corrected residuals ().

Figure 10 NWM-based and CORS observations-based methods.

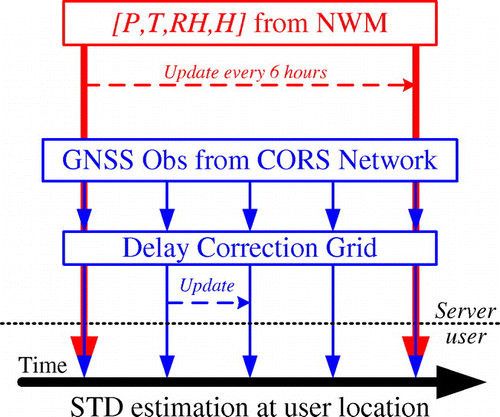
The correction updating procedure is repeated at a variable updating rate to keep track of troposphere variations. This requires the RMS to be monitored at the network level. When the troposphere variation is very active, which leads to a high RMS value, the correction update rate is increased accordingly (e.g. up to 10 min); and when the variation is not quite active, the correction update rate is reduced (e.g. 1 h). Dramatic weather variations are only an occasional event, and for most of the, NWM can predict the quite troposphere condition well, thus the correction grid may not even be needed. This variable update rate can significantly reduce the correction data volume transmitting from the network server to the user.

The correction grid generation procedure is carried out at the server side. To implement this integrated STD estimation at the user side, both NWM grid and the delay correction grid generated from the CORS network need to be broadcast to the user, as shown in Figure 11. The NWM grid provides the main prediction information on the whole troposphere; the correction grid contains more detailed near-to-real information on the lower troposphere, and steers the user’s STD estimation with the local tropospheric variation. For a service covering the UK region, the required NWM grid would have a file size roughly 150 Mb, and would be updated every 6 h; meanwhile the correction grid file is less than 1 Mb, but would be updated at a higher rate. The large NWM file could allow a longer transmission time (up to an hour), as it is based on a prediction and is available before the actual reporting epoch. However, the correction file would need to be transmitted in real time when it is available. These transmission requirements could be met comfortably with the modern communication technologies.

Figure 11 Timeline of the NWM and the correction grid data transmission.

After receiving both of the NWM and the correction grids, the user can perform ray tracing and estimate the STD at their own location. In contrast to the CORS stations, the user does not have pre-determined precise coordinates, therefore, cannot estimate the STD via the inverse PPP approach ( in Figure 10. However, by benefiting from the correction grid established by the CORS network, the integrated ray tracing STD estimation can be close to , with only small differences (validated later as less than 2 cm). This STD estimation can then be applied in the user’s PPP processing, replacing the traditional zenith modeling plus mapping function approach.

This new approach benefits from both meteorology measurements and the CORS observations. The CORS observations serve like probes to the atmosphere, as illustrated in Figure 12. Clearly, the more observations used in the least squares procedure, the better the optimization result that can be achieved. Therefore, the use of a reference station network is necessary for the generation of the correction grid.

Figure 12 CORS observations “probing” through the NWM correction grids.

4.3 Correction grid generation

As the NWM forecast product can predict the major variation of troposphere, the correction grid need only reflect the discrepancy between the prediction and the reality, which comes mainly from the changed distribution of water vapor. In the proposed correction grid, the values given at its nodes are, as mentioned earlier, the delay discrepancy densities.

To solve this correction grid, a few simplifications are made. First, the correction grid is defined up to a maximum of 12 km in height, as the water vapor gradually diminishes above this height, and the troposphere condition is more predictable in the NWM. Second, it is assumed that the discrepancy delay density varies linearly in both vertical and horizontal directions. This assumption enables the determination of delay density by linear-interpolation in the correction grid. Third, the delay correction is added onto the NWM ray path without altering the signal trace, which means the delay discrepancy is mainly due to the slowed, rather than bended signal. This simplification is based on the fact that the origin of the delay discrepancy is mainly the unpredicted variation of water vapor, rather than the air pressure. This assumption makes the correction additive to the NWM-based ray tracing.

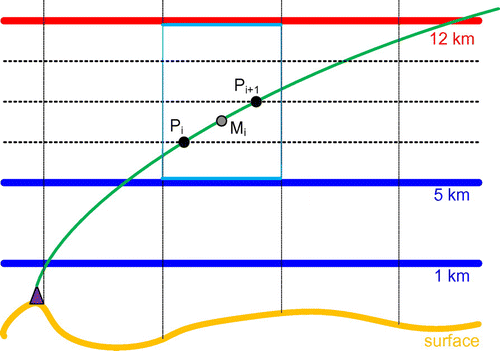
Based on these simplifications and assumptions, the correction grid is constructed as below. Horizontally, it is designed the same as the NWM horizontal grid, i.e. with regular spacing of 0.11° in either latitude or longitude (∼12.3 km). Vertically, it consists of three layers, which includes one constraining layer and two controlling layers. The constraining layer is at 12 km in height, denoted as red in Figure 12, on which the grid node values (representing the delay discrepancy density) are fixed as zero. The two controlling layers are at the 5 and 1 km heights, denoted as blue in Figure 12. The delay discrepancy density varies linearly between the 12-km layer and the 5-km layer, and also between the 5-km layer and the 1-km layer. It is assumed that the delay discrepancy density below the 1-km layer is the same as the value given on the 1-km layer.

Not all the observations collected at the CORS stations can be used in the least square for the correction grid. The input to the least square solving is the noise contaminated troposphere delay discrepancy (, or ), thus the only valid observations are those that have their lower path under 12 km height and are fully covered by the defined correction grid. In other words, only the observations, of which the receiving CORS station and the pierce point on the 12-km layer are within the correction grid horizontal coverage, are considered valid to be used in determining the correction grid. Illustrated in Figure 12, there are two observations excluded (marked as red dash lines), on which the delay discrepancy cannot be fully represented within the correction grid.

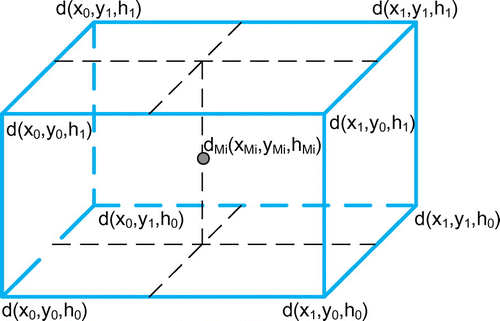
From the definition of the horizontal grid and vertical layers, the valid observation may travel through multiple voxels in the 3D correction grid. Figure 13 shows the front view of a signal traveling path, where one of the voxel on this path is marked as light blue as an example. Within each voxel, the path of the signal can be further described by the multiple thin layers (marked as dashed lines in Figure 13, which have been introduced in the earlier NWM ray tracing algorithm. The pierce points of the signal on each thin layer are computed in the NWM ray tracing, which is denoted as P_i in Figure 13 for the lower surface pierce point of the i-th thin layer. Then the delay correction is the sum over the delay in all voxels and thin layers,(14) (15) where is the delay correction within a voxel , is the delay density at a point with coordinates [x, y, h], and the integral term gives the delay correction within the i-th thin layer. As the path of the signal in each thin layer is assumed as a straight line in the ray tracing algorithm, and also as the delay density is assumed to be linear-varying, Equation (15) can be simplified as(16) where L_i is the signal travel distance in the i-th thin layer, and is the delay density at the middle point M_i of the signal path in the i-th thin layer. From the linear assumption of the delay density variation, can be considered as an interpolation from the densities given at the eight corners of the voxel_v, which is shown in Figure 14 and expressed as(17) where is the weight at the voxel corners, computed from the linear interpolation of point M_i. Substituting Equation (17) into Equation (16), the delay correction within the voxel v can be expressed as a weighted sum of the delay densities at its eight voxel corners.

Figure 13 Front view of a signal piercing through the correction grid.

Figure 14 Linear interpolation within a voxel.

For an observation n, if the delays in all the voxels, through which the signals travels, are summed as in Equation (14), the total correction delay, denoted by , can be given as(18) where denotes a weight given at a certain node in the correction grid. For the nodes of the voxels through which the signal travels, this weight can be computed from the above procedure; for the joints of the voxels through which the signal does not travel, this weight is set as zero. Using Equation (18), the total delay correction of a certain observation n can be expressed as the sum of all the elements in the dot-product of the 3D delay density grid and a 3D weights grid with the same size. This re-writes Equation (18) as(19)

Here the delay density grid is the correction grid to be solved in the least squares procedure; the weight grid is specific for the individual signal trace of each observation, and can be determined in the NWM ray tracing algorithm. Linking with Equation (13), the least squares solution of the correction grid is an optimization procedure which minimizes the sum of the corrected residuals of all the valid observations and can be written as(20)

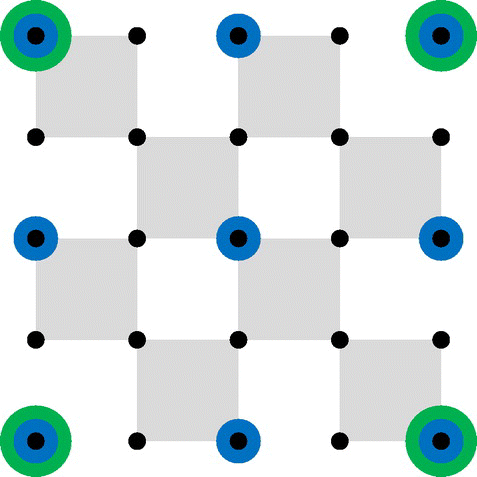
Depending on the size of the correction area, an issue may be raised that the number of unknowns to be solved on the correction grid joints is much larger than that of the input observations. In this case, the least squares process is ill-conditioned and may not provide a satisfactory performance. To solve this particular problem, multiple correction rounds with different horizontal resolutions are suggested. Figure 15 illustrates this idea. In this figure, the black dots denote the horizontal NWM grid. If there are too many variables to be optimized directly in the least squares process (25 in this case), the correction can be carried out in several progressive rounds. In the first round, correction for the grid with the largest horizontal resolution is solved, which are the green dots in Figure 15. With the same number of inputs and reduced number of unknowns, the task for the least squares optimization could be easier. However, the drawback is that, because of the linear-variation of the delay density within the large unit square, the correction accuracy is limited. The residual of this first round correction () can be computed in Equation (13).If it is higher than expected, a second round correction can be applied, on the grids with a higher resolution, illustrated in Figure 15 as blue dots. The resulting residuals after the earlier round are used as the inputs for the following round. Clearly, higher resolution correction grid will be able to describe the more detailed variation in the covered area, thus improving the correction performance, unless the least squares process becomes ill-conditioned.

Figure 15 Illustration of multiple correction sets with different horizontal resolutions.

The above procedure can be iterated for several rounds, until either the highest horizontal resolution met (which is the same as the NWM horizontal resolution), or the least square becomes ill-conditioned (insufficient inputs compared to the number of unknowns) and cannot provide improvement. Using to denote the correction grid solved in the t-round, the overall correction grid generated in this multiple-round scheme can be expressed as the sum of the corrections sets in the individual rounds, as shown in Equation (20). This step is based on the earlier correction additive assumption.(21)

4.4 Performance validation with multi-GNSS

The proposed STD estimation correction scheme, which integrates the NWM and CORS, was validated with a case study. Its performance, in terms of both the estimation accuracy and the convergence time in PPP are discussed below.

The GNSS CORS observations used were obtained from the UK national CORS network, called OS Net which was established and is maintained by the UK mapping agency, the ordnance survey. OS Net is a dense regional network consisting of over 100 precisely surveyed stations, with 50–60 km inter-station distances. Each station can provide real time dual frequency observations with 30 s interval.

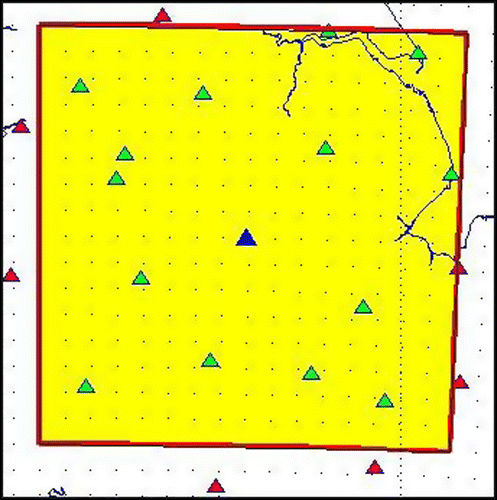
The test area was selected as the East Midland area in the UK, marked as yellow in Figure 16. This area contains 16 by 16 horizontal unit squares of NWM grid, shown by the black dots. It also contains15 OS Net CORS stations, marked as triangles in Figure 16. The test period in the case study is 6 h (06:0012:00, 2009/10/13). It was identified in the earlier section that the NWM-alone-based STD estimation had decreased accuracy in this period, due to the very high level of troposphere variations.

Figure 16 Test area in East Midlands, UK.

In the test area 14 CORS stations, marked as green triangles in Figure 16, are used to determine the correction grid. Another CORS station KEYW, marked as blue triangle, is treated as the user site to validate the performance of the integrated STD estimation.

Table 3 gives the number of the observations from these 14 stations, which are valid for the generation of the correction grid. This number has been averaged over epochs. Note that here, and also in the following test, the Galileo observations come from a simulated data-set. Table 4 gives the number of points to be solved in each correction round. It can be seen that for this test area configuration, 5 rounds of correction were allowed. The first round will treat the space covering the whole area as a single voxel, and the last round will had the same horizontal resolution as the NWM.

Table 3. Average number of qualified observations per epoch in the test area for the multi-GNSSs.

System	Average number of observations
GPS	125
GPS + GLO	232
GPS + GLO + GAL	336

Table 4. Number of points to be solved in each correction round.

Round	Unit square size	Total points to solve
1	16 × 16	8
2	8 × 8	18
3	4 × 4	50
4	2 × 2	162
5	1 × 1	578

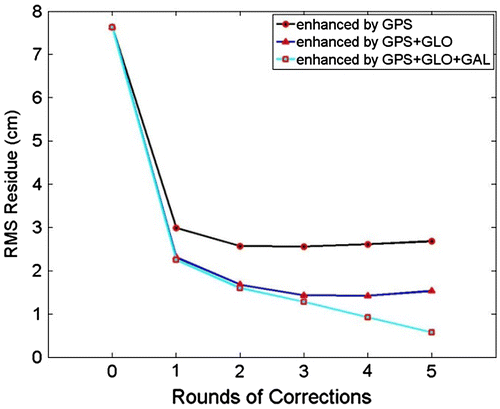
At the KEYW location, the NWM-based estimation was corrected by the correction grid generated from the other 14 stations, and is compared against the STD estimation from the inverse PPP approach. The difference between them, or the residual of the integrated estimation (), is evaluated in Figure 17. In this figure, each point represents the RMS of all the residuals in the whole test period. It can be seen that after two rounds of corrections, the performance of the GPS-based correction cannot be improved anymore; for the GPS + GLONASS dual systems-based correction, the improvement can be continued until the third round of corrections; and for the GPS + GLONASS + GALILEO triple systems-based correction, every round of the correction can provide improvement. This could be explained from Tables 3 and 4. On average, there are only 125 valid observations in the GPS-based correction. When the unit square is small, the solution of the correction grid will be difficult, as there is insufficient signal paths crossing to determine the unknowns on the grid nodes (mathematically this means the least squares algorithm is ill-conditioned). Increasing the number of the observation from the dual or triple systems could overcome this shortfall, and enhance the correction performance. As a comparison, if there is no correction applied, the RMS residual is 7.7 cm. This can be reduced to 2.7 cm in the best GPS-based correction, 1.5 cm in the best dual systems-based correction, and to 0.6 cm in the best triple systems-based correction. Thus, the improvement by applying multi-GNSSs is clear.

Figure 17 Improvement of multiple rounds of corrections on the RMS residuals for multi-GNSSs.

The traditional PPP can be revised by taking the integrated STD estimation () as its inputs, and removing the a priori zenith dry troposphere delay modeling, the zenith wet troposphere delay solving, and also the associated mapping function. The convergence time of this revised PPP can be assessed. Figure 18 shows the revised PPP performance, with different correction schemes, in the same case shown in Figure 8. It can be seen that, in comparison to the NWM-based STD estimation, the integrated STD estimation can provide a clear improvement to the PPP convergence time. There is a small improvement by using the correction based on multi-GNSSs, rather than GPS only; and there is nearly no difference by using dual or triple systems-based corrections. This is because in this particular case, although the RMS residual can be further reduced with more systems involved in the correction, it is already under or quite close to the 2 cm noise floor. Therefore, the further improvement on the STD estimation will not be reflected in the PPP as the troposphere delay is no longer the dominating factor which constrains the PPP performance. The 6-h period of high tropospheric variation used in the test was the only available from one month of archived data. It is expected that searching over a longer period (e.g. in a year) and more locations, more periods dramatic tropospheric behavior could be found to demonstrate further, the impact of the multi-GNSSs on PPP.

Figure 18 Multi-GNSS comparison on the PPP performance with the integrated STD estimation.

5 Conclusions

This paper set out to improve real time tropospheric delay estimation in rapidly changing and spatially variable atmosphere conditions. Instead of simply mapping the zenith troposphere delay, direct estimation of the slant troposphere delay is proposed, which can be obtained from the ray tracing of high resolution NWM products. This NWM-based STD estimation procedure is introduced and validated in this paper. From the preliminary results, it has been shown that the RMS residual of the NWM analysis field-based STD estimation is lower than 3.5 cm, when the elevation is above 15° and lower than 2 cm when the elevation is above 30°. Therefore, the new STD estimation can provide sufficient accuracy to reduce the convergence time in PPP.

If used in real time, the new method is based on the NWM forecast field. Statistical results have shown that its performance is only slightly degraded compared to the use of the NWM analysis field. However, the performance of the new method may be reduced during periods of high tropospheric variations, due to decreased NWM prediction accuracy. To enhance the performance of the new STD estimation method during these periods, a correction scheme has been proposed, in which a 3D correction grid is established by integrating the GNSS observations from a CORS network. It has been demonstrated in a case study that this correction scheme is quite effective in reducing the integrated STD estimation residual.

The new STD estimation and its integrated correction can be implemented for real-time applications. Both the NWM grid and the correction grid information have the capability to be produced in real time, and could be transmitted to the users at different rates, to enable the direct STD estimation by the users. The server does not need to be informed of the user’s location, and therefore, a broadcasting service could be established to support a large number of users with the same NWM and correction information.

Notes on contributors

Lei Yang is a research fellow at Nottingham Geospatial Institute (NGI) of the University of Nottingham.

Chris Hill is a principal research officer at the NGI. He has a PhD from the University of Nottingham on the subject of Satellite Laser Ranging, and has worked on a variety of GPS and GNSS research projects over the last 20 years. He is a fellow of the RIN.

Terry Moore is the director of NGI at the University of Nottingham, where he is the professor of Satellite Navigation and also currently associate dean within the Faculty of Engineering. He has 30 years of research experience in surveying, positioning and navigation technologies. He is a member of Council and a fellow of the Royal Institute of Navigation.

Acknowledgments

This study is carried out as part of the project Innovative Navigation using new GNSS Signals with Hybridized Technologies (iNsight), which is funded by the UK Engineering and Physical Sciences Research Council (EPSRC). The authors acknowledge the support from the project academic partners, University College of London, Imperial College London, and University of Westminster, and also the project industry partners, Ordnance Survey, ST Microsystems, QinetiQ, EADS Astrium, Thales Research and Technology, Leica Geosystems, Civil Aviation Authority and Nottingham Scientific Limited.

The authors also acknowledge the support of the British Atmospheric Data Center (BADC) and the NERC British Isles continuous GNSS Facility(BIGF),for the NWM and GNSS archived data, respectively, and the authors of the PPP processing software suit POINT and PANDA, which have been used as the development and quality checking tools, respectively, in this paper.