Abstract
GNSS signals have previously been modulated using binary phase shift keying but this modulation scheme is being replaced by binary offset carrier (BOC) modulation. Research has considered how the BOC signals might be affected differently when passed through a surface acoustic wave (SAW) filter. The concern has been that because of the split spectrum nature of the BOC signals, the upper and lower side-lobes will be delayed significantly differently. This was suggested because SAW filters have nonlinear phase characteristics and therefore different frequencies are delayed differently. It was suggested that this difference in delay will result in greater distortion of the correlation triangle. A delay magnification effect was also mentioned when analyzing the delay of a BOC signal. It was not understood why the theoretical delay calculations did not match up with the actual results in both hardware and simulation. This paper clarifies some of the confusion and explains why the “delay magnification” applies to phase delay but not group delay. This paper also takes a look at how the code phase delay can vary with frequency and correlator spacing as a result of the SAW filter properties.
1 A simple sinusoid model
To explain the delay magnification idea proposed in Ref. Citation(1), we start with a model of two sinusoids being passed through a filter. These two sinusoids are generated by multiplying a carrier sinusoid with a signal sinusoid and are the input to a filter:(1) where x(t) is the input,
is the frequency of the information signal which for our purposes is assumed to be a simple sinusoid, and
is the frequency of the carrier. The input to the filter is equivalent to two sinusoids added together:
(2) where
and
.
In the original analysis in Ref. Citation(1), when these two sinusoids ( and
) were passed through a SAW filter, the sinusoids were delayed according to the group delay of the SAW filter at the two frequencies. Because of this, any slight difference in group delay between the two frequencies results in a much greater delay in the information signal sinusoid. This effect is demonstrated below.
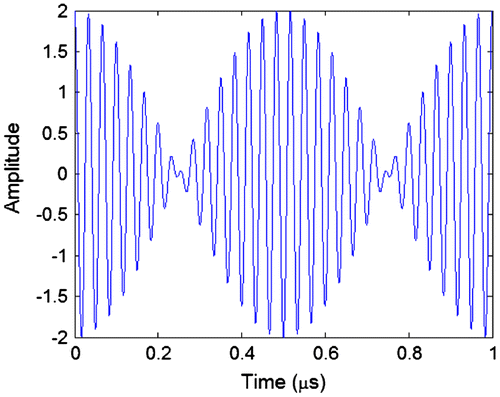
Figure shows the input to the filter . In this example,
and
. This results in
and
. Although these are not GPS frequencies, they were chosen so that both the carrier and information signal sinusoid are clearly visible on the plots.
Figure 1 Filter input signal .
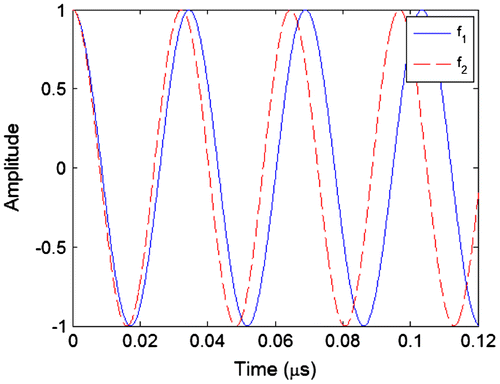
Figure shows the two sinusoids and
. It clearly shows that the phases of the two sinusoids start aligned but gradually separate due to the difference in frequency.
Figure 2 Plot of sinusoids with frequencies and
.
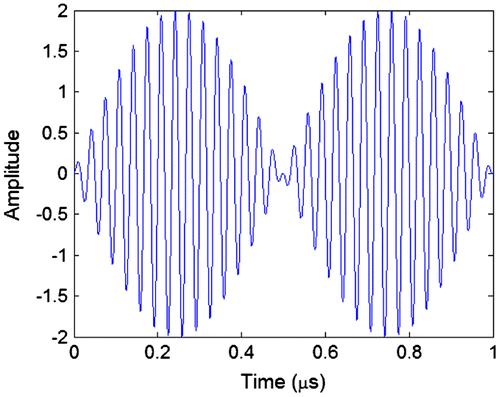
If the sinusoid of frequency was delayed by a small amount, we would see that the envelope of the signal would be delayed much more. Let the filter have no delay for frequency
but have a phase delay of 16 ns at
. Figure shows the output of the filter
. This shows that the envelope of the signal has been delayed by approximately 250 ns even though the phase delay of the filter for
was only 16 ns. This demonstrates the idea of delay magnification, as proposed in Ref. Citation(1), where a small delay results in a much larger delay.
Figure 3 Output of the filter
We have already used the term “phase delay” in the previous paragraph so we had better also define it here. The delay of a filter can be measured in terms of the “phase delay” but more commonly the “group delay” is used instead. Both the phase and the group delays are calculated using the phase of the filter. The equations describing the different delay definitions were taken from Ref. Citation(2) and are defined here as:(3)
(4) where
is the phase delay of the filter at frequency
,
is the group delay of the filter at frequency
, and
is the phase of the filter at frequency
.
It is important to know the difference between these two definitions of delay measurement and how they affect a signal differently. First, we look at how a pure sinusoid is affected by these two delay definitions and show that group delay does not apply to such a signal.
We start with the filter input sinusoid :
(5)
Let be the phase of the filter at frequency
. Therefore, the output of the filter
is:
(6)
We know that, however we define the phase and group delays to affect the sinusoid input , the resultant equations for the filter output
must be equivalent to Equation (6). For phase delay, the sinusoid is delayed by the value
. This results in the output of the filter
being defined as:
(7)
Substituting for using Equation (5) gives:
(8)
After substituting for using Equation (3), Equation (8) above is equivalent to Equation (6). If one were to apply the group delay value
to the input signal
in the same way as has just been done for the phase delay value
then the equation for
would no longer be equivalent to Equation (6). This analysis explains why group delay does not apply to a pure sinusoid.
If it is the case that group delay does not apply to a continuous sinusoid signal then how does it apply to signals? Ref. Citation(3) mentions that group delay defines the delay of the envelope of a signal. To explain this in more detail, we construct a new input signal for the filter input. This time this signal is a sinusoid shaped by an envelope signal
. The equation for the filter input
is shown below:
(9)
For this signal, both the phase delay and the group delay values need to be applied when passing through a filter. The sinusoid is delayed by the phase delay and the envelope
is delayed by the group delay. This results in the output of the filter
becoming:
(10) where
is the phase delay of the filter at frequency
, and
is the group delay of the filter at
. Equation (10) is only an approximation if the group delay varies over the range of frequencies that are included in the spectrum of
. However, Equation (10) is a close approximation to the actual response of the filter if the group delay varies only very slightly over the frequency range of
. If the group delay of the filter varies greatly with frequency then the bandwidth of the signal
can be reduced until the changes in group delay are small enough to be neglected.
In the case of a linear phase filter, the values for the phase delay are identical to the group delay
values for all frequencies. In this case, even though the phase and group delay definitions are not equivalent, the group delay values
could be applied in the same way as the phase delay values
to get the same results. However, one must be cautious because, in the case of a nonlinear phase filter, the group and phase delay values are not the same and therefore, if applied incorrectly the calculations will not match the measured or simulated results.
We now return to our original model of two sinusoids being passed through a filter as described by Equations (11) and (12). The output of the filter is:
(11) where
is the phase of the filter at
and
is the phase of the filter at
. Therefore, in terms of the original carrier and information signal, the output of the filter is:
(12)
This equation can be compared with Equation (10) where the sinusoid in (10) is the carrier signal in (12) and the envelope function in (10) is the information signal in (12). It should be noted that the carrier signal is the cosine with the term and the information signal is the cosine with the
term.
In Equation (10), the group delay of the filter delays the envelope signal
. In Equation (12), the information signal is equivalent to the envelope signal in Equation (10). Therefore, the group delay
of the filter can be found from the phase of the information signal in equation (12) and is defined as:
(13)
We know that is the difference in frequency between
and
which is equivalent to
. We also know that
is equivalent to
. Therefore, Equation (13) is equivalent to Equation (4). This confirms the validity of Equation (10) where the group delay defines the delay of the envelope of a signal.
So far, we have demonstrated that the “delay magnification” effect applies to phase delay. We have shown that group delay does not apply to continuous signals but it defines the delay of the envelope of a signal. Equation (10) also shows that the phase delay defines the steady-state response of a filter.
2 Modeling using spread-spectrum signals
Up to this point, the signals used in the analysis have been useful for the initial explanation of delay but they are inadequate for the analysis of how the real signals and the correlation peaks will be affected by a SAW filter in the front end of a receiver. The signals used previously have consisted of pure sinusoids meaning that they are continuous signals with no transients and therefore their spectra contained only two frequencies. Also the signals previously used carried no real information.
GPS signals have a spread spectrum meaning that, their spectra do not contain just a few frequencies but, they use a range of frequencies to represent the signals. In order to be able to model such signals, the modeling was done in MATLAB. This allows the effects that a SAW filter has on the signals and their correlation peaks to be observed. For the analysis, both BPSK and BOC(1, 1) signals were simulated separately by being passed through a model of a SAW filter. The first SAW filter modeled was a B3521 GPS filter from EPCOS.
This shows whether or not the BOC(1, 1) signals will be delayed differently or will have a different distortion of the correlation triangles when compared with the BPSK signals.
The model of the signals and SAW filter calculates the response of the filter for 1 ms of signal, this being the length of a complete chipping sequence for the C/A code. The signals were first generated in the time domain and then passed through a model of the SAW filter by multiplying the spectrum of the signals in the frequency domain with the frequency response of the SAW filter. The data provided by the manufacturer for the SAW filter contained the magnitude and phase response of the filter in 312.5 kHz steps. Because the simulation length is 1 ms, the points in the frequency domain are spaced every 1 kHz meaning that the SAW filter data had to be up-sampled and interpolated using a first-order hold to have data points every 1 kHz.
Once the signals had been passed through the SAW filter by means of multiplication in the frequency domain, the signals are converted back to the time domain using an IFFT. After this the signals are demodulated by multiplying them with the carrier signal. And finally, the signals are correlated. The correlation is achieved by multiplication in the frequency domain as this requires less processing than direct correlation in the time domain.
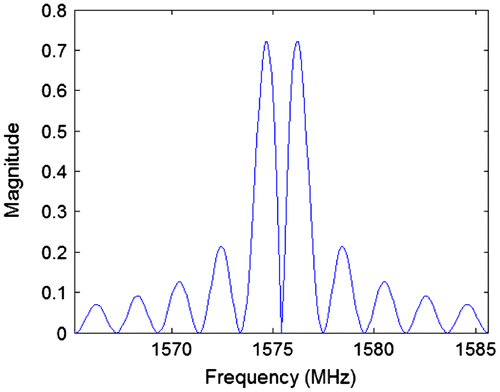
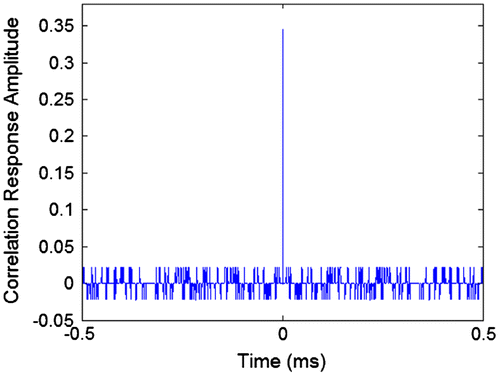
Figures show the frequency spectrums of the BPSK and BOC(1, 1) signals, respectively. The following Figures show the correlation responses for both BPSK and BOC(1, 1) signals after they have been passed through a SAW filter and demodulated.
Figure 4 Frequency spectrum of a GPS BPSK signal.
Figure 5 Frequency spectrum of BOC(1, 1) signal.
Figure 6 Correlation response of BPSK signal.
Figure 7 Correlation triangle of BPSK signal.
Figure 8 Close-up of correlation triangle for BPSK.
Figure 9 Correlation response of BOC(1, 1) signal.
Figure 10 Correlation triangle of BOC(1, 1) signal.
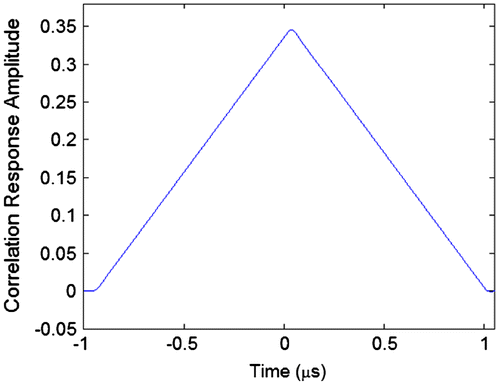
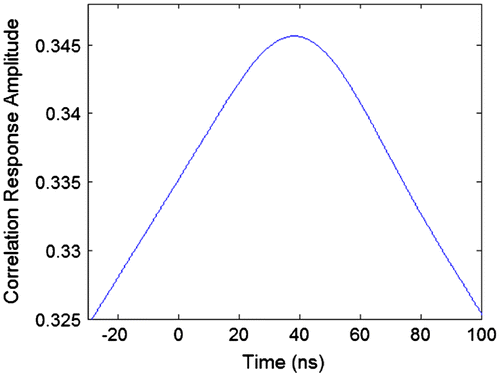
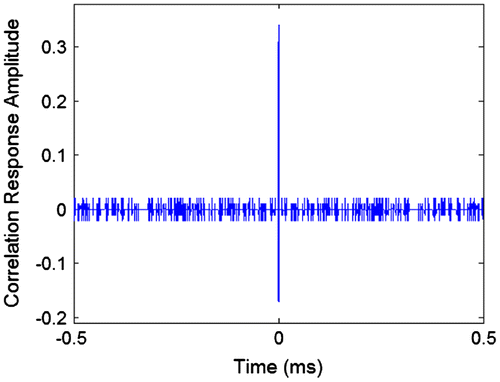
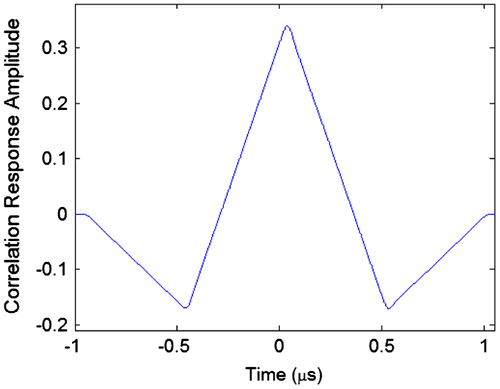
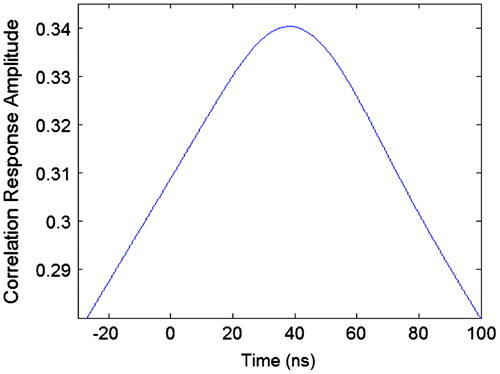
By contrasting Figures it can be seen that there is no noticeable difference in the way the correlation triangles have been distorted. The most significant effect is the smoothing of the peaks due to the limited bandwidth of the filter. Both correlation triangles look symmetrical. The maximum values of the correlation triangles occur at 38.40 ns (484 samples) for both signals showing no difference in delay.
Figure 11 Close-up of correlation triangle for BOC(1, 1).
Another method to calculate the delay of the correlation triangles was used. The two sample points of the correlation triangle that have a value half that of the peak value were found. Then the time values of the two samples were averaged resulting in a delay of 465 samples for the BPSK signal and 464 samples for the BOC(1, 1) signal. This delay is about 1.6 ns smaller than the delay of the peak value. This shows that the SAW filter not only delays the correlation peak, but it also distorts the shape of the correlation triangle. However, the distortion is not much different for the BOC(1, 1) signals as it is for the GPS signals.
3 Impulse response analysis
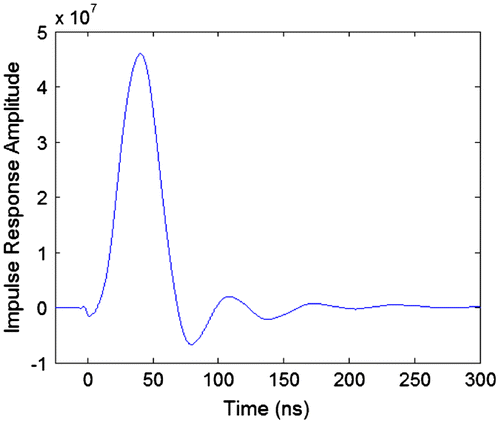
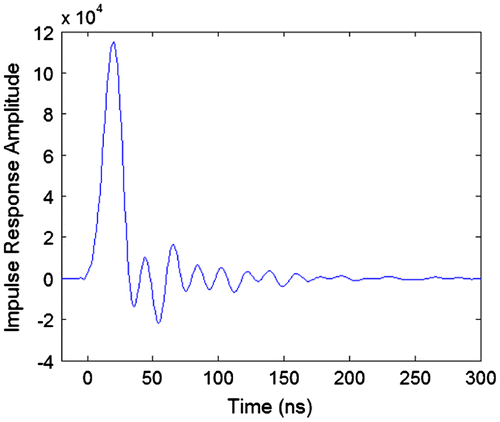
In order to understand more fully what is going on with the SAW filter and its effect on the signals, it is useful to look at its impulse response in the time domain. Figure shows the impulse response of the GPS narrowband SAW filter which was calculated using an IFFT. The figure shows that the peak of the impulse response (at 40.6 ns) is very close to the delay of the correlation peak observed in simulation (38.40 ns) when passing BPSK and BOC(1, 1) signals.
Figure 12 Impulse response of SAW filter.
The effective impulse response of the system that the signal sees after it has been modulated, filtered, demodulated, and low-pass filtered can be constructed by shifting the frequency points of the filter down to baseband frequencies. This was done by shifting the filter frequencies down by the carrier frequency of 1575.42 MHz. Figure shows the resultant impulse response which is effectively what the original signals will be filtered by at the output of the receiver. So, instead of modulating the signal by the carrier, filtering it through the SAW filter, and demodulating the signal. All these steps can be replaced by simply convolving the signal with the impulse response shown in Figure .
Figure 13 Effective impulse response of system.
Both BPSK and BOC(1, 1) signals are filtered by the same effective impulse response and Figure shows that split correlation peaks cannot practically exist. This is because there is no significant secondary peak in the impulse response. More importantly, the ripples in the impulse response are mostly filtered out because the correlation triangles of both BPSK and BOC(1, 1) signals are much wider than the length of the ripples.
To verify that this effective impulse response of the system results in an accurate model, both ways of simulating the system were done side-by-side. The two correlation peaks calculated in each way were subtracted one from another to find the error. This error was found to be approximately 8 × 10−5 relative to the actual value at any given point. After zooming in on the errors, it was found that the errors were oscillatory and were at a frequency twice the carrier frequency. This shows that the first way of simulating the system that modulates the signal, filters, and then demodulates it, does not completely filter out the frequencies. This is because no special filtering was used after demodulation. However, when the demodulated signal is convolved with the flipped version of the original signal, this filters out the high frequencies. Because of this, it was assumed that the demodulated signal did not need to be low-pass filtered first.
4 Modeling the system at baseband
This section goes about to explain why it is possible to model the system only at baseband frequencies rather than at RF frequencies. Modeling at baseband reduces the sampling rates required and hence reduces computation time. To explain, we first look at what happens to the signals at each stage in their modulation, filtering and demodulation. The example given in this section uses low frequencies to aid explanation, but the process is still the same for the actual GPS frequencies.
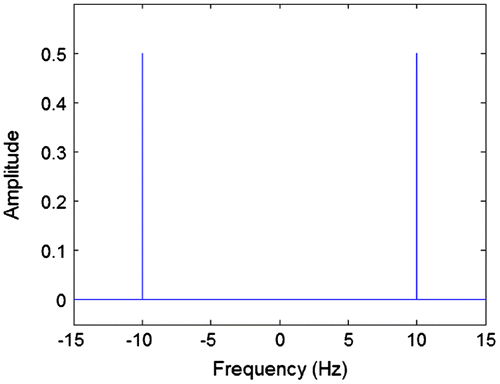
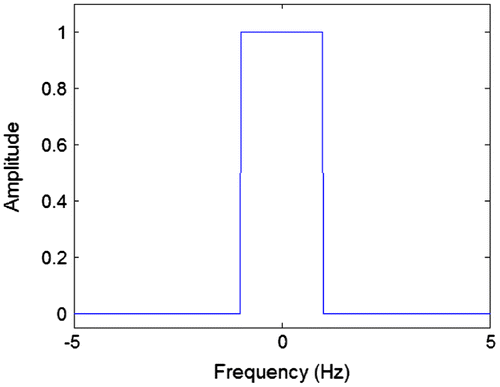
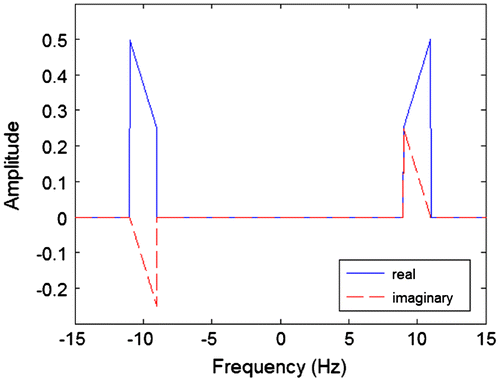
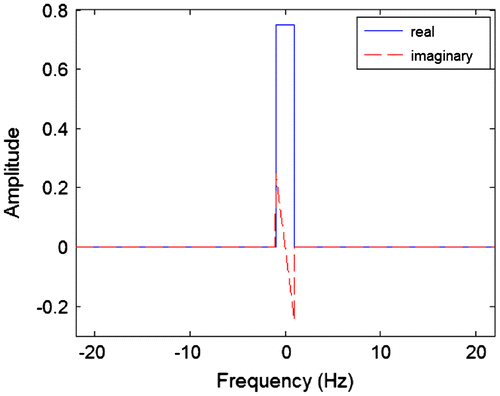
Figure shows the spectrum of a 10 Hz carrier signal. Figure shows the spectrum of the baseband signal being transmitted. For both of these signals, they have a purely positive and real spectrum and so only the magnitude is shown.
Figure 14 Spectrum of carrier signal.
Figure 15 Spectrum of baseband signal.
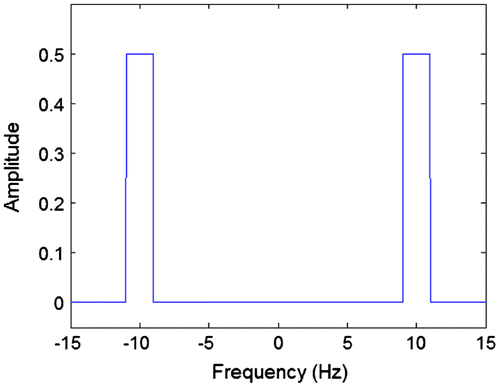
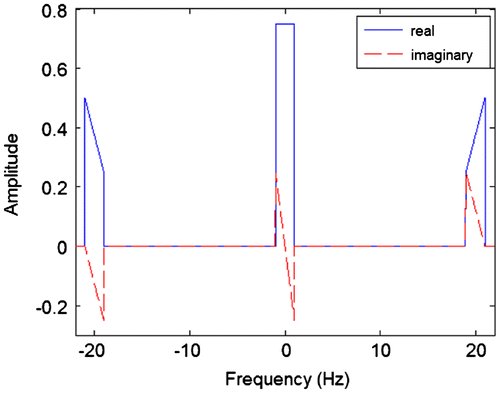
Figure shows the transmitted signal that is generated by multiplying the baseband signal with the carrier. In the frequency domain, the two signals are convolved resulting in the spectra in Figure . Again the spectrum of the transmitted signal is purely positive and real.
Figure 16 Spectrum of transmitted signal.
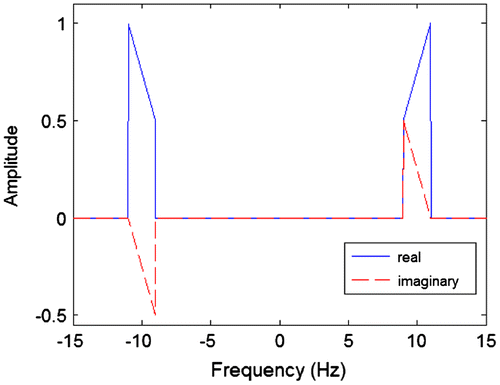
Figure shows the spectrum of the filter’s response. This time both real and imaginary parts are shown on the same figure. When the transmitted signal is passed through the filter it results in the signal shown in Figure .
Figure 17 Spectrum of filter response.
Figure 18 Spectrum of filtered signal.
The spectrum of the modulated and filtered signal shown in Figure is next demodulated. This results in the demodulated signal in Figure . Before the signal is correlated, it is first low-pass filtered to remove the signal replicas at (20 Hz). In the MATLAB model of the system, the correlation acts as a low-pass filter, hence this step is not included as the correlation implicitly does the high-frequency component filtering. However, Figure shows the spectrum of the demodulated signal after it has been low-pass filtered.
Figure 19 Spectrum of demodulated signal.
Figure 20 Spectrum of low-pass filtered demodulated signal.
Instead of having to modulate the signal before filtering and then demodulating the signal before low-pass filtering, all these steps can be replaced by making a new filter. This filter takes the baseband signal in Figure and produces a signal identical to Figure . This is done by modulating the filter response in the time-domain with the sinusoid carrier signal. Afterwards, the filter response is low-pass filtered to remove the higher frequencies.
To avoid the need to modulate and low-pass filter the original filter’s response the equivalent filter is actually made in the frequency domain by shifting, flipping, conjugating, and adding, thereby circumventing the need to sample at the high RF frequencies.
One thing that has not been mentioned yet is the carrier phase. If the phase of the carrier being used to demodulate is different from the phase of the transmitted carrier after filtering, then there will be gain errors in the received signal. For example, if the phase of the carriers had a phase shift of 90° between them, then after multiplying the resultant signal would have no DC component (i.e. no signal). One option would be to leave the equivalent filter as having a complex response. This would result in an I and Q component signal which would then require two parallel convolutions. However, we are only interested in the magnitude response of the correlation. Therefore, we can align the carrier signals and have only one resultant correlation signal.
In the previous way (time-domain approach) of modeling the system at RF frequencies, we can align the demodulating carrier with the filtered carrier by subtracting the phase of the filter at the carrier frequency from the phase of the demodulating carrier. In our equivalent baseband filter, this can be achieved by adjusting the phase of the original filter before using it to create the baseband filter. By subtracting the phase of the original filter at the carrier frequency from all the frequency points of the filter, the carrier phases are now aligned.
5 GPS and GLONASS filter
Previously, the SAW filter used was a GPS narrowband filter. Next, we look at a GPS/GLONASS filter that has a wide enough pass-band to let both signals through. GPS is centered at 1575.42 MHz and GLONASS has frequencies centered at 1602 MHz. Although GLONASS uses several channels with much smaller bandwidths than GPS, it was decided to use a GPS signal at 1602 MHz instead for simplicity.
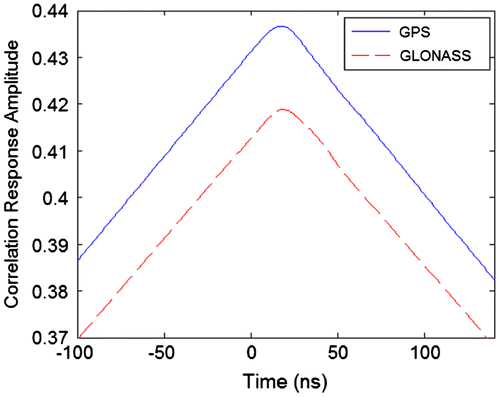
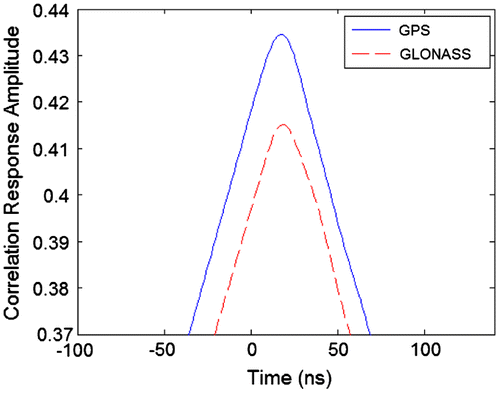
Figure shows the correlation signal for BPSK signals at GPS and GLONASS frequencies. In Figure are the correlation signals for BOC(1, 1) also at GPS and GLONASS frequencies. There is no noticeable difference between the signals except a small scale factor between GPS and GLONASS, which is highly likely due to the different gains in the pass-band of the GPS/GLONASS SAW filter. Also, the BOC signals obviously have narrower peaks.
Figure 21 The peak of the correlation triangles for BPSK signals.
Figure 22 Correlation response for BOC signals.
The peaks for the BPSK signals are at 17.2 ns for GPS and 18.1 ns for GLONASS. The positions of the peaks for the BOC signals are identical to those for the BPSK signals. This difference in delay is due to the difference in the group delay of the GPS/GLONASS filter throughout its pass-band.
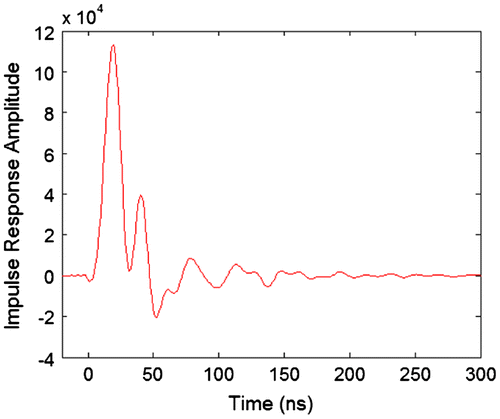
Next, we look at the impulse response of the system for both GPS and GLONASS frequencies. Figure shows the GPS impulse response. Figure shows the GLONASS impulse response.
Figure 23 Impulse response of system for GPS frequencies.
Figure 24 Impulse response of system for GLONASS frequencies.
The GLONASS impulse response explains the slight hump in the right hand side of the correlation triangle. This is due to the second but smaller peak in the impulse response. The GPS impulse response does not have such a large second peak. Again, the first peaks in the impulse responses correspond very closely to the delay of the correlation peaks. And finally, Figure shows the impulse response of the SAW filter.
Figure 25 Impulse response of GPS/GLONASS SAW filter.
6 Correlator spacing and delay
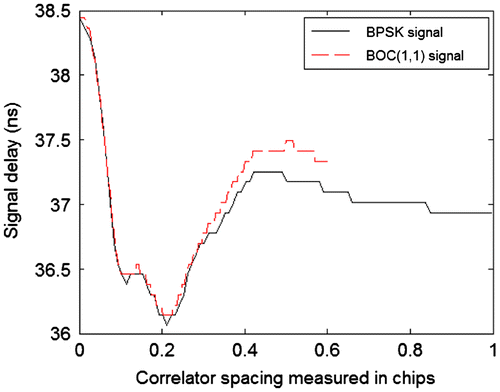
Because the SAW filter has nonlinear phase, the symmetrical shape of the correlation peak is not maintained. The nonlinear phase results in a slightly nonsymmetric correlation peak. This means that the delay caused by the SAW filter varies with correlator spacing when two correlating arms are used. Note that the correlator spacing here is defined as the spacing between the early and late correlators used to find the center of the correlation triangle. Figure is a plot of the signal delay against correlator spacing.
Figure 26 Signal delay against correlator spacing.
Figure shows that there is little difference in delay between the BPSK signal and the BOC(1, 1) modulated signal. The maximum difference in delay between the two is about 0.2–0.3 ns for when the correlator spacing is about half a chip. This is of course assuming identical correlator spacings for both BPSK and BOC(1, 1). In practice, a typical early to late correlator spacing for GPS BPSK signals is 1 chip Citation(4). However, the BOC(1, 1) correlator spacing will be much narrower due to the slope of the main correlation peak being three times steeper Citation(5).
This analysis of delay vs. correlator spacing shows that a change of carrier frequency is not the only cause of a change in delay due to non-linear phase filtering. When designing a GNSS receiver and compensating for delay errors across multiple signal types, the effect of correlator spacing is another characteristic which needs to be considered. For designs using variable correlator spacing to maximize code phase accuracy, the delay compensation will have to be dynamically changed according to any changes of correlator spacing. Figure also suggests that step changes in correlator spacing would also result in step changes in code phase delay, this would in turn cause unwanted transients in the code phase loop. Therefore, changing correlator spacing must be done slowly and gradually.
7 Conclusions
It was found and demonstrated that the delay magnification mentioned in Ref. Citation(1) does apply but only when using the phase delay of the filter to calculate the signal delay. Using MATLAB, models of realistic GNSS signals passing through two types of SAW filters were tested. This showed very little or no difference in the delay of the correlation peaks of BPSK and BOC(1, 1) signals. This was followed by the analysis of the impulse response of the SAW filters. The filters’ responses were converted to baseband to make the analysis of how the signals are affected by the SAW filters easier. The effective impulse response of the system explained why split correlation peaks do not occur.
A GPS/GLONASS filter showed that, as expected, there was a small difference in delay between signals transmitted at GPS frequencies and signals transmitted at the GLONASS frequencies. It was also shown that the delay was not noticeably different for BPSK and BOC(1, 1) signals.
A comparison of delay vs. correlator spacing was undertaken for both BPSK and BOC(1, 1) signals passing through the GPS SAW filter. This revealed the importance of considering correlator spacing and not just carrier frequency when determining the actual code phase delay as seen by the tracking loops. For a given correlator spacing, the delay difference between BPSK and BOC was negligible. However, the difference in the modulation types will force different correlator spacings to be used which may result in a more significant difference between BPSK and BOC(1, 1) delay.
The analysis done for this paper involved only the effect of a SAW filter. A practical GNSS receiver will have a more complex signal chain introducing more nonlinearity’s, in which case a more in depth analysis would need to be done to determine the overall system effect on the code phase and carrier delay.
Notes on contributors
Reuben Berry was awarded Master of Engineering (MEng) with Distinction in Electronic Engineering at the University of Westminster in 2012. He is currently working for the Applied DSP and VLSI Research Group (ADVRG) at the University of Westminster contributing to the design of a research enabling GNSS receiver.
Philip G. Mattos joined STMicroelectronics in 1979. He was made a visiting research fellow at Bristol University, awarded an external PhD on his GPS work in 1996, and then appointed as a visiting professor at Westminster in 2011. In 2012, he is leading the team on L1C and Compass implementation, and the creation of totally generic hardware that can handle even future unknown systems.
Izzet Kale received the PhD degree in techniques for reducing digital filter complexity from the University of Westminster, London. He is currently a professor of applied Digital Signal Processing (DSP) and Very Large Scale Integration (VLSI) systems. He is also the founder and the Director of the Applied DSP and VLSI Research Group, at the University of Westminster, where he has undertaken numerous applied research and development projects and contracts for European, U.SA, and Japanese corporations working on innovative silicon-integrated product development for commercial applications. He is currently working on efficiently implementable ultralow-power DSP algorithms/architectures and sigma–delta modulator structures for use in the communications and biomedical industries and hybrid Global Navigation Satellite Systems GPS/Galileo/Glonass/Compass receiver structures and systems.
Acknowledgments
This research is being carried out within iNsight (www.insight-gnss.org). It is a collaborative research project funded by the UK’s Engineering and Physical Sciences Research Council (EPSRC) to extend the applications and improve the efficiency of positioning through the exploitation of new global navigation satellite systems signals. It is being undertaken by a consortium of 12 UK University and industrial groups: Imperial College London, University College London, the University of Nottingham, the University of Westminster, EADS Astrium, Nottingham Scientific Ltd, Leica Geosystems, Ordnance Survey of Great Britain, QinetiQ, STMicroelectronics, Thales Research and Technology UK Limited, and the UK Civil Aviation Authority.
Thanks are also due to Alper Ucar from the University of Westminster for providing MATLAB code for GPS signal generation.
References
- Mattos, P.G. In Multi Constellation and BOC-Signal Problems with Group Delay, Proceedings of the 2012 International Technical Meeting of the Institute of Navigation, Newport Beach, CA, January, 2012, 1875–1909.
- Antoniou, A. Digital Signal Processing – Signals, Systems and Filters; McGraw Hill; ISBN 0-07-145424-1, 2006; p 426.
- Maher, R.C. In All About Phase, Proc. IEEE Signal Processing Society 5th Signal Processing Education Workshop, Marco Island, FL, Jan, 2009, 218–222.
- van Dierendonck, A.J.; Fenton P.; Ford T. Theory and Performance of Narrow Corelator Spacing in a GPS Receiver. Navig. J. Inst. Navig. 1992, 39, 265–283.
- Borre, K.; Akos, D.M.; Bertelsen, N.; Rinder, P.; Jensen, S.H. A Software-Defined GPS and Galileo Receiver; Birkhaüser, Boston, MA, 2007 p 60.