A star-based data structure to store efficiently 3D topography in a database

Abstract

For storing and modeling three-dimensional (3D) topographic objects (e.g. buildings, roads, dykes, and the terrain), tetrahedralizations have been proposed as an alternative to boundary representations. While in theory they have several advantages, current implementations are either not space efficient or do not store topological relationships (which makes spatial analysis and updating slow, or require the use of an expensive 3D spatial index). We discuss in this paper an alternative data structure for storing tetrahedralizations in a database management system (DBMS). It is based on the idea of storing only the vertices and stars of edges; triangles and tetrahedra are represented implicitly. It has been used previously in main memory, but not in a DBMS. We describe how to modify it to obtain an efficient implementation in a DBMS, and we describe how it can be used for modeling 3D topography. As we demonstrate with different real-world examples, the structure is compacter than known alternatives, it permits us to store attributes for any primitives, and has the added benefit of being topological, which permits us to query it efficiently. The structure can be easily implemented in most DBMS (we describe our implementation in PostgreSQL), and we present some of the engineering choices we made for the implementation.

Keywords:

• 3D GIS
• tetrahedralization
• database management system (DBMS)
• data structures

1. Introduction

Several data models to represent three-dimensional (3D) topographic objects (e.g. buildings, roads, dykes, or the ground) and to store them in a database management system (DBMS) have been proposed. Some of them store only the geometry of single objects while others permit us to explicitly store the topological relationships between objects (and also those between the lower dimensionality primitives of the representation of an object). Geometry models usually store objects with a boundary representation, called b-rep, and one popular data structure used in practice is the Geography Markup Language (1). It can be seen in the overview of Zlatanova et al. (2) that many topological models are variations of the formal data structure (FDS) (3, 4), which, unlike its name implies, is a conceptual model – with rules and constraints to preserve the validity – that can be implemented in a DBMS. The FDS is a boundary representation in which four primitives are kept (nodes, arc, edge, and face; bodies are implicit) and where the topological relationships between them are stored.

An alternative to b-rep models is to use tetrahedralizations, where 3D objects are decomposed into tetrahedra and where empty space (e.g. between buildings) is also decomposed into tetrahedra (dubbed the “air” tetrahedra) and integrated in the model.¹ Carlson (5) and Pilouk (6), among others, argue that tetrahedralizations have several advantages to represent 3D objects, in the same way that triangulations have advantages in 2D (7). The advantages the most often cited are: storage is simplified as only one convex primitive is needed (8), spatial analysis operations can be performed more efficiently (9), and the overall implementation is simpler, thus more robust. However, tetrahedralizations also have theoretical drawbacks, Zlatanova et al. (2) state in their comparison of the different 3D GIS models: “An additional disadvantage of TEN is its much larger database size compared with other representations.” However, as Penninga and van Oosterom (10) state, the storage penalty is true only if all the primitives of the tetrahedra are explicitly represented (nodes, edges, and faces, as with the FDS). To design a compact data structure, they propose two variations of a data structure where only vertices and tetrahedra are represented: edges and triangles are extracted on the fly when needed. The first approach can be seen as akin to Simple Features (11): a tetrahedron is formed by the concatenation of the four coordinates of the four vertices and only one table is stored. The second approach is a variation: vertices are stored in one table and have an ID, and one tetrahedron is formed by the concatenation of four vertex IDs into a series of bits. For both approaches they ensure that all tetrahedra are correctly oriented (i.e. the ordering of the vertices is the same for all tetrahedra), which speeds up spatial analysis and the incremental update of the model.

While Penninga and van Oosterom’s data structures are compact, the topological relationships between the tetrahedra are not explicitly stored (neither adjacency between tetrahedra nor incidence from one tetrahedron to primitives in other tetrahedra). These can be extracted in views, but still require a global scan of the tables. That means that spatial analysis operations will perform slowly on big data-sets, and so will incremental updates. Penninga and van Oosterom (10) advocate using an auxiliary spatial index for each tetrahedron, such as an R-tree (12), although that has not been implemented nor tested. The main problems with an auxiliary index are: (i) storage space is expensive, the bounding box of a tetrahedron (required by the R-tree) has only one point less than the tetrahedron itself and (ii) an R-tree is a rather complex structure, and updating incrementally a large tree can be slow. Triangulations in 2D often are not indexed at the triangle level for the same reasons, referring to Ref. (13).

We discuss in this paper an alternative data structure for storing tetrahedralizations in a DBMS. Instead of storing explicitly tetrahedra, we store only two lower dimensionality primitives (vertices and edges) and the stars of edges. It has been used previously in 3D in main memory (14), but to our knowledge no attempt has been made to implement it in a DBMS. We define in Section 2 the concept of stars, which is related to that of a tetrahedralization. We present in Section 3 the data structure and we detail how attributes and constraints can be stored. One important advantage of our star-based structure is that it permits us to avoid the use of an auxiliary 3D spatial index, the topological relationships between the tetrahedra are instead exploited; only a standard binary-tree (B-tree) is needed to index the tetrahedra. As explained in Section 4, the structure is very compact, can be implemented easily in a DBMS, and can be efficiently queried. We report in Section 5 on the storage space needed in PostgreSQL/PostGIS for different real-world 3D city models. It can be seen that the size of the DBMS tables required for our structure (including the indexing) is smaller than simply the R-tree needed to index the tetrahedra when stored with Penninga and van Oosterom’s structure (10). We finally discuss in Section 6 some of the engineering choices that we made while implementing the structure and our future challenges.

2. Constrained tetrahedralization and stars

2.1. Constrained tetrahedralization

Given a set S of points in R^d (the Euclidean space of dimension d), a triangulation decomposes the convex hull of S into nonoverlapping simplices. A simplex is the simplest element in a given dimension. Specifically, a k-dimensional simplex is called a k-simplex and it is the convex hull of a set of (k + 1) linearly independent points in R^k; a 0-simplex is a node, a 1-simplex an edge, a 2-simplex a triangle, a 3-simplex a tetrahedron, and so on. To simplify the notation, a k-simplex σ formed by the vertices a, b, and c, is simply denoted abc. The facets of σ are the (k − 1)-simplices forming it.

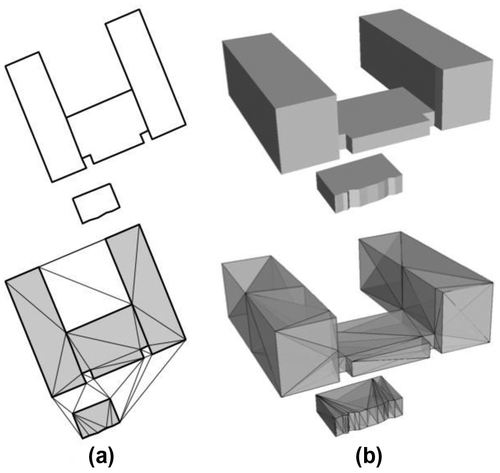
If the set S contains both points and constraints, then a constrained triangulation (CT) decomposes the convex hull of S into simplices that are nonoverlapping, and every input constraint appears in the triangulation of CT(S). As shown in Figure 1(a), the constraints in R² are (straight-line) segments in the plane; if several segments form a loop (which defines a polygon), a CT permits us to triangulate the interior of this polygon. In R³ the constraints are planar surfaces, as Figure 1(b) shows. In our case, these constraints are the walls of buildings for instance; as is the case in 2D, if several adjacent surfaces form a closed polyhedron, a CT will permit us to tetrahedralize its interior.

Figure 1. (a) 2D polygons representing buildings footprints, and their constrained Delaunay triangulation. (b) 3D representation of the same buildings (polyhedra in this case, obtained by extruding the footprints in (a)) and their CDT (for clarity only the tetrahedra inside the polyhedra are shown here, but the whole convex hull in 3D is partitioned into tetrahedra).

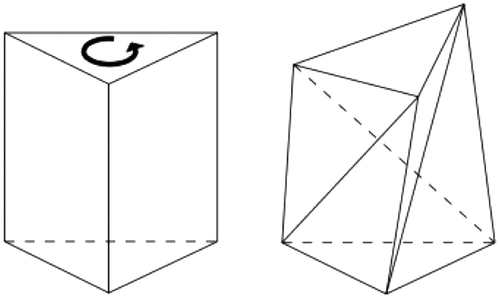
It is known that the CT of a set of points and segments in R² is always possible (15). However, in 3D the problem is more complex. This is because some arbitrary polyhedra cannot be tetrahedralized without the addition of extra vertices, the so-called Steiner points. Figure 2 shows an example, as it was first illustrated by Schönhardt (16). This polyhedron is formed by twisting the top face of a triangular prism to form a six-vertex polyhedron having eight triangular faces (each one of the three quadrilateral faces adjacent to the top face will fold into two triangles). It is impossible to select four vertices of the polyhedron such that a tetrahedron is totally contained inside the polyhedron, as none of the vertices of the bottom face can directly “see” the three vertices of the top triangular face. Adding one Steiner in the center of the prism allows the CT to be constructed.

Figure 2. The Schönhardt polyhedron is impossible to tetrahedralize without adding extra vertices.

To construct a CT in 3D, there are three approaches. The first one is the conforming Delaunay tetrahedralization, where additional vertices are inserted and where each tetrahedron respects the Delaunay criteria, i.e. its circumsphere is empty of any other vertex. While in certain disciplines having well-shaped tetrahedra is important (e.g. in finite-element analysis), in the case of 3D topography it is most likely less as the partitioning of space is used as a data structure, and the shape of the element is not used directly. Moreover, conforming Delaunay tetrahedralizations often insert several new vertices, although there are techniques to reduce them in practice (17). The second solution is the constrained Delaunay tetrahedralization (CDT) (18, 19), where the tetrahedra are not fully Delaunay but where the number of Steiner points is minimized. A third approach consists of creating tetrahedra without any guarantee on their shapes, this requires the use of Steiner points but these can be minimized. Robust and efficient implementations of the last two approaches exist, we use for the experiments in Section 4 the software TetGen (20).

2.2. Stars and links

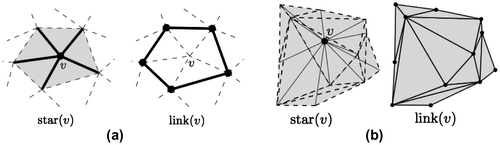
Let v be a vertex in a d-dimensional triangulation. Referring to Figure 3, the star of v, denoted star(v), consists of all the simplices that contain v; it forms a star-shaped polytope P. For example, in 2D, all the triangles and edges incident to v form star(v). Notice, however, that the edges and vertices disjoint from v – but still part of the triangles incident to v – are not contained in star(v). From a point-set topology point of view, star(v) is the interior of P. Also, observe that the vertex v itself is part of star(v), and that a simplex can be part of a star(v), but not some of its facets.

Figure 3. The star and the link of a vertex v in 2D (a) and 3D (b).

The boundary of P is defined as the link of v. It is formed by the set of simplices incident to the d-simplices forming star(v), but “left out” by star(v). For example, if v is a vertex in a 2D triangulation, link(v) is formed by the vertices and edges that are incident to the triangles incident to v. In 2D it is a polyline, and in a tetrahedralization, link(v) is a 2D triangulation formed by the vertices, edges, and triangular faces that are contained by the tetrahedra of star(v), but are disjoint from v. In a d-dimensional triangulation, the link of a given vertex is a (d−1) triangulation.

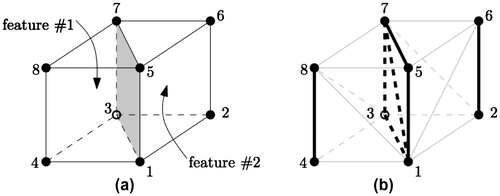
The closely related concepts of star and link also apply to edges in 3D: in Figure 4 star(ab) is formed by all the incident simplices (six in this case), and link(ab) is a 1D triangulation.

Figure 4. The link of the edge ab in 3D is formed by the bold dashed polyline cde f ghc.

3. A star-based data structure

To our knowledge, Cline and Renka (21) are the first to design a data structure where stars of vertices are used to represent a triangulation, albeit in 2D. Their structure is compact, but does not allow incremental updates (which is arguably important for a GIS data model). Schewchuk (22) uses a star-based data structure to manipulate 3D triangulations, but his structure is very verbose since the star of every vertex is stored as a 2D triangulation, itself stored with stars. Blandford et al. (14) fix both issues with their structure, which is valid for 2D and 3D triangulations. Their representation indeed uses about a factor 3 less memory than traditional representations in 3D and at the same time can be queried and dynamically modified. To achieve this compression, they designed a pointer-less structure where each vertex is assigned a label (an integer) and they compress based on labels: if possible they store the integers using four bits (they use differences between the labels to achieve that) and use different optimizations to keep the memory footprint low.

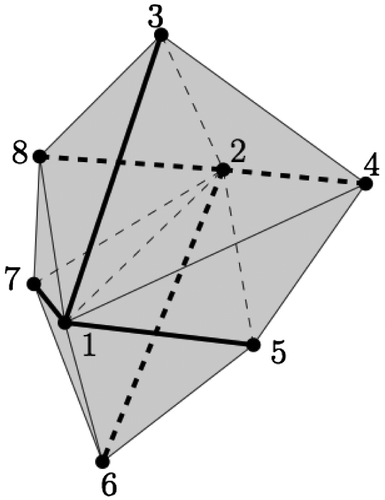
While it would theoretically be possible to implement the compression in a DBMS, we are interested in their basic idea of using labels for vertices and storing the stars of edges in 3D. In a nutshell, a star-based data structure for a tetrahedralization in a DBMS is as follows. First, each vertex is given a label. For an edge ab of the tetrahedralization, we store its link as an ordered list of labels. The orientation of all the edges must be the same; we use in this paper the right-hand rule: if the thumb points from a to b, the vertices of link(ab) are ordered in the direction of the curled fingers of the right hand. In Figure 4, link(ab) is the ordered list [c, d, e, f, g, h, c]; notice that this is a circular list and that the starting vertex could be any vertex. The link list is of variable length: its minimum is two (one tetrahedron) and its theoretical maximum is the number of vertices in the tetrahedralization minus two. A tetrahedron is formed by ab and two consecutive vertices in the list; abcd and abhc are two examples of tetrahedra implicitly represented in link(ab). Notice that the length of the list gives the number of incident tetrahedra to ab. Also, lower dimensionality simplices (triangles and edges) are implicitly represented in links: for instance, referring to Figure 4, the triangle abc is present in the links of its three edges. Since the link is an ordered list, the simplices implicitly represented are also ordered.

The key idea behind the structure is that if we represent the link of each edge then we obtain a data structure where relationships such as incidence and adjacency between tetrahedra and their lower dimensionality simplices are present. It is the overlap between the (ordered) links that permits us to represent explicitly that information. Observe that each tetrahedron is represented in the link of its six edges, and that since these are ordered, we can easily navigate from tetrahedron to tetrahedron. We demonstrate in Section 4.3 queries that can be efficiently answered with such a data structure.

3.1. Representative edges

Storing the link for each edge of a tetrahedralization yields a powerful and topological data structure, but also one that is not space efficient. Indeed, if the CT of a set S of n points contains t tetrahedra, then the number e of edges is significantly higher: Blandford et al. (14) estimate it at (7/6)t for a CT where the points are uniformly distributed in space. The real-world data-sets of buildings used for the experiments in Section 5 corroborate this. Since, as explained in the Introduction, one of the disadvantages of using tetrahedralizations to model topography is the larger storage requirements, this is clearly not optimal.

To reduce the number of edges whose star is stored, we store only the representative edges (RE), as Blandford et al. (14) suggest. If the label given to each vertex is an integer, an RE is one where its two vertex labels are either odd or even. If we randomly label the vertices, which should reduce by a factor of about 2 the number of edges to be stored and still permits us to represent at least once each triangle and each tetrahedron (which is fundamental to ensure that all topological relationships are present). Indeed, it ensures that each triangle has at least one RE: a triangle has either three REs (three odd or three even labels) or one RE (one odd/two even; two odd/one even).

Figure 5 shows the same six tetrahedra as in Figure 4, and the REs are in bold. It can be seen that out of the 19 edges, six are representative, and that each triangle, and each tetrahedron, contains at least one RE.

Figure 5. A set of eight vertices yields a tetrahedralization with six tetrahedra. Out of the total 19 edges the six REs are stored (and shown in bold): <1, 3>,<1, 5>,<1, 7>,<2, 4>,<2, 6>,<2, 8>.

3.2. Storage space

Evaluating the theoretical storage space for a given data-set is difficult since the number of tetrahedra in a CT depends on the locations of the points and the constraints (16). However, to obtain an order of magnitude, we can state that we need on average 3 labels per tetrahedron. Indeed, each tetrahedron has four triangles, which are shared by two tetrahedra (if we ignore those on the convex hull); thus two triangles per tetrahedron. A triangle has three labels, but since it appears in three stars and that only half of the edges are represented, we obtain . Thus, labels per tetrahedron. Our experiments with real-world data-sets corroborate that, see Section 5.

3.3. Attributes and constraints

Attaching attributes to the tetrahedra is possible, although one must be careful since tetrahedra are present in multiple stars and only implicitly. As Blandford et al. (14) suggest, we exploit the fact that each vertex has a unique label (which can be ordered) and attach the attributes to the star of the REs whose origin is the lowest; in case there are more than one, the one having the lowest destination is chosen. For example, an attribute for the tetrahedron abcd is stored in the star of the RE ab. Given a tetrahedron abcd, we can find out in constant time which RE stores its attributes. Each attribute is stored in its own list having the same length as the list of the star. Table 1 shows one example for a specific data-set, and a concrete example is given in Section 4.3.

Table 1. The three tables for the data-set shown in Figure 8.

(a) Vertex table				(b) RE table				(c) Feature table
ID	x	y	z	Start	End	Link [ ]	Attribute [ ]	ID	Owner	Tetra [ ]
1	0.0	0.0	0.0	1	3	[−1, 4, 8, 7, 2]	[−1, 1, 1, 2, −1]	1	‘John Smith’	[1, 3, 4, 8]
2	1.0	0.0	0.0	1	5	[−1, 6, 7, 8]	[−1, 2, 1, −1]	2	‘Bob Brown’	[1, 5, 6, 7]
3	1.0	1.0	0.0	1	7	[6, 2, 3, 8, 5]	[2, −1, −1, −1, −1]
4	0.0	1.0	0.0	2	6	[−1, 7, 1]	[ ]
5	0.0	0.0	1.0	3	7	[−1, 8, 1, 2]	[ ]
6	1.0	0.0	1.0	4	8	[−1, 1, 3]	[ ]
7	1.0	1.0	1.0	5	7	[−1, 6, 1, 8]	[ ]
8	0.0	1.0	1.0

In the context of modeling 3D city models, an example of an attribute would be the ID (or name) of the building inside which a tetrahedron lies. If we store this ID for each tetrahedron (and assign also an ID for the “air” tetrahedra), then we can also explicitly represent the original constraints in the data-set: they are formed by the triangles whose incident tetrahedra have different IDs.

3.4. Spatial indexing: using the tetrahedralization itself

An advantage of a star-based structure – or of any structure in which adjacency and incidence relationships are stored – is that a spatial index, such as an R-tree (12) is not necessary to access efficiently the tetrahedra. Instead, the tetrahedralization itself can be used to determine which tetrahedron contains a query point q: the adjacency relationships between the tetrahedra are used to navigate in the tetrahedralization. The latter can be implemented with the walking algorithm as described in Mücke et al. (23). It is a sub-optimal algorithm that is favored by practitioners since it does not require an auxiliary data structure and yields fast practical performances (23, 24).

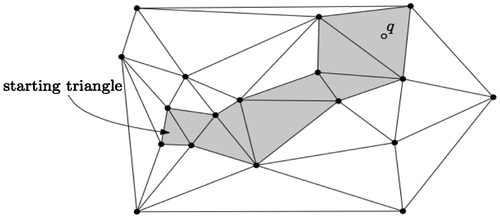
The idea is as follows: starting from a given tetrahedron σ, we move to one of the neighbors of σ (we choose one neighbor such that the query point q and σ are on each side of the triangular face shared by σ and its neighbor) until there is no such neighbor, then the tetrahedron containing q is σ. In Figure 6, only the grey triangles are visited during the walk.

Figure 6. Walking in a 2D triangulation, starting from a given triangle to the query point q. In 3D, the principle is the same: the walk is performed from tetrahedron to tetrahedron.

To minimize the number of tetrahedra visited, the starting tetrahedron should be close to q. Mücke et al. (23) investigated a “bucketing” approach where a certain number of triangles are randomly selected, and each walk starts from the closest one (selected by a simple Euclidean distance test); it is called the jump-and-walk method. The result of a query can be either a tetrahedron, or one RE in that tetrahedron. Modifying this algorithm to start from a RE is trivial.

4. Implementation in a DBMS

This section describes a prototype implementation of the star-based data structure in a specific object-relational DBMS (PostgreSQL), but since the data structure is based solely on lists of labels, implementing it in another DBMS is straightforward. Several engineering decisions were taken while implementing the structure in PostgreSQL, and we report here on the main ones.

4.1. Data model

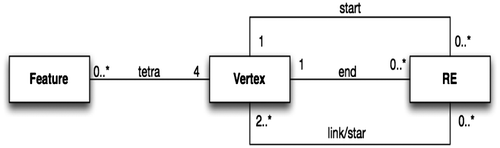
Figure 7 shows the UML class diagram for the data structure. The tetrahedralization itself is represented with two classes: one for the vertices and one for the REs. The third class is used to represent features in a data-set, e.g. solids such as buildings.

Figure 7. The UML diagram of the data model for our star-based data structure.

Each vertex has a location with 3D coordinates. An RE has a start and an end vertex, and a link (which is an array of vertices). The relationship “tetra” between the classes “Feature” and “RE” represents one tetrahedron (four vertices) located inside a feature: it permits us to efficiently locate one RE for a tetrahedron inside the feature without performing a global search.

4.2. PostgreSQL tables

These three classes are straightforward to implement in a DBMS supporting an array type of variable length such as PostgreSQL. An example of the tables filled with data, for the two features shown in Figure 8, is shown in Table 1. In our implementation, we define an ID for each Vertex and it is the primary key (which creates a B-tree index on the column). This ensures efficient access and enforces uniqueness. The primary key of the table RE is defined as the concatenation of the columns “start” and “end”. It should be noticed that these two columns could be merged into one column, but that would require using a data type twice as large (64-bit integers for instance) and would not permit us to compress the storage. Table 1 also shows how attributes are stored in the “RE” table.

Figure 8. (a) Two adjacent 3D features (both triangular prisms) sharing a surface (in grey). (b) The two features tetrahedralized with the seven REs in bold black.

Also, to be able to represent triangles and tetrahedra two custom types have been defined. Both types are a sequence of vertex IDs, where triangles are represented by three vertex IDs and tetrahedra by four. Based on these custom types, a view can be defined that “glues” the geometry of the vertices and edges together to triangles and tetrahedra (performed by a database join).

4.3. Examples of topological queries

We describe in the following how a few typical queries are answered with a star-based structure. All the queries refer to the example in Figure 8 and the resulting tables in PostgreSQL (Table 1).

Observe that out of the 19 edges in the tetrahedralization, seven are REs. In Table 1, in the link column of the RE table the ID “−1” is used for links that do not form a cycle, i.e. the edge is on the boundary of the convex hull of the data-set.

Observe also that the array of the column attribute is filled only for some tetrahedra: as explained in Section 3.3, for a given tetrahedron, we attach an attribute to it in the RE whose origin is the lowest. If a given RE is one such RE for a tetrahedron, then an array of the same length as that of the link column is used and “−1” is used when the tetrahedron’s attribute is stored in another RE. If an RE is not used to store the attributes of any tetrahedra (i.e. the attributes of the incident tetrahedra to the RE are stored in other REs), then the array can be empty to save storage space. The last four rows in the Table 1(b) have an empty array.

Since triangles and tetrahedra can be present multiple times in the structure, querying the structure has to be done with care. For example, tetrahedron [1, 5, 6, 7] is present in the edge table in the links of all its REs: [1, 5], [1, 7], and [5, 7].

Is the tetrahedron [1, 2, 6, 7] present? First, one RE has to be found: [1, 7] is one of them. Observe that an RE is found in constant time only by finding locally two odd or even IDs in the tetrahedron. Second, the IDs 2 and 6 have to appear consecutively (not necessarily in that order) in the link of that RE. It is the case, thus the tetrahedron is present.

What attribute has tetrahedron [1, 2, 6, 7]? First, make sure the tetrahedron exists, as above. In the attribute[ ] column of its RE ([1, 7]), find the first instance of either 6 or 2: first position in the link. The attribute (value is 2) is at the same position in the attribute list.

Which tetrahedra are adjacent to [6, 7, 1, 5]? First, find one RE, as above ([1, 5]) and find the position of vertices 6 and 7 in the link. The vertices before and after the tuple give two adjacent tetrahedra: [1, 5, 0, 6] and [1, 5, 7, 8]; the former does not exist since 0 is in the link. Second, find another RE ([1, 7]) and repeat the same operations in its link: tetrahedra [1, 7, 8, 5] and [1, 7, 6, 2] are found, the former having been previously identified. Since we know that each triangle is represented in at least one RE, this operation will always return the four tetrahedra, unless the tetrahedron is on the boundary of the convex hull. Notice that this is also a mechanism to identify which triangles are on the boundary of the convex hull (triangles [5, 6, 7] and [6, 5, 1] in this case).

Total number of tetrahedra? Here, we apply the same criteria as for storing attributes in Section 3.3: the lowest concatenation of the IDs is the one representing the tetrahedron. For instance, tetrahedron [7, 8, 1, 5] is conceptually stored in edge [1, 5] and not [1, 7]. Thus, it suffices to scan the RE table and take a local decision to extract tetrahedra: six tetrahedra are present in Figure 8.

Volume of a given feature? From the Feature table we obtain a tetrahedron inside the feature; let us find the volume of the feature 1 in Table 1. First find an RE for the tetrahedron [1, 3, 4, 8] ([1, 3]) and identify the adjacent tetrahedra. If these tetrahedra also have the same attribute (same as above), then add them to the list of tetrahedra. Repeat this step for all the found tetrahedra, and sum the volume of the tetrahedra.

Are features #1 and #2 adjacent? As in the case of finding the volume of a feature, we need to visit all the tetrahedra inside the feature 1 and test if one of their adjacent tetrahedra has the attribute 2. For the feature 1 in Table 1, we would first find the RE [1, 3] and the tetrahedron [1, 3, 8, 7]. From this tetrahedron, we repeat the same operation and find [1, 3, 7, 2], which has the attribute 2 in the list. Features 1 and 2 are thus adjacent.

5. Experiments with real-world data

To test the star-based data structure in PostgreSQL/PostGIS, we have made experiments with three real-world data-sets containing 3D buildings. These were all obtained by extruding the 2D footprints to their height (which was obtained by averaging the height of the LiDAR samples inside a footprint). To be able to tetrahedralize the resulting 3D data-sets, the surfaces of the buildings should be unique, i.e. if two buildings are adjacent, their shared wall should be present only once. We have created such a topologically consistent data-set with the methodology described by Ledoux and Meijers (25). In a nutshell, it consists of ensuring that the 2D footprints are topologically consistent (i.e. no two footprints overlap and the graph of the footprint is a planar graph), and extrude each edge to a vertical wall.

We have constructed the constrained tetrahedralization of the models with TetGen² (26). For populating the DBMS, we have created a program that takes as input the result of the tetrahedralization (a list of vertices and tetrahedra) and outputs a list of REs and their links.

5.1. Data-sets used

The three data-sets, shown in Figure 9, are areas in the Netherlands: “campus” is the campus of the Delft University of Technology; “kvz” is an area of Rotterdam; “engelen” an area of the municipality of Den Bosch. Table 2 gives the details of the 3D extruded data-sets, and the results of the construction of the tetrahedralization. It should be noticed here that we tried to minimize the number of Steiner points when tetrahedralizing the data-sets; as it can be seen this was very satisfactory as only one point needed to be inserted for the data-set “campus”, and none for the other two. The cuboid shape of the buildings explains this.

Figure 9. Part of the footprints of the data-sets (a) campus, (b) kvz, and (c) engelen. In (d) a view on the kvz data-set tetrahedralized; notice that the ‘air’ tetrahedra are not shown.

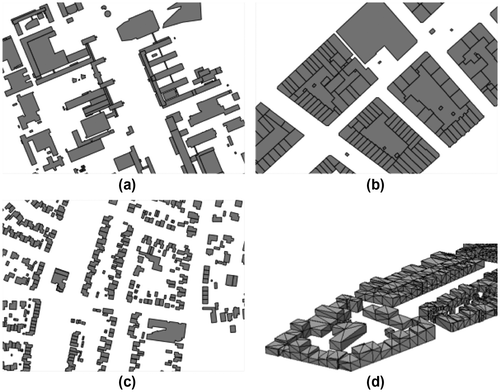
Table 2. Details concerning the data-sets used for the experiments.

3D model			Input		CDT
Area	Solids	Faces	Vertices	Constraints	Vertices	Edges	Tets
campus	370	4298	5970	3976	5971	36,790	28,024
kvz	637	6549	8951	13,571	8951	59,332	50,376
engelen	1629	15,870	23,732	15,868	23,732	145,296	110,232

5.2. Comparisons with alternatives

For each data-set, we have created three databases in PostgreSQL 9.2.2/PostGIS 2.0.2:

b-rep: each building is stored as a 3D primitive, the type POLYHEDRALSURFACE was used, which is a boundary representation. The original surfaces of a building were used, no triangulation was performed. A 3D R-tree index was used to index each building.

tetrahedra: each tetrahedron was stored as a POLYHEDRALSURFACE, which is conceptually similar to what Penninga and van Oosterom (10) propose. They originally propose to concatenate the four xyz coordinates of the four vertices. This is not possible without creating a totally new data type. We have instead opted to use a POLYHEDRALSURFACE for each tetrahedron – more storage is used since this is a generic type and the ordering of the vertices cannot be inferred. We estimate that the storage penalty is around a factor 3 since each vertex is stored in three surfaces. As is the case for the buildings, a 3D index was used to index each tetrahedron. Notice that we could not test the other approach of Penninga and van Oosterom (10) (where a tetrahedron is formed by the concatenation of four IDs, and another table with vertices is used for the coordinates), since it is not possible to spatially index the table of tetrahedra. A join between the two tables should first be performed, and then this table can be indexed; that would increase significantly the size and duplicate the information.

our star-based structure: as was described in Section 4.

It should be noticed that for the experiments we do not consider the features, we focus only on the tetrahedra. The first observation is that for a given data-set with n solids, the CT of the data-set contains several tetrahedra: in our experiments, this number is around 75 times more. If every tetrahedron is stored individually, a direct consequence is that the table will have several more rows, and more importantly, the R-tree will be significantly bigger and more complex to update.

Table 3 presents the details of our star-based data structure for the three data-sets. Notice that around half of the edges of the CT are stored as RE, as theory states. In our experiments, the number of REs is around 60% of that of the number of tetrahedra. This is inline with what theory states for a tetrahedralization in which the points are uniformly distributed in space: (7/6)t (where t is the number of tetrahedra), and only half of the edges are REs. This is therefore expected for most data-sets. It should be noticed here that this translates into less rows in a table to store the tetrahedra, but also into a leaner index to build and maintain.

Table 3. Details of the stars.

Link
Area	REs	Avg	Max	Min	Sum	ID/tet
campus	16,004	4.79	27	3	76,693	2.73
kvz	28,763	5.04	35	3	145,158	2.88
engelen	71,841	4.98	23	3	357,984	3.25

Table 3 also shows the details of the links of the REs. The average number of IDs stored in a link is about 5, its maximum is 35 for one data-set, and its minimum is 3 (an edge on the boundary of the convex hull). The column “sum” is the sum of all the IDs in all the links. As described in Section 3.2, the number of IDs used for one tetrahedron is in theory 3 – we obtain similar results with real-world data-sets.

This number is however higher in practice in a DBMS since we must also assign IDs to the REs (“start” and “end” attributes), but is nonetheless of the same magnitude as Penninga and van Oosterom (10). As an example, for the kvz data-set we need to have (28,763 × 2) IDs for the REs, plus 145,158 IDs in the links; the total is thus 202,684 IDs. If the second approach of Penninga and van Oosterom (10) was used to store the tetrahedra (where IDs of vertices are used), then each tetrahedron would need exactly 4 IDs: 50,376 × 4 = 201,504 IDs.

Table 4 shows the size of the tables and the indices in PostgreSQL/PostGIS for the three data-sets; for the star-based structure both tables are shown, and the index used is a B-tree for both. The total size of the tables for the star-based structure is around four times that of the b-rep structure, but around eight times less than with the tetrahedra structure. The former was expected since far less objects/solids are stored with the b-rep, and the connections between nonadjacent buildings (the “air” tetrahedra) are not stored. The latter is explained by the fact that Penninga and van Oosterom (10) cannot be stored with generic types; even if the storage was reduced by a factor 3, the size of the tetrahedra structure would still be larger. Furthermore, the size of the indices for the star-based structure is around six times less than that of the R-tree for the tetrahedra structure. In fact, both tables and both indices for the star-based structure take around 33% less storage space than the R-tree index alone for the tetrahedra structure.

Table 4. Size of the PostgreSQL/PostGIS tables.

b-rep			Tetrahedra		Star-based
Area	Table (kB)	Index (kB)	Table (MB)	Index (kB)	Vertex (kB)	Index (kB)	RE (kB)	Index (kB)
campus	424	320	15	3440	408	152	1408	368
kvz	768	224	26	5072	600	216	2560	648
engelen	1936	304	57	12,000	1584	536	6360	1592

The size of the tables of the b-rep option is obviously smaller than that of the star-based structure, but it should be noticed that we are comparing apples to oranges here, especially since, as the number of solids grow in a data-set, the number of tetrahedra will grow even more (depending on the complexity and distribution of the points). A star-based structure permits us to represent more than simply the features: their adjacency and even their connection are encoded in the tetrahedralization, which is useful for several applications. Topological queries are much faster answered as no comparison of coordinates need to be performed, and it is for instance possible to query for features that are neighbors, but do not touch.

6. Discussion and future work

We have shown that a star-based data structure implemented in a DBMS can be both compact and topological at the same time, two criteria that are usually contradictory. Our structure is in theory as compact as the most compact structure implemented in a DBMS so far (that of Penninga and van Oosterom (10)), but if we consider that spatial indexing is needed then our structure is several times compacter. While storage space in a DBMS is not the most important factor, having smaller tables (in terms of rows) with leaner indices means faster updating and maintenance when a data-set is modified. As 3D data-sets become more available and grow in size, this is becoming more important.

Another strong point of the star-based structure is that it can be easily implemented in any DBMS supporting variable length arrays with two simple tables, and that no complex spatial index is needed. While the structure seems more cumbersome to maintain when the data are updated, the users need not be aware that this is the structure used. We plan to add functionalities to the DBMS so that views can be created over the edges and stars, so that only features (e.g. buildings) are shown to the user, which is what van Oosterom et al. (27) advocate for storing 3D GIS data-sets in a DBMS. We have plans to make the data structure fully dynamic, i.e. supporting insertions and deletionss of tetrahedra and of features, updating the already stored tetrahedra in the database.

Object relational DBMS systems keep evolving and new powerful features have been added to mainstream systems. One example is Common Table Expressions (SQL-99) which paves the way to deal with more complex data structures like trees and graph storage inside such systems natively. We intend to see how far these features are useful during implementation of the query part of our data structure and how much custom procedural functionality still needs to be built.

Apart from 3D topography, 3D models can also be useful for modeling space and map scale in one integrated 3D data structure, e.g. van Oosterom and Meijers (28). Hence, one operation we want to investigate in more detail is to create a cross-section through the stored 3D model: selecting intersecting tetrahedra, performing intersection and then create a topologically clean output of the intersected elements to see whether this tetrahedra-based model can be useful underlying technology for producing vario-scale data.

Notes on contributors

Hugo Ledoux is an assistant professor in GIS at the Delft University of Technology in the Netherlands. His research focuses on topological data structures, the development of algorithms for three-dimensional modeling, and the use of Voronoi diagram for environmental modeling.

Martijn Meijers is a postdoctoral researcher at the same university. His research interests include geo-database management systems, map generalization, cartography and geo-visualization, (applied) computational geometry for GIS, handling large data-sets, and topological consistency.

Acknowledgments

This research is supported by the Dutch Technology Foundation STW, which is part of the Netherlands Organization for Scientific Research (NWO), and which is partly funded by the Ministry of Economic Affairs (project codes: 11300 and 11185).

Notes

1. Notice that this model is often called “TEN”, which stands for either TEtrahedral Network, TEtrahedral irregular Network, TEtrahedronized irregular Network, or TEtrahedron Network, depending on the authors. For the purpose of this paper, they are all equivalent and a TEN is a tetrahedralization, as defined in Section 2.

2. http://www.tetgen.org.