Tessellations in GIS: Part II–making changes

Abstract

We attempt to describe the role of tessellated models of space within the discipline of Geographic Information Systems (GIS) – a speciality coming largely out of Geography and Land Surveying, where there was a strong need to represent information about the land’s surface within a computer system rather than on the original paper maps. We look at some of the basic operations in GIS, including dynamic and kinetic applications. We examine issues of topology and data structures, and produced a tessellation model that may be widely applied both to traditional “object” and “field” data types. The Part I of this study examined object and field spatial models, the Voronoi extension of objects, and the graphs that express the resulting adjacencies. The required data structures were also briefly described, along with 2D and 3D structures and hierarchical indexing. The importance of graph duality was emphasized. Here, this second paper builds on the structures described in the first, and examines how these may be modified: change may often be associated with either viewpoint or time. Incremental algorithms permit additional point insertion, and applications involving the addition of skeleton points, for map scanning, contour enrichment or watershed delineation and simulation. Dynamic algorithms permit skeleton smoothing, and higher order Voronoi diagram applications, including Sibson interpolation. Kinetic algorithms allow collision detection applications, free-Lagrange flow modeling, and pen movement simulation for map drawing. If desired these methods may be extended to 3D. Based on this framework, it can be argued that tessellation models are fundamental to our understanding and processing of geographical space, and provide a coherent framework for understanding the “space” in which we exist.

Keywords:

• GIS
• tessellation model
• dynamic structure
• topology
• data structure
• object and field
• Voronoi diagram
• kinetic algorithm

1. Introduction

The first paper of this study completed our exploration of static tessellations for geographic information systems (GIS) (Gold 2016). However, few things remain unchanged, whether due to editing or real-world changes. In this paper we discuss various types of “Change” in a map, and look at a variety of algorithms and applications: incremental methods, where items are added one at a time; dynamic algorithms, where deletion is possible without having to rebuild the whole graph data structure; and kinetic algorithms, intended to handle topological changes induced by point movement in the real or simulated exterior world. Some of the most interesting applications here involve collision detection problems, e.g. for shipping, and map-drawing algorithms, where the moving point represents the pen that is drawing cartographic objects such as roads and buildings. Here the lower dimensional entities (points or lines) are embedded in the higher (2D) map space – but their spatial extensions provide a tessellated model with many useful properties based on their adjacency structure.

Based on this framework, it can be argued that tessellation models are fundamental to our understanding and processing of geographical space, and provide a coherent framework for understanding the “space” in which we exist.

2. Change

A growing concern in GIS is the management not of static map displays but also of changes to them. Traditionally, for example in forest maps, these were redrawn every few years to indicate the changes – giving several “snapshots” of the changing situation. “Dynamic mapping” now suggests that the observer can see changes happen to the map. This requires considerable thought: while adding or removing points in simulated real-time is straightforward, this becomes more complicated for topologically connected entities.

By “Dynamic”, we are referring to some kind of change (usually over time). Examples include interaction, editing, viewpoint change, and modification of the data structure. One form of dynamism is based on the act of changing the viewpoint, selecting an object, querying it and viewing or changing its attributes. A more fundamental form consists of modifying the spatial properties of entities in the map space. This could consist of manual editing involving the insertion, deletion or movement of an entity; it could also consist of the automatic update of the data structure because of geometric changes or for simulation of geographic processes.

The word dynamic can have many meanings in GIS. The simplest use of dynamic might be the case of dynamically generated maps, for example on a web site or a GPS-based navigation system. Here the issue is to receive the request and compile the map from standard objects and layers as quickly as possible. A relatively easy extension of this issue is to add the locations of moving vehicles, for example, as points on this map – e.g. for fleet monitoring and delivery services. (Note that there is often no interaction of these vehicles with the map itself – their locations are merely plotted. However, for GPS-based navigation there is often some form of road-following algorithm involved.)

A somewhat more advanced approach assigns ranges of temporal existence to these entities and permits queries about snapshots in time (Langran 1992; Marchand, Bédard, and Brisebois 2005). Essentially, this is a database approach, where the objects retrieved by the temporal query are displayed on the map.

Where the map objects themselves change over time, traditional GIS is frequently used to produce snapshots of attribute values at some particular date, usually for polygon maps and raster images (Albrecht 2007). Various map-matching techniques are then used to examine the differences. Note that this is usually done for field-type data, where attribute values exist throughout the map area. In the case of polygon maps, the boundaries usually remain unchanged between snapshots – if this is not the case, then the problem becomes more difficult. Dynamic fields, such as temperature, are usually managed as sequences of snapshots, using raster images. These images can be compared using traditional image analysis techniques. Typical questions are concerned with the values, changes and history of attributes at specific locations.

When we consider discrete map objects, as opposed to fields, the appropriate techniques are related to database management methods, tracking the existence of individual objects over time, or perhaps the coexistence of two or more. If an object’s status changes, then an event has taken place, which may also be treated as a database entity.

When objects are elastic, their boundaries may change, as for clouds or forest fires, and the usual approach is to process them as fields – e.g. using image analysis. However, in this case the object itself is not the primary entity, but becomes an attribute attached to particular pixels. The same situation holds if the object as a whole moves – as in the case of clouds. Definitions here can become difficult if clouds split or merge: how are individual objects defined? What happens if there are internal variations, such as fire temperature? Treating the whole map as a field or image is often the most practical, but the object definition is lost.

Currently it appears that the primary problems occur with questions of spatial object proximity, both static and dynamic, where objects exist as defined entities with their spatial location as a fundamental part of their definition – they lose their meaning if they have no position. However, spatial proximity or adjacency is not easy to define, or to maintain under object movement.

3. Time

3.1. Change of viewpoint

Our primary emphases so far are the issues of interaction and visualization. These are intimately linked to change in data structures. In 2D we may often want to edit our map or spatial representation, which requires a vertical view at the appropriate location and scale, as well as tools to edit the objects and, if necessary, the topology. In 3D the change in view is more complex, involving perspective transformations and the ability of the observer to navigate within the simulated world. This must involve an intuitive interface, as poor interfaces (especially for spatial movement) often disorient the user, rendering the system useless. Changing or editing the data requires an effective set of graphics tools to allow easy “picking” of the appropriate map elements within the 3D display, as well as allowing modification of the spatial data structure. (It is rare that a 3D model consists entirely of discrete objects.) Game technology is a basic resource for scene visualization and navigation, but it rarely permits all but the most basic editing or scene modification – usually by blowing the object up!

3.2. Change as simulation

If we intend to model change with time, then we are starting to look at aspects of “simulation” that are not necessarily a data structure problem. By “simulation” here we may mean modeling the change over time of our attributes (e.g. within a population density map organized as polygons), change over time of the spatial location of our objects (e.g. marine navigation) or change over time of our connectivity (topology) (e.g. the movement of a foam of bubbles). By “simulation” we may initially mean entering the changes by hand on a paper map (e.g. population after each census), followed by computer automation of the procedure (and of the visualization), or full simulation by defining some mathematical function that attempts to describe the behavior of the process, and letting this drive the previously described automation.

It should be noted here that “change” does not necessarily mean attribute change over time (dz/dt) – it could also mean attribute change over space (dz/dx), spatial change over time (dx/dt) or even their inverses. Examples of these include forest growth within stands (dz/dt), height change over the landscape (dz/dx) and polygon boundary migration over time (dx/dt). These changes may be continuous (as in a smooth landscape or steady forest growth) or discrete (as in a cliff, a forest fire or a manual map update). For details see Gold (1996). All of these types of change are forms of simulation (and this idea classifies terrain surface interpolation as simulation of attribute change with changing location – which is reasonable).

“Managing change” can therefore be applied to many problems. The simplest in concept is map updating: read a “log file” ordered by date, and insert or remove the features that have changed. The log file can be read from the beginning to any specified date, giving a map for that time. This usually requires local topological update, although simulation of attribute change, such as population, is straightforward.

Movement of topologically connected objects, such as Voronoi cells around moving objects in a collision-avoidance system, requires a dynamic topology maintenance system, not a static one. A good illustration of the two is to compare Eulerian and Lagrangian fluid flow modeling. In Eulerian simulation, a network of cells (usually a regular grid or Voronoi cell structure) is initially constructed, and flow is assumed to be a transfer of fluid between adjacent cells, as in Figure 1, which illustrates runoff modeling. In Lagrangian simulation each node is assumed to be a fixed mass of the fluid, and their interaction produces movement of the nodes. In free-Lagrangian simulation the topology is capable of being updated as the nodes move – often by using dynamic Voronoi data structures (Mostafavi and Gold 2004). These methods may be implemented in 2D or 3D. The fundamental kinetic operation is node movement, with associated update of the data structure. Applications include navigation and collision avoidance, fluid flow, robotic exploration of the environment and interactive construction of the 2D line-segment Voronoi diagram (VD) or constrained Delaunay triangulation (DT).

Figure 1. IFD flow modeling.

3.3. Managing change

We can now examine our mapping (and tessellations) from a temporal point of view. The simplest case is a static map – either where nothing changes, or where only the viewpoint changes (pan and zoom in 2D, or fly-throughs in terrain or city models). Alternatively, the map structure remains unchanged, but attributes vary – as in the previous surface runoff simulation, or slide-shows illustrating population change. Algorithms may be for batch processes, where intermediate results are not available until construction is finished, or for incremental ones where objects are added one at a time. (Batch processes are often faster, but incremental ones are often easier and more robust.) A useful example is DT construction, where Fortune’s (1987) algorithm is faster, but where the incremental algorithm (Guibas and Stolfi 1985), with one point inserted at a time, is frequently used.

Algorithms are called dynamic not, as is frequently supposed, because they model dynamic actions in the real world, but because the related data structures may be updated locally, without the need to rebuild everything for each change. In many cases this simply requires object or point deletion methods, as well as the previous incremental insertion ones. Kinetic algorithms allow the related data structures to be preserved during object movement – where full topology (e.g. tessellations) are present this still remains a challenging job. We will summarize algorithms and applications based on whether they are static (incremental), dynamic, or kinetic.

The incremental algorithm (Guibas and Stolfi 1985) starts with a bounding triangle and inserts one data point at a time. In the first step the current triangulation is searched for the triangle enclosing the point, using the CCW test, which is then split in three. Each new triangle is then checked with the Incircle test to see if its circumcircle is empty – if not the appropriate edge is flipped, the results put on a stack, and the process repeated until the stack is empty.

The dynamic algorithm consists of the insertion algorithm above plus point deletion, which is more or less the inverse of insertion: flip “ears” of the set of neighbors to the deletion point, until only three are left – then remove the point. See Devillers (1999) and Mostafavi, Gold, and Dakowicz (2003) for details.

The kinematic algorithm examines the locus of the current moving point to determine when it moves into the circumcircle of a neighboring triangle, or out of the circumcircle of an “ear” of the neighbors. At this topological event an edge is flipped. See Roos (1993) and Gold and Dakowicz (2006) for details. As a result the Voronoi/Delaunay structure is always maintained under point movement.

4. Incremental algorithms and applications

Batch algorithms, such as by Fortune (1987), process all input points together. Incremental algorithms process one at a time, and can therefore be used to add subsequent points as needed. We will examine GIS applications for this approach.

4.1. Triangulation: TIN models

Constructing a continuous terrain model from scattered elevation data used to be done by estimating values on a grid by averaging the values of nearby points: a form of interpolation. Today a TIN model (Triangulated Irregular Network) is more common: for simple cases assuming flat triangular plates is sufficient. The DT is used as local data changes are guaranteed to make only local changes to the network.

4.2. Volume estimation

Where total volume estimates of rock (e.g. coal) are needed, the most stable approach is not to attempt to construct upper and lower bounding surfaces, but to assign the estimated thickness at any location to that of the nearest data point. This produces Voronoi prisms, similar to Figure 1 below.

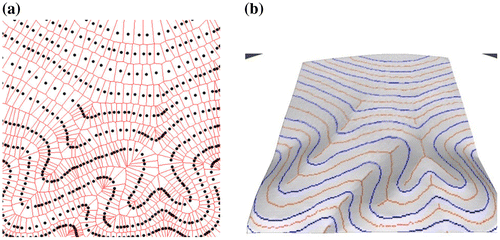
4.3. Runoff modeling

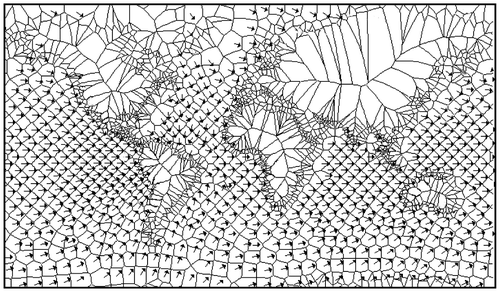
Integrated Finite Difference (IFD) flow modeling simulates flow between adjacent irregular cells that have boundaries perpendicular to the dual edges connecting adjacent elevation values: this is a property of the VD. Figure 1 illustrates a simulation model using random elevation estimates based on the Sibson interpolation method described below. A large rejection radius is used to prevent generators being too close, which would give awkwardly shaped Voronoi cells. (Gold and Dakowicz 2007).

4.4. Geological mapping

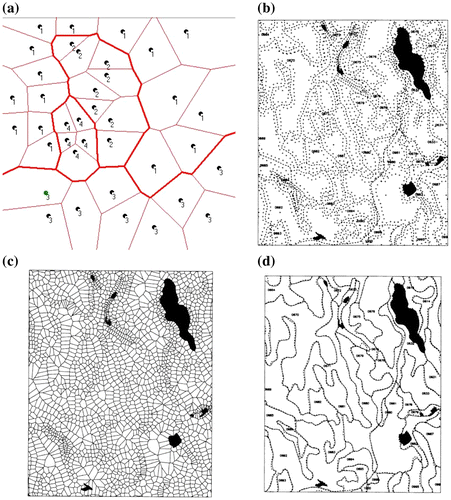
Figure 2a shows the VD of a set of rock outcrops of types 1−4. The heavy boundary separates cells with different labels, and thus gives an approximate geological map. This is termed a “labelled skeleton”.

Figure 2. (a) Skeleton between rock types; (b) Labeled points inside polygons; (c) Voronoi cells; (d) Labeled-point Skeleton.

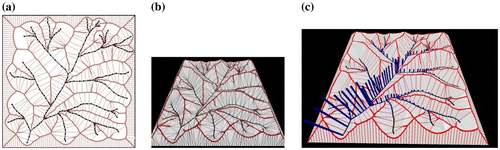
4.5. Rapid digitizing

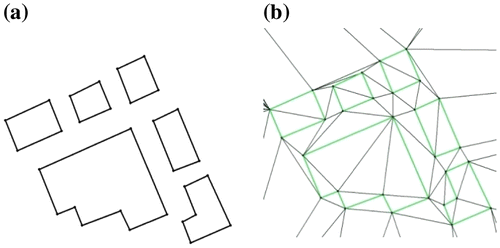
Where it is necessary to construct polygon maps rapidly, e.g. for annual forest mapping, an effective method is to “roll” the digitizing cursor round the interior of each polygon, generating multiple points, each with the polygon label (Figure 2(b)). Generating the VD (Figure 2(c)) and extracting the labeled skeleton (Figure 2(d)) provides a simple topologically connected polygon map (Gold, Nantel, and Yang 1996).

4.6. Crust and skeleton

The labeled skeleton is only effective for closed polygons, and requires digitizing both sides of each boundary. For open networks or scanned polygon boundaries with sufficient point density the “geometric skeleton”, as well as the “crust” of connected boundary points may be extracted from the simple DT/VD (Gold 1999; Gold and Snoeyink 2001). Figure 3(a) shows the DT/VD and Figure 3(b) shows the crust and skeleton obtained by accepting only one part of each Voronoi/Delaunay edge pair. The skeleton is “hairy” due to irregularities in the scanned boundary. Figure 3(c) shows the smoothed results obtained by iterative adjustment of boundary points so that they fall on adjacent circumcircles (Thibault and Gold 2000). Note both the interior and exterior skeletons.

Figure 3. (a) Delaunay plus Voronoi; (b) Crust plus skeleton; (c) Smoothed crust plus skeleton.

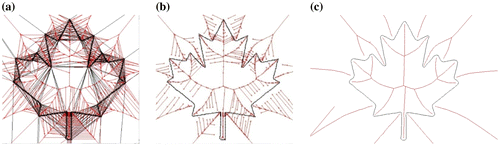
4.7. Text recognition

If the polygons were formed by the boundaries of text characters the generated skeletons form a simplified representation of the character, this can assist in character recognition (Figure 4).

Figure 4. Scanned cadastral map: crust and skeleton.

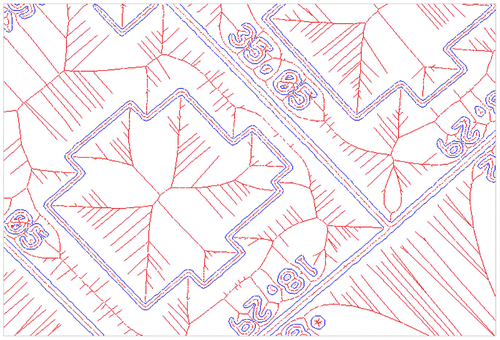
4.8. Scanned maps

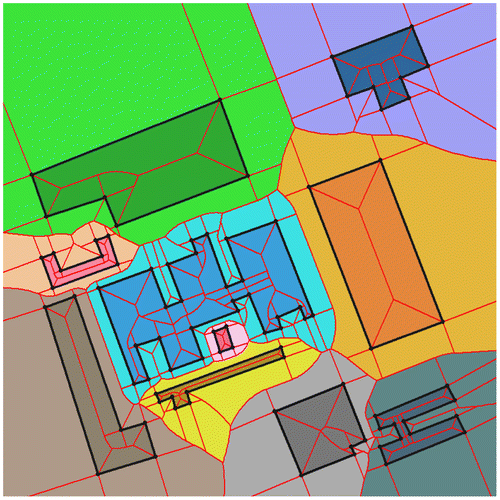
Figure 4 shows a portion of a scanned cadastral map, where image filtering has identified the boundaries between light (background) and dark (text). Generating the skeleton gives a connected topological set of property boundaries, the position of buildings within properties, characters forming labels, the grouping of characters to form labels, and the identification of labels with properties (Gold 1997).

4.9. Contour enhancement

Scanned contour maps (Figure 5(a)) may be used to generate TIN type terrain models, but along ridges and valleys some triangles will be “flat”, with the same elevation at all vertices. Using the ridge and valley portions of the skeleton generates intermediate secondary data points that break up the flat triangles, and their elevations may be estimated by using certain assumptions of constant slope (Dakowicz and Gold 2003). The results (interpolated by Sibson’s method, described below) are shown in Figure 5(b). Koshel (2012) described an algorithm for the topologically correct gridding of contour data, to ensure that the neighboring points used were within the particular contour interval. Vanek, Jezek, and Milkova (2012) gave an overview of terrain reconstruction from contours.

Figure 5. (a) Contour data and Voronoi cells; (b) Interpolated surface with ridges and valleys.

4.10. Watersheds

Figure 6(a) shows the crust and skeleton for a digitized river system, together with the remaining edges of the Voronoi cells, similar to Figure 2(a). Blum (1967) originally defined the skeleton, or “Medial Axis Transform”, and also suggested that the height of a skeleton point could be estimated as equivalent to the radius of the Voronoi vertex forming the skeleton point. Figure 6(b) shows a TIN terrain model with constant 45 degree valley-wall slopes, based on this approach.

Figure 6. (a) Crust, skeleton, Voronoi cells; (b) Terrain from crust and skeleton; (c) Cumulative catchment areas.

Assuming a fixed rainfall throughout the map, the volume of water in each Voronoi cell of Figure 6(a) is proportional to the cell size, and the cumulative sum of these volumes downstream gives an estimate of the total water flow at any river node (Figure 6(c)). This cumulative catchment model provides a first-order approximation of the total flow, based on the drainage network alone. Note that no time-based simulation is involved.

4.11. Building plane recognition

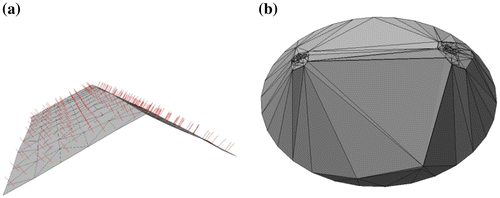
Continuing from the surface model and runoff idea, Tse, Gold, and Kidner (2007) were involved in extracting building models from LiDAR (laser altimetry) data. A major part of this work was to recognize planar roof features. A TIN model was used to obtain the vector normals (Figure 7(a)) and these were plotted on the unit hemisphere with a DT (Figure 7(b)). Clusters of points indicated common slopes, often roof planes, and the Minimum Spanning Tree was obtained directly from the DT. Removing long edges identified clusters that could be identified with roof planes. These planes may then be incorporated in the landscape to assist in runoff estimation.

Figure 7. Clusters of roof vector normals (a) on the unit hemisphere (b).

5. Dynamic algorithms and applications

The number of dynamic algorithms for maintaining GIS data structures is limited, because they are usually based on a line-intersection spatial model, rather than a tessellation. The primary tessellation model that can be used in GIS is the constrained DT (Jones, Bundy, and Ware 1995), which is usually static, in that all vertices are added first to give a simple DT (Chew 1989), and then constrained edges are added to give enforced boundaries . Deletion of these edges is not addressed, and even point deletion in the simple DT is only described in some studies (Devillers 1999; Mostafavi, Gold, and Dakowicz 2003).

We have described dynamic algorithms as those permitting both the insertion and deletion of data points in a VD/DT – we now give some applications.

5.1. Crust and skeleton smoothing

The skeletons produced for some of the earlier examples are very sensitive to perturbations of the boundary points – point misalignment produces narrow triangles along the boundary, with circumcircle centers on the medial axis. A relatively simple first-order adjustment of point position largely eliminates the “hairiness” of the skeleton by deleting and re-inserting boundary points, as in Figure 3(c) (Thibault and Gold 2000).

5.2. Second-order VDs

As the VD of a set of points gives the regions closest to each point, this may be used to find the closest service (e.g. hospital) to any map location. However, if this service is out of order, perhaps in a disaster, the closest service needs to be recalculated. This can be done by deleting the appropriate point in the VD. (More formally, the ordered order-2 VD gives the regions with particular closest and second-closest services – see Okabe et al. 2000). Figure 8(a) illustrates how the removal of point Z indicates the extended regions of the secondary service sites if site Z was out of order.

Figure 8. (a) Area-stealing; (b) Natural neighbors.

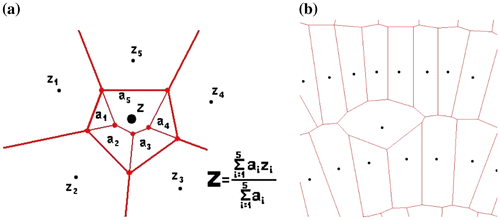
5.3. Sibson interpolation

The same approach may be used as an interpolation method. Traditionally local interpolation (based on a small set of neighboring data points) used some form of inverse distance to weight the contribution of the elevation of each data point. The difficulties with this approach are described in Gold (1989). Sibson interpolation (Sibson 1981) removed many of these problems by inserting a dummy point at the location of interest, then removing it, and calculating the areas of the adjacent Voronoi cells “stolen” by the point insertion (Figure 8(a)). See (Gold 1989). This has proved to be a very convenient approach for many applications: for example where data points are anisotropically distributed around the query point (Figure 8(b)).

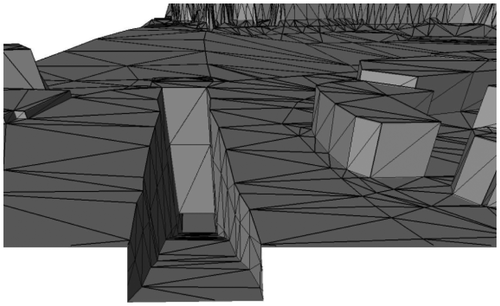
5.4. CAD B-Rep operators and map editing

A surface model may be modified in other ways besides point insertion and deletion. In CAD modeling systems a set of “Euler Operators” are defined that can modify the surface model (often a triangulation) by switching edges as well as inserting or removing points, while guaranteeing surface continuity (Mäntylä 1988; Tse and Gold 2002). This allows the construction of a surface that is not monotonic in X and Y and may have bridges and tunnels (Figure 9). In many cases these operations are called manually, in order to construct the desired model. In a similar fashion ordinary TIN models may be edited manually to produce the desired result – perhaps to remove erroneous data, or to add extra points along river valleys.

Figure 9. Triangulated terrain: CAD modeling.

6. Kinetic algorithms and applications

Many dynamic applications may be performed with these two operations. Examples are: Sibson interpolation (Sibson 1981), map editing, simulation of robot movement by removing the point from one location and placing it in the next, etc. The data structures themselves are also dynamic, being capable of local update. However, for further applications true kinetic properties are required, where it is necessary to know when the topology will change (given the current trajectory of the point), to move there, to update the topology, and to continue. This has been achieved in 2D (Guibas, Mitchell, and Roos 1991; Mostafavi and Gold 2004; Roos 1993) and in 3D (Ledoux 2006; Ledoux, Gold, and Baciu 2005) – when change (movement etc.) destroys these kinetic properties then local updating is required.

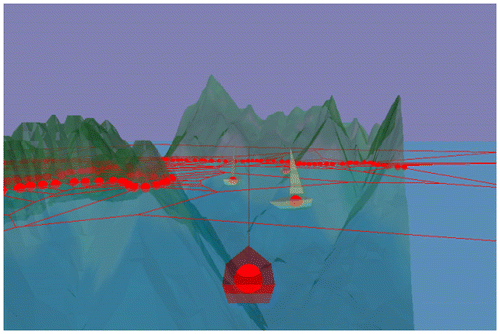
Applications of the kinetic VD include ship navigation (Gold et al. 2004; see Figure 10), free-Lagrange fluid flow simulation (Mostafavi and Gold 2004) and interactive constrained DT and line-segment VDs (Gold 1994; Gold and Dakowicz 2006). Mostafavi, Beni, and Mallet (2009, 2010) used VDs to represent dynamic spatial processes. In 3D we anticipate a variety of applications in oceanographic and atmospheric simulation.

Figure 10. Collision prediction using Voronoi neighbors.

6.1. Collision

With the kinetic VDs a new type of GIS system for maritime navigation safety has been developed. The system takes advantage of the properties of the kinetic VD (which implies that the first possible collision must be with one of the moving point’s Voronoi neighbors) and uses the Quad-Edge data structure for the real-time maintenance of the spatial relationships of ships and other navigational objects (see Figure 10). The locations of ships are updated using a standard onboard automatic identification system transponder, and moving-point Voronoi algorithms. The spatial relationships are used for collision detection and avoidance (Goralski and Gold 2007). The system is aimed at tackling the main cause of marine accidents (human errors) by providing navigational aid and decision support to navigators. Lekkas (2014) looks at various methods for path planning for autonomous vehicles, and Marvell and Bostelman (2014) survey various approaches for evaluating possible collisions.

6.2. Free-Lagrange

Mostafavi and Gold (2004) used the kinetic VD to simulate global tides (Figure 11). Shorelines were marked by double lines of fixed points, and a regular pattern of Voronoi cells were placed throughout the oceans, each representing a fixed volume of water. The Free-Lagrange method (Fritts, Crowley, and Trease 1985) was used to handle the forces on each cell – both from the neighboring cells and from the moon.

Figure 11. Free-Lagrange model of global tides.

6.3. Constrained

Managing the Voronoi structure during point movement has obvious applications in the simulation of real-world processes. However, the same approach may be used for the simulation of the map drawing process itself: the moving point simulates the pen, which leaves a trace of its path behind.

The most obvious example of this is the construction of the “constrained” DT, where certain triangle edges are forced to conform to some cartographic feature, such as a building boundary. The trace of the pen’s path is formed by forbidding the triangle edge connecting the starting point and the pen to be switched, no matter how far the pen moves (Figure 12). See Gold and Dakowicz (2006). Constrained edges/line segments are deleted by reversing the movement of the pen. Ohori, Ledoux, and Meijers (2012) used the constrained DT for the validation and repair of general planar partitions.

Figure 12. (a) Building outlines; (b) Constrained triangulation.

6.4. Line-segment Voronoi

Since line segments are required to define cartographic features, and not just points, the kinetic model allowed the VD/DT to be maintained as the pen point moved through the tessellation. While the dynamic model could be developed with only the CCW and InCircle geometric predicates used in Computational Geometry (Guibas and Stolfi 1985; and Shewchuk 1997), giving a guaranteed robustness, the kinetic model requires additional tests to handle near-degenerate cases, especially point collision.

In either the constrained DT or the line-segment VD, all the update operations used have their inverses, as point movement may expand or contract the trailing line (Mioc et al. 1999). Preserving the topological relationships during construction means that potential collisions may be detected in advance, and the appropriate join operations implemented. This is simplified as the lines and their proximal regions are embedded in the two-dimensional space, guaranteeing that, for example, one VD line segment may detect an imminent collision and form the appropriate junction that preserves the correct node and region ordering around the junction point. Mioc et al. (2013) discussed operations applied in the simplification of map objects: these are usually lost in the generalization process. With the hierarchical Voronoi data structure described previously these relations may be recovered. These are needed for reasoning about dynamic aspects of the world, primarily actions, events and processes.

The difficulties with this approach have been that the algorithms (Roos 1993) for the construction of the line-segment VD are extremely complex (Imai 1996; Sugihara et al. 2000) and sensitive to the limitations of computer floating-point arithmetic (Shewchuk 1997). Held (2001) stated that it took him ten years to achieve this for a static algorithm. Gold, Remmele, and Roos (1995) constructed a line-segment VD of unconnected line segments. Imai (1996) constructed an incremental algorithm for line segments and closed polygons, where a maximum of two line segments meet at a vertex. Karavelas (2004) described a robust incremental algorithm (without deletion). Yang and Gold (1995) developed an incremental line-segment VD algorithm, but it suffered from a lack of arithmetic robustness. Gold and Dakowicz (2006) built a kinetic line-segment VD algorithm, where points and line segments may be inserted, intersected, and deleted – which is particularly useful for a dynamic GIS. Figure 13 illustrates the spatial relationships that may be obtained from this spatial model. The difficulties associated with this approach are primarily concerned with preserving the correct order of tangent points around the Delaunay circumcircles at locations where line segments meet.

Figure 13. Neighbor relationships from Line-Segment VD.

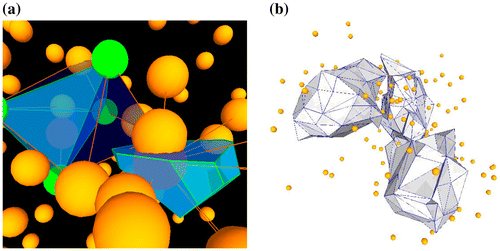
7. 3D models

Many of the methods described above for 2D may equally be implemented in 3D. Ledoux (2006) built a 3D kinetic VD model for various applications (Figure 14(a)). Figure 14(b) shows the contour surface generated by slicing the 3D DT – data points inside the shell have higher values than the specified contour surface. Boguslawski and Gold (2016) developed a half-edge-based data structure, the Dual Half-Edge (DHE), for the incremental construction of building models where full navigation within and between rooms may be achieved by examining both of the linked primal and dual graphs. This again is a tessellation, in the full 3D sense. Jamali et al. (2014) discussed rapid surveying of building interiors based on incrementally modifying the DHE as the survey progressed. Ohori, Boguslawski, and Ledoux (2013) described a four-dimensional GIS, based on the DHE plus a time dimension, and Anton, Boguslawski, and Mioc (2014) extended the DHE as the dual half-arc, giving increasing generality.

Figure 14. (a) Tetrahedron and 3D Voronoi cell; (b) 3D contour surface.

8. Conclusions

This second paper has built on the structures described in the first, and examined how these may be modified: change may often be associated with either viewpoint or time. Incremental algorithms permit additional point insertion, and applications involving the addition of skeleton points, for map scanning, contour enrichment, or watershed delineation and simulation. Dynamic algorithms permit skeleton smoothing, and higher order VD applications, including Sibson interpolation. Kinetic algorithms allow collision detection applications, free-Lagrange flow modeling, and pen movement simulation for map drawing. If desired, these methods may be extended to 3D. Based on this framework, it can be argued that tessellation models are fundamental to our understanding and processing of geographical space, and provide a coherent framework for understanding the “space” in which we exist.

Notes on contributor

Christopher Gold is an emeritus professor at the University of South Wales, a visiting professor at Southwest Jiaotong University and a visiting professor at LIESMARS, Wuhan University. He has held research chairs at Laval University, Quebec, Canada and at the University of South Wales. He received the Wang Zhizhuo Award from the Chinese Society of Geodesy, Photogrammetry and Cartography in 2008. His research has been devoted to the development of appropriate spatial models for various aspects of GIS, and the promotion of Voronoi diagrams as a fundamental tool for spatial analysis.