Markov partition in the attractor of Lozi maps

Abstract

In this paper, we study iterations of two-dimensional maps, in particular iterations of Lozi maps in the region of the parameter space where it has a strange attractor. Using symbolic dynamics techniques for two-dimensional maps, based on the kneading theory of Milnor and Thurston and also in the symbolic dynamic formalism developed by Sousa Ramos, through the kneading sequence for the Lozi maps, we characterize the region in the parameter space that contains the kneading curves and present a method to define a Markov partition for the Lozi attractors. Consequently, the topological entropy for the Lozi map is computed.

Keywords:

• Lozi maps
• kneading sequence
• symbolic sequences
• Markov partitions
• topological entropy

Mathematics Subject Classifications:

• 37E05
• 37D45
• 37E30

1. Introduction

Consider the following parametrized family of Lozi maps: (1) ${\mathcal{L}}_{ab}(x,y)=(1-a|x|+y,bx),(x,y)\in {\mathbb{R}}^2.$(1) These piecewise linear plane invertible maps were introduced in 1978 by René Lozi  [5] as a simplified version of the parametrized family of Hénon maps, without loosing the capacity to show chaotic behaviour. Since then, Lozi maps has been an important tool to understand complex behaviour of iterated maps on the plane.

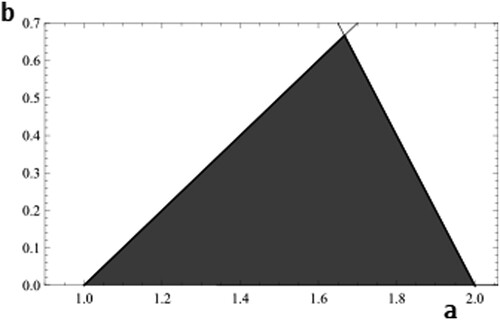
Since it is an invertible map, it is possible to define its inverse, ${\mathcal{L}}_{ab}^{-1}$, given by ${\mathcal{L}}_{ab}^{-1}(x,y)=(\frac{y}{b},x-1+a\left|\frac{y}{b}\right|).$In 1992  [6] Liu et al. showed that for parameters $(a,b)$ satisfying (2) $\{\begin{array}{l}0<b<1;\\ a>b+1;\\ a>2-b/2,\end{array}$(2) every map ${\mathcal{L}}_{ab}$ has indeed a strange attractor. Let ${\mathrm{△}}_{\mathcal{L}}$ denote the corresponding region of the parameter space; see Figure 1.

Figure 1. The parameter space region for which ${\mathcal{L}}_{ab}$ has a strange attractor.

From this point the Lozi maps considered will have parameter values $a$ and $b$ belonging to ${\mathrm{△}}_{\mathcal{L}}$. For simplification purposes, ${\mathcal{L}}_{ab}$ will be denoted by $\mathcal{L}$.

Earlier, Michał Misiurewicz  [7] introduced a region ${\mathrm{\nabla }}_{\mathcal{L}}$ in ${\mathbb{R}}^2$ satisfying (3) $\mathcal{L}({\mathrm{\nabla }}_{\mathcal{L}})\subseteq {\mathrm{\nabla }}_{\mathcal{L}},$(3) allowing to present the Lozi map attractor, ${\mathcal{A}}_{\mathcal{L}}$, from its successive forward iteration, (4) ${\mathcal{A}}_{\mathcal{L}}=\bigcap _{n=0}^{\mathrm{\infty }}{\mathcal{L}}^n({\mathrm{\nabla }}_{\mathcal{L}}).$(4) Considering the fixed point that lies in the first quadrant $A=(\frac{1}{a+1-b},\frac{b}{a+1-b})\mathrm{if}b<a+1,$and computing its local stability by evaluating the eigenvalues of the jacobian matrix of the map at the fixed point, in the domain of the parameters for $a>|b|+1$, the fixed point is a saddle point. Let $L^s(A)$ and $L^u(A)$ be the stable and unstable manifolds of $A$, respectively.

Definition 1.1

The Lozi map fundamental domain ${\mathrm{\nabla }}_{\mathcal{L}}$ is the triangle with vertices $\mathbf{\text{I}}$, $\mathcal{L}(I)$, and ${\mathcal{L}}^2(I)$, where (5) $I=(\frac{2+a+\sqrt{a^2+4b}}{2(1+a-b)},0)$(5) is the intersection point of the unstable manifold of the fixed point $A$, $L_A^u$, with the horizontal axis.

Next, some definitions of Lozi maps symbolic dynamics are presented, following [4].

Definition 1.2

Given $X\in \mathbb{R}$, the itinerary of $X$ is the bi-infinite symbolic sequence (6) $\mathsf{i}\mathsf{t}(X)=\dots {\delta }_{-2}{\delta }_{-1}\cdot {\delta }_0{\delta }_1{\delta }_2\dots ,$(6) where the symbols ${\delta }_n$, for $n\in \mathbb{Z}$, are defined as (7) ${\delta }_n\equiv \{\begin{array}{cl}-1,& {\mathcal{L}}^n(X{)}_x<0,\\ \star ,& {\mathcal{L}}^n(X{)}_x=0,\\ +1,& {\mathcal{L}}^n(X{)}_x>0,\end{array}$(7) where $X_x$ corresponds to the $x$ component of $X$.

By the previous definition, $\mathsf{i}\mathsf{t}(X)$ is a bi-infinite symbolic sequence of $\{-1,\ast ,+1{\}}^{\mathbb{Z}}$.  It is important to distinguish the itinerary for the past and the itinerary for the future of a point X; let $\underset{\_}{\delta }(X)=\cdots {\delta }_{-2}{\delta }_{-1}\cdot {\delta }_0{\delta }_1{\delta }_2\cdots$ be an itinerary of $X$. The symbolic subsequence ${\underset{\_}{\delta }}^u(X)=\cdots {\delta }_{-2}{\delta }_{-1}$ is the itinerary for the past of $X$ and the symbolic subsequence ${\underset{\_}{\delta }}^s(X)={\delta }_0{\delta }_1{\delta }_2\cdots$ is the itinerary for the future. Thus, $\underset{\_}{\delta }(X)={\underset{\_}{\delta }}^u(X)\cdot {\underset{\_}{\delta }}^s(X)$.

2. Critical set

Let $\mathcal{V}$ be the vertical axis, such that $\mathcal{V}={\mathcal{V}}^{+1}\cup {\mathcal{V}}^{-1},$where ${\mathcal{V}}^{+1}$ is the nonnegative part of the vertical axis and ${\mathcal{V}}^{-1}$ is the negative part of the vertical axis.

According to the construction process suggested by Ishii  [4] and Baptista et al. [3], some points belonging to ${\mathcal{A}}_{\mathcal{L}}\cap \mathcal{V}$play a very important role in the study of Lozi's maps dynamics, especially the point ${\mathcal{L}}^{-1}(I)$. The orbit associated with the forward itinerary of the point $I$ is the orbit whose itinerary, for the future, corresponds to the maximum symbolic sequence within the set of all admissible symbolic sequences for the future.

Definition 2.1

Given a Lozi map $\mathcal{L}$, its kneading sequence $K(\mathcal{L})$ is the itinerary for the future of $I$, i.e. $K(\mathcal{L})={\underset{\_}{\delta }}^s\left(I\right).$

Definition 2.2

Let $(a,b)\in {\mathrm{△}}_{\mathcal{L}}$. Given a Lozi map $\mathcal{L}$, its pruned kneading sequence, $k_n(\mathcal{L}),$ is the initial subsequence of symbols of $K(\mathcal{L})$ such that the first symbol ★ appears at position $n$, that is, ${\mathcal{L}}^{n-1}(I{)}_x=0$.

From the inverse map ${\mathcal{L}}^{-1}$, two maps can be introduced, ${\mathcal{L}}_{+1}^{-1}$ and ${\mathcal{L}}_{-1}^{-1}$, as follows: ${\mathcal{L}}_{+1}^{-1}(x,y)=(\frac{y}{b},x-1+a\frac{y}{b})$and ${\mathcal{L}}_{-1}^{-1}(x,y)=(\frac{y}{b},x-1-a\frac{y}{b}).$Using these two maps and a pruned kneading sequence, $k_n(\mathcal{L}),$ we will define a certain type of line segments, in ${\mathrm{\nabla }}_{\mathcal{L}},$ as follows:

Definition 2.3

Let $(a,b)\in {\mathrm{△}}_{\mathcal{L}}$ and ${\underset{\_}{\delta }}^s=k_n(\mathcal{L})={\delta }_0{\delta }_1\cdots {\delta }_{n-2}\ast$ for $n>3$.

The line segments ${\mathcal{S}}^{{\delta }_i\cdots {\delta }_{n-2}\ast }$, with $2\le i\le n-2$, in ${\mathrm{\nabla }}_{\mathcal{L}}$, are defined by $\begin{array}{rl}& {\mathcal{S}}^{{\delta }_{n-2}\ast }={\mathcal{L}}_{{\delta }_{n-2}}^{-1}({\mathrm{\nabla }}_{\mathcal{L}}\cap {\mathcal{V}}^{{\delta }_{n-2}})\cap {\mathrm{\nabla }}_{\mathcal{L}};\\ & {\mathcal{S}}^{{\delta }_{n-3}{\delta }_{n-2}\ast }={\mathcal{L}}_{{\delta }_{n-3}}^{-1}({\mathcal{S}}^{{\delta }_{n-2}\ast })\cap {\mathrm{\nabla }}_{\mathcal{L}};\\ & \cdot \cdot \cdot \\ & {\mathcal{S}}^{{\delta }_2\cdots {\delta }_{n-2}\ast }={\mathcal{L}}_{{\delta }_2}^{-1}({\mathcal{S}}^{{\delta }_3\cdots {\delta }_{n-2}\ast })\cap {\mathrm{\nabla }}_{\mathcal{L}}.\end{array}$

After the definition of the line segments ${\mathcal{S}}^{{\delta }_i\cdots {\delta }_{n-2}\ast }$ with $2\le i\le n-2$, for n>3, its possible to define the critical set for $\mathcal{L}$ when $(a,b)\in {\mathrm{△}}_{\mathcal{L}}$.

Definition 2.4

Let $(a,b)\in {\mathrm{△}}_{\mathcal{L}}$ and ${\underset{\_}{\delta }}^s=k_n(\mathcal{L})$. The critical set ${\mathcal{C}}_{{\underset{\_}{\delta }}^s}(\mathcal{L})$ is defined as the set containing the line segments ${\mathcal{S}}^{{\delta }_i\cdots {\delta }_{n-2}\ast }$, with $2\le i\le n-2$, the vertical line segment ${\mathcal{S}}^{\ast }=\mathcal{V}\cap {\mathrm{\nabla }}_{\mathcal{L}}$ and the points $\mathcal{L}(I)$ and I.

The following proposition presents the slope of each line segment ${\mathcal{S}}^{{\delta }_i\cdots {\delta }_{n-2}\ast }$, with $2\le i\le n-2$ (for n>3).

Proposition 2.5

Let $(a,b)\in {\mathrm{△}}_{\mathcal{L}}$ and ${\underset{\_}{\delta }}^s=k_n(\mathcal{L})$ $={\delta }_0{\delta }_1\cdots {\delta }_{n-2}\ast$. The line segments ${\mathcal{S}}^{{\delta }_i\cdots {\delta }_{n-2}\ast }$, with $0\le i\le n-2$, are given by ${\mathcal{S}}^{{\delta }_i\cdots {\delta }_{n-2}\ast }={\mathrm{\nabla }}_{\mathcal{L}}\cap \{(x,y):y=m_i(x-x_i)+y_i\},$where $(x_i,y_i)={\mathcal{L}}^i(I)$ and $m_i=\{\begin{array}{cc}a{\delta }_{n-2},& i=n-2,\\ a{\delta }_i+{\displaystyle \frac{b}{m_{i+1}}},& 0\le i<n-2.\end{array}$

Proof.

Let ${\underset{\_}{\delta }}^s=k_n(\mathcal{L})={\delta }_0{\delta }_1\cdots {\delta }_{n-2}\ast$ be the pruned kneading sequence of $\mathcal{L}$ with dimension $n$.

Consider the jacobian matrix of ${\mathcal{L}}^{-1}$ at the point $X\in \mathbb{R}$, defined as follows: $D{\mathcal{L}}_{+1}^{-1}=\left[\begin{array}{cc}0& {\displaystyle \frac{1}{b}}\\ 1& {\displaystyle \frac{a}{b}}\end{array}\right]\mathrm{if}{X}_y>0$and $D{\mathcal{L}}_{-1}^{-1}=\left[\begin{array}{cc}0& {\displaystyle \frac{1}{b}}\\ 1& {\displaystyle \frac{-a}{b}}\end{array}\right]\mathrm{if}{X}_y<0,$where $X_y$ corresponds to the y component of $X$.

Let $\overrightarrow{v}=(0,1)$ be the vector of the line segment ${\mathcal{V}}^{{\delta }_{n-2}}$. The vector of a line segment ${\mathcal{L}}_{{\delta }_{n-2}}^{-1}({\mathcal{V}}^{{\delta }_{n-2}})\cap {\mathrm{\nabla }}_{\mathcal{L}}$ is given by $\begin{array}{rl}{\overrightarrow{v}}^{{\delta }_{n-2}}& =\overrightarrow{v}{\left(D{\mathcal{L}}_{{\delta }_{n-2}}^{-1}\right)}^T=\left[\begin{array}{cc}0& 1\end{array}\right]\left[\begin{array}{cc}0& 1\\ {\displaystyle \frac{1}{b}}& {\displaystyle \frac{a{\delta }_{n-2}}{b}}\end{array}\right]\\ & =\left[\begin{array}{cc}{\displaystyle \frac{1}{b}}& {\displaystyle \frac{a}{b}}{\delta }_{n-2}\end{array}\right].\end{array}$Depending on the value of ${\delta }_{n-2}$, the point ${\mathcal{L}}^{n-1}(I)$ will belong to ${\mathcal{V}}^{+1}$ or ${\mathcal{V}}^{-1}$. By the definition of ${\mathcal{L}}_{{\delta }_{n-2}}^{-1}$, ${\mathcal{S}}^{{\delta }_{n-2}\ast }={\mathcal{L}}_{{\delta }_{n-2}}^{-1}({\mathcal{V}}^{{\delta }_{n-2}})\cap {\mathrm{\nabla }}_{\mathcal{L}}$ will be a line segment that passes through the point ${\mathcal{L}}^{n-2}(I),$ with vector ${\overrightarrow{v}}^{{\delta }_{n-2}}=({\displaystyle \frac{1}{b}},{\displaystyle \frac{a}{b}}{\delta }_{n-2})$ and slope $m_{n-2}=a{\delta }_{n-2}$.

Let ${\overrightarrow{v}}^{{\delta }_{n-2}}=(v_x,v_y)$. As $\left[\begin{array}{cc}{v}_x& v_y\end{array}\right]\left[\begin{array}{cc}0& 1\\ {\displaystyle \frac{1}{b}}& {\displaystyle \frac{a{\delta }_{n-3}}{b}}\end{array}\right]=\left[\begin{array}{cc}{\displaystyle \frac{1}{b}}{v}_y& v_x+{\displaystyle \frac{a}{b}}{v}_y{\delta }_{n-3}\end{array}\right],$the slope of the line segment ${\mathcal{S}}^{{\delta }_{n-3}{\delta }_{n-2}\ast }={\mathcal{L}}_{{\delta }_{n-3}}^{-1}({\mathcal{S}}^{{\delta }_{n-2}\ast })\cap {\mathrm{\nabla }}_{\mathcal{L}}$ will be $\begin{array}{rl}{m}_{n-3}& =b\frac{v_x}{v_y}+a{\delta }_{n-3}\\ & =a{\delta }_{n-3}+\frac{b}{m_{n-2}}.\end{array}$Therefore, for $2\le i\le n-2$, the line segment ${\mathcal{S}}^{{\delta }_i\cdots {\delta }_{n-2}\ast }$ that passes through the point $(x_i,y_i)={\mathcal{L}}^i(I)$ has the vector given by ${\overrightarrow{v}}^{{\delta }_i\cdots {\delta }_{n-2}}={\overrightarrow{v}}^{{}^{{\delta }_{i+1}\cdots {\delta }_{n-2}}}{\left(D{\mathcal{L}}_{{\delta }_i}^{-1}\right)}^T$and slope given by $m_i=a{\delta }_i+\frac{b}{m_{i+1}}.$

Proposition 2.6

Let $(a,b)\in {\mathrm{△}}_{\mathcal{L}}$, ${\underset{\_}{\delta }}^s=k_n(\mathcal{L})$. The intersection of the line segment ${\mathcal{S}}^{{\delta }_i\cdots {\delta }_{n-2}\ast }$ with the $x\text{-}axis$ is the point $({\xi }_i,0)$ where ${\xi }_i=\{\begin{array}{ll}0& ifi=n-1.\\ {\displaystyle \frac{1}{m_i}}(1-{\xi }_{i+1})& if2\le i\le n-2.\end{array}$

Proof.

The line segment ${\mathcal{S}}^{\ast }$ (when $i=n-1$) is the vertical line, and its intersection with the $x\text{-}axis$ occurs at the point $({\xi }_{n-1},0)=(0,0)$. The pre-image of $({\xi }_{n-1},0)$ is ${\mathcal{L}}_{{\delta }_{n-2}}^{-1}(0,0)=(-1,0)$. Let $m_i$ be the slope of the line segments ${\mathcal{S}}^{{\delta }_i\cdots {\delta }_{n-2}\ast }$ with $2\le i\le n-2$, for $n>3$. Therefore, the line segment that passes through the points $(0,-1)$ and ${\mathcal{L}}^{n-2}(I)$ has slope $m_{n-2}$ and can be given by $y=m_{n-2}x-1$. Since this line segment contains the segment ${\mathcal{S}}^{{\delta }_{n-2}\ast },$ the intersection of the line segment ${\mathcal{S}}^{{\delta }_{n-2}\ast }$ with the $x\text{-}axis$ occurs at the point $({\xi }_{n-2},0)=(\frac{1}{m_{n-2}},0)$.

Continuing this process, the pre-image of the point $({\xi }_{n-2},0)$ is the point $(0,{\xi }_{n-2}-1)$. Therefore, the line segment ${\mathcal{S}}^{{\delta }_{n-3}{\delta }_{n-2}\ast }$ is contained in a line segment that passes through the point $(0,{\xi }_{n-2}-1)$ with slope $m_{n-3}$ and intersects the $x\text{-}axis$ at the point $({\xi }_{n-3},0)=(\frac{1}{m_{n-3}}(1-{\xi }_{n-2}),0)$ . In general, the pre-image of a point $(\xi ,0)$ is the point $(0,\xi -1)$ and consequently the line segment ${\mathcal{S}}^{{\delta }_i\cdots {\delta }_{n-2}\ast }$ with $2\le i\le n-2$, for $n>3,$ intersects the $x\text{-}axis$ at the point $({\xi }_i,0)$, where ${\xi }_i=\frac{1}{m_i}(1-{\xi }_{i+1}).\text{■}$

Considering Propositions 2.5 and 2.6, the next result follows.

Proposition 2.7

Let $(a,b)\in {\mathrm{△}}_{\mathcal{L}}$ and ${\underset{\_}{\delta }}^s=k_n(\mathcal{L})$. The line segments ${\mathcal{S}}^{{\delta }_i\cdots {\delta }_{n-2}\ast }$, with $2\le i\le n-2$, for $n>3,$ and the vertical line segment ${\mathcal{S}}^{\ast }$ do not intersect.

2.1. Order relation in the set $\{-1,\ast ,+1{\}}^{\mathbb{N}}$

From [4], the attractor points with the same fixed itinerary for the past ${\underset{\_}{\epsilon }}^u$ lie in a segment ${\mathsf{L}}^u$, called the unstable leaf, completely characterized by the parameter values $(a,b)$ and ${\underset{\_}{\epsilon }}^u$. Moreover, attractor points with the same fixed itinerary for the future ${\underset{\_}{\epsilon }}^s$ lie in a segment ${\mathsf{L}}^s$, called the stable leaf, also completely characterized by $(a,b)$ and ${\underset{\_}{\epsilon }}^s$. If a point $X\in {\mathcal{A}}_{\mathcal{L}}$ has a fixed itinerary $\underset{\_}{\epsilon }$, $X$ is the intersection of the line segments previously defined, denoted by ${\mathsf{L}}^u(X)$ and ${\mathsf{L}}^s(X)$, respectively.

In order to rewrite the order relation established by Ishii [4] for the set $\{-1,\ast ,+1{\}}^{\mathbb{N}}$, consider the following definition.

Definition 2.8

Let ${\underset{\_}{\epsilon }}^s$ and ${\underset{\_}{\delta }}^s$ be two symbolic subsequences for the future.

${\underset{\_}{\epsilon }}^s{<}_s{\underset{\_}{\delta }}^s$ if one of the following conditions is satisfied:

1. ${\epsilon }_0<{\delta }_0;$

2. ${\epsilon }_0\cdots {\epsilon }_{i-1}={\delta }_0\cdots {\delta }_{i-1}$ and ${\epsilon }_i\ne {\delta }_i$,:

1. the number of $+1^{\mathrm{\prime }}s$ in $\cdot {\epsilon }_0\cdots {\epsilon }_{i-1}$ is even and ${\epsilon }_i<{\delta }_i$;

2. the number of $+1^{\mathrm{\prime }}s$ in $\cdot {\epsilon }_0\cdots {\epsilon }_{i-1}$ is odd and ${\epsilon }_i>{\delta }_i$;

where the order on the symbols is $-1<\ast <+1$.

If ${\epsilon }_i={\delta }_i$ for all $i\ge 0$, ${\underset{\_}{\epsilon }}^s={\underset{\_}{\delta }}^s$.

From the previous definition it can be establish that, for any point $X\in {\mathrm{\nabla }}_{\mathcal{L}}$, (8) ${\underset{\_}{\delta }}^s(\mathcal{L}(I)){<}_s{\underset{\_}{\delta }}^s\left(X\right){<}_s{\underset{\_}{\delta }}^s\left(I\right).$(8) Considering the set $\{{\sigma }^i({\underset{\_}{\delta }}^s){\}}_{i=0}^{n-1}$, where $\sigma$is the shift-operator, the set $\{{\xi }_i{\}}_{i=2}^{n-2}\cup \{I_x,\mathcal{L}(I{)}_x\}$ and denoting by $p$ as a permutation in the set $\{2,\dots ,n-1\}$ such that (9) $\sigma \left({\underset{\_}{\delta }}^s\right){<}_s{\sigma }^{p(2)}\left({\underset{\_}{\delta }}^s\right){<}_s\cdots {<}_s{\sigma }^{p(n-1)}\left({\underset{\_}{\delta }}^s\right){<}_s{\underset{\_}{\delta }}^s$(9) it follows that (10) $\mathcal{L}{\left(I\right)}_x⟨{\mathcal{S}}^{{\sigma }^{p(2)}\left({\underset{\_}{\delta }}^s\right)}⟨\cdots ⟨{\mathcal{S}}^{{\sigma }^{p(n-1)}\left({\underset{\_}{\delta }}^s\right)}⟨I_x,$(10) and where $A⟨B$ means that $A$ is on the left side of $B$, and consequently (11) $\mathcal{L}{\left(I\right)}_x<{\xi }_{{}^{p(2)}}<\cdots <{\xi }_{{}^{p(n-1)}}<I_x.$(1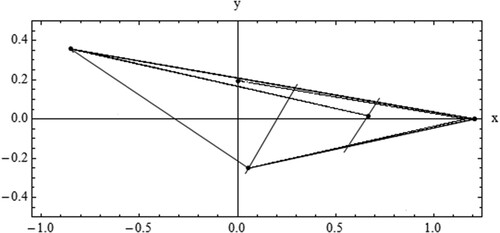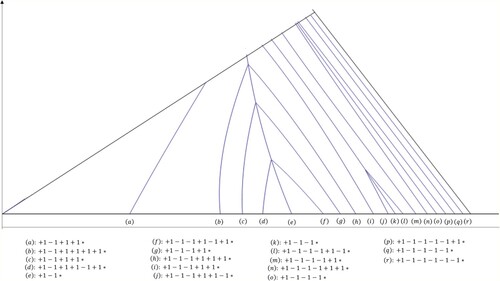1)  Figure 2 illustrates the critical set, the attractor and the invariant triangle ${\mathrm{\nabla }}_{\mathcal{L}}$, considering the pruned kneading sequence ${\underset{\_}{\delta }}^s$ $=+1-1+1+1\ast$.

Figure 2. The critical set and the Lozi map attractor for the pruned kneading sequence ${\delta }^s=+1-1+1+1\ast$.

2.2. Markov partition on ${\mathcal{A}}_{\mathcal{L}}$

Using the elements of the critical set ${\mathcal{C}}_{{\underset{\_}{\delta }}^s}(\mathcal{L}),$ where ${\underset{\_}{\delta }}^s=k_n(\mathcal{L})$, it is possible to construct a partition, with $n-1$ regions, for the set ${\mathrm{\nabla }}_{\mathcal{L}}$ and therefore to ${\mathcal{A}}_{\mathcal{L}}$.

Considering the Definition 2.8 and the order relations given in (9(9) $\sigma \left({\underset{\_}{\delta }}^s\right){<}_s{\sigma }^{p(2)}\left({\underset{\_}{\delta }}^s\right){<}_s\cdots {<}_s{\sigma }^{p(n-1)}\left({\underset{\_}{\delta }}^s\right){<}_s{\underset{\_}{\delta }}^s$(9) ), (10(10) $\mathcal{L}{\left(I\right)}_x⟨{\mathcal{S}}^{{\sigma }^{p(2)}\left({\underset{\_}{\delta }}^s\right)}⟨\cdots ⟨{\mathcal{S}}^{{\sigma }^{p(n-1)}\left({\underset{\_}{\delta }}^s\right)}⟨I_x,$(10) ) and (11(11) $\mathcal{L}{\left(I\right)}_x<{\xi }_{{}^{p(2)}}<\cdots <{\xi }_{{}^{p(n-1)}}<I_x.$(11) ) we define the $n-1$ regions on the triangle ${\mathrm{\nabla }}_{\mathcal{L}}$ as follows:

let $p$ be a permutation in the set $\{2,\dots ,n-1\}$ such that $\mathcal{L}{\left(I\right)}_x⟨{\mathcal{S}}^{{\sigma }^{p(2)}\left({\underset{\_}{\delta }}^s\right)}⟨\cdots ⟨{\mathcal{S}}^{{\sigma }^{p(n-1)}\left({\underset{\_}{\delta }}^s\right)}⟨I_x.$The $n-1$ regions on the triangle ${\mathrm{\nabla }}_{\mathcal{L}}$ are defined as follows: $\begin{array}{rl}{R}_1& =\{(x,y)\in {\mathrm{\nabla }}_{\mathcal{L}}:(x,y)⟨{\mathcal{S}}^{{\sigma }^{p(2)}\left({\underset{\_}{\delta }}^s\right)}\}\\ & ⋮\\ R_k& =\{(x,y)\in {\mathrm{\nabla }}_{\mathcal{L}}:{\mathcal{S}}^{{\sigma }^{p(k)}\left({\underset{\_}{\delta }}^s\right)}\underset{\_}{⟨}(x,y)⟨{\mathcal{S}}^{{\sigma }^{p(k+1)}\left({\underset{\_}{\delta }}^s\right)}\},k=3,\dots ,n-2\\ & ⋮\\ R_{n-1}& =\{(x,y)\in {\mathrm{\nabla }}_{\mathcal{L}}:{\mathcal{S}}^{{\sigma }^{p(n-1)}\left({\underset{\_}{\delta }}^s\right)}\underset{\_}{⟨}(x,y)\},\end{array}$where $A\underset{\_}{⟨}(x,y)$ means that $(x,y)$ is on the right side of $A$ or $(x,y)$ belongs to $A$ and $(x,y)⟨A$ means that $(x,y)$ is on the left side of $A$.

Considering the previous construction the next result follows:

Theorem 2.9

The set $\mathcal{P}=\{R_1,\dots ,R_{n-1}\}$ is a topological partition of ${\mathrm{\nabla }}_{\mathcal{L}}$.

Let $X$ belong to the interior of a set $R_i$. Suppose that $\mathcal{L}\left(R_i\right)\subset R_j,$where $R_j$ is single region or a union of two or more regions of the topological partition $\mathcal{P}$. Assume, without loss of generality, that it is a single region. Thus, $\mathcal{L}\left(X\right)\in R_j.$Moreover, by Ishii [4], the unstable leaf and the stable leaf of $X$ lie in a segment denoted by ${\mathsf{L}}^u(X)$ and ${\mathsf{L}}^s(X)$, respectively, and X is the intersection point of the segments previously defined. Therefore, and due to the Lozi map linearity, we can state that $\mathcal{L}(L^u\left(X\right)\cap R_i)\supset L^u\left(\mathcal{L}\left(X\right)\right)\cap R_j$and $\mathcal{L}(L^s\left(X\right)\cap R_i)\subset L^s\left(\mathcal{L}\left(X\right)\right)\cap R_j.$Thus, by Bowen [2], it follows:

Theorem 2.10

The topological partition $\{R_1,\dots ,R_{n-1}\}$ provides a Markov partition of ${\mathrm{\nabla }}_{\mathcal{L}}$ associated to ${\underset{\_}{\delta }}^s=k_n(\mathcal{L})$.

3. Transition matrix and topological entropy

Definition 3.1

Let $\{R_1,\dots ,R_{n-1}\}$ be a Markov partition of ${\mathrm{\nabla }}_{\mathcal{L}}$ associated to ${\underset{\_}{\delta }}^s=k_n(\mathcal{L})$. The transition matrix over ${\mathrm{\nabla }}_{\mathcal{L}}$ is a square matrix $A_{{\underset{\_}{\delta }}^s}$, of order $n-1$, such that $A_{{\underset{\_}{\delta }}^s}=\left(a_{ij}\right)=\{\begin{array}{cc}1& if\mathcal{L}\left(R_i\right)\cap R_j\ne \mathrm{\varnothing }\\ 0& if\mathcal{L}\left(R_i\right)\cap R_j=\mathrm{\varnothing }\end{array}.$

Following [8] and [1], the topological entropy of $\mathcal{L}$ can be calculated using the corresponding transition matrix. This result can be stated as follows:

Proposition 3.2

Let ${\underset{\_}{\delta }}^s=k_n(\mathcal{L})={\delta }_0{\delta }_1\cdots {\delta }_{n-2}\ast$ and $(a,b)\in {\mathrm{△}}_{\mathcal{L}}$. Let $A_{{\underset{\_}{\delta }}^s}$ be the transition matrix associated to ${\underset{\_}{\delta }}^s$. The topological entropy of $\mathcal{L}$ is given by $h_{top}\left(\mathcal{L}\right)=\log \left({\lambda }_{max}\left(A_{{\underset{\_}{\delta }}^s}\right)\right),$where ${\lambda }_{max}(A_{{\underset{\_}{\delta }}^s})$ is the spectral radius of $A_{{\underset{\_}{\delta }}^s}$.

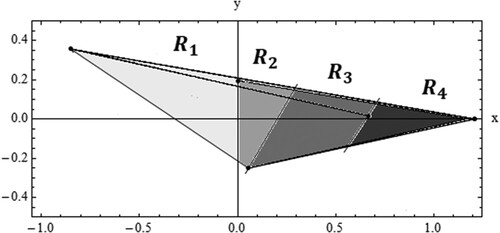
Example 3.3

Let consider $(a,b)\approx (1.518,0.185728)$ and the pruned kneading sequence associated ${\underset{\_}{\delta }}^s=+1-1+1+1\ast$The itinerary given by the pruned kneading sequence $\underset{\_}{\delta }$ for $(a,b)\approx (1.518,0.185728)$ is given in Figure 3.

Figure 3. Itinerary given by the pruned kneading sequence and Lozi attractor for $(a,b)\approx (1.518,0.185728)$.

Applying the shift map to the pruned kneading sequence ${\underset{\_}{\delta }}^s,$ it follows: $\begin{array}{rl}{\underset{\_}{\delta }}^s& =+1-1+1+1\ast \\ \sigma \left({\underset{\_}{\delta }}^s\right)& =-1+1+1\ast \\ {\sigma }^2\left({\underset{\_}{\delta }}^s\right)& =+1+1\ast \\ {\sigma }^3\left({\underset{\_}{\delta }}^s\right)& =+1\ast \\ {\sigma }^4\left({\underset{\_}{\delta }}^s\right)& =\ast \end{array}$By Definition 2.8, the following order relation is valid $\sigma \left({\underset{\_}{\delta }}^s\right){<}_s{\sigma }^4\left({\underset{\_}{\delta }}^s\right){<}_s{\sigma }^2\left({\underset{\_}{\delta }}^s\right){<}_s{\sigma }^3\left({\underset{\_}{\delta }}^s\right){<}_s{\underset{\_}{\delta }}^s$and consequently $\mathcal{L}{\left(I\right)}_x⟨{\mathcal{S}}^{\ast }⟨{\mathcal{S}}^{+1+1\ast }⟨{\mathcal{S}}^{+1\ast }⟨I_x.$The partition of ${\mathrm{\nabla }}_{\mathcal{L}}$ is given through the regions (Figure 4) $\begin{array}{rl}{R}_1& =\{(x,y)\in {\mathrm{\nabla }}_{\mathcal{L}}:(x,y)⟨{\mathcal{S}}^{\ast }\}\\ R_2& =\{(x,y)\in {\mathrm{\nabla }}_{\mathcal{L}}:{\mathcal{S}}^{\ast }\underset{\_}{⟨}(x,y)⟨{\mathcal{S}}^{+1+1\ast }\}\\ R_3& =\{(x,y)\in {\mathrm{\nabla }}_{\mathcal{L}}:{\mathcal{S}}^{+1+1\ast }\underset{\_}{⟨}(x,y)⟨{\mathcal{S}}^{+1\ast }\}\\ R_4& =\{(x,y)\in {\mathrm{\nabla }}_{\mathcal{L}}:{\mathcal{S}}^{+1\ast }\underset{\_}{⟨}(x,y)\}\end{array}$which can be associated to the following transition matrix $A_{{\underset{\_}{\delta }}^s}$ given by $A_{{\underset{\_}{\delta }}^s}=\left[\begin{array}{cccc}0& 0& 1& 1\\ 0& 0& 0& 1\\ 0& 1& 1& 0\\ 1& 0& 0& 0\end{array}\right].$The transition matrix $A_{{\underset{\_}{\delta }}^s}$ has maximum eigenvalue ${\lambda }_{max}\approx 1.51288$ and the topological entropy is approximately $h_{top}\approx \log \left(1.51288\right)\approx \mathrm{0.41402.}$

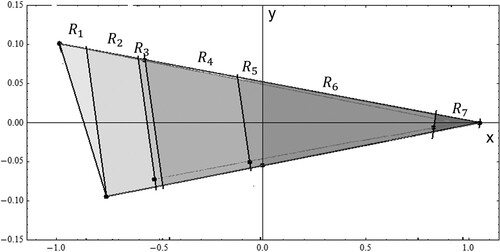
Example 3.4

Consider $(a,b)\approx (1.887,0.0957356)$ and the pruned kneading sequence associated ${\underset{\_}{\delta }}^s=+1-1-1-1-1+1-1\ast .$Applying the shift map to ${\underset{\_}{\delta }}^s$ $\begin{array}{rl}{\underset{\_}{\delta }}^s& =+1-1-1-1-1+1-1\ast \\ \sigma ({\underset{\_}{\delta }}^s)& =-1-1-1-1+1-1\ast \\ {\sigma }^2({\underset{\_}{\delta }}^s)& =-1-1-1+1-1\ast \\ {\sigma }^3({\underset{\_}{\delta }}^s)& =-1-1+1-1\ast \\ {\sigma }^4({\underset{\_}{\delta }}^s)& =-1+1-1\ast \\ {\sigma }^5({\underset{\_}{\delta }}^s)& =+1-1\ast \\ {\sigma }^6({\underset{\_}{\delta }}^s)& =-1\ast \\ {\sigma }^7({\underset{\_}{\delta }}^s)& =\ast \end{array}$that verifies the following order relationship: $\sigma ({\underset{\_}{\delta }}^s){<}_s{\sigma }^2({\underset{\_}{\delta }}^s){<}_s{\sigma }^3({\underset{\_}{\delta }}^s){<}_s{\sigma }^6({\underset{\_}{\delta }}^s){<}_s{\sigma }^4({\underset{\_}{\delta }}^s){<}_s{\sigma }^7({\underset{\_}{\delta }}^s){<}_s{\sigma }^5({\underset{\_}{\delta }}^s){<}_s{\underset{\_}{\delta }}^s$and $\mathcal{L}{\left(I\right)}_x⟨{\mathcal{S}}^{{\sigma }^2({\underset{\_}{\delta }}^s)}⟨{\mathcal{S}}^{{\sigma }^3({\underset{\_}{\delta }}^s)}⟨{\mathcal{S}}^{{\sigma }^6({\underset{\_}{\delta }}^s)}⟨{\mathcal{S}}^{{\sigma }^4({\underset{\_}{\delta }}^s)}⟨{\mathcal{S}}^{{\sigma }^7({\underset{\_}{\delta }}^s)}⟨{\mathcal{S}}^{{\sigma }^5({\underset{\_}{\delta }}^s)}⟨I_x.$The partition of ${\mathrm{\nabla }}_{\mathcal{L}}$ is given through the regions (Figure 5) $\begin{array}{rl}{R}_1& =\{(x,y)\in {\mathrm{\nabla }}_{\mathcal{L}}:(x,y)⟨{\mathcal{S}}^{{\sigma }^2({\underset{\_}{\delta }}^s)}\},\\ R_2& =\{(x,y)\in {\mathrm{\nabla }}_{\mathcal{L}}:{\mathcal{S}}^{{\sigma }^2({\underset{\_}{\delta }}^s)}\underset{\_}{⟨}(x,y)⟨{\mathcal{S}}^{{\sigma }^3({\underset{\_}{\delta }}^s)}\},\\ R_3& =\{(x,y)\in {\mathrm{\nabla }}_{\mathcal{L}}:{\mathcal{S}}^{{\sigma }^3({\underset{\_}{\delta }}^s)}\underset{\_}{⟨}(x,y)⟨{\mathcal{S}}^{{\sigma }^6({\underset{\_}{\delta }}^s)}\},\\ R_4& =\{(x,y)\in {\mathrm{\nabla }}_{\mathcal{L}}:{\mathcal{S}}^{{\sigma }^6({\underset{\_}{\delta }}^s)}\underset{\_}{⟨}(x,y)⟨{\mathcal{S}}^{{\sigma }^4({\underset{\_}{\delta }}^s)}\},\\ R_5& =\{(x,y)\in {\mathrm{\nabla }}_{\mathcal{L}}:{\mathcal{S}}^{{\sigma }^4({\underset{\_}{\delta }}^s)}\underset{\_}{⟨}(x,y)⟨{\mathcal{S}}^{{\sigma }^7({\underset{\_}{\delta }}^s)}\},\\ R_6& =\{(x,y)\in {\mathrm{\nabla }}_{\mathcal{L}}:{\mathcal{S}}^{{\sigma }^7({\underset{\_}{\delta }}^s)}\underset{\_}{⟨}(x,y)⟨{\mathcal{S}}^{{\sigma }^5({\underset{\_}{\delta }}^s)}\},\\ R_7& =\{(x,y)\in {\mathrm{\nabla }}_{\mathcal{L}}:{\mathcal{S}}^{{\sigma }^5(\underset{\_}{\delta })}\underset{\_}{⟨}(x,y)\},\end{array}$which can be associated to the following transition matrix $A_{{\underset{\_}{\delta }}^s}$: $A_{{\underset{\_}{\delta }}^s}=\left[\begin{array}{ccccccc}0& 1& 0& 0& 0& 0& 0\\ 0& 0& 1& 1& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 0& 1\\ 0& 0& 0& 1& 1& 1& 1\\ 1& 1& 1& 0& 0& 0& 0\end{array}\right].$The transition matrix $A_{{\underset{\_}{\delta }}^s}$ has a maximum eigenvalue ${\lambda }_{max}\approx 1.9363$ and the topological entropy is approximately $h_{top}=\log \left(1.9363\right)\approx \mathrm{0.66078.}$

Figure 4. Itinerary of point I, the critical set and the regions $R_j$, j = 1, 2, 3, 4.

3.1. Isentropics curves for Lozi maps

From [3], a pruned kneading sequence corresponds to an algebraic condition on the parameters and, therefore, to a curve on the parameter plane. For example, a simple computation shows that the kneading curve for the pruned kneading sequence ${\underset{\_}{\delta }}^s=+1-1\star$ is described by the following condition: $2+4a-a^3-ab-a^2\sqrt{a^2+4b}+b\sqrt{a^2+4b}=0.$

Definition 3.5

Given a pruned kneading sequence ${\underset{\_}{\delta }}^s$ of dimension $n$, its kneading curve $\mathrm{\Gamma }({\underset{\_}{\delta }}^s)$ is the parameter space curve corresponding to parameter values such that $k_n(\mathcal{L})={\underset{\_}{\delta }}^s$.

Following the work [3], and considering Proposition 3.2, the topological entropy of $\mathcal{L}$ along the curve $\mathrm{\Gamma }({\underset{\_}{\delta }}^s)$ is equal to $\log (a_{{\underset{\_}{\delta }}^s})$, where $(a_{{\underset{\_}{\delta }}^s},0)$ is the point of the horizontal axis given by the limit, as $b\to 0$, of $\mathrm{\Gamma }({\underset{\_}{\delta }}^s)$ and therefore $0\le h_{top}\left(\mathcal{L}\right)\le \log \left(2\right).$Figure 6 illustrates the kneading curves (isentropic curves) for pruned kneading sequence up to dimension 7.

Figure 5. Itinerary and the partition associated to the pruned kneading sequence ${\delta }^s=+1-1-1-1-1+1-1\ast$  when $(a,b)\approx (1.887,0.0957356)$.

Figure 6. Isentropic curves associated to a pruned kneading sequence.

Acknowledgments

The author expresses his gratitude to Ricardo Severino and Sandra Vinagre for all their support and encouragement in obtaining these results.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This work was partially supported by projects UIBD/00308/2020 and UIDB/04-674/2020, by FCT-Portuguese Foundation for Science and Technology