Chaos and mixing homeomorphisms on fans

Abstract

We construct a mixing homeomorphism on both the Lelek fan and the Cantor fan. We also construct a family of uncountably many pairwise non-homeomorphic smooth (and non-smooth) fans that admit mixing homeomorphisms.

Keywords:

• Closed relations
• Mahavier products
• transitive dynamical systems
• transitive homeomorphisms
• mixing homeomorphisms
• smooth fan

2020 Mathematics Subject Classifications:

• 37B02
• 37B45
• 54C60
• 54F15
• 54F17

1. Introduction

In this paper we study mixing homeomorphisms on compact metric spaces. By mixing, in this paper, we mean topologically mixing. First, we study how one can use Mahavier products of closed relations on compact metric spaces to construct dynamical systems $(X,f)$, where f is a mixing homeomorphism. Next, we study quotients of dynamical systems. We start with a dynamical system $(X,f)$ and define an equivalence relation ∼ on X. Then we discuss when the mixing of $(X,f)$ implies the mixing of $(X{/}_{\sim },f^{\star })$. Finally, we use these techniques

1. to obtain a mixing homeomorphism on the Lelek fan,

2. to obtain a mixing homeomorphism on the Cantor fan, and

3. to construct a family of uncountably many pairwise non-homeomorphic smooth (non-smooth) fans that admit a mixing homeomorphism.

In addition, we show that

1. there are continuous functions $f,h:L\to L$ on the Lelek fan L such that

   1. h is a homeomorphism and f is not,

   2. $(L,f)$ and $(L,h)$ are both mixing as well as chaotic in the sense of Robinson but not in the sense of Devaney.

2. there are continuous functions $f,h:C\to C$ on the Cantor fan C such that

   1. h is a homeomorphism and f is not,

   2. $(C,f)$ and $(C,h)$ are both mixing as well as chaotic in the sense of Devaney, and

3. there are continuous functions $f,h:C\to C$ on the Cantor fan C such that

   1. h is a homeomorphism and f is not,

   2. $(C,f)$ and $(C,h)$ are both mixing as well as chaotic in the sense of Robinson but not in the sense of Devaney.

Note that the example which is mixing and chaotic in the sense of Knudsen, but not in the sense of Devaney, is not possible since mixing implies transitivity.

We proceed as follows. In Section 2, we introduce the definitions, notation and the well-known results that will be used later in the paper. In Section 3, we study mixing of Mahavier dynamical systems and mixing of quotients of dynamical systems. Then, we use these results in Sections 4– 6 to produce mixing homeomorphisms on various examples of fans.

2. Definitions and notation

The following definitions, notation and well-known results are needed in the paper.

Definition 2.1

Let X be a metric space, $x\in X$ and $\epsilon >0$. We use $B(x,\epsilon )$ to denote the open ball centered at x with radius ε.

Definition 2.2

We use $\mathbb{N}$ to denote the set of positive integers and $\mathbb{Z}$ to denote the set of integers.

Definition 2.3

Let $(X,d)$ be a compact metric space. Then we define $2^X$ by $\begin{array}{r}{2}^X=\{A\subseteq X|A\text{ is a non-empty closed subset of }X\}.\end{array}$Let $\epsilon >0$ and let $A\in 2^X$. Then we define $N_d(\epsilon ,A)$ by $\begin{array}{r}{N}_d(\epsilon ,A)=\bigcup _{a\in A}B(a,\epsilon ).\end{array}$Let $A,B\in 2^X$. The function $H_d:2^X\times 2^X\to \mathbb{R}$, defined by $\begin{array}{r}{H}_d(A,B)=inf\{\epsilon >0|A\subseteq N_d(\epsilon ,B),B\subseteq N_d(\epsilon ,A)\},\end{array}$is called the Hausdorff metric. The Hausdorff metric is in fact a metric and the metric space $(2^X,H_d)$ is called a hyperspace of the space $(X,d)$.

Remark 2.1

Let $(X,d)$ be a compact metric space, let A be a non-empty closed subset of X, and let $(A_n)$ be a sequence of non-empty closed subsets of X. When we say ${\displaystyle A=\underset{n\to \mathrm{\infty }}{lim}{A}_n}$, we mean ${\displaystyle A=\underset{n\to \mathrm{\infty }}{lim}{A}_n}$ in $(2^X,H_d)$.

Definition 2.4

A continuum is a non-empty compact connected metric space. A subcontinuum is a subspace of a continuum, which is itself a continuum.

Definition 2.5

Let X be a continuum.

1. The continuum X is unicoherent if for any subcontinua A and B of X such that $X=A\cup B$, the compactum $A\cap B$ is connected.

2. The continuum X is hereditarily unicoherent provided that each of its subcontinua is unicoherent.

3. The continuum X is a dendroid if it is an arcwise connected hereditarily unicoherent continuum.

4. Let X be a continuum. If X is homeomorphic to $[0,1]$, then X is an arc.

5. A point x in an arc X is called an endpoint of the arc X if there is a homeomorphism $\phi :[0,1]\to X$ such that $\phi (0)=x$.

6. Let X be a dendroid. A point $x\in X$ is called an endpoint of the dendroid X if for every arc A in X that contains x, x is an endpoint of A. The set of all endpoints of X will be denoted by $E(X)$.

7. A continuum X is a simple triod if it is homeomorphic to $([-1,1]\times \{0\})\cup (\{0\}\times [0,1])$.

8. A point x in a simple triod X is called the top-point or just the top of the simple triod X if there is a homeomorphism $\phi :([-1,1]\times \{0\})\cup (\{0\}\times [0,1])\to X$ such that $\phi (0,0)=x$.

9. Let X be a dendroid. A point $x\in X$ is called a ramification point of the dendroid X if there is a simple triod T in X with the top x. The set of all ramification points of X will be denoted by $R(X)$.

10. The continuum X is a fan if it is a dendroid with at most one ramification point v, which is called the top of the fan X (if it exists).

11. Let X be a fan. For all points x and y in X, we define $A_X[x,y]$ to be the arc in X with endpoints x and y if $x\ne y$. If x=y, then we define $A_X[x,y]=\{x\}$.

12. Let X be a fan with top v. We say that that the fan X is smooth if for any $x\in X$ and for any sequence $(x_n)$ of points in X, $\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}{x}_n=x⟹\underset{n\to \mathrm{\infty }}{lim}{A}_X[v,x_n]=A_X[v,x].\end{array}$

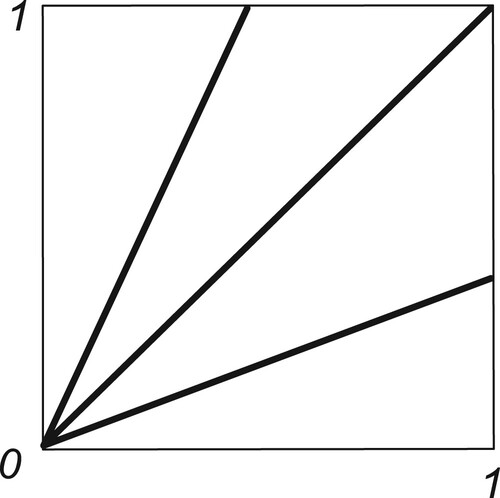
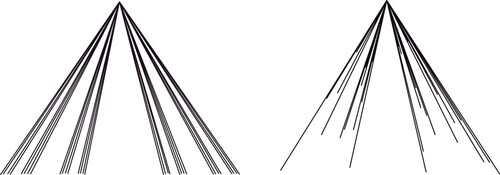
13. Let X be a fan. We say that X is a Cantor fan if X is homeomorphic to the continuum $\begin{array}{r}\bigcup _{c\in C}{S}_c,\end{array}$where $C\subseteq [0,1]$ is the standard Cantor set and for each $c\in C$, $S_c$ is the straight line segment in the plane from $(0,0)$ to $(c,1)$. See Figure 1 where a Cantor fan is pictured.

    Figure 1. A Cantor fan and a Lelek fan.

    

14. Let X be a fan. We say that X is a Lelek fan if it is smooth and $\mathrm{Cl}(E(X))=X$. See Figure 1 where a Lelek fan is pictured.

Observation 2.6

The Cantor fan is universal for smooth fans, i.e. every smooth fan embeds into it (for details see [12, Theorem 9, p. 27], [17, Corollary 4], and [15]).

Also, note that a Lelek fan was constructed by A. Lelek in [19]. An interesting property of the Lelek fan L is that the set of its endpoints is a dense one-dimensional set in L. It is also unique, i.e. any two Lelek fans are homeomorphic, for the proofs see [11,13].

In this paper, X will always be a non-empty compact metric space.

Definition 2.7

Let X be a non-empty compact metric space and let $f:X\to X$ be a continuous function. We say that $(X,f)$ is a dynamical system.

Definition 2.8

Let $(X,f)$ be a dynamical system and let $x\in X$. The sequence $\begin{array}{r}\mathbf{x}=(x,f(x),f^2(x),f^3(x),\dots )\end{array}$is called the trajectory of x. The set $\begin{array}{r}{\mathcal{O}}_f^{\oplus }(x)=\{x,f(x),f^2(x),f^3(x),\dots \}\end{array}$is called the forward orbit set of x.

Definition 2.9

Let $(X,f)$ be a dynamical system and let $x\in X$. If $\mathrm{Cl}({\mathcal{O}}_f^{\oplus }(x))=X$, then x is called a transitive point in $(X,f)$. Otherwise it is an intransitive point in $(X,f)$. We use $\text{tr}(f)$ to denote the set $\begin{array}{r}\text{tr}(f)=\{x\in X|x\text{is a transitive point in}(X,f)\}.\end{array}$

Definition 2.10

Let $(X,f)$ be a dynamical system. We say that $(X,f)$ is transitive if for all non-empty open sets U and V in X, there is a non-negative integer n such that $f^n(U)\cap V\ne \mathrm{\varnothing }$. We say that the mapping f is transitive if $(X,f)$ is transitive.

The following theorem is a well-known result. See [18] for more information about transitive dynamical systems.

Theorem 2.11

Let $(X,f)$ be a dynamical system. Then the following hold.

(1)	If $(X,f)$ is transitive, then for each $x\in \text{tr}(f)$ and for each positive integer n, $f^n(x)\in \text{tr}(f)$.
(2)	If $(X,f)$ is transitive, then $\text{tr}(f)$ is dense in X.

Definition 2.12

Let $(X,f)$ be a dynamical system. We say that $(X,f)$ is mixing if for all non-empty open sets U and V in X, there is a non-negative integer $n_0$ such that for each positive integer n, $\begin{array}{r}n\ge n_0⟹f^n(U)\cap V\ne \mathrm{\varnothing }.\end{array}$We say that the mapping f is mixing if $(X,f)$ is mixing.

Definition 2.13

Let $(X,f)$ and $(Y,g)$ be dynamical systems. We say that

1. $(Y,g)$ is topologically conjugate to $(X,f)$ if there is a homeomorphism $\phi :X\to Y$ such that $\phi \circ f=g\circ \phi$.

2. $(Y,g)$ is topologically semi-conjugate to $(X,f)$ if there is a continuous surjection $\alpha :X\to Y$ such that $\alpha \circ f=g\circ \alpha$.

Definition 2.14

Let X be a compact metric space. We say that X

1. admits a transitive homeomorphism if there is a homeomorphism $f:X\to X$ such that $(X,f)$ is transitive.

2. admits a mixing homeomorphism if there is a homeomorphism $f:X\to X$ such that $(X,f)$ is mixing.

Theorems 2.15 and 2.16 are well-known results. Their proofs may be found in [1,2,18].

Theorem 2.15

Let $(X,f)$ be a dynamical system such that f is a homeomorphism. Then the following hold.

(1)	$(X,f^{-1})$ is transitive if and only if $(X,f)$ is transitive.
(2)	$(X,f^{-1})$ is mixing if and only if $(X,f)$ is mixing.

Theorem 2.16

Let $(X,f)$ and $(Y,g)$ be dynamical systems.

(1)	If $(X,f)$ is transitive and if $(Y,g)$ is topologically semi-conjugate to $(X,f)$, then $(Y,g)$ is transitive.
(2)	If $(X,f)$ is mixing and if $(Y,g)$ is topologically semi-conjugate to $(X,f)$, then $(Y,g)$ is mixing.

Definition 2.17

Let X be a compact metric space and let $f:X\to X$ be a continuous function. The inverse limit generated by $(X,f)$ is the subspace $\begin{array}{r}\underleftarrow{\lim }(X,f)=\{(x_1,x_2,x_3,\dots )\in \prod _{i=1}^{\mathrm{\infty }}X|\text{for each positive integer}i,x_i=f(x_{i+1})\}\end{array}$of the topological product $\prod _{i=1}^{\mathrm{\infty }}X$. The function $\sigma :\underleftarrow{\lim }(X,f)\to \underleftarrow{\lim }(X,f)$, defined by $\begin{array}{r}\sigma (x_1,x_2,x_3,x_4,\dots )=(x_2,x_3,x_4,\dots )\end{array}$for each $(x_1,x_2,x_3,\dots )\in \underleftarrow{\lim }(X,f)$, is called the shift map on $\underleftarrow{\lim }(X,f)$.

Observation 2.18

Note that the shift map σ on the inverse limit $\underleftarrow{\lim }(X,f)$ is a homeomorphism. Also, note that for each $(x_1,x_2,x_3,\dots )\in \underleftarrow{\lim }(X,f)$, $\begin{array}{r}{\sigma }^{-1}(x_1,x_2,x_3,\dots )=(f(x_1),x_1,x_2,x_3,\dots ).\end{array}$

Theorem 2.19 is a well-known result. Its proof may be found in [2] or in [18].

Theorem 2.19

Let $(X,f)$ be a mixing dynamical system such that f is surjective and let $\sigma :\underleftarrow{\lim }(X,f)\to \underleftarrow{\lim }(X,f)$ be the shift map on $\underleftarrow{\lim }(X,f)$. Then the following hold.

(1)	$(X,f)$ is transitive if and only if $(\underleftarrow{\lim }(X,f),\sigma )$ is transitive.
(2)	$(X,f)$ is mixing if and only if $(\underleftarrow{\lim }(X,f),\sigma )$ is mixing.

Definition 2.20

Let $(X,f)$ be a dynamical system. We say that $(X,f)$ has sensitive dependence on initial conditions if there is an $\epsilon >0$ such that for each $x\in X$ and for each $\delta >0$, there are $y\in B(x,\delta )$ and a positive integer n such that $\begin{array}{r}d(f^n(x),f^n(y))>\epsilon .\end{array}$

Observation 2.21

Let $(X,f)$ be a dynamical system. Note that $(X,f)$ has sensitive dependence on initial conditions if and only if there is $\epsilon >0$ such that for each non-empty open set U in X, there is a positive integer n such that $\mathrm{diam}(f^n(U))>\epsilon$. See [8, Theorem 2.29] for more information.

Definition 2.22

Let $(X,f)$ be a dynamical system and let A be a non-empty closed subset of X. We say that $(X,f)$ has sensitive dependence on initial conditions with respect to A if there is $\epsilon >0$ such that for each non-empty open set U in X, there are $x,y\in U$ and a positive integer n such that¹ $\begin{array}{r}min\{d(f^n(x),f^n(y)),d(f^n(x),A)+d(f^n(y),A)\}>\epsilon .\end{array}$

Proposition 2.23

Let $(X,f)$ be a dynamical system and let A be a non-empty closed subset of X. If $(X,f)$ has sensitive dependence on initial conditions with respect to A, then $(X,f)$ has sensitive dependence on initial conditions.

Proof.

Suppose that $(X,f)$ has sensitive dependence on initial conditions with respect to A and let $\epsilon >0$ be such that for each non-empty open set U in X, there are $x,y\in U$ and a positive integer n such that $\begin{array}{r}min\{d(f^n(x),f^n(y)),d(f^n(x),A)+d(f^n(y),A)\}>\epsilon .\end{array}$To see that $(X,f)$ has sensitive dependence on initial conditions, we use Observation 2.21. Let U be any non-empty open set in X and let $x,y\in U$ and let n be a positive integer such that $\begin{array}{r}min\{d(f^n(x),f^n(y)),d(f^n(x),A)+d(f^n(y),A)\}>\epsilon .\end{array}$Then $\begin{array}{r}\mathrm{diam}(f^n(U))\ge d(f^n(x),f^n(y))\ge min\{d(f^n(x),f^n(y)),d(f^n(x),A)+d(f^n(y),A)\}>\epsilon \end{array}$and we are done.

We use the following result.

Theorem 2.24

Let $(X,f)$ be a dynamical system such that f is surjective, let A be a non-empty closed subset of X such that $f(A)\subseteq A$, and let σ be the shift homeomorphism on $\underleftarrow{\lim }(X,f)$. If f is surjective and $(X,f)$ has sensitive dependence on initial conditions with respect to A, then $(\underleftarrow{\lim }(X,f),{\sigma }^{-1})$ has sensitive dependence on initial conditions with respect to $\underleftarrow{\lim }(A,f{|}_A)$.

Proof.

See [8, Theorem 3.14].

We conclude this section by defining three different types of chaos. First, we define periodic points.

Definition 2.25

Let $(X,f)$ be a dynamical system and $p\in X$. We say that p is a periodic point in $(X,f)$ if there is a positive integer n such that $f^n(p)=p$. We use $\mathcal{P}(f)$ to denote the set of periodic points in $(X,f)$.

Definition 2.26

Let $(X,f)$ be a dynamical system. We say that $(X,f)$ is chaotic in the sense of Robinson [20] if

1. $(X,f)$ is transitive, and

2. $(X,f)$ has sensitive dependence on initial conditions.

Definition 2.27

Let $(X,f)$ be a dynamical system. We say that $(X,f)$ is chaotic in the sense of Knudsen [16] if

1. $\mathcal{P}(f)$ is dense in X, and

2. $(X,f)$ has sensitive dependence on initial conditions.

Definition 2.28

Let $(X,f)$ be a dynamical system. We say that $(X,f)$ is chaotic in the sense of Devaney [14], if

1. $(X,f)$ is transitive, and

2. $\mathcal{P}(f)$ is dense in X.

Observation 2.29

Note that it is proved in [10, Theorem] that for any dynamical system $(X,f)$, $(X,f)$ has sensitive dependence on initial conditions if $(X,f)$ is transitive and if the set $\mathcal{P}(f)$ is dense in X.

We also use special kind of projections that are defined in the following definition.

Definition 2.30

For each (positive) integer i and for each $\mathbf{x}=(x_1,x_2,x_3,\dots )\in \prod _{k=1}^{\mathrm{\infty }}X$ (or $\mathbf{x}=(\dots ,x_{-2},x_{-1},x_0,x_1,x_2,\dots )\in \prod _{k=-\mathrm{\infty }}^{\mathrm{\infty }}X$ or $\mathbf{x}=(x_1,x_2,x_3,\dots ,x_m)\in \prod _{k=1}^{m}X$), we use ${\pi }_i(\mathbf{x})$ or $\mathbf{x}(i)$ or ${\mathbf{x}}_i$ to denote the ith coordinate $x_i$ of the point $\mathbf{x}$.

We also use $p_1:X\times X\to X$ and $p_2:X\times X\to X$ to denote the standard projections defined by $p_1(s,t)=s$ and $p_2(s,t)=t$ for all $(s,t)\in X\times X$.

3. Mixing, Mahavier dynamical systems and quotients of dynamical systems

We give new results about how Mahavier products of closed relations on compact metric spaces can be used to construct dynamical systems $(X,f)$ such that f is a mixing homeomorphism. Then we study quotients of dynamical systems. Explicitly, we start with a dynamical system $(X,f)$ and an equivalence relation ∼ on X. Then, we discuss when the mixing of $(X,f)$ implies the mixing of $(X{/}_{\sim },f^{\star })$.

3.1. Mixing and Mahavier dynamical systems

First, we define Mahavier products of closed relations.

Definition 3.1

Let X be a non-empty compact metric space and let $F\subseteq X\times X$ be a non-empty relation on X. If $F$ is closed in $X\times X$, then we say that $F$ is a closed relation on X.

Definition 3.2

Let X be a non-empty compact metric space and let $F$ be a closed relation on X. For each positive integer m, we call $\begin{array}{r}{X}_F^m=\{(x_1,x_2,\dots ,x_{m+1})\in \prod _{i=1}^{m+1}X|\text{for each}i\in \{1,2,\dots ,m\},(x_i,x_{i+1})\in F\}\end{array}$the mth Mahavier product of F; we call $\begin{array}{r}{X}_F^{+}=\{(x_1,x_2,x_3,\dots )\in \prod _{i=1}^{\mathrm{\infty }}X|\text{for each positive integer}i,(x_i,x_{i+1})\in F\}\end{array}$the Mahavier product of $F$; and $\begin{array}{r}{X}_F=\{(\dots ,x_{-3},x_{-2},x_{-1},x_0;x_1,x_2,x_3,\dots )\in \prod _{i=-\mathrm{\infty }}^{\mathrm{\infty }}X|\text{for each integer}i,(x_i,x_{i+1})\in F\}\end{array}$the two-sided Mahavier product of $F$.

Definition 3.3

Let X be a non-empty compact metric space and let $F$ be a closed relation on X. The function ${\sigma }_F^{+}:X_F^{+}\to X_F^{+}$, defined by $\begin{array}{r}{\sigma }_F^{+}(x_1,x_2,x_3,x_4,\dots )=(x_2,x_3,x_4,\dots )\end{array}$for each $(x_1,x_2,x_3,x_4,\dots )\in X_F^{+}$, is called the shift map on $X_F^{+}$. The function ${\sigma }_F:X_F\to X_F$, defined by $\begin{array}{r}{\sigma }_F(\dots ,x_{-3},x_{-2},x_{-1},x_0;x_1,x_2,x_3,\dots )=(\dots ,x_{-3},x_{-2},x_{-1},x_0,x_1;x_2,x_3,\dots )\end{array}$for each $(\dots ,x_{-3},x_{-2},x_{-1},x_0;x_1,x_2,x_3,\dots )\in X_F$, is called the shift map on $X_F$.

Observation 3.4

Note that ${\sigma }_F$ is always a homeomorphism while ${\sigma }_F^{+}$ may not be a homeomorphism.

Definition 3.5

Let X be a compact metric space and let F be a closed relation on X. The dynamical system

1. $(X_F^{+},{\sigma }_F^{+})$ is called a Mahavier dynamical system.

2. $(X_F,{\sigma }_F)$ is called a two-sided Mahavier dynamical system.

Observation 3.6

Let X be a compact metric space and let F be a closed relation on X such that $p_1(F)=p_2(F)=X$. Note that $(X_F^{+},{\sigma }_F^{+})$ is semi-conjugate to $(X_F,{\sigma }_F)$: for $\alpha :X_F\to X_F^{+}$, defined by $\alpha (\mathbf{x})=(\mathbf{x}(1),\mathbf{x}(2),\mathbf{x}(3),\dots )$ for any $\mathbf{x}\in X_F$, $\alpha \circ {\sigma }_F={\sigma }_F^{+}\circ \alpha$.

Theorems 3.7 and 3.8 are proved in [7] (Theorems 4.1 and 4.4, respectively). We use these theorems to prove Theorems 3.9 and 3.13.

Theorem 3.7

Let X be a compact metric space and let F be a closed relation on X. Then

(1)	$\underleftarrow{\lim }(X_F^{+},{\sigma }_F^{+})$ is homeomorphic to the two-sided Mahavier product $X_F$.
(2)	The inverse ${\sigma }_F^{-1}$ of the shift map ${\sigma }_F$ on $X_F$ is topologically conjugate to the shift map σ on $\underleftarrow{\lim }(X_F^{+},{\sigma }_F^{+})$.

Theorem 3.8

Let X be a compact metric space and let F be a closed relation on X such that $p_1(F)=p_2(F)=X$. Then the following statements are equivalent.

(1)	$(X_F^{+},{\sigma }_F^{+})$ is transitive.
(2)	$(X_F,{\sigma }_F)$ is transitive.

Next, we show that if $p_1(F)=p_2(F)=X$, then $(X_F^{+},{\sigma }_F^{+})$ is mixing if and only if $(X_F,{\sigma }_F)$ is mixing.

Theorem 3.9

Let X be a compact metric space and let F be a closed relation on X such that $p_1(F)=p_2(F)=X$. Then the following statements are equivalent.

(1)	$(X_F^{+},{\sigma }_F^{+})$ is mixing.
(2)	$(X_F,{\sigma }_F)$ is mixing.

Proof.

Let σ be the shift map on $\underleftarrow{\lim }(X_F^{+},{\sigma }_F^{+})$. First, suppose that $(X_F^{+},{\sigma }_F^{+})$ is mixing. It follows from $p_1(F)=p_2(F)=X$ that ${\sigma }_F^{+}$ is surjective. By Theorem 2.19, $(\underleftarrow{\lim }(X_F^{+},{\sigma }_F^{+}),\sigma )$ is also mixing. By Theorem 3.7, σ is topologically conjugate to ${\sigma }_F^{-1}$, therefore, $(X_F,{\sigma }_F^{-1})$ is mixing. It follows from Theorem 2.15 that $(X_F,{\sigma }_F)$ is mixing.

Next, suppose that $(X_F,{\sigma }_F)$ is mixing. By Theorem 2.15, $(X_F,{\sigma }_F^{-1})$ is also mixing and it follows from Theorem 3.7 that $(\underleftarrow{\lim }(X_F^{+},{\sigma }_F^{+}),\sigma )$ is mixing. Since ${\sigma }_F^{+}$ is surjective, it follows from Theorem 2.19 that $(X_F^{+},{\sigma }_F^{+})$ is mixing.

Definition 3.10

Let X be a compact metric space. We use ${\mathrm{\Delta }}_X$ to denote the diagonal set $\begin{array}{r}{\mathrm{\Delta }}_X=\{(x,x)|x\in X\}.\end{array}$

We use the following lemma to prove Theorem 3.12, where we prove that for each transitive system $(X_F^{+},{\sigma }_F^{+})$ if ${\mathrm{\Delta }}_X\subseteq F$, then $(X_F^{+},{\sigma }_F^{+})$ is mixing.

Lemma 3.11

Let X be a compact metric space, let F be a closed relation on X and let U be a non-empty open set in $X_F^{+}$. Then for each $\mathbf{x}\in U$, there is a positive integer $n_0$ such that for each $\mathbf{y}\in X_F^{+}$, $\begin{array}{r}(\text{for each integer}n\le n_0,{\pi }_n(\mathbf{y})={\pi }_n(\mathbf{x}))⟹\mathbf{y}\in U.\end{array}$

Proof.

Let k be a positive integer and let $U_1$, $U_2$, $U_3$, …, $U_k$ be open sets in X such that $\begin{array}{r}\mathbf{x}\in U_1\times U_2\times U_3\times \cdots \times U_k\times \prod _{i=k+1}^{\mathrm{\infty }}X\subseteq U.\end{array}$Let $n_0=k$ and let $\mathbf{y}\in X_F^{+}$ be such that for each positive integer $n\le n_0$, ${\pi }_n(\mathbf{y})={\pi }_n(\mathbf{x})$. Then $\mathbf{y}\in U_1\times U_2\times U_3\times \cdots \times U_k\times \prod _{i=k+1}^{\mathrm{\infty }}X$ and since $U_1\times U_2\times U_3\times \cdots \times U_k\times \prod _{i=k+1}^{\mathrm{\infty }}X\subseteq U$, it follows that $\mathbf{y}\in U$.

Theorem 3.12

Let X be a compact metric space and let F be a closed relation on X. If

(1)	$(X_F^{+},{\sigma }_F^{+})$ is transitive, and
(2)	${\mathrm{\Delta }}_X\subseteq F$,

then $(X_F^{+},{\sigma }_F^{+})$ is mixing.

Proof.

Let U and V be non-empty open sets in $X_F^{+}$. Since $(X_F^{+},{\sigma }_F^{+})$ is transitive, it follows from Theorem 2.11 that $\text{tr}({\sigma }_F^{+})$ is dense in $X_F^{+}$. Therefore, $\text{tr}({\sigma }_F^{+})\cap U\ne \mathrm{\varnothing }$. Let $\mathbf{x}\in \text{tr}({\sigma }_F^{+})\cap U$. By Lemma 3.11, there is a positive integer $m_0$ such that for each $\mathbf{y}\in X_F^{+}$, $\begin{array}{r}(\text{for each positive integer}n\le m_0,{\pi }_n(\mathbf{y})={\pi }_n(\mathbf{x}))⟹\mathbf{y}\in U.\end{array}$Choose and fix such a positive integer $m_0$. Next, let m be a positive integer such that $m>m_0$ and such that $({\sigma }_F^{+}{)}^m(\mathbf{x})\in V$, and let $\begin{array}{r}{\mathbf{x}}_1=(\mathbf{x}(1),\mathbf{x}(2),\mathbf{x}(3),\dots ,\mathbf{x}(m-1),\underset{2}{\underbrace{\mathbf{x}\mathbf{(}\mathbf{m}\mathbf{)}\mathbf{,}\mathbf{x}\mathbf{(}\mathbf{m}\mathbf{)}}},\mathbf{x}(m+1),\mathbf{x}(m+2),\mathbf{x}(m+3),\dots ).\end{array}$Then for each positive integer $n\le m$, ${\pi }_n({\mathbf{x}}_1)={\pi }_n(\mathbf{x})$. Therefore, ${\mathbf{x}}_1\in U$. Also, note that $({\sigma }_F^{+}{)}^{m+1}({\mathbf{x}}_1)=({\sigma }_F^{+}{)}^m(\mathbf{x})$, therefore, $({\sigma }_F^{+}{)}^{m+1}({\mathbf{x}}_1)\in V$. It follows that $({\sigma }_F^{+}{)}^{m+1}(U)\cap V\ne \mathrm{\varnothing }$.

Next, let $\begin{array}{rl}{\mathbf{x}}_2& =(\mathbf{x}(1),\mathbf{x}(2),\mathbf{x}(3),\dots ,\mathbf{x}(m-1),\underset{3}{\underbrace{\mathbf{x}\mathbf{(}\mathbf{m}\mathbf{)}\mathbf{,}\mathbf{x}\mathbf{(}\mathbf{m}\mathbf{)}\mathbf{,}\mathbf{x}\mathbf{(}\mathbf{m}\mathbf{)}}},\mathbf{x}(m+1),\\ & \mathbf{x}(m+2),\mathbf{x}(m+3),\dots ).\end{array}$Then for each positive integer $n\le m$, ${\pi }_n({\mathbf{x}}_2)={\pi }_n(\mathbf{x})$. Therefore, ${\mathbf{x}}_2\in U$. Also, note that $({\sigma }_F^{+}{)}^{m+2}({\mathbf{x}}_2)=({\sigma }_F^{+}{)}^m(\mathbf{x})$, therefore, $({\sigma }_F^{+}{)}^{m+2}({\mathbf{x}}_2)\in V$. It follows that $({\sigma }_F^{+}{)}^{m+2}(U)\cap V\ne \mathrm{\varnothing }$.

In general, let k be any positive integer and let $\begin{array}{rl}{\mathbf{x}}_k& =(\mathbf{x}(1),\mathbf{x}(2),\mathbf{x}(3),\dots ,\mathbf{x}(m-1),\underset{k}{\underbrace{\mathbf{x}\mathbf{(}\mathbf{m}\mathbf{)}\mathbf{,}\mathbf{x}\mathbf{(}\mathbf{m}\mathbf{)}\mathbf{,}\dots \mathbf{,}\mathbf{x}\mathbf{(}\mathbf{m}\mathbf{)}}},\\ & \mathbf{x}(m+1),\mathbf{x}(m+2),\mathbf{x}(m+3),\dots ).\end{array}$Then for each positive integer $n\le m$, ${\pi }_n({\mathbf{x}}_k)={\pi }_n(\mathbf{x})$. Therefore, ${\mathbf{x}}_k\in U$. Also, note that $({\sigma }_F^{+}{)}^{m+k}({\mathbf{x}}_k)=({\sigma }_F^{+}{)}^m(\mathbf{x})$, therefore, $({\sigma }_F^{+}{)}^{m+k}({\mathbf{x}}_k)\in V$. It follows that $({\sigma }_F^{+}{)}^{m+k}(U)\cap V\ne \mathrm{\varnothing }$. This proves that for any positive integer n, $\begin{array}{r}n\ge m⟹({\sigma }_F^{+}{)}^n(U)\cap V\ne \mathrm{\varnothing },\end{array}$therefore, $(X_F^{+},{\sigma }_F^{+})$ is mixing.

Theorem 3.13 is a variant of Theorem 3.12 where $(X_F^{+},{\sigma }_F^{+})$ from Theorem 3.12 is replaced by $(X_F,{\sigma }_F)$.

Theorem 3.13

Let X be a compact metric space and let F be a closed relation on X. If

(1)	$(X_F,{\sigma }_F)$ is transitive, and
(2)	${\mathrm{\Delta }}_X\subseteq F$,

then $(X_F,{\sigma }_F)$ is mixing.

Proof.

Suppose that $(X_F,{\sigma }_F)$ is transitive, and that ${\mathrm{\Delta }}_X\subseteq F$. Note that $p_1(F)=p_2(F)=X$ since ${\mathrm{\Delta }}_X\subseteq F$. By Theorem 3.8, $(X_F^{+},{\sigma }_F^{+})$ is transitive. Since ${\mathrm{\Delta }}_X\subseteq F$, it follows from Theorem 3.12 that $(X_F^{+},{\sigma }_F^{+})$ is mixing. By Theorem 3.9, $(X_F,{\sigma }_F)$ is mixing since ${\mathrm{\Delta }}_X\subseteq F$.

In Theorem 3.14, we show that adding the diagonal to the closed relation, preserves the transitivity of the Mahavier dynamical system.

Theorem 3.14

Let X be a compact metric space, let G be a closed relation on X such that $p_1(G)=p_2(G)=X$ and let $F=G\cup {\mathrm{\Delta }}_X$. Then the following hold.

(1)	If $(X_G^{+},{\sigma }_G^{+})$ is transitive, then $(X_F^{+},{\sigma }_F^{+})$ is transitive.
(2)	If $(X_G,{\sigma }_G)$ is transitive, then $(X_F,{\sigma }_F)$ is transitive.

Proof.

To prove Theorem 3.14(1), suppose that $(X_G^{+},{\sigma }_G^{+})$ is transitive, let m and n be positive integers, let $U_1$, $U_2$, $U_3$, …, $U_m$, $V_1$, $V_2$, $V_3$, …, $V_n$ be non-empty open sets in X, and let $\begin{array}{r}U=U_1\times U_2\times U_3\times \cdots \times U_m\times \prod _{k=m+1}^{\mathrm{\infty }}X\end{array}$and $\begin{array}{r}V=V_1\times V_2\times V_3\times \cdots \times V_n\times \prod _{k=n+1}^{\mathrm{\infty }}X\end{array}$be such that $U\cap X_F^{+}\ne \mathrm{\varnothing }$ and $V\cap X_F^{+}\ne \mathrm{\varnothing }$. To see that $(X_F^{+},{\sigma }_F^{+})$ is transitive, we prove that there is a non-negative integer ℓ such that $({\sigma }_F^{+}{)}^{\ell }(U\cap X_F^{+})\cap (V\cap X_F^{+})\ne \mathrm{\varnothing }$.

First, let $\mathbf{y}\in U\cap X_F^{+}$ be such that $({\sigma }_F^{+}{)}^{m-1}(\mathbf{y})\in X_G^{+}$, and let $\begin{array}{r}D=\{k\in \{1,2,3,\dots ,m-1\}|\mathbf{y}(k)\ne \mathbf{y}(k+1)\}.\end{array}$Next, let $s\in \{1,2,3,\dots ,m-1\}$ and let $k_1,k_2,k_3,\dots ,k_s\in \{1,2,3,\dots ,m-1\}$ be such that

1. for each $i\in \{1,2,3,\dots ,s\}$, $k_i<k_{i+1}$ and

2. $D=\{k_1,k_2,k_3,\dots ,k_s\}$.

Also, let $\begin{array}{rl}\hat{U}& =\underset{k_1}{\underbrace{\left(\bigcap _{i=1}^{k_1}{U}_i\right)\times \left(\bigcap _{i=1}^{k_1}{U}_i\right)\times \left(\bigcap _{i=1}^{k_1}{U}_i\right)\times \cdots \times \left(\bigcap _{i=1}^{k_1}{U}_i\right)}}\\ & \times \underset{k_2-k_1}{\underbrace{\left(\bigcap _{i=k_1+1}^{k_2}{U}_i\right)\times \left(\bigcap _{i=k_1+1}^{k_2}{U}_i\right)\times \left(\bigcap _{i=k_1+1}^{k_2}{U}_i\right)\times \cdots \times \left(\bigcap _{i=k_1+1}^{k_2}{U}_i\right)}}\\ & \times \cdots \times \underset{k_s-k_{s-1}}{\underbrace{\left(\bigcap _{i=k_{s-1}+1}^{k_s}{U}_i\right)\times \left(\bigcap _{i=k_{s-1}+1}^{k_s}{U}_i\right)\times \left(\bigcap _{i=k_{s-1}+1}^{k_s}{U}_i\right)\times \cdots \times \left(\bigcap _{i=k_{s-1}+1}^{k_s}{U}_i\right)}}\\ & \times \cdots \times \underset{m-k_s}{\underbrace{\left(\bigcap _{i=k_s+1}^m{U}_i\right)\times \left(\bigcap _{i=k_s+1}^m{U}_i\right)\times \left(\bigcap _{i=k_s+1}^m{U}_i\right)\times \cdots \times \left(\bigcap _{i=k_s+1}^m{U}_i\right)}}\\ & \times \prod _{k=m+1}^{\mathrm{\infty }}X\end{array}$and let $\begin{array}{rl}\overline{U}& =\left(\bigcap _{i=1}^{k_1}{U}_i\right)\times \left(\bigcap _{i=k_1+1}^{k_2}{U}_i\right)\times \left(\bigcap _{i=k_2+1}^{k_3}{U}_i\right)\times \cdots \times \left(\bigcap _{i=k_{s-1}+1}^{k_s}{U}_i\right)\times \left(\bigcap _{i=k_s+1}^m{U}_i\right)\\ & \times \prod _{k=s+2}^{\mathrm{\infty }}X.\end{array}$Then, let $\mathbf{z}\in V\cap X_F^{+}$ be such that $({\sigma }_F^{+}{)}^{n-1}(\mathbf{z})\in X_G^{+}$, and let $\begin{array}{r}E=\{k\in \{1,2,3,\dots ,n-1\}|\mathbf{z}(k)\ne \mathbf{z}(k+1)\}.\end{array}$Next, let $t\in \{1,2,3,\dots ,m-1\}$ and let $l_1,l_2,l_3,\dots ,l_t\in \{1,2,3,\dots ,m-1\}$ be such that

1. for each $i\in \{1,2,3,\dots ,t\}$, $l_i<l_{i+1}$ and

2. $D=\{l_1,l_2,l_3,\dots ,l_t\}$.

Also, let $\begin{array}{rl}\hat{V}=& \underset{l_1}{\underbrace{\left(\bigcap _{i=1}^{l_1}{V}_i\right)\times \left(\bigcap _{i=1}^{l_1}{V}_i\right)\times \left(\bigcap _{i=1}^{l_1}{V}_i\right)\times \cdots \times \left(\bigcap _{i=1}^{l_1}{V}_i\right)}}\\ & \times \underset{l_2-l_1}{\underbrace{\left(\bigcap _{i=l_1+1}^{l_2}{V}_i\right)\times \left(\bigcap _{i=l_1+1}^{l_2}{V}_i\right)\times \left(\bigcap _{i=l_1+1}^{l_2}{V}_i\right)\times \cdots \times \left(\bigcap _{i=l_1+1}^{l_2}{V}_i\right)}}\\ & \times \cdots \times \underset{l_t-l_{t-1}}{\underbrace{\left(\bigcap _{i=l_{t-1}+1}^{l_t}{V}_i\right)\times \left(\bigcap _{i=l_{t-1}+1}^{l_t}{V}_i\right)\times \left(\bigcap _{i=l_{t-1}+1}^{l_t}{V}_i\right)\times \cdots \times \left(\bigcap _{i=l_{t-1}+1}^{l_t}{V}_i\right)}}\\ & \times \cdots \times \underset{n-l_t}{\underbrace{\left(\bigcap _{i=l_t+1}^n{V}_i\right)\times \left(\bigcap _{i=l_t+1}^n{V}_i\right)\times \left(\bigcap _{i=l_t+1}^n{V}_i\right)\times \cdots \times \left(\bigcap _{i=l_t+1}^n{V}_i\right)}}\times \prod _{k=n+1}^{\mathrm{\infty }}X\end{array}$and let $\begin{array}{rl}\overline{V}& =\left(\bigcap _{i=1}^{l_1}{V}_i\right)\times \left(\bigcap _{i=l_1+1}^{l_2}{V}_i\right)\times \left(\bigcap _{i=l_2+1}^{l_3}{V}_i\right)\times \cdots \times \left(\bigcap _{i=l_{t-1}+1}^{k_t}{V}_i\right)\times \left(\bigcap _{i=l_t+1}^n{V}_i\right)\\ & \times \prod _{k=t+2}^{\mathrm{\infty }}X.\end{array}$Note that

1. $\hat{U}$ and $\hat{V}$ are both open in $\prod _{k=1}^{\mathrm{\infty }}X$ such that $\mathbf{y}\in \hat{U}\subseteq U$ and $\mathbf{z}\in \hat{V}\subseteq V$, and

2. $\overline{U}$ and $\overline{V}$ are both open in $\prod _{k=1}^{\mathrm{\infty }}X$ such that $\begin{array}{r}(\mathbf{y}(1),\mathbf{y}(k_1+1),\mathbf{y}(k_2+1),\dots ,\mathbf{y}(k_s+1),\mathbf{y}(k_s+2),\mathbf{y}(k_s+3),\dots )\in \overline{U}\cap X_G^{+}\end{array}$and $\begin{array}{r}(\mathbf{z}(1),\mathbf{z}(l_1+1),\mathbf{z}(l_2+1),\dots ,\mathbf{z}(l_t+1),\mathbf{z}(l_t+2),\mathbf{z}(l_t+3),\dots )\in \overline{V}\cap X_G^{+}.\end{array}$

Next, let ℓ be a positive integer such that $\ell >m$ and $({\sigma }_G^{+}{)}^{\ell }(\overline{U}\cap X_G^{+})\cap (\overline{V}\cap X_G^{+})\ne \mathrm{\varnothing }$ and let $\overline{\mathbf{x}}\in \overline{U}\cap X_G^{+}$ be such that $({\sigma }_G^{+}{)}^{\ell }(\overline{\mathbf{x}})\in \overline{V}\cap X_G^{+}$. Note that such an integer ℓ does exist by Theorem 2.11. Finally, let $\begin{array}{rl}\mathbf{x}& =(\underset{k_1}{\underbrace{\overline{\mathbf{x}}(1),\overline{\mathbf{x}}(1),\overline{\mathbf{x}}(1),\dots ,\overline{\mathbf{x}}(1)}},\underset{k_2-k_1}{\underbrace{\overline{\mathbf{x}}(2),\overline{\mathbf{x}}(2),\overline{\mathbf{x}}(2),\dots ,\overline{\mathbf{x}}(2)}},\dots \\ & \dots ,\underset{m-k_s}{\underbrace{\overline{\mathbf{x}}(s+1),\overline{\mathbf{x}}(s+1),\overline{\mathbf{x}}(s+1),\dots ,\overline{\mathbf{x}}(s+1)}},\overline{\mathbf{x}}(s+2),\overline{\mathbf{x}}(s+3),\dots ,\overline{\mathbf{x}}(\ell ),\\ & \underset{l_1}{\underbrace{\overline{\mathbf{x}}(\ell +1),\overline{\mathbf{x}}(\ell +1),\overline{\mathbf{x}}(\ell +1),\dots ,\overline{\mathbf{x}}(\ell +1)}},\underset{l_2-l_1}{\underbrace{\overline{\mathbf{x}}(\ell +2),\overline{\mathbf{x}}(\ell +2),\overline{\mathbf{x}}(\ell +2),\dots ,\overline{\mathbf{x}}(\ell +2)}},\\ & \dots \dots ,\underset{n-l_s}{\underbrace{\overline{\mathbf{x}}(\ell +t+1),\overline{\mathbf{x}}(\ell +t+1),\overline{\mathbf{x}}(\ell +t+1),\dots ,\overline{\mathbf{x}}(\ell +t+1)}},\\ & \phantom{\underset{n-l_s}{\underbrace{\overline{\mathbf{x}}(\ell +t+1),\overline{\mathbf{x}}(\ell +t+1),\overline{\mathbf{x}}(\ell +t+1),\dots ,\overline{\mathbf{x}}(\ell +t+1)}}}\overline{\mathbf{x}}(\ell +t+2),\overline{\mathbf{x}}(\ell +t+3),\dots )\end{array}$Note that $\mathbf{x}\in U\cap X_F^{+}$ and that ${\sigma }_F^{\ell }(\mathbf{x})\in V\cap X_F^{+}$. Therefore, $({\sigma }_F^{+}{)}^{\ell }(U\cap X_F^{+})\cap (V\cap X_F^{+})\ne \mathrm{\varnothing }$ and it follows that $(X_F^{+},{\sigma }_F^{+})$ is transitive.

To prove Theorem 3.14(2), suppose that $(X_G,{\sigma }_G)$ is transitive. By Theorem 3.8, $(X_G^{+},{\sigma }_G^{+})$ is transitive, therefore, by Theorem 3.14(1), so is $(X_F^{+},{\sigma }_F^{+})$. Finally, it follows from Theorem 3.8 that $(X_F,{\sigma }_F)$ is transitive.

Corollary 3.15

Let X be a compact metric space, let G be a closed relation on X such that $p_1(G)=p_2(G)=X$ and let $F=G\cup {\mathrm{\Delta }}_X$. Then the following hold.

1. If $(X_G^{+},{\sigma }_G^{+})$ is transitive, then $(X_F^{+},{\sigma }_F^{+})$ is mixing.

2. If $(X_G,{\sigma }_G)$ is transitive, then $(X_F,{\sigma }_F)$ is mixing.

Proof.

To prove Corollary 3.15(1), suppose that $(X_G^{+},{\sigma }_G^{+})$ is transitive. By Theorem 3.14, $(X_F^{+},{\sigma }_F^{+})$ is transitive. Therefore, by Theorem 3.12, $(X_F^{+},{\sigma }_F^{+})$ is mixing since ${\mathrm{\Delta }}_X\subseteq F$.

To prove Corollary 3.15(2), suppose that $(X_G,{\sigma }_G)$ is transitive. By Theorem 3.14, $(X_F,{\sigma }_F)$ is transitive. Therefore, by Theorem 3.13, $(X_F,{\sigma }_F)$ is mixing since ${\mathrm{\Delta }}_X\subseteq F$.

3.2. Mixing and quotients of dynamical systems

Theorem 3.22 is the main result of this section. First, we introduce quotients of dynamical systems and recall some of their properties.

Definition 3.16

Let X be a compact metric space and let ∼ be an equivalence relation on X. For each $x\in X$, we use $[x]$ to denote the equivalence class of the element x with respect to the relation ∼. We also use $X{/}_{\sim }$ to denote the quotient space $X{/}_{\sim }=\{[x]|x\in X\}$.

Observation 3.17

Let X be a compact metric space, let ∼ be an equivalence relation on X, let $q:X\to X{/}_{\sim }$ be the quotient map that is defined by $q(x)=[x]$ for each $x\in X$, and let $U\subseteq X{/}_{\sim }$. Then $\begin{array}{r}U\text{is open in}X{/}_{\sim }⟺q^{-1}(U)\text{is open in}X.\end{array}$

Definition 3.18

Let X be a compact metric space, let ∼ be an equivalence relation on X, and let $f:X\to X$ be a function such that for all $x,y\in X$, $\begin{array}{r}x\sim y⟺f(x)\sim f(y).\end{array}$Then we let $f^{\star }:X{/}_{\sim }\to X{/}_{\sim }$ be defined by $f^{\star }([x])=[f(x)]$ for any $x\in X$.

Proposition 3.19

Let X be a compact metric space, let ∼ be an equivalence relation on X, and let $f:X\to X$ be a function such that for all $x,y\in X$, $\begin{array}{r}x\sim y⟺f(x)\sim f(y).\end{array}$Then the following hold.

(1)	$f^{\star }$ is a well-defined function from $X{/}_{\sim }$ to $X{/}_{\sim }$.
(2)	If f is continuous, then $f^{\star }$ is continuous.
(3)	If f is a homeomorphism, then $f^{\star }$ is a homeomorphism.
(4)	If $(X,f)$ is transitive and $X{/}_{\sim }$ is metrizable, then $(X{/}_{\sim },f^{\star })$ is transitive.

Proof.

See [7, Theorem 3.4].

Definition 3.20

Let $(X,f)$ be a dynamical system and let ∼ be an equivalence relation on X such that for all $x,y\in X$, $\begin{array}{r}x\sim y⟺f(x)\sim f(y).\end{array}$Then we say that $(X{/}_{\sim },f^{\star })$ is a quotient of the dynamical system $(X,f)$ or it is the quotient of the dynamical system $(X,f)$ that is obtained from the relation ∼.

Observation 3.21

Let $(X,f)$ be a dynamical system. Note that we have defined a dynamical system as a pair consisting of a compact metric space and a continuous function and that in this case, $X{/}_{\sim }$ is not necessarily metrizable. So, if $X{/}_{\sim }$ is metrizable, then also $(X{/}_{\sim },f^{\star })$ is a dynamical system. Note that for the quotient map $q:X\to X{/}_{\sim }$, $q\circ f=f^{\star }\circ q$. Therefore, $(X{/}_{\sim },f^{\star })$ is semi-conjugate to $(X,f)$.

Theorem 3.22

Let X be a compact metric space, let ∼ be an equivalence relation on X, and let $f:X\to X$ be a function such that for all $x,y\in X$, $\begin{array}{r}x\sim y⟺f(x)\sim f(y).\end{array}$If $(X,f)$ is mixing and $X{/}_{\sim }$ is metrizable, then $(X{/}_{\sim },f^{\star })$ is mixing.

Proof.

Suppose that $(X,f)$ is mixing and that $X{/}_{\sim }$ is metrizable. It follows from Theorem 2.16 and Observations 3.21 that $(X{/}_{\sim },f^{\star })$ is mixing.

4. Mixing on the Lelek fan

In this section, we produce on the Lelek fan a mixing homeomorphism as well as a mixing mapping, which is not a homeomorphism.

Definition 4.1

In this section, we use X to denote $X=[0,1]$. For each $(r,\rho )\in (0,\mathrm{\infty })\times (0,\mathrm{\infty })$, we define the sets $L_r$, $L_{\rho }$ and $L_{r,\rho }$ as follows: $L_r=\{(x,y)\in X\times X|y=\mathrm{rx}\}$, $L_{\rho }=\{(x,y)\in X\times X|y=\mathrm{\rho x}\}$, and $L_{r,\rho }=L_r\cup L_{\rho }$. We also define the set $M_{r,\rho }$ by $M_{r,\rho }=X_{L_{r,\rho }}^{+}$.

Definition 4.2

Let $(r,\rho )\in (0,\mathrm{\infty })\times (0,\mathrm{\infty })$. We say that r and ρ never connect or $(r,\rho )\in \mathcal{NC}$ if

1. r<1, $\rho >1$ and

2. for all integers k and ℓ, $\begin{array}{r}{r}^k={\rho }^{\ell }⟺k=\ell =0.\end{array}$

In [5], the following theorem is the main result.

Theorem 4.3

Let $(r,\rho )\in \mathcal{NC}$. Then $M_{r,\rho }$ is a Lelek fan with top $(0,0,0,\dots )$.

Proof.

See [5, Theorem 14].

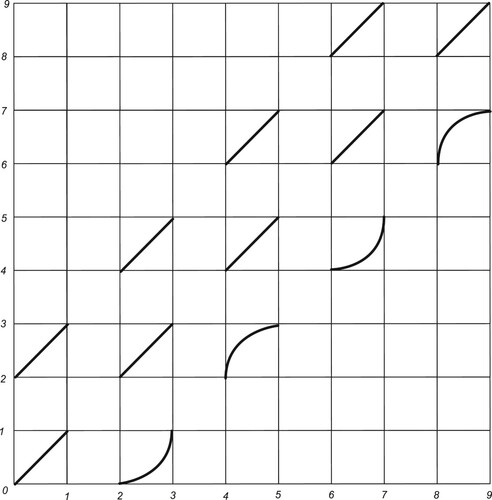
Definition 4.4

Let $(r,\rho )\in \mathcal{NC}$. We use $F_{r,\rho }$ to denote the following closed relation on X: $\begin{array}{r}{F}_{r,\rho }=L_{r,\rho }\cup \{(t,t)|t\in X\},\end{array}$see Figure 2.

Figure 2. The relation F from Definition 3.14.

Theorem 4.5

Let $(r,\rho )\in \mathcal{NC}$. Then $X_{F_{r,\rho }}^{+}$ and $X_{F_{r,\rho }}$ are both Lelek fans.

Proof.

It follows from the proof of [4, Theorem 3.1] that $X_{F_{r,\rho }}^{+}$ is a Lelek fan. To see that $X_{F_{r,\rho }}$ is a Lelek fan, let $\begin{array}{r}{B}_{\mathbf{a}\mathbf{,}\mathbf{b}}=\{(\dots ,\mathbf{b}(2)\mathbf{b}(1)\cdot t,\mathbf{b}(1)\cdot t,t;\mathbf{a}(1)\cdot t,\mathbf{a}(2)\mathbf{a}(1)\cdot t,\dots )|t\in [0,1]\}\end{array}$and $\begin{array}{r}{A}_{\mathbf{a}\mathbf{,}\mathbf{b}}=B_{\mathbf{a}\mathbf{,}\mathbf{b}}\cap X_F\end{array}$for each $\mathbf{a}=(\mathbf{a}(1),\mathbf{a}(2),\mathbf{a}(3),\dots )\in \{1,r,\rho {\}}^{\mathbb{N}}$ and each $\mathbf{b}=(\mathbf{b}(1),\mathbf{b}(2),\mathbf{b}(3),\dots )\in \{1,\frac{1}{r},\frac{1}{\rho }{\}}^{\mathbb{N}}$. Note that for each $\mathbf{a}\in \{1,r,\rho {\}}^{\mathbb{N}}$ and each $\mathbf{b}\in \{1,\frac{1}{r},\frac{1}{\rho }{\}}^{\mathbb{N}}$, $B_{\mathbf{a}\mathbf{,}\mathbf{b}}$ is a straight line segment in the Hilbert cube $\prod _{k=-\mathrm{\infty }}^{-1}[0,r^k]\times \prod _{k=0}^{\mathrm{\infty }}[0,{\rho }^k]$ from $(\dots ,0,0,0;0,0,\dots )$ to $(\dots ,\mathbf{b}(2)\mathbf{b}(1)\cdot 1,\mathbf{b}(1)\cdot 1,1;\mathbf{a}(1)\cdot 1,\mathbf{a}(2)\mathbf{a}(1)\cdot 1,\dots )$, and that for all ${\mathbf{a}}_1,{\mathbf{a}}_2\in \{1,r,\rho {\}}^{\mathbb{N}}$ and all ${\mathbf{b}}_1,{\mathbf{b}}_2\in \{1,\frac{1}{r},\frac{1}{\rho }{\}}^{\mathbb{N}}$, $\begin{array}{r}{B}_{{\mathbf{a}}_{\mathbf{1}}\mathbf{,}{\mathbf{b}}_{\mathbf{1}}}\cap B_{{\mathbf{a}}_{\mathbf{2}}\mathbf{,}{\mathbf{b}}_{\mathbf{2}}}=\{(\dots ,0,0,0;0,0,\dots )\}⟺({\mathbf{a}}_1,{\mathbf{b}}_1)\ne ({\mathbf{a}}_2,{\mathbf{b}}_2).\end{array}$Since $\begin{array}{r}\{(\dots ,\mathbf{b}(2)\mathbf{b}(1)\cdot 1,\mathbf{b}(1)\cdot 1,1;\mathbf{a}(1)\cdot 1,\mathbf{a}(2)\mathbf{a}(1)\cdot 1,\dots )|\mathbf{a}\in \{1,r,\rho {\}}^{\mathbb{N}},\mathbf{b}\in {\{1,\frac{1}{r},\frac{1}{\rho }\}}^{\mathbb{N}}\}\end{array}$is a Cantor set, it follows that $\begin{array}{r}C=\bigcup _{(\mathbf{a},\mathbf{b})\in \{1,r,\rho {\}}^{\mathbb{N}}\times {\{1,\frac{1}{r},\frac{1}{\rho }\}}^{\mathbb{N}}}{B}_{\mathbf{a},\mathbf{b}}\end{array}$is a Cantor fan. Therefore, $X_{F_{r,\rho }}$ is a subcontinuum of the Cantor fan C. Note that for each $\mathbf{a}\in \{1,r,\rho {\}}^{\mathbb{N}}$ and each $\mathbf{b}\in \{1,\frac{1}{r},\frac{1}{\rho }{\}}^{\mathbb{N}}$, $A_{\mathbf{a}\mathbf{,}\mathbf{b}}$ is either degenerate or it is an arc from $(\dots ,0,0,0;0,0,\dots )$ to some other point, denote it by ${\mathbf{e}}_{\mathbf{a}\mathbf{,}\mathbf{b}}$. Let $\begin{array}{r}\mathcal{U}=\{(\mathbf{a},\mathbf{b})\in \{1,r,\rho {\}}^{\mathbb{N}}\times {\{1,\frac{1}{r},\frac{1}{\rho }\}}^{\mathbb{N}}|A_{\mathbf{a}\mathbf{,}\mathbf{b}}\text{is an arc}\}.\end{array}$Then $\begin{array}{r}{X}_{F_{r,\rho }}=\bigcup _{(\mathbf{a},\mathbf{b})\in \mathcal{U}}{A}_{\mathbf{a}\mathbf{,}\mathbf{b}}\text{and}E(X_{F_{r,\rho }})=\{{\mathbf{e}}_{\mathbf{a}\mathbf{,}\mathbf{b}}|(\mathbf{a},\mathbf{b})\in \mathcal{U}\}.\end{array}$Next, we show that for each $\mathbf{x}\in X_{F_{r,\rho }}$, $\begin{array}{r}\mathbf{x}\in E(X_{F_{r,\rho }})⟺sup\{\mathbf{x}(k)|k\text{is an integer}\}=1.\end{array}$Let $\mathbf{x}\in X_{F_{r,\rho }}$. We treat the following possible cases.

Case 1.	For each integer k, there are integers ${\ell }_1$ and ${\ell }_2$ such that ${\ell }_1<k<{\ell }_2$ and $\mathbf{x}(k)\notin \{\mathbf{x}({\ell }_1),\mathbf{x}({\ell }_2)\}$. The proof that in this case $\begin{array}{r}\mathbf{x}\in E(X_{F_{r,\rho }})⟺sup\{\mathbf{x}(k)|k\text{is an integer}\}=1\end{array}$follows from [3, Theorem 3.5] by using the obvious homeomorphism from $X_{L_{r,\rho }}$ to the inverse limit $M=\underleftarrow{\lim }(M_{r,\rho },{\sigma }_{r,\rho })$, which is used in [3, Section 5] to prove that M is a Lelek fan.
Case 2.	There is an integer $k_0$ such that for each positive integer j, $\mathbf{x}(k_0-j)=\mathbf{x}(k_0)$ and for each integer k, there is an integer ${\ell }_0$ such that $k<{\ell }_0$ and $\mathbf{x}(k)\ne \mathbf{x}({\ell }_0)$. The proof that in this case $\begin{array}{r}\mathbf{x}\in E(X_{F_{r,\rho }})⟺sup\{\mathbf{x}(k)|k\text{is an integer}\}=1,\end{array}$is analogous to the proof of [3, Theorem 3.5].
Case 3.	There is an integer $k_0$ such that for each positive integer j, $\mathbf{x}(k_0+j)=\mathbf{x}(k_0)$ and for each integer k, there is an integer ${\ell }_0$ such that $k>{\ell }_0$ and $\mathbf{x}(k)\ne \mathbf{x}({\ell }_0)$. This case is analogous to the previous case.
Case 4.	There are integers $k_1$ and $k_2$ such that $k_1\le k_2$ and such that for each positive integer ℓ, $\mathbf{x}(k_1-\ell )=\mathbf{x}(k_1)$ and $\mathbf{x}(k_2+\ell )=\mathbf{x}(k_2)$. In this case, $\begin{array}{r}sup\{\mathbf{x}(k)|k\text{is an integer}\}=max\{\mathbf{x}(k)|k\text{is an integer}\}.\end{array}$Let $\mathbf{x}\in E(X_{F_{r,\rho }})$ and suppose that $$\begin{gathered} sup\{\mathbf{x}(k)|k \\ \mathrm{textrm}\mathrm{isaninteger}\}=m<1 \end{gathered}$$. Also, let $k_0$ be an integer such that $\mathbf{x}(k_0)=m$ and let $(\mathbf{a},\mathbf{b})\in \{1,r,\rho {\}}^{\mathbb{N}}\times \{1,\frac{1}{r},\frac{1}{\rho }{\}}^{\mathbb{N}}$ be such that $\begin{array}{r}\mathbf{x}=(\dots ,\mathbf{b}(2)\mathbf{b}(1)\cdot m,\mathbf{b}(1)\cdot m,m=\mathbf{x}(k_0),\mathbf{a}(1)\cdot m,\mathbf{a}(2)\mathbf{a}(1)\cdot m,\dots ).\end{array}$Then $\begin{array}{r}\mathbf{x}\in \{(\dots ,\mathbf{b}(2)\mathbf{b}(1)\cdot t,\mathbf{b}(1)\cdot t,t,\mathbf{a}(1)\cdot t,\mathbf{a}(2)\mathbf{a}(1)\cdot t,\dots )|t\in [0,m]\},\end{array}$and $\begin{array}{r}\{(\dots ,\mathbf{b}(2)\mathbf{b}(1)\cdot t,\mathbf{b}(1)\cdot t,t,\mathbf{a}(1)\cdot t,\mathbf{a}(2)\mathbf{a}(1)\cdot t,\dots )|t\in [0,m]\}\end{array}$is a proper subarc of the arc $\begin{array}{r}\{(\dots ,\mathbf{b}(2)\mathbf{b}(1)\cdot t,\mathbf{b}(1)\cdot t,t,\mathbf{a}(1)\cdot t,\mathbf{a}(2)\mathbf{a}(1)\cdot t,\dots )|t\in [0,1]\}\end{array}$in $X_{F_{r,\rho }}$ and is, therefore, not an endpoint of $X_{F_{r,\rho }}$. It follows that the supremum $sup\{\mathbf{x}(k)|k\text{is an integer}\}$ equals 1. To prove the other implication, suppose that $sup\{\mathbf{x}(k)|k\text{is an integer}\}=1$. Then $\mathbf{x}$ is the endpoint of some arc $A_{\mathbf{a}\mathbf{,}\mathbf{b}}$ in $X_{F_{r,\rho }}$, which is not equal to $(\dots ,0,0;0,0,0,\dots )$. Therefore, it is an endpoint of $X_{F_{r,\rho }}$.

We have just proved that $\begin{array}{r}\mathbf{x}\in E(X_{F_{r,\rho }})⟺sup\{\mathbf{x}(k)|k\text{is an integer}\}=1.\end{array}$To see that $X_{F_{r,\rho }}$ is a Lelek fan, let $\mathbf{x}\in X_{F_{r,\rho }}$ be any point and let $\epsilon >0$. We prove that there is a point $\mathbf{e}\in E(X_{F_{r,\rho }})$ such that $\mathbf{e}\in B(\mathbf{x},\epsilon )$. Without loss of generality, we assume that $\mathbf{x}\ne (\dots ,0,0;0,0,0,\dots )$. Let $k_0$ be a positive integer such that $\sum _{k=k_0}^{\mathrm{\infty }}\frac{1}{2^k}<\epsilon$. It follows from [5, Theorem 9] that there is a sequence $(a_1,a_2,a_3,\dots )\in \{r,\rho {\}}^{\mathbf{N}}$ such that $\begin{array}{r}sup\{(a_1\cdot a_2\cdot a_3\cdot \dots \cdot a_n)\cdot \mathbf{x}(k_0)|n\text{is a positive integer}\}=1.\end{array}$Choose and fix such a sequence $(a_1,a_2,a_3,\dots )$. Let $\begin{array}{r}\mathbf{e}=(\dots ,\mathbf{x}(-1),\mathbf{x}(0),\mathbf{x}(1),\dots ,\mathbf{x}(k_0),a_1\cdot \mathbf{x}(k_0),a_2{a}_1\cdot \mathbf{x}(k_0),a_3{a}_2{a}_1\cdot \mathbf{x}(k_0),\dots ).\end{array}$Then $\mathbf{e}\in E(X_{F_{r,\rho }})$ since $$\begin{gathered} sup\{\mathbf{e}(k)|k \\ \mathrm{textrm}\mathrm{isaninteger}\}=1 \end{gathered}$$ and $\begin{array}{r}D(\mathbf{e},\mathbf{x})\le \sum _{k=k_0}^{\mathrm{\infty }}\frac{1}{2^k}<\epsilon ,\end{array}$where D is the metric on $X_{F_{r,\rho }}$. This proves that also $X_{F_{r,\rho }}$ is a Lelek fan.

Theorem 4.6

Let $(r,\rho )\in \mathcal{NC}$. The dynamical systems $(X_{F_{r,\rho }}^{+},{\sigma }_{F_{r,\rho }}^{+})$ and $(X_{F_{r,\rho }},{\sigma }_{F_{r,\rho }})$ are both mixing.

Proof.

It follows from [3, Theorem 4.3 and Observation 5.3] that $(X_{L_{r,\rho }}^{+},{\sigma }_{L_{r,\rho }}^{+})$ and $(X_{L_{r,\rho }},{\sigma }_{L_{r,\rho }})$ are transitive. Since $F_{r,\rho }=L_{r,\rho }\cup {\mathrm{\Delta }}_X$, it follows from Corollary 3.15 that $(X_{F_{r,\rho }}^{+},{\sigma }_{F_{r,\rho }}^{+})$ and $(X_{F_{r,\rho }},{\sigma }_{F_{r,\rho }})$ are both mixing.

Theorem 4.7

The following hold for the Lelek fan L.

(1)	There is a continuous mapping f on the Lelek fan L, which is not a homeomorphism, such that $(L,f)$ is mixing.
(2)	There is a homeomorphism h on the Lelek fan L such that $(L,h)$ is mixing.

Proof.

Let $(r,\rho )\in \mathcal{NC}$. We prove each part of the theorem separately.

1. Let $L=X_{F_{r,\rho }}^{+}$ and let $f={\sigma }_F^{+}$. Note that f is a continuous function which is not a homeomorphism. By Theorem 4.6, $(L,f)$ is mixing.

2. Let $L=X_{F_{r,\rho }}$ and let $h={\sigma }_F$. Note that h is a homeomorphism. By Theorem 4.6, $(L,h)$ is mixing.

5. Mixing on the Cantor fan

In this section, we produce on the Cantor fan a mixing homeomorphism as well as a mixing mapping, which is not a homeomorphism. Furthermore, we produce

1. continuous functions $f,h:C\to C$ on the Cantor fan C such that

   1. h is a homeomorphism and f is not,

   2. $(C,f)$ and $(C,h)$ are both mixing as well as chaotic in the sense of Devaney, and

2. continuous functions $f,h:C\to C$ on the Cantor fan C such that

   1. h is a homeomorphism and f is not,

   2. $(C,f)$ and $(C,h)$ are both mixing as well as chaotic in the sense of Robinson but not in the sense of Devaney

Note that for every dynamical system $(X,f)$, it holds that if $(X,f)$ is mixing, then $(X,f)$ is transitive. Therefore, there are no continuous functions, and hence no homeomorphisms, $f:C\to C$ on the Cantor fan C such that $(C,f)$ is mixing and chaotic in the sense of Knudsen but not chaotic in the sense of Devaney.

We use the following theorems to prove results about periodic points.

Theorem 5.1

Let $(X,f)$ be a dynamical system, let A be a nowhere dense closed subset of X such that $f(A)\subseteq A$ and $f(X\setminus A)\subseteq X\setminus A$, and let ∼ be the equivalence relation on X, defined by $\begin{array}{r}x\sim y⟺x=y\text{or}x,y\in A\end{array}$for all $x,y\in X$. Then the following statements are equivalent.

(1)	The set $\mathcal{P}(f)$ of periodic points in $(X,f)$ is dense in X.
(2)	The set $\mathcal{P}(f^{\star })$ of periodic points in the quotient $(X{/}_{\sim },f^{\star })$ is dense in $X{/}_{\sim }$.

Proof.

See [8, Theorem 3.16].

Theorem 5.2

Let X be a compact metric space and let F be a closed relation on X. If for each $(x,y)\in F$, there are a positive integer n and a point $\mathbf{z}\in X_F^n$ such that $\mathbf{z}(1)=y$ and $\mathbf{z}(n+1)=x$, then the set of periodic points $\mathcal{P}({\sigma }_F^{+})$ is dense in $X_F^{+}$.

Proof.

See [8, Theorem 2.21].

Theorem 5.3

Let $(X,f)$ be a dynamical system and let σ be the shift homeomorphism on $\underleftarrow{\lim }(X,f)$. The following statements are equivalent.

(1)	The set $\mathcal{P}(f)$ of periodic points in $(X,f)$ is dense in X.
(2)	The set $\mathcal{P}({\sigma }^{-1})$ of periodic points in $(\underleftarrow{\lim }(X,f),{\sigma }^{-1})$ is dense in $\underleftarrow{\lim }(X,f)$.

Proof.

[8, Theorem 2.22].

We use Theorem 5.5 to prove results about transitive dynamical systems on the Cantor fan.

Definition 5.4

Let X be a compact metric space, let F be a closed relation on X and let $x\in X$. Then we define $\begin{array}{r}{\mathcal{U}}_F^{\oplus }(x)=\{y\in X|\text{there are}n\in \mathbb{N}\text{and}\mathbf{x}\in X_F^n\text{such that}\mathbf{x}(1)=x,\mathbf{x}(n)=y\}\end{array}$and we call it the forward impression of x by F.

Theorem 5.5

Let X be a compact metric space, let F be a closed relation on X and let $\{f_{\alpha }|\alpha \in A\}$ and $\{g_{\beta }|\beta \in B\}$ be non-empty collections of continuous functions from X to X such that $\begin{array}{r}{F}^{-1}=\bigcup _{\alpha \in A}\mathrm{\Gamma }(f_{\alpha })\text{and}F=\bigcup _{\beta \in B}\mathrm{\Gamma }(g_{\beta }).\end{array}$If there is a dense set D in X such that for each $s\in D$, $\mathrm{Cl}({\mathcal{U}}_F^{\oplus }(s))=X$, then $(X_F^{+},{\sigma }_F^{+})$ is transitive.

Proof.

See [7, Theorem 4.8].

Finally, we use the following theorem when studying sensitive dependence on initial conditions.

Theorem 5.6

Let $(X,f)$ be a dynamical system, let A be a nowhere dense closed subset of X such that $f(A)\subseteq A$ and $f(X\setminus A)\subseteq X\setminus A$, and let ∼ be the equivalence relation on X, defined by $\begin{array}{r}x\sim y⟺x=y\text{or}x,y\in A\end{array}$for all $x,y\in X$. The following statements are equivalent.

(1)	$(X,f)$ has sensitive dependence on initial conditions with respect to A.
(2)	$(X{/}_{\sim },f^{\star })$ has sensitive dependence on initial conditions.

Proof.

See [8, Theorem 3.15].

5.1. Mixing and Devaney's chaos on the Cantor fan

Here, we study functions f on the Cantor fan C such that $(C,f)$ is mixing as we well as chaotic in the sense of Devaney.

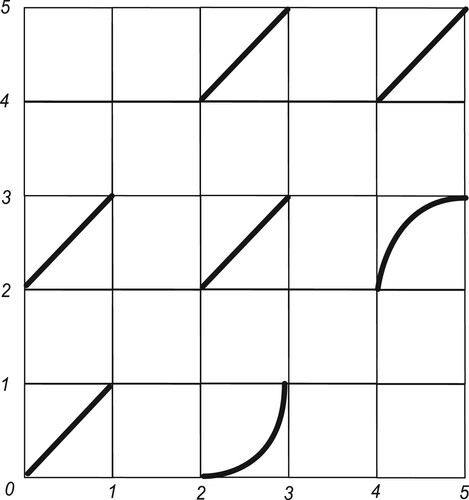
Definition 5.7

In this subsection, we use X to denote $X=[0,1]\cup [2,3]\cup [4,5]\cup [6,7]\cup [8,9]$, and we let $f_1,f_2,f_3:X\to X$ to be the homeomorphisms from X to X that are defined by $f_1(x)=x$, $\begin{array}{rl}{f}_2(x)& =\{\begin{array}{ll}x;& x\in [8,9]\\ x+2;& x\in [0,1]\cup [4,5]\\ x-2{)}^2;& x\in [2,3]\\ (x-6{)}^3+4;& x\in [6,7],\end{array}\\ f_3(x)& =\{\begin{array}{ll}x;& x\in [0,1]\\ x+2;& x\in [2,3]\cup [6,7]\\ (x-4{)}^{\frac{1}{2}}+2;& x\in [4,5]\\ (x-8{)}^{\frac{1}{3}}+6;& x\in [8,9]\end{array}\end{array}$for each $x\in X$. Then we use F to denote the relation $F=\mathrm{\Gamma }(f_1)\cup \mathrm{\Gamma }(f_2)\cup \mathrm{\Gamma }(f_3)$; see Figure 3.

Figure 3. The relation F from Definition 5.7.

Definition 5.8

We define two equivalence relations.

1. For all $\mathbf{x},\mathbf{y}\in X_F^{+}$, we define the relation ${\sim }_{+}$ as follows: $\begin{array}{r}\mathbf{x}{\sim }_{+}\mathbf{y}⟺\mathbf{x}=\mathbf{y}\text{or for each positive integer}k,\{\mathbf{x}(k),\mathbf{y}(k)\}\subseteq \{0,2,4,6,8\}.\end{array}$

2. For all $\mathbf{x},\mathbf{y}\in X_F$, we define the relation ∼ as follows: $\begin{array}{r}\mathbf{x}\sim \mathbf{y}⟺\mathbf{x}=\mathbf{y}\text{or for each integer}k,\{\mathbf{x}(k),\mathbf{y}(k)\}\subseteq \{0,2,4,6,8\}.\end{array}$

Observation 5.9

Essentially the same proof as the one from [7, Example 4.14] shows that the quotient spaces $X_F^{+}{/}_{{\sim }_{+}}$ and $X_F{/}_{\sim }$ are both Cantor fans. Also, note that $({\sigma }_F^{+}{)}^{\star }$ is not a homeomorphism on $X_F^{+}{/}_{{\sim }_{+}}$ while ${\sigma }_F^{\star }$ is a homeomorphism on $X_F{/}_{\sim }$.

Theorem 5.10

The following hold for the sets of periodic points in $(X_F^{+}{/}_{{\sim }_{+}},({\sigma }_F^{+}{)}^{\star })$ and $(X_F{/}_{\sim },{\sigma }_F^{\star })$.

(1)	The set $\mathcal{P}(({\sigma }_F^{+}{)}^{\star })$ of periodic points in the quotient $(X_F^{+}{/}_{{\sim }_{+}},({\sigma }_F^{+}{)}^{\star })$ is dense in $X_F^{+}{/}_{{\sim }_{+}}$.
(2)	The set $\mathcal{P}({\sigma }_F^{\star })$ of periodic points in the quotient $(X_F{/}_{\sim },{\sigma }_F^{\star })$ is dense in $X_F{/}_{\sim }$.

Proof.

Using Theorem 5.1, we prove each of the statements separately.

1. We use Theorem 5.2 to prove the first part of the theorem. Let $(x,y)\in F$ be any point. We show that there are a positive integer n and a point $\mathbf{z}\in X_F^n$ such that $\mathbf{z}(1)=y$ and $\mathbf{z}(n+1)=x$. We consider the following cases for x.

   1. $x\in [0,1]$. If y=x, then let n=1 and $\mathbf{z}=(x,x)$. If y=x+2, then let n=3 and $\mathbf{z}=(x+2,x+4,x^{\frac{1}{2}}+2,x)$.

   2. $x\in [2,3]$. If $y=(x-2{)}^2$, then let n=3 and $\mathbf{z}=((x-2{)}^2,(x-2{)}^2+2,(x-2{)}^2+4,x)$. If y=x, then let n=1 and $\mathbf{z}=(x,x)$. If y=x+2, then let n=3 and $\mathbf{z}=(x+2,(x-2{)}^{\frac{1}{2}}+2,x-2,x)$.

   3. $x\in [4,5]$. If $y=(x-4{)}^{\frac{1}{2}}+2$, then let n=3 and $\mathbf{z}=((x-4{)}^{\frac{1}{2}}+2,x-4,x-2,x)$. If y=x, then let n=1 and $\mathbf{z}=(x,x)$. If y=x+2, then let n=3 and $\mathbf{z}=(x+2,x+4,(x-4{)}^{\frac{1}{3}}+6,x)$.

   4. $x\in [6,7]$. If $y=(x-6{)}^3+4$, then let n=3 and $\mathbf{z}=((x-6{)}^3+4,(x-6{)}^3+6,(x-6{)}^3+8,x)$. If y=x, then let n=1 and $\mathbf{z}=(x,x)$. If y=x+2, then let n=3 and $\mathbf{z}=(x+2,(x-6{)}^{\frac{1}{3}}+6,x-2,x)$.

   5. $x\in [8,9]$. If $y=(x-8{)}^{\frac{1}{3}}+6$, then let n=3 and $\mathbf{z}=((x-8{)}^{\frac{1}{3}}+6,x-4,x-2,x)$. If y=x, then let n=1 and $\mathbf{z}=(x,x)$.

2. It follows from Theorem 5.10(1) and from Theorem 5.3 that the set $\mathcal{P}({\sigma }^{-1})$ of periodic points in $(\underleftarrow{\lim }(X_F^{+},{\sigma }_F^{+}),{\sigma }^{-1})$ is dense in $\underleftarrow{\lim }(X_F^{+},{\sigma }_F^{+})$. By Theorem 3.7, the set $\mathcal{P}({\sigma }_F^{\star })$ of periodic points in the quotient $(X_F{/}_{\sim },{\sigma }_F^{\star })$ is dense in $X_F{/}_{\sim }$.

Theorem 5.11

The dynamical systems $(X_F^{+}{/}_{{\sim }_{+}},({\sigma }_F^{+}{)}^{\star })$ and $(X_F{/}_{\sim },{\sigma }_F^{\star })$ are both transitive.

Proof.

To prove that $(X_F^{+}{/}_{{\sim }_{+}},({\sigma }_F^{+}{)}^{\star })$ is transitive, we prove that $(X_F^{+},{\sigma }_F^{+})$ is transitive. Note that both F and $F^{-1}$ are unions of three graphs of homeomorphisms. Hence, all the initial conditions from Theorem 5.5 are satisfied. To see that $(X_F^{+},{\sigma }_F^{+})$ is transitive, we prove that there is a dense set D in X such that for each $s\in D$, $\mathrm{Cl}({\mathcal{U}}_H^{\oplus }(s))=X$. Let $D=(0,1)\cup (2,3)\cup (4,5)\cup (6,7)\cup (8,9)$. Then D is dense in X. Let $s\in D$ be any point. We consider the following cases for s.

1. $s\in [8,9]$. Then $s,(s-8{)}^{\frac{1}{3}}+6,s-4,(s-8{)}^{\frac{1}{2}}+2,s-8\in {\mathcal{U}}_H^{\oplus }(s)$.

2. $s\in [6,7]$. Then $s,(s-6{)}^3+4,(s-6{)}^{\frac{3}{2}}+2,(s-6{)}^3\in {\mathcal{U}}_H^{\oplus }(s)$.

3. $s\in [4,5]$. Then $s,(s-4{)}^{\frac{1}{2}}+2,s-4\in {\mathcal{U}}_H^{\oplus }(s)$.

4. $s\in [2,3]$. Then $s,(s-2{)}^2\in {\mathcal{U}}_H^{\oplus }(s)$.

Depending on the case, denote $s-8,(s-6{)}^3,s-4$ or $(s-2{)}^2$ with t. Then $t\in (0,1).$ It follows from the definition of F that for all integers m, n and for each $k\in \{0,1,2,3,4\}$, $\begin{array}{r}{t}^{\frac{2^m}{3^n}}+k\cdot 2\in {\mathcal{U}}_F^{\oplus }(t).\end{array}$It follows from Theorem [7, Lemma 4.9] that $\{t^{\frac{2^m}{3^n}}+k\cdot 2|m,n\in \mathbb{Z},k\in \{0,1,2,3,4\}\}$ is dense in X. Since $\begin{array}{r}\{t^{\frac{2^m}{3^n}}+k\cdot 2|m,n\in \mathbb{Z},k\in \{0,1,2,3,4\}\}\subseteq {\mathcal{U}}_F^{\oplus }(t)\subseteq {\mathcal{U}}_F^{\oplus }(s),\end{array}$it follows that ${\mathcal{U}}_F^{\oplus }(s)$ is dense in X. Therefore, by Theorem 5.5, $(X_F^{+},{\sigma }_F^{+})$ is transitive and it follows from Theorem 3.8 that $(X_F,{\sigma }_F)$ is transitive since $p_1(F)=p_2(F)=X$. It follows from Theorem 3.19 that $(X_F^{+}{/}_{{\sim }_{+}},({\sigma }_F^{+}{)}^{\star })$ and $(X_F{/}_{\sim },{\sigma }_F^{\star })$ are both transitive.

Theorem 5.12

The dynamical systems $(X_F^{+}{/}_{{\sim }_{+}},({\sigma }_F^{+}{)}^{\star })$ and $(X_F{/}_{\sim },{\sigma }_F^{\star })$ both have sensitive dependence on initial conditions.

Proof.

The dynamical systems $(X_F^{+}{/}_{{\sim }_{+}},({\sigma }_F^{+}{)}^{\star })$ and $(X_F{/}_{\sim },{\sigma }_F^{\star })$ are both transitive by Theorem 5.11. Also, by Theorem 5.10, the set $\mathcal{P}(({\sigma }_F^{+}{)}^{\star })$ of periodic points in the quotient $(X_F^{+}{/}_{{\sim }_{+}},({\sigma }_F^{+}{)}^{\star })$ is dense in $X_F^{+}{/}_{{\sim }_{+}}$, and the set $\mathcal{P}({\sigma }_F^{\star })$ of periodic points in the quotient $(X_F{/}_{\sim },{\sigma }_F^{\star })$ is dense in $X_F{/}_{\sim }$. It follows from [10, Theorem] that $(X_F^{+}{/}_{{\sim }_{+}},({\sigma }_F^{+}{)}^{\star })$ and $(X_F{/}_{\sim },{\sigma }_F^{\star })$ both have sensitive dependence on initial conditions.

Theorem 5.13

The following hold for the Cantor fan C.

(1)	There is a continuous mapping f on the Cantor fan C, which is not a homeomorphism, such that $(C,f)$ is mixing as well as chaotic in the sense of Devaney.
(2)	There is a homeomorphism h on the Cantor fan C such that $(C,h)$ is mixing as well as chaotic in the sense of Devaney.

Proof.

We prove each part of the theorem separately.

1. Let $C=X_F^{+}{/}_{{\sim }_{+}}$ and let $f=({\sigma }_F^{+}{)}^{\star }$. Note that f is a continuous function which is not a homeomorphism. By Theorem 5.12, $(C,f)$ has sensitive dependence on initial conditions, by Theorem 5.11, $(C,f)$ is transitive, and by Theorem 5.10, the set $\mathcal{P}(f)$ of periodic points in $(C,f)$ is dense in C. Therefore, $(C,f)$ is chaotic in the sense of Devaney.

   It follows from Theorem 3.12 that $(X_F^{+},{\sigma }_F^{+})$ is mixing since ${\mathrm{\Delta }}_X\subseteq F$. It follows from Theorem 3.22 that $(C,f)$ is also mixing.

2. Let $C=X_F{/}_{\sim }$ and let $h={\sigma }_F^{\star }$. Note that h is a homeomorphism. By Theorem 5.12, $(C,h)$ has sensitive dependence on initial conditions, by Theorem 5.11, $(C,h)$ is transitive, and by Theorem 5.10, the set $\mathcal{P}(h)$ of periodic points in $(C,h)$ is dense in C. Therefore, $(C,h)$ is chaotic in the sense of Devaney.

   It follows from Theorem 3.13 that $(X_F,{\sigma }_F)$ is mixing since ${\mathrm{\Delta }}_X\subseteq F$. It follows from Theorem 3.22 that $(C,h)$ is also mixing.

5.2. Mixing and Robinson's chaos but not Devaney's chaos on the Cantor fan

Here, we study functions f on the Cantor fan C such that $(C,f)$ is mixing as we well as chaotic in the sense of Robinson but not in the sense of Devaney.

Definition 5.14

In this subsection, we use X to denote $\begin{array}{r}X=[0,1]\cup [2,3]\cup [4,5]\end{array}$and we let $f_1,f_2,f_3:X\to X$ to be the homeomorphisms from X to X that are defined by $f_1(x)=x$, $\begin{array}{rl}{f}_2(x)& =\{\begin{array}{ll}x+2;& x\in [0,1]\\ (x-2{)}^2;& x\in [2,3]\\ x;& x\in [4,5],\end{array}\\ f_3(x)& =\{\begin{array}{ll}x;& x\in [0,1]\\ x+2;& x\in [2,3]\\ (x-4{)}^{\frac{1}{3}}+2;& x\in [4,5]\end{array}\end{array}$for each $x\in X$. Then we use F to denote the relation $F=\mathrm{\Gamma }(f_1)\cup \mathrm{\Gamma }(f_2)\cup \mathrm{\Gamma }(f_3)$; see Figure 4.

Figure 4. The relation F from Definition 5.14.

Definition 5.15

We define two equivalence relations.

1. For all $\mathbf{x},\mathbf{y}\in X_F^{+}$, we define the relation ${\sim }_{+}$ as follows: $\begin{array}{r}\mathbf{x}{\sim }_{+}\mathbf{y}⟺\mathbf{x}=\mathbf{y}\text{or for each positive integer}k,\{\mathbf{x}(k),\mathbf{y}(k)\}\subseteq \{0,2,4\}.\end{array}$

2. For all $\mathbf{x},\mathbf{y}\in X_F$, we define the relation ∼ as follows: $\begin{array}{r}\mathbf{x}\sim \mathbf{y}⟺\mathbf{x}=\mathbf{y}\text{or for each integer}k,\{\mathbf{x}(k),\mathbf{y}(k)\}\subseteq \{0,2,4\}.\end{array}$

Observation 5.16

Note that it follows from [7, Example 4.14] that the quotient spaces $X_F^{+}{/}_{{\sim }_{+}}$ and $X_F{/}_{\sim }$ are both Cantor fans. Also, note that $({\sigma }_F^{+}{)}^{\star }$ is not a homeomorphism on $X_F^{+}{/}_{{\sim }_{+}}$ while ${\sigma }_F^{\star }$ is a homeomorphism on $X_F{/}_{\sim }$.

First, we prove the following theorems about sensitive dependence on initial conditions.

Theorem 5.17

Let $A=\{\mathbf{x}\in X_F^{+}|\text{for each positive integer}k,\mathbf{x}(k)\in \{0,2,4\}\}$. Then

(1)	${\sigma }_F^{+}(A)\subseteq A$ and ${\sigma }_F^{+}(X_F^{+}\setminus A)\subseteq X_F^{+}\setminus A$, and
(2)	$(X_F^{+},{\sigma }_F^{+})$ has sensitive dependence on initial conditions with respect to A.

Proof.

First, note that ${\sigma }_F^{+}(A)\subseteq A$ and ${\sigma }_F^{+}(X_F^{+}\setminus A)\subseteq X_F^{+}\setminus A$. Next, let $f={\sigma }_F^{+}$ and let $\epsilon =\frac{1}{4}$. We show that for each basic open set U of the product topology on $\prod _{k=1}^{\mathrm{\infty }}X$ such that $U\cap X_F^{+}\ne \mathrm{\varnothing }$, there are $\mathbf{x},\mathbf{y}\in U\cap X_F^{+}$ such that for some positive integer m, $\begin{array}{r}min\{d(f^m(\mathbf{x}),f^m(\mathbf{y})),d(f^m(\mathbf{x}),A)+d(f^m(\mathbf{y}),A)\}>\epsilon ,\end{array}$where d is the product metric on $\prod _{k=1}^{\mathrm{\infty }}X$, defined by $\begin{array}{r}d((x_1,x_2,x_3,\dots ),(y_1,y_2,y_3,\dots ))=max\left\{\frac{|y_k-x_k|}{2^k}|k\text{is a positive integer}\right\}\end{array}$for all $(x_1,x_2,x_3,\dots ),(y_1,y_2,y_3,\dots )\in \prod _{k=1}^{\mathrm{\infty }}X$. Let U be a basic set of the product topology on $\prod _{k=1}^{\mathrm{\infty }}X$ such that $U\cap X_F^{+}\ne \mathrm{\varnothing }$. Also, let n be a positive integer and for each $i\in \{1,2,3,\dots ,n\}$, let $U_i$ be an open set in X such that $\begin{array}{r}U=U_1\times U_2\times U_3\times \cdots \times U_n\times \prod _{k=n+1}^{\mathrm{\infty }}X.\end{array}$Next, let $\mathbf{z}=(z_1,z_2,z_3,\dots )\in U\cap X_F^{+}$ be any point such that $z_n\notin \{0,1,2,3,4,5\}$. We consider the following possible cases for the coordinate $z_n$ of the point $\mathbf{z}$.

1. $z_n\in (0,1)$. Then let $\mathbf{x}=(x_1,x_2,x_3,\dots )\in X_F^{+}$ be defined by $\begin{array}{r}(x_1,x_2,x_3,\dots ,x_n)=(z_1,z_2,z_3,\dots ,z_n)\end{array}$and for each positive integer k, $x_{n+k}=z_n$. Also, we define $\mathbf{y}=(y_1,y_2,y_3,\dots )\in X_F^{+}$ as follows. First, let $\begin{array}{r}(y_1,y_2,y_3,\dots ,y_n)=(z_1,z_2,z_3,\dots ,z_n).\end{array}$Next, we define $\begin{array}{rl}& (y_{n+1},y_{n+2},y_{n+3},\dots )\\ & =(z_n+2,z_n+4,z_n^{\frac{1}{3}}+2,z_n^{\frac{1}{3}}+4,z_n^{\frac{1}{3^2}}+2,z_n^{\frac{1}{3^2}}+4,z_n^{\frac{1}{3^3}}+2,z_n^{\frac{1}{3^3}}+4,\dots ).\end{array}$Note that $\begin{array}{r}\underset{k\to \mathrm{\infty }}{lim}{y}_{n+4+2k}=5\text{and}\underset{k\to \mathrm{\infty }}{lim}{y}_{n+3+2k}=3.\end{array}$Let $k_0$ be an even positive integer such that for each positive integer k, $\begin{array}{r}k\ge k_0⟹5-y_{n+4+2k}<\frac{1}{10}\text{and}3-y_{n+3+2k}<\frac{1}{10}.\end{array}$Let $m=n+k_0+1$. Then, $\begin{array}{r}d(f^m(\mathbf{x}),f^m(\mathbf{y}))=max\{\frac{|y_k-x_k|}{2^{k-m+1}}|k\in \{m,m+1,m+2,m+3,\dots \}\}\ge 1>\epsilon \end{array}$and $\begin{array}{rl}& d(f^m(\mathbf{x}),A)+d(f^m(\mathbf{y}),A)\ge d(f^m(\mathbf{y}),A)=min\{d(f^m(\mathbf{y}),\mathbf{a})|\mathbf{a}\in A\}\\ & =min\{max\{\frac{|\mathbf{a}(k)-y_{k+m}|}{2^k}|k\in \{1,2,3,\dots \}\}|\mathbf{a}\in A\}\\ & \ge \frac{{\mathbf{y}}_{\mathbf{k}\mathbf{+}\mathbf{m}}\mathbf{-}\mathbf{4}}{2}\ge \frac{9}{20}>\epsilon \end{array}$

2. $z_n\notin (0,1)$. Then there is an integer $j\in \{1,2,3\}$ such that $z_n\in (2j,2j+1)$. In this case, the proof is analogous to the proof of the previous case. We leave the details to the reader.

This proves that $(X_F^{+},{\sigma }_F^{+})$ has sensitive dependence on initial conditions with respect to A.

Corollary 5.18

Let $B=\{\mathbf{x}\in X_F|\text{for each integer}k,\mathbf{x}(k)\in \{0,2,4\}\}$. Then

(1)	${\sigma }_F(B)\subseteq B$ and ${\sigma }_F(X_F\setminus B)\subseteq X_F\setminus B$, and
(2)	$(X_F,{\sigma }_F)$ has sensitive dependence on initial conditions with respect to B.

Proof.

First, note that ${\sigma }_F(B)\subseteq B$ and ${\sigma }_F(X_F\setminus B)\subseteq X_F\setminus B$. Next, let $\begin{array}{r}A=\{\mathbf{x}\in X_F^{+}|\text{for each positive integer}k,\mathbf{x}(k)\in \{0,2,4,6\}\}.\end{array}$By Theorem 5.17,

1. ${\sigma }_F^{+}(A)\subseteq A$ and ${\sigma }_F^{+}(X_F^{+}\setminus A)\subseteq X_F^{+}\setminus A$, and

2. $(X_F^{+},{\sigma }_F^{+})$ has sensitive dependence on initial conditions with respect to A.

Note that ${\sigma }_F^{+}$ is surjective. By Theorem 2.24, $(\underleftarrow{\lim }(X_F^{+},{\sigma }_F^{+}),{\sigma }^{-1})$ has sensitive dependence on initial conditions with respect to $\underleftarrow{\lim }(A,{\sigma }_F^{+}{|}_A)$, where σ is the shift homeomorphism on $\underleftarrow{\lim }(X_F^{+},{\sigma }_F^{+})$. By Theorem 3.7, the inverse limit $\underleftarrow{\lim }(X_F^{+},{\sigma }_F^{+})$ is homeomorphic to the two-sided Mahavier product $X_F$ and the inverse of the shift homeomorphism ${\sigma }_F$ on $X_F$ is topologically conjugate to the shift homeomorphism σ on $\underleftarrow{\lim }(X_F^{+},{\sigma }_F^{+})$. Let $\phi :\underleftarrow{\lim }(X_F^{+},{\sigma }_F^{+})\to X_F$ be the homeomorphism, used to prove Theorem 3.7 in [7, Theorem 4.1]. Then $\phi (\underleftarrow{\lim }(A,{\sigma }_F^{+}{|}_A))=B$. Therefore, $(X_F,{\sigma }_F)$ has sensitive dependence on initial conditions with respect to B.

Theorem 5.19

The dynamical systems $(X_F^{+}{/}_{{\sim }_{+}},({\sigma }_F^{+}{)}^{\star })$ and $(X_F{/}_{\sim },{\sigma }_F^{\star })$ both have sensitive dependence on initial conditions.

Proof.

For each of the dynamical systems, we prove separately that it has sensitive dependence on initial conditions.

1. Let $C=X_F^{+}{/}_{{\sim }_{+}}$ and let $f=({\sigma }_F^{+}{)}^{\star }$, i.e. for each $\mathbf{x}\in X_F$, $f([\mathbf{x}])=[{\sigma }_F^{+}(\mathbf{x})]$. We show that $(C,f)$ has sensitive dependence on initial conditions. Let $\begin{array}{r}A=\{\mathbf{x}\in X_F^{+}|\text{for each positive integer}k,\mathbf{x}(k)\in \{0,2,4\}\}.\end{array}$By Theorem 5.17,

   1. ${\sigma }_F(A)\subseteq A$ and ${\sigma }_F(X_F^{+}\setminus A)\subseteq X_F^{+}\setminus A$ and

   2. $(X_F^{+},{\sigma }_F^{+})$ has sensitive dependence on initial conditions with respect to A.

   Since A is a closed nowhere dense set in $X_F^{+}$, it follows from Theorem 5.6 that $(C,f)$ has sensitive dependence on initial conditions.

2. Let $C=X_F{/}_{\sim }$ and let $h={\sigma }_F^{\star }$, i.e. for each $\mathbf{x}\in X_F$, $h([\mathbf{x}])=[{\sigma }_F(\mathbf{x})]$. We show that $(C,h)$ has sensitive dependence on initial conditions. The rest of the proof is analogous to the proof above – instead of the set A, the set $\begin{array}{r}B=\{\mathbf{x}\in X_F|\text{for each integer}k,\mathbf{x}(k)\in \{0,2,4\}\}\end{array}$is used in the proof. We leave the details to a reader.

Theorem 5.20

The following hold for the sets of periodic points in $(X_F^{+}{/}_{{\sim }_{+}},({\sigma }_F^{+}{)}^{\star })$ and in $(X_F{/}_{\sim },{\sigma }_F^{\star })$.

(1)	The set $\mathcal{P}(({\sigma }_F^{+}{)}^{\star })$ of periodic points in the quotient $(X_F^{+}{/}_{{\sim }_{+}},({\sigma }_F^{+}{)}^{\star })$ is not dense in $X_F^{+}{/}_{{\sim }_{+}}$.
(2)	The set $\mathcal{P}({\sigma }_F^{\star })$ of periodic points in the quotient $(X_F{/}_{\sim },{\sigma }_F^{\star })$ is not dense in $X_F{/}_{\sim }$.

Proof.

We prove each of the statements separately.

1. Let $U=(0,1)\times (2,3)\times \prod _{k=3}^{\mathrm{\infty }}X$. Then U is open in $\prod _{k=1}^{\mathrm{\infty }}X$ and $U\cap X_F^{+}\ne \mathrm{\varnothing }$. However, note that $U\cap \mathcal{P}({\sigma }_F^{+})=\mathrm{\varnothing }$. This is true since for each $x\in (0,1)$, for each $\mathbf{x}=(x_1,x_2,x_3,\dots )\in X_F^{+}$ such that $x_1=x$, and for each positive integer n>1, $\begin{array}{r}{x}_n\in (0,1)⟹\text{there are positive integers}k\text{and}\ell \text{such that}{x}_n=x^{\frac{2^k}{3^{\ell }}},\end{array}$and such an $x_n$ is not equal to x. It follows that the set $\mathcal{P}({\sigma }_F^{+})$ of periodic points in $(X_F^{+},{\sigma }_F^{+})$ is not dense in $X_F^{+}$. Therefore, by Theorem 5.1, the set $\mathcal{P}({\sigma }_F^{+})$ of periodic points in $(X_F^{+},{\sigma }_F^{+})$ is not dense in $X_F^{+}$.

2. Suppose that the set $\mathcal{P}({\sigma }_F^{\star })$ of periodic points in the quotient $(X_F{/}_{\sim },{\sigma }_F^{\star })$ is dense in $X_F{/}_{\sim }$. Therefore, by Theorem 5.1, the set $\mathcal{P}({\sigma }_F)$ of periodic points in $(X_F,{\sigma }_F)$ is dense in $X_F$. It follows from Theorem 3.7, the set $\mathcal{P}({\sigma }^{-1})$ of periodic points in $(\underleftarrow{\lim }(X_F^{+},{\sigma }_F^{+}),{\sigma }^{-1})$ is dense in $\underleftarrow{\lim }(X_F^{+},{\sigma }_F^{+})$. By Theorem 5.3, the set $\mathcal{P}({\sigma }_F^{+})$ of periodic points in $(X_F^{+},{\sigma }_F^{+})$ is dense in $X_F^{+}$, which contradicts with Theorem 5.20(1).

Theorem 5.21

The dynamical systems $(X_F^{+}{/}_{{\sim }_{+}},({\sigma }_F^{+}{)}^{\star })$ and $(X_F{/}_{\sim },{\sigma }_F^{\star })$ are both transitive.

Proof.

The proof of this theorem is analogous to the proof of Theorem 5.11. We leave the details to a reader.

Theorem 5.22

The following hold for the Cantor fan C.

(1)	There is a continuous mapping f on the Cantor fan C, which is not a homeomorphism, such that $(C,f)$ is mixing as well as chaotic in the sense of Robinson but not in the sense of Devaney.
(2)	There is a homeomorphism h on the Cantor fan C such that $(C,h)$ is mixing as well as chaotic in the sense of Robinson but not in the sense of Devaney.

Proof.

We prove each part of the theorem separately.

1. Let $C=X_F^{+}{/}_{{\sim }_{+}}$ and let $f=({\sigma }_F^{+}{)}^{\star }$. Note that f is a continuous function which is not a homeomorphism. By Theorem 5.19, $(C,f)$ has sensitive dependence on initial conditions. By Theorem 5.21, $(C,f)$ is transitive. It follows from Theorem 5.20 that the set $\mathcal{P}(f)$ of periodic points in the quotient $(C,f)$ is not dense in C. Therefore, $(C,f)$ is chaotic in the sense of Robinson but it is not chaotic in the sense of Devaney.

   It follows from Theorem 3.12 that $(X_F^{+},{\sigma }_F^{+})$ is mixing since ${\mathrm{\Delta }}_X\subseteq F$. It follows from Theorem 3.22 that $(C,f)$ is also mixing.

2. Let $C=X_F{/}_{\sim }$ and let $h={\sigma }_F^{\star }$. Note that h is a homeomorphism. The rest of the proof is analogous to the proof above. We leave the details to a reader.

6. Uncountable family of (non-)smooth fans that admit mixing homeomorphisms

In this section, an uncountable family $\mathcal{G}$ of pairwise non-homeomorphic smooth fans that admit mixing homeomorphisms is constructed. Our construction of the family $\mathcal{G}$ follows the idea from [6], where an uncountable family $\mathcal{F}$ of pairwise non-homeomorphic smooth fans that admit transitive homeomorphisms is constructed: every step of the construction of family $\mathcal{F}$ from [6] is essentially copied here to construct the family $\mathcal{G}$. The only difference is a small modification of the relation H on X that is used in [6, Definition 4.13] to obtain the family $\mathcal{F}$: in H, the graph in $(I_1\times I_1)\cup (I_2\times I_2)$ is replaced with the graph in $(I_2\times I_1)\cup (I_3\times I_2)$ and the graph in $(I_2\times I_1)\cup (I_3\times I_2)$ is replaced with the graph in $(I_1\times I_1)\cup (I_2\times I_2)$; see [6, Figure 5] and Figure 5. Therefore, in this section, we omit the details and simply state our first theorem.

Figure 5. The relation H on X.

Theorem 6.1

There is a family $\mathcal{G}$ of uncountable many pairwise non-homeomorphic smooth fans that admit mixing homeomorphisms.

In [9], a family of uncountably many pairwise non-homeomorphic non-smooth fans that admit transitive homeomorphisms is constructed from the family $\mathcal{F}$ from [6]. This is done in such a way that for each smooth fan $F\in \mathcal{F}$, a special equivalence relation ∼ on F is defined in such a way that $F{/}_{\sim }$ is a non-smooth fan that admits a transitive homeomorphism. The same procedure as the one from [9] for the family $\mathcal{F}$, works also for our family $\mathcal{G}$. It transforms every smooth fan $F\in \mathcal{G}$ to a non-smooth fan $F{/}_{\sim }$ that admits a mixing homeomorphism. The following theorem is, therefore, a good place to finish the paper. Since its proof is essentially the same as the proof of [9, Theorem 3.23], we leave the details to a reader.

Theorem 6.2

There is a family of uncountable many pairwise non-homeomorphic non-smooth fans that admit mixing homeomorphisms.

Acknowledgments

The authors thank the anonymous referees for their careful reading. The suggestions of the referees have helped to improve the paper.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This work is supported in part by the Slovenian Research Agency (research projects J1-4632, BI-HR/23-24-011, BI-US/22-24-086 and BI-US/22-24-094, and research program P1-0285).

Notes

1 For each $z\in X$, $d(z,A)=inf\{d(z,a)|a\in A\}$.