?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.
?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.Abstract
We investigate the conditions on an integer sequence ,
, with
, such that the sequence
, computed recursively via
, with
, exists. We prove that
is ‘slow’, that is,
,
, is a sufficient but not necessary condition for the existence of sequence q. Sequences q defined in this way typically display non-trivial dynamics: in particular, they are generally aperiodic with no obvious patterns. We discuss and illustrate this behavior with some examples.
1. Motivation
In his 1979 book [Citation3], author D.R. Hofstadter mentions an integer sequence, , defined, for n>2, by
(1)
(1) In order for
to exist for all positive integers n, that is, for
, it must be true, again for all
, that
, since only then does the right-hand side of (Equation1
(1)
(1) ) refer to terms that are already known:
is undefined for
. Should it happen that
for some n, the sequence is said to die at n. Although direct computation shows that
exists for
[Citation5], the existence of
for all positive n is still an open question.
The sequence is non-monotonic, aperiodic and its dynamical behavior appears to be complex. In [Citation9] for instance, small scale ‘chaotic’ behavior is described, with some order apparent at larger scales, and several statistical properties of the sequence are also investigated.
This complex behavior has inspired several authors to study variations of Hofstadter's original recursion. For instance, Tanny [Citation11] considers
for n>2 [Citation6]. Another variant is considered in [Citation1], in which the authors investigate
for n>4 [Citation7]. Both these variants give rise to sequences that are monotonic, unlike
, and hit every positive integer.
A different approach is followed in [Citation2], in which the recursion formula in (Equation1(1)
(1) ) is retained but different initial conditions are used. For certain initial conditions, ‘eventually quasi-polynomial’ solutions can be found. For a given integer m>0 and a given fixed set of polynomials
,
, a quasi-polynomial function of n,
, say, is defined by
, where
. If this holds only for n greater than some positive integer
say, then
is said to be eventually quasi-polynomial. In [Citation2], families of eventually quasi-polynomial solutions to
(2)
(2) with suitable initial conditions, are constructed. As an example of such a solution with m = 5 and where the
are of degree at most 1, we give
along with the initial conditions . (Values of
and
are not needed to compute
.) For all
here,
satisfying (Equation2
(2)
(2) ) is then given by the quasi-polynomial above.
In this paper, we also consider a variation on the original problem, one which consists of an infinite number of variants rather than just a single case. In particular, we discuss a ‘diluted’ version of the problem of the existence of . In order to describe this version, we first need the notation
for an infinite sequence. We use this notation in formal contexts, such as in definitions and lemmas, but where it it is clear what is intended, we just write a to mean the whole sequence. Naturally, when the nth term is meant, we write
. We also need the following definitions:
Definition 1.1
Slow sequence
If integer sequence obeys
for
, then the sequence is said to be ‘slow’.
Definition 1.2
Property 

If integer sequence is slow and additionally
, then it is said to have property
.
We drop the quotation marks around the word ‘slow’ from now on.
The problem that we consider is the question of the existence of sequences q defined recursively by
(3)
(3) for
, n>1, and where
has property
(so in particular
). All sequences in the paper start from index 1 and we apply the conditions
and
strictly throughout, even though
is never needed to compute the sequence q. Computations suggest that, under these conditions, the sequence q corresponding to any f with property
exists for all
.
We think of sequences generated by (Equation3(3)
(3) ) as ‘diluted’ Hofstadter sequences because of the similarity of their definition to that of the original
-sequence. In particular, in (Equation3
(3)
(3) ), one ‘difficult’ – nested – term is retained,
, but the second nested term is replaced by
, which is under our control.
Clearly the existence of the sequence q is also equivalent to the inequality holding for all
. If this is the case, then we simply say that q exists. The lower bound on
here is easy: by (Equation3
(3)
(3) ), for any n for which q exists,
is the sum of a positive integer and a non-negative one, and so is also greater than or equal to unity.
The upper bound on q, however, is less obvious. In what follows, after some preliminaries, we give a proof of the following theorem.
Theorem 1.3
For all sequences having property
, the corresponding sequence
with
and with
, for n>1, computed from (Equation3
(3)
(3) ), exists for all
.
The proof of this theorem is the main result of the paper, but the recursion (Equation3(3)
(3) ) can also be viewed as a non-linear (in the light of the nested term), non-autonomous (because of
) dynamical system, discrete in both time and space. Hence, having proved the existence of q for all f with property
, we make some observations about the dynamics of sequences q, which are also interesting.
2. Preliminaries
The first term of all sequences in this paper has index 1. We start by giving the following definitions:
Two sequences
and
differ if there exists
such that
; otherwise, they are equal.
A sequence
obeying (Equation3
(3)
(3) ) exists if and only if
is defined for all
; or, equivalently, if
for all
.
A sequence
is the sequence corresponding to sequence
if
exists and is defined by (Equation3
(3)
(3) ).
A sequence
is the sequence corresponding to sequence
if
exists and
is defined by
and
for n>1.
Where we need to refer explicitly to the first few terms of a sequence, say, we list the values starting from
– for example
means
,
,
.
Let us define as the set of all sequences having property
: that is
We will also need the set of finite sequences with property
:
It is easily established that the cardinality of
is the same as that of the real numbers. To do so, let
and consider the sequence of differences
, which will be a sequence consisting of the symbols 0 and 1. Interpreting this as a binary decimal, we see that each distinct
gives rise to a distinct real number
.
One important subset of , with same cardinality, is
It is easy to see (i) that , and that in fact (ii)
. Property (i) comes directly from the definition
, from which we deduce that, for
,
is either 0 or 1. For property (ii), consider the sequence
, which are the first four terms of a sequence in
. Now assume that these terms are generated by
for some α. Then
implies that
, but
implies that
, leading to a contradiction. Hence, there are sequences in
that are not in
.
Furthermore, the condition that successive terms in a sequence differ by at most unity turns out to be sufficient but not necessary for the corresponding
to exist. There are examples where f increases by more than unity, and where it is not monotonic, but for which
nonetheless exists. Consider, for instance, (a)
, for which
and (b)
, for which
. Statements (a) and (b) are proved in
Lemma 2.1
If
and if
for all
Proof.
These just boil down to computation.
For , we have
so
for all n. Hence,
, as claimed.
For , we have
Hence,
is odd, and so
, both for all n. Therefore,
.
Remark 2.2
Example (b) is in fact a special case of
On the other hand, it is easy to find examples of for which
does not exist – for instance,
, for which
and so
which is undefined.
We also prove
Lemma 2.3
If f and are different sequences, and
and
both exist, then
.
Proof.
Let for
but
. Write
,
. Now,
for
and
,
. Also,
, but
. Hence
and so the sequences q,
differ.
We remark here that the recursion (Equation3(3)
(3) ) can be used in either direction. That is, given any sequence f for which
exists, sequence q can obviously be computed, term-by-term, in order of increasing index, from (Equation3
(3)
(3) ); and, given any sequence q obeying
for all n, (Equation3
(3)
(3) ) can be used to compute
for all n. A case where computing f given q gives an interesting result is
Lemma 2.4
Let sequence obey (i)
and (ii)
, both for
, and let
. Define
for
with
. Then, for
,
.
Proof.
Throughout the proof, we assume integer . Assumption (i) tells us that q exists and (ii), that q is slow. By the definition of
,
Assumption (ii) implies immediately that
.
Now define : by (i),
. Then
, again by (ii). Hence,
is either
, or
. Therefore,
. Thus we have
and the lemma is proven.
Note that the converse of Lemma 2.4 is not true: if then q is not necessarily slow: a counterexample is given by
in Lemma 2.1.
Finally, we point out that cases in which gives rise to a monotonic sequence q appear to be rare – a few examples, each of which is also slow, are given in Section 4.
3. The main theorem
We now give a proof of Theorem 1.3. We need several lemmas, the first of which is
Lemma 3.1
The shift property
Let , with
, be any sequence of integers for which the corresponding sequence
, with
, exists. Define
Then we have that
implies
and
implies
.
Proof.
A ⇒ B. We use strong induction and the fact that both q and obey (Equation3
(3)
(3) ).
First, by definition, and
. Hence,
.
Next, assume that
(4)
(4) Now, by assumption (Equation4
(4)
(4) ), we have that
. For the inductive step
, we have that
where
. We have
, since q exists, and so, by (Equation4
(4)
(4) ),
and hence
.
B ⇒ A. This is straightforward. By definition, we have . Then, by B, we have
and
. Hence, by (Equation3
(3)
(3) ),
. Then, letting
, we have
as claimed. Here we have used B and (Equation3
(3)
(3) ) for the second-last and last equalities respectively.
We will also need the following two special cases of , each of which, unusually, leads to a slow sequence q:
Lemma 3.2
Let and
, both for all
, and define sequences
,
. Then
and
, also for all n.
Proof.
For , (Equation3
(3)
(3) ) gives
since
. By induction, with base case
, we make the assumption that for some k>1 we have
. Then, by the recursion formula, we have
, as claimed.
For , (Equation3
(3)
(3) ) gives
since
. With
, we assume that
for some k>1. Then
and the proof is complete.
In the remainder of this section, f will always have property and we will assume that f is such that
exists. We introduce the handy notation
, with
, to designate the set of successive integers
.
We now consider the question: for a particular n, given that , what are the possible values of
? That is, we investigate the sets
, where f ranges over
. The lower bound on each of these sets is given by
Lemma 3.3
If for
exists, then (i) for
and
,
; and (ii) a sequence f that gives rise to this minimum value is
Proof.
For (i), if n = 1 then, by the initial conditions, and
; and so the claimed lower bound holds. Therefore, fix n>1 and recall that
. Then, provided that q exists,
for
. In particular
and so
. Recall now that we are considering
. Hence,
, where
, so
. Therefore,
, and this gives the required minimum.
For (ii), we use Lemmas 3.1 and 3.2. In order that , we must have
, otherwise f cannot have property
. If
, then, by Lemma 3.2,
can be achieved by choosing
. Otherwise,
and in this case, the shift property of Lemma 3.1 applied
times gives
.
We have easily found the minimum of the sets , but the corresponding maximum is not so straightforward. There is, however, a way round the problem. We require the definition of two collections of finite sets of integers,
and
, both of which have the same triangular structure. Taking
first, this is the collection of sets
, where
and
, which can be pictured as a triangular arrangement with n indexing rows and i indexing the position within row n. The definition of
is
Definition 3.4
is the collection of sets
with
and
.
By Lemma 3.2 we have
(5)
(5) for
. For (a), if
and
, then it must be that
for
and so the first part of Lemma 3.2 applies. For (b), if
, the only way that
is if
for
, so the second part of Lemma 3.2 applies.
We have not succeeded in computing explicitly for all valid i and n. In principle,
can be computed by finding all the values that
can take given that
and
. This would in turn require knowledge of all the values that
can take (and then adding
to them). In practice, though, it seems that we have insufficient knowledge of the sequences
as f ranges over
.
However, we can explicitly construct a collection of sets, , and the sets in
will turn out to contain the corresponding sets in
. This is sufficient to prove Theorem 1.3. The collection
consists of the sets
(6)
(6) for
.
We now prove
Lemma 3.5
Let collections of sets and
be as in Definition 3.4 and Equation (Equation6
(6)
(6) ) respectively. Then
for
and
.
Proof.
First, note that for i = 0, (Equation5(5)
(5) )(a) applies and gives
. Furthermore, for i= k, (Equation5
(5)
(5) )(b) applies, giving
. Both of these are true for all positive k.
The rest of the proof proceeds by strong induction, starting from . We assume that
for all allowed values of i and
, which assumption we refer to as (H). We then study what happens when
. The lemma having been proved for i = 0 and i = k, it only remains to study the case
.
Let us therefore consider with
. Equation (Equation3
(3)
(3) ) now reads
since, by definition,
. We first need the set of possible values of
, which, by (H), is
. Only sets with indices
and
are allowed because f has property
:
can only be true if
or
. Thus,
. Note that
, since
, so
is defined only in terms of q with argument strictly less than k + 1. Hence, informally put,
{union of rows 1 to k−i + 1 of
; that is, using assumption (H) and (Equation6
(6)
(6) ),
(7)
(7) Therefore, for
, we have
and so
. Hence, from (Equation6
(6)
(6) ), we have
and this completes the proof.
Finally, we are in a position to prove Theorem 1.3.
Proof of Theorem 1.3
An immediate consequence of Lemma 3.5 is that for ,
. Hence,
for all
and Theorem 1.3 is proven.
We return to . In words,
is the set of all values that
attains in practice, given that
, as f ranges over
, is equal to i. Clearly, since f has property
,
. It is important to note that
is not equal to
because approximations were made in the proof of Lemma 3.5 in order to compute the values that
can assume in principle. In particular, the unions in (Equation7
(7)
(7) ) are typically over more – and larger – sets
than necessary. These approximations almost always overestimate, and never underestimate
, giving a collection of sets
such that those in
are contained within the corresponding sets in
: that is
.
As stated earlier, can be visualized as a triangular array of sets – see Figure . This was computed by brute force. For instance, the last row corresponds to n = 8 and was computed by generating all
sequences
, finding the sequences q corresponding to each and noting the different values of
, for
. As an example, the fourth row of Figure implies that, for instance,
If
,
can only be 1, that is,
. This is obvious since the sequence f,
, can only be
. See Lemma 3.2.
Now suppose that
. In this case, the allowed sequences f are
,
and
. Using (Equation3
(3)
(3) ) to compute
in each case, we find that the first two give
and the third one,
. Thus,
(cf.
).
4. Examples of sequences q that are slow
In Lemma 3.2, we gave the examples and
, both of which lead to sequences q that are slow. We are aware of three other examples, which we now present.
The first example is given in
Lemma 4.1
Proof.
Let
for
. Then it can easily be verified that
for
. Furthermore, direct calculation gives
Finally, it is straightforward to check that, for
,
and this proves the lemma.
Remark 4.2
We have proved more here, viz. that ,
as given above obey
for all
: a continuous solution to (Equation3
(3)
(3) ). The same is true of
, which implies that
, and
, which implies that
, both for
– an extension of Lemma 3.2.
For the second example, define
(8)
(8) for
. Another instance of a slow sequence q is found when
: in fact,
, where each positive integer k occurs k times. This sequence can also be written
We summarize these observations in the following lemma:
Lemma 4.3
Let . Then
, where each positive integer appears in turn, with integer k occurring k times in succession. That is,
where
and
.
This sequence [Citation8] is a special case of a generalized Golomb triangular recursion [Citation4]. A proof of Lemma 4.3 by S.W. Golomb can be found in the ‘Links’ section of [Citation8].
Remark 4.4
This result can also be written as
as can be easily shown by considering
for
. However, we lack a direct proof of Lemma 4.3 starting from this expression.
Remark 4.5
This result relates immediately to the fact that : we have explicitly constructed
above, from which it is clear that
for n>2. See the second column from the left in Figure .
The third example of a slow sequence q is especially interesting and involves γ, the reciprocal of the golden ratio:
Theorem 4.6
Let , so that
. Then
obeys (Equation3
(3)
(3) ) with
.
Since , clearly
as defined here is slow, and, furthermore,
.
In the course of the proof of the theorem, we need a few small results:
Footnote1
, which implies that
,
,
.
,
, where
is the fractional part of x
,
for
.
Proof of Theorem 4.6
We first show that the theorem is equivalent to identity (Equation9(9)
(9) ) below, then we prove the identity itself.
Starting from , clearly
. It is convenient to shift n by 1, giving
, which we will show obeys (Equation3
(3)
(3) ) for
. When this is substituted in
we have
Now, using (i), (iii) and (iv), we find that
Hence, Theorem 4.6 holds if the right-hand side of the above expression is equal to
for
, that is, if
(9)
(9) To prove (Equation9
(9)
(9) ), we consider separately three cases which are demarcated according to
For n>1, these intervals are all open because γ and
are irrational. Hence, we first dispose of the case n = 1, where we find
since
.
We assume that throughout the rest of this proof. Proving cases A–C for
amounts primarily to rearranging
into a first-degree polynomial in n, plus the floor of a bounded function of n.
Case A. Note that implies that
and
. Thus, in case A we have
Consider the first term in
:
where we have used (i), (iv), (iii) and then (ii). Replacing the first
with
, we get
using (iii). We can now use (ii) and (v) to obtain
Hence, using (iv),
and
is now in the required form.
Since , we have, in case A,
, using (i), and so
. Therefore,
.
Case B. For case B, we have and this implies that
. Hence, in case B
Since
is an integer, we immediately have
. Now,
by (ii) and (i). Hence,
(10)
(10) using (iii). Now, by the definition of case B,
Hence,
and
.
Case C. Case C is similar to case B. We now have , giving
but
. Hence, in case C
From the definition of
, we see immediately that
and so, from (Equation10
(10)
(10) ), we have
. Hence, for case C,
Therefore,
and so
, concluding the proof of the theorem.
5. Heuristic and experimental results
In this section we present heuristic plausibility arguments to give simple descriptions of the behavior of q for certain sequences f. As we shall see, computation suggests that the actual behavior of q follows our predictions closely. We consider three types of sequence f.
5.1. 
 ,
, 

The following lemma summarizes what we can say about the behavior of in this case.
Lemma 5.1
Let with
. Assume that
, where
is a constant, and that
. Then
.
Proof.
Substituting in Equation (Equation3
(3)
(3) ) gives
and solving for
gives
Dividing both sides by n and letting
gives
and so
(11)
(11)
This turns out to be a good approximation. For an example, see Figure , which shows when
. For
, we find from the data used to produce this figure that
.
Theorem 4.6 is a particular case of Equation (Equation11(11)
(11) ) with
.
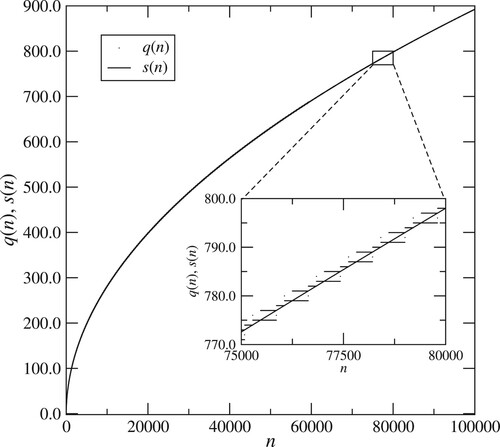
5.2. 

The case tends to a constant
as
is interesting, and is a special case of a nested recursion studied in [Citation10]. We argue by proposing the ansatz
,
, and then deducing the
that this implies. Starting from the asymptotic expansion:
we let
in order to eliminate the second term. This gives
This short calculation suggests that, for
,
(12)
(12) where
and
as
, i = 1, 2.
This appears to work surprisingly well – see Figure , which compares q when , so that
, with
for
. Over this range, we find that
.
Figure 2. Plot of , black dots, for
, so that
as
. According to the argument in Section 5.2, we expect that
, this curve being plotted as a continuous black line. The approximation appears to hold remarkably well, the two plots being almost exactly superimposed. Inset: enlargement of the region
.
Other examples were tried: ,
and
if
and
otherwise. In all cases, a, b were chosen so as to ensure that
had property
, and every time, (Equation12
(12)
(12) ) gave an excellent approximation to
: in these cases at least, it is the asymptotic behavior of
that determines the asymptotic behavior of
.
5.3. 
 with
with 

Arguing in reverse as in the previous case, we can obtain useful approximations to when
is the sum of fractional powers of n, at least in certain special cases. We use the ansatz
and calculate the asymptotic expansion for
Note that the powers of x here are p−i,
and ip−j,
,
. We cannot order the powers of x unless a value of p is specified. Letting, for example, a = 1,
and
, we have
and
. Then, with
, which has property
, we generate
via (Equation3
(3)
(3) ) and compare this with our approximation
. The agreement is good, with
for
, where
.
5.4. Dynamics
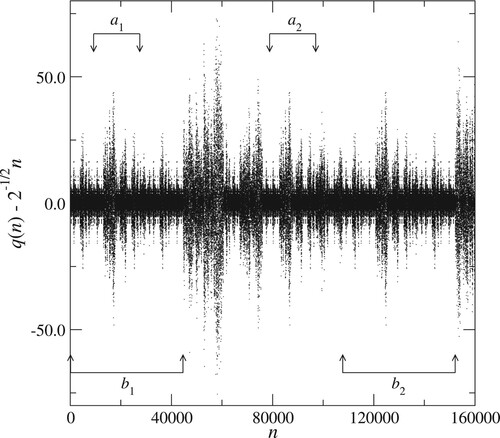
We close this section with some figures illustrating examples of the dynamics of q for particular sequences f.
An interesting case is , shown in Figure . This shows the de-trended sequence
– see (Equation11
(11)
(11) ) – for
. At first sight, no obvious patterns appear in the plot, but in fact there are several regions of exact self-similarity, even in this limited range of n. Specifically, among others, we observe
(regions
); and
(regions
).
Our final figure gives an intuitive idea of what happens if we make a small perturbation. It is tempting to describe the behavior of many of the sequences as ‘chaotic’. However, since (Equation3
(3)
(3) ) is discrete in time and space, there is no sense in which the system can be infinitesimally perturbed; perhaps the best we can do is to compute sequences q,
, where
is computed identically to q – using (Equation3
(3)
(3) ) in the usual way – except that we artificially adjust a single term,
say, for some small integer
. The result of such a computation, with
,
, so that
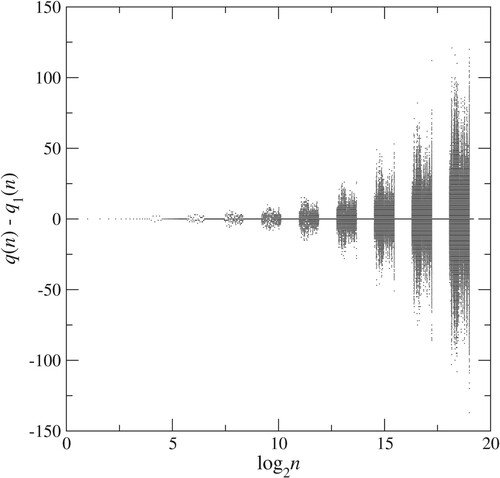
, is shown in Figure . This figure is a plot of the difference
versus
, the scaling bringing out the approximate periodicity visible on a logarithmic scale. We see regions where
exactly, interspersed with regions where this difference is far from zero: the memory of the perturbation seems to persist indefinitely.
6. Conclusions and further work
We have investigated the problem of the conditions on an integer sequence ,
, with
, such that the sequence
, with
, computed from
, exists. We think of the sequence q as a solution to this difference equation. We have proved that if
,
, then the solution q exists, the existence of q being exactly equivalent to the inequality
holding for all
.
We have defined as the set of semi-infinite slow sequences (that is, sequences with differences between successive terms equal to 0 or 1)Footnote2. In Lemma 2.1 examples were given of sequences
but for which q nonetheless exists – the condition that f be slow is sufficient but not necessary – and this suggests that we define a second set of semi-infinite integer sequences,
, which is the set of all sequences f with
such that the corresponding sequence q exists. Clearly,
.
It would be fruitful to investigate the structure of further. The question naturally arises as to whether the proof of Theorem 1.3 could be extended to include more sequences f. A better characterization of
might be a useful step on the way to settling the question of the existence of the Hofstadter sequence, this problem being the original motivation for our work. In fact, the question would have been settled by Theorem 1.3, were the sequence
, with
defined by (Equation1
(1)
(1) ), to be slow. It is not – in fact
.
Solutions arising from typically appear to display non-trivial dynamics: in particular, they are generally aperiodic and display no obvious patterns. For some special sequences f, for instance
with
, the average behavior appears to be well-defined, however, and we give a heuristic argument for this.
Less typical seem to be sequences for which the corresponding solution is also monotonic, and we construct exact solutions in the cases of which we are aware.
Both from the point of view of the existence of solutions and from the study of their dynamics, the difference Equation (Equation3(3)
(3) ) appears to be an interesting subject for further study, even in its own right.
Acknowledgments
The Authors would like to acknowledge helfpul discussions with Dr Peter Gallagher and the valuable comments of the anonymous referees of this journal.
Disclosure statement
No potential conflict of interest was reported by the author(s).
Notes
1 (i), (ii) etc would be clearer labels than i, ii
2 It would be useful to add "and with first term equal to zero" here, i for consistency with the original definition of S.
References
- B. Balamohan, A. Kuznetsov, and S. Tanny, On the behavior of a variant of Hofstadter's Q-sequence, J. Integer Seq. 10 (2007), Article 07.7.1.
- N. Fox, Quasipolynomial solutions to the Hofstadter Q-recurrence, Integers 16 (2016), paper A68, 6 pp.
- D.R. Hofstadter, Gödel, Escher, Bach: An Eternal Golden Braid, Basic Books, Springer, New York, 1979. ISBN 0-465-026850.
- A. Isgur, V. Kuznetsov, and S.M. Tanny, A combinatorial approach for solving certain nested recursions with non-slow solutions, J. Differ. Equ. Appl. 19(4) (2013), pp. 604–615. https://doi.org/10.1080/10236198.2012.662967.
- OEIS Foundation Inc., Entry A005185 in the On-Line Encyclopedia of Integer Sequences, 2024; Available at https://oeis.org/A005185 (in particular the reference to a computation by M. Eric Carr (2 July 2023)).
- OEIS Foundation Inc., Entry A006949 in the On-Line Encyclopedia of Integer Sequences, 2024; Available at https://oeis.org/A006949.
- OEIS Foundation Inc., Entry A063882 in the On-Line Encyclopedia of Integer Sequences, 2024; Available at https://oeis.org/A063882.
- OEIS Foundation Inc., Entry A002024 in the On-Line Encyclopedia of Integer Sequences, 2024; Available at https://oeis.org/A002024.
- K. Pinn, Order and chaos in Hofstadter's Q(n) sequence, Complexity 4(3) (1999), pp. 41–46.
- M. Sunohara and S.M. Tanny, On the solution space of the Golomb recursion, J. Differ. Equ. Appl. 24(8) (2018), pp. 1273–1294. https://doi.org/10.1080/10236198.2018.1471471.
- S.M. Tanny, A well-behaved cousin of the Hofstadter sequence, Discrete Math. 105(1–3) (1992), pp. 227–239.