Comparison of rotation tensor extracted from affine approximation and least square optimization

Keywords:

• Movement Analysis
• Continuum Mechanics
• Soft Tissues Artefact

1. Introduction

Biomechanics of human movements relies on kinematics data from skins markers. The main challenge is to obtain the underlying bone orientation and displacement while skin markers based kinematics are affected by soft tissues artefact. The accuracy of kinematics measurement is also affected by noise and depends on orientation and spreading of markers cluster (Leardini et al. 2005).

Table 1. Mean, max and RMSE of rotation matrices.

	Mean	Max	RMSE
Pin-LSQ/Ref	0.39	1.19	0.45
Skin-Affine/Ref	7.23	11.76	7.71
Skin-LSQ/Ref	11.44	16.93	12.41

Often, computation of underlying bone kinematics are made by least squares (lsq) optimization based on an assumption of rigid bodies (Carman & Milburn 2006). This assumption could be legit if deformations are small. However, it can produce bad results when skin markers are close to a joint where deformation can be important (Cappozzo et al. 1996).

Based on recent works of Rubin and Solav (2016), the rigid body assumption can be replaced by an affine transformation behaviour law. Basically, it consists in replacing the rotation matrix $\overline{\overline{R}}$ with an affine tensor $\overline{\overline{\text{F}}}$ which is a combination of a rigid rotation tensor $\overline{\overline{Rr}}$ and a pure deformation tensor $\overline{\overline{U}}$ . The advantage of this model is that $\overline{\overline{Rr}}$ is not a function of the orientation nor the spreading of the skin markers. As hypothesis in Rubin and Solav(2016), this assumption would be closer to bone movements. Our objective was to experimentally validate the benefit of this approach. Our first hypothesis was that the kinematics obtained using lsq or affine assumptions are equivalent for rigid bodies captured by optoelectronic systems. The second hypothesis is that affine transformation will performed better than the lsq approach in presence of soft tissue artefact.

2. Methods

One participant performed rotations and abductions of the right upper limb. An optoelectronic device (frequency 300 Hz) was used to track trajectories of two marker sets. The first one was composed of four markers attached to a pin screwed into the humerus and the second one composed of four markers spread on the arm skin (Begon et al. 2015).

Movement of a rigid solid can be described as a combination of a translation independent of the observed points and a rotation such as:(1) $$\overrightarrow{x}\left(\overrightarrow{X},t\right)=\overrightarrow{T}\left(t\right)+\overline{\overline{R}}\left(\text{t}\right).\overrightarrow{X}(t)$$(1)

with $\overrightarrow{T}\left(t\right)$ the translation vector, $\overline{\overline{R}}$ the rotation matrix satisfying ${\overline{\overline{RR}}}^{\text{T}}=\overline{\overline{I}}$ and $det\left(\overline{\overline{R}}\right)=1$. $\overline{\overline{R}}$ can be obtained with lsq optimization.

For an affine transformation the cluster position estimation, ${\widehat{x}}_i$ of x_i is defined by:(2) $$\widehat{\overrightarrow{x_i}}=\overrightarrow{X}+\overrightarrow{t}+\overline{\overline{F}}\overrightarrow{\mathrm{\Delta }{X}_i}$$(2)

where $\overrightarrow{\mathit{\Delta }{X}_i}=\overrightarrow{X_i}-\overrightarrow{X}$, is the difference between the cluster at the i^th instant and the reference, $\overrightarrow{t}$ the translation vector and $\overline{\overline{F}}$ the affine tensor.

$\overline{\overline{F}}$ is then decomposed by polar decomposition into two tensors as: $\overline{\overline{F}}=\overline{\overline{Rr}}\overline{\overline{U}}$ where $\overline{\overline{R}}$ is the rigid rotation tensor and $\overline{\overline{U}}$ the pure deformation tensor.

We applied those two methods to the two markers sets and four rotation matrices were computed:

1.	pin-Affine (considered as reference)
2.	pin-LSQ
3.	skin-Affine
4.	skin-LSQ

To test our hypothesis, each rotation matrix had been computed in the reference one, and then the quaternion of these matrices has been computed as well. If reference and rotation matrix are equal, the quaternion angle is zero. So mean and max value of quaternion angle and also root mean square error (RMSE) were computed between each of these angles and zero.

3. Results and discussion

Because the cluster of markers attached to the pin is a rigid body, RMSE between Pin-LSQ and the reference was the closest to 0° (0.45°), with mean = 0.39° and maximum error = 1.19°.

However, bigger differences were found with the two rotation matrices derived from skin marker set.

The skin-Affine rotation matrix shows smaller error than skin-LSQ one: 7.71° vs 12.41° for RMSE with smallest mean and maximum value.

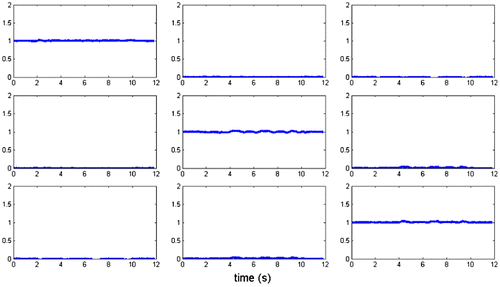
Pin markers set $\overline{\overline{U}}$ tensor (Figure 1) is close to an identity matrix, wich shows that the transformation of this markers set is only a rotation, since $\overline{\overline{F}}=\overline{\overline{Rr}}\overline{\overline{U}}$.

Figure 1. Pure deformation tensor of Pin markers set.

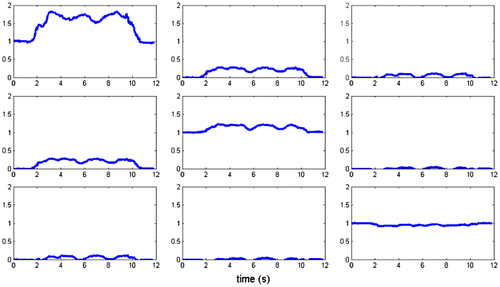
However, $\overline{\overline{U}}$ tensor calculated from the Skin markers set (Figure 2) is not close to an identity matrix, which means that $\overline{\overline{F}}$ is not only a rigid rotation transformation. So we can a priori conclude that the assumption of solid rigid movement is less relevant than affine transformation.

Figure 2. Pure deformation tensor of Skin markers set.

As promising as this approach seems to be in terms of decrease of orientation error, further studies have to be made to cross-validate our results, with more subjects and more movements. Other methods than lsq approach have to be used for the same experimental configuration to validate the advantage of affine transformation.

Another advantage of this method is the simplicity of the algorithm implementation. Basically $\overline{\overline{F}}$ have to be computed from marker set and polar decomposition of $\overline{\overline{F}}$ have to be computed to extract $\overline{\overline{R}}$.

To improve the results, best set of markers have to been find for rotation matrix computing, because despite the fact that rotation matrix obtained with affine tensor is independent of how the marker cluster is spread, soft tissues artefacts are not the same anywhere on the segment.

Another way to improve results is distinguish soft tissues artefact and measurement noise to have a better kinematics.

4. Conclusions

The proposed method using affine tensor allows to obtain a rotation matrix independent of the orientation or how spread the marker cluster is.

Rotation matrix extracted from affine tensor provides better approximation of the underlying bone movement from a skin cluster than the commonly used lsq approach.

We recommend using affine tensor to compute rotation matrices for kinematics analysis.

Acknowledgements

This work has been sponsored by the French government research program “Investissements d’Avenir” through the Robotex Equipment of Excellence (ANR-10-EQPX-44).