A micromechanical framework of arterial tissue growth in the context of medial calcification

Keywords:

• Medial calcification
• arterial growth
• multiscale formulation
• generalized eshelby problem

1. Introduction

Growth and remodelling (G&R) of biological tissues are mechanisms which respectively involve a change in mass and material properties. In particular, arterial media calcification (AMC) is a pathological process involving both processes. AMC mainly consists in an ectopic mineralization process within its elastin-rich inner layer called tunica media. This pathology is linked to various conditions including type II diabetes and chronic kidney disease. AMC induces arterial stiffening, which promotes a mechanically-driven vicious cycle but also cardiovascular events and mortality (Van den Bergh et al. 2019).

Biomechanical G&R theories help understand and quantify the evolution of the biological tissues. In the specific case of arteries, several theoretical frameworks generally focusing on the question of aneurysm development (Baek et al. 2006; DiCarlo et al. 2009; Watton et al. 2009) adopt a macroscopic point of view describing the evolution of tissue growth as an irreversible (as opposed to elastic) component of the deformation gradient (Kuhl 2014).

In this study, we propose to utilize a biomechanical point of view to capture local strains and stresses during calcification. We translate the classical Kröner-Lee decomposition of the deformation gradient to the microscale using a continuum micromechanical framework. We obtain the macroscopic consequences on the tissue (e.g., in terms of tissue growth and deformation) from average rules.

2. Methods

2.1. Framework and kinematics

The present approach entails the definition of a representative volume element (RVE) of the arterial media made of a matrix and embedded spherical mineral (calcification) inclusions.

The constituents of this RVE can deform as a consequence to an imposed macroscopic loading, and also to pathological crystal growth. The (microscopic) gradient of the deformation ${\mathit{f}}^c$ of the mineral phase is decomposed as the product of an elastic (reversible) component ${\mathit{f}}_e^c$ and an imposed component attributed to growth ${\mathit{f}}_g^c,$ leading to ${\mathit{f}}^c={\mathit{f}}_e^c·{\mathit{f}}_g^c.$

Both tissue growth and elastic deformation generate a change in the macroscopic deformation $\mathit{F}$ and stress, as well as an evolution of the respective volume fractions of mineral $f^c$ and matrix $f^m$ which are calculated using micromechanics.

2.2. Micromechanical framework

The micromechanical framework is based on a Mori-Tanaka homogenization method. Both matrix and mineral phases are modelled as isotropic materials, whose elastic properties are displayed in Table 1.

Table 1. Bulk ($k_X)$ and shear (${\mu }_X)$ moduli of the matrix (X = m) and mineral (X = c) phases.

$k_m$	${\mu }_m$	$k_c$	${\mu }_c$
70.0 MPa	18.5 MPa	82.6 GPa	44.9 GPa

A hypoelastic constitutive law is formulated for each phase $X,$ connecting the objective stress rate ${\sigma }_X^{\nabla }$ to the local (microscopic) elastic strain rate ${\mathit{d}}_e^X$ via an hypoelastic stiffness tensor ${\mathbb{C}}_X:$ (1) $${\mathit{\sigma }}_X^{\nabla }={\mathbb{C}}_X:{\mathit{d}}_{\mathit{e}}^{\mathrm{X}},\mathrm{ }{\mathit{d}}_{\mathit{e}}^{\mathrm{X}}=\mathrm{ }{\mathit{d}}^X-{\mathit{d}}_{\mathit{g}}^X,$$(1) where the double dot refers to double contraction, ${\mathit{d}}^X$ is the total strain rate and ${\mathit{d}}_{\mathit{g}}^X$ refers to its component associated with the growth velocity gradient ${\mathit{l}}_g^{\mathit{X}}={\mathit{f}}_{\mathit{e}}^X\cdot {\dot{\mathit{f}}}_{\mathit{g}}^X\cdot {\mathit{f}}_{\mathit{g}}^{X,-1}\cdot {\mathit{f}}_{\mathit{e}}^{X,-1},$ null in the matrix (${\mathit{f}}_{\mathit{g}}^m=\mathit{I},$ no matrix growth; the superimposed dot refers to the time derivative and $\mathit{I}$ is the second-order unit tensor). Phase-specific total strain rates follow from the prescribed macroscopic strain rate $\mathit{D}$ through the use of strain-rate concentration tensors ${\mathbb{A}}_X$ and influence tensors ${\mathbb{D}}_{XY}$ to account for the existence of growth-induced eigenstrain rates (Pichler and Hellmich 2010): (2) $${\mathit{d}}^X={\mathbb{A}}_X:\mathit{D}+\sum _Y{\mathbb{D}}_{XY}{\mathit{d}}_{\mathit{g}}^Y.$$(2)

Computation of the growth-driven evolution of local stresses and their average over the representative volume element enables the recalculation of the macroscopic homogenized stiffness tensor. Note that, in this strain-driven formulation the evolution of the macroscopic deformation $\mathit{F}$ directly results from the prescribed strain rate $\mathit{D}.$ Finally, the ratio of volume change between the calcification phase and the whole RVE gives access to the change in volume fraction.

2.3. Computation of growth

In following simulations, a macroscopic constant uniaxial strain rate $\mathit{D}$ of magnitude $D=100\mu ϵ.{\tau }^{-1}$ is applied ($\tau$ time unit). Meanwhile, calcification is modelled with an increase in the irreversible deformation ${\mathit{f}}_g^c,$ independent from mechanics: (3) $${\mathit{f}}_g^c=f_g^c(t)\mathit{I}=(1+\alpha (1-\exp (-t/t_{\mathit{crit}})))\mathit{I}$$(3) where $t_{\mathit{crit}}=10\mathrm{ }\tau \mathrm{ }$ and $\alpha =0.5$ (unless otherwise specified) are parameters accounting respectively for the mineralization characteristic time and the maximum calcification-induced growth.

3. Results and discussion

In this section, we present preliminary results of our model using an initial volume fraction of calcifications of $5\mathrm{\%}.$ One can observe in Figure 1 the evolution of the spherical part of the deformation gradients associated to mineral (${\mathit{f}}^c,$ light blue) and matrix deformations (${\mathit{f}}^m,$ dark).

Figure 1. Evolution of the mineral (light blue) ${\mathit{f}}^c$ and matrix (dark) ${\mathit{f}}^m$ respective deformations with time. Dark dotted: total matrix deformation with no growth ($\alpha =0$). Light dashed curve: evolution of the growth component of the mineral deformation ${\mathit{f}}_g^c.$

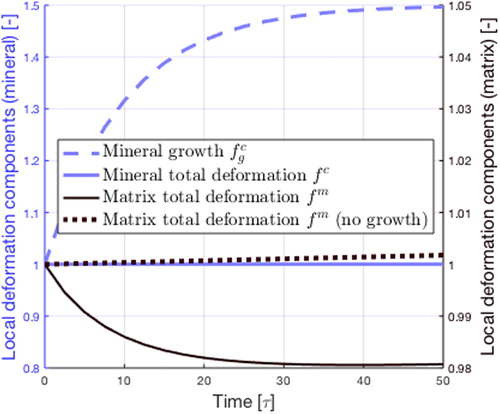
While calcifications grow, the matrix deformation ${\mathit{f}}^m$ decreases, denoting the compression of the matrix resulting from calcification. The increase in mineral total deformation gradient ${\mathit{f}}^c$ is less substantial than the growth part ${\mathit{f}}_g^c:$ the elastic component ${\mathit{f}}_e^c$ ensures the compatibility of deformations.

4. Conclusions

Our numerical study shows that our model is able to reproduce the trends of calcification-induced changes in mineral volume fraction and induced local deformations. To consolidate this framework, model parameters need to be identified using tissue imaging to characterize adaptation and tissue properties. The role of smooth muscle cells, embedded in the medial tissue, is critical to calcification (Van den Bergh et al. 2019). Moreover, these cells are sensitive to their mechanical environment, which regulates their osteogenic phenotype (Humphrey et al. 2015). Micromechanics provide an excellent framework to study these mechanisms, by providing a quantification of local strains sensed by the cells (Scheiner et al. 2013). Hence, describing mechanobiology is a key future work to capture the mechanisms of AMC.

Additional information

Funding

This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement No. 647067, project ERC Consolidator Grant 2014 Biolochanics).