A new musculoskeletal AnyBody™ detailed hand model

Abstract

Musculoskeletal research questions regarding the prevention or rehabilitation of the hand can be addressed using inverse dynamics simulations when experiments are not possible. To date, no complete human hand model implemented in a holistic human body model has been fully developed. The aim of this work was to develop, implement, and validate a fully detailed hand model using the AnyBody Modelling System (AMS) (AnyBody, Aalborg, Denmark). To achieve this, a consistent multiple cadaver dataset, including all extrinsic and intrinsic muscles, served as a basis. Various obstacle methods were implemented to obtain with the correct alignment of the muscle paths together with the full range of motion of the fingers. These included tori, cylinders, and spherical ellipsoids. The origin points of the lumbrical muscles within the tendon of the flexor digitorum profundus added a unique feature to the model. Furthermore, the possibility of an entire patient-specific scaling based on the hand length and width were implemented in the model. For model validation, experimental datasets from the literature were used, which included the comparison of numerically calculated moment arms of the wrist, thumb, and index finger muscles. In general, the results displayed good comparability of the model and experimental data. However, the extrinsic muscles showed higher accordance than the intrinsic ones. Nevertheless, the results showed, that the proposed developed inverse dynamics hand model offers opportunities in a broad field of applications, where the muscles and joint forces of the forearm play a crucial role.

Keywords:

• Musculoskeletal
• hand
• AnyBody
• inverse dynamics
• moment arm

Introduction

The human hand is a highly developed and sophisticated grasping organ containing 27 bones with 36 articulations and 39 active muscles (Hirt et al. 2017). This contributes to a wide range of motion (ROM) (31 degrees of freedom – DOF) while possessing sensitive haptic properties. For controlling this complex system, a high level of interaction between the human brain and the musculoskeletal structure is required. To address various malfunctions because of to disorders of the musculoskeletal system, the inverse dynamics modelling approach is an increasingly applied method.

With this method, the complex dynamic force distribution in all hand structures can be analyzed in numerous kinds of tasks for physiological as well as for pathological simulations. Research questions regarding the prevention or rehabilitation of the biomechanics of the hand can be explained without the requirement for in vivo or in vitro experiments. Mechanical loads within the hand do not only affect muscle activities and forces in the surrounding joints but also lead to balancing forces in the entire body.

Therefore, a diversified field of problems does not rely on the biomechanics of an isolated hand model alone, but an embedment into a holistic human body model. Numerous research groups conducted musculoskeletal simulations of the human hand over recent decades.

Holzbaur et al. (2005) implemented an entire upper limb model, including the human hand within the OpenSim (Seth et al. 2018) framework. This model is based on the experimental and anatomical data of An et al. (1979), Jacobson et al. (1992), Lieber et al. (1990, 1992), and Murray et al. (2000). The model copes with 26 muscles crossing the wrist and finger joints, but lacks the intrinsic muscles.

Lee et al. (2015b) solved this limitation by implementing intrinsic muscles for the fingers. On the basis of the experimental data of An et al. (1979), the muscle pathing was optimized to achieve an improved alignment with the moment arm behavior of each joint (Lee et al. 2015a; MacIntosh and Keir 2017). Further enhancements regarding the length-dependent passive properties of the extrinsic index finger muscles was done by Binder-Markey and Murray (2017).

The model from Ma’touq et al. (2019) also included the biomechanics of the thumb and its intrinsic muscles based on the same literature data as Lee et al. (2015a) and Lippert (2006). In contrast to the previous models, this one implements the human forearm and hand as a standalone framework in Simulink® (The MathWorks, Inc., USA).

As proposed by Mirakhorlo et al. (2018) and Kerkhof et al. (2018), the usage of one consitent source for anatomic data is fundamental.

Goislard de Monsabert et al. (2018) showed that using multiple sources instead of a single one can lead to errors of up to 180% in the calculated muscle forces. Therefore, Mirakhorlo et al. (2018) implemented an OpenSim hand/wrist model, based on an anatomical study of a single cadaver specimen (Mirakhorlo et al. 2016).

Nevertheless, it is a standalone model of the upper extremity based on one cadaver and can thus not be used in a broader scope.

The AnyBody^TM Modelling System (AMS) (Anybody, Aalborg, Denmark) is a musculoskeletal modeling platform containing body scaling functions that incorporate body mass and percentage of fat and influence the muscle and bone dimensions accordingly, which features a patient-specific scaling of the hand model. The AMS is a widely applied simulation platform for musculoskeletal modeling using an inverse dynamics approach. Furthermore, it contains sophisticated algorithms to optimize complex motion capture data, like the movements of thumb and fingers.

The AMS also provides the AnyBody Managed Model Repository (AMMR) (Lund et al. 2019), which includes a generic human body model and a collection of human body parts. The AMMR contained only single fingers in detail by Wu et al. (2008, 2009), which are not implemented in the full-body model. Therefore, a complete comprehensive model of the hand was still lacking.

Therefore, the aim of this study was the development and validation of a detailed human hand model within an existing, commonly used framework for inverse dynamics simulation, including:

1. Anatomical data from a consitent source containing sixteen cadaveric specimens

2. All intrinsic and extrinsic muscles of the entire hand (fingers and thumb)

3. The possibility of patient-specific scaling

4. Full body model implementation (AMMR)

5. Validation of the Model

Materials and methods

The model

The detailed hand model was embedded in the AMS Version 7.2 and AMMR 2.2.2 (Lund et al. 2019).

The AMMR full-body model was used as a basis. Only the forearm and hand were modified. For the proposed detailed hand model, 22 hand segments (including ulna and radius) modelled as rigid bodies linked by physiological idealized joints were used, allowing 31 DOF. The joints of the distal interphalangeal (DIP) and proximal interphalangeal (PIP) were modelled as revolute joints for flexion/extension movements and the metacarpophalangeal (MCP) joint as a universal joint. Hereby flexion/extension and ab/adduction were achieved. Joint positioning and orientation was acchieved in accordance to literature studies (An et al. 1979; Buchholz et al. 1992) and an anatomical study by the UWB (Havelkova et al. 2020b), following the International Society of Biomechanics recommendations for joint coordinate systems (Wu et al. 2005). Further, the axes of rotation of the thumb’s joints were modeled in separated revolute joints as depicted by Hollister et al. (1995). To reduce the complexity, the carpal bones were treated as one rigid body as in other models described in the literature (Lee et al. 2015b; Mirakhorlo et al. 2018; Ma’touq et al. 2019). The wrist joint has two rotational axes according to Kobayashi et al. (1997), which implies flexion/extension and ab/adduction.

Anatomical dataset

Anatomical data were obtained by a study at the UWB by Havelkova et al. (2020b), which included dissecting sixteen cadaveric forearms and Magnetic resonance imaging scans. Through this study, the patient-specific bone surfaces and muscle properties like physiological cross-sectional area (PCSA), muscle length, and origin, via-, and insertion points, as well as the alignment of the muscles were obtained. The whole data set, including a short description of the data obtaining procedure, is freely available (Havelkova et al. 2020a). The means of all values were calculated and implemented into the model. Because the use of mutiple anatomical data can lead to large deviations in the result according to Goislard de Monsabert et al. (2018), the mean values of the sixteen measured samples were calculated and implemented into the model. Further, the muscle alignment was obtained according to the MRI scans of one exemplary cadaver specimen of the anatomical study.

Patient-specific scaling and muscle alignment

Regarding patient-specific scaling, it is not always feasible to measure all dimensions of each finger segment. However, Buchholz et al. (1992) proposed a linear correlation between the hand length and that of each finger bone. Because the study of Buchholz et al. only included the dimensions of six hands, we performed a study with the X-ray data of 71 patients to determine a more accurate relationship (details can be found in the appendix). The length of the metacarpal (MC) and the proximal-, middle-, and distal phalanges (PP, MP, DP) can be scaled according to the hand length (compare with Table 1).

Table 1. Relative segment lengths (to hand length) of each finger bone (distal phalanx (DP), middle phalanx (MP), proximal phalanx (PP), and metacarpal (MC)) in percent and corresponding standard deviation.

Fingers	DP	MP	PP	MC
Thumb	11.52 (0.99)	–	15.76 (1.32)	23.38 (1.72)
Index	8.82 (1.10)	11.75 (1.00)	20.27 (1.44)	34.82 (2.44)
Middle	9.30 (0.77)	14.31 (1.11)	22.54 (1.54)	33.41 (2.36)
Ring	9.54 (0.84)	13.62 (1.04)	21.05 (1.40)	29.48 (2.07)
Little	8.43 (0.92)	9.56 (1.04)	16.72 (1.20)	27.11 (1.88)

The scaling of the model affects not only the length of the segments but also the dimension of the wrapping surfaces, assuring an appropriate alignment of the muscle paths. Therefore, various obstacles like tori, cylinders, and ellipsoids were implemented to guarantee a correct and physiological alignment of the muscle tendons – also in extreme positions of the fingers. Detailed information can be found in the published AMMR repository.

Choice of model accuracy

Because this detailed representation and guidance of each muscle increased the computational time during the calculation of kinematics and kinetics, the model contains four different stages of accuracy:

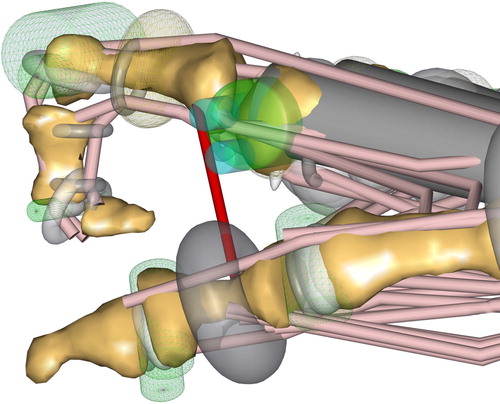
1. Switch between fully detailed muscle alignment in the fingers through wrapping obstacles (WRAP) or via-points (VIA) (see Figure 1).

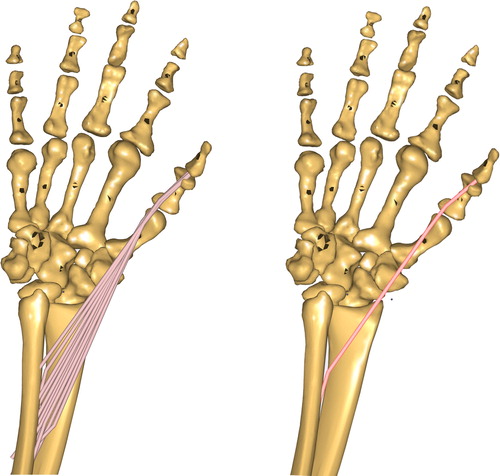
2. Selection between a splitting of the extrinsic hand muscles in various representatives according to their anatomical origins (MULTIPLE) or one representative for each extrinsic hand muscle (SINGLE) (see Figure 2).

Figure 1. Visualization of all wrapping obstacles of the new hand model.

Figure 2. Detailed hand model with several representatives of one muscle (FPL) – left side. Hand model with only one representative for the same muscle – right side.

In addition, the detailed hand model can be switched from a simple muscle representation to a Hill-type muscle model. Via these options, the model can be adapted to different research questions.

Modelling characteristics

Another unique feature of the human hand is the origin points of the lumbricals. In contrast to regular muscles, the lumbricals do not origin from a bone, rather the tendon of the FDP. Therefore, the force of the lumbrical is transmitted onto the FDP tendon. Regarding the modeling, this behavior was realized by a massless substitute segment, which was placed between two via-points on the FDP tendon.

If motion-capture data lacks information for the distal phalangeal, a finger rhythm according to the data from van Zwieten et al. (2015) was implemented. This feature uses the strong relationship between the DIP and PIP joints. Thereby the angle of the DIP joint is driven by the PIP joint.

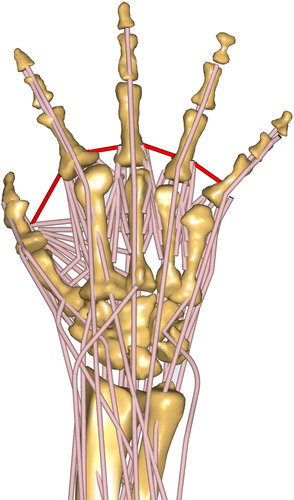
To model the strengthening of the skin between the fingers during ab/adduction, ligaments simulate the skin resistance. Properties are according to the material investigations by Gallagher et al. (2012). The zero position was assumed according to the positioning of the fingers shown in Figure 3. The red line depicts the ligament representing the purlicue skin resistance.

Figure 3. The proposed detailed musculoskeletal hand model in the AMS (configuration WRAP – SINGLE). The position of the fingers corresponds to the calibration position of ligaments to simulate the purlicue skin resistance (red).

On the basis of the study of Wu et al. (2008) the moments of inertia of each finger segment were calculated under the assumption of a tubular representation of the bone.

The entire developed hand model is shown in Figure 3.

Model validation

For validation purposes, moment arms numerically calculated by the model and experimentally measured moment arms from the literature were compared. This approach was chosen because studies of Maury et al. (1995) and Raikova and Prilutsky (2001) indicated that the line of action and moment arms are critical parameters for muscles to predict muscle and joint reaction forces. Previous validation studies of the AMS by Zee et al. (2007) and Marra et al. (2015) showed, that simulated muscle activities and joint reaction forces fit quite accurately to experimental data. Therefore, when the moment arms of the proposed model fit experimental data, the resulting muscle activities and joint reaction forces of the hand should also correspond to reality.

Even though the model is able to calculate inverse dynamics, this study placed particular emphasis on the importance of the muscle moment arms, and thus on the correct kinematics.

Loren et al. (1996) obtained the muscle moment arm in five upper extremities for the extension/flexion as well as for the ulnar/radial abduction of the wrist.

Smutz et al. (1998) used seven cadaveric specimens to obtain the moment arm considering the thumb. The ROM contained the flexion/extension of the DIP joint, the flexion/extension and ab/adduction of the MCP joint, and the flexion/extension and ab/adduction of the carpometacarpal (CMC) joint.

In case of the index finger, An et al. (1983) conducted movements of the flexion/extension of the MCP, PIP, and DIP as well as ab/adduction of the MCP joint. Thereby seven cadaveric hands were evaluated.

The results of Franko et al. (2011) stated that the moment arms are nearly identical across all digits for each joint (MCP, PIP, DIP). Therefore, for validation purposes, only one finger (the index finger) needed to be addressed. The muscles examined in all three studies are summarized in Table 2.

Table 2. Examined muscles according to the studies of Loren et al. (1996), Smutz et al. (1998) and An et al. (1983)

Wrist JOINT
Extensor carpi radialis brevis	(ECRB)
Extensor carpi radialis longus	(ECRL)
Extensor carpi ulnaris	(ECU)
Flexor carpi radialis	(FCR)
Flexor carpi ulnaris	(FCU)
Thumb
Flexor pollicis longus	(FPL)
Extensor pollicis longus	(EPL)
Extensor pollicis brevis	(EPB)
Abductor pollicis longus	(APL)
Flexor pollicis brevis	(FPB)
Abductor pollicis brevis	(APB)
Adductor pollicis oblique head	(APo)
Adductor pollicis transverse head	(APt)
opponens pollicis	(OP)
Index finger
Flexor digitorum superficialis	(FDS)
Flexor digitorum profundus	(FDP)
Extensor digitorum communis	(EC)
Extensor indicis	(EI)
First dorsal interosseous	(FDI)
Lumbrical	(LU)
First palmar interosseous	(FPI)

The tendon excursion method introduced by Landsmeer (1961) was used to compute moment arms in experiments (An et al. 1983; Loren et al. 1996; Smutz et al. 1998; Franko et al. 2011) and simulation models. The tendon excursion method uses the length variation of the tendon (dx), because only one axis of a joint is moved, and the angular change of the joint (dɸ) to calculate the moment arm (M) of the specific muscle in respect to the chosen joint (An et al. 1983). $$\frac{dx}{d\mathrm{ɸ}}=M$$

The model was scaled to an average 50 percentile male person (hand length: 182 mm, handbreadth: 85 mm) unless the literature data provided anthropometrics of single specimens (An et al. 1983). To compare the numerical and experimental results, the same kinematic motion was performed in the simulations as in the experiments. Thereby, only the investigated joints were moved through the ROM provided by the literature, all others were locked in neutral position.

Results

Figures 4–6 show exemplary the comparison of the experimentally gained literature data and the numerically calculated muscle moment arms of selected muscles. The main flexors and extensors of the wrist follow the trend of the experimental data (Loren et al. 1996) for the flexion/extension of the wrist and remains mostly within the standard deviation; only the FCR muscle displays a small offset (Figure 4). Regarding the flexion/extension of the MCP finger joint (Figure 5) the model prediction shows a comparable progression as the literature data (An et al. 1983), whereby it should be noted that the experimental data is based only on a single finger. Additionally, for the MCP joint of the thumb, the numerically calculated moment arms of the selected flexor/extensor thumb muscles remain within the standard deviation of the literature experiments (Smutz et al. 1998) (Figure 6). The progression of all muscles over the flexion/extension and ab/adduction ranges can be found in the appendix.

Figure 4. Progression of the moment arms for the wrist regarding the extensor and flexor muscles during the extension/flexion phase. Negative angles represent the extension of the wrist, and positives the flexion. Lines represent the simulated results, whereas the shaded areas are the experimental results with standard deviation from Loren et al. (1996).

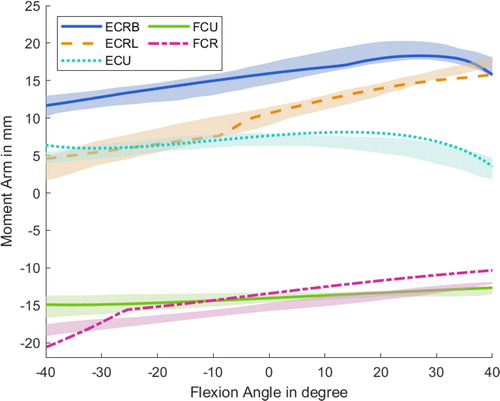
Figure 5. Progression of the moment arms for the index finger regarding extrinsic and intrinsic hand muscles during the flexion of the MCP joint. Lines represent the simulated results, whereas the shaded areas highlight the experimental data of one subject with standard deviation from An et al. (1983).

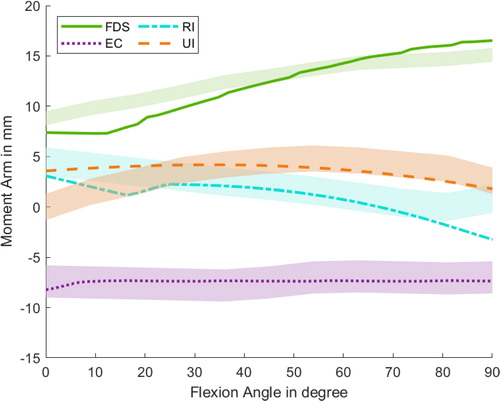
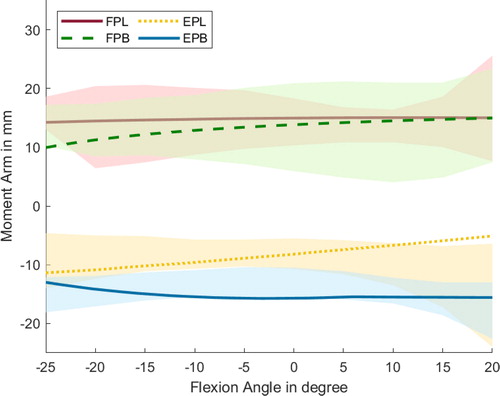
Figure 6. Progression of the moment arms for the thumb regarding extensor and flexor muscles during flexion around the CMC joint. Negative angles represent the extension of the CMC joint, and positives the flexion. Lines represent the simulated results, whereas the shaded areas highlight the experimental data with standard deviation from Smutz et al. (1998).

However, An et al. (1983) only provided the exact progression of an exemplary finger for the flexion/extension and ab/adduction along the MCP joint. For the measurements of all examined patients’ fingers and all joints (including the PIP and DIP joints), only the mean values along the ROM are given. For this reason, the mean moment arms along the ROM for all muscles and joints are summarized in Table 3 for a better comparability. For all simulations, a detailed muscle alignment through wrapping obstacles and one representative for each extrinsic hand muscle were chosen (configuration: WRAP – SINGLE). According to the literature data, the hand model was scaled in size.

Table 3. Mean muscle moment arms of the index finger, thumb and wrist during the range of motion (extension/flexion, abduction/adduction).

		Mean muscle moment arms (and stand. dev.) in mm
		FDS	FDP	EC	EI	RI	LU	UI
MCP Flex/Ext	Model	12.18	8.79	−7.37	−7.37	1.38	10.39	3.81
	Exp.	11.9 (0.7)	11.1 (1.1)	−8.6 (1.6)	−9 (1.3)	3.7 (1.4)	9.3 (2.1)	6.6 (2.1)
MCP Abd/Add	Model	0.13	0.82	0.80	0.29	−7.81	−7.66	12.79
	Exp.	1.7 (2.0)	1.1 (1.7)	−0.2 (2.5)	1.3 (1.6)	−6.1 (2.1)	−4.8 (1.6)	5.8 (1.7)
PIP Flex/Ext	Model	5.75	7.77	−4.09	−4.02	–	0	0
	Exp.	6.2 (1.0)	7.9 (1.1)	−2.8 (1.1)	−2.6 (1.1)	–	−1.8 (1.3)	−2.6 (0.8)
DIP Flex/Ext	Model	0	4.29	−3.67	−3.68	–	0	0
	Exp.	0	4.2 (1.4)	−2.2 (0.4)	−1.9 (0.5)	–	−0.7 (0.6)	−1.6 (0.5)
Thumb
		FPL	FPB	EPL	EPB	APL	APB	APt	APo	OP
CMC Flex/Ext	Model	14.81	13.24	−8.44	−15.18	−13.07	−0.07	32.15	13.91	0.79
	Exp.	14.49 (5.02)	13.43 (6.52)	−9.62 (3.93)	−14.39 (2.75)	−7.69 (3.57)	3.36 (3.70)	31.32 (7.68)	22.91 (10.80)	12.56 (5.08)
CMC Abd/Add	Model	−4.45	−9.72	1.12	−0.35	−0.09	−17.95	17.47	−0.24	−8.52
	Exp.	−1.18 (3.84)	−9.41 (5.83)	7.42 (5.28)	−3.58 (4.59)	−9.71 (2.99)	−15.13 (7.08)	16.46 (11.38)	13.62 (12.04)	−4.72 (5.00)
MCP Flex/Ext	Model	8.86	6.83	−6.58	−8.49	0	5.04	9.6	–	–
	Exp.	9.91 (2.16)	6.64 (1.65)	−9.69 (1.44)	−9.04 (1.16)	1.36 (2.21)	6.78 (4.56)	5.26 (3.06)	–	–
MCP Abd/Add	Model	−0.57	−5.17	3.64	1.64	−7.58	8.4	3.27	–	–
	Exp.	−0.06 (2.41)	−8.83 (3.27)	4.37 (1.86)	−1.04 (1.43)	−10.77 (4.39)	4.93 (4.23)	2.96 (4.36)	–	–
DIP Flex/Ext	Model	5.86		−4.97	–	–	–	–	–	–
	Exp.	7.82 (1.31)		−4.18 (0.77)	–	–	–	–	–	–
Wrist
		ECRB	ECRL	ECU	FCR	FCU
Wrist Flex/Ext	Model	15.58	10.24	6.86	13.84	13.96
	Exp.	13.47–16.42	8.49–10.87	4.21–6.35	15.00–16.22	13.27–15.05
Wrist Abd/Add	Model	16.32	21.73	20.03	5.04	16.28
	Exp.	13.99–15.79	21.08–23.09	25.83–29.51	4.01–7.13	19.82–23.59

The predicted moment arms (and standard deviations) in the developed detailed hand model coincide well with the experimental data by An et al. (1983), Smutz et al. (1998), and Loren et al. (1996).

Discussion

The aim of this work was the implementation and validation of a developed, detailed hand model in the simulation environment of AMS.

In addition to the successful implementation of a scalable, anatomically representative hand model, the validation by moment arm patterns displays matching results.

Wrist joint

Moment arm patterns inside the wrist display a good alignment with data from the literature, according to Loren et al. (1996). Furthermore, the decay in the ECU muscle during high flexions is predicted accurately, whereas the FCR follows the trend of the data from Loren et al. but showing a small offset.

Regarding the mean moment arm through the ROM, only small deviations from the literature data for the ECU and FCR in extension/flexion and during ab/adduction for the ECRB are notable. All other muscle moment arm averages are within the standard deviation of the compared data. Exceptions are the ECU and FCU muscle during the ab/adduction phase, which show up to 5.8 mm differences. This deviation could result in the patient specification or measure inaccuracies of the experimental data set, because a moment arm of approximately 20 mm/16 mm for the ECU/FCU appears reasonable.

Index finger

The comparison with the data from An et al. (1983) shows that the majority of the respective muscles are within the average moment arms standard deviation or display divergences of less than 1 mm apart. In particular, the intrinsic muscles (LU, RI, UI) show a greater discrepancy in the experimental data than the extrinsic ones. One reason could be that the moment arms of intrinsic muscles are more patient-specific than the extrinsic muscles, which was previously noted by Mirakhorlo et al. (2018). Regarding the progression of the muscle moment arms during the MCP flexion phase, the simulated muscle paths agree well with the experimental observations.

Thumb

The large standard deviation of the experimental dataset from Smutz et al. (1998) shows that the anatomical structure of the thumb can vary considerably among subjects, particularly for the intrinsic muscles. Alternatively, the high standard deviation of the experimental data by Smutz et al. could originate from measurement errors.

Regarding the mean moment arm along the ROM, the majority of the thumb muscles are within the standard deviation. Greater differences occur at the CMC joint for the OP, APo, and APL. The divergence for the APL might originate from the insertion point of the underlying anatomical data set from Havelkova et al. (2020b), because the insertion point is located closer to the joint than in the experimental data, which restricts the moment arm of the APL. Nevertheless, the simulated moment arm progressions of the extrinsic muscles align well with the data from Smutz et al. (1998).

The depicted results show similar moment arm patterns as previously published models by Ma’touq et al. (2019), Mirakhorlo et al. (2018), and Lee et al. (2015b).

Together with the generalized anatomical dataset, this leads to the conclusion, that the proposed model represents the musculoskeletal mechanics of the human hand in an accurate manner. Therefore, the muscle forces and joint reaction forces calculated with this model should reflect reality as closely as possible.

Anatomical variability needs to be emphasized in any type of musculoskeletal model, it therefore needs to be kept in mind, that patient specific variations of muscle aligments and unique musculatures can not be considered by such a generalized model. The patient specific scaling in size might cope the most significant anatomical changes in muscle alignment and joint placement, but is limited to this scaling.

To ensure the most accurate possible answers to any research questions, the model is scalable to subject-specific anthropometric data. The necessary degree of detail (WRAP, VIA, MULTIPLE, and SINGLE) can be adapted. Additionally, the use of the consistent anatomical dataset (Havelkova et al. 2020b) from multiple specimens provides generalizability of the model, as claimed by Goislard de Monsabert et al. (2018).

In addition to many features that contribute to the preciseness of the model, the first implementation of the LU muscles with origins on the FDP tendon leads to a more accurate prediction of the intrinsic muscle activities. Thereby, the force equilibrium between, for example, the two LU of the index finger, is achieved more physiologically, because each crosses the MCP joint on each side.

Nevertheless, the model is limited, because the origins of the LU muscles are fixed on the neutral position of the FDP tendons, but do not change position when the FDP muscles are contracted. By contrast, simulations show that a manual shifting of the LU origin point according to the calculated shortening of the FDP tendon would only lead to a change in the LU moment arm of 1 mm. Considering the way the moment arm is calculated using the tendon excursion method, this limitation of the LU being fixed explains that the intrinsic muscles have no moment arm in the PIP and DIP joint compared to the experimental data (see Table 3).

Regarding the different configurations, computational costs, and the accuracy of the results, the following could be stated: the most detailed model includes more wrapping obstacles within the fingers and more muscle representatives. This increased level of detail leads to the most precise outcome but also more computational expenses and, thus, to an approximately five times longer computational time compared to the simplest detailed model (see Figure 7).

Figure 7. The progression (SINGLE)/ mean progression (MULTIPLE) of the FDS moment arms during flexion of the MCP index joint with different detailed stages of the model. Clearly notable is, that the model with obstacle methods predicts a better moment arm behaviour. The simple model drastically decreases the computational effort from 100 % (MULTIPLE-WRAP) to 14 % (MULTIPLE-VIA) and from 92 % (SINGLEWRAP) to 12 % (SINGLE-VIA).

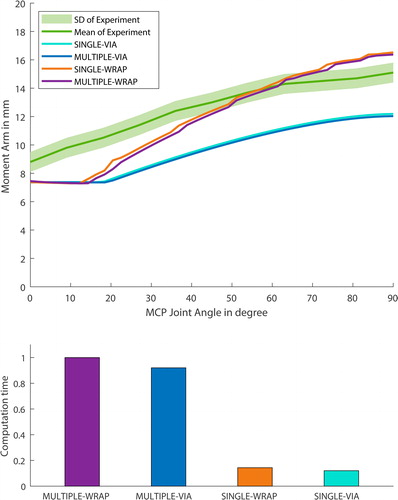
As seen in Figure 7, the progression of the moment arm is quite similar for the MULTIPLE and SINGLE configurations. This can be explained by the fact that these two configurations differ in the size of the muscles’ origin and insertion zone, as indicated in Figure 2. The respective muscle representatives have different muscle paths and correspondingly different moment arms along the wrist and the CMC joint. However, from the MCP onwards, these are all very similar, which leads to only a slight difference in the moment arm for the MCP joint.

The axis of rotation of each joint is not adjusted according to the mean cadaveric specimen data, and therefore, small deviations or offsets of the moment arms can be explained.

The skin resistance between the fingers during ab/adduction is only assumptions according to the data of Gallagher et al. (2012). The material properties of the skin in the forearm by Gallagher et al. are directly transferred to the skin properties because no specific material tests were conducted in the presented anatomic study by Havelkova et al. (2020b).

Although Eschweiler et al. (2016) had already developed a detailed model of the human wrist within the AMS, this model is not implemented in the proposed detailed hand model, mainly because of the reduction of complexity of the model. The eight carpal bones in the presented model are defined as one rigid segment, allowing no movement between the carpal bones. When the research questions do not address the force distribution inside the wrist joint, Schuind et al. (1995) showed that this lack does not have a great influence on the outcome of the muscle activities. This limitation can be addressed in a future version of the model, where splitting of the wrist joint into an ulnar and radial side might be convenient. Further enhancements might be the implementation of helical joint axes in the thumb joints, as proposed by Kerkhof et al. (2016).

Another point for improvement is the implementation of the extensor mechanism in the fingers. Although the kinematics of the extensor mechanism is partially represented by the finger rhythm, the passive tension whenever it is elongated is currently still omitted when calculating forces in an inverse dynamics simulation. Consequently, slightly altered joint reaction forces on the finger joints could be found, as well as a possible co-contraction in the finger muscles, as stated by MacIntosh and Keir (2017) could be lacking.

In general, the anatomical complexity of the fingers is quite high and the extensor hood is just one example of the interconnectivity within the human hand. Although the model is capable of correctly mapping tendon pulling forces using the obstacle, which transfers forces to segments, passive joint stiffness or damping moments are not yet implemented in the model. How the implementation of these parameters can affect a forward dynamic finger model is shown by Lee and Kamper (2009).

A further step to enhance confidence in the model could be an experimental validation, like a comparison with electromyographical data, as well as testing the outcome of predicted joint reaction forces against measured ones, using instrumentalized prostheses similar to Bergmann’s (2008) implants for the shoulder.

Conclusion

The current study presented the development of a musculoskeletal hand model using the AMS framework, that is capable of kinematics as well as inverse dynamics predictions, based on a consistent anatomical dataset. Comparison with experimental moment arm studies showed good correlation and emphasizes the motivation to use the model in an inverse dynamics validation and later in a broad field of applications.

Many research questions can be answered within this new framework, through the adaptive implementation of the hand within the holistic human body system (AMMR). Thereby, also influences of the entire body motion on the hand and vice versa can be addressed.

The presented generic model will become available in the AMMR and can be used for the biomechanical investigation of important clinical problems affecting the human forearm.

Disclaimers

Maximilian Melzner and Lucas Engelhardt contributed equally to this work and share the first authorship.

Sebastian Dendorfer and Ulrich Simon contributed equally to this work and share the last authorship.

Disclosure statement

All authors of this manuscript have no conflict of interest.

Additional information

Funding

Funding from the SNF (320030L_170205), DFG (SI 2196/2-1, IG 18/19-1), and FWF (I 3258-B27) for the DACH_FX Project and funding from the EFRE, Ziel ETZ BY-CZ 2014-2020 (Interreg V) (Pr. 182) and BayWISS is gratefully acknowledged.