A scale conjugate neural network approach for the fractional schistosomiasis disease system

Abstract

This study presents the numerical solutions of the fractional schistosomiasis disease model (SDM) using the supervised neural networks (SNNs) and the computational scaled conjugate gradient (SCG), i.e. SNNs-SCG. The fractional derivatives are used for the precise outcomes of the fractional SDM. The preliminary fractional SDM is categorized as: uninfected, infected with schistosomiasis, recovered through infection, expose and susceptible to this virus. The accurateness of the SNNs-SCG is performed to solve three different scenarios based on the fractional SDM with synthetic data obtained with fractional Adams scheme (FAS). The generated data of FAS is used to execute SNNs-SCG scheme with 81% for training samples, 12% for testing and 7% for validation or authorization. The correctness of SNNs-SCG approach is perceived by the comparison with reference FAS results. The performances based on the error histograms (EHs), absolute error, MSE, regression, state transitions (STs) and correlation accomplish the accuracy, competence, and finesse of the SNNs-SCG scheme.

Keywords:

• Fractional schistosomiasis model
• biological system
• supervised neural networks
• comparison
• scaled conjugate gradient

1. Introduction

Schistosomiasis is known as a parasitic disease that produce to worm the Schistosoma species. Almost seven years ago, Schistosomiasis targeted around 206 million, while 89.2 million individuals were found expected to treat (World Health Organization 2013). Schistosomiasis originated by the tapeworms that presents the species Schistosoma and the monophyletic Platyhelminthes members (Toor et al. 2018; Dejon-Agobé et al. 2022). In 1905, Schistosoma is discovered by the camellia eggs, which is introduced an eighteen-year boy who works on the farms (Kong et al. 2019). Schistosomiasis has a complicated life cycle that contains two rapacious host steps initially (larva and human) along with two free pelagic steps (miracidia and cercariae). In the process of host bacterium eggs, the roundworms can cross the large intestine along with the ecosystem (Kincaid-Smith et al. 2021). These eggs pledge to grow and hatch into the miracidia after mixing in the fresh water. The clear miracidia contaminate the hosts based on the snail that is recognized as a larval growth. The snails create a huge quantity of cercariae and with the use of asexual reproduction release in the water. The free movement of the cercariae can affect the skin, where the adults can face sophistication into the water (Jaber et al. 2021).

The mathematical analysis based on the Schistosomiasis has been typically presented by using the boundary conditions. There were many scholars that applied the deterministic schemes along with some modified versions to solve the schistosomiasis mathematical model (SDM) (Zhang and Zhao 2020; Lowe et al. 2023). The study based on the fractional calculus has widely been investigated in recent years with real-world applications to describe the energy dissipation impacts, genetic properties, damage structures and cognition (Diethelm et al., 2020). The Caputo fractional and Riemann–Liouville are excellent operators to handle the fractional order models that present the complication of the polynomial function along with its corresponding derivative (Shaikh and Qureshi 2022). Newton proposed the fractional calculus that has recently annoyed the interest of various researchers. The most captivating leaps in the sectors of industry have been introduced in the last three decades by using the fractional calculus structure (Hejazi et al. 2022). The updated form of the fractional derivative involves more complications by using the inhomogeneity characteristics. The multifaceted media behavior using the diffusion procedure can be applied in the fractional operators. These valuable tools have been used in various models that demonstrate the reliable and precise solutions of the differential systems of any order. Many investigators worked on the simplistic calculus to describe a wider range of intricate occurrences of rapid development with different computational methods in terms of computer software. Some recent fractional calculus applications using the efficient integer-order schemes have been applied to examine the real-world models based mathematical systems (Fernandez and Fahad 2022; Azizi 2022). The differential form of the derivative associated with the non-singular kernel is used to study the fibroid observation system presented in (Baleanu et al. 2019). A novel fractional impression by using a control approach in the dengue infection is reported in (Jajarmi et al. 2019). A review study based on the infection disease during the process of pregnancy is reported in (Farah et al. 2023).

The recent investigations of the theory of fractional calculus have been obtained by using the two noteworthy operators, Atangana–Baleanu (AB) and Caputo–Fabrizio (CF), the necessary mathematical details and expression regarding AB and CF differential operators can be seen in (Balasubramaniam 2022; Lin et al. 2022). These operator performances represent the non-singularity and have not been applied in the energy supply. The AB operator is generally concentrated to the simple Mittag-Leffler scheme that present the powerful forces due to the diffusion impacts of associations along with good molds. The operator based on CF indicates the exponential law that shows the diversity of natural phenomena along with the fusion impacts. The AB and CF operators demonstrate the variety of scientific evaluations, e.g. life processes, turbulence theory, financial problems, heat flux models, and operations research (Balasubramaniam 2022; Lin et al. 2022).

This work aims to present the solutions of the fractional SDM numerically using the supervised neural networks (SNNs) and scaled conjugate gradient (SCG), i.e. SNNs-SCG. The stochastic computing solvers have been explored in various complicated models (Wang et al. 2021; Sabir et al. 2022). Few of the stochastic applications are reported as, infection control system (Sabir et al. 2022), dynamics of nonlinear combined drug therapy model (Bilal et al. 2024), cyber warfare model with attack–defend strategies on critical infrastructures (Majeed et al. 2023) singular models of nonlinear fractional Lane–Emden equations (Sabir et al. 2021), nonlinear delay differential systems governing avian influenza spread dynamics (Anwar et al. 2023), nonlinear singular models of third kind (Sabir and Wahab 2021), dynamical HIV infection system with latently infected cells (Umar et al. 2021), magnetohydrodynamic (MHD) boundary layer problems (Ullah et al. 2023), non-linear tumor-immune delayed system (Anwar et al. 2023), and MHD Casson nanofluid involving Darcy-Forchheimer porous medium (Shoaib et al. 2023), biological based chemical production or biorefining modelling (Pomeroy et al. 2022), effective prediction of date fruit quality attributes during cold storage by exploiting electrical characteristics (Mohammed et al. 2022), electroencephalogram signals analysis (Jia et al. 2022), and steady-state Bratu differential systems arising from solid biofuel combustion theory (Hosseini et al. 2023). Based on all these reports, the authors are inspired or motivation to implement AI based computing paradigm to access the dynamical behaviour of the fractional schistosomiasis disease model numerically by applying the hybrid computing of SNNs-SCG procedure. As per authors literature survey the AI-based computing paradigm via SNNs-SCG has not implemented for solving the fractional SMD (Jaber et al. 2021; Anwar et al. 2023).

The insights, contribution and novel features of the SNNs-SCG algorithm-based computing paradigm are given in brief as follows:

• The nonlinear fractional SDM is presented to get more precise and accurate performances disease spread dynamics.

• The Caputo fractional operator has been used to develop the fractional SDM and solve it numerically.

• The dynamical performances of the fractional SDM are obtainable by exploiting the novel application of the supervised neural networks along with the computational scaled conjugate gradient scheme, i.e. SNNs-SCG

• The overlapping of the SNNs-SCG paradigm results and reference fractional Adam scheme solutions have been performed to solve the fractional SDM.

• The negligible absolute error (AE) performances show the preciseness of SNNs-SCG solver to solve the fractional SDM.

• The performances based on the error histograms (EHs), absolute error, MSE, regression, state transitions (STs) and correlation accomplish the accuracy, competence, and finesse of the SNNs-SCG scheme for solving the fractional SDM.

The remaining sections of the paper are given as: Sect 2 is related to the fractional model, Sect 3 presents the SNNs-SCG scheme, Sect 4 shows the numerical results, and the conclusions are presented in final Sect.

2. Fractional SDM

The mathematical fractional SDM is presented in this section. The aim to exploit the fractional derivatives is to achieve the precise results of the SDM. The general integer order form of the SDM is presented with five differential class based categories as: uninfected $W(\tau ),$ infected with schistosomiasis $A(\tau ),$ recovered through infection $Q(\tau ),$ expose $E(\tau )$ and susceptible to this virus $S(\tau )$ (Botmart et al. 2022): (1) $$\{\begin{array}{l}\frac{\mathit{\text{dW}}(\tau )}{d\tau }=l_1-a_1\mathit{\text{SW}}(\tau )+\delta Q(\tau )-b_{1}W(\tau ),\\ \frac{\mathit{\text{dA}}(\tau )}{d\tau }=a_1\mathit{\text{SW}}(\tau )-(b_1+\mu )A(\tau ),\text{}\\ \frac{\mathit{\text{dQ}}(\tau )}{d\tau }=\mu -(\delta +b_1)Q(\tau ),\\ \frac{\mathit{\text{dE}}(\tau )}{d\tau }=l_2-a_{2}A(\tau )E(\tau )-b_{2}E(\tau ),\\ \frac{\mathit{\text{dS}}(\tau )}{d\tau }=a_{2}A(\tau )E(\tau )-b_{2}S(\tau ).\end{array}$$(1)

The parameters define in Table 1 while the further elaborative information regarding SDM in (1)(1) $$\{\begin{array}{l}\frac{\mathit{\text{dW}}(\tau )}{d\tau }=l_1-a_1\mathit{\text{SW}}(\tau )+\delta Q(\tau )-b_{1}W(\tau ),\\ \frac{\mathit{\text{dA}}(\tau )}{d\tau }=a_1\mathit{\text{SW}}(\tau )-(b_1+\mu )A(\tau ),\text{}\\ \frac{\mathit{\text{dQ}}(\tau )}{d\tau }=\mu -(\delta +b_1)Q(\tau ),\\ \frac{\mathit{\text{dE}}(\tau )}{d\tau }=l_2-a_{2}A(\tau )E(\tau )-b_{2}E(\tau ),\\ \frac{\mathit{\text{dS}}(\tau )}{d\tau }=a_{2}A(\tau )E(\tau )-b_{2}S(\tau ).\end{array}$$(1) can be seen in (Botmart et al. 2022). In SDM in Equation (1)(1) $$\{\begin{array}{l}\frac{\mathit{\text{dW}}(\tau )}{d\tau }=l_1-a_1\mathit{\text{SW}}(\tau )+\delta Q(\tau )-b_{1}W(\tau ),\\ \frac{\mathit{\text{dA}}(\tau )}{d\tau }=a_1\mathit{\text{SW}}(\tau )-(b_1+\mu )A(\tau ),\text{}\\ \frac{\mathit{\text{dQ}}(\tau )}{d\tau }=\mu -(\delta +b_1)Q(\tau ),\\ \frac{\mathit{\text{dE}}(\tau )}{d\tau }=l_2-a_{2}A(\tau )E(\tau )-b_{2}E(\tau ),\\ \frac{\mathit{\text{dS}}(\tau )}{d\tau }=a_{2}A(\tau )E(\tau )-b_{2}S(\tau ).\end{array}$$(1) presents the total mortality at the time $\tau ,$ represented by $N(\tau ),$ into susceptible individuals that are not infected due to schistosomiasis $W(\tau ).$ Those who suffer infection with this disease $A(\tau ),$ and recovered through this infection $Q(\tau ).$ Accordingly, the whole population is $A(\tau )+W(\tau )+Q(\tau )=N(\tau ).$ Moreover, $N_1$ categorized the snail total populations into exposed snails. The uninfected individuals from the schistosomiasis are $U$ and infested from the schistosomiasis are $V.$ It is shown that $N_1=V+U$ is the total population of the vectors. Table 1 indicates the characteristics of the parameter using the mathematical SDM.

Table 1. Parameter details based on the SDM.

Parameter	Descriptions
$l_{{}_1}$	Human rate based susceptible
$\delta$	Loss of immunity rate
$a_1$	Those susceptible who got infection through schistosomiasis
$b_1,b_2$	Snails’ and human morality
$\mu$	Infected to recovered individuals
$l_2$	Population of snail
$a_2$	Diseased snail
$\tau$	Time

These numerical performances of the fractional SDM are presented by applying the artificial intelligence (AI) procedures based on the SNNs-SCG. The fractional SDM is mathematically presented as: (2) $$\{\begin{array}{l}\frac{d^{\alpha }W(\tau )}{d{\tau }^{\alpha }}=l_1-a_1\mathit{\text{SW}}(\tau )+\delta Q(\tau )-b_{1}W(\tau ),\text{}\\ \frac{d^{\alpha }A(\tau )}{d{\tau }^{\alpha }}=a_1\mathit{\text{SW}}(\tau )-(b_1+\mu )A(\tau ),\text{}\\ \frac{d^{\alpha }Q(\tau )}{d{\tau }^{\alpha }}=\mu -(\delta +b_1)Q(\tau ),\\ \frac{d^{\alpha }E(\tau )}{d{\tau }^{\alpha }}=l_2-a_{2}A(\tau )E(\tau )-b_{2}E(\tau ),\\ \frac{d^{\alpha }S(\tau )}{d{\tau }^{\alpha }}=a_{2}A(\tau )E(\tau )-b_{2}S(\tau ),\end{array}$$(2) where $\alpha$ is the fractional Caputo operator and taken between 0 and 1 to present the solutions of the fractional SDM.

3. Proposed SNNs-SCG solver

The stochastic SNNs-SCG procedure for the numerical representation of solution dynamics for fractional SDM is presented in this section briefly.

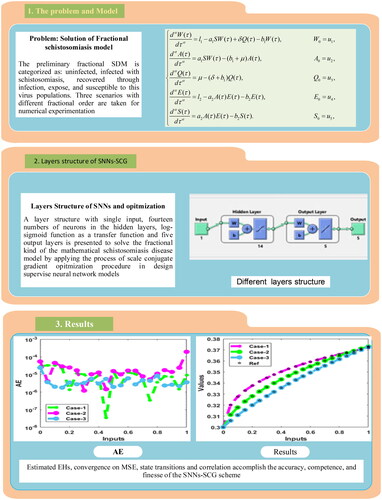
The design of SNNs-SCG procedure is presented in two phases: In phases one, necessary description of generation of the data for fractional SDM models portrayed in (2)(2) $$\{\begin{array}{l}\frac{d^{\alpha }W(\tau )}{d{\tau }^{\alpha }}=l_1-a_1\mathit{\text{SW}}(\tau )+\delta Q(\tau )-b_{1}W(\tau ),\text{}\\ \frac{d^{\alpha }A(\tau )}{d{\tau }^{\alpha }}=a_1\mathit{\text{SW}}(\tau )-(b_1+\mu )A(\tau ),\text{}\\ \frac{d^{\alpha }Q(\tau )}{d{\tau }^{\alpha }}=\mu -(\delta +b_1)Q(\tau ),\\ \frac{d^{\alpha }E(\tau )}{d{\tau }^{\alpha }}=l_2-a_{2}A(\tau )E(\tau )-b_{2}E(\tau ),\\ \frac{d^{\alpha }S(\tau )}{d{\tau }^{\alpha }}=a_{2}A(\tau )E(\tau )-b_{2}S(\tau ),\end{array}$$(2) is given while in phase two, the design of SNNs-SCG scheme along with its execution performances to be selected for the effective solution strategies for the fractional SDM. The overall flow of proposed procedural steps in process block structure to solve the SDM is presented in Figure 1. The process flow structure consists of three steps, first steps define the problem along with its mathematical representation of the system model, step 2 for solution methodology of SNNs-SCG scheme, while step 3 portrayed the outcomes and analysis of the performance as compared with reference/standard available numerical solutions.

Figure 1. Flow chart based on the mathematical model, layer structure and outputs using the SNNs-SCG.

3.1. Synthetics data generation for fractional SDM

The synthetics data generation for Fractional SDM as in set of Equation (2)(2) $$\{\begin{array}{l}\frac{d^{\alpha }W(\tau )}{d{\tau }^{\alpha }}=l_1-a_1\mathit{\text{SW}}(\tau )+\delta Q(\tau )-b_{1}W(\tau ),\text{}\\ \frac{d^{\alpha }A(\tau )}{d{\tau }^{\alpha }}=a_1\mathit{\text{SW}}(\tau )-(b_1+\mu )A(\tau ),\text{}\\ \frac{d^{\alpha }Q(\tau )}{d{\tau }^{\alpha }}=\mu -(\delta +b_1)Q(\tau ),\\ \frac{d^{\alpha }E(\tau )}{d{\tau }^{\alpha }}=l_2-a_{2}A(\tau )E(\tau )-b_{2}E(\tau ),\\ \frac{d^{\alpha }S(\tau )}{d{\tau }^{\alpha }}=a_{2}A(\tau )E(\tau )-b_{2}S(\tau ),\end{array}$$(2) is provided in this sub-section, which is used later in the study for not only the execution of proposed SNNs-SCG scheme but also for reference to compare the results.

Real or experimental data for Fractional SDM model is not available, even for integer order cases as (1)(1) $$\{\begin{array}{l}\frac{\mathit{\text{dW}}(\tau )}{d\tau }=l_1-a_1\mathit{\text{SW}}(\tau )+\delta Q(\tau )-b_{1}W(\tau ),\\ \frac{\mathit{\text{dA}}(\tau )}{d\tau }=a_1\mathit{\text{SW}}(\tau )-(b_1+\mu )A(\tau ),\text{}\\ \frac{\mathit{\text{dQ}}(\tau )}{d\tau }=\mu -(\delta +b_1)Q(\tau ),\\ \frac{\mathit{\text{dE}}(\tau )}{d\tau }=l_2-a_{2}A(\tau )E(\tau )-b_{2}E(\tau ),\\ \frac{\mathit{\text{dS}}(\tau )}{d\tau }=a_{2}A(\tau )E(\tau )-b_{2}S(\tau ).\end{array}$$(1) not available; therefore, one must develop the synthetics dataset for Fractional SDM model with the help of appropriate fractional numerical procedure/algorithm. Three fractional order cases based on value $\alpha =0.5$0, 0.75 and 0.9 are selection with fixed parameters, $a_1=0.12,$ $a_2=0.3,$ $b_1=0.15,$ $b_2=0.18,$ $\mu =0.2,$ $\delta =0.23,$ $l_1=0.1,$ and $l_2=0.23,$ having the initial conditions (ICs) are 0.1, 0.2, 0.3, 0.4 and 0.5 for fractional SDM as inspired by the reported study (Botmart et al. 2022), where necessary justification and theoretical verification are available. Generalized schistosomiasis disease model is formulated by the introduction of fractional derivative which have capabilities of not only the integer order cases but also for real order (fractional) cases, thus fractional SDM model is more accurate, precise, and robust to model the complex dynamics of disease spread that that of integer counterpart.

Now the desire is to generate the synthetics dataset for the models for $\tau$ between 0 and 1 while the step size is taken as 0.01, thus we have 101 grid of inputs and response or solution set of 101 each for dependable differential class of uninfected $W(\tau ),$ infected with schistosomiasis $A(\tau ),$ recovered through infection $Q(\tau ),$ expose $E(\tau )$ and susceptible to this virus $S(\tau ).$ The numerical procedure of fractional Adams scheme (FAS) is exploited to generate the datasets by adopting the defaults procedure (stopping criteria, tolerances, and accuracy goals) of FAS as reported in (Baskonus and Bulut 2015; Prakash and Rahul 2023). The mathematical details with theoretical justification of the FAS can be seen in (Baskonus and Bulut 2015; Prakash and Rahul 2023), here our aim is to implement the FAS to generate the data for fractional SDM.

3.2. Implementation of SNNs-SCG

Necessary description for formulation and implemented the SNNs-SCG to solve fractional SDM is provided in this sub-section for ease in the reproduction of the results presented throughout in this article.

To implement SNNs-SCG first of all, we acquired the synthetics dataset for 101 inputs in case of $\tau$ between 0 and 1 with step of 0.01, and accordingly 505 instances in total with 101 instances for each uninfected $W(\tau ),$ infected with schistosomiasis $A(\tau ),$ recovered through infection $Q(\tau ),$ expose $E(\tau )$ and susceptible to this virus $S(\tau )$ populations of fractional SDM for all three scenarios on fractional order. Now the datasets are splits into 81% for training, i.e. 409 instances, 12% for testing, i.e. 60 samples and 7% for validation or authorization, i.e. 35 instances.

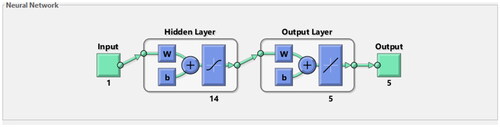
The SNNs via feedforward neuro-structure are executed with the help of ‘nstool’ function/routine in MATLAB environment while training/learning is conducted with SCG optimization scheme for efficient local search. SNNs structure is based on single input, output and hidden layer with layer size 14, i.e. hidden neurons, while the default settings initialize parameter of SCG optimization is exploited. All these structural setting of networks, neurons, volume distribution between testing/validation/training and parameters of SCG scheme are set after performing a lot of experimentations, experience, knowledge, and care on the basis of best tradeoff between the over/under fitting scenario.

4. Results and discussions

This section presents three cases of fractional SDM using the SNNs-SCG. The mathematical formulations and representations are given as:

• Case 1: Consider a fractional SDM with $\alpha =0.5,$ $a_1=0.12,$ $a_2=0.3,$ $b_1=0.15,$ $b_2=0.18,$ $\mu =0.2,$ $\delta =0.23,$ $l_1=0.1,$ and $l_2=0.23,$ where the initial conditions (ICs) are 0.1, 0.2, 0.3, 0.4 and 0.5. (3) $$\{\begin{array}{l}\frac{d^{0.5}W(\tau )}{d{\tau }^{0.5}}=0.1-0.12S(\tau )W(\tau )+0.23Q(\tau )-0.15W(\tau ),W_0=0.1,\\ \frac{d^{0.5}A(\tau )}{d{\tau }^{0.5}}=0.12W(\tau )S(\tau )-0.35A(\tau ),A_0=0.2,\\ \frac{d^{0.5}Q(v)}{d{\tau }^{0.5}}=0.2-0.38Q(\tau ),Q_0=0.3,\\ \frac{d^{0.5}E(\tau )}{d{\tau }^{0.5}}=0.23-0.3E(\tau )A(\tau )-0.15E(\tau ),E_0=0.4,\\ \frac{d^{0.5}S(\tau )}{d{\tau }^{0.5}}=0.15E(\tau )A(\tau )-0.15S(\tau ).S_0=\mathrm{0.5.}\end{array}$$(3)

• Case 2: Consider the fractional SDM with $\alpha =0.7,$ $a_1=0.12,$ $a_2=0.3,$ $b_1=0.15,$ $b_2=0.18,$ $\mu =0.2,$ $\delta =0.23,$ $l_1=0.1,$ $l_2=0.23,$ with ICs 0.1, 0.2, 0.3, 0.4 and 0.5. (4) $$\{\begin{array}{l}\frac{d^{0.7}W(\tau )}{d{\tau }^{0.7}}=0.1-0.12S(\tau )W(\tau )+0.23Q(\tau )-0.15W(\tau ),W_0=0.1,\\ \frac{d^{0.7}A(\tau )}{d{\tau }^{0.7}}=0.12W(\tau )S(\tau )-0.35A(\tau ),A_0=0.2,\\ \frac{d^{0.7}Q(v)}{d{\tau }^{0.7}}=0.2-0.38Q(\tau ),\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}{Q}_0=0.3,\\ \frac{d^{0.7}E(\tau )}{d{\tau }^{0.7}}=0.23-0.3E(\tau )A(\tau )-0.15E(\tau ),\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}{E}_0=0.4,\\ \frac{d^{0.7}S(\tau )}{d{\tau }^{0.7}}=0.15E(\tau )A(\tau )-0.15S(\tau ).\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}{S}_0=\mathrm{0.5.}\end{array}$$(4)

• Case 3: Consider the fractional SDM with $\alpha =0.5,$ $a_1=0.12,$ $a_2=0.3,$ $b_1=0.15,$ $b_2=0.18,$ $\mu =0.2,$ $\delta =0.23,$ $l_1=0.1,$ $l_2=0.23,$ with ICs 0.1, 0.2, 0.3, 0.4 and 0.5. (5) $$\{\begin{array}{l}\frac{d^{0.9}W(\tau )}{d{\tau }^{0.9}}=0.1-0.12S(\tau )W(\tau )+0.23Q(\tau )-0.15W(\tau ),W_0=0.1,\\ \frac{d^{0.9}A(\tau )}{d{\tau }^{0.9}}=0.12W(\tau )S(\tau )-0.35A(\tau ),A_0=0.2,\\ \frac{d^{0.9}Q(v)}{d{\tau }^{0.9}}=0.2-0.38Q(\tau ),\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}{Q}_0=0.3,\\ \frac{d^{0.9}E(\tau )}{d{\tau }^{0.9}}=0.23-0.3E(\tau )A(\tau )-0.15E(\tau ),\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}{E}_0=0.4,\\ \frac{d^{0.9}S(\tau )}{d{\tau }^{0.9}}=0.15E(\tau )A(\tau )-0.15S(\tau ).S_0=\mathrm{0.5.}\end{array}$$(5)

The results of the SDM are accessible numerically with the proposed SNNs-SCG procedure with 14 neurons. The selection of data is proposed as 81% for training, 12% for testing and 7% for validation or authorization. Figure 2 presents a layer structure with single input, fourteen numbers of neurons in the hidden layers, log-sigmoid as a transfer function and five output layers to solve the fractional kind of the mathematical SDM by applying the process of SNNs-SCG.

Figure 2. Designed input, output, and hidden layer structure.

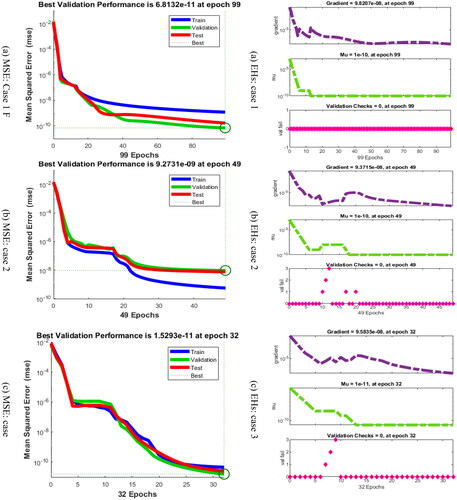
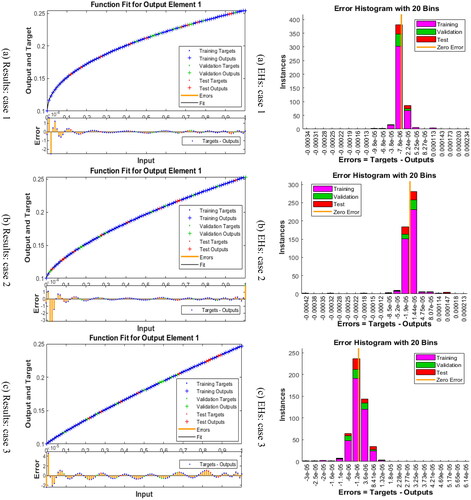
The solutions of the mathematical fractional SDM have been presented in Figures 3–5 using the SNNs-SCG. The performances of the EHs, corroborations, and STs based on the mathematical fractional SDM have been presented in Figure 3. The best outcomes based on the mathematical fractional SDM have been performed at epochs 99, 49, and 32 that are provided as 9.82 × 10⁻⁰⁸, 9.37 × 10⁻⁰⁸ and 9.58 × 10⁻⁰⁸. The gradient operator values are considered as 1.16 × 10⁻⁰⁹, 5.40 × 10⁻¹⁰, and 4.35 × 10⁻¹¹. These graphical observations represent the SNNs-SCG procedure convergence for the mathematical fractional SDM. The result assessment and EHs performances to solve the mathematical fractional SDM using the SNNs-SCG procedure are presented in Figure 4. The testing, training, and corroboration performances based on the fractional SDM have been drawn. Figure 4(d–f) provides the EHs measures that are calculated as −7.8 × 10⁻⁰⁶, −1.9 × 10⁻⁰⁵, and −1.2 × 10⁻⁰⁶ for 1^st to 3^rd case. The correlation measures for the fractional SDM using the stochastic SNNs-SCG procedure are plotted in Figure 5(a–c). These performances for the fractional SDM are calculated 1 for each variation. The outcomes of supervised neural networks (SNNs) aided with the computational scaled conjugate gradient (SCG), i.e. SNNs-SCG, for the numerical solutions of the fractional schistosomiasis disease model (SDM) for three different scenarios are presented in Table 2, in terms of MSE level attained for validations, testing, and training samples, best validation performance, total number of epoch executed, values of adaptive controlling parameter, i.e. gradient and step size, of optimizer and computational time taken for training of the weights of networks by SCG optimization. The MSE performances of the fractional SDM using the SNNs-SCG procedure have been tabulated in Table 2.

Figure 3. MSE and STs values based on the fractional SDM.

Figure 4. Fitness and EHs values to solve the fractional SDM.

Figure 5. Regression values of fractional SDM. (a) Regression measures for 1st case; (b) Regression measures for 2nd case; (c) Regression measures for 3rd case.

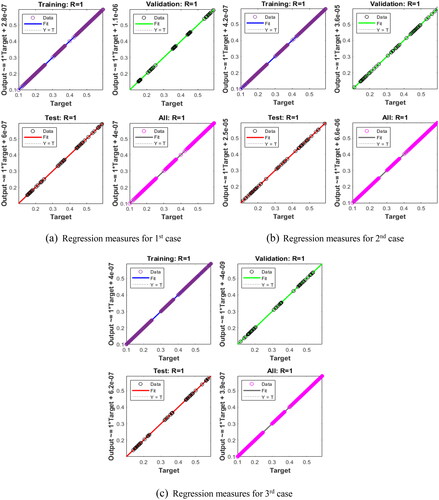
Table 2. Proposed SNNs-SCG procedure for the fractional SDM.

Case	MSE			Performance	Gradient	Mu	Epoch	Time (seconds)
	Validation	Training	Testing
I	1.16 × 10^-09	6.81 × 10^-11	1.62 × 10^-10	1.16 × 10^-09	9.82 × 10^-08	1 × 10^-10	99	3
2	5.27 × 10^-09	9.27 × 10^-09	7.38 × 10^-09	5.40 × 10^-10	9.37 × 10^-08	1 × 10^-10	49	3
3	4.34 × 10^-11	1.52 × 10^-11	2.40 × 10^-11	4.35 × 10^-11	9.58 × 10^-08	1 × 10^-11	32	2

The convergence curves for numerical solutions of the fractional schistosomiasis disease model (SDM) using the supervised neural networks (SNNs) and the computational scaled conjugate gradient (SCG), i.e. SNNs-SCG, are portrayed in Figure 3, it can be seen from Figure 3 and Table 2 that the fitness function, i.e. MSE, reached to the study state at epochs 99, 49 and 32 for cases 1, 2, and 3, respectively with validation performance on MSE as 1.16 × 10⁻⁰⁹, 5.40 × 10⁻¹⁰, and 4.35 × 10⁻¹¹.

The performance of convergence of SNNs-SCG reached to the steady state with reasonably accurate fitness so the execution of the optimizer stops. These graphs in Figure 3 and numerical data in Table 2 shows the stable performance of the SNNs-SCG algorithm for solving fractional schistosomiasis disease model as given in set of Equation (2)(2) $$\{\begin{array}{l}\frac{d^{\alpha }W(\tau )}{d{\tau }^{\alpha }}=l_1-a_1\mathit{\text{SW}}(\tau )+\delta Q(\tau )-b_{1}W(\tau ),\text{}\\ \frac{d^{\alpha }A(\tau )}{d{\tau }^{\alpha }}=a_1\mathit{\text{SW}}(\tau )-(b_1+\mu )A(\tau ),\text{}\\ \frac{d^{\alpha }Q(\tau )}{d{\tau }^{\alpha }}=\mu -(\delta +b_1)Q(\tau ),\\ \frac{d^{\alpha }E(\tau )}{d{\tau }^{\alpha }}=l_2-a_{2}A(\tau )E(\tau )-b_{2}E(\tau ),\\ \frac{d^{\alpha }S(\tau )}{d{\tau }^{\alpha }}=a_{2}A(\tau )E(\tau )-b_{2}S(\tau ),\end{array}$$(2) . Computational time-based complexity of SNNs-SCG scheme for optimization of the parameter of networks to solve the fractional SDM for all three fractional order cases is also embedded in the last column of Table 2. Almost same 2 to 3 s are required by SNNs-SCG scheme for each case of fractional SDM.

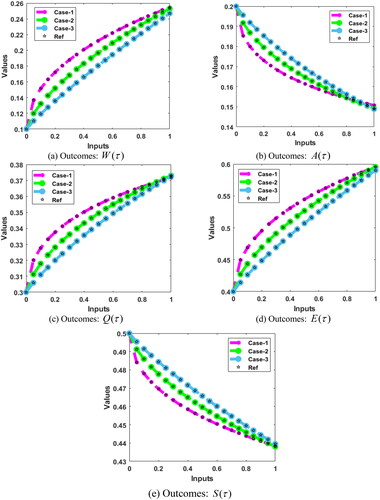
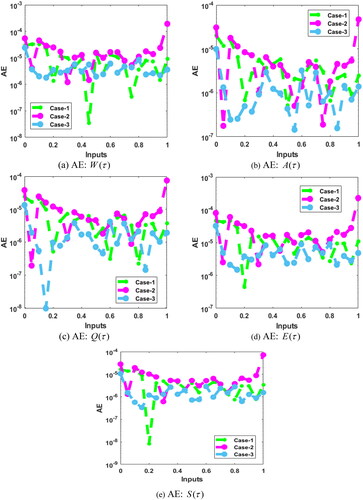
The exactness of the SNNs-SCG to solve the fractional SDM is presented in Figures 6 and 7 based on the comparison performances and the values of the AE. The calculated performances have been illustrated for the fractional SDM by implementing the SNNs-SCG procedure. Figure 6 shows the performances of the calculated and reference results. These illustrations indicate the precision and exactness of the proposed SNNs-SCG scheme to solve the fractional SDM. Figure 7 presents the AE measures of fractional SDM using the stochastic performances.

Figure 6. Matching of the outcomes for the fractional SDM.

Figure 7. The values of AE for the fractional SDM.

The AE is illustrated for classes uninfected with the schistosomiasis disease $W(\tau ),$ infected $A(\tau ),$ recovered from schistosomiasis $Q(\tau ),$ not afflicted susceptible snail from schistosomiasis $E(\tau )$ and afflicted susceptible snail from schistosomiasis $S(\tau ).$ These AE plots indicate that the uninfected class with the schistosomiasis $W(\tau )$ is found as 10⁻⁰⁵–10⁻⁰⁶, 10⁻⁰⁵–10⁻⁰⁷ and 10⁻⁰⁵–10⁻⁰⁶ for case 1 to 3. These values for infected individuals $A(\tau )$ are found as 10⁻⁰⁵–10⁻⁰⁶, 10⁻⁰⁵–10⁻⁰⁷ and 10⁻⁰⁶–10⁻⁰⁷ for case 1 to 3. The values of AE for the recovered from schistosomiasis $Q(\tau )$ are found as 10⁻⁰⁶–10⁻⁰⁷, 10⁻⁰⁵–10⁻⁰⁶ and 10⁻⁰⁶–10⁻⁰⁷ for 1^st to 3^rd case. The AE performances for unafflicted susceptible snail from schistosomiasis $E(\tau )$ are calculated as 10⁻⁰⁴–10⁻⁰⁴, 10⁻⁰⁵–10⁻⁰⁴ and 10⁻⁰⁵–10⁻⁰⁶ for respective cases. Likewise, the AE for the afflicted susceptible snail from schistosomiasis $S(\tau )$ lie as 10⁻⁰⁵–10⁻⁰⁷, 10⁻⁰⁴–10⁻⁰⁶ and 10⁻⁰⁵–10⁻⁰⁶ for each case of the fractional SDM. These AE best performances present the correctness of SNNs-SCG technique of the model.

5. Concluding remarks

The motive of this research is to implement the numerical results of the mathematical form of the fractional schistosomiasis system. The fractional derivative has been applied to accomplish more accurate routines of the fractional schistosomiasis model. The preliminary fractional SDM is categorized as: uninfected, infected with disease, recovered through infection, susceptible to this virus. Few concluding remarks for the fractional schistosomiasis system are presented as:

• The numerical representations of the fractional schistosomiasis model have been performed by using the supervised neural networks together with the computational scaled conjugate gradient values.

• The correctness of the stochastic performances has been observed for three variations of mathematical fractional schistosomiasis model.

• The data performances have been calculated as 81% for training, 12% for learning and 7% for authorization to solve the model along with 14 numbers of neurons.

• The values of the absolute error have been operated in good procedures, which authenticate the exactness of SNNs-SCG method.

• The absolute error, MSE, regression, and STs performances have been presented to accomplish the competence, and finesse of the SNNs-SCG scheme.

Beside above-mentioned advantages of proposed SNNs-SCG methodology, only limitation for execution of SNNs-SCG is the availability of the synthetic data or real data implementation, which some time become challengeable to acquire for stiff nonlinear fractional order systems.

In future, the proposed solver based SNNs-SCG along with its variants based on deep neural structures can be used for the numerical outcomes of the biological models (Zheng and Yu 2023; Wang et al. 2023), fluid dynamics (Pranjivan Mehta 2023; Golzar et al. 2023), information security models (Jaber et al. 2021; Zakhem et al. 2022; Bouclaous et al. 2023) and another related nonlinear stiff differential model (Kassis et al. 2019; Issa 2022; Nie and Li 2023; Tian et al. 2023) and disease models (Salvi et al. 2021; Anwar et al. 2023).

Credit author statement

All authors contribute equally.

Data availability statement

The data used in this manuscript is within the manuscript.

Disclosure statement

There are no potential conflicts of interest among the authors.

Additional information

Funding

The author(s) reported there is no funding associated with the work featured in this article.