Derivation of the tumour control probability (TCP) from a cell cycle model

Abstract

In this paper, a model for the radiation treatment of cancer which includes the effects of the cell cycle is derived from first principles. A malignant cell population is divided into two compartments based on radiation sensitivities. The active compartment includes the four phases of the cell cycle, while the quiescent compartment consists of the G ₀ state. Analysis of this active-quiescent radiation model confirms the classical interpretation of the linear quadratic (LQ) model, which is that a larger α/β ratio corresponds to a fast cell cycle, while a smaller ratio corresponds to a slow cell cycle. Additionally, we find that a large α/β ratio indicates the existence of a significant quiescent phase. The active-quiescent model is extended as a nonlinear birth–death process in order to derive an explicit time dependent expression for the tumour control probability (TCP). This work extends the TCP formula from Zaider and Minerbo and it enables the TCP to be calculated for general time dependent treatment schedules.

Keywords:

• Radiation treatment
• Cell cycle
• Tumor control probability
• Birth–death process

Keywords:

• 92C50

1. Introduction

Cancer is a disease that affects millions of people worldwide. According to the World Health Organization, 12.5% of total deaths every year worldwide are caused by cancer [14]. Also, in 30% of these cases, the patients could have been cured had they received early diagnosis and effective treatment. Time and cost are two factors that limit the number of patients eligible to receive early treatment. For these reasons, mathematical modelling is a helpful tool in not only predicting tumour growth and cancer spread, but also in determining the effectiveness of a specific treatment.

One of the common therapies used to treat cancer is external beam radiotherapy. This treatment works by transferring energy to a cell, which causes structural damage that affects cell viability. Based on the interaction of radiation with individual cells, we derive radiation dependent death rates for tumour cells. The main objective in this work is to derive a mathematical model for the radiation treatment of cancer, which includes cell cycle dynamics, that can be used explicitly to compute the tumour control probability (TCP). The TCP can be used to predict the outcome of a given treatment schedule.

A widely used mathematical model of the radiation treatment of cancer is the linear quadratic (LQ) model, which predicts the surviving fraction of clonogens after a treatment of dose D is applied to a tumour. This model, in its basic form, assumes that the tumour cell population is uniform and that the effect of the treatment is independent of the cell cycle. This assumption leads to an oversimplification which prevents complete understanding of the system dynamics. In this paper, we divide the cell population into two compartments: active cells, representing cells in the G ₁, S, G ₂ and M phases and quiescent cells, representing cells in the G ₀ phase. We use this simple, two compartment setup to explain the derivation of a TCP formula. We believe that the method used can be extended to describe a system with more compartments; however, the computations would become very tedious. In this work, we consider only a two-compartment model and leave the inclusion of more compartments for future studies. Let u(t) represent the active cells and q(t) the quiescent cells. The basic cell cycle radiation model of this paper is then

The reproduction kinetics of the cells are described by the term f(u). When an active cell undergoes mitosis, two daughter cells are formed and we assume these two new cells enter directly into the quiescent compartment. The negative reproduction term in the first equation represents the occurrence of cell division and the 2f(u) term in the second equation represents the two daughter cells entering into the quiescent compartment. Cells in the quiescent compartment can re-enter the active compartment with rate γ>0.

The assumption that new daughter cells enter directly into the G ₀ phase is supported by many experimental observations and has been used in Swierniak [22].

Formerly, as in Ref. [17], the G ₀-phase was not distinguished from the G ₁-phase. Pioneering cellular biologists believed there to be only four cell cycle phases: G ₁, S, G ₂ and M. However, the G ₁ phase was recognized as being highly variable in length and in cellular activity. This phase variability was due to the fact that many cells were in a period of inactivity, now known as the G ₀ phase. Our model is equally valid for a model for a u-compartment consisting of S, G ₂ and M phases and a q compartment consisting of the G ₀ and G ₁ phases. The model's ability to describe the basic biological system demonstrates one of the strengths of mathematical modelling, which is that we can generalize and derive basic properties that are valid for a wide range of applications. In model (1), the time dependent parameters Γ _u (t) and Γ _q (t) denote the radiation damage to the two cell compartments, respectively.

To derive radiation induced death rates Γ _u and Γ _q , we begin modelling on the subcellular scale. A critical event is DNA double strand breaks (DSB) that occur by the interaction of two radiation energy depositions, referred to as single-hit events. We make the transition to the cellular level and derive probabilities of cell death. Based on these probabilities, we define macroscopic death rates, Γ _u and Γ _q to make the transition to a fully macroscopic model (1). In this procedure, we follow the scaling hierarchy from microscopic to macroscopic that was also suggested in Bellomo and Maini [3].

To finally derive a formula for the TCP, we go back to the cellular scale and consider a nonlinear birth–death process describing the cell kinetics, where we assume f(u) = μu. The main result of this paper is the extension of the active-quiescent model (1) to a nonlinear birth–death process (see equations (32) and (33)) which is explicitly solved to obtain the dynamic equation for the TCP, which is given by

where

and u(t), q(t) are the solutions of the active-quiescent model (1) with f(u) = μu. The details of this derivation are given in section 4.

We use the remainder of the introduction to present a brief overview of the cell cycle in section 1.1, and of radiation treatment in section 1.2. In section 1.3, we review existing TCP models, in particular the work of Zaider and Minerbo [25]. In section 2, we give a detailed, physically based derivation of the radiation cell cycle model (1). We use singular perturbation arguments in section 3 to investigate the effects of the model parameters μ and γ on the model dynamics. This analysis allows us to compare model (1) to the LQ-model. We relate the standard α/β ratio to our model parameters and we find that a large α/β ratio indicates the presence of a significant quiescent compartment. In section 4, we extend the active-quiescent model (1) to a nonlinear birth–death process such that the mean field equations are given by (1). We derive a system of hyperbolic partial differential equations for the corresponding moment generating functions and we explicitly solve this hyperbolic system. This procedure leads to the explicit TCP formula in equation (2). Lastly, in section 5, we summarise and discuss our results. The TCP formula (2) is used in Yurtseven et al. [24] to investigate various treatment schedules.

1.1 The cell cycle

Here, we review some basic facts about the cell cycle from Refs. [1,7,13]. The cell cycle can be split into four phases, where the culmination occurs when the cell divides and two daughter cells are formed. Although not considered part of the cell cycle, it is also important to recognize that there is a resting phase that cells may enter. This phase is very important when modelling radiation treatment of cancer because the cell is less sensitive to radiation when in this phase.

The first phase is known as the gap 1 phase . It occurs just after the cell has split, but must not be mistaken for the resting phase . During this phase, the cell begins to manufacture more proteins in preparation for division. It also experiences other growth: metabolism increases, RNA synthesis is elevated, and organelles duplicate. This phase lasts about 12 h. The second phase is known as the stationary phase, although a cell in the S phase is biologically active. During the S phase, the DNA is copied so that when the cell divides, both cells will have a copy of this genetic information. This phase lasts about 6–10 h. The S phase is followed by the gap 2 phase . The gap 2 phase occurs just before the cell begins to divide into two cells and is a preparation stage for its chromosome duplication. This phase lasts about 2–6 h. The cell can then enter the M phase where the cell division occurs and two new cells are formed. The chromosomes are first lined up and pulled to either end of the cell, the membrane is pinched together and two daughter cells are formed. This phase lasts about 30 min. After cell division occurs, the cell may enter a resting state, referred to as the phase. During this phase of inactivity, cells have not begun to divide. This period of inactivity can last anywhere from a few hours to a lifetime and is the phase with the most variable time frame. Once the cell is signalled to reproduce, it then moves into the phase. Most stem cells found in normal tissues are in the phase and are not committed to division. Also, tumor spheroids show an inner necrotic core surrounded by a ring of resting cells due to lack of nutrients [4].

1.2 Radiation treatment of cancer

Radiation therapy works to treat cancer by attacking reproducing cancer cells, but also inadvertently affects the normal, healthy cells that are proliferating. This damage to normal cells is the cause of side effects. Every time radiotherapy is given there must be a balance between attacking cancer cells and avoiding destruction of healthy cells.

Radiation can be simply described as energy that is carried by waves or streams of particles. The key aspect in using this energy to treat cancer is that radiation has the capability of altering genetic material in a cell. As seen in the cell cycle description, this genetic code controls cell growth and proliferation. A cell's sensitivity to radiation, referred to as radiosensitivity, depends on its current position in the cell cycle. Radiation is more effective on cells that are active and dividing quickly, while it is much less effective on cells that are in the resting phase, as well as on cells that divide slowly [15].

In radiation therapy, ionizing radiation is used to destroy or shrink tumours. Ionizing radiation causes ionization, which is the loss of an electron in atoms or molecules. When an electron is lost, energy is transferred and this energy disrupts chemical bonds, resulting in ionization. These ionizations, when induced by radiation, can act directly on molecules forming cellular components, or indirectly on water molecules. When acting on water, the ionizations cause water-derived radicals (highly reactive molecules that can bind to and destroy cellular components). These radicals quickly react with molecules near them and this results in chemical bond breakage or oxidation of the affected molecules. In cells, there is a variety of possible radiation induced lesions, although the most harmful to the cell are the lesions which effect the DNA structure.

DNA occurs in pairs of complementary strands and radiation can induce single strand breaks, or DSB. Single strand breaks are the more common lesion of the two and can usually be repaired by the cell (undamaged strand serves as template for production of complementary strand). DSB are caused by either a single event, which severs both DNA strands, or by two independent single strand break events close in time and space. DSB are considered more harmful than single strand breaks, as they are difficult to repair. Even when repair is attempted, broken ends may be joined together, leading to misrepairs. These misrepairs cause mutations, aberrations (of chromosomes), or cell death.

Deletion of DNA segments is the most common form of radiation damage in cells that survive radiation treatment. The deletion may be caused by the misrepair of two separate DSB in a DNA molecule by joining of the two outer ends and loss of the section between the breaks. However, it may also be a result of the cleaning process, where enzymes digest nucleotides (component molecules of DNA) of the broken ends prior to rejoining them to repair a single double strand break [12].

The LQ model is the most common cell survival formalism used when modelling radiation treatment of tumours. The LQ expression was originally used by Sinclair in 1966 [16], who found that an expression of this form fit the cell survival data he analysed, although he did not biologically justify this discovery. The model determines the surviving fraction of cells after radiation of a specified dose, where a cell survives the dose application if it is able to act as a progenitor for significant line of offspring. (The operational definition commonly used for cell survival is that a cell survives if it produces at least 50 offspring.) The LQ formula is written as

where is the surviving fraction of cells after application of dose D and α and β are the model parameters.

The ratio of the two adjustable parameters in the LQ model, α and β, has been found to correlate with the cell cycle length. Tissues which have a slow cell cycle are composed of cells which proliferate slowly. These slow cycling tissues correspond with a smaller ratio. Brain tissue and the spinal cord are examples of slow cycling tissues, both of which have an ratio of about 3 Gy [5]. Tissues which have a fast cell cycle are composed of cells that proliferate quickly and are associated with a larger ratio. Most tumours are composed of cells which cycle quickly, and have an ratio of approximately 10 Gy. It is important to note that in radiotherapy, it is usually the case that the slow cycling tissues are those which we are trying to protect.

1.3 The tumour control probability

The probability that no malignant cells are left in a specified location after irradiation is known as the TCP. This probability is used to determine an optimal treatment strategy where the dose to the tumour is increased without increasing the damaging effects of radiation of healthy tissues.

1.3.1 Poisson statistics

The most common and simplest expression for the TCP is one which relies on Poisson statistics.

If the number of cells present before treatment, n, is large, and if cell survival after treatment is a rare event, the probability that k cells survive is given by

where X denotes the random variable of the number of surviving cells. We assume that the observed surviving cell number, , is a good estimation of the expected value of X and hence assume . The TCP denotes the probability of having no tumour cells, so

Expression (4) is only valid when the cell survival probability is small and the number of cells surviving irradiation is much less than the initial number of tumour cells, which are the usual conditions in radiotherapy treatments.

1.3.2 Binomial statistics

Let p denote the survival probability of an individual cell. If we assume that all cells are identical and independent, then we obtain from a binomial distribution

Again we assume that the observed surviving cell number is a good estimator of the expectation of X, so which gives . In this case, the TCP is

The limit of equation (5) as and , such that , results in the Poisson statistics expression (4).

1.3.3 Zaider and Minerbo TCP formulation

Zaider and Minerbo [25] were the first who found a method to express the TCP as a time-dependent dynamical expression that could be applied to all treatment protocols. In their formulation, Zaider and Minerbo apply a birth–death model (see Kendall [9]) to the radiation treatment of cancer. This birth–death process has been solved explicitly to obtain an expression for the TCP, which satisfies where is the probability that i clonogens are alive at time t. In their model, the cell birth rate is denoted by b and the cell death rate is denoted by δ. The death rate δ is composed of death due to radiation, , and radiation-independent death, d. That is, . The radiation death term is known as the hazard rate, which for the LQ survival probability (3), is .

The master equation for the birth–death process of cancer growth and radiation treatment is given by an infinite system of ordinary differential equations (ODEs) for the ,

with the convention that . To solve equation (6), they introduce the generating function , implicitly assuming that the moment generating function exists on an interval where and T>0. From equation (6), they derive a hyperbolic equation for , namely

If initially there are n tumour cells, then the initial condition is . The TCP is given by . The expression obtained for the TCP is as follows:

where

is the cell survival probability for a given hazard function and is defined via the differential equation .

The mean field equation of (6) for the expectation is given by

Using the solution of the mean field equation, we can directly calculate the TCP as

The solution of the mean field equation (10) is the mean cell number of the cancer cells. Hence denotes the surviving fraction of tumour cells. Note that this interpretation of is not used in the original formula (8) of Zaider and Minerbo. There the term denotes the survival probability for a given hazard function and it should not be mixed up with the surviving fraction of the cells .

Note that for no birth, b = 0, we obtain the binomial model (5).

The active-quiescent model presented in this paper extends Zaider and Minerbos model by including the effects of varying sensitivities within a tumour. The detailed derivation of equation (2) is given in section 2. Before we do this, we give a detailed derivation of the active-quiescent radiation model (1).

1.3.4 The normal tissue complication probability

During the radiation treatment of cancer, healthy tissue is inadvertently irradiated. For treatment to be useful, it is important that the damage of healthy tissue is kept to a minimum. The normal tissue complication probability (NTCP) is used as a measure for the sensitivity of normal tissue for a given radiation treatment schedule. NTCP models are based on the damage probability of so called “functional subunits” (FSU) [8,18]. Of course, it is desirable to achieve a TCP close to 1, however, at the same time the NTCP must be at an acceptably low level. Hence, for real treatments it is important to look at both the TCP and the NTCP simultaneously. In Stavreva et al. [20], the above mentioned Poissonian TCP formula and related NTCP formulas are computed for various model assumptions. The model of Zaider and Minerbo [25] has been compared to NTCP models in Weldon [19]. For the TCP formula derived in this paper, there is no corresponding NTCP model available. We plan in future research to extend existing NTCP models to NTCP models of comparable detail to the TCP model studied here.

2. Derivation of an active-quiescent radiation model from first principles

In this section, a model for the radiation treatment of cancer cells that includes active and quiescent cell phases is derived. The derivation begins from first principles, at the microscopic level, by considering target sites inside a cell that can potentially be damaged by radiation. A target site is damaged when an energy deposition via radiation occurs at that site. These energy depositions are modelled as stochastic events referred to as hits. The model includes a quiescent state, , and an active state, which combines the and M-phases.

Target theories for radiation damage on living tissues have been discussed since the work of Lea presented in 1955 in Ref. [10]. We give a complete new derivation here to include time dependent treatment schedules, rather than considering only the total dose.

The model derivation is divided into five steps. In Step 1, a single cell is considered and the probabilities that this cell is damaged by radiation are defined. In Step 2, a group of cells is considered. In Step 3, using radiation physics, the expressions for the damage probabilities are derived. In Step 4, the radiation induced death rates for active and quiescent cell compartments are derived. Lastly, in Step 5, the death rates are used to formulate our active-quiescent radiation model (1).

Step 1: one cell

We consider a single cell, which contains specific sites, called active sites, that are susceptible to radiation damage. We assume that a single cell has n active sites, labelled , where need two-hits to be damaged and need only one hit to be damaged.

We assume radiation has energy E and we define as the probability that radiation with energy E causes the site to experience a single-hit event in a given unit of time . Similarly, we define as the probability that radiation with energy E causes the site to experience a two-hit event in a given unit of time . A two-hit event consists of two separate single-hit events, close in both time and space, so it is expected that these two probabilities are related (see Step 3).

The probability that at least one site experiences a single-hit event can be computed. Any of the n sites susceptible to radiation damage can experience a single-hit event:

Similarly, the probability that at least one site experiences a two-hit event can be computed, where only the sites susceptible to two-hit damage need to be considered:

Step 2: many cells

Consider a group of cells , where each cell has an associated number of active sites susceptible to single-hit damage and two-hit damage, respectively. In this step, the probabilities that the k-th cell dies after a single-hit, or a two-hit event are defined, where a cell is considered dead if it produces less than 50 offspring.

The probability that a cell dies after experiencing single-hit event is denoted by , and the probability that a cell dies after experiencing a two-hit event is defined as . The numbers of single-hit and two-hit active sites for cell are denoted by and , respectively. Recall that hit events are stochastically independent and that two single-hit events close enough in time and space comprise a two-hit event. Then the probability that a cell dies is

Using expressions (12) and (13) we obtain

In order to simplify the above probability, it is assumed that all cells are identical. Later, we will split cells into active and quiescent compartments and then we assume that all active cells are identical and all quiescent cells are identical. Here we assume for all that

As a result of this assumption, probability (14) reduces to

Step 3: radiation physics

In this step, expressions for the single-hit and two-hit event probabilities previously defined as and are derived. The probability that an active site is hit by radiation in the time interval is proportional to the energy E of the radiation beam as well as to the time interval , hence . Let denote the dose accumulated at time t and so is the radiation dose rate. This dose rate is proportional to the energy E of the radiation beam. Hence we obtain

with proportionality constants and δ, respectively. Here, becomes the probability density function of .

In order to compute , the probability that two stochastically independent one-hit events occur close in time and space must be calculated. The assumption is made that two single-hits must occur in a time interval of length ω>0 in order to produce a two-hit event.

Suppose that a single-hit event occurred in the time interval . In order to have a two-hit event at time t, another single-hit must have occurred in the interval . From above, the probability density of a single-hit event is . Now define

Using the total dose , we can write

Then can be computed as

These results are substituted into equation (15). The expression becomes a function of , which we denote as for the probability of cell death due to radiation administered in an interval of . This results in the following:

Step 4: radiation induced death rates

If P(death) denotes the probability of death in a time unit , then

defines the death rate. In order to find the death rates of a cell population, we expand about . Which gives

We define , and . Then the radiation-induced death rate becomes

At this point, it is necessary to discern between active and quiescent cells. The cells are separated into these two respective compartments, where the active compartment u includes the cell cycle phases , S, , M and the quiescent compartment q includes only the phase. Hence, we obtain corresponding radiation death rates as

In the sequel, we assume that two-hit events, that include DSB, play a minor role for the quiescent cells and that when these cells do receive a DSB they have a good chance of repairing this lesion. Hence, in general, we expect . In parts of the analysis and numerical simulations, we will simply assume .

Step 5: ODE model

In order to use the above radiation induced death rates and in an ODE model, first consider a cell cycle model for active and quiescent cells without the effects of radiation. Let denote the density of active cells and denote the density of quiescent cells. Further, let denote the reproduction of active cells, where it is assumed that the two daughter cells enter the quiescent compartment at birth. Moreover, γ>0 denotes the rate at which a quiescent cell becomes active. Then a simple cell cycle model is given as (see Swierniak [22])

If additionally we include the effect of radiation damage, as expressed through the death rates and , we arrive at the active-quiescent radiation model (1).

3. Singular perturbation analysis for a time dependent dose rate

In this section, we consider a time dependent dose rate and study scaling limits for the model parameters to compare the model (1) to the standard LQ model. To do this, we assume that is linear, that and that . The model is then given by

Then the effects of the parameters μ and γ on the system (19) are examined. In section 3.1, we study the case of a slow transition through the cell cycle (γ and μ both small) and we derive a modified LQ model that takes the quiescent state into account. In section 3.2, we introduce new variables to enable us to separate the actions of the parameters and in section 3.2.1, we study γ large and . Finally in section 3.2.2, we consider and μ large.

3.1 Slow transition between active and quiescent compartments, and slow proliferation

In the first case when both γ and μ are small, let and , where ε is small. These values are substituted into the active-quiescent model (19), which yields

Both u and q are expanded in powers of ε:

These expansions are then substituted into the model and the leading-order terms are

This system is solved to obtain

To obtain an LQ model, we make the following assumption.

(LQ-assumption): The total dose D is given in a time interval that is smaller than the mean two-hit interaction time: . Moreover, we observe the result after treatment is completed for some T with .Under assumption (LQ-assumption) the remaining integral term in equation (20) is zero and we obtain an LQ-model

The linear dependence for large D is dominated by the term and the quadratic term is given by . Hence for the LQ model, we find qualitatively and . In particular, if the initial condition of the resting cells is , then we obtain the LQ model with .

3.2 A transformation with radiation

To investigate the behaviour of equation (19) if the parameters γ and μ are of different sizes, we transform to a set of new variables and . The new variable Z is equal to the total number of cells and W corresponds to the total number of cells making a transition between the compartments. This transformation is applied to the cell cycle model (19) to obtain the transformed system:

3.2.1 The case of γ large and

Now consider the case where the transition rate from the quiescent to the active cell compartment is large compared to the proliferation rate. This assumption implies that and the system (21) becomes

As in the previous section, we formally expand Z and W in powers of ε and we denote the leading order terms by , respectively. To leading order, we find from equation (23) that which can be rearranged to give . This result is substituted into equation (22) to get

The solution of this equation is given by

Under assumption (LQ-assumption), we again obtain an LQ-model with and . Notice that the one-hit event damage on the resting cells, , has no effect in this case. This means that the active cells control the system dynamics when the transition rate γ is large. This agrees with the biological behaviour, since new cells would spend much less time in the quiescent compartment before entering the active phase of the cell cycle.

3.2.2 The case of μ large and

Now consider the case where the proliferation rate is large relative to the transition rate. This implies that and so the system (21) becomes

The leading order terms of equation (26) are taken to obtain

which implies that . This result is used to simplify equation (27) to

Solving equation (28) gives

We obtain the LQ model with and β = 0. In this case, where the transition from quiescent to active is slow relative to proliferation, the -term dominates, while the effect of the radiation on the active cells does not contribute to the leading order system behaviour. Again, this makes sense because new cells quickly accumulate in the quiescent compartment and therefore, although less sensitive to radiation, the higher density of cells found here causes this compartment to control the system dynamics.

3.3 Model comparison

Using the results from the perturbation analysis and the additional assumption (LQ-assumption), a relationship between the parameters in the active-quiescent model, μ and γ, and the parameters in the LQ Model, α and β, can be established. Typically, a small ratio corresponds with a slow cell cycle, whereas a larger parameter ratio indicates a fast cell cycle. The parameter relationships are summarized in table 1.

Table 1. Comparison between the parameters in the active-quiescent model, μ and γ and the parameters in the LQ Model, α and β.

Case	μ	γ	α	β
1	small	small		B/2
2	large	small	A q	0
3	small	large	A u	B/2

Case 1

In this case, both μ and γ are small, which corresponds with a slow cell cycle and a significant quiescent phase. The ratio is equal to the active-quiescent model ratio . In the classical interpretation, a slow cell cycle corresponds with a small ratio. The ratio is relatively small, compared with the cases 2 and 3 below.

Case 2

In this case, μ is large and γ is small, which corresponds with a fast cell cycle. The ratio is obtained for the active-quiescent model, which confirms the classical interpretation, in which the ratio is assumed to be large.

Case 3

In this third case, μ is small and γ is large. This corresponds with slow reproduction and effectively no quiescent compartment. The active-quiescent ratio in this case is . In the classical interpretation, the ratio should be relatively small.

In addition to the classical understanding of the ratio, we derive the following biologically relevant conclusion from our model:

Biotheorem: Based on our model, we conclude that a large ratio indicates the presence of a significant quiescent compartment.

4. Tumour control probability

In this section, an expression for the TCP of system (1) is derived. The TCP is the probability that no malignant cells are left in an affected region. This is a useful tool in predetermining the success of radiotherapy treatment over time for a cancer patient.

Here, we do not make use of the specific radiation death terms as given in equation (17). The TCP derivation given here is valid for general, time dependent radiation death rates and (that are integrable and bounded).

The active-quiescent model (19) is a deterministic ODE-model for cancer growth and radiation treatment. As such it is valid for relatively large cell densities where stochastic effects are negligible. When we talk about tumour control, we aim to reduce the tumour population to a level close to extinction. Hence, we are interested in small cell levels, where stochastic effects play an important role. To address this appropriately, we follow the ideas of Zaider and Minerbo [25] and extend the ODE-model (19) into a nonlinear birth–death process. A birth–death process is a Markov process, where birth and death events are modelled as stochastic events. In this context, it makes sense to talk about TCP as the extinction probability of cancer cells (see also [9]). To be consistent with the ODE model (1) derived earlier, we show that the birth–death process leads to equation (19) in a mean field approximation, i.e. the mean values of the cell numbers satisfy equation (19).

4.1 The corresponding birth–death process

We define as the probability that i active cells are alive at time t and similarly, as the probability that j resting cells are alive at time t. If , then we use the convention that and are equal to zero. Initially, at time equal to zero, the density of active cells is defined to be , which implies that . At time zero, the density of resting cells is defined as , which implies that . The probability that no malignant cells are left in the affected region, i.e. the TCP, is given by .

In order to determine equations for both and , the biological process that the system intends to describe is recalled. First, we consider a single active cell. This cell must have entered the active compartment from the resting cell compartment. Once a cell becomes active, it can: leave the active cell compartment by replicating; undergo cell death due to radiation; or it can remain in the active cell compartment.

Also, consider a single quiescent cell. This cell must have entered the quiescent compartment from the active compartment. It is important to note, however, that when a cell leaves the active compartment, it replicates and two cells must enter the quiescent compartment. This implies that it is never the case that the number of resting cells increases by only one. Once a cell has become quiescent, it can: leave the quiescent cell compartment by becoming active; undergo cell death due to radiation; or it can remain in the quiescent cell compartment.

In order to mathematically describe the birth–death process, we consider events that can occur in a very small time interval, .

For ,

For ,

For , equations (30) and (31) are rewritten in differential form to obtain:

and

Equations (32) and (33) describe the birth–death process of the active-quiescent radiation model.

The expected values of and are given by the respective densities of the active and quiescent cells, earlier defined as and , so

Also, it is straightforward to show that the active-quiescent radiation model (1) derived earlier is the mean field approximation of the birth–death process described by equations (32) and (33).

In order to solve the birth–death process given by the system of equations (32) and (33), define the moment generating functions and as:

We assume that the moment generating functions and their first order derivatives exist. First, we consider . We use that

We multiply equation (32) by and sum over all indices from to obtain a hyperbolic partial differential equation for :

with initial condition . Similarly, for , we find

with initial condition .

Using the method of characteristics for , we find the solutions as

and

Finally, using the solutions for and , we obtain an explicit expression for the TCP from

given by equation (2).

Note that in order to compute the TCP from equation (19), the solutions and of the mean field equation (19) are needed. For this reason, in numerical studies we first solve the ODE-model (19) and then substitute these solutions into the TCP.

4.2 An example of constant irradiation

In Yurtseven et al. [24], a detailed sensitivity analysis of the parameters of the TCP model is given and various treatment schedules are simulated and compared. Here, we only show the TCP curve for constant radiation and we assume that the two-hit interaction interval length ω>0 is small compared to the observation period. Then the radiation death rates (17) take the form

In order to do this, realistic parameter values must be determined. For an initial number of tumour cells, an estimate given in Wyatt et al. [23] is used, which is 10⁸ cells at diagnosis. This estimate for the initial number of tumour cells must be divided into two compartments: active and quiescent. Since there is no readily available data on the states of tumour cells, it is assumed that half of the cells are in the active state and half are in the quiescent state. The parameter that is the most difficult to determine is γ, the transition rate from the quiescent to the active cell compartment. Prior to the recognition of this resting state, was included in the phase, which accounted for a highly variable length in the cell cycle. For the parameter γ, an estimate for the transition rate from the phase to the S phase is used.

For the parameters and , estimates for the α parameter in the LQ model are used, since in both cases the parameters represent damage due to single-hit events. For , the parameter for the active cell single-hit damage, a value of α for radiosensitive prostate tumour cells is used. For , the single-hit damage parameter for the resting cell compartment, an α estimate for radioresistant prostate tumour cells is used. Similarly, for B, the term which represents damage due to two-hit events, an estimate for the β parameter in the LQ model for radiosensitive prostate tumour cells is used. These α and β estimates were taken from Leith et al. [11]. Lastly, the estimate for the length of time in which two single-hits must occur to cause a two-hit event, defined as ω, is obtained from Carlson et al. [6].

The values of the parameters used are given in table 2.

Table 2. Parameter estimates for the active-quiescent TCP.

Parameter	Value used	Units	Reference
u 0	10^8/2	Cells	[23]
q 0	10^8/2	Cells	[23]
μ	0.0655	1/day	[21]
γ	0.0476	1/day	[2]
A u	0.487	Gy^− 1	[11]
A q	0.155	Gy^− 1	[11]
B	0.055	Gy^− 2	[11]
ω	570.4	Minutes	[6]

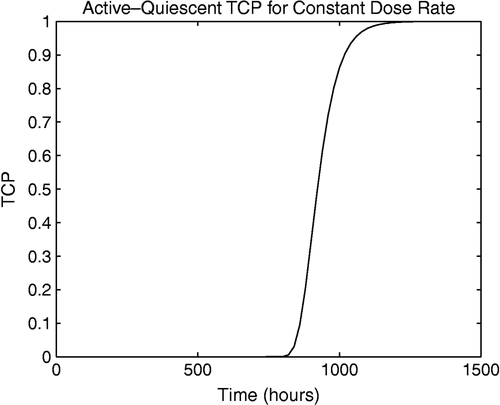
Assume the dose rate is a constant value of 2.75 Gy day^− 1. Figure 1 depicts a plot of the TCP as a function of time for this treatment schedule. The plot shows that at approximately 750 h, or 1 month, the TCP begins to increase, which suggests this is when the treatment begins to have a positive effect. By 1200 h, or 50 days, the TCP has reached its maximum value, which indicates a high probability of tumour eradication. The TCP for specific treatment schedules that are used to treat cancer is considered in the paper by Yurtseven et al. [24].

Figure 1 Plot of TCP vs. time with constant dose rate.

5. Discussion

In this paper, the radiation treatment of cancer cells, beginning at the cellular level, is mathematically described. Using this mathematical description, which consists of a system of two ODEs (1), an expression for the TCP (2), which is useful in determining the outcome of a specific treatment schedule, is subsequently derived.

The effects of radiotherapy on cancer cells have been studied extensively for many years. The first widely recognized mathematical model of this process came in 1966, when the LQ model was first developed. Many later mathematical models of the radiation treatment of cancer have considered an inhomogeneous cell population of varying radiosensitivities, without classifying the mechanism behind these variations. It is only recently that the quiescent, or , phase was recognized as a cellular state which the cell can enter from the classical four phase cell cycle. It has been shown that cells in this quiescent state are less sensitive to radiation than cells which are proliferating. For this reason, it is important to consider this resting state when developing a model of this process. In the active-quiescent model presented here, the cell population is divided into two compartments: a quiescent compartment and an active compartment, which includes the , S, and M phases of the cell cycle. The derivation of the active-quiescent radiation model began from first principles, by considering how radiation affects a single cell. Once cell specific target sites that could be damaged via energy deposits were established, the model was extended to groups of cells in the two respective compartments. The result of this derivation was a system of two ODEs, which includes the effects of a time-dependent radiation dose rate and incorporates the dynamics of the active-quiescent cell cycle (see equation (1)).

Once the active-quiescent radiation model was established, the effects of the two parameters which governed a cell's transition through the quiescent and active phases were considered. The first parameter, μ, describes the proliferation rate and the second parameter, γ, describes the transition rate from the quiescent to the active cell compartment. Perturbation analysis showed that the relative sizes of these parameters have a significant effect on the solutions of the active-quiescent system. When μ and γ are both small, a modified linear-quadratic model is obtained. When γ is large and μ is small, the one-hit event damage on resting cells has no effect, while when μ is large and γ is small, the effect of radiation on the active cells does not contribute to the leading order system behaviour. The comparison to the LQ-model leads to the confirmation that a large ratio corresponds to a fast cell cycle and a smaller ratio corresponds with a slow cell cycle. Also, this comparison led to the hypothesis that a large ratio indicates a significant quiescent compartment.

Following the model analysis, the results of Zaider and Minerbo [25] were extended by deriving an expression for the active-quiescent TCP. To do this, a method similar to that used in Ref. [25] was employed. The first step was to extend the active-quiescent model to a nonlinear birth–death process (see equations (32) and (33)). The resulting system of infinitely many differential equations was then solved using generating functions. Once the solution was obtained, an explicit expression for the active-quiescent TCP, or the probability that there are zero tumour cells at time t, could be calculated. This expression can be used to analyze a variety of treatment plans of varying dose rates, number of fractions, and overall treatment time (see [24]).

Acknowledgements

We thank G. de Vries, O. Yurtseven and the members of the Mathematical Physiology Group at University of Alberta for helpful remarks and discussions. We are grateful to have continued support through NSERC and through the MITACS project on Mathematical Modeling in Pharmaceutical Development under the leadership of Jack Tuszynski.

Additional information

Notes on contributors

A. Dawson

† †Supported by MITACS.

T. Hillen

‡ ‡ [email protected]. Supported by NSERC and MITACS.

Notes

^†Supported by MITACS.

^‡ [email protected]. Supported by NSERC and MITACS.