Local modal regression

Abstract

A local modal estimation procedure is proposed for the regression function in a nonparametric regression model. A distinguishing characteristic of the proposed procedure is that it introduces an additional tuning parameter that is automatically selected using the observed data in order to achieve both robustness and efficiency of the resulting estimate. We demonstrate both theoretically and empirically that the resulting estimator is more efficient than the ordinary local polynomial regression (LPR) estimator in the presence of outliers or heavy-tail error distribution (such as t-distribution). Furthermore, we show that the proposed procedure is as asymptotically efficient as the LPR estimator when there are no outliers and the error distribution is a Gaussian distribution. We propose an expectation–maximisation-type algorithm for the proposed estimation procedure. A Monte Carlo simulation study is conducted to examine the finite sample performance of the proposed method. The simulation results confirm the theoretical findings. The proposed methodology is further illustrated via an analysis of a real data example.

Keywords:

• adaptive regression
• local polynomial regression
• M-estimator
• modal regression
• robust nonparametric regression

1. Introduction

Local polynomial regression (LPR) has been popular in the literature due to its simplicity of computation and nice asymptotic properties (Fan and Gijbels 1996). The local M-estimator (LM) has been investigated in the presence of outliers by many authors; see Härdle and Gasser (1984), Tsybakov (1986), Härdle and Tsybakov (1988), Hall and Jones (1990), Fan, Hu, and Truong (1994), Fan and Jiang (2000), Jiang and Mack (2001), among others. As usual, a nonparametric M-type of regression will be more efficient than least-squares-based nonparametric regression when there are outliers or the error distribution has a heavy tail. However, these methods lose some efficiency when there are no outliers or the error distribution is normal. Thus, it is desirable to develop a new local modelling procedure which can achieve both robustness and efficiency by adapting to different types of error distributions.

In this paper, we propose a local modal regression (LMR) procedure. The sampling properties of the proposed estimation procedure are systematically studied. We show that the proposed estimator is more efficient than the ordinary least-squares-based LPR estimator in the presence of outliers or heavy-tail error distribution. Furthermore, the proposed estimator achieves a full asymptotic efficiency of the ordinary LPR estimator when there are no outliers and the error distribution is a Gaussian distribution. We further develop a modal expectation–maximisation (MEM) algorithm for the LMR. Thus, the proposed modal regression can be implemented easily in practice. We conduct a Monte Carlo simulation to assess the finite sample performance of the proposed procedure. The simulation results show that the proposed procedure is robust to outliers and performs almost as well as the local likelihood regression (LLH) estimator (Tibshirani and Hastie 1987) constructed using the true error function. In other words, the proposed estimator is almost as efficient as an omniscient estimator.

The remainder of the paper is organised as follows. In Section 2, we propose the LMR, develop the MEM algorithm for the LMR estimator, and study the asymptotic properties of the resulting estimator. In Section 3, we describe the Monte Carlo simulation study conducted and use a real data example to illustrate the proposed methodology. Technical conditions and proofs are given in Appendix 1.

2. The LMR estimator

Suppose that are independent and identically distributed (iid) random samples from

where , , and m(·) is an unknown nonparametric smoothing function to be estimated. LPR is to locally approximate by a polynomial function. That is, for x in a neighbourhood of x ₀, we approximate

where

The local parameter is estimated by minimising the following weighted least-squares function:

where , a rescaled kernel function of K(t) with a bandwidth h. The properties of LPR have been well studied (see e.g. Fan and Gijbels 1996). It is also well known that the least-squares estimate is sensitive to outliers. In this section, we propose an LMR procedure to achieve both robustness and efficiency.

Our LMR estimation procedure is to maximise over

where and φ(t) is a kernel density function. The choice of φ is not very crucial. For ease of computation, we use the standard normal density for φ(t) throughout this paper. See Equation (5). It is well known that the choice of K(·) is not very important. In our examples, we also use Gaussian kernel for K(·). The choices of the bandwidths h ₁ and h ₂ will be discussed later. Denote the maximiser of to be . Then, the estimator of the vth derivative of m(x), m ^(v)(x), will be

We will refer to as the LMR estimator. Specially, when p=1 and v=0, we refer to this method as local linear modal regression (LLMR). When p=0, Equation (2) reduces to

which is a kernel density estimate of (X, Y) at (x ₀, y ₀) with y ₀=β₀. Hence, the resulting estimate βˆ₀, by maximising Equation (4), is indeed the mode of the kernel density estimate in the y direction given X=x ₀ (Scott 1992, sec. 8.3.2). This is why we call our method LMR. In this paper, we mainly consider univariate X. The proposed estimate is applicable for multivariate X, but is practically less useful due to the ‘curse of dimensionality’.

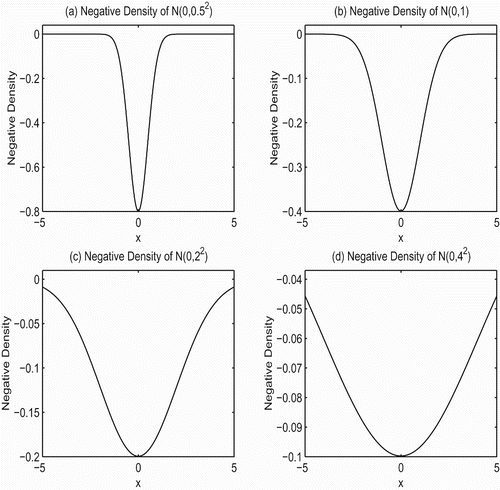
In general, it is known that the sample mode is inherently insensitive to outliers as an estimator for the population mode. The robustness of the proposed procedure can be further interpreted from the point of view of M-estimation. If we treat as a loss function, the resulting M-estimator is an LMR estimator. The bandwidth h ₂ determines the degree of robustness of the estimator. Figure 1 provides insights into how the LMR estimator achieves the adaptive robustness. Note that corresponds to the variance in the normal density. From Figure 1, it can be seen that the negative normal density with small h ₂, such as h ₂=0.5, looks like an outlier-resistant loss function, while the shape of the negative normal density with large h ₂, for example, h ₂=4, is similar to that of the L ₂-loss function. In practice, h ₂ is selected by a data-driven method so that the resulting local estimate is adaptively robust. The issue of selection of both bandwidths h ₁ and h ₂ will be addressed later on.

Figure 1. Plot of negative normal densities.

2.1. The MEM algorithm

In this section, we extend the MEM algorithm, proposed by Li, Ray, and Lindsay (2007), to maximise Equation (2). Similar to an expectation–maximisation (EM) algorithm, the MEM algorithm also consists of two steps: E-step and M-step. Let be the initial value and start with k=0:

	E-step: In this step, we update by
	M-step: In this step, we update : since φ(·) is the density function of a standard normal distribution. Here, with W k is an n×n diagonal matrix with diagonal elements s, and .

The MEM algorithm requires one to iterate the E-step and the M-step until the algorithm converges. The ascending property of the proposed MEM algorithm can be established along the lines of the study of Li et al. (2007). The closed-form solution for is one of the benefits of using the normal density function in Equation (2). If , it can be seen in the E-step that

Thus, the LMR converges to the ordinary LPR. That is, the LPR is a limiting case of the LMR. This can also be roughly seen by the following approximation:

(Note that this approximation only holds when h ₂ is quite large.) This is another benefit of using the normal density for the LMR. This property makes the LMR estimator achieve full asymptotic efficiency under the normal error distribution.

From the MEM algorithm, it can be seen that the major difference between the LPR and the LMR lies in the E-step. The contribution of observation (x _i , y _i ) to the LPR depends on the weight , which in turn depends on how close x _i is to x ₀ only. On the other hand, the weight in the LMR depends on both how close x _i is to x ₀ and how close y _i is to the regression curve. This weight scheme allows the LMR to downweight the observations further away from the regression curve to achieve adaptive robustness.

The iteratively reweighted least-squares (IRWLS) algorithm can be also applied to our proposed LMR. When normal kernel is used for φ(·), the reweighted least-squares algorithm is actually equivalent to the proposed EM algorithm (but they are different if φ(·) is not normal). In addition, the IRWLS algorithm has been proved to have monotone and convergence properties if −φ(x)/x is non-increasing. But the proposed EM algorithm has been proved to have monotone property for any kernel density φ(·). Note that −φ(x)/x is not non-increasing if φ(x) has normal density. Therefore, the proposed EM algorithm provides a better explanation why the IRWLS algorithm is monotone for normal kernel density.

2.2. Theoretical properties

We first establish the convergence rate of the LMR estimator in the following theorem, the proof of which is given in Appendix 1.

Theorem 2.1

Under the regularity conditions (A1)– (A7) given in Appendix 1, with probability approaching 1, there exists a consistent local maximiser of Equation (2) such that

where is the estimate of m ^(v)(x ₀) and m ^(v)(x ₀) is the v th derivative of m(x) at x ₀.

To derive the asymptotic bias and variance of the LMR estimator, we need the following notation. The moments of K and K ² are denoted, respectively, by

Let S, [Stilde], and S* be the matrix with (j, l)-element μ _j+l−2, μ _j+l−1, and ν _j+l−2, respectively, and c _p and [ctilde] _p be the p×1 vector with jth element μ _p+j and μ _p+j+1, respectively. Furthermore, let , a p×1 vector with 1 in the (v+1)th position.

Let

where is the first derivative of and is the second derivative of .

If ε and X are independent, then F(x, h ₂) and G(x, h ₂) are independent of x and we will use F(h ₂) and G(h ₂) to denote them, respectively, in this situation. Furthermore, denote the marginal density of X, that is, the design density, by f(·).

Theorem 2.2

Under the regularity conditions (A1)– (A7) given in Appendix 1, the asymptotic variance of given in Theorem 2.1, is given by

The asymptotic bias of denoted by b _v (x ₀), for p−v odd is given by

Furthermore, the asymptotic bias for p−v even is

provided that are continuous in a neighbourhood of x ₀ and where

The proof of Theorem 2.2 is given in Appendix 1. Based on Equation (7) and the asymptotic variance of the LPR estimator given in Fan and Gijbels (1996), we can show that the ratio of the asymptotic variance of the LMR estimator to that of the LPR estimator is given by

The ratio R(x ₀, h ₂) depends on x ₀ and h ₂ only, and it plays an important role in the discussion of relative efficiency in Section 2.5. Furthermore, the ideal choice of h ₂ is

From Equation (12), we can see that h _{2, opt} dose not depend on n and only depends on the conditional error distribution of ε given X.

Based on Equations (8) and (9) and the asymptotic bias of the LPR estimator (Fan and Gijbels 1996), we know that the LMR estimator and the LPR estimator have the same asymptotic bias when p−v is odd. When p−v is even, they are still the same provided that ε and X are independent as a(x ₀) defined in Equation (10) equals , but they are different if ε and X are not independent. Similar to the LPR, the second term in Equation (9) often creates extra bias. Thus, it is preferable to use odd values of p−v in practice. Thus, it is consistent with the selection order of p for the LPR (Fan and Gijbels 1996). From now on, we will concentrate on the case when p−v is odd.

Theorem 2.3

Under the regularity conditions (A1)– (A7) given in Appendix 1, the estimate given in Theorem 2.1, has the following asymptotic distribution:

The proof of Theorem 2.3 is given in Appendix 1.

2.3. Asymptotic bandwidth and relative efficiency

Note that the mean squared error (MSE) of the LMR estimator, , is

The asymptotic optimal bandwidth for odd p−v, which minimises the MSE, is

where h _LPR is the asymptotic optimal bandwidth for LPR (Fan and Gijbels 1996),

with

The asymptotic relative efficiency (ARE) between the LMR estimator with h _{1, opt} and h _{2, opt} and the LPR estimator with h _LPR of m ^(v)(x ₀) with order p is

From Equation (16), we can see that R(x ₀, h ₂) completely determines the ARE for fixed p and v. Let us study the properties of R(x, h ₂) further.

Theorem 2.4

Let be the conditional density of ε given X=x. For R(x, h ₂) defined in Equation (11), given any x, we have the following results.

	(a)  and hence
	(b) If is a normal density, R(x, h 2)>1 for any finite h 2 and
	(c) Assuming has bounded third derivative, if .

The proof of Theorem 2.4 is given in Appendix 1. From (a) and Equation (16), one can see that the supremum (over h ₂) of the relative efficiency between the LMR and the LPR is greater than or equal to 1. Hence, the LMR works at least as well as the LPR for any error distribution. If there exists some h ₂ such that R(x, h ₂)<1, then the LMR estimator has a smaller asymptotic MSE than the LPR estimator.

As discussed in Section 2.3, when , the LMR converges to the LPR. The equation of (a) confirms this result. It can be seen from (b) that when , the optimal LMR (with ) is the same as the LPR. This is why the LMR will not lose efficiency under normal distribution. From (c), one can see that the optimal h ₂ should not be too small, which is quite different from the needed locality effect of h ₁.

Table 1 lists the ARE between the LLMR estimator (LMR with p=1 and v=0) and the local linear regression (LLR) estimator for a normal error distribution and some special error distributions that are generally used to evaluate the robustness of a regression method. The normal mixture is used to mimic the outlier situation. This kind of mixture distribution is also called the contaminated normal distribution. The t-distributions with degrees of freedom ranging from 3 to 5 are often used to represent heavy-tail distributions. From Table 1, one can see that the improvement of the LLMR over the LLR is substantial when there are outliers or the error distribution has heavy tails.

Table 1. Relative efficiency between the LLMR estimator and the LLR estimator.

Error distribution	Relative efficiency
N(0, 1)	1
	1.1745
	1.6801
t-distribution with df=5	1.1898
t-distribution with df=3	1.7169

3. Simulation study and application

In this section, we describe the Monte Carlo simulation conducted to assess the performance of the proposed LLMR estimator and compare it with the LLR estimator and some commonly used robust estimators. We first address how to select the bandwidths h ₁ and h ₂ in practice.

3.1. Bandwidth selection in practice

In our simulation setting, ε and X are independent. Thus, we need to estimate F(h ₂) and G(h ₂) defined in Equation (6) in order to find the optimal bandwidth h _{2, opt} based on Equation (12). To this end, we first get an initial estimate of m(x), denoted by , and the residual , by fitting the data using any simple robust smoothing method, such as locally weighted scatterplot smoothing (LOWESS). Then, we estimate F(h ₂) and G(h ₂) by

respectively. Then, R(h ₂) can be estimated by , where σˆ is estimated based on the pilot estimates, , of the error term. Using the grid search method, we can easily find to minimise [Rcirc](h ₂). (Note that would not depend on x.) From Theorem 2.4(c), we know that the asymptotically optimal h ₂ is never too small. Based on our empirical experience, the size of the chosen h ₂ is usually comparable to the standard deviation of the error distribution. Hence, the possible grid points for h ₂ can be , j=0, …, k, for some fixed k (such as k=90).

The asymptotically optimal bandwidth h ₁ is much easier to estimate after finding . Based on formula (14) given in Section 2.5, the asymptotically optimal bandwidth for h ₁ of the LLMR is h _LLR multiplied by a factor . After finding , we can estimate by . We can then employ an existing bandwidth selector for the LLR, such as the plug-in method (Ruppert, Sheather, and Wand 1995). If the optimal bandwidth selected for the LLR is , then h ₁ is estimated by .

When ε and X are independent, the relationship (14) also holds for the global optimal bandwidth that is obtained by minimising the weighted mean integrated square error where w≥0 is some weight function, such as 1 or design density f(x). Hence, the above proposed method of finding also works for the global optimal bandwidth. For simplicity of computation, we use the global optimal bandwidth for and thus for our examples in Sections 3.2 and 3.3.

3.2. Simulation study

For comparison, in our simulation study, we included the LLH estimator (Tibshirani and Hastie 1987) assuming that the error distribution is known. Specifically, suppose the error distribution is g(t), the LLH estimator finds by maximising the following local likelihood:

The estimate of regression function m(x ₀) is .

If the error density g(t) is assumed to be known, the LLH estimator (17) is the most efficient estimator. However, in reality, we seldom know the true error density. The LLH estimator is just used as a benchmark, omniscient estimator to check how well the LLMR estimator adapts to different true densities.

We generated the iid data from the model , where X _i ∼ U(0, 1). We considered the following three cases:

	Case I:
	Case II: . The 5% data from N(0, 52) are most likely to be outliers.
	Case III: .

We compared the following five estimators:

	(1) LLR. We used the plug-in bandwidth (Ruppert et al. 1995).
	(2) Local ℓ1 regression/median regression (LMED).
	(3) LM using Huber's function . As in Fan and Jiang (2000), we took , where σˆ is the estimated standard deviation of the error term by the median absolute deviation (MAD) estimator, that is, where are the pilot estimates of the error term.
	(4) LLMR (LMR with p=1 and v=0).
	(5) LLH using the true error density.

For comparison, in Table 2, we report the relative efficiency between different estimators and the benchmark estimator LLH, where RE(LLMR) is the relative efficiency between the LLMR estimator and the LLH estimator. That is, RE(LLMR) is the ratio of MSE(LLH) to MSE(LLMR) (based on 50 equally spaced grid points from 0.05 to 0.95 and 500 replicates). The same notation applies to other methods.

Table 2. Relative efficiency between different estimators and the LLH estimator.

Error distribution	n	RE(LLR)	RE(LMED)	RE(LM)	RE(LLMR)
N(0, 1)	50	1	0.6676	0.9235	0.9979
	100	1	0.6757	0.9358	0.9992
	250	1	0.6753	0.9455	0.9997
	500	1	0.6818	0.9488	0.9998
	50	0.6446	0.7314	0.9392	0.9127
	100	0.5828	0.7113	0.9298	0.9210
	250	0.5598	0.7222	0.9375	0.9675
	500	0.5691	0.7246	0.9402	0.9859
t 3	50	0.6948	0.8196	0.9809	0.9514
	100	0.6429	0.8386	0.9611	0.9350
	250	0.5462	0.8470	0.9428	0.9617
	500	0.5743	0.8497	0.9442	0.9747

From Table 2, it can be seen that for a normal error, the LLMR had a relative efficiency very close to 1 from the small sample size 50 to the large sample size 500. Note that in Case I, we need not use a robust procedure and the LLR should work the best in this case. Note that in this case, the LLR is the same as the LLH. However, the newly proposed method LLMR worked almost as well as the LLR/LLH when the error distribution was exactly the normal distribution. Hence, the LLMR adapted to normal errors very well. In addition, we can see that the LM lost about 8% efficiency for the small size 50 and lost about 5% efficiency for the large sample size 500. The LMED lost more than 30% efficiency under normal errors.

For contaminated normal errors, the LLMR still had a relative efficiency close to 1 and worked better than the LM, especially for large sample sizes. Hence, the LLMR adapted to contaminated normal error distributions quite well. In this case, the LLR lost more than 40% efficiency and the LMED lost about 30% efficiency.

For t ₃ error, it can be seen from Table 2 that the LLMR also worked similarly to the LLH and a little better than the LM, especially for large sample sizes. Hence, the LLMR also adapted to t-distribution errors quite well. In this case, the LLR lost more than 40% efficiency and the LMED lost about 15% efficiency.

3.3. An application

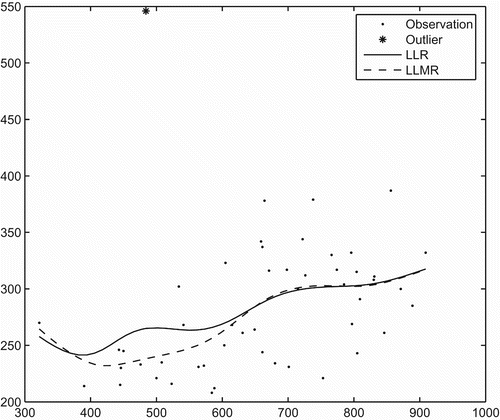
In this section, we illustrate the proposed methodology by analysis of the Education Expenditure Data (Chatterjee and Price 1977). This data set consists of 50 observations from 50 states, one for each state. The two variables to be considered here are X, the number of residents per thousand residing in urban areas in 1970, and Y, the per capita expenditure on public education in a state, projected for 1975. For this example, one can easily identify the outlier. We use this example to show how the obvious outlier will affect the LLR fit and the LLMR fit.

Figure 2 shows the scatter plot of the original observations and the fitted regression curves by the LLR and the LLMR. From Figure 2, one can see that there is an extreme observation (outlier). This extreme observation is from Hawaii, which has a very high per capita expenditure on public education with x value being close to 500. This observation created the biggest difference between the two fitted curves around x=500. The observations with x around 500 appear to go down in that area compared with the observations with x around 600. Thus, the regression function should also go down when x moves from 600 to 500. The LLMR fit reflected this fact. (For this example, the robust estimators LMED and LM provided results that were similar to those of the estimator LLMR.) However, the LLR fit went up in that area due to the big impact of the extreme observation from Hawaii. In fact, this extreme observation received about a 10% weight in the LLR fit at x=500, compared with nearly 0% weight in the LLMR fit. Hence, unlike the LLR, the LLMR adapts to, and is thereby robust to, outliers.

Figure 2. Plot of fitted regression curves for the Education Expenditure Data. The star point represents the extreme observation from Hawaii. The solid curve represents the LLR fit. The dashed curve represents the LLMR fit.

4. Discussion

In this paper, we have proposed an LMR procedure. It introduces an additional tuning parameter that is automatically selected using the observed data in order to achieve both robustness and efficiency of the resulting nonparametric regression estimator. Modal regression has been briefly discussed in Scott (1992, sec. 8.3.2) without any detailed asymptotic results. Scott (1992, sec. 8.3.2) used a constant β₀ to estimate the local mode as Equation (4). Due to the advantage of the LPR over the local constant regression, we extended the local constant structure to a local polynomial structure and provided a systematic study of the asymptotic results of the LMR estimator. As a measure of centre, the modal regression uses the ‘most likely’ conditional values rather than the conditional average. When the conditional density is symmetric, these two criteria match. However, as stated by Scott (1992, sec. 8.3.2), the modal regression, besides robustness, can explore a more complicated data structure when there are multiple local modes. Hence, the LMR may be applied to a mixture of regressions (Goldfeld and Quandt 1976; Fruhwirth-Schnatter 2001; Green and Richardson 2002; Rossi, Allenby, and McCulloch 2005) and ‘change point’ problems (Lai 2001; Bai and Perron 2003; Goldenshluger, Tsbakov, and Zeevi 2006). This requires further research.

Chu, Glad, Godtliebsen, and Marron (1998) also used the Gaussian kernel as the outlier-resistant function in their proposed local constant M-smoother for image processing. However, they let and aimed at edge-preserving smoothing when there is a jump in the regression curves. In this paper, the goal was different; we sought to provide an adaptive robust regression estimate for the smooth regression function m(x) by adaptively choosing h ₂. In addition, we proved that for a regression estimate, the optimal h ₂ does not depend on n and should not be too small.

In addition, note that the LMR does not estimate the mean function in general. It requires the assumption , which holds if the error density is symmetric about zero. If the above assumption about the error density does not hold, the proposed estimate is actually estimating the function

which converges to the mode of f(Y| X=x) if and the bias depends on h ₂. For the general error distribution and fixed h ₂, all the asymptotics provided in this paper still apply if we replace the mean function m(x) by [mtilde](x).

Acknowledgements

The authors are grateful to the editors and the referees for their insightful comments on this paper. Bruce G. Lindsay's research was supported by an NSF grant CCF 0936948. Runze Li's research was supported by the National Natural Science Foundation of China grant 11028103, NSF grant DMS 0348869, and National Institute on Drug Abuse (NIDA) grant P50-DA10075. The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIDA or the NIH.

Appendix 1: Proofs

The following technical conditions are imposed in this section:

	(A1) m(x) has a continuous (p+1)th derivative at the point x 0.
	(A2) f(x) has a continuous first derivative at the point x 0 and f(x 0)>0.
	(A3) F(x, h 2) and G(x, h 2) are continuous with respect to x at the point x 0, where F(x, h 2) and G(x, h 2) are defined in Equation (6).
	(A4) K(·) is a symmetric (about zero) probability density with compact support [−1, 1].
	(A5) F(x 0, h 2)<0 for any h 2>0.
	(A6)  and , , and are continuous with respect to x at the point x 0.
	(A7) The bandwidth h 1 tends to zero such that and the bandwidth h 2 is a constant and does not depend on n.

The above conditions are not the weakest possible conditions, but they are imposed to facilitate the proofs. For example, the compact support restriction on K(·) is not essential and can be removed if we put a restriction on the tail of K(·). Condition (A5) ensures that there exists a local maximiser of Equation (2). In addition, although h ₁ is assumed to tend to zero when , h ₂ is assumed to be a fixed constant and its optimal values only depend on the error density and not on n. The condition ensures that the proposed estimate is consistent and it is satisfied if the error density is symmetric about zero. However, we do not require the error distribution to be symmetric about zero. If the assumption does not hold, the proposed estimate is actually estimating the function

Denote , , , , and , where , j=0, 1, …, p. The following lemmas are needed for our technical proofs.

Lemma A.1

Assume that conditions A1–A6 hold. We have

and

Proof

We shall prove Equation (A1), since Equation (A2) can be shown by the same arguments. Denote . In lines of arguments that are the same as those in Lemma 5.1 of Fan and Jiang (2000), we have

and

Based on the result and the assumption , it follows that .   ▪

Proof

[Proof of Theorem 2.1] Denote . It is sufficient to show that for any given η>0, there exists a large constant c such that

where is defined in Equation (2).

Using Taylor expansion, it follows that

where z _i is between and .

By directly calculating the mean and the variance, we obtain

Hence,

Similarly,

From Lemma A.1, it follows that

Noting that S is a positive matrix, |μ|=c, and F(x ₀, h ₂)<0, we can choose c large enough such that I ₂ dominates both I ₁ and I ₃ with a probability of at least 1−η. Thus, Equation (A3) holds. Hence, with the probability approaching 1 (wpa1), there exists a local maximiser such that , where . Based on the definition of , we can get, wpa1, .   ▪

Define

We have the following asymptotic representation.

Lemma A.2

Under conditions (A1)– (A6), it follows that

Proof

Let

Then,

The solution satisfies the following equation:

where ε* is between ε _i and . Note that the second term on the left-hand side of Equation (A7) is

Applying Lemma A.1, we obtain

and

From Theorem 2.1, we know that ; hence,

and

Also similar to the proof of Lemma A.1, we have

Based on Equations (A9) and (A10) and condition (A6),

and

Hence, for the third term on the left-hand side of Equation (A7),

Then, it follows from Equations (A5) and (A7) that

which is Equation (A6).   ▪

Proof

[Proof of Theorem 2.2] Based on Equation (A5) and condition (A6), we can easily get . Similar to the proof in Lemma A.1, we have

So,

Based on the result (A6), the asymptotic bias b _v (x ₀) and the variance of are naturally given by

and

By simple calculations, we can know that the (v+1)th element of S ⁻¹ c _p is zero for p−v even. So, we need a higher order expansion of asymptotic bias for p−v even. Following arguments that are similar to those in Lemma A.1, if , we can easily prove that

where J ₁ and J ₂ are defined in Equation (A8) and .

Then, it follows from Equation (A7) that

where

For p−v even, since the (v+1)th element of S ⁻¹ c _p and is zero (see Fan and Gijbels 1996 for more details), the asymptotic bias b _v (x ₀) of is naturally given by

  ▪

Proof

[Proof of Theorem 2.3] It is sufficient to show that

where because using Slutsky's theorem, it follows from Equations (A6) and (A12) and Theorem 2.2 that

Next, we give Equation (A12). For any unit vector , we prove that

Let

Then, . We check Lyapunov's condition. Based on Equation (A11), we can get and . So, we only need to prove . Noting that is bounded, and K(·) has compact support,

So, the asymptotic normality for W _n * holds with the covariance matrix .   ▪

Proof

[Proof of Theorem 2.4]

	(a) Note that Based on Equation (6), when , we have Then, , when . So, for any x, From Equation (A13), we can get for any x.
	(b) Suppose is the density function of . By some simple calculations, we can get Hence, From (a), we can get for any x.
	(c) Suppose that , then So, we can easily see that as .

  ▪