Methods for the analysis of multiple endpoints in small populations: A review

ABSTRACT

While current guidelines generally recommend single endpoints for primary analyses of confirmatory clinical trials, it is recognized that certain settings require inference on multiple endpoints for comprehensive conclusions on treatment effects. Furthermore, combining treatment effect estimates from several outcome measures can increase the statistical power of tests. Such an efficient use of resources is of special relevance for trials in small populations. This paper reviews approaches based on a combination of test statistics or measurements across endpoints as well as multiple testing procedures that allow for confirmatory conclusions on individual endpoints. We especially focus on feasibility in trials with small sample sizes and do not solely rely on asymptotic considerations. A systematic literature search in the Scopus database, supplemented by a manual search, was performed to identify research papers on analysis methods for multiple endpoints with relevance to small populations. The identified methods were grouped into approaches that combine endpoints into a single measure to increase the power of statistical tests and methods to investigate differential treatment effects in several individual endpoints by multiple testing.

Key Words:

• Combined outcomes
• composite endpoints
• multiple endpoints
• multiple testing
• multivariate responses
• rare diseases
• small populations

1 Introduction

For the assessment of drug efficacy in confirmatory trials, the current ICH E9 guidance on statistical principles in clinical trials recommends to select a single primary endpoint that is “capable of providing the most clinically relevant and convincing evidence directly related to the primary objective of the trial” (International Conference on Harmonisation, 1998). The purpose of secondary variables that describe different aspects of the patients’ condition and course of disease is either to support the primary objective (after a treatment effect has been demonstrated in the primary endpoint) or to address secondary objectives.

However, the ICH E9 guideline also recognizes that in certain settings the primary analysis of clinical trials should be based on inference on multiple endpoints. The European Medicines Agency issued a guideline concerning multiplicity issues in clinical trials that especially addresses issues arising from the use of multiple endpoints (European Medicines Agency, Committee for Proprietary Medicinal Products, 2002) and recently a draft of an update was released (European Medicines Agency, Committee for Proprietary Medicinal Products, 2017). Similarly, the US Food and Drug Administration recently released a draft guideline on multiple endpoints in clinical trials (U.S. Department of Health and Human Services Food and Drug Administration, 2017). There are two main objectives for including multiple endpoints in the primary analysis: (i) to increase the power of statistical tests (or reduce the required sample size, respectively) by aggregating information from multiple endpoints and (ii) to describe treatment effects more comprehensively in diseases that manifest in a multifaceted way where a single outcome measure does not suffice to fully represent the treatment effect.

When aiming for a global assessment of treatment effects, the information from multivariate summary statistics can be aggregated into a single univariate test statistic. Alternatively, multiple endpoints can be aggregated in a single combined endpoint for each patient and a univariate test may be applied to the combined endpoint.

Assessing effects in terms of combined endpoints is common in many areas of clinical development. Summary scores based on a rating scale, like the HAMD score applied in depression trials or the ACR20 or ACR50 in rheumatoid arthritis trials, provide examples. Multiple binary or time-to-event endpoints may be comprised in a composite endpoint, defined as occurrence of at least one event or the time to the first event. E.g. in transplantation studies, a composite endpoint for treatment failure could be defined as the occurrence of rejection, graft loss or death within a certain time period after start of treatment. In cardiovascular outcome studies, a composite endpoint may be the time to the myocardial infarction, stroke or death, whichever occurs first (Chi, 2005).

Examples where combined endpoints are used in trials in small populations are indications as pulmonary arterial hypertension with the endpoint time to clinical worsening comprising six components (Gomberg-Maitland et al., 2013) or systemic mastocytosis where the cumulative number of responses across five visits and four symptoms (75% improvement in pruritus score, flushes per week, HAMD or Fatigue Impact Scale) was used as primary endpoint (Gomberg-Maitland et al., 2013; Lortholary et al., 2017).

A consequence of any aggregation strategy is that only an overall null hypothesis is tested and no conclusions can be drawn on individual endpoints. If there is a treatment effect in all considered endpoints and the correlation between endpoints is not too large, an aggregated measure will have a better effect to variance ratio than a single endpoint (Senn and Bretz, 2007; Tang et al., 1989b). Especially in settings where an increase of sample size is not feasible (as, e.g., in rare diseases), the gain in power of approaches that consider an overall hypothesis only may outweigh the price to be paid in terms of less detailed inference. Even if a combined endpoint shows some statistically significant and clinically relevant effect, the effect in its components may be of different magnitude or even point in different directions (Rauch and Kieser, 2013). For this reason the effect in the individual components should be evaluated as well (European Medicines Agency, Committee for Proprietary Medicinal Products, 2002), which could be done either in a descriptive or in a confirmatory way.

If inference for several individual endpoints is intended in a confirmatory clinical trial, several hypotheses need to be tested and some adjustment for multiple testing is required to control the familywise type I error rate (FWER). Although these adjustments may result in larger sample sizes to achieve appropriate power, the required number of patients may still be lower than for performing separate clinical trials to investigate different endpoints. In small populations, therefore, the investigation of multiple testing procedures with favorable small sample properties is of special importance.

In this context, “small” constitutes a sample size that is restrictive in some aspect of the study design or analysis. This includes the case of a sample too small to justify the use of purely asymptotic inference methods in terms of type I error rate control, requiring the application of exact tests. It also covers the case of sample sizes that are limited by the number of eligible patients due to low prevalence of the disease, which may result in underpowered studies. A recent investigation in trials registered at ClinicalTrials.gov shows that the sample size of trials in rare diseases is positively associated with the disease prevalence (Hee et al., 2017). The study reports median sample sizes of 74.5, 112 and 122.5 in completed phase 3 studies in, respectively, 8, 64, and 44 trials in rare diseases with prevalences 1–9/1,000,000, 1–9/100,000 and 1–5/10,000 (Hee et al., 2017). The first quartiles of the sample size distribution were 22, 34.5 and 46, the third quartiles were 100, 301 and 256. These numbers provide some range for small sample sizes encountered in practice. Note that with binary and time-to-event endpoints, the observed number of events determines the precision of an analysis method, and this number may be substantially smaller than the number of recruited patients.

In this literature review, we discuss methods that are suitable to test hypotheses concerning treatment effects in multiple endpoints when the sample size is small in the sense defined above. These include methods based on a combination of marginal test statistics for several endpoints, the combination of endpoints on a patient level and multiple testing procedures that allow for confirmatory inference on multiple individual endpoints. Table 1 clarifies the terminology of multiple endpoint tests used in our systematic review.

Table 1. Terminology of multiple endpoint tests used in the review.

Form of test/endpoint	Description
Combined endpoint	Univariate measure observable in each subject that is constructed from observations in that subject on multiple endpoints
Composite endpoint	Special case of a combined endpoint, either the occurrence of at least one event out of a defined set of events, or the time to the first such event
Co-primary endpoints	Collection of endpoints that have to be affected by treatment to acknowledge an effect
Global test	Test designed to reject the intersection null hypothesis of no effect on any of several endpoints versus the alternative of an effect on at least one endpoint
Multiple testing	Enables inferences on the individual endpoints while controlling the family-wise type I error rate
Family-wise type I error rate (FWER)	The probability to reject at least one true null hypothesis from a set of null hypotheses of interest, regardless of which null hypotheses are true

This article is organized as follows: The search strategy and results of the systematic literature search are reported in Section 2. In Section 3, we focus on methods that combine endpoints to test a global null hypothesis of no treatment effect in any endpoint. The section is structured by the scale level of the regarded endpoints and the small sample aspects are summarized at the end of each subsection. Section 4 is concerned with multiple testing procedures on individual endpoints while controlling the FWER. Most methods considered in this section are applicable to p-values which may result from hypothesis tests of any type of endpoint. Therefore the section is not structured by the type of endpoint but by tests based on marginal or joint distributions of test statistics and different objectives of multiple testing procedures. A special focus is put on procedures that have been assessed in settings with small sample sizes and that do not solely rely on asymptotic considerations. Section 5 gives examples of small-sample trials that employed some of the discussed methods, or for which such methods could be recommended. In Section 6, we conclude with a discussion on the suitability of the methodology for drawing inferences and possible extensions such as group sequential/adaptive designs.

2 Literature search

The literature presented in this review was collected in a two-tier approach, consisting of a systematic search in the electronic database Scopus and supplemented by manually searched papers. Scopus was used to identify research articles published up to 26th September 2016 on methods for confirmative hypothesis tests of multiple endpoints. Reflecting the two objectives to base inference on multiple endpoints discussed above, two search queries were defined to identify (i) papers covering methodology based on the combination of multiple endpoints (“combined endpoints query”) and (ii) papers addressing multiple testing methodology for tests of multiple endpoints (“multiple testing query”). Both queries were restricted to research articles in the areas of mathematics, medicine (including human, dental or veterinary medicine), pharmaceutics, health sciences and multidisciplinary research (see Table 3 and Appendix for the exact search terms).

The search yielded 830 hits for the combined endpoint and 867 hits for the multiple testing query. After removal of 182 duplicates, 1515 articles were screened for relevance based on the titles and abstracts. Papers that did not address statistical methods for multiple endpoints and non-methodological papers were excluded based on their title. Articles not relevant for small clinical trials were excluded based on their title and abstract, accessing the full text where necessary. Only articles addressing exact tests, non-parametric test procedures (such as resampling based tests) or asymptotic tests whose finite sample size properties were assessed, were included. Furthermore, review papers and methods not based on hypothesis testing were excluded. Fifty-one articles satisfied the above inclusion-exclusion criteria. The manual search resulted in 52 additional papers leading to a total number of 103 relevant papers whose full text was reviewed. The work-flow of the literature search is depicted in Figure 1

Figure 1. Flow diagram of inclusion and exclusion strategy for the two queries about combination of multiple endpoints and multiple testing. The detailed search terms are listed in the Appendix. The numbers refer to a search in the Scopus database on 26.09.2016.

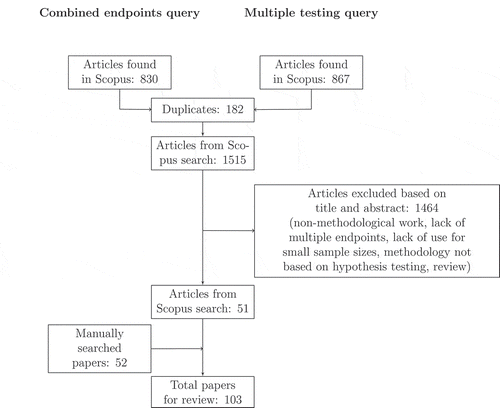
A full list of these papers and their classification according to the structure of this review is provided in Table 2 for methods based on combining multiple endpoints and for multiple testing strategies. The articles concerned with different methodology for combining endpoints were treated according to the scale of measurement they primarily apply to.

Table 2. Articles concerned with the combination of endpoints by scale of measurement (some papers fitting in several categories were put into the most applicable class) and articles concerned with multiple testing based on the used information level and testing strategy.

	Combining multiple endpoints
Continuous	Ordinal	Binary	Time-to-event
Bathke et al. (2008)	Buyse (2010)	Agresti and Klingenberg (2005)	Dong et al. (2016)
Bittman et al. (2009)	Chenouri et al. (2011)	Barnard (1947)	Ferreira-González et al. (2007)
Bregenzer and Lehmacher (1998)	Chenouri and Small (2012)	Baraniuk et al. (2012)	Lachin and Bebu (2015)
Frick (1996)	Claggett et al. (2015)	Boschloo (1970)	Luo and Turnbull (1999)
Glimm and Läuter (2010)	Häberle et al. (2009)	Guo et al. (2005)	Luo et al. (2013)
Läuter (1996)	Huang et al. (2005)	Han et al. (2004)	Pocock et al. (2012)
Kudo (1963)	Klingenberg et al. (2009)	Mascha and Imrey (2010)	Rauch and Kieser (2013)
Logan and Tamhane et al. (2004)	Liu et al. (1999)	Rom (1992)	Rauch and Beyersmann (2013)
Minas et al. (2014)	Ramchandani et al. (2016)	Ristl et al. (2018)	Rauch et al. (2014b)
Minhajuddin et al. (2007)	Rauch et al. (2014a)	Westfall and Young (1989)	Schüler et al. (2014)
O’Brien (1984)	Wittkowski et al. (2004)	Whitehead et al. (2010)	Wei and Lachin (1984)
Perlman (1969)			Yin et al. (2003)
Perlman and Wu (2002)
Pocock et al. (1987)
Pollard and Van Der Laan (2004)
Tamhane and Logan (2002)
Tang et al. (1989a)
	Multiple testing
Information from marginal distributions	Information from joint distribution	Tests for co-primary endpoints	Tests for non-inferiority/superiority	General
Agresti (2001)	Boyett and Shuster (1977)	Bretz et al. (2011)	Boyett and Shuster (1977)	Bauer (1991)
Bretz et al. (2011)	Brannath et al. (2009a)	Chuang-Stein et al. (2007)	Bloch et al. (2001)	Lehmacher et al. (1991)
Bretz et al. (2009b)	Calian et al. (2008)	Kordzakhia et al. (2010)	Bloch et al. (2007)	Romano and Wolf (2007)
Burman et al. (2009)	Hothorn et al. (2008)	Offen et al. (2007)	Logan and Tamhane (2008)	Senn and Bretz (2007)
Dmitrienko et al. (2003)	Lafaye De Micheaux et al. (2014)	Ristl et al. (2016)	Perlman and Wu (2004)	Su et al. (2012)
Dmitrienko et al. (2008)	Logan and Tamhane (2001)	Sozu et al. (2012)	Röhmel et al. (2006)
Dmitrienko et al. (2007)	Pauly et al. (2015)	Sugimoto et al. (2012)	Tamhane and Logan (2004)
Holm (1979)	Sexton et al. (2012)
Hommel and Krummenauer (1998)	Simes (1986)
Hommel et al. (2007)	Westfall and Young (1993)
Huque and Alosh (2012)	Westfall and Troendle (2008)
Klinglmüller et al. (2014a)	Westfall (2011)
Liu and Hsu (2009)	Zaykin et al. (2002)
Maurer et al. (1995)	Xi and Tamhane (2015)
Posch and Futschik (2008)
Tarone (1990)
Westfall et al. (1998)
Westfall and Krishen (2001)
Westfall and Wolfinger (1997)

Table 3. Structure of the combined endpoints query and the multiple testing query: The (TITLE-ABS-KEY) words are restricted by the (AUTHKEY) words, the subject area and document type for each search query. The number of hits are given in brackets and refer to a search in the Scopus data base on 26.09.2016.

Combined endpoints	Multiple testing	AND	AND	AND
(TITLE-ABS-KEY)	(TITLE-ABS-KEY)	(AUTHKEY)	(SUBJAREA)	(DOCTYPE)
Composite endpoint* (76)	Multiple comparison* (330)	Multiple endpoint*	math	ar
combin* W/2 endpoint*(15)	Multiple test* (244)	Multivariate	medi
Multiple endpoint* (123)	Composite endpoint* (76)	Small	phar
Multivariate response* (12)	Multiple outcome* (66)	Non*parametric	dent
Multivariate endpoint*(3)	Multiple response* (79)	Sum statistic	vete
Multivariate comparison* (12)	Multiplicity adjustment (12)	Composite endpoint*	heal
Multivariate W/2 test (524)	Closed test* (36)	Concordance	mult
Multivariate outcome*(25)	Closure principle (1)	Rank
	Gatekeeping (12)	Robust
	Partitioning principle (2)	Bootstrap
	Reverse multiplicity (2)	Resampling
	Co-primary endpoints (12)	Permutation test
	Simultaneous confidence intervals (96)	minP
	Intersection-union (21)	Exact test
	Adjusted p-value (29)
	Family wise error rate (32)

The multiple testing strategies, on the other hand, were first categorized according to their objectives, namely identifying at least one endpoint for which the treatment is effective, showing a treatment effect in several co-primary endpoints, or showing non-inferiority of all endpoints and superiority in at least one. Strategies aiming for the rejection of at least one endpoint were further categorized according to the utilization of either marginal or joint distributions of test statistics.

Note that throughout the review further (more general) references are cited to provide relevant background information.

3 Combination of endpoints

In small clinical trials the interpretation of individual endpoints may be difficult due to the high variability of estimates. Combining the information from several endpoints may result in higher power to detect a treatment effect and allow for a better overall assessment of that effect. A standard approach combines the information on a patient level by defining a new outcome variable as a summary score or composite endpoint and applies an appropriate univariate hypothesis test. However, in principle any function of the multivariate sample space to a univariate measure can be used to combine multiple endpoints. Important criteria for the choice of the combination function are the interpretability of the resulting outcome measure and the statistical power of the corresponding hypothesis test. Sum statistics achieve a high power in case of an effect pointing in the same direction in many components. Statistics based on sum of squares are suitable for hypothesis tests with non-directional alternatives and maximum statistics may lead to a high power if a strong effect in at least one endpoint is expected. Alternatively, multivariate orderings have been proposed for a non-parametric combination of endpoints. For time-to-event endpoint data the composite endpoint is most often chosen as the time to the first event of a candidate set of relevant events. Information from several endpoints can also be combined in terms of univariate tests for each component. This option will be discussed in Section 4.

3.1 Continuous endpoints

A direct way to compare multivariate metric outcomes from two or more populations is to test equality of the mean vectors. In clinical trials we are mostly interested in equidirected differences, for example, that at least one component of the mean vector of the treatment group exceeds that of a placebo group. The well-known Hotelling’s $T^2$ test does not account for the direction of component differences and therefore does not allow for a directional interpretation of the test results. O’Brien (1984) studied several directed tests of the null hypothesis of equal mean vectors against the alternative of at least one non-negative difference: an ordinary least squares (OLS) test on the standardized observations and a generalized least squares test (GLS) where the standardized values are further weighted by the inverse of the estimated correlation matrix. Small sample properties of these directional tests allowing for incomplete data are discussed by Bregenzer and Lehmacher (1998).

If the treatment effects are identical for all endpoints, the power of O’Brien’s tests is always larger than the power of tests for individual endpoints and consequently the required sample size is reduced accordingly (Tang et al., 1989b). The power gain of the GLS test over the OLS test is typically small, the weights in the GLS test may become negative and the convergence of the resulting statistic to a limiting distribution is slower for the GLS test, such that some authors argue in favor of the OLS test (Logan and Tamhane et al., 2004). In contrast to Hotelling’s $T^2$ test, simulations show good power of O’Brien’s tests for directional alternatives and sample sizes in the range of 5 to 50 per group and a range of distributions (O’Brien, 1984).

Läuter (1996) pointed out that even for normally distributed data the OLS test statistics is not exactly t-distributed. This may cause inflation of type I error rates for small sample sizes. He developed sum statistics with weights derived from the total covariance matrix estimate under the global null hypothesis or a principal component decomposition of this matrix. These statistics are exactly t-distributed for normally distributed data, but the tests may fail to reach sufficient power if the true treatment effect in at least one endpoint equals zero, even if the effect sizes in the other endpoints tend to infinity (Frick, 1996). Logan and Tamhane et al. (2004) empirically derived a formula to calculate the degrees of freedom for the approximating t-distribution of the OLS test for two samples, which results in type I error rates close to the nominal level and good power for sample sizes from 5 to 25 per group.

O’Brien type statistics of weighted and standardized sums can be generalized to combine any vector of multivariate normal test statistics (Pocock et al., 1987). If the covariance matrix is known and identical under the null and alternative hypothesis, the GLS statistic provides the optimal test for the global null hypothesis versus an alternative of common standardized effect in all endpoints (Bittman et al., 2009). Further weights can be derived to achieve optimal power for any specified directional alternative. Minas et al. (2014) proposed a stage-wise adaptive weighting scheme which calculates separate sum statistics at each stage and chooses the weights from the observed effects in previous stages. The stage-wise tests are combined using a p-value combination function (see e.g. Bauer and Köhne, 1994).

For testing the null hypothesis of two equal mean vectors versus the alternative that their difference is in the positive orthant, that is all differences are non-negative and at least one difference is positive, likelihood ratio tests have been derived by Kudo (1963) and Perlman (1969). However, their null distribution is not well tractable. Tang et al. (1989a) proposed an approximate likelihood ratio test, which is easier to calculate. Since the sampling variation of the covariance matrix estimate is not taken into account, the test is liberal for small sample sizes. A refinement described by Tamhane and Logan (2002) suggests type I error rate control in simulations for small sample sizes of 20 to 50 patients per group. Perlman and Wu (2002) give a detailed discussion on likelihood ratio tests for multivariate outcomes.

A common issue with the tests discussed so far is that the positive orthant alternative is not the full complement of the (point) null hypothesis. As a consequence, such a test may well reject the null hypothesis even if the true parameter vector is not in the alternative of interest. If needed though, it is often not difficult to restrict the rejection region to outcomes in line with the aimed for alternative. Glimm and Läuter (2010) propose a simple modification of Hotelling’s $T^2$ test to perform a directional test for the null hypothesis of a mean vector being in the negative orthant versus the alternative that at least one component of the mean vector is positive. The small sample properties of this test are inherited from Hotelling’s $T^2$ test. In particular, it takes into account uncertainty due to estimation of the covariance matrix and it is exact for multivariate normal data. Minhajuddin et al. (2007) consider the complement of the positive orthant as appropriate null space and describe a bootstrap test (see also Pollard and Van Der Laan (2004)) that does not require distributional assumptions.

Summary of small sample aspects

Directional tests provide larger power for the relevant alternative in superiority trials and may therefore be preferred over undirected tests, particularly in small sample trials. As a common feature, the small sample adjustments for these tests utilize t- or F-distributions instead of normal or Chi-square distributions. While these distributions are not the exact sampling distributions of the statistics under deviations from normally distributed data, they can be expected to perform much better in terms of type I error rate control than the large sample limiting distribution (Bathke et al., 2008).

3.2 (At least) Ordinally scaled outcomes

Wittkowski et al. (2004) and Häberle et al. (2009) discuss different ways of obtaining a partial ordering of patients based on a multivariate metric or ordinally scaled observations. A univariate score for each patient is calculated from a pair-wise comparison of patients based on that ordering as the basis for statistical inference. In the simplest approach, the multivariate outcome of a patient is considered superior to that of another patient if all component-wise differences are non-negative and one difference is strictly positive. The outcome is inferior if all differences are non-positive and at least one is strictly negative, otherwise the two patients are not comparable. For each patient, a score can be calculated as the number of all other patients in the sample with superior outcome minus the number of all other patients with inferior outcome. A t-test or a permutation test can then be applied to the scores. A significant (one-sided) test based on multivariate ordering allows for the interpretation that for two patients randomly assigned to treatment and control, the patient receiving treatment has on average a better outcome than the control patient. The approach is quite generic and can be extended to censored observations (Buyse, 2010; Rauch et al., 2014a).

O’Brien (1984) also suggested a non-parametric test, in which observations of each variable are ranked across groups and inference is based on rank sums of each patient. This rank ordering typically results in a smaller number of ties and may provide larger power than tests based on the pair-wise multivariate order (Häberle et al., 2009). Under the non-parametric null hypothesis the multivariate distributions in both groups are identical. However it is often of interest to detect differences in location between groups while deviations in scale are considered less relevant. For O’Brien’s test Huang et al. (2005) suggest a solution in which consistent estimates for the variance of the difference in mean ranks are applied. Simulation results for 2 and 10 dimensional outcomes and sample sizes as small as 20 per group show type I error rate control of the improved tests.

Ramchandani et al. (2016) subsume the approaches above under a general framework of U-statistics allowing for derivations of asymptotic distributions and sample size formulas. For special cases, including O’Brien’s rank sum test, the global U-statistic can be written as a sum of endpoint-specific U-statistics. Weighted sums may be defined to reflect utilities or to optimize the power for a particular alternative.

For categorical endpoints a finite set of all possible outcome combinations can be obtained. Claggett et al. (2015) proposed to order such outcome categories based on medical considerations. This results in a new univariate ordinal outcome measure that may be analyzed by appropriate methods for this single endpoint. Bathke et al. (2008) studied ANOVA-type, Lawley–Hotelling-type and Bartlett–Nanda–Pillai-type statistics of rank transformed multivariate outcomes to obtain non-directional tests. ANOVA-type statistics performed best for positive and Lawley–Hotelling-type tests for negative correlations. They developed finite sample approximations of the null distribution of these statistics with good results according to a large simulation study.

A general concept for ordering multivariate data points with respect to the center of a distribution is data depth, with the half-space depth (Tukey, 1975) and the simplex depth (Liu et al., 1990) being the best known examples. The half-space depth of a point is defined as the minimum of the number of points in any half-space resulting from a separation of the sample space by a hyperplane through the point of interest. The simplex depth is the number of possible simplex regions with vertices in observed data points containing the point of interest. Tests for equality of location or scale of two multivariate distributions based on the notion of depth have been suggested (Chenouri and Small, 2012; Chenouri et al., 2011), however, for directed alternatives, the ordering methods considered above (Claggett et al., 2015; Häberle et al., 2009; O’Brien, 1984; Wittkowski et al., 2004) appear to be easier to interpret. If the main goal of a study is to describe or visualize the multivariate distribution of multiple outcome measures, though, depth-based methods provide robust estimates of the center and the quantiles (Donoho and Gasko, 1992; Liu et al., 1999).

Klingenberg et al. (2009) propose a test for the null hypothesis of simultaneous marginal homogeneity of multiple ordinal endpoints between two groups versus a directed alternative. They construct a test statistic as weighted sum of endpoint-specific mean score differences, where the weights are derived from a covariance estimate of the summands. In small samples, the covariance structure has to be restricted to obtain stable estimates. The reference distribution of the test statistic is found by permutation, such that restrictions to the weighting co-variance matrix estimate may affect the efficiency but not the type I error rate of the test. Importantly, under the assumption that the multivariate ordinal outcome in one group is stochastically larger or equal to that in the other group, the null hypothesis of simultaneous marginal homogeneity is equivalent to the null hypothesis of identical joint distributions, which justifies the use of a permutation test (see the discussion in Section 4.2 on the assumptions required for permutation tests).

Summary of small sample aspects

Methods of multivariate ordering do not require asymptotic arguments or distributional assumptions other than at least ordinal data to combine the information from multiple endpoints into a new univariate measure. The combined outcome may then be analyzed by a non-parametric test, controlling the type I error rate also with small samples. Furthermore, the scores resulting from ordering ameliorate the impact of extreme outliers by construction due to floor and ceiling effects inherent to ordinal measures. Therefore applying approximate asymptotic tests to such scores will in most cases be appropriate. With small samples, multivariate orderings that generate too many ties should be avoided, as the ties may severely affect the power of the subsequent between-groups comparison. External information from other trials or expert opinion can be used to construct an ordering with high sensitivity for a particular study to enhance power, similar to choosing a test for a particular directed alternative with continuous data.

3.3 Binary endpoints

For comparing two vectors of multiple binary proportions, Wald and score tests analogous to Hotelling’s $T^2$ test have been proposed by Agresti and Klingenberg (2005). The test statistic is defined as a quadratic form of the observed differences in marginal proportions and the inverse of a covariance matrix estimate. Here the covariance matrix estimate is the sum of group-wise estimates in case of the Wald test, whereas a pooled-sample estimate is applied for the score test. Both tests use a chi-squared distribution to approximate the sampling distribution of the test statistic. In simulations with sample sizes as low as 50 per group this approximation was found to be accurate for the score test but not for the Wald test. To explicitly test the null hypothesis of identical joint distributions, a permutation test may be used, similar to the method by Klingenberg et al. (2009) discussed in Section 3.2.

Whitehead et al. (2010) combine information from multiple binary endpoints similarly to O’Brien’s GLS test. They use a weighted sum of the marginal score statistics for the tests of equality of two groups where the weights are derived from a sample estimate of the covariance matrix of the statistics. Their approach may also be applied to ordinal data under a proportional-odds model for each endpoint. A stratified analysis, accounting for categorical covariables, is possible by performing the calculations for each stratum and then combining the statistics. Alternatively, a logistic regression model can be fitted using a generalized estimating equation (GEE) approach to account for correlations between endpoints (Baraniuk et al., 2012). Global test statistics for such models have also been derived (Mascha and Imrey, 2010). Simulations show that for a total sample size of 100 patients the test by Whitehead controls the type I error rate while the Wald test applied to the estimator in the GEE approach shows some inflation. For large sample sizes the tests perform similarly (Whitehead et al., 2010). This comparison may be criticized, though, for not using a score test for the GEE model too, which has better small sample properties (Guo et al., 2005).

For the test decision in clinical trials, Whitehead et al. (2010) suggest to reject the null hypothesis of equal marginal proportions in favor of the alternative of at least one proportion being larger under treatment if the weighted sum score statistic exceeds some critical value and in addition all individual score statistics are greater than zero. This strategy prevents a positive test decision if the observed effect in one of the variables points in the unfavorable direction. Furthermore, by narrowing the rejection region this approach allows one to apply a smaller critical value what may result in a larger power in case of a treatment effect in all endpoints.

The approaches discussed so far in this section require the estimation of a potentially large number of nuisance parameters. Especially for the case of multiple binary endpoints and a small number of observations, the data may be too sparse to reliably estimate all pair-wise covariances individually, necessitating a restricted covariance structure.

Another method to overcome the problem of unknown nuisance parameters is to perform tests conditional on a sufficient statistic. One of the probably best known examples is Fisher’s exact test for 2 × 2 tables. Furthermore, if some simplifying assumptions on the data generating process are justified, the model complexity can be reduced and small sample inference is possible. Han et al. (2004) model the relationship of the dose of a drug and a set of binary adverse events with an exponential family model due to Molenberghs and Ryan (1999). For this example the authors argue in favor of assuming a common correlation between all endpoints in the model and a common effect of the dose level on all endpoints. The intercepts and the correlation parameter in the model were accounted for by conditioning on their sufficient statistics and an exact conditional test and confidence intervals for the regression slope were derived.

When comparing two treatment groups with respect to multiple binary endpoints, the exact conditional joint distribution of marginal success numbers can be found by permutation (Westfall and Young, 1989). For this joint distribution a multivariate rejection region can be defined to test the global null hypothesis of no overall treatment effect. Using a multivariate null-distribution, the inherent conservatism resulting from discreteness can be largely alleviated by allowing for rejection regions that are not restricted to some particular shape (Ristl et al., 2018; Rom, 1992). Numeric optimization algorithms can be applied to find multivariate rejection regions of arbitrary shape that result in exact tests with maximal exhaustion of the nominal type I error rate or maximal power under a pre-specified alternative (Ristl et al., 2018). These tests are in particular advantageous for small sample sizes when asymptotic tests fail to control the type I error rate and non-optimal exact tests would have low power due to discreteness.

An alternative approach to address the problem of unknown nuisance parameters that alleviates the discreteness and conservatism of exact conditional tests is to consider the distribution of a test statistic for all possible values of the nuisance parameter (or some subset of plausible values) and to take the supremum of the resulting p-values. Barnard (1947) used this approach to develop unconditional exact tests to compare two binomial proportions. In a related approach, Boschloo proposed to perform Fisher’s exact test at an elevated significance level such that the nominal level is still controlled for all possible values of the nuisance parameter. This results in a uniform improvement of Fisher’s exact test in terms of power. Applying the same idea to multiple binary endpoints is computationally challenging due to the larger number of nuisance parameters needed to specify the joint distribution. Also, with a larger number of nuisance parameters, a test based on maximization may be more conservative than a test based on conditioning (Mehta and Hilton, 1993).

Summary of small sample aspects

When relying on asymptotic tests for multiple binary endpoints with small to moderate sample sizes, approaches based on score tests show superior performance in terms of type I error rate control compared to Wald tests (Agresti and Klingenberg, 2005; Whitehead et al., 2010). This might be due to the fact that the score test statistic is calculated under the restriction of the null hypothesis which reduces the number of nuisance parameters in this setting. However, (multivariate) normal approximations for statistics of multiple binary endpoints may require simplifying model assumptions when the sample size is too small to estimate a large number of nuisance parameters. When aiming for strict type I error rate control, similar to Fisher’s exact test for a single binary endpoint, exact conditional tests can be derived from the joint distribution of multiple binary endpoints. In contrast to the single endpoint case, conservatism due to discreteness of the reference distribution can be alleviated in the multivariate setting by defining appropriate multivariate rejection regions.

3.4 Time-to-event endpoints

In clinical trials time-to-event endpoints are often the outcome variables of interest. Typical endpoints are death or specific causes of death, but also non-fatal events like progression of disease or hospitalization. Test statistics from proper parametric or non-parametric models for censored data may in principle be combined (also with other outcome measures) using the methods discussed above, however the estimation of covariance matrices, which is crucial for many methods, may be more involved. Wei and Lachin (1984) showed that the vector of several two-sample log-rank test statistics applied to multiple survival endpoints is asymptotically multivariate normal and derived an estimator for the covariance matrix. They used these results to construct a chi-squared statistic for the non-directed global test and a sum statistic analogous to O’Brien’s OLS statistic for a directed global test. Extensions to tests from proportional hazards models, robust variance estimators and weighted sums similar to O’Brien’s GLS statistic have been proposed (Lachin and Bebu, 2015).

In settings where one event, typically death, precludes the observations of other events, methods for the analysis of competing events can be applied. Luo and Turnbull (1999) derive approximately multivariate normal test statistics for the comparison of two groups with respect to cumulative incidence or cause-specific hazard functions for competing events. Simulations for sample sizes of 50 patients per group, two competing events with exponential failure times and censoring rates up to 50%, that is on average 25 observed events per group, show good accuracy of the distributional approximation. This suggests that the standard methods for the analysis of competing events are valid also for lower number of events. However, if event rates are low, still a considerable number of patients may be required to reach a sufficient number of events.

Yin et al. (2003) studied the inference for quantiles of the marginal survival functions of multiple, possibly correlated, survival endpoints. They show asymptotic multivariate normality of estimators of the same marginal quantile for the survival functions of multiple endpoints. A method using kernel smoothing and a bootstrap approach are described for estimation of the covariance matrix. In a simulation study the coverage probability of the resulting confidence intervals (based on normal approximations) for quantiles from exponential and Weibull distributed survival times was found to be close to the nominal level for sample sizes of 200 and no censoring. However for censoring rates of 20% or 40% or smaller sample sizes of 100 or 50, the coverage rates were mostly 1 to 2 percentage points too low.

Methods of multivariate orderings can be applied also to censored data if a pair-wise ordering can be defined. For univariate analyses, a pair-wise ordering is the basis for Harrell’s well-known concordance index (Harrell et al., 1996). For multiple time-to-event endpoints one approach that avoids large numbers of non-comparable pairs is to order the endpoints by clinical importance first. A pair of patients is then scored using the most important endpoint for which they are comparable and inference is based on “win-ratio” type statistics that are based on the number of pairs in which the outcome of either the treated or the untreated patient is superior (Buyse, 2010; Pocock et al., 2012; Rauch et al., 2014a). Luo et al. (2015) and Dong et al. (2016) investigated the distributional properties of different “win-ratio” type statistics and provide consistent estimates of the variance of their limiting normal distributions. Simulations in Dong et al. (2016) show that the normal approximation of the logarithm of the win ratio is satisfactory with sample sizes as small as 25 per group.

A widely applied method to combine multiple survival endpoints in clinical trials is to define a composite endpoint as the time to the first event out of a pre-defined set of possible events. Especially with small trials, this measure can increase the event rate, which may result in a larger power of the study. However, the actual treatment effect in terms of the composite endpoint will depend on the effect and on the baseline event rate of each component endpoint. If a component with high overall event rate but a small difference between treatments is added, the effect of the other components may be masked and the trial may become inconclusive. See Ferreira-González et al. (2007) for a detailed review and discussion on advantages and disadvantages of composite survival endpoints.

As a significant result on a composite endpoint is not readily extended to the individual components, interpretation of a test for a composite endpoint is only straight forward, if homogeneous effects for all components are assumed. In all other cases a multiple testing strategy should be applied to enable inference on the individual endpoints as is further discussed in Section 4. The overall hypothesis on the composite endpoint and elementary hypotheses on one or several important components can be included in such a framework (Rauch and Beyersmann, 2013; Rauch and Kieser, 2013; Rauch et al., 2014b; Schüler et al., 2014).

If one component is time to a terminal event precluding the subsequent observation of other endpoints, marginal estimates of the component specific treatment effect can be severely biased (Rosenkranz, 2011). Methods for competing risks or models for a joint distribution of the components provide more reliable evaluation of the component specific effects (Fine and Gray, 1999; Fine et al., 2001; Rosenkranz, 2011).

Summary of small sample aspects

Due to censoring, achieving a sufficient effective sample size in terms of the number of events may not be possible with a limited number of patients. Combining multiple time-to-event endpoints in a composite endpoint or in terms of multivariate orderings utilizes more information and provides larger power. However, in both approaches the observed effect may depend on the censoring distribution and may be dominated by high rates of less important event types, such that the interpretation of results may be ambiguous (Luo et al., 2015; Rauch et al., 2014a). More complex methods for the analysis of multiple time-to-event outcomes typically use asymptotic approximations, which may have inflated type I error rates in small samples.

4 Multiple testing

Following rejection of the global null hypothesis of no treatment effect on any endpoint, it is natural to ask for the effect in specific endpoints. If the effect of individual endpoints is to be tested in a confirmatory clinical trial, control of the familywise type I error rate (FWER) in the strong sense is required (European Medicines Agency, Committee for Proprietary Medicinal Products, 2002). This means that the probability to reject at least one true null hypothesis in the family of considered hypotheses must not exceed the nominal significance level $\alpha$, regardless of how many and which null hypotheses hold. In small samples it may be appealing to relax this standard in favor of higher power and control the probability for at least $k>1$ false rejections, the so-called k-FWER (Lehmann and Romano, 2005; Romano and Wolf, 2007) or gFWER (Xu and Hsu, 2007), or the false discovery rate (Benjamini and Hochberg, 1995) (FDR). However, at the moment these approaches are less common and we will therefore focus on approaches that control the FWER.

A general concept to construct multiple testing procedures with strong FWER control is the closed testing principle (Marcus et al., 1976). To perform a closed test, for all elementary null hypotheses and all corresponding intersection null hypotheses a local level $\alpha$ test is specified. The closed test then rejects an elementary (or intersection) null hypothesis at multiple level $\alpha$, if all intersection hypotheses it is contained in are rejected locally. The closed test controls the FWER in the strong sense. Thus, following rejection of the global null hypothesis, the closed testing procedure allows one to test individual endpoints as well as subsets of endpoints.

An alternative concept is the partitioning principle (Finner and Strassburger, 2002; Hayter and Hsu, 1994; Stefansson et al., 1988): The parameter space is divided in disjoint sets and the null hypothesis corresponding to each set is tested by a level $\alpha$ test. The partitioning approach is a useful tool to account for specific restrictions, for example if testing a hypothesis depends on the result of a test for another hypothesis, and to construct confidence intervals corresponding to multiple testing procedures.

A multiple testing procedure is consonant, if the rejection of the global intersection null hypothesis also leads to rejection of at least one individual null hypothesis (Gabriel, 1969). A consonant multiple testing procedure avoids to conclude a treatment effect in some endpoint without being able to identify in which one. However, for some alternative hypotheses, non-consonant multiple testing procedures may be more powerful to reject the global null hypothesis. Especially in the small sample case, this potential trade-off between the power for the global and elementary hypothesis tests has to be considered when choosing a specific test.

Lehmacher et al. (1991) simulated the power of the closure of O’Brien’s OLS and GLS tests under alternatives with equal effects in all endpoints. These tests have superior power for the rejection of intersection and individual hypotheses compared to the Bonferroni-Holm procedure. However, the scenarios covered only alternatives for which O’Brien’s OLS test is especially powerful. The closed OLS and GLS tests are not consonant, but the rejection of an intersection null hypothesis for a subset of endpoints is a valuable finding in itself. Bittman et al. (2009) provided a consonant version by removing all points from the rejection region that lead to non-consonant decisions and in turn increasing the rejection region by including points that lead to consonant test decisions. This modification is a uniform improvement with respect to the rejection of individual null hypotheses. For the case of two endpoints, a comprehensive comparison of these two procedures with the Bonferroni test and the Simes test (see Section 4.1) is given by Su et al. (2012). For unequal effect sizes, their simulations show that the O’Brien based consonant closed test is considerably more powerful for the rejection of the global null hypothesis than the original non-consonant version. For homogeneous effects, the non-consonant test is optimal. Simulations with more than two endpoints are outstanding.

4.1 Methods based on the marginal null distributions

Taking the maximum over standardized individual test statistics (called the maxT statistic) is a valid way to aggregate information from multiple endpoints. If the test statistics are not on the same scale, each statistic can be transformed into a p-value and the minimal p-value (called the minP statistic) can be used to test the global null hypothesis of no effect in any of the endpoints. A critical boundary for the minP statistic can be derived from the Bonferroni inequality. In case of $n$ endpoints, the resulting Bonferroni test rejects the global null hypothesis if the minimum p-value is below $\alpha /n$. Likewise the elementary hypotheses of no treatment effect in an individual endpoint can be rejected, if the respective p-value is below $\alpha /n$. The Bonferroni test controls the familywise error rate in the strong sense at level $\alpha$. The procedure ignores information on the correlation between endpoints which is attractive if the correlation is unknown. On the other hand, this robustness comes at the cost of possibly conservative critical boundaries. The Bonferroni test exhausts the significance level only under a specific least favorable configuration where the probability that two (or more) test statistics exceed the critical boundary simultaneously is zero.

An improvement that does not require additional assumptions on the dependence of test statistics is the Bonferroni-Holm test (Holm, 1979). Denoting the ordered p-values by $p_{(1)}\le p_{(2)}\le ...\le p_{(n)}$ it rejects the null hypothesis corresponding to the smallest p -value if $p_{(1)}\le \alpha /n$. If this hypothesis can be rejected, the next is rejected if $p_{(2)}\le \alpha /(n-1)$ and so on. The procedure stops if a hypothesis cannot be rejected. Posch and Futschik (2008) developed a testing procedure where it is assumed that patients sequentially enter the trial and a test decision is possible each time the data on a new subject has become available. The procedure uniformly improves the Bonferroni-Holm test in terms of power without increasing the maximum sample size, regardless of the dependence structure of the test statistics.

In weighted Bonferroni tests each marginal p-value is compared to an individual local level ${\alpha }_i\in [0,\alpha ]$, with ${\sum }_{i=1}^n{\alpha }_i=\alpha$. Thus different weights are assigned to the individual hypotheses, such that effects in highly relevant endpoints can be given a higher chance to be rejected. Alternatively, endpoints with smaller expected effect sizes can be tested at larger local levels in order to optimize the expected number of rejected hypotheses. Westfall et al. (1998) derived optimal weights for the latter case depending on prior assumptions on the true effect sizes. When a Bonferroni correction is applied to tests with discrete test statistics, weights may be chosen such that the Bonferroni bound on the type I error rate is as close as possible to the nominal level and conservatism is reduced (Ristl et al., 2018; Westfall and Troendle, 2008).

Applying the closed testing principle (Bauer, 1991; Hommel et al., 2007) or the partitioning principle (Liu and Hsu, 2009), sequentially rejective testing procedures can be constructed that reflect the relevance and structure between endpoints onto the testing procedure. A simple example for a sequentially rejective weighted Bonferroni test is the hierarchical (also called “fixed sequence”) test in which the hypotheses are tested at full level $\alpha$ in a pre-defined order. Testing stops as soon as a hypothesis cannot be rejected. The hierarchical test is the multiple testing procedure with the largest power to reject the first hypothesis in the order and is preferable if this constitutes the main aim of the study. Another, more complex example for sequentially rejective weighted Bonferroni tests are gate-keeping procedures where secondary endpoints can only be tested after the null hypotheses for the primary endpoints have been rejected (Dmitrienko et al., 2003, 2008, 2007; Huque and Alosh, 2012; Klinglmüller et al., 2014b; Maurer et al., 1995; Westfall and Krishen, 2001). Sequentially rejective Bonferroni test procedures can be conveniently created by graphs (Bretz et al., 2009b, 2011; Burman et al., 2009). In case that information on the joint distribution of a subset of endpoints is available, Bonferroni tests and parametric tests (see Section 4.2) may be combined in a (weighted) closed testing approach, resulting in increased power (Xi et al., 2017).

Another improvement of the Bonferroni procedure is a closed test where the intersection hypotheses are tested with the Simes test (Simes, 1986) which rejects the global null hypothesis if $p_{(k)}\le \alpha k/n$ for some $k$. However, Simes’ test is not a level $\alpha$ test in general, but conservative under appropriate assumptions on the distribution of the test statistics, for example multivariate total positivity of order two (Sarkar, 1998) or multivariate normal respectively t-distributed with non-negative correlations and $\alpha \le 1/2$ (Block et al., 2013). With two endpoints, the trimmed Simes test (Brannath et al., 2009b) and the uniformly more powerful diagonally trimmed Simes test (Ristl et al., 2016) provide strict type I error rate control for multivariate normal or multivariate t-distributed test statistics with arbitrary correlation. The Hochberg (1988) and Hommel (1988) procedures are short-cuts of the closure of the Simes test. Both are uniformly more powerful than the Bonferroni-Holm procedure but rely on the same assumptions on the joint distribution as the Simes test.

Exact marginal tests for multiple categorical endpoints

The exact distributions of test statistics and p-values from categorical data are discrete which can result in conservative tests, especially for small samples. While randomized tests could, in principle, alleviate this problem, they are hardly acceptable for the analysis of clinical trial data because, with the same observed data, application of the same test can lead to different conclusions. As a compromise, the use of mid-p-values has been proposed (Agresti, 2001). The mid-p-value is the probability for a more extreme event than the one observed plus half the probability of the observed event. This approach results in actual type I error rates closer to but not necessarily below the nominal significance level.

When testing multiple categorical endpoints with a maximum-type test, the level can often be better exhausted than for univariate tests. Tarone (1990) proposed an improvement of discrete exact Bonferroni tests that is best illustrated for the comparison of two treatments and multiple binary endpoints. Discrete tests for some endpoints may never reject because the lowest possible p-value is still above the Bonferroni adjusted local level of significance. These endpoints do not contribute to the test decision and have not to be considered in the Bonferroni correction. Therefore a larger adjusted level can be applied. For Tarone’s test, the smallest positive number $k$ is selected, such that maximally $k$ tests can reach significance at level $\alpha /k$. Since $\alpha /k$ can be considerably larger than the original Bonferroni adjusted level, the power of the global maximum-type test is improved. Tarone’s procedure has been criticized because of its lack of $\alpha$-consistency, i.e. the test decision is not monotone in $\alpha$. Hommel and Krummenauer (1998) and, independently, Roth (1999) improved Tarone’s test and defined a procedure that controls the FWER in the strong sense, which is $\alpha$-consistent and even more powerful.

4.2 Methods based on the joint distribution

If the joint distribution of the individual test statistics is known, exact critical boundaries can be computed which are less conservative than boundaries derived by the Bonferroni inequality. Furthermore, if the sample sizes are large enough, the joint null distribution of many test statistics can be approximated by a multivariate normal distribution. If in addition a consistent estimate for the covariance matrix is available, inference can be based on the asymptotic joint distribution (Hothorn et al., 2008; Lafaye De Micheaux et al., 2014). Type I error rate control of these tests holds asymptotically, however recent work in the related field of multiple contrast tests suggests that in many cases a satisfactory small sample performance can be achieved if the multivariate normal distribution is replaced by a multivariate t-distribution (Hasler et al., 2013; Hasler and Hothorn, 2011).

When sample sizes are small, permutation tests provide a viable alternative (Boyett and Shuster, 1977). In the minP test by Westfall and Young (1993) group labels are permuted randomly between the observational units. For each random permutation, the minP statistic is calculated. The empirical distribution from a large number of permutations provides a p-value for the observed minP statistic. If the p-value is below $\alpha$, the global null hypothesis is rejected. If all hypotheses are rejected whose local p-values (also obtained by permutation) are below the $\alpha$ quantile of the permutation distribution of minP values, the single step minP test results. This test controls the FWER in the strong sense if the so called subset-pivotality condition holds, which essentially states that the joint null distribution of any subset of test statistics does not depend on the distribution of the remaining test statistics. An improvement of the single step minP test is closed tests where each intersection hypothesis is tested by a minP test. Since permutation is applied at the level of the observational unit, the correlation structure between the multiple endpoints respectively their local test statistics is preserved. As an alternative to permutation tests, bootstrap methods can be used to approximate the null distribution. The bootstrap approach is especially suitable for models with higher complexity than that of a mere between groups comparison, however it is not an exact method. Also additional steps, e.g. centering of the data, may be required to provide resampling under the null hypothesis (Westfall, 2011).

Choosing the maximum or minimum as a global test statistic results in a consonant procedure and provides good power if there is a strong effect in at least one endpoint. Still, resampling approaches are not limited to maximum or minimum statistics and other choices may provide better power, depending on the true alternative.

Logan and Tamhane (2001) propose a bootstrap resampling procedure for testing multiple endpoints in which the minP test is supplemented by a global test, exemplified by O’Brien’s OLS test, aiming at combining the benefits of both test statistics. For each intersection hypothesis, the test decision is based on the minimum of the corresponding marginal p-values and the p-value calculated for the OLS test. The authors argue that the significance level adjusted for this combined minimum p-value will not be much smaller than the level for the minP test, due to the positive correlation between the marginal p-values and the OLS test p-value. Thus, the combined minimum should provide the advantages of both procedures at only a small cost. This conjecture was confirmed by a simulation study for a comparison of two groups with 50 observational units each and four or eight endpoints.

The “truncated product method” also follows the idea of balancing between the merits of a minP statistic and an average statistic (Zaykin et al., 2002). Only those p-values are included in the combination that are below some pre-set threshold. The null distribution of the resulting combination statistic can be found by resampling, like in the minP test. The approach was extended by Sexton et al. (2012) by considering different choices for the threshold simultaneously. In particular, each observed p-value may be used as potential threshold, resulting in a family of nested subsets of p-values to combine. The rationale is, that the optimal threshold will be included in any case, and this advantage may outweigh the additional multiplicity that is introduced. For the combination function value of each subset, a p-value is calculated by permutation. The overall test statistic is formed as minimum over the subset-derived p-values and the permutation distribution of this statistic is used for the final test decision. Simulations suggest that this approach is particularly powerful if only a part of all null hypotheses is false.

When comparing treatment groups in a parallel group design, the minP test and other resampling based tests can be applied to binary or categorical data as well (see Section 3.3). Since resampling of subjects accounts for the dependence structure between endpoints within subjects, these procedures can be more powerful than marginal approaches such as Tarone’s test and its improvement (Ristl et al., 2018; Westfall and Wolfinger, 1997).

Summary of small sample aspects

Small sample properties of the closed testing procedures are inherited from the local tests employed to the intersection hypotheses. Similar to the discussion in Section 3, approximate methods based on a multivariate t-distribution or resampling methods are preferred over asymptotically valid methods in studies with small sample sizes. Without any further assumptions, the null hypothesis for a multivariate permutation test is that of equal joint distributions of the multiple endpoints in all treatment groups. Equivalently, the permutation test can be seen as a test for exchangeability of subjects between treatment groups with respect to the studied endpoints (Calian et al., 2008; Westfall and Troendle, 2008; Xu and Hsu, 2007). This implies that in principle a significant result of, for example, the minP test can result from different correlation structures while the marginal distributions are identical (Calian et al., 2008; Westfall and Troendle, 2008). Bootstrap methods rely on the approximation of the true distribution through the empirical sample distribution, which may not be accurate enough with very small samples.

4.3 Adaptations to tests for co-primary endpoints

For some diseases (like Alzheimer’s dementia) efficacy of a treatment can only be concluded if the effect is shown for several endpoints, which are then referred to as co-primary. The standard approach to this problem is to test each individual hypothesis at level $\alpha$ and conclude efficacy only if all of these tests are significant. The power of this global test is lower than the power of each individual endpoint test and it decreases with the number of co-primary endpoints. This will especially affect small clinical trials if one is not able to increase the sample size to achieve the required power.

The null hypothesis of a co-primary endpoint test is the union of all individual null hypotheses. The least favorable configuration in this union is any point with zero effect in one endpoint and an infinite effect in the others. Since in reality treatment effects cannot be arbitrarily large, it is sufficient to consider parameter configurations where the effect sizes are bounded. This allows to perform the individual tests at a local level larger than $\alpha$ and still control the type I error rate (Chuang-Stein et al., 2007; Kordzakhia et al., 2010; Offen et al., 2007). For large sample sizes the extent of the increase is negligible, for small sample sizes in combination with rather strict assumptions on the maximal effect some gain can be achieved. Alternatively one could control an average type I error rate using prior weights for each point in the null space (Chuang-Stein et al., 2007). For uniform weights, averaging the type I error rates of the most extreme points in the unrestricted null space and the type I error rate of the point of no effect in any endpoint provides an upper bound. The latter approach results in a reduction of sample size in the order of 10% to 30% for two to five moderately correlated co-primary endpoints when a power of 80% is aimed for. However, the determination of the increased local levels requires knowledge of the joint distribution of the test statistics. Kordzakhia et al. (2010) propose a compromise between slight relaxation and strict type I error rate control. In their approach the significance level for an individual endpoint is adjusted upward only if the treatment effect is highly significant in one or more of the remaining endpoints. This procedure controls the type I error rate at a level slightly above $\alpha$. However, this value can be chosen such that the maximal type I error rate over an restricted null space or an average type I error rate is controlled exactly at level $\alpha$. For small clinical trials the features of this procedure may be an acceptable compromise between slight relaxation of strict type I error control and increased power to conclude efficacy for co-primary endpoints.

Fallback tests for co-primary endpoints augment the standard co-primary endpoint test by additional rejection rules for elementary or intersection hypotheses, while retaining FWER control (Ristl et al., 2016). For two endpoints a diagonally trimmed Simes test controls the FWER for bivariate normal or t-distributed test statistics with arbitrary correlation. This test rejects both null hypotheses if both marginal p-values fall below $\alpha$ and otherwise allows for rejection of an elementary null hypothesis if the respective p-value is below $\alpha /2$ and the sum of both p-values is not greater than 1. Simulations for scenarios with a true effect in either one or both endpoints and different correlations between the endpoints show superior power of this procedure over the Bonferroni-Holm test and the minP test (which are not fallback tests) with the exception of scenarios with large correlations and heterogeneous effect sizes. For three co-primary endpoints a fallback test can be derived for multivariate normal test statistics. Note that also closed testing procedures based on the Simes test, such as the Hochberg and Hommel procedures, are fallback tests for co-primary endpoints that control the FWER in the strong sense under dependence structures where the Simes test is conservative (Block et al., 2013; Sarkar, 1998).

The calculation of sample size and power for tests of co-primary endpoints, including the particular setting of continuous and binary co-primary endpoints, was studied in detail by Sozu et al. (2012) and Sugimoto et al. (2012).

4.4 Non-inferiority in all and superiority in some endpoints

In some situations it may be sufficient to show superiority in one and at least non-inferiority in the remaining endpoints. This strategy offers a more stringent conclusion than a superiority test of the global null hypothesis of no treatment effect in any endpoint (Bloch et al., 2007, 2001; Logan and Tamhane, 2008; Perlman and Wu, 2004; Röhmel et al., 2006; Tamhane and Logan, 2004). The primary null hypothesis in this setting is the union of all individual non-inferiority null hypotheses and of the intersection of all superiority null hypotheses. The first step for testing this combined hypothesis are marginal non-inferiority tests for all endpoints, all of which have to be significant at the local level $\alpha$. Next a global test for superiority is applied. This test may account for the fact that some outcomes in the rejection region of the superiority test will contradict overall non-inferiority and not contribute to the type I error rate.

Bloch et al. (2001) proposed the use of Hotelling’s $T^2$ test as the global superiority test. The $T^2$ test statistic is set to zero if the test for overall non-inferiority is not significant. The actual critical values are calculated as empirical quantiles of the test statistics from bootstrap samples. Perlman and Wu (2004) noted that this test can become non-monotone in the effect sizes because of the circular shape of the $T^2$ test rejection boundary. They suggest to use a one-sided likelihood ratio test instead, which results in a monotone test with otherwise similar properties. In the same framework, Tamhane and Logan (2004) investigated the use of the maximum test statistic to decide on the superiority intersection hypothesis. The critical boundary for this test, too, is found by a bootstrap approach. Simulation results show a small power advantage of the likelihood ratio test over the maximum test. The bootstrap approach for these tests was generalized by Bloch et al. (2007) to allow not only for tests of mean differences but for general functionals of distributions, such as a ratio of means.

In all these tests the critical boundary of the superiority test depends on the choice of the non-inferiority margin such that a larger non-inferiority margin makes rejection of the superiority null hypothesis more difficult. This property was criticized by Röhmel et al. (2006) and they suggested to rather use an unmodified superiority test. In defense, Logan and Tamhane (2008) pointed out that rejection of the overall non-inferiority null hypothesis at a lower non-inferiority margin conveyed more information on a possible positive effect in some endpoint and hence it was natural that the consecutive superiority test could reject more easily compared to a test with a larger non-inferiority margin.

5 Clinical trial examples with multiple endpoints

In this section we briefly discuss four exemplary small sample studies to illustrate the application of selected methods described in this review.

Example 1: Charcot-Marie-Tooth disease type 1A. A clinical trial in Charcot-Marie-Tooth disease type 1A (CMT1A) (Attarian et al., 2014), a rare orphan inherited neuropathy, is an example of a study in a rare disease with two efficacy endpoints. This randomized, double-blind and placebo-controlled phase 2 study compared 3 doses of a combination of baclofen, naltrexone and sorbitol (PXT3003) with placebo in patients with CMT1A. The total sample size was 80, with 19 to 21 patients per group. The Charcot-Marie-Tooth Neuropathy Score (CMTNS) and the Overall Neuropathy Limitations Scale (ONLS) were the two primary efficacy endpoints. Differences between treatment groups were assessed by analysis of covariance on the log-transformed values by adjusting for baseline. The results of the comparison of high dose (HD) and placebo indicated an improvement of 5.5 percentage points $(p=0.16)$ for CMTNS and 14.4 percentage points $(p=0.043)$ for ONLS. The comparison of both endpoints by O’Brien’s OLS test confirmed a global improvement of the HD group over placebo $(p=0.036)$. While this means to reject a global intersection null hypothesis of no effect, application of the closed testing principle allows to conclude an effect for ONLS with FWER control at the 5% level.

Example 2: Trial in panic disorder and agoraphobia patients. A randomized clinical trial in 46 patients with a diagnosis of panic disorder and agoraphobia was reported by Broocks et al. (1998). The study participants were assigned equally to clomipramine (an antidepressant), regular aerobic exercise, or placebo. For the efficacy assessment four clinical and self-rated measures were taken repeatedly 7 times for 10 weeks. A group-wise comparison of each of the scales could be done separately for every week, but this would result in at least 28 tests. The analysis in the paper was a two-factor repeated measures analysis of variance. This relieves the multiplicity issue but does not account for the direction of the treatment effect. Bregenzer and Lehmacher (1998) suggested to use O’Brien’s OLS or GLS test to answer the question of whether one of the treatments is superior with respect to all endpoints at all times. When they simultaneously analyzed all four scales at all time points, the comparison of exercise and clomipramine with the OLS rank test resulted in a statistically significant difference ($p=0.022$).

Example 3: Trial in advanced colorectal cancer patients. In a randomized trial in advanced colorectal cancer 420 patients, 210 in each arm, received a standard regimen of 5-fluorouracil and leucovorin either with or without addition of oxaliplatin (De Gramont et al., 2000). Two time-to-event variables were considered as efficacy endpoints: Overall-survival and progression-free survival, the latter defined as the time from randomization to objective disease progression or death. As the trial showed a significant benefit of oxaliplatin for progression-free survival, but failed to reach significance for the effect of oxaliplatin on overall survival, interpretation of results was difficult. A method to estimate an overall treatment benefit for this example using pairwise comparisons of prioritized outcomes was proposed by Buyse (2010). In this approach a patient on oxaliplatin was considered to have a better treatment outcome than a patient on standard regimen if his or her overall survival was longer or, if that could not be decided due to censoring, if progression free survival was longer. All possible pairs between the two groups were compared according to this rule. In 51.7% of these pairs the patient receiving oxaliplatin had the more favorable outcome, in 36.9% the standard regimen was preferable and the remaining 11.4% remained undecided. Buyse (2010) presents the difference of 14.8% as effect measure and tests the null hypothesis of zero difference via a permutation test, resulting in a p-value of 0.0054 and suggesting a clear benefit for oxaliplatin.

Example 4: Late-onset Pompe’s disease. A randomized, placebo-controlled trial of alglucosidase alfa for the treatment of late-onset Pompe’s disease, which is a rare, progressive neuromuscular disease, was conducted by Van Der Ploeg et al. (2010). The two primary efficacy endpoints, measured repeatedly over time, were 6-minute walking distance and percentage of predicted forced vital capacity. The final sample size of 60 patients on active treatment and 30 patients on placebo was chosen in an adaptive way to allow for 90% power to detect an increase in the between group difference of the 6-minute walking distance of 3.75 meters per month using a linear mixed model. Due to unmet model assumptions for the mixed model, analysis of covariance models for the last observed values and accounting for baseline values were used for the main analysis of the two primary endpoints. To control the family-wise type I error rate, a fixed sequence hierarchical testing procedure (see Section 4.1) was applied. The treatment effect on the 6-minute walking distance was tested first, followed by testing the effect on the forced vital capacity, subject to a significant result of the first test. Thus no power was lost due to correcting for multiplicity when testing the first endpoint in the hierarchy. Given the relatively large power of 90% for this test, the power loss for the second endpoint in the hierarchy would be small under the assumed effect in the first endpoint. The p-values resulting from the trial were $p_1=0.03$ for the 6-minute walking distance and $p_2=0.006$ for the forced vital capacity. A significant effect for both endpoints, with FWER control at the 5% level, was declared using the hierarchical test. If both endpoints were to be considered equally important, planning for a Bonferroni-Holm adjustment would by a suitable alternative multiple testing strategy, in this case yielding the same conclusions as the hierarchical test.

6 Discussion

In this review we wanted to give an overview of the different analysis methods available for analyzing clinical trials with multiple endpoints. In diseases that manifest in complex ways, several endpoints are often deemed relevant and their investigation in a single clinical trial aims at better capturing the disease of interest or lowering the needed number of patients. First and foremost, the choice of endpoints must be guided by the objectives of the trial. Clinical relevance and interpretability of the resulting outcome measures are paramount. In small clinical trials, however, feasibility considerations, for example, the maximal available sample size, may influence the selection of study endpoints and analysis methods to a larger extent than in less restricted situations (Parmar et al., 2016). The choice of statistical methods has an impact on both the power and interpretation of results.

In the first part of the review we explain parametric and non-parametric methods to combine multiple endpoints and their corresponding assumptions. The methods are ordered according to the different scale of measurement required. In general we can conclude that normal approximations of the distribution of test statistics are typically sufficiently accurate even for smaller samples as long as the underlying distribution is not too discrete and not too heavily tailed. The quality of the normal approximation is however reduced if test statistics that rely on variance estimates are used, resulting in a noticeable inflation of the type I error rate for small sample sizes. In these settings, t(or F-) distributions with appropriately chosen degrees of freedom provide a better approximation (Läuter, 1996; O’Brien, 1984; Tamhane and Logan, 2002).

If normal approximations are not accurate enough, non-parametric procedures based on resampling of the outcomes provide a valuable alternative. As the resampling of multivariate outcomes is performed at the level of the observational unit, they account for the correlation of endpoints (Westfall and Young, 1993). A limitation of permutation tests is that they provide inference on the general null hypothesis of identical distributions in two (or more) groups rather than testing equality of relevant parameters (Calian et al., 2008; Klingenberg et al., 2009; Westfall and Troendle, 2008; Xu and Hsu, 2007). In the context of multiple comparison of means, Pauly et al. (2015) showed that this limitation can be relaxed, at least asymptotically, for appropriately standardized test statistics. Furthermore, even with small sample sizes, evaluation of all possible permutations is not feasible. Instead a set of random permutations is selected and the resulting permutation tests are exact up to a sampling error that can be reduced by increasing the number of random permutations. An alternative to permutation tests that can be applied in tests of parameters of more complex statistical models are bootstrap methods to estimate the null distribution of test statistics (Bloch et al., 2007; Logan and Tamhane, 2001; Minhajuddin et al., 2007; Rauch and Beyersmann, 2013; Westfall and Young, 1989). Furthermore, methods of multivariate ordering in combination with a permutation test provide robust non-parametric inference for multiple endpoints (Wittkowski et al., 2004).

For some parametric models, especially for binary data, exact tests can be derived (Agresti, 2002; Boschloo, 1970; Han et al., 2004). These often do not exhaust the nominal significance level, because the distributions of their statistics are discrete. This conservatism can become severe with small sample sizes and reduce the power to identify a treatment as efficacious. When analyzing multiple endpoints, this problem can be reduced by appropriately distributing the nominal level across marginal distributions or within a multivariate joint distribution of test statistics (Ristl et al., 2018; Rom, 1992; Tarone, 1990; Westfall and Wolfinger, 1997). More powerful procedures can be obtained if specific assumptions on the underlying statistical model are made, for example assumptions on the correlation between endpoints or the assumption that there is a common effect in all endpoints, as in the model for binary data proposed by Han et al. (Han et al., 2004).

Additional challenges arise if a global test for endpoints of different scale levels is warranted. In the small sample setting, a robust and most general testing approach is given by the methods of multivariate ordering described in Section 3.2. Another general approach is to approximate the joint distribution of test statistics for different, non-commensurate endpoints by a multivariate normal distribution and define a combined test statistic as in O’Brien’s GLS test (Pocock et al., 1987). The joint covariance matrix required for this approach may in principle be estimated through a GEE model, see e.g. Teixeira-Pinto and Normand (2009) for the important case of a model for a binary and a continuous endpoint. However, the small sample properties of this combination of methods remains to be assessed.

In the second part of the article we reviewed different methodology either based on the marginal distributions or the joint distribution of the test statistics to extend inference to individual endpoints while controlling the familywise error rate. Multivariate normal or t-distributed test statistics with non-negative correlations allows one to use the more powerful Hommel or Hochberg tests instead of the Bonferroni-Holm test (Block et al., 2013; Hochberg, 1988; Hommel, 1988; Simes, 1986). If one supposes a positive effect in all endpoints, the rejection region of global null hypothesis tests can be optimized to increase the power for such alternatives (Su et al., 2012; Whitehead et al., 2010). Assumptions on the individual effect sizes in the endpoints can be used to select optimal weights in a multiple testing procedure (Westfall et al., 1998). Parametric methods based on the joint distribution of test statistics have a power advantage compared to the non-parametric and semi-parametric procedures (Hothorn et al., 2008; Lafaye De Micheaux et al., 2014), but their performance depends on the accuracy of the approximation of their distribution. If the assumptions on the dependence structure of the test statistics are violated, the type I and type II error rate may be inflated. Erroneous assumptions on the effect sizes have an impact on the type II error. Small samples will typically not provide sufficient information to verify the assumptions such that they need to be justified by data from other trials or subject matter knowledge, e.g. knowledge on the course of the disease or on the mechanism of action of the investigated treatments.

Intermediate approaches between testing the global null hypothesis or specific individual null hypotheses have been proposed where the global null hypothesis is tested with strict type I error control and the individual endpoints are assessed in a descriptive manner (e.g. requiring a positive point estimate only) (Huque and Alosh, 2012; Rauch and Beyersmann, 2013; Rauch et al., 2014b). An alternative considered way is to establish non-inferiority in all endpoints in combination with superiority in at least one endpoint (Bloch et al., 2007, 2001; Logan and Tamhane, 2008; Perlman and Wu, 2004; Röhmel et al., 2006; Tamhane and Logan, 2004). These methods should help with the interpretability of a combined endpoint in a clinical trial. Another approach to avoid correcting for multiple testing would be to require all endpoints to show a significant effect for the trial to be considered positive. Such co-primary endpoint designs (Sozu et al., 2012; Sugimoto et al., 2012) and ways of still making sound inference in case some hypotheses can not be rejected (Ristl et al., 2016) are discussed.

The combination of multiple testing procedures with the adaptive design framework (Bauer and Köhne, 1994; Bretz et al., 2009a; Kieser et al., 1999; Müller and Schäfer, 2001; Urach and Posch, 2016), although important due to the lower expected sample size of the trial design, has not been in the scope of the review. Additionally these designs would be more flexible, allowing for example for sample size adaptations and the dropping of hypotheses in interim analyses (Bauer and Köhnee, 1994). However the application of sequential or adaptive designs may have to be re-considered under the aspect that interim decisions must be taken at potentially very small sample sizes. Other relevant topics outside the limits of the review is avoidance of and coping with missing data and the longitudinal analysis of multiple endpoints. Also we did not discuss methods to deal with multiplicity issues arising from simultaneously analyzing a full population and subgroups. The methods of multiple testing covered in Section 4 are applicable also to this setting. However, when analyzing subgroups and a full population, the correlation between test statistics is typically determined through the proportion of sample sizes in the subgroups and this information can be incorporated in methods based on the assumption that the joint distribution of test statistics is known (Graf et al., 2018; Spiessens and Debois, 2010).

This review outlines several methods to analyze multiple endpoints for various data types and study objectives with a focus on applications to small sample problems. The different assumptions involved in the application of the methods and the conclusions to be drawn based on the different tested hypotheses shall help investigators to find the optimal procedure for evaluating specific clinical trials with multiple endpoints.

Acknowledgments

We wish to thank Armin Koch for helpful discussions.

Additional information

Funding

This work has been funded by the FP7 Health project Advances in Small Trials Design for Regulatory Innovation and Excellence (ASTERIX). Grant Agreement No. 2013-603160. Website: http://www.asterix-fp7.eu/

Appendices

Combined endpoints query

( TITLE-ABS-KEY(“composite endpoint*”) OR TITLE-ABS-KEY(combin* W/2 endpoint*) OR TITLE-ABS-KEY(“multiple endpoint*”) OR TITLE-ABS-KEY(“multivariate comparison*”) OR TITLE-ABS-KEY(multivariate W/2 test) OR TITLE-ABS-KEY(“multivariate endpoint*”) OR TITLE-ABS-KEY(“multivariate outcome*”) OR TITLE-ABS-KEY(“multivariate response*”) ) AND (AUTHKEY (“multiple endpoint*”) OR AUTHKEY(“multivariate”) OR AUTHKEY(“small”) OR AUTHKEY(“non*parametric”) OR AUTHKEY(“sum statistic”) OR AUTHKEY(“composite”) OR AUTHKEY(“concordance”) OR AUTHKEY(“rank”) OR AUTHKEY(“robust”) OR AUTHKEY(“bootstrap”) OR AUTHKEY(“resampling”) OR AUTHKEY(“permutation test”) OR AUTHKEY(“minP”) OR AUTHKEY(“exact test”) ) AND ( SUBJAREA(math) OR SUBJAREA(medi) OR SUBJAREA(phar) OR SUBJAREA(dent) OR SUBJAREA(vete) OR SUBJAREA(heal) OR SUBJAREA(mult) ) AND DOCTYPE(ar)

Multiple testing query

( TITLE-ABS-KEY(“multiple comparison*”) OR TITLE-ABS-KEY(“multiple test*”) OR TITLE-ABS-KEY(“composite endpoint*”) OR TITLE-ABS-KEY(“multiple outcome*”) OR TITLE-ABS-KEY(“multiple response*”) OR TITLE-ABS-KEY(“multiplicity adjustment”) OR TITLE-ABS-KEY(“closed test*”) OR TITLE-ABS-KEY(“closure principle”) OR TITLE-ABS-KEY(“gatekeeping”) OR TITLE-ABS-KEY(“partitioning principle”) OR TITLE-ABS-KEY(“reverse multiplicity”) OR TITLE-ABS-KEY(“co-primary endpoints”) OR TITLE-ABS-KEY(“simultaneous confidence intervals”) OR TITLE-ABS-KEY(“intersection-union”) OR TITLE-ABS-KEY(“adjusted p-value”) OR TITLE-ABS-KEY(“family wise error rate”) ) AND ( AUTHKEY (“multiple endpoint*”) OR AUTHKEY(“multivariate”) OR AUTHKEY(“small”) OR AUTHKEY(“non*parametric”) OR AUTHKEY(“sum statistic”) OR AUTHKEY(“composite”) OR AUTHKEY(“concordance”) OR AUTHKEY(“rank”) OR AUTHKEY(“robust”) OR AUTHKEY(“bootstrap”) OR AUTHKEY(“resampling”) OR AUTHKEY(“permutation test”) OR AUTHKEY(“minP”) OR AUTHKEY(“exact test”) ) AND ( SUBJAREA(math) OR SUBJAREA(medi) OR SUBJAREA(phar) OR SUBJAREA(dent) OR SUBJAREA(vete) OR SUBJAREA(heal) OR SUBJAREA(mult) ) AND DOCTYPE(ar)