Tensor methods for finding approximate stationary points of convex functions

Abstract

In this paper, we consider the problem of finding ε-approximate stationary points of convex functions that are p-times differentiable with ν-Hölder continuous pth derivatives. We present tensor methods with and without acceleration. Specifically, we show that the non-accelerated schemes take at most $\mathcal{O}\left({ϵ}^{-1/(p+\nu -1)}\right)$ iterations to reduce the norm of the gradient of the objective below given $ϵ\in (0,1)$. For accelerated tensor schemes, we establish improved complexity bounds of $\mathcal{O}\left({ϵ}^{-(p+\nu )/\left[\right(p+\nu -1\left)\right(p+\nu +1\left)\right]}\right)$ and $\mathcal{O}\left(|\log \left(ϵ\right)|{ϵ}^{-1/(p+\nu )}\right)$, when the Hölder parameter $\nu \in [0,1]$ is known. For the case in which ν is unknown, we obtain a bound of $\mathcal{O}\left({ϵ}^{-(p+1)/\left[\right(p+\nu -1\left)\right(p+2\left)\right]}\right)$ for a universal accelerated scheme. Finally, we also obtain a lower complexity bound of $\mathcal{O}\left({ϵ}^{-2/\left[3\right(p+\nu )-2]}\right)$ for finding ε-approximate stationary points using p-order tensor methods.

Keywords:

• Unconstrained minimization
• high-order methods
• tensor methods
• Hölder condition
• worst-case complexity

2010 Mathematics Subject Classifications:

• 49M15
• 49M37
• 58C15
• 90C25
• 90C30

1. Introduction

1.1. Motivation

In this paper, we study tensor methods for unconstrained optimization, i.e. methods in which the iterates are obtained by the (approximate) minimization of models defined from high-order Taylor approximations of the objective function. This type of method is not new in the optimization literature (see, e.g. [1,4,33]). Recently, the interest for tensor methods has been renewed by the work in [2], where p-order tensor methods were proposed for unconstrained minimization of nonconvex functions with Lipschitz continuous pth derivatives. It was shown that these methods take at most $\mathcal{O}\left({ϵ}^{-\frac{p+1}{p}}\right)$ iterations to find an ε-approximate first-order stationary point of the objective, generalizing the bound of $\mathcal{O}\left({ϵ}^{-3/2}\right)$, originally established in [31] for the Cubic Regularization of Newton's Method (p = 2). After [2], several high-order methods have been proposed and analysed for nonconvex optimization (see, e.g. [9–11,23]), resulting even in worst-case complexity bounds for the number of iterations that p-order methods need to generate approximate qth order stationary points [7,8].

More recently, in [27], p-order tensor methods with and without acceleration were proposed for unconstrained minimization of convex functions with Lipschitz continuous pth derivatives. As it is usual in Convex Optimization, these methods aim the generation of a point $\overline{x}$ such that $f\left(\overline{x}\right)-f^{\ast }\le ϵ$, where f is the objective function, $f^{\ast }$ is its optimal value and $ϵ>0$ is a given precision. Specifically, it was shown that the non-accelerated scheme takes at most $\mathcal{O}\left({ϵ}^{-1/p}\right)$ iterations to reduce the functional residual below a given $ϵ>0$, while the accelerated scheme takes at most $\mathcal{O}\left({ϵ}^{-1/(p+1)}\right)$ iterations to accomplish the same task. Auxiliary problems in these methods consist in the minimization of a $(p+1)$-regularization of the pth order Taylor approximation of the objective, which is a multivariate polynomial. A remarkable result shown in [27] (which distinguishes this work from [1]) is that, in the convex case, the auxiliary problems in tensor methods become convex when the corresponding regularization parameter is sufficiently large. Since [27], several high-order methods have been proposed for convex optimization (see, e.g. [13,14,18,20]), including near-optimal methods [5,15,21,28,29] motivated by the second-order method in [24]. In particular, in [18], we have adapted and generalized the methods in [16,17,27] to handle convex functions with ν-Hölder continuous pth derivatives. It was shown that the non-accelerated schemes take at most $\mathcal{O}\left({ϵ}^{-1/(p+\nu -1)}\right)$ iterations to generate a point with functional residual smaller than a given $ϵ\in (0,1)$, while the accelerated variants take only $\mathcal{O}\left({ϵ}^{-1/(p+\nu )}\right)$ iterations when the parameter ν is explicitly used in the scheme. For the case in which ν is not known, we also proposed a universal accelerated scheme for which we established an iteration complexity bound of $\mathcal{O}\left({ϵ}^{-p/\left[\right(p+1\left)\right(p+\nu -1\left)\right]}\right)$.

As a natural development, in this paper, we present variants of the p-order methods ($p\ge 2$) proposed in [18] that aim the generation of a point $\overline{x}$ such that $\parallel \mathrm{\nabla }f\left(\overline{x}\right){\parallel }_{\ast }\le ϵ$, for a given threshold $ϵ\in (0,1)$. In the context of nonconvex optimization, finding approximate stationary points is usually the best one can expect from local optimization methods. In the context of convex optimization, one motivation to search for approximate stationary points is the fact that the norm of the gradient may serve as a measure of feasibility and optimality when one applies the dual approach for solving constrained convex problems (see, e.g. [26]). Another motivation comes from the inexact high-order proximal-point methods, recently proposed in [28,29], in which the iterates are computed as approximate stationary points of uniformly convex models.

Specifically, our contributions are the following:

1. We show that the non-accelerated schemes in [18] take at most $\mathcal{O}\left({ϵ}^{-1/(p+\nu -1)}\right)$ iterations to reduce the norm of the gradient of the objective below a given $ϵ\in (0,1)$, when the objective is convex, and $\mathcal{O}\left({ϵ}^{-(p+\nu )/(p+\nu -1)}\right)$ iterations, when f is nonconvex. These complexity bounds extend our previous results reported in [16] for regularized Newton methods (case p = 2). Moreover, our complexity bound for the nonconvex case agrees in order with the bounds obtained in [9,23] for different tensor methods.

2. For accelerated tensor schemes, we establish improved complexity bounds of $\mathcal{O}\left({ϵ}^{-(p+\nu )/\left[\right(p+\nu -1\left)\right(p+\nu +1\left)\right]}\right)$, when the Hölder parameter $\nu \in [0,1]$ is known. This result generalizes the bound of $\mathcal{O}\left({ϵ}^{-2/3}\right)$ obtained in [26] for the accelerated gradient method ($p=\nu =1$). In contrast, when ν is unknown, we prove a bound of $\mathcal{O}\left({ϵ}^{-(p+1)/\left[\right(p+\nu -1\left)\right(p+2\left)\right]}\right)$ for a universal accelerated scheme.

3. For the case in which ν and the corresponding Hölder constant are known, we propose tensor schemes for the composite minimization problem. In particular, we prove a bound of $\mathcal{O}(R^{\frac{p+\nu -1}{p+\nu }}|{\log }_2(ϵ\left)|{ϵ}^{-\frac{1}{p+\nu }}\right)$ iterations, where R is an upper bound for the initial distance to the optimal set. This result generalizes the bounds obtained in [26] for first-order and second-order accelerated schemes combined with a regularization approach (p = 1, 2 and $\nu =1$). We also prove a bound of $\mathcal{O}(S^{\frac{p+\nu -1}{p+\nu }}|{\log }_2(ϵ\left)|{ϵ}^{-1}\right)$ iterations, where S is an upper bound for the initial functional residual.

4. Considering the same class of difficult functions described in [18], we derive a lower complexity bound of $\mathcal{O}\left({ϵ}^{-2/\left[3\right(p+\nu )-2]}\right)$ iterations (in terms of the initial distance to the optimal set), and a lower complexity bound of $\mathcal{O}\left({ϵ}^{-2(p+\nu )/\left[3\right(p+\nu )-2]}\right)$ iterations (in terms of the initial functional residual), for p-order tensor methods to find ε-approximate stationary points of convex functions with ν-Hölder continuous pth derivatives. These bounds generalize the corresponding bounds given in [6] for first-order methods ($p=\nu =1$).

The paper is organized as follows. In Section 2, we define our problem. In Section 3, we present complexity results for tensor schemes without acceleration. In Section 4, we present complexity results for accelerated schemes. In Section 5, we analyse tensor schemes for the composite minimization problem. Finally, in Section 6, we establish lower complexity bounds for tensor methods find ε-approximate stationary points of convex functions under the Hölder condition. Some auxiliary results are left in the Appendix.

1.2. Notations and generalities

Let $\mathbb{E}$ be a finite-dimensional real vector space, and ${\mathbb{E}}^{\ast }$ be its dual space. We denote by $⟨s,x⟩$ the value of the linear functional $s\in {\mathbb{E}}^{\ast }$ at point $x\in \mathbb{E}$. Spaces $\mathbb{E}$ and ${\mathbb{E}}^{\ast }$ are equipped with conjugate Euclidean norms: (1) $\parallel x\parallel =⟨Bx,x{⟩}^{1/2},x\in \mathbb{E},\parallel s{\parallel }_{\ast }=⟨s,B^{-1}s{⟩}^{1/2},s\in {\mathbb{E}}^{\ast }.$(1) where $B:\mathbb{E}\to {\mathbb{E}}^{\ast }$ is a self-adjoint positive definite operator ($B\succ 0$). For a smooth function $f:\mathbb{E}\to \mathbb{R}$, denote by $\mathrm{\nabla }f\left(x\right)$ its gradient, and by ${\mathrm{\nabla }}^{2}f\left(x\right)$ its Hessian evaluated at point $x\in \mathbb{E}$. Then $\mathrm{\nabla }f\left(x\right)\in {\mathbb{E}}^{\ast }$ and ${\mathrm{\nabla }}^{2}f\left(x\right)h\in {\mathbb{E}}^{\ast }$ for $x,h\in \mathbb{E}$.

For any integer $p\ge 1$, denote by $D^{p}f\left(x\right)[h_1,\dots ,h_p]$ the directional derivative of function f at x along directions $h_i\in \mathbb{E}$, $i=1,\dots ,p$. For any $x\in \mathrm{d}\mathrm{o}\mathrm{m}f$ and $h_1,h_2\in \mathbb{E}$ we have $Df\left(x\right)\left[h_1\right]=⟨\mathrm{\nabla }f\left(x\right),h_1⟩\mathrm{a}\mathrm{n}\mathrm{d}{D}^{2}f\left(x\right)[h_1,h_2]=⟨{\mathrm{\nabla }}^{2}f\left(x\right)h_1,h_2⟩.$ If $h_1=\dots =h_p=h\in \mathbb{E}$, we denote $D^{p}f\left(x\right)[h_1,\dots ,h_p]$ by $D^{p}f\left(x\right)[h{]}^p$. Using this notation, the pth order Taylor approximation of function f at $x\in \mathbb{E}$ can be written as follows: (2) $f(x+h)={\mathrm{\Phi }}_{x,p}(x+h)+o(\parallel h{\parallel }^p),$(2) where (3) ${\mathrm{\Phi }}_{x,p}\left(y\right)\equiv f\left(x\right)+\sum _{i=1}^p\frac{1}{i!}{D}^{i}f\left(x\right)[y-x{]}^i,y\in \mathbb{E}.$(3) Since $D^{p}f\left(x\right)[\cdot ]$ is a symmetric p-linear form, its norm is defined as: $\parallel D^{p}f\left(x\right)\parallel =\underset{h_1,\dots ,h_p}{max}\left\{\left|D^{p}f\left(x\right)[h_1,\dots ,h_p]\right|:\parallel h_i\parallel \le 1,i=1,\dots ,p\right\}.$ It can be shown that (see, e.g. Appendix 1 in [30]) $\parallel D^{p}f\left(x\right)\parallel =\underset{h}{max}\left\{\left|D^{p}f\left(x\right)[h{]}^p\right|:\parallel h\parallel \le 1\right\}.$ Similarly, since $D^{p}f\left(x\right)[.,\dots ,.]-D^{p}f\left(y\right)[.,\dots ,.]$ is also a symmetric p-linear form for fixed $x,y\in \mathbb{E}$, it follows that $\parallel D^{p}f\left(x\right)-D^{p}f\left(y\right)\parallel =\underset{h}{max}\left\{\left|D^{p}f\left(x\right)[h{]}^p-D^{p}f(y\left)\right[h{]}^p\right|:\parallel h\parallel \le 1\right\}.$

2. Problem statement

In this paper, we consider methods for solving the following minimization problem (4) $\underset{x\in \mathbb{E}}{min}f\left(x\right),$(4) where $f:\mathbb{E}\to \mathbb{R}$ is a convex function p-times differentiable. We assume that (4(4) $\underset{x\in \mathbb{E}}{min}f\left(x\right),$(4) ) has at least one optimal solution $x^{\ast }\in \mathbb{E}$. As in [18], the level of smoothness of the objective f will be characterized by the family of Hölder constants (5) $H_{f,p}\left(\nu \right)\equiv \underset{x,y\in \mathbb{E}}{sup}\left\{\frac{\parallel D^{p}f\left(x\right)-D^{p}f\left(y\right)\parallel }{\parallel x-y{\parallel }^{\nu }}\right\},0\le \nu \le 1.$(5) From (5(5) $H_{f,p}\left(\nu \right)\equiv \underset{x,y\in \mathbb{E}}{sup}\left\{\frac{\parallel D^{p}f\left(x\right)-D^{p}f\left(y\right)\parallel }{\parallel x-y{\parallel }^{\nu }}\right\},0\le \nu \le 1.$(5) ), it can be shown that, for all $x,y\in \mathbb{E}$, (6) $\begin{array}{rl}& |f\left(y\right)-{\mathrm{\Phi }}_{x,p}\left(y\right)|\le \frac{H_{f,p}\left(\nu \right)}{p!}\parallel y-x{\parallel }^{p+\nu },\end{array}$(6) (7) $\begin{array}{rl}& \parallel \mathrm{\nabla }f\left(y\right)-\mathrm{\nabla }{\mathrm{\Phi }}_{x,p}\left(y\right){\parallel }_{\ast }\le \frac{H_{f,p}\left(\nu \right)}{(p-1)!}\parallel y-x{\parallel }^{p+\nu -1},\end{array}$(7) and (8) $\parallel {\mathrm{\nabla }}^{2}f\left(y\right)-{\mathrm{\nabla }}^2{\mathrm{\Phi }}_{x,p}\left(y\right){\parallel }_{\ast }\le \frac{H_{f,p}\left(\nu \right)}{(p-2)!}\parallel y-x{\parallel }^{p+\nu -2}.$(8) Given $x\in \mathbb{E}$, if $H_{f,p}\left(\nu \right)<+\mathrm{\infty }$ and $H\ge H_{f,p}\left(\nu \right)$, by (6(6) $\begin{array}{rl}& |f\left(y\right)-{\mathrm{\Phi }}_{x,p}\left(y\right)|\le \frac{H_{f,p}\left(\nu \right)}{p!}\parallel y-x{\parallel }^{p+\nu },\end{array}$(6) ) we have (9) $f\left(y\right)\le {\mathrm{\Phi }}_{x,p}\left(y\right)+\frac{H}{p!}\parallel y-x{\parallel }^{p+\nu },y\in \mathbb{E}.$(9) This property motivates the use of the following class of models of f around $x\in \mathbb{E}$: (10) ${\mathrm{\Omega }}_{x,p,H}^{\left(\alpha \right)}\left(y\right)={\mathrm{\Phi }}_{x,p}\left(y\right)+\frac{H}{p!}\parallel y-x{\parallel }^{p+\alpha },\alpha \in [0,1].$(10) Note that, by (9(9) $f\left(y\right)\le {\mathrm{\Phi }}_{x,p}\left(y\right)+\frac{H}{p!}\parallel y-x{\parallel }^{p+\nu },y\in \mathbb{E}.$(9) ), if $H\ge H_{f,p}\left(\nu \right)$ then $f\left(y\right)\le {\mathrm{\Omega }}_{x,p,H}^{\left(\nu \right)}\left(y\right)$ for all $y\in \mathbb{E}$.

3. Tensor schemes without acceleration

Let us consider the following assumption:

H1	$H_{f,p}\left(\nu \right)<+\mathrm{\infty }$ for some $\nu \in [0,1]$.

Regarding the smoothness parameter ν, there are only two possible situations: either ν is known, or ν is unknown. In order to cover both cases in a single framework, as in [18], we shall consider the parameter (11) $\alpha =\left\{\begin{array}{ll}\nu ,& \mathrm{i}\mathrm{f}\nu \mathrm{i}\mathrm{s}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}\mathrm{n},\\ 1,& \mathrm{i}\mathrm{f}\nu \mathrm{i}\mathrm{s}\mathrm{u}\mathrm{n}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}\mathrm{n}.\end{array}\right.-1.5pc$(11)

Remark 3.1

If ν is unknown, by (11(11) $\alpha =\left\{\begin{array}{ll}\nu ,& \mathrm{i}\mathrm{f}\nu \mathrm{i}\mathrm{s}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}\mathrm{n},\\ 1,& \mathrm{i}\mathrm{f}\nu \mathrm{i}\mathrm{s}\mathrm{u}\mathrm{n}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}\mathrm{n}.\end{array}\right.-1.5pc$(11) ) we set $\alpha =1$ in Algorithm 1. The resulting algorithm is a universal scheme that can be viewed as a generalization of the universal second-order method (6.10) in [16]. Moreover, it is worth mentioning that for p = 3 and $\alpha =\nu$, one can use Gradient Methods with Bregman distance [19] to approximately solve (12) in the sense of (13).

For both cases (ν known or unknown), Algorithm 1 is a particular instance of Algorithm 1 in [18] in which $M_t=2^{i_t}{H}_t$ for all $t\ge 0$. Let us define the following function of ε: (15) $N_{\nu }\left(ϵ\right)=\left\{\begin{array}{ll}max\left\{\frac{3H_{f,p}\left(\nu \right)}{2},3\theta (p-1)!\right\},& \mathrm{i}\mathrm{f}\nu \mathrm{i}\mathrm{s}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}\mathrm{n},\\ max\left\{\theta ,{\left(\frac{3H_{f,p}\left(\nu \right)}{2}\right)}^{\frac{p}{p+\nu -1}}{4}^{\frac{1-\nu }{p+\nu -1}}\right\}{ϵ}^{-\frac{1-\nu }{p+\nu -1}},& \mathrm{i}\mathrm{f}\nu \mathrm{i}\mathrm{s}\mathrm{u}\mathrm{n}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}\mathrm{n}.\end{array}\right.$(15) The next lemma provides upper bounds on $M_t$ and on the number of calls of the oracle in Algorithm 1.

Lemma 3.1

Suppose that H1 holds. Given $ϵ\in (0,1)$, assume that $\{x_t{\}}_{t=0}^T$ is a sequence generated by Algorithm 1 such that (16) $\parallel \mathrm{\nabla }f\left(x_t\right){\parallel }_{\ast }>ϵ,t=0,\dots ,T.$(16) Then, (17) $H_t\le max\left\{H_0,N_{\nu }\left(ϵ\right)\right\},fort=0,\dots ,T,$(17) and, consequently, (18) $M_t=2^{i_t}{H}_t\le 2max\left\{H_0,N_{\nu }\left(ϵ\right)\right\},fort=0,\dots ,T-1,$(18) Moreover, the number $O_T$ of calls of the oracle after T iterations is bounded as follows: (19) $O_T\le 2T+{\log }_{2}max\left\{H_0,N_{\nu }\left(ϵ\right)\right\}-{\log }_2{H}_0.$(19)

Proof.

Let us prove (17(17) $H_t\le max\left\{H_0,N_{\nu }\left(ϵ\right)\right\},fort=0,\dots ,T,$(17) ) by induction. Clearly, it holds for t = 0. Assume that (17(17) $H_t\le max\left\{H_0,N_{\nu }\left(ϵ\right)\right\},fort=0,\dots ,T,$(17) ) is true for some t, $0\le t\le T-1$. If ν is known, then by (11(11) $\alpha =\left\{\begin{array}{ll}\nu ,& \mathrm{i}\mathrm{f}\nu \mathrm{i}\mathrm{s}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}\mathrm{n},\\ 1,& \mathrm{i}\mathrm{f}\nu \mathrm{i}\mathrm{s}\mathrm{u}\mathrm{n}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}\mathrm{n}.\end{array}\right.-1.5pc$(11) ) we have $\alpha =\nu$. Thus, it follows from H1 and Lemma A.2 in [18] that the final value of $2^{i_t}{H}_t$ cannot be bigger than $2max\left\{\right(3/2\left)H_{f,p}\right(\nu ),3\theta (p-1)!\}$, since otherwise we should stop the line search earlier. Therefore, $H_{t+1}=\frac{1}{2}{2}^{i_t}{H}_t\le max\left\{\frac{3H_{f,p}\left(\nu \right)}{2},3\theta (p-1)!\right\}=N_{\nu }\left(ϵ\right)\le max\left\{H_0,N_{\nu }\left(ϵ\right)\right\},$ that is, (17(17) $H_t\le max\left\{H_0,N_{\nu }\left(ϵ\right)\right\},fort=0,\dots ,T,$(17) ) holds for t = t + 1. On the other hand, if ν is unknown, we have $\alpha =1$. In view of (16(16) $\parallel \mathrm{\nabla }f\left(x_t\right){\parallel }_{\ast }>ϵ,t=0,\dots ,T.$(16) ), Corollary A.5 [18] and $ϵ\in (0,1)$, we must have $2^{i_t}{H}_t\le 2max\left\{\theta ,{\left(\frac{3H_{f,p}\left(\nu \right)}{2}\right)}^{\frac{p}{p+\nu -1}}{\left(\frac{4}{ϵ}\right)}^{\frac{1-\nu }{p+\nu -1}}\right\}\le 2N_{\nu }\left(ϵ\right).$ Consequently, it follows that $H_{t+1}=\frac{1}{2}{2}^{i_t}{H}_t\le N_{\nu }\left(ϵ\right)\le max\left\{H_0,N_{\nu }\left(ϵ\right)\right\},$ that is, (17(17) $H_t\le max\left\{H_0,N_{\nu }\left(ϵ\right)\right\},fort=0,\dots ,T,$(17) ) holds for t + 1. This completes the induction argument. Using (17(17) $H_t\le max\left\{H_0,N_{\nu }\left(ϵ\right)\right\},fort=0,\dots ,T,$(17) ), for $t=0,\dots ,T-1$ we get $M_t=2H_{t+1}\le 2max\{H_0,N_{\nu }(ϵ\left)\right\}$. Finally, note that at the tth iteration of Algorithm 1, the oracle is called $i_t+1$ times. Since $H_{t+1}=2^{i_t-1}{H}_t$, it follows that $i_t-1={\log }_2{H}_{t+1}-{\log }_2{H}_t$. Thus, by (17(17) $H_t\le max\left\{H_0,N_{\nu }\left(ϵ\right)\right\},fort=0,\dots ,T,$(17) ) we get $\begin{array}{rl}{O}_T& =\sum _{t=0}^{T-1}(i_t+1)=\sum _{t=0}^{T-1}2+{\log }_2{H}_{t+1}-{\log }_2{H}_t=2T+{\log }_2{H}_T-{\log }_2{H}_0\\ & \le 2T+{\log }_{2}max\left\{H_0,N_{\nu }\left(ϵ\right)\right\}-{\log }_2{H}_0,\end{array}$ and the proof is complete.

Let us consider the additional assumption:

H2	The level sets of f are bounded, that is, $\underset{x\in \mathcal{L}\left(x_0\right)}{max}\parallel x-x^{\ast }\parallel \le D_0\in (1,+\mathrm{\infty })$ for $\mathcal{L}\left(x_0\right)\equiv \{x\in \mathbb{E}:f(x)\le f(x_0\left)\right\}$, with $x_0$ being the starting point.

The next theorem gives global convergence rates for Algorithm 1 in terms of the functional residual.

Theorem 3.2

Suppose that H1 and H2 are true and let $\{x_t{\}}_{t=0}^T$ be a sequence generated by Algorithm 1 such that, for $t=0,\dots ,T,$ we have $\parallel \mathrm{\nabla }f\left(x_{t,i}^{+}\right){\parallel }_{\ast }>ϵ,i=0,\dots ,i_t.$ Let m be the first iteration number such that $f\left(x_m\right)-f\left(x^{\ast }\right)\le 4\left[8\right(p+1)!{]}^{p+\alpha -1}max\left\{H_0,N_{\nu }\left(\nu \right)\right\}{D}_0^{p+\alpha },$ and assume that m<T. Then (20) $m\le \frac{1}{\ln \left(\frac{p+\alpha }{p+\alpha -1}\right)}\ln max\left\{1,{\log }_2\frac{f\left(x_0\right)-f\left(x^{\ast }\right)}{2\left[8\right(p+1)!{]}^{p+\alpha -1}max\left\{H_0,N_{\nu }\left(ϵ\right)\right\}{D}_0^{p+\alpha }}\right\}$(20) and, for all k, $m<k\le T,$ we have (21) $f\left(x_k\right)-f\left(x^{\ast }\right)\le \frac{\left[24p\right(p+1)!{]}^{p+\alpha -1}2max\left\{H_0,N_{\nu }\left(ϵ\right)\right\}{D}_0^{p+\alpha }}{(k-m{)}^{p+\alpha -1}}.$(21)

Proof.

By Lemma 3.1, this result follows from Theorem 3.2 in [18] with $M_{\nu }=2max\{H_0,N_{\nu }(ϵ\left)\right\}$.

Now, we can derive global convergence rates for Algorithm 1 in terms of the norm of the gradient.

Theorem 3.3

Under the same assumptions of Theorem 3.2, if T = m + 3s for some $s\ge 1,$ then (22) $g_T^{\ast }\equiv \underset{0\le t\le T}{min}\parallel \mathrm{\nabla }f\left(x_t\right){\parallel }_{\ast }\le 2{\left[\frac{288p(p+1)!D_0}{T-m}\right]}^{p+\alpha -1}max\left\{H_0,N_{\nu }\left(ϵ\right)\right\}.$(22) Consequently, (23) $T<m+{\kappa }_1^{\left(\nu \right)}\left[288p\right(p+1)!D_0]{ϵ}^{-\frac{1}{p+\nu -1}},$(23) with ${\kappa }_1^{\left(\nu \right)}=\left\{\begin{array}{ll}{\left(2max\left\{H_0,\frac{3H_{f,p}\left(\nu \right)}{2},3\theta (p-1)!\right\}\right)}^{\frac{1}{p+\nu -1}},& \mathrm{i}\mathrm{f}\nu \mathrm{i}\mathrm{s}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}\mathrm{n},\\ {\left(2max\left\{H_0,\theta ,{\left(\frac{3H_{f,p}\left(\nu \right)}{2}\right)}^{\frac{p}{p+\nu -1}}{4}^{\frac{1-\nu }{p+\nu -1}}\right\}\right)}^{\frac{1}{p}},& \mathrm{i}\mathrm{f}\nu \mathrm{i}\mathrm{s}\mathrm{u}\mathrm{n}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}\mathrm{n}.\end{array}\right.$

Proof.

By Theorem 3.2, we have (24) $f\left(x_k\right)-f\left(x^{\ast }\right)\le \frac{\left[24p\right(p+1)!{]}^{p+\alpha -1}2max\left\{H_0,N_{\nu }\left(ϵ\right)\right\}{D}_0^{p+\alpha }}{(k-m{)}^{p+\alpha -1}},$(24) for all k, $m<k\le T$. In particular, it follows from (14) and (24(24) $f\left(x_k\right)-f\left(x^{\ast }\right)\le \frac{\left[24p\right(p+1)!{]}^{p+\alpha -1}2max\left\{H_0,N_{\nu }\left(ϵ\right)\right\}{D}_0^{p+\alpha }}{(k-m{)}^{p+\alpha -1}},$(24) ) that $\begin{array}{rl}& \frac{\left[24p\right(p+1)!{]}^{p+\alpha -1}2max\left\{H_0,N_{\nu }\left(ϵ\right)\right\}{D}_0^{p+\alpha }}{(2s{)}^{p+\alpha -1}}\\ & \ge f\left(x_{m+2s}\right)-f\left(x^{\ast }\right)\\ & =f\left(x_T\right)-f\left(x^{\ast }\right)+\sum _{k=m+2s}^{T-1}\left(f\right(x_k)-f(x_{k+1}\left)\right)\\ & \ge \frac{s}{8(p+1)!}{\left[\frac{1}{2max\left\{H_0,N_{\nu }\left(ϵ\right)\right\}}\right]}^{\frac{1}{p+\alpha -1}}(g_T^{\ast }{)}^{\frac{p+\alpha }{p+\alpha -1}}.\end{array}$ Therefore, $\begin{array}{rl}(g_T^{\ast }{)}^{\frac{p+\alpha }{p+\alpha -1}}& \le \frac{8(p+1)!\left[24p\right(p+1)!{]}^{p+\alpha -1}{\left(2max\left\{H_0,N_{\nu }\left(ϵ\right)\right\}\right)}^{\frac{p+\alpha }{p+\alpha -1}}{D}_0^{p+\alpha }}{2^{p+\alpha -1}{s}^{p+\alpha }}\\ & \le \frac{\left(96p{)}^{p+\alpha -1}{3}^{p+\alpha }\right[(p+1)!{]}^{p+\alpha }{\left(2max\left\{H_0,N_{\nu }\left(ϵ\right)\right\}\right)}^{\frac{p+\alpha }{p+\alpha -1}}{D}_0^{p+\alpha }}{(T-m{)}^{p+\alpha }},\end{array}$ and so (22(22) $g_T^{\ast }\equiv \underset{0\le t\le T}{min}\parallel \mathrm{\nabla }f\left(x_t\right){\parallel }_{\ast }\le 2{\left[\frac{288p(p+1)!D_0}{T-m}\right]}^{p+\alpha -1}max\left\{H_0,N_{\nu }\left(ϵ\right)\right\}.$(22) ) holds. By assumption, we have $g_T^{\ast }>ϵ$. Thus, by (22(22) $g_T^{\ast }\equiv \underset{0\le t\le T}{min}\parallel \mathrm{\nabla }f\left(x_t\right){\parallel }_{\ast }\le 2{\left[\frac{288p(p+1)!D_0}{T-m}\right]}^{p+\alpha -1}max\left\{H_0,N_{\nu }\left(ϵ\right)\right\}.$(22) ) we get (25) $\begin{array}{rl}& ϵ<2{\left(\frac{288p(p+1)!D_0}{T-m}\right)}^{p+\alpha -1}max\left\{H_0,N_{\nu }\left(ϵ\right)\right\}\\ ⟹& T<m+\left[288p\right(p+1)!D_0]{\left(2max\left\{H_0,N_{\nu }\left(ϵ\right)\right\}\right)}^{\frac{1}{p+\alpha -1}}{ϵ}^{-\frac{1}{p+\alpha -1}}.\end{array}$(25) Finally, by analysing separately the cases in which ν is known and unknown, it follows from (25(25) $\begin{array}{rl}& ϵ<2{\left(\frac{288p(p+1)!D_0}{T-m}\right)}^{p+\alpha -1}max\left\{H_0,N_{\nu }\left(ϵ\right)\right\}\\ ⟹& T<m+\left[288p\right(p+1)!D_0]{\left(2max\left\{H_0,N_{\nu }\left(ϵ\right)\right\}\right)}^{\frac{1}{p+\alpha -1}}{ϵ}^{-\frac{1}{p+\alpha -1}}.\end{array}$(25) ) and (15(15) $N_{\nu }\left(ϵ\right)=\left\{\begin{array}{ll}max\left\{\frac{3H_{f,p}\left(\nu \right)}{2},3\theta (p-1)!\right\},& \mathrm{i}\mathrm{f}\nu \mathrm{i}\mathrm{s}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}\mathrm{n},\\ max\left\{\theta ,{\left(\frac{3H_{f,p}\left(\nu \right)}{2}\right)}^{\frac{p}{p+\nu -1}}{4}^{\frac{1-\nu }{p+\nu -1}}\right\}{ϵ}^{-\frac{1-\nu }{p+\nu -1}},& \mathrm{i}\mathrm{f}\nu \mathrm{i}\mathrm{s}\mathrm{u}\mathrm{n}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}\mathrm{n}.\end{array}\right.$(15) ) that (23(23) $T<m+{\kappa }_1^{\left(\nu \right)}\left[288p\right(p+1)!D_0]{ϵ}^{-\frac{1}{p+\nu -1}},$(23) ) is true.

Remark 3.2

Suppose that the objective f in (4(4) $\underset{x\in \mathbb{E}}{min}f\left(x\right),$(4) ) is nonconvex and bounded from below by $f^{\ast }$. Then, it follows from (14) and (18(18) $M_t=2^{i_t}{H}_t\le 2max\left\{H_0,N_{\nu }\left(ϵ\right)\right\},fort=0,\dots ,T-1,$(18) ) that $f\left(x_t\right)-f\left(x_{t+1}\right)\ge \frac{1}{8(p+1)!}{\left[\frac{1}{2max\left\{H_0,N_{\nu }\left(ϵ\right)\right\}}\right]}^{\frac{1}{p+\alpha -1}}{ϵ}^{\frac{p+\alpha }{p+\alpha -1}},t=0,\dots ,T-1.$ Summing up these inequalities, we get $f\left(x_0\right)-f^{\ast }\ge f\left(x_0\right)-f\left(x_T\right)\ge \frac{T}{8(p+1)!}{\left[\frac{1}{2max\left\{H_0,N_{\nu }\left(ϵ\right)\right\}}\right]}^{\frac{1}{p+\alpha -1}}{ϵ}^{\frac{p+\alpha }{p+\alpha -1}}$ and so, by (15(15) $N_{\nu }\left(ϵ\right)=\left\{\begin{array}{ll}max\left\{\frac{3H_{f,p}\left(\nu \right)}{2},3\theta (p-1)!\right\},& \mathrm{i}\mathrm{f}\nu \mathrm{i}\mathrm{s}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}\mathrm{n},\\ max\left\{\theta ,{\left(\frac{3H_{f,p}\left(\nu \right)}{2}\right)}^{\frac{p}{p+\nu -1}}{4}^{\frac{1-\nu }{p+\nu -1}}\right\}{ϵ}^{-\frac{1-\nu }{p+\nu -1}},& \mathrm{i}\mathrm{f}\nu \mathrm{i}\mathrm{s}\mathrm{u}\mathrm{n}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}\mathrm{n}.\end{array}\right.$(15) ), we obtain $T\le \mathcal{O}\left({ϵ}^{-\frac{p+\nu }{p+\nu -1}}\right)$. This bound generalizes the bound of $\mathcal{O}\left({ϵ}^{-\frac{2+\nu }{1+\nu }}\right)$ proved in [16] for p = 2. It agrees in order with the complexity bounds proved in [23] and [9] for different universal tensor methods.

4. Accelerated tensor schemes

The schemes presented here generalize the procedures described in [26] for p = 1 and p = 2. Specifically, our general scheme is obtained by adding Step 2 of Algorithm 1 at the end of Algorithm 4 in [18], in order to relate the functional decrease with the norm of the gradient of f in suitable points:

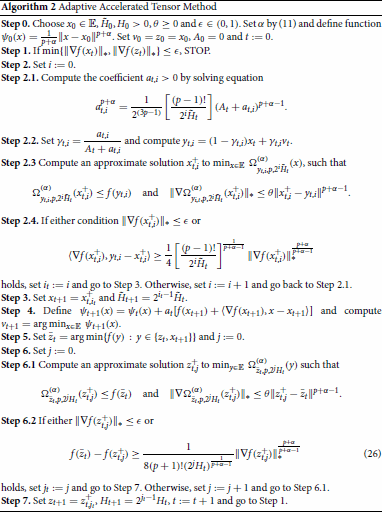
Let us define the following function of ε: (27) ${\tilde{N}}_{\nu }\left(ϵ\right)=\left\{\begin{array}{ll}(p+\nu -1)\left(H_{f,p}\right(\nu )+\theta (p-1)!),& \mathrm{i}\mathrm{f}\nu \mathrm{i}\mathrm{s}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}\mathrm{n},\\ max\left\{4\theta (p-1)!,\left(4H_{f,p}\right(\nu ){)}^{\frac{p}{p+\nu -1}}{\left(\frac{4}{ϵ}\right)}^{\frac{1-\nu }{p+\nu -1}}\right\},& \mathrm{i}\mathrm{f}\nu \mathrm{i}\mathrm{s}\mathrm{u}\mathrm{n}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}\mathrm{n}.\end{array}\right.$(27) In Algorithm 2, note that $\left\{x_t\right\}$ is independent of $\left\{z_t\right\}$. The next theorem establishes global convergence rates for the functional residual with respect to $\left\{x_t\right\}$.

Theorem 4.1

Assume that H1 holds and let the sequence $\{x_t{\}}_{t=0}^T$ be generated by Algorithm 2 such that, for $t=0,\dots ,T$ we have (28) $\parallel \mathrm{\nabla }f\left(x_{t,i}^{+}\right){\parallel }_{\ast }>ϵ,i=0,\dots ,i_t.$(28) Then, (29) $f\left(x_t\right)-f\left(x^{\ast }\right)\le \frac{2^{3p}max\left\{{\tilde{H}}_0,{\tilde{N}}_{\nu }\left(ϵ\right)\right\}(p+\alpha {)}^{p+\alpha -1}\parallel x_0-x^{\ast }{\parallel }^{p+\alpha }}{(p-1)!(t-1{)}^{p+\alpha }},$(29) for $t=2,\dots ,T$.

Proof.

As in the proof of Lemma 3.1, it follows from (28(28) $\parallel \mathrm{\nabla }f\left(x_{t,i}^{+}\right){\parallel }_{\ast }>ϵ,i=0,\dots ,i_t.$(28) ), (27(27) ${\tilde{N}}_{\nu }\left(ϵ\right)=\left\{\begin{array}{ll}(p+\nu -1)\left(H_{f,p}\right(\nu )+\theta (p-1)!),& \mathrm{i}\mathrm{f}\nu \mathrm{i}\mathrm{s}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}\mathrm{n},\\ max\left\{4\theta (p-1)!,\left(4H_{f,p}\right(\nu ){)}^{\frac{p}{p+\nu -1}}{\left(\frac{4}{ϵ}\right)}^{\frac{1-\nu }{p+\nu -1}}\right\},& \mathrm{i}\mathrm{f}\nu \mathrm{i}\mathrm{s}\mathrm{u}\mathrm{n}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}\mathrm{n}.\end{array}\right.$(27) ) and Lemmas A.6 and A.7 in [18] that ${\tilde{H}}_t\le max\left\{{\tilde{H}}_0,{\tilde{N}}_{\nu }\left(ϵ\right)\right\},t=0,\dots ,T,$ which gives ${\tilde{M}}_t=2^{i_t}{\tilde{H}}_t=2\left(2^{i_t}{\tilde{H}}_t\right)=2{\tilde{H}}_{t+1}\le 2max\left\{{\tilde{H}}_0,{\tilde{N}}_{\nu }\left(ϵ\right)\right\},t=0,\dots ,T-1.$ Then, (29(29) $f\left(x_t\right)-f\left(x^{\ast }\right)\le \frac{2^{3p}max\left\{{\tilde{H}}_0,{\tilde{N}}_{\nu }\left(ϵ\right)\right\}(p+\alpha {)}^{p+\alpha -1}\parallel x_0-x^{\ast }{\parallel }^{p+\alpha }}{(p-1)!(t-1{)}^{p+\alpha }},$(29) ) follows directly from Theorem 4.3 in [18] with $M_{\nu }=2max\{{\tilde{H}}_0,{\tilde{N}}_{\nu }(ϵ\left)\right\}$.

Now we can obtain global convergence rates for Algorithm 2 in terms of the norm of the gradient.

Theorem 4.2

Suppose that H1 holds and let sequences $\{x_t{\}}_{t=0}^T$ and $\{z_t{\}}_{t=0}^T$ be generated by Algorithm 2. Assume that, for $t=0,\dots ,T,$ we have (30) $min\left\{\parallel \mathrm{\nabla }f\left(x_{t,i}^{+}\right){\parallel }_{\ast },\parallel \mathrm{\nabla }f\left(z_{t,j}^{+}\right){\parallel }_{\ast }\right\}>ϵ,i=0,\dots ,i_t,j=0,\dots ,j_t.$(30) If T = 2s for some $s>1,$ then (31) $g_T^{\ast }\equiv \underset{0\le k\le T}{min}\parallel \mathrm{\nabla }f\left(z_t\right){\parallel }_{\ast }\le C_{\nu }\left(ϵ\right)\parallel x_0-x^{\ast }{\parallel }^{p+\alpha -1}{\left[\frac{p+1}{T-2}\right]}^{\frac{(p+\alpha -1)(p+\alpha +1)}{p+\alpha }}$(31) where $C_{\nu }\left(ϵ\right)={\left[2^{(4p+6)}max\left\{{\tilde{H}}_0,{\tilde{N}}_{\nu }\left(ϵ\right)\right\}max{\left\{H_0,N_{\nu }\left(ϵ\right)\right\}}^{\frac{1}{p+\alpha -1}}\right]}^{\frac{p+\alpha -1}{p+\alpha }},$

with $N_{\nu }\left(ϵ\right)$ and ${\tilde{N}}_{\nu }\left(ϵ\right)$ defined in (15(15) $N_{\nu }\left(ϵ\right)=\left\{\begin{array}{ll}max\left\{\frac{3H_{f,p}\left(\nu \right)}{2},3\theta (p-1)!\right\},& \mathrm{i}\mathrm{f}\nu \mathrm{i}\mathrm{s}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}\mathrm{n},\\ max\left\{\theta ,{\left(\frac{3H_{f,p}\left(\nu \right)}{2}\right)}^{\frac{p}{p+\nu -1}}{4}^{\frac{1-\nu }{p+\nu -1}}\right\}{ϵ}^{-\frac{1-\nu }{p+\nu -1}},& \mathrm{i}\mathrm{f}\nu \mathrm{i}\mathrm{s}\mathrm{u}\mathrm{n}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}\mathrm{n}.\end{array}\right.$(15) ) and (27(27) ${\tilde{N}}_{\nu }\left(ϵ\right)=\left\{\begin{array}{ll}(p+\nu -1)\left(H_{f,p}\right(\nu )+\theta (p-1)!),& \mathrm{i}\mathrm{f}\nu \mathrm{i}\mathrm{s}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}\mathrm{n},\\ max\left\{4\theta (p-1)!,\left(4H_{f,p}\right(\nu ){)}^{\frac{p}{p+\nu -1}}{\left(\frac{4}{ϵ}\right)}^{\frac{1-\nu }{p+\nu -1}}\right\},& \mathrm{i}\mathrm{f}\nu \mathrm{i}\mathrm{s}\mathrm{u}\mathrm{n}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}\mathrm{n}.\end{array}\right.$(27) ), respectively. Consequently, (32) $T\le 2+2^{(4p+6)}(p+1)max\left\{1,{\tilde{H}}_0,H_0,3p\left(H_{f,p}\left(\nu \right)+\theta (p-1)!\right)\right\}\parallel x_0-x^{\ast }{\parallel }^{\frac{p+\nu }{p+\nu +1}}{ϵ}^{-\frac{p+\nu }{(p+\nu -1)(p+\nu +1)}},$(32) if ν is known (i.e. $\alpha =\nu$), and

(33) $\begin{array}{r}T<2+2^{(2p+3)}(p+1)max{\left\{1,{\tilde{H}}_0,H_0,4\left[\left(4H_{f,p}\right(\nu ){)}^{\frac{p}{p+\nu -1}}+\theta (p-1)!\right]\right\}}^{\frac{1}{2}}\parallel x_0-x^{\ast }{\parallel }^{\frac{p+1}{p+2}}{ϵ}^{-\frac{p+1}{(p+\nu -1)(p+2)}},\end{array}$(33)

if ν is unknown (i.e. $\alpha =1$).

Proof.

By Theorem 4.1, we have (34) $f\left(x_t\right)-f\left(x^{\ast }\right)\le \frac{2^{3p}max\left\{{\tilde{H}}_0,{\tilde{N}}_{\nu }\left(ϵ\right)\right\}(p+\alpha {)}^{p+\alpha -1}\parallel x_0-x^{\ast }{\parallel }^{p+\alpha }}{(p-1)!(t-1{)}^{p+\alpha }}$(34) for $t=2,\dots ,T$. On the other hand, as in Lemma 3.1, by (30(30) $min\left\{\parallel \mathrm{\nabla }f\left(x_{t,i}^{+}\right){\parallel }_{\ast },\parallel \mathrm{\nabla }f\left(z_{t,j}^{+}\right){\parallel }_{\ast }\right\}>ϵ,i=0,\dots ,i_t,j=0,\dots ,j_t.$(30) ) we get $2^{j_t}{H}_t\le 2max\left\{H_0,N_{\nu }\left(ϵ\right)\right\},t=0,\dots ,T-1,$ where $N_{\nu }\left(ϵ\right)$ is defined in (15(15) $N_{\nu }\left(ϵ\right)=\left\{\begin{array}{ll}max\left\{\frac{3H_{f,p}\left(\nu \right)}{2},3\theta (p-1)!\right\},& \mathrm{i}\mathrm{f}\nu \mathrm{i}\mathrm{s}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}\mathrm{n},\\ max\left\{\theta ,{\left(\frac{3H_{f,p}\left(\nu \right)}{2}\right)}^{\frac{p}{p+\nu -1}}{4}^{\frac{1-\nu }{p+\nu -1}}\right\}{ϵ}^{-\frac{1-\nu }{p+\nu -1}},& \mathrm{i}\mathrm{f}\nu \mathrm{i}\mathrm{s}\mathrm{u}\mathrm{n}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}\mathrm{n}.\end{array}\right.$(15) ). Then, in view of (26), it follows that (35) $f\left({\overline{z}}_t\right)-f\left(z_{t+1}\right)\ge \frac{1}{8(p+1)!}{\left[\frac{1}{2max\left\{H_0,N_{\nu }\left(ϵ\right)\right\}}\right]}^{\frac{1}{p+\alpha -1}}\parallel \mathrm{\nabla }f\left(z_{t+1}\right){\parallel }_{\ast }^{\frac{p+\alpha }{p+\alpha -1}},$(35) for $t=0,\dots ,T-1$. In particular, $f\left(z_{t+1}\right)\le f\left({\overline{z}}_t\right)$ for $t=0,\dots ,T-1$. Moreover, by the definition of ${\overline{z}}_t$, we get $f\left({\overline{z}}_t\right)\le f\left(x_{t+1}\right)$ and $f\left({\overline{z}}_t\right)\le f\left(z_t\right)$. Therefore (36) $f\left(z_t\right)\le f\left(x_t\right),t=0,\dots ,T,$(36) and (37) $f\left(z_t\right)-f\left(z_{t+1}\right)\ge \frac{1}{8(p+1)!}{\left[\frac{1}{2max\left\{H_0,N_{\nu }\left(ϵ\right)\right\}}\right]}^{\frac{1}{p+\alpha -1}}\parallel \mathrm{\nabla }f\left(z_{t+1}\right){\parallel }_{\ast }^{\frac{p+\alpha }{p+\alpha -1}}.$(37) Now, since T = 2s, summing up (37(37) $f\left(z_t\right)-f\left(z_{t+1}\right)\ge \frac{1}{8(p+1)!}{\left[\frac{1}{2max\left\{H_0,N_{\nu }\left(ϵ\right)\right\}}\right]}^{\frac{1}{p+\alpha -1}}\parallel \mathrm{\nabla }f\left(z_{t+1}\right){\parallel }_{\ast }^{\frac{p+\alpha }{p+\alpha -1}}.$(37) ), we get $\begin{array}{rl}& \frac{2^{3p}max\left\{{\tilde{H}}_0,{\tilde{N}}_{\nu }\left(ϵ\right)\right\}(p+\alpha {)}^{p+\alpha -1}\parallel x_0-x^{\ast }{\parallel }^{p+\alpha }}{(p-1)!(s-1{)}^{p+\alpha }}\\ & \ge f\left(x_s\right)-f\left(x^{\ast }\right)\ge f\left(z_s\right)-f\left(x^{\ast }\right)\\ & =f\left(z_T\right)-f\left(x^{\ast }\right)+\sum _{k=s}^{T-1}\left(f\right(z_k)-f(z_{k+1}\left)\right)\\ & \ge \frac{(s-1)}{8(p+1)!}{\left[\frac{1}{2max\left\{H_0,N_{\nu }\left(ϵ\right)\right\}}\right]}^{\frac{1}{p+\alpha -1}}(g_T^{\ast }{)}^{\frac{p+\alpha }{p+\alpha -1}}.\end{array}$ Thus, $(g_T^{\ast }{)}^{\frac{p+\alpha }{p+\alpha -1}}\le \frac{2^{(4p+6)}max\left\{{\tilde{H}}_0,{\tilde{N}}_{\nu }\left(ϵ\right)\right\}max{\left\{H_0,N_{\nu }\left(ϵ\right)\right\}}^{\frac{1}{p+\alpha -1}}(p+1{)}^{p+\alpha +1}\parallel x_0-x^{\ast }{\parallel }^{p+\alpha }}{(T-2{)}^{p+\alpha +1}},$ and so (31(31) $g_T^{\ast }\equiv \underset{0\le k\le T}{min}\parallel \mathrm{\nabla }f\left(z_t\right){\parallel }_{\ast }\le C_{\nu }\left(ϵ\right)\parallel x_0-x^{\ast }{\parallel }^{p+\alpha -1}{\left[\frac{p+1}{T-2}\right]}^{\frac{(p+\alpha -1)(p+\alpha +1)}{p+\alpha }}$(31) ) holds. By assumption, we have $g_T^{\ast }>ϵ$. Thus, it follows from (31(31) $g_T^{\ast }\equiv \underset{0\le k\le T}{min}\parallel \mathrm{\nabla }f\left(z_t\right){\parallel }_{\ast }\le C_{\nu }\left(ϵ\right)\parallel x_0-x^{\ast }{\parallel }^{p+\alpha -1}{\left[\frac{p+1}{T-2}\right]}^{\frac{(p+\alpha -1)(p+\alpha +1)}{p+\alpha }}$(31) ) that (38) $\begin{array}{rl}& ϵ<C_{\nu }\left(ϵ\right)\parallel x_0-x^{\ast }{\parallel }^{p+\alpha -1}{\left[\frac{p+1}{T-2}\right]}^{\frac{(p+\alpha -1)(p+\alpha +1)}{(p+\alpha )}}\\ ⟹& T<2+(p+1){\left[\frac{C_{\nu }\left(ϵ\right)}{ϵ}\right]}^{\frac{p+\alpha }{(p+\alpha -1)(p+\alpha +1)}}\parallel x_0-x^{\ast }{\parallel }^{\frac{p+\alpha }{p+\alpha +1}}.\end{array}$(38) If ν is known, by (15(15) $N_{\nu }\left(ϵ\right)=\left\{\begin{array}{ll}max\left\{\frac{3H_{f,p}\left(\nu \right)}{2},3\theta (p-1)!\right\},& \mathrm{i}\mathrm{f}\nu \mathrm{i}\mathrm{s}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}\mathrm{n},\\ max\left\{\theta ,{\left(\frac{3H_{f,p}\left(\nu \right)}{2}\right)}^{\frac{p}{p+\nu -1}}{4}^{\frac{1-\nu }{p+\nu -1}}\right\}{ϵ}^{-\frac{1-\nu }{p+\nu -1}},& \mathrm{i}\mathrm{f}\nu \mathrm{i}\mathrm{s}\mathrm{u}\mathrm{n}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}\mathrm{n}.\end{array}\right.$(15) ) and (27(27) ${\tilde{N}}_{\nu }\left(ϵ\right)=\left\{\begin{array}{ll}(p+\nu -1)\left(H_{f,p}\right(\nu )+\theta (p-1)!),& \mathrm{i}\mathrm{f}\nu \mathrm{i}\mathrm{s}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}\mathrm{n},\\ max\left\{4\theta (p-1)!,\left(4H_{f,p}\right(\nu ){)}^{\frac{p}{p+\nu -1}}{\left(\frac{4}{ϵ}\right)}^{\frac{1-\nu }{p+\nu -1}}\right\},& \mathrm{i}\mathrm{f}\nu \mathrm{i}\mathrm{s}\mathrm{u}\mathrm{n}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}\mathrm{n}.\end{array}\right.$(27) ) we have $max\left\{N_{\nu }\right(ϵ),{\tilde{N}}_{\nu }(ϵ\left)\right\}\le 3p\left(H_{f,p}\right(\nu )+\theta (p-1)!)$. Then, $max\left\{{\tilde{H}}_0,{\tilde{N}}_{\nu }\left(ϵ\right)\right\}max{\left\{H_0,N_{\nu }\left(ϵ\right)\right\}}^{\frac{1}{p+\nu -1}}\le max{\left\{{\tilde{H}}_0,H_0,3p\left(H_{f,p}\left(\nu \right)+\theta (p-1)!\right)\right\}}^{\frac{p+\nu }{p+\nu -1}},$ and so (39) $C_{\nu }\left(ϵ\right)\le 2^{(4p+6)}max\left\{{\tilde{H}}_0,H_0,3p\left(H_{f,p}\left(\nu \right)+\theta (p-1)!\right)\right\}.$(39) Combining (38(38) $\begin{array}{rl}& ϵ<C_{\nu }\left(ϵ\right)\parallel x_0-x^{\ast }{\parallel }^{p+\alpha -1}{\left[\frac{p+1}{T-2}\right]}^{\frac{(p+\alpha -1)(p+\alpha +1)}{(p+\alpha )}}\\ ⟹& T<2+(p+1){\left[\frac{C_{\nu }\left(ϵ\right)}{ϵ}\right]}^{\frac{p+\alpha }{(p+\alpha -1)(p+\alpha +1)}}\parallel x_0-x^{\ast }{\parallel }^{\frac{p+\alpha }{p+\alpha +1}}.\end{array}$(38) ), (39(39) $C_{\nu }\left(ϵ\right)\le 2^{(4p+6)}max\left\{{\tilde{H}}_0,H_0,3p\left(H_{f,p}\left(\nu \right)+\theta (p-1)!\right)\right\}.$(39) ) and $\frac{p+\nu }{(p+\nu -1)(p+\nu +1)}\le 1$, we obtain (32(32) $T\le 2+2^{(4p+6)}(p+1)max\left\{1,{\tilde{H}}_0,H_0,3p\left(H_{f,p}\left(\nu \right)+\theta (p-1)!\right)\right\}\parallel x_0-x^{\ast }{\parallel }^{\frac{p+\nu }{p+\nu +1}}{ϵ}^{-\frac{p+\nu }{(p+\nu -1)(p+\nu +1)}},$(32) ). If ν is unknown, it follows from (15(15) $N_{\nu }\left(ϵ\right)=\left\{\begin{array}{ll}max\left\{\frac{3H_{f,p}\left(\nu \right)}{2},3\theta (p-1)!\right\},& \mathrm{i}\mathrm{f}\nu \mathrm{i}\mathrm{s}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}\mathrm{n},\\ max\left\{\theta ,{\left(\frac{3H_{f,p}\left(\nu \right)}{2}\right)}^{\frac{p}{p+\nu -1}}{4}^{\frac{1-\nu }{p+\nu -1}}\right\}{ϵ}^{-\frac{1-\nu }{p+\nu -1}},& \mathrm{i}\mathrm{f}\nu \mathrm{i}\mathrm{s}\mathrm{u}\mathrm{n}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}\mathrm{n}.\end{array}\right.$(15) ) and (27(27) ${\tilde{N}}_{\nu }\left(ϵ\right)=\left\{\begin{array}{ll}(p+\nu -1)\left(H_{f,p}\right(\nu )+\theta (p-1)!),& \mathrm{i}\mathrm{f}\nu \mathrm{i}\mathrm{s}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}\mathrm{n},\\ max\left\{4\theta (p-1)!,\left(4H_{f,p}\right(\nu ){)}^{\frac{p}{p+\nu -1}}{\left(\frac{4}{ϵ}\right)}^{\frac{1-\nu }{p+\nu -1}}\right\},& \mathrm{i}\mathrm{f}\nu \mathrm{i}\mathrm{s}\mathrm{u}\mathrm{n}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}\mathrm{n}.\end{array}\right.$(27) ) that $max\left\{N_{\nu }\left(ϵ\right),{\tilde{N}}_{\nu }\left(ϵ\right)\right\}\le 4\left[\left(4H_{f,p}\right(\nu ){)}^{\frac{p}{p+\nu -1}}+\theta (p-1)!\right]{ϵ}^{-\frac{1-\nu }{p+\nu -1}}.$ Then, $\begin{array}{rl}& max\left\{{\tilde{H}}_0,{\tilde{N}}_{\nu }\left(ϵ\right)\right\}max{\left\{H_0,N_{\nu }\left(ϵ\right)\right\}}^{\frac{1}{p}}\\ & \le {\left[max\left\{{\tilde{H}}_0,H_0,4\left[\left(4H_{f,p}\right(\nu ){)}^{\frac{p}{p+\nu -1}}+\theta (p-1)!\right]\right\}{ϵ}^{-\frac{1-\nu }{p+\nu -1}}\right]}^{\frac{p+1}{p}},\end{array}$ and so (40) $C_{\nu }\left(ϵ\right)\le 2^{(4p+6)}max\left\{{\tilde{H}}_0,H_0,4\left[\left(4H_{f,p}\right(\nu ){)}^{\frac{p}{p+\nu -1}}+\theta (p-1)!\right]\right\}{ϵ}^{-\frac{1-\nu }{p+\nu -1}}.$(40) Combining (38(38) $\begin{array}{rl}& ϵ<C_{\nu }\left(ϵ\right)\parallel x_0-x^{\ast }{\parallel }^{p+\alpha -1}{\left[\frac{p+1}{T-2}\right]}^{\frac{(p+\alpha -1)(p+\alpha +1)}{(p+\alpha )}}\\ ⟹& T<2+(p+1){\left[\frac{C_{\nu }\left(ϵ\right)}{ϵ}\right]}^{\frac{p+\alpha }{(p+\alpha -1)(p+\alpha +1)}}\parallel x_0-x^{\ast }{\parallel }^{\frac{p+\alpha }{p+\alpha +1}}.\end{array}$(38) ), (40(40) $C_{\nu }\left(ϵ\right)\le 2^{(4p+6)}max\left\{{\tilde{H}}_0,H_0,4\left[\left(4H_{f,p}\right(\nu ){)}^{\frac{p}{p+\nu -1}}+\theta (p-1)!\right]\right\}{ϵ}^{-\frac{1-\nu }{p+\nu -1}}.$(40) ) and $\frac{p+1}{p(p+2)}<\frac{1}{2}$, we obtain (33(33) $\begin{array}{r}T<2+2^{(2p+3)}(p+1)max{\left\{1,{\tilde{H}}_0,H_0,4\left[\left(4H_{f,p}\right(\nu ){)}^{\frac{p}{p+\nu -1}}+\theta (p-1)!\right]\right\}}^{\frac{1}{2}}\parallel x_0-x^{\ast }{\parallel }^{\frac{p+1}{p+2}}{ϵ}^{-\frac{p+1}{(p+\nu -1)(p+2)}},\end{array}$(33) ).

Remark 4.1

When $\nu =1$, bounds (32(32) $T\le 2+2^{(4p+6)}(p+1)max\left\{1,{\tilde{H}}_0,H_0,3p\left(H_{f,p}\left(\nu \right)+\theta (p-1)!\right)\right\}\parallel x_0-x^{\ast }{\parallel }^{\frac{p+\nu }{p+\nu +1}}{ϵ}^{-\frac{p+\nu }{(p+\nu -1)(p+\nu +1)}},$(32) ) and (33(33) $\begin{array}{r}T<2+2^{(2p+3)}(p+1)max{\left\{1,{\tilde{H}}_0,H_0,4\left[\left(4H_{f,p}\right(\nu ){)}^{\frac{p}{p+\nu -1}}+\theta (p-1)!\right]\right\}}^{\frac{1}{2}}\parallel x_0-x^{\ast }{\parallel }^{\frac{p+1}{p+2}}{ϵ}^{-\frac{p+1}{(p+\nu -1)(p+2)}},\end{array}$(33) ) have the same dependence on ε. However, when $\nu \ne 1$, the bound of $\mathcal{O}\left({ϵ}^{-(p+1)/\left[\right(p+\nu -1\left)\right(p+2\left)\right]}\right)$ obtained for the universal scheme (i.e. $\alpha =1$) is worse than the bound of $\mathcal{O}\left({ϵ}^{-(p+\nu )/\left[\right(p+\nu -1\left)\right(p+\nu +1\left)\right]}\right)$ obtained for the non-universal scheme (i.e. $\alpha =\nu$). In both cases, these complexity bounds are better than the bound of $\mathcal{O}\left({ϵ}^{-1/(p+\nu -1)}\right)$ proved for Algorithm 1.

5. Composite minimization

From now on, we will assume that ν and $H_{f,p}\left(\nu \right)$ are known. In this setting, we can consider the composite minimization problem: (41) $\underset{x\in \mathbb{E}}{min}\tilde{f}\left(x\right)\equiv f\left(x\right)+\varphi \left(x\right),$(41) where $f:\mathbb{E}\to \mathbb{R}$ is a convex function satisfying H1 (see page 5), and $\varphi :\mathbb{E}\to \mathbb{R}\cup \{+\mathrm{\infty }\}$ is a simple closed convex function whose effective domain has nonempty relative interior, that is, $\mathrm{r}\mathrm{i}\left(\mathrm{d}\mathrm{o}\mathrm{m}\varphi \right)\ne \mathrm{\varnothing }$. We assume that there exists at least one optimal solution $x^{\ast }\in \mathbb{E}$ for (41(41) $\underset{x\in \mathbb{E}}{min}\tilde{f}\left(x\right)\equiv f\left(x\right)+\varphi \left(x\right),$(41) ). By (6(6) $\begin{array}{rl}& |f\left(y\right)-{\mathrm{\Phi }}_{x,p}\left(y\right)|\le \frac{H_{f,p}\left(\nu \right)}{p!}\parallel y-x{\parallel }^{p+\nu },\end{array}$(6) ), if $H\ge H_{f,p}\left(\nu \right)$ we have $\tilde{f}\left(y\right)\le {\mathrm{\Omega }}_{x,p,H}^{\left(\nu \right)}\left(y\right)+\varphi \left(y\right),\mathrm{\forall }y\in \mathbb{E}.$ This motivates the following class of models of $\tilde{f}$ around a fixed point $x\in \mathbb{E}$: (42) ${\tilde{\mathrm{\Omega }}}_{x,p,H}^{\left(\nu \right)}\left(y\right)\equiv {\mathrm{\Omega }}_{x,p,H}^{\left(\nu \right)}\left(y\right)+\varphi \left(y\right),$(42) where ${\mathrm{\Omega }}_{x,p,H}^{\left(\nu \right)}(\cdot )$ is defined in (10(10) ${\mathrm{\Omega }}_{x,p,H}^{\left(\alpha \right)}\left(y\right)={\mathrm{\Phi }}_{x,p}\left(y\right)+\frac{H}{p!}\parallel y-x{\parallel }^{p+\alpha },\alpha \in [0,1].$(10) ). The next lemma gives a sufficient condition for function ${\mathrm{\Omega }}_{x,p,H}^{\left(\nu \right)}(\cdot )$ to be convex. Its proof is an adaptation of the proof of Theorem 1 in [27].

Lemma 5.1

Suppose that H1 holds for some $p\ge 2$. Then, for any $x,y\in \mathbb{E}$ we have (43) ${\mathrm{\nabla }}^{2}f\left(y\right)⪯{\mathrm{\nabla }}^2{\mathrm{\Phi }}_{x,p}\left(y\right)+\frac{H_{f,p}\left(\nu \right)}{(p-2)!}\parallel y-x{\parallel }^{p+\nu -2}B.$(43) Moreover, if $H\ge (p-1)H_{f,p}\left(\nu \right),$ then function ${\mathrm{\Omega }}_{x,p,H}^{\left(\nu \right)}(\cdot )$ is convex for any $x\in \mathbb{E}$.

Proof.

For any $u\in \mathbb{E}$, it follows from (8(8) $\parallel {\mathrm{\nabla }}^{2}f\left(y\right)-{\mathrm{\nabla }}^2{\mathrm{\Phi }}_{x,p}\left(y\right){\parallel }_{\ast }\le \frac{H_{f,p}\left(\nu \right)}{(p-2)!}\parallel y-x{\parallel }^{p+\nu -2}.$(8) ) that $\begin{array}{rl}⟨\left({\mathrm{\nabla }}^{2}f\left(y\right)-{\mathrm{\nabla }}^2{\mathrm{\Phi }}_{x,p}\left(y\right)\right)u,u⟩& \le \parallel {\mathrm{\nabla }}^{2}f\left(y\right)-{\mathrm{\nabla }}^2{\mathrm{\Phi }}_{x,p}\left(y\right){\parallel }_{\ast }\parallel u{\parallel }^2\\ & \le \frac{H_{f,p}\left(\nu \right)}{(p-2)!}\parallel y-x{\parallel }^{p+\nu -2}\parallel u{\parallel }^2.\end{array}$ Since $u\in \mathbb{E}$ is arbitrary, we get (43(43) ${\mathrm{\nabla }}^{2}f\left(y\right)⪯{\mathrm{\nabla }}^2{\mathrm{\Phi }}_{x,p}\left(y\right)+\frac{H_{f,p}\left(\nu \right)}{(p-2)!}\parallel y-x{\parallel }^{p+\nu -2}B.$(43) ).

Now, suppose that $H\ge (p-1)H_{f,p}\left(\nu \right)$. Then, by (43(43) ${\mathrm{\nabla }}^{2}f\left(y\right)⪯{\mathrm{\nabla }}^2{\mathrm{\Phi }}_{x,p}\left(y\right)+\frac{H_{f,p}\left(\nu \right)}{(p-2)!}\parallel y-x{\parallel }^{p+\nu -2}B.$(43) ) we have $\begin{array}{rl}0⪯{\mathrm{\nabla }}^{2}f\left(y\right)& ⪯{\mathrm{\nabla }}^2{\mathrm{\Phi }}_{x,p}\left(y\right)+\frac{H_{f,p}\left(\nu \right)(p-1)}{(p-1)!}\parallel y-x{\parallel }^{p+\nu -2}B\\ & ⪯{\mathrm{\nabla }}^2{\mathrm{\Phi }}_{x,p}\left(y\right)+\frac{H}{(p-1)!}\parallel y-x{\parallel }^{p+\nu -2}B\\ & ⪯{\mathrm{\nabla }}^2{\mathrm{\Phi }}_{x,p}\left(y\right)+\frac{H(p+\nu )}{p!}\parallel y-x{\parallel }^{p+\nu -2}B\\ & ⪯{\mathrm{\nabla }}^2{\mathrm{\Phi }}_{x,p}\left(y\right)+{\mathrm{\nabla }}^2\left(\frac{H}{p!}\parallel y-x{\parallel }^{p+\nu }\right)={\mathrm{\nabla }}^2{\mathrm{\Omega }}_{x,p,H}^{\left(\nu \right)}\left(y\right).\end{array}$ Therefore, ${\mathrm{\Omega }}_{x,p,H}^{\left(\nu \right)}\left(y\right)$ is convex.

From Lemma 5.1, if $H\ge (p-1)H_{f,p}\left(\nu \right)$, it follows that ${\tilde{\mathrm{\Omega }}}_{x,p,H}^{\left(\nu \right)}(\cdot )$ is also convex. In this case, since $\mathrm{r}\mathrm{i}\left(\mathrm{d}\mathrm{o}\mathrm{m}\varphi \right)\ne \mathrm{\varnothing }$, any solution $x^{+}$ of (44) $\underset{y\in \mathbb{E}}{min}{\tilde{\mathrm{\Omega }}}_{x,p,H}^{\left(\nu \right)}\left(y\right)$(44) satisfies the first-order optimality condition: (45) $0\in \mathrm{\partial }{\tilde{\mathrm{\Omega }}}_{x,p,H}^{\left(\nu \right)}\left(x^{+}\right)=\mathrm{\partial }{\mathrm{\Omega }}_{x,p,H}^{\left(\nu \right)}\left(x^{+}\right)+\mathrm{\partial }\varphi \left(x^{+}\right)=\left\{\mathrm{\nabla }{\mathrm{\Omega }}_{x,p,H}^{\left(\nu \right)}\left(x^{+}\right)\right\}+\mathrm{\partial }\varphi \left(x^{+}\right).$(45) Therefore, there exists $g_{\varphi }\left(x^{+}\right)\in \mathrm{\partial }\varphi \left(x^{+}\right)$ such that (46) $\mathrm{\nabla }{\mathrm{\Omega }}_{x,p,H}^{\left(\nu \right)}\left(x^{+}\right)+g_{\varphi }\left(x^{+}\right)=0.$(46) Instead of solving (44(44) $\underset{y\in \mathbb{E}}{min}{\tilde{\mathrm{\Omega }}}_{x,p,H}^{\left(\nu \right)}\left(y\right)$(44) ) exactly, in our algorithms we consider inexact solutions $x^{+}$ such that¹ (47) ${\tilde{\mathrm{\Omega }}}_{x,p,H}^{\left(\nu \right)}\left(x^{+}\right)\le \tilde{f}\left(x\right)\mathrm{a}\mathrm{n}\mathrm{d}\parallel \mathrm{\nabla }{\mathrm{\Omega }}_{x,p,H}^{\left(\nu \right)}\left(x^{+}\right)+g_{\varphi }\left(x^{+}\right){\parallel }_{\ast }\le \theta \parallel x^{+}-x{\parallel }^{p+\nu -1},$(47) for some $g_{\varphi }\left(x^{+}\right)\in \mathrm{\partial }\varphi \left(x^{+}\right)$ and $\theta \ge 0$. For such points $x^{+}$, we define (48) $\mathrm{\nabla }\tilde{f}\left(x^{+}\right)\equiv \mathrm{\nabla }f\left(x^{+}\right)+g_{\varphi }\left(x^{+}\right),$(48) with $g_{\varphi }\left(x^{+}\right)$ satisfying (47(47) ${\tilde{\mathrm{\Omega }}}_{x,p,H}^{\left(\nu \right)}\left(x^{+}\right)\le \tilde{f}\left(x\right)\mathrm{a}\mathrm{n}\mathrm{d}\parallel \mathrm{\nabla }{\mathrm{\Omega }}_{x,p,H}^{\left(\nu \right)}\left(x^{+}\right)+g_{\varphi }\left(x^{+}\right){\parallel }_{\ast }\le \theta \parallel x^{+}-x{\parallel }^{p+\nu -1},$(47) ). Clearly, we have $\mathrm{\nabla }\tilde{f}\left(x^{+}\right)\in \mathrm{\partial }\tilde{f}\left(x^{+}\right)$.

Lemma 5.2

Suppose that H1 holds and let $x^{+}$ be an approximate solution of (44(44) $\underset{y\in \mathbb{E}}{min}{\tilde{\mathrm{\Omega }}}_{x,p,H}^{\left(\nu \right)}\left(y\right)$(44) ) such that (47(47) ${\tilde{\mathrm{\Omega }}}_{x,p,H}^{\left(\nu \right)}\left(x^{+}\right)\le \tilde{f}\left(x\right)\mathrm{a}\mathrm{n}\mathrm{d}\parallel \mathrm{\nabla }{\mathrm{\Omega }}_{x,p,H}^{\left(\nu \right)}\left(x^{+}\right)+g_{\varphi }\left(x^{+}\right){\parallel }_{\ast }\le \theta \parallel x^{+}-x{\parallel }^{p+\nu -1},$(47) ) holds for some $x\in \mathbb{E}$. If (49) $H\ge max\left\{p{H}_{f,p}\left(\nu \right),3\theta (p-1)!\right\},$(49) then (50) $\tilde{f}\left(x\right)-\tilde{f}\left(x^{+}\right)\ge \frac{1}{8(p+1)!H^{\frac{1}{p+\nu -1}}}\parallel \mathrm{\nabla }\tilde{f}\left(x^{+}\right){\parallel }_{\ast }^{\frac{p+\nu }{p+\nu -1}}.$(50)

Proof.

By (48(48) $\mathrm{\nabla }\tilde{f}\left(x^{+}\right)\equiv \mathrm{\nabla }f\left(x^{+}\right)+g_{\varphi }\left(x^{+}\right),$(48) ), (7(7) $\begin{array}{rl}& \parallel \mathrm{\nabla }f\left(y\right)-\mathrm{\nabla }{\mathrm{\Phi }}_{x,p}\left(y\right){\parallel }_{\ast }\le \frac{H_{f,p}\left(\nu \right)}{(p-1)!}\parallel y-x{\parallel }^{p+\nu -1},\end{array}$(7) ), (10(10) ${\mathrm{\Omega }}_{x,p,H}^{\left(\alpha \right)}\left(y\right)={\mathrm{\Phi }}_{x,p}\left(y\right)+\frac{H}{p!}\parallel y-x{\parallel }^{p+\alpha },\alpha \in [0,1].$(10) ), (47(47) ${\tilde{\mathrm{\Omega }}}_{x,p,H}^{\left(\nu \right)}\left(x^{+}\right)\le \tilde{f}\left(x\right)\mathrm{a}\mathrm{n}\mathrm{d}\parallel \mathrm{\nabla }{\mathrm{\Omega }}_{x,p,H}^{\left(\nu \right)}\left(x^{+}\right)+g_{\varphi }\left(x^{+}\right){\parallel }_{\ast }\le \theta \parallel x^{+}-x{\parallel }^{p+\nu -1},$(47) ) and (49(49) $H\ge max\left\{p{H}_{f,p}\left(\nu \right),3\theta (p-1)!\right\},$(49) ) we have (51) $\begin{array}{rl}\parallel \mathrm{\nabla }\tilde{f}\left(x^{+}\right){\parallel }_{\ast }& =\parallel \mathrm{\nabla }f\left(x^{+}\right)+g_{\varphi }\left(x^{+}\right){\parallel }_{\ast }\\ & \le \parallel \mathrm{\nabla }f\left(x^{+}\right)-\mathrm{\nabla }{\mathrm{\Phi }}_{x,p}\left(x^{+}\right){\parallel }_{\ast }+\parallel \mathrm{\nabla }{\mathrm{\Phi }}_{x,p}\left(x^{+}\right)-\mathrm{\nabla }{\mathrm{\Omega }}_{x,p,H}^{\left(\nu \right)}\left(x^{+}\right){\parallel }_{\ast }\\ & +\parallel \mathrm{\nabla }{\mathrm{\Omega }}_{x,p,H}^{\left(\nu \right)}\left(x^{+}\right)+g_{\varphi }\left(x^{+}\right){\parallel }_{\ast }\\ & \le \left[\frac{H_{f,p}\left(\nu \right)}{(p-1)!}+\frac{H(p+\nu )}{p!}+\theta \right]\parallel x^{+}-x{\parallel }^{p+\nu -1}\le 2H\parallel x^{+}-x{\parallel }^{p+\nu -1},\end{array}$(51) where the last inequality is due to $p\ge 2$. On the other hand, by (6(6) $\begin{array}{rl}& |f\left(y\right)-{\mathrm{\Phi }}_{x,p}\left(y\right)|\le \frac{H_{f,p}\left(\nu \right)}{p!}\parallel y-x{\parallel }^{p+\nu },\end{array}$(6) ), (42(42) ${\tilde{\mathrm{\Omega }}}_{x,p,H}^{\left(\nu \right)}\left(y\right)\equiv {\mathrm{\Omega }}_{x,p,H}^{\left(\nu \right)}\left(y\right)+\varphi \left(y\right),$(42) ), (49(49) $H\ge max\left\{p{H}_{f,p}\left(\nu \right),3\theta (p-1)!\right\},$(49) ), we have $\begin{array}{rl}\tilde{f}\left(x^{+}\right)& \le {\tilde{\mathrm{\Omega }}}_{x,p,H_{f,p}\left(\nu \right)}^{\left(\nu \right)}\left(x^{+}\right)={\mathrm{\Phi }}_{x,p}\left(x^{+}\right)+\frac{H_{f,p}\left(\nu \right)}{p!}\parallel x^{+}-x{\parallel }^{p+\nu }+\varphi \left(x^{+}\right)\\ & ={\mathrm{\Phi }}_{x,p}\left(x^{+}\right)+\frac{H}{p!}\parallel x^{+}-x{\parallel }^{p+\nu }-\frac{(H-H_{f,p}(\nu \left)\right)}{p!}\parallel x^{+}-x{\parallel }^{p+\nu }+\varphi \left(x^{+}\right)\\ & ={\tilde{\mathrm{\Omega }}}_{x,p,H}^{\left(\nu \right)}\left(x^{+}\right)-\frac{H-H_{f,p}\left(\nu \right)}{p!}\parallel x^{+}-x{\parallel }^{p+\nu }\le \tilde{f}\left(x^{+}\right)-\frac{H-H_{f,p}\left(\nu \right)}{p!}\parallel x^{+}-x{\parallel }^{p+\nu }.\end{array}$ Note that $H\ge p{H}_{f,p}\left(\nu \right)\ge \left(\frac{p+1}{p}\right)H_{f,p}\left(\nu \right)$. Thus, (52) $\begin{array}{rl}\tilde{f}\left(x\right)-\tilde{f}\left(x^{+}\right)& \ge \frac{H-H_{f,p}\left(\nu \right)}{p!}\parallel x^{+}-x{\parallel }^{p+\nu }\ge \frac{\left(H-\frac{1}{p+1}H\right)}{p!}\parallel x^{+}-x{\parallel }^{p+\nu }\\ & =\frac{H}{(p+1)!}\parallel x^{+}-x{\parallel }^{p+\nu }.\end{array}$(52) Finally, combining (51(51) $\begin{array}{rl}\parallel \mathrm{\nabla }\tilde{f}\left(x^{+}\right){\parallel }_{\ast }& =\parallel \mathrm{\nabla }f\left(x^{+}\right)+g_{\varphi }\left(x^{+}\right){\parallel }_{\ast }\\ & \le \parallel \mathrm{\nabla }f\left(x^{+}\right)-\mathrm{\nabla }{\mathrm{\Phi }}_{x,p}\left(x^{+}\right){\parallel }_{\ast }+\parallel \mathrm{\nabla }{\mathrm{\Phi }}_{x,p}\left(x^{+}\right)-\mathrm{\nabla }{\mathrm{\Omega }}_{x,p,H}^{\left(\nu \right)}\left(x^{+}\right){\parallel }_{\ast }\\ & +\parallel \mathrm{\nabla }{\mathrm{\Omega }}_{x,p,H}^{\left(\nu \right)}\left(x^{+}\right)+g_{\varphi }\left(x^{+}\right){\parallel }_{\ast }\\ & \le \left[\frac{H_{f,p}\left(\nu \right)}{(p-1)!}+\frac{H(p+\nu )}{p!}+\theta \right]\parallel x^{+}-x{\parallel }^{p+\nu -1}\le 2H\parallel x^{+}-x{\parallel }^{p+\nu -1},\end{array}$(51) ) and (52(52) $\begin{array}{rl}\tilde{f}\left(x\right)-\tilde{f}\left(x^{+}\right)& \ge \frac{H-H_{f,p}\left(\nu \right)}{p!}\parallel x^{+}-x{\parallel }^{p+\nu }\ge \frac{\left(H-\frac{1}{p+1}H\right)}{p!}\parallel x^{+}-x{\parallel }^{p+\nu }\\ & =\frac{H}{(p+1)!}\parallel x^{+}-x{\parallel }^{p+\nu }.\end{array}$(52) ), we get (50(50) $\tilde{f}\left(x\right)-\tilde{f}\left(x^{+}\right)\ge \frac{1}{8(p+1)!H^{\frac{1}{p+\nu -1}}}\parallel \mathrm{\nabla }\tilde{f}\left(x^{+}\right){\parallel }_{\ast }^{\frac{p+\nu }{p+\nu -1}}.$(50) ).

In this composite context, let us consider the following scheme:

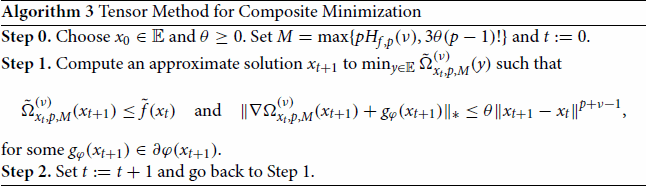
For p = 3, point $x_{t+1}$ at Step 1 can be computed by Algorithm 2 in [19], which is linearly convergent. As far as we know, the development of efficient algorithms to approximately solve (44(44) $\underset{y\in \mathbb{E}}{min}{\tilde{\mathrm{\Omega }}}_{x,p,H}^{\left(\nu \right)}\left(y\right)$(44) )–(42(42) ${\tilde{\mathrm{\Omega }}}_{x,p,H}^{\left(\nu \right)}\left(y\right)\equiv {\mathrm{\Omega }}_{x,p,H}^{\left(\nu \right)}\left(y\right)+\varphi \left(y\right),$(42) ) with p>3 is still an open problem.

Theorem 5.3

Suppose that H1 holds and that $\tilde{f}$ is bounded from below by ${\tilde{f}}^{\ast }$. Given $ϵ\in (0,1),$ assume that $\{x_t{\}}_{t=0}^T$ is a sequence generated by Algorithm 3 such that $\parallel \mathrm{\nabla }\tilde{f}\left(x_t\right){\parallel }_{\ast }>ϵ$ for $t=0,\dots ,T$. Then, (53) $T\le 8(p+1)!M^{\frac{1}{p+\nu -1}}\left(\tilde{f}\left(x_0\right)-{\tilde{f}}^{\ast }\right){ϵ}^{-\frac{p+\nu }{p+\nu -1}}.$(53)

Proof.

By Lemma 5.2, bound (53(53) $T\le 8(p+1)!M^{\frac{1}{p+\nu -1}}\left(\tilde{f}\left(x_0\right)-{\tilde{f}}^{\ast }\right){ϵ}^{-\frac{p+\nu }{p+\nu -1}}.$(53) ) follows as in Remark 3.2.

5.1. Extended accelerated scheme

Let us consider the following variant of Algorithm 2 for composite minimization:

The next theorem gives the global convergence rate for Algorithm 4 in terms of the norm of the gradient. Its proof is a direct adaptation of the proof of Theorem 4.2.

Theorem 5.4

Suppose that H1 holds. Assume that $\{z_t{\}}_{t=0}^T$ is a sequence generated by Algorithm 4 such that (56) $\parallel \mathrm{\nabla }\tilde{f}\left(z_t\right){\parallel }_{\ast }>ϵ,t=0,\dots ,T.$(56) If T = 2s for some $s>1,$ then (57) ${\tilde{g}}_T\equiv \underset{0\le k\le T}{min}\parallel \mathrm{\nabla }\tilde{f}\left(z_t\right){\parallel }_{\ast }\le \frac{{\left[2^{4(p+1)}\right]}^{\frac{p+\nu -1}{p+\nu }}M\parallel x_0-x^{\ast }{\parallel }^{p+\nu -1}}{(T-2{)}^{\frac{(p+\nu -1)(p+\nu +1)}{p+\nu }}}.$(57) Consequently, (58) $T\le 2+{\left[2^{4(p+1)}\right]}^{\frac{1}{p+\nu +1}}\parallel x_0-x^{\ast }{\parallel }^{\frac{p+\nu }{p+\nu +1}}{\left(\frac{M}{ϵ}\right)}^{\frac{p+\nu }{(p+\nu -1)(p+\nu +1)}}.$(58)

Proof.

In view of Theorem A.2, we have (59) $\tilde{f}\left(x_t\right)-\tilde{f}\left(x^{\ast }\right)\le \frac{2^{3p-1}M(p+\nu {)}^{p+\nu -1}\parallel x_0-x^{\ast }{\parallel }^{p+\nu }}{(p-1)!(t-1{)}^{p+\nu }},$(59) for $t=2,\dots ,T$. On the other hand, by (55) and Lemma 5.2, we have (60) $\tilde{f}\left({\overline{z}}_t\right)-\tilde{f}\left(z_{t+1}\right)\ge \frac{1}{8(p+1)!M^{\frac{1}{p+\nu -1}}}\parallel \mathrm{\nabla }\tilde{f}\left(z_{t+1}\right){\parallel }_{\ast }^{\frac{p+\nu }{p+\nu -1}},$(60) for $t=0,\dots ,T-1$. Thus, $f\left(z_{t+1}\right)\le f\left({\overline{z}}_t\right)\le min\left\{f\right(x_{t+1}),f(z_t\left)\right\}$ and, consequently, (61) $\tilde{f}\left(z_t\right)\le \tilde{f}\left(x_t\right),t=0,\dots ,T,$(61) and (62) $\tilde{f}\left(z_t\right)-\tilde{f}\left(z_{t+1}\right)\ge \frac{1}{8(p+1)!M^{\frac{1}{p+\nu -1}}}\parallel \mathrm{\nabla }\tilde{f}\left(z_{t+1}\right){\parallel }_{\ast }^{\frac{p+\nu }{p+\nu -1}},t=0,\dots ,T-1.$(62) Since T = 2s, combining (59(59) $\tilde{f}\left(x_t\right)-\tilde{f}\left(x^{\ast }\right)\le \frac{2^{3p-1}M(p+\nu {)}^{p+\nu -1}\parallel x_0-x^{\ast }{\parallel }^{p+\nu }}{(p-1)!(t-1{)}^{p+\nu }},$(59) ), (61(61) $\tilde{f}\left(z_t\right)\le \tilde{f}\left(x_t\right),t=0,\dots ,T,$(61) ) and (62(62) $\tilde{f}\left(z_t\right)-\tilde{f}\left(z_{t+1}\right)\ge \frac{1}{8(p+1)!M^{\frac{1}{p+\nu -1}}}\parallel \mathrm{\nabla }\tilde{f}\left(z_{t+1}\right){\parallel }_{\ast }^{\frac{p+\nu }{p+\nu -1}},t=0,\dots ,T-1.$(62) ), we obtain $\begin{array}{rl}\frac{2^{3p-1}M(p+\nu {)}^{p+\nu -1}\parallel x_0-x^{\ast }{\parallel }^{p+\nu }}{(p-1)!(s-1{)}^{p+\nu }}& \ge \tilde{f}\left(x_s\right)-\tilde{f}\left(x^{\ast }\right)\ge \tilde{f}\left(z_s\right)-\tilde{f}\left(x^{\ast }\right)\\ & =\tilde{f}\left(z_T\right)-\tilde{f}\left(x^{\ast }\right)+\sum _{k=s}^{T-1}\tilde{f}\left(z_t\right)-\tilde{f}\left(z_{t+1}\right)\\ & \ge \frac{(s-1)}{8(p+1)!M^{\frac{1}{p+\nu -1}}}{\left({\tilde{g}}_T\right)}^{\frac{p+\nu }{p+\nu -1}},\end{array}$ where ${\tilde{g}}_T=\underset{0\le k\le T}{min}\parallel \mathrm{\nabla }\tilde{f}\left(z_t\right){\parallel }_{\ast }$. Therefore, ${\left({\tilde{g}}_T\right)}^{\frac{p+\nu }{p+\nu -1}}\le \frac{2^{4(p+1)}{M}^{\frac{p+\nu }{p+\nu -1}}(p+1{)}^{p+\nu +1}\parallel x_0-x^{\ast }{\parallel }^{p+\nu }}{(T-2{)}^{p+\nu +1}},$ which gives (57(57) ${\tilde{g}}_T\equiv \underset{0\le k\le T}{min}\parallel \mathrm{\nabla }\tilde{f}\left(z_t\right){\parallel }_{\ast }\le \frac{{\left[2^{4(p+1)}\right]}^{\frac{p+\nu -1}{p+\nu }}M\parallel x_0-x^{\ast }{\parallel }^{p+\nu -1}}{(T-2{)}^{\frac{(p+\nu -1)(p+\nu +1)}{p+\nu }}}.$(57) ). Finally, by (56(56) $\parallel \mathrm{\nabla }\tilde{f}\left(z_t\right){\parallel }_{\ast }>ϵ,t=0,\dots ,T.$(56) ) we have ${\tilde{g}}_T>ϵ$. Thus, (58(58) $T\le 2+{\left[2^{4(p+1)}\right]}^{\frac{1}{p+\nu +1}}\parallel x_0-x^{\ast }{\parallel }^{\frac{p+\nu }{p+\nu +1}}{\left(\frac{M}{ϵ}\right)}^{\frac{p+\nu }{(p+\nu -1)(p+\nu +1)}}.$(58) ) follows directly from (57(57) ${\tilde{g}}_T\equiv \underset{0\le k\le T}{min}\parallel \mathrm{\nabla }\tilde{f}\left(z_t\right){\parallel }_{\ast }\le \frac{{\left[2^{4(p+1)}\right]}^{\frac{p+\nu -1}{p+\nu }}M\parallel x_0-x^{\ast }{\parallel }^{p+\nu -1}}{(T-2{)}^{\frac{(p+\nu -1)(p+\nu +1)}{p+\nu }}}.$(57) ).

5.2. Regularization approach

Now, let us consider the ideal situation in which ν, $H_{f,p}\left(\nu \right)$ and $R\ge \parallel x_0-x^{\ast }\parallel$ are known. In this case, a complexity bound with a better dependence on ε can be obtained by repeatedly applying an accelerated algorithm to a suitable regularization of $\tilde{f}$. Specifically, given $\delta >0$, consider the regularized problem (63) $\underset{x\in {\mathbb{R}}^n}{min}{\tilde{F}}_{\delta }\left(x\right)\equiv F_{\delta }\left(x\right)+\varphi \left(x\right),$(63) for (64) $F_{\delta }\left(x\right)=f\left(x\right)+\frac{\delta }{p+\nu }\parallel x-x_0{\parallel }^{p+\nu }.$(64)

Lemma 5.5

Given $x_0\in \mathbb{E}$ and $\nu \in [0,1],$ let $d_{p+\nu }:\mathbb{E}\to \mathbb{R}$ be defined by $d_{p+\nu }\left(x\right)=\parallel x-x_0{\parallel }^{p+\nu }$, where $\parallel \cdot \parallel$ is the Euclidean norm defined in (1(1) $\parallel x\parallel =⟨Bx,x{⟩}^{1/2},x\in \mathbb{E},\parallel s{\parallel }_{\ast }=⟨s,B^{-1}s{⟩}^{1/2},s\in {\mathbb{E}}^{\ast }.$(1) ). Then, $\parallel D^p{d}_{p+\nu }\left(x\right)-D^p{d}_{p+\nu }\left(y\right)\parallel \le C_{p,\nu }\parallel x-y{\parallel }^{\nu },\mathrm{\forall }x,y\in \mathbb{E},$ where $C_{p,\nu }=2{\mathrm{\Pi }}_{i=1}^p(\nu +i)$.

Proof.

See [32].

As a consequence of the lemma above, we have the following property.

Lemma 5.6

If H1 holds, then the pth derivative of $F_{\delta }(\cdot )$ in (64(64) $F_{\delta }\left(x\right)=f\left(x\right)+\frac{\delta }{p+\nu }\parallel x-x_0{\parallel }^{p+\nu }.$(64) ) is ν-Hölder continuous with constant $H_{F_{\delta },p}\left(\nu \right)=H_{f,p}\left(\nu \right)+\frac{\delta }{p+\nu }{C}_{p,\nu }$.

In view of Lemma 5.6, to solve (63(63) $\underset{x\in {\mathbb{R}}^n}{min}{\tilde{F}}_{\delta }\left(x\right)\equiv F_{\delta }\left(x\right)+\varphi \left(x\right),$(63) ) we can use the following instance of Algorithm A1 (see Appendix):

Let us consider the following restart procedure based on Algorithm 5.

Theorem 5.7

Suppose that H1 holds and let $\{u_k{\}}_{k=0}^T$ be a sequence generated by Algorithm 6 such that (68) $\parallel \mathrm{\nabla }{\tilde{F}}_{\delta }\left(u_k\right)\parallel >\frac{ϵ}{2},k=0,\dots ,T.$(68) Then, (69) $T\le 1+{\log }_2\left(\frac{32(p+1)!H_{\delta }^{\frac{1}{p+\nu -1}}\delta R^{p+\nu }}{2^{p+\nu -1}(p+\nu ){ϵ}^{\frac{p+\nu }{p+\nu -1}}}\right).$(69)

Proof.

Let $x_{\delta }^{\ast }=\arg \underset{x\in \mathbb{E}}{min}{\tilde{F}}_{\delta }\left(x\right)$. By Theorem A.2 and (66), we have (70) $\begin{array}{rl}{\tilde{F}}_{\delta }\left(y_{k+1}\right)-{\tilde{F}}_{\delta }\left(x_{\delta }^{\ast }\right)& ={\tilde{F}}_{\delta }\left(x_m^{\left(k\right)}\right)-{\tilde{F}}_{\delta }\left(x_{\delta }^{\ast }\right)\\ & \le \frac{2^{3p-1}{H}_{\delta }(p+\nu {)}^{p+\nu -1}\parallel x_0^{\left(k\right)}-x_{\delta }^{\ast }{\parallel }^{p+\nu }}{(p-1)!(m-1{)}^{p+\nu }}\\ & \le \frac{\delta 2^{-(p+\nu -2)}}{2(p+\nu )}\parallel y_k-x_{\delta }^{\ast }{\parallel }^{p+\nu }.\end{array}$(70) On the other hand, by Lemma 5 in [12] and Lemma 1 in [25], function $F_{\delta }(\cdot )$ is uniformly convex of degree $p+\nu$ with parameter $2^{-(p+\nu -2)}$. Thus, (71) ${\tilde{F}}_{\delta }\left(y_{k+1}\right)-{\tilde{F}}_{\delta }\left(x_{\delta }^{\ast }\right)\ge \frac{\delta 2^{-(p+\nu -2)}}{p+\nu }\parallel y_{k+1}-x_{\delta }^{\ast }{\parallel }^{p+\nu }.$(71) Combining (70(70) $\begin{array}{rl}{\tilde{F}}_{\delta }\left(y_{k+1}\right)-{\tilde{F}}_{\delta }\left(x_{\delta }^{\ast }\right)& ={\tilde{F}}_{\delta }\left(x_m^{\left(k\right)}\right)-{\tilde{F}}_{\delta }\left(x_{\delta }^{\ast }\right)\\ & \le \frac{2^{3p-1}{H}_{\delta }(p+\nu {)}^{p+\nu -1}\parallel x_0^{\left(k\right)}-x_{\delta }^{\ast }{\parallel }^{p+\nu }}{(p-1)!(m-1{)}^{p+\nu }}\\ & \le \frac{\delta 2^{-(p+\nu -2)}}{2(p+\nu )}\parallel y_k-x_{\delta }^{\ast }{\parallel }^{p+\nu }.\end{array}$(70) ) and (71(71) ${\tilde{F}}_{\delta }\left(y_{k+1}\right)-{\tilde{F}}_{\delta }\left(x_{\delta }^{\ast }\right)\ge \frac{\delta 2^{-(p+\nu -2)}}{p+\nu }\parallel y_{k+1}-x_{\delta }^{\ast }{\parallel }^{p+\nu }.$(71) ), we obtain $\parallel y_{k+1}-x_{\delta }^{\ast }{\parallel }^{p+\nu }\le {\displaystyle \frac{1}{2}}\parallel y_k-x_{\delta }^{\ast }{\parallel }^{p+\nu }$, and so (72) $\parallel y_k-x_{\delta }^{\ast }{\parallel }^{p+\nu }\le {\left(\frac{1}{2}\right)}^k\parallel y_0-x_{\delta }^{\ast }{\parallel }^{p+\nu }={\left(\frac{1}{2}\right)}^k\parallel x_0-x_{\delta }^{\ast }{\parallel }^{p+\nu }.$(72) Thus, it follows from (70(70) $\begin{array}{rl}{\tilde{F}}_{\delta }\left(y_{k+1}\right)-{\tilde{F}}_{\delta }\left(x_{\delta }^{\ast }\right)& ={\tilde{F}}_{\delta }\left(x_m^{\left(k\right)}\right)-{\tilde{F}}_{\delta }\left(x_{\delta }^{\ast }\right)\\ & \le \frac{2^{3p-1}{H}_{\delta }(p+\nu {)}^{p+\nu -1}\parallel x_0^{\left(k\right)}-x_{\delta }^{\ast }{\parallel }^{p+\nu }}{(p-1)!(m-1{)}^{p+\nu }}\\ & \le \frac{\delta 2^{-(p+\nu -2)}}{2(p+\nu )}\parallel y_k-x_{\delta }^{\ast }{\parallel }^{p+\nu }.\end{array}$(70) ) and (72(72) $\parallel y_k-x_{\delta }^{\ast }{\parallel }^{p+\nu }\le {\left(\frac{1}{2}\right)}^k\parallel y_0-x_{\delta }^{\ast }{\parallel }^{p+\nu }={\left(\frac{1}{2}\right)}^k\parallel x_0-x_{\delta }^{\ast }{\parallel }^{p+\nu }.$(72) ) that (73) ${\tilde{F}}_{\delta }\left(y_{k+1}\right)-{\tilde{F}}_{\delta }\left(x_{\delta }^{\ast }\right)\le \frac{\delta }{2^{p+\nu -1}(p+\nu )}{\left(\frac{1}{2}\right)}^k\parallel x_0-x_{\delta }^{\ast }{\parallel }^{p+\nu }.$(73) In view of Lemma 5.2, by (67) and (65), we get (74) ${\tilde{F}}_{\delta }\left(y_{k+1}\right)-{\tilde{F}}_{\delta }\left(u_{k+1}\right)\ge \frac{1}{8(p+1)!H_{\delta }^{\frac{1}{p+\nu -1}}}\parallel \mathrm{\nabla }{\tilde{F}}_{\delta }\left(u_{k+1}\right){\parallel }_{\ast }^{\frac{p+\nu }{p+\nu -1}}.$(74) Then, combining (73(73) ${\tilde{F}}_{\delta }\left(y_{k+1}\right)-{\tilde{F}}_{\delta }\left(x_{\delta }^{\ast }\right)\le \frac{\delta }{2^{p+\nu -1}(p+\nu )}{\left(\frac{1}{2}\right)}^k\parallel x_0-x_{\delta }^{\ast }{\parallel }^{p+\nu }.$(73) ) and (74(74) ${\tilde{F}}_{\delta }\left(y_{k+1}\right)-{\tilde{F}}_{\delta }\left(u_{k+1}\right)\ge \frac{1}{8(p+1)!H_{\delta }^{\frac{1}{p+\nu -1}}}\parallel \mathrm{\nabla }{\tilde{F}}_{\delta }\left(u_{k+1}\right){\parallel }_{\ast }^{\frac{p+\nu }{p+\nu -1}}.$(74) ), it follows that $\frac{1}{8(p+1)!H_{\delta }^{\frac{1}{p+\nu -1}}}\parallel \mathrm{\nabla }{\tilde{F}}_{\delta }\left(u_{k+1}\right){\parallel }_{\ast }^{\frac{p+\nu }{p+\nu -1}}\le \frac{\delta }{2^{p+\nu -1}(p+\nu )}{\left(\frac{1}{2}\right)}^k\parallel x_0-x_{\delta }^{\ast }{\parallel }^{p+\nu }.$ In particular, for k = T−1, it follows from (68(68) $\parallel \mathrm{\nabla }{\tilde{F}}_{\delta }\left(u_k\right)\parallel >\frac{ϵ}{2},k=0,\dots ,T.$(68) ) that (75) $2^{T-1}\le \frac{32(p+1)!H_{\delta }^{\frac{1}{p+\nu -1}}\delta \parallel x_0-x_{\delta }^{\ast }{\parallel }^{p+\nu }}{2^{p+\nu -1}(p+\nu ){ϵ}^{\frac{p+\nu }{p+\nu -1}}}.$(75) Since ${\tilde{F}}_{\delta }\left(x_{\delta }^{\ast }\right)\le {\tilde{F}}_{\delta }\left(x^{\ast }\right)$, it follows that $\parallel x_0-x_{\delta }^{\ast }\parallel \le \parallel x_0-x^{\ast }\parallel \le R$. Thus, combining this with (75(75) $2^{T-1}\le \frac{32(p+1)!H_{\delta }^{\frac{1}{p+\nu -1}}\delta \parallel x_0-x_{\delta }^{\ast }{\parallel }^{p+\nu }}{2^{p+\nu -1}(p+\nu ){ϵ}^{\frac{p+\nu }{p+\nu -1}}}.$(75) ), we get (69(69) $T\le 1+{\log }_2\left(\frac{32(p+1)!H_{\delta }^{\frac{1}{p+\nu -1}}\delta R^{p+\nu }}{2^{p+\nu -1}(p+\nu ){ϵ}^{\frac{p+\nu }{p+\nu -1}}}\right).$(69) ).

Corollary 5.8

Suppose that H1 holds and that $R\ge 1$. Then, Algorithm 6 with (76) $\delta =\frac{ϵ}{2^{(p+\nu )}{R}^{p+\nu -1}}.$(76) perform at most (77) $\mathcal{O}\left({\log }_2\left(\frac{R^{p+\nu -1}}{ϵ}\right){\left(\frac{R^{p+\nu -1}}{ϵ}\right)}^{\frac{1}{p+\nu }}\right).$(77) iterations of Algorithm 5 in order to generate $u_T$ such that $\parallel \mathrm{\nabla }\tilde{f}\left(u_T\right){\parallel }_{\ast }\le ϵ$.

Proof.

By Theorem 5.7, we can obtain $\parallel \mathrm{\nabla }{\tilde{F}}_{\delta }\left(u_T\right){\parallel }_{\ast }\le ϵ/2$ with (78) $T\le 2+{\log }_2\left(\frac{32(p+1)!H_{\delta }^{\frac{1}{p+\nu -1}}\delta R^{p+\nu }}{2^{p+\nu -1}(p+\nu ){ϵ}^{\frac{p+\nu }{p+\nu -1}}}\right).$(78) Moreover, it follows from (65), (76(76) $\delta =\frac{ϵ}{2^{(p+\nu )}{R}^{p+\nu -1}}.$(76) ), the definition of $H_{F_{\delta },p}\left(\nu \right)$ in Lemma 5.6, $ϵ\in (0,1)$ and $R\ge 1$ that (79) $\begin{array}{rl}{H}_{\delta }& =p\left(H_{F_{\delta },p}+3\theta (p-1)!\right)=p\left(H_{f,p}\left(\nu \right)+\frac{\delta }{p+\nu }{C}_{p,\nu }+3\theta (p-1)!\right)\\ & =p\left(H_{f,p}\left(\nu \right)+\frac{ϵ}{2^{(p+\nu )}{R}^{p+\nu -1}}\frac{C_{p,\nu }}{(p+\nu )}+3\theta (p-1)!\right)\\ & \le p\left(H_{f,p}\left(\nu \right)+C_{p,\nu }+3\theta (p-1)!\right).\end{array}$(79) Combining (78(78) $T\le 2+{\log }_2\left(\frac{32(p+1)!H_{\delta }^{\frac{1}{p+\nu -1}}\delta R^{p+\nu }}{2^{p+\nu -1}(p+\nu ){ϵ}^{\frac{p+\nu }{p+\nu -1}}}\right).$(78) ), (79(79) $\begin{array}{rl}{H}_{\delta }& =p\left(H_{F_{\delta },p}+3\theta (p-1)!\right)=p\left(H_{f,p}\left(\nu \right)+\frac{\delta }{p+\nu }{C}_{p,\nu }+3\theta (p-1)!\right)\\ & =p\left(H_{f,p}\left(\nu \right)+\frac{ϵ}{2^{(p+\nu )}{R}^{p+\nu -1}}\frac{C_{p,\nu }}{(p+\nu )}+3\theta (p-1)!\right)\\ & \le p\left(H_{f,p}\left(\nu \right)+C_{p,\nu }+3\theta (p-1)!\right).\end{array}$(79) ) and (76(76) $\delta =\frac{ϵ}{2^{(p+\nu )}{R}^{p+\nu -1}}.$(76) ), we have (80) $T\le 2+{\log }_2\left(\frac{32(p+1)!{\left[p\left(H_{f,p}\left(\nu \right)+C_{p,\nu }+3\theta (p-1)!\right)\right]}^{\frac{1}{p+\nu -1}}R}{2^{2(p+\nu -2)}(p+\nu ){ϵ}^{\frac{1}{p+\nu -1}}}\right).$(80) At this point $u_T$, we have (81) $\parallel \mathrm{\nabla }\tilde{f}\left(u_T\right){\parallel }_{\ast }\le \parallel \mathrm{\nabla }{\tilde{F}}_{\delta }\left(u_T\right){\parallel }_{\ast }+\frac{\delta }{p+\nu }\parallel \mathrm{\nabla }{d}_{p+\nu }\left(u_T\right)\parallel \le \frac{ϵ}{2}+\delta \parallel u_T-x_0{\parallel }^{p+\nu -1}.$(81) Since ${\tilde{F}}_{\delta }(\cdot )$ is uniformly convex of degree $p+\nu$ with parameter $2^{-(p+\nu -2)}$, it follows from (74(74) ${\tilde{F}}_{\delta }\left(y_{k+1}\right)-{\tilde{F}}_{\delta }\left(u_{k+1}\right)\ge \frac{1}{8(p+1)!H_{\delta }^{\frac{1}{p+\nu -1}}}\parallel \mathrm{\nabla }{\tilde{F}}_{\delta }\left(u_{k+1}\right){\parallel }_{\ast }^{\frac{p+\nu }{p+\nu -1}}.$(74) ) and (73(73) ${\tilde{F}}_{\delta }\left(y_{k+1}\right)-{\tilde{F}}_{\delta }\left(x_{\delta }^{\ast }\right)\le \frac{\delta }{2^{p+\nu -1}(p+\nu )}{\left(\frac{1}{2}\right)}^k\parallel x_0-x_{\delta }^{\ast }{\parallel }^{p+\nu }.$(73) ) that $\begin{array}{rl}\frac{\delta 2^{-(p+\nu -2)}}{p+\nu }\parallel u_T-x_{\delta }^{\ast }{\parallel }^{p+\nu }& \le {\tilde{F}}_{\delta }\left(u_T\right)-{\tilde{F}}_{\delta }\left(x_{\delta }^{\ast }\right)\le {\tilde{F}}_{\delta }\left(y_T\right)-{\tilde{F}}_{\delta }\left(x_{\delta }^{\ast }\right)\\ & \le \frac{\delta }{2^{p+\nu -1}(p+\nu )}{\left(\frac{1}{2}\right)}^{T-1}\parallel x_0-x_{\delta }^{\ast }{\parallel }^{p+\nu }.\end{array}$ Therefore, $\parallel u_T-x_{\delta }^{\ast }\parallel \le \parallel x_0-x_{\delta }^{\ast }\parallel$, and so (82) $\begin{array}{rl}\parallel u_T-x_0{\parallel }^{p+\nu -1}& \le {\left[\parallel u_T-x_{\delta }^{\ast }\parallel +\parallel x_{\delta }^{\ast }-x_0\parallel \right]}^{p+\nu -1}\\ & \le 2^{p+\nu -1}\parallel x_0-x_{\delta }^{\ast }{\parallel }^{p+\nu -1}\end{array}$(82) (83) $\begin{array}{rl}& \le 2^{p+\nu -1}{R}^{p+\nu -1}.\end{array}$(83) Now, combining (81(81) $\parallel \mathrm{\nabla }\tilde{f}\left(u_T\right){\parallel }_{\ast }\le \parallel \mathrm{\nabla }{\tilde{F}}_{\delta }\left(u_T\right){\parallel }_{\ast }+\frac{\delta }{p+\nu }\parallel \mathrm{\nabla }{d}_{p+\nu }\left(u_T\right)\parallel \le \frac{ϵ}{2}+\delta \parallel u_T-x_0{\parallel }^{p+\nu -1}.$(81) ), (83(83) $\begin{array}{rl}& \le 2^{p+\nu -1}{R}^{p+\nu -1}.\end{array}$(83) ) and (76(76) $\delta =\frac{ϵ}{2^{(p+\nu )}{R}^{p+\nu -1}}.$(76) ), we obtain (84) $\parallel \mathrm{\nabla }\tilde{f}\left(u_T\right)\parallel \le \frac{ϵ}{2}+\frac{ϵ}{2}=ϵ.$(84) The conclusion is obtained by noticing that, for δ given in (76(76) $\delta =\frac{ϵ}{2^{(p+\nu )}{R}^{p+\nu -1}}.$(76) ) we have (85) $\begin{array}{rl}m& =1+⌈{\left(\frac{2^{4p+\nu -2}(p+\nu {)}^{p+\nu }{H}_{\delta }}{\delta (p-1)!}\right)}^{\frac{1}{p+\nu }}⌉\\ & \le 1+⌈{\left(\frac{2^{4p+\nu -2}(p+\nu {)}^{p+\nu }\left[p\left(H_{f,p}\left(\nu \right)+C_{p,\nu }+3\theta (p-1)!\right)\right]}{\delta (p-1)!}\right)}^{\frac{1}{p+\nu }}⌉\\ & =1+⌈{\left(\frac{2^{5p+2\nu -2}(p+\nu {)}^{p+\nu }{R}^{p+\nu -1}\left[p\left(H_{f,p}\left(\nu \right)+C_{p,\nu }+3\theta (p-1)!\right)\right]}{ϵ(p-1)!}\right)}^{\frac{1}{p+\nu }}⌉\end{array}$(85) Thus, (77(77) $\mathcal{O}\left({\log }_2\left(\frac{R^{p+\nu -1}}{ϵ}\right){\left(\frac{R^{p+\nu -1}}{ϵ}\right)}^{\frac{1}{p+\nu }}\right).$(77) ) follows from multiplying (80(80) $T\le 2+{\log }_2\left(\frac{32(p+1)!{\left[p\left(H_{f,p}\left(\nu \right)+C_{p,\nu }+3\theta (p-1)!\right)\right]}^{\frac{1}{p+\nu -1}}R}{2^{2(p+\nu -2)}(p+\nu ){ϵ}^{\frac{1}{p+\nu -1}}}\right).$(80) ) and (85(85) $\begin{array}{rl}m& =1+⌈{\left(\frac{2^{4p+\nu -2}(p+\nu {)}^{p+\nu }{H}_{\delta }}{\delta (p-1)!}\right)}^{\frac{1}{p+\nu }}⌉\\ & \le 1+⌈{\left(\frac{2^{4p+\nu -2}(p+\nu {)}^{p+\nu }\left[p\left(H_{f,p}\left(\nu \right)+C_{p,\nu }+3\theta (p-1)!\right)\right]}{\delta (p-1)!}\right)}^{\frac{1}{p+\nu }}⌉\\ & =1+⌈{\left(\frac{2^{5p+2\nu -2}(p+\nu {)}^{p+\nu }{R}^{p+\nu -1}\left[p\left(H_{f,p}\left(\nu \right)+C_{p,\nu }+3\theta (p-1)!\right)\right]}{ϵ(p-1)!}\right)}^{\frac{1}{p+\nu }}⌉\end{array}$(85) ).

Suppose now that $S\ge \tilde{f}\left(x_0\right)-\tilde{f}\left(x^{\ast }\right)$ is known. In this case, we have the following variant of Theorem 5.7.

Theorem 5.9

Suppose that H1 holds and let $\{u_k{\}}_{k=0}^T$ be a sequence generated by Algorithm 6 such that (86) $\parallel \mathrm{\nabla }{\tilde{F}}_{\delta }\left(u_k\right){\parallel }_{\ast }>\frac{ϵ}{2},k=0,\dots ,T.$(86) Then, (87) $T\le 1+{\log }_2\left(\frac{16(p+1)!H_{\delta }^{\frac{1}{p+\nu -1}}S}{{ϵ}^{\frac{p+\nu }{p+\nu -1}}}\right).$(87)

Proof.

By (75(75) $2^{T-1}\le \frac{32(p+1)!H_{\delta }^{\frac{1}{p+\nu -1}}\delta \parallel x_0-x_{\delta }^{\ast }{\parallel }^{p+\nu }}{2^{p+\nu -1}(p+\nu ){ϵ}^{\frac{p+\nu }{p+\nu -1}}}.$(75) ), we have (88) $T\le 1+{\log }_2\left(\frac{32(p+1)!H_{\delta }^{\frac{1}{p+\nu -1}}}{2{ϵ}^{\frac{p+\nu }{p+\nu -1}}}\frac{\delta }{2^{p+\nu -2}(p+\nu )}\parallel x_0-x_{\delta }^{\ast }{\parallel }^{p+\nu }\right).$(88) Since ${\tilde{F}}_{\delta }(\cdot )$ is uniformly convex of degree $p+\nu$ with parameter $\delta 2^{-(p+\nu -2)}$ we have (89) $\begin{array}{rl}\frac{\delta }{2^{p+\nu -2}(p+\nu )}\parallel x_0-x_{\delta }^{\ast }{\parallel }^{p+\nu }& \le {\tilde{F}}_{\delta }\left(x_0\right)-{\tilde{F}}_{\delta }\left(x_{\delta }^{\ast }\right)\\ & =\tilde{f}\left(x_0\right)-\tilde{f}\left(x_{\delta }^{\ast }\right)-\frac{\delta }{p+\nu }\parallel x_{\delta }^{\ast }-x_0{\parallel }^{p+\nu }\\ & \le \tilde{f}\left(x_0\right)-\tilde{f}\left(x_{\delta }^{\ast }\right)\\ & \le \tilde{f}\left(x_0\right)-\tilde{f}\left(x^{\ast }\right)\\ & \le S.\end{array}$(89) Combining (88(88) $T\le 1+{\log }_2\left(\frac{32(p+1)!H_{\delta }^{\frac{1}{p+\nu -1}}}{2{ϵ}^{\frac{p+\nu }{p+\nu -1}}}\frac{\delta }{2^{p+\nu -2}(p+\nu )}\parallel x_0-x_{\delta }^{\ast }{\parallel }^{p+\nu }\right).$(88) ) and (89(89) $\begin{array}{rl}\frac{\delta }{2^{p+\nu -2}(p+\nu )}\parallel x_0-x_{\delta }^{\ast }{\parallel }^{p+\nu }& \le {\tilde{F}}_{\delta }\left(x_0\right)-{\tilde{F}}_{\delta }\left(x_{\delta }^{\ast }\right)\\ & =\tilde{f}\left(x_0\right)-\tilde{f}\left(x_{\delta }^{\ast }\right)-\frac{\delta }{p+\nu }\parallel x_{\delta }^{\ast }-x_0{\parallel }^{p+\nu }\\ & \le \tilde{f}\left(x_0\right)-\tilde{f}\left(x_{\delta }^{\ast }\right)\\ & \le \tilde{f}\left(x_0\right)-\tilde{f}\left(x^{\ast }\right)\\ & \le S.\end{array}$(89) ) we get (87(87) $T\le 1+{\log }_2\left(\frac{16(p+1)!H_{\delta }^{\frac{1}{p+\nu -1}}S}{{ϵ}^{\frac{p+\nu }{p+\nu -1}}}\right).$(87) ).

Corollary 5.10

Suppose that H1 holds and that $S\ge 1$. Then, Algorithm 6 with (90) $\delta ={\left[\frac{ϵ}{2^{p+\nu }{\left[2^{p+\nu -2}(p+\nu )S\right]}^{\frac{p+\nu -1}{p+\nu }}}\right]}^{p+\nu }$(90) performs at most (91) $\mathcal{O}\left({\log }_2\left(\frac{S}{{ϵ}^{\frac{p+\nu -1}{p+\nu }}}\right)\left(\frac{S^{\frac{p+\nu -1}{p+\nu }}}{ϵ}\right)\right)$(91) iterations of Algorithm 5 in order to generate $u_T$ such that $\parallel \mathrm{\nabla }\tilde{f}\left(u_T\right){\parallel }_{\ast }\le ϵ$.

Proof.

By Theorem 5.9, we can obtain $\parallel \mathrm{\nabla }{\tilde{F}}_{\delta }\left(u_T\right){\parallel }_{\ast }\le ϵ/2$ with (92) $T\le 2+{\log }_2\left(\frac{16(p+1)!H_{\delta }^{\frac{1}{p+\nu -1}}S}{{ϵ}^{\frac{p+\nu }{p+\nu -1}}}\right).$(92) In view of (90(90) $\delta ={\left[\frac{ϵ}{2^{p+\nu }{\left[2^{p+\nu -2}(p+\nu )S\right]}^{\frac{p+\nu -1}{p+\nu }}}\right]}^{p+\nu }$(90) ), $ϵ\in (0,1)$ and $S\ge 1$, we also have (93) $H_{\delta }\le p\left(H_{f,p}\left(\nu \right)+C_{p,\nu }+3\theta (p-1)!\right).$(93) Thus, from (92(92) $T\le 2+{\log }_2\left(\frac{16(p+1)!H_{\delta }^{\frac{1}{p+\nu -1}}S}{{ϵ}^{\frac{p+\nu }{p+\nu -1}}}\right).$(92) ) and (93(93) $H_{\delta }\le p\left(H_{f,p}\left(\nu \right)+C_{p,\nu }+3\theta (p-1)!\right).$(93) ), it follows that (94) $T\le 2+{\log }_2\left(\frac{16(p+1)!{\left[p\left(H_{f,p}\left(\nu \right)+C_{p,\nu }+3\theta (p-1)!\right)\right]}^{\frac{1}{p+\nu -1}}S}{{ϵ}^{\frac{p+\nu }{p+\nu -1}}}\right).$(94) At this point $u_T$ we have $\parallel \mathrm{\nabla }\tilde{f}\left(u_T\right){\parallel }_{\ast }\le \parallel \mathrm{\nabla }{\tilde{F}}_{\delta }\left(u_T\right){\parallel }_{\ast }+\frac{\delta }{p+\nu }\parallel \mathrm{\nabla }{d}_{p+\nu }\left(u_T\right){\parallel }_{\ast }\le \frac{ϵ}{2}+\delta \parallel u_T-x_0{\parallel }^{p+\nu -1}.$ By (82(82) $\begin{array}{rl}\parallel u_T-x_0{\parallel }^{p+\nu -1}& \le {\left[\parallel u_T-x_{\delta }^{\ast }\parallel +\parallel x_{\delta }^{\ast }-x_0\parallel \right]}^{p+\nu -1}\\ & \le 2^{p+\nu -1}\parallel x_0-x_{\delta }^{\ast }{\parallel }^{p+\nu -1}\end{array}$(82) ) and (89(89) $\begin{array}{rl}\frac{\delta }{2^{p+\nu -2}(p+\nu )}\parallel x_0-x_{\delta }^{\ast }{\parallel }^{p+\nu }& \le {\tilde{F}}_{\delta }\left(x_0\right)-{\tilde{F}}_{\delta }\left(x_{\delta }^{\ast }\right)\\ & =\tilde{f}\left(x_0\right)-\tilde{f}\left(x_{\delta }^{\ast }\right)-\frac{\delta }{p+\nu }\parallel x_{\delta }^{\ast }-x_0{\parallel }^{p+\nu }\\ & \le \tilde{f}\left(x_0\right)-\tilde{f}\left(x_{\delta }^{\ast }\right)\\ & \le \tilde{f}\left(x_0\right)-\tilde{f}\left(x^{\ast }\right)\\ & \le S.\end{array}$(89) ), (95) $\begin{array}{rl}\parallel u_T-x_0{\parallel }^{p+\nu -1}& \le 2^{p+\nu -1}\parallel x_0-x_{\delta }^{\ast }{\parallel }^{p+\nu -1}\le 2^{p+\nu -1}{\left[\frac{2^{p+\nu -2}(p+\nu )S}{\delta }\right]}^{\frac{p+\nu -1}{p+\nu }}\\ & ={\left(\frac{1}{\delta }\right)}^{\frac{p+\nu -1}{p+\nu }}{2}^{p+\nu -1}{\left[2^{p+\nu -2}(p+\nu )S\right]}^{\frac{p+\nu -1}{p+\nu }}.\end{array}$(95) Thus, it follows from (95(95) $\begin{array}{rl}\parallel u_T-x_0{\parallel }^{p+\nu -1}& \le 2^{p+\nu -1}\parallel x_0-x_{\delta }^{\ast }{\parallel }^{p+\nu -1}\le 2^{p+\nu -1}{\left[\frac{2^{p+\nu -2}(p+\nu )S}{\delta }\right]}^{\frac{p+\nu -1}{p+\nu }}\\ & ={\left(\frac{1}{\delta }\right)}^{\frac{p+\nu -1}{p+\nu }}{2}^{p+\nu -1}{\left[2^{p+\nu -2}(p+\nu )S\right]}^{\frac{p+\nu -1}{p+\nu }}.\end{array}$(95) ), (95(95) $\begin{array}{rl}\parallel u_T-x_0{\parallel }^{p+\nu -1}& \le 2^{p+\nu -1}\parallel x_0-x_{\delta }^{\ast }{\parallel }^{p+\nu -1}\le 2^{p+\nu -1}{\left[\frac{2^{p+\nu -2}(p+\nu )S}{\delta }\right]}^{\frac{p+\nu -1}{p+\nu }}\\ & ={\left(\frac{1}{\delta }\right)}^{\frac{p+\nu -1}{p+\nu }}{2}^{p+\nu -1}{\left[2^{p+\nu -2}(p+\nu )S\right]}^{\frac{p+\nu -1}{p+\nu }}.\end{array}$(95) ) and (90(90) $\delta ={\left[\frac{ϵ}{2^{p+\nu }{\left[2^{p+\nu -2}(p+\nu )S\right]}^{\frac{p+\nu -1}{p+\nu }}}\right]}^{p+\nu }$(90) ) that $\parallel \mathrm{\nabla }\tilde{f}\left(u_T\right){\parallel }_{\ast }\le \frac{ϵ}{2}+{\delta }^{\frac{1}{p+\nu }}{2}^{p+\nu -1}{\left[2^{p+\nu -2}(p+\nu )S\right]}^{\frac{p+\nu -1}{p+\nu }}\le \frac{ϵ}{2}+\frac{ϵ}{2}=ϵ.$ Finally, by (66) and (90(90) $\delta ={\left[\frac{ϵ}{2^{p+\nu }{\left[2^{p+\nu -2}(p+\nu )S\right]}^{\frac{p+\nu -1}{p+\nu }}}\right]}^{p+\nu }$(90) ) we have $\begin{array}{rl}m& =1+⌈{\left(\frac{2^{4p+\nu -2}(p+\nu {)}^{p+\nu }{H}_{\delta }}{\delta (p-1)!}\right)}^{\frac{1}{p+\nu }}⌉\le 1\\ & +⌈{\left(\frac{2^{4p+\nu -2}(p+\nu {)}^{p+\nu }\left[p{H}_{f,p}\left(\nu \right)+C_{p,\nu }+3\theta (p-1)!\right]}{(p-1)!}\right)}^{\frac{1}{p+\nu }}\\ & \frac{2^{p+\nu }{\left[2^{p+\nu -2}(p+\nu )S\right]}^{\frac{p+\nu -1}{p+\nu }}}{ϵ}⌉.\end{array}$ Thus, (91(91) $\mathcal{O}\left({\log }_2\left(\frac{S}{{ϵ}^{\frac{p+\nu -1}{p+\nu }}}\right)\left(\frac{S^{\frac{p+\nu -1}{p+\nu }}}{ϵ}\right)\right)$(91) ) follows by multiplying (94(94) $T\le 2+{\log }_2\left(\frac{16(p+1)!{\left[p\left(H_{f,p}\left(\nu \right)+C_{p,\nu }+3\theta (p-1)!\right)\right]}^{\frac{1}{p+\nu -1}}S}{{ϵ}^{\frac{p+\nu }{p+\nu -1}}}\right).$(94) ) by the upper bound on m given above.

6. Lower complexity bounds under Hölder condition

In this section, we derive lower complexity bounds for p-order tensor methods applied to the problem (4(4) $\underset{x\in \mathbb{E}}{min}f\left(x\right),$(4) ) in terms of the norm of the gradient of f, where the objective f is convex and $H_{f,p}\left(\nu \right)<+\mathrm{\infty }$ for some $\nu \in [0,1]$.

For simplicity, assume that $\mathbb{E}={\mathbb{R}}^n$ and $B=I_n$. Given an approximation $\overline{x}$ for the solution of (4(4) $\underset{x\in \mathbb{E}}{min}f\left(x\right),$(4) ), we consider p-order methods that compute trial points of the form $x^{+}=\overline{x}+\overline{h}$, where the search direction $\overline{h}$ is the solution of an auxiliary problem of the form (96) $\underset{h\in {\mathbb{R}}^n}{min}{\phi }_{a,\gamma ,q}\left(h\right)\equiv \sum _{i=1}^p{a}^{\left(i\right)}{D}^{i}f\left(\overline{x}\right)[h{]}^i+\gamma \parallel h{\parallel }^q,$(96) with $a\in {\mathbb{R}}^p$, $\gamma >0$ and q>1. Denote by ${\mathrm{\Gamma }}_{\overline{x},f}(a,\gamma ,q)$ the set of all stationary points of function ${\phi }_{a,\gamma ,q}(\cdot )$ and define the linear subspace (97) $S_f\left(\overline{x}\right)=\mathrm{L}\mathrm{i}\mathrm{n}\left({\mathrm{\Gamma }}_{\overline{x},f}(a,\gamma ,q)|a\in {\mathbb{R}}^p,\gamma >0,q>1\right).$(97) More specifically, we consider the class of p-order tensor methods characterized by the following assumption.

Assumption 6.1

Given $x_0\in {\mathbb{R}}^n$, the method generates a sequence of test points $\{x_k{\}}_{k\ge 0}$ such that (98) $x_{k+1}\in x_0+\sum _{i=0}^k{S}_f\left(x_i\right),k\ge 0.$(98) Given $\nu \in [0,1]$, we consider the same family of difficult problems discussed in [18], namely: (99) $f_k\left(x\right)=\frac{1}{p+\nu }\left[\sum _{i=1}^{k-1}|x^{\left(i\right)}-x^{(i+1)}{|}^{p+\nu }+\sum _{i=k}^n|x^{\left(i\right)}{|}^{p+\nu }\right]-x^{\left(1\right)},2\le k\le n.$(99) The next lemma establishes that for each $f_k(\cdot )$ we have $H_{f_k,p}\left(\nu \right)<+\mathrm{\infty }$.

Lemma 6.1

Given an integer $k\in [2,n],$ the pth derivative of $f_k(\cdot )$ is ν-Hölder continuous with (100) $H_{f_k,p}\left(\nu \right)=2^{\frac{2+\nu }{2}}{\mathrm{\Pi }}_{i=1}^{p-1}(p+\nu -i).$(100)

Proof.

See Lemma 5.1 in [18].

The next lemma provides additional properties of $f_k(\cdot )$.

Lemma 6.2

Given an integer $k\in [2,n]$, let function $f_k(\cdot )$ be defined by (99(99) $f_k\left(x\right)=\frac{1}{p+\nu }\left[\sum _{i=1}^{k-1}|x^{\left(i\right)}-x^{(i+1)}{|}^{p+\nu }+\sum _{i=k}^n|x^{\left(i\right)}{|}^{p+\nu }\right]-x^{\left(1\right)},2\le k\le n.$(99) ). Then, $f_k(\cdot )$ has a unique global minimizer $x_k^{\ast }$. Moreover, (101) $f_k^{\ast }=-\frac{(p+\nu -1)k}{p+\nu }and\parallel x_k^{\ast }\parallel <\frac{(k+1{)}^{\frac{3}{2}}}{\sqrt{3}}.$(101)

Proof.

See Lemma 5.2 in [18].

Our goal is to understand the behaviour of the tensor methods specified by Assumption 1 when applied to the minimization of $f_k(\cdot )$ with a suitable k. For that, let us consider the following subspaces: ${\mathbb{R}}_k^n=\left\{x\in {\mathbb{R}}^n|x^{\left(i\right)}=0,i=k+1,\dots ,n\right\},1\le k\le n-1.$

Lemma 6.3

For any $q\ge 0$ and $x\in {\mathbb{R}}_k^n,$ $f_{k+q}\left(x\right)=f_k\left(x\right)$.

Proof.

It follows directly from (99(99) $f_k\left(x\right)=\frac{1}{p+\nu }\left[\sum _{i=1}^{k-1}|x^{\left(i\right)}-x^{(i+1)}{|}^{p+\nu }+\sum _{i=k}^n|x^{\left(i\right)}{|}^{p+\nu }\right]-x^{\left(1\right)},2\le k\le n.$(99) ).

Lemma 6.4

Let $\mathcal{M}$ be a p-order tensor method satisfying Assumption 1. If $\mathcal{M}$ is applied to the minimization of $f_t(\cdot )$ $(2\le t\le n)$ starting from $x_0=0,$ then the sequence $\{x_k{\}}_{k\ge 0}$ of test points generated by $\mathcal{M}$ satisfies $x_{k+1}\in \sum _{i=0}^k{S}_{f_t}\left(x_i\right)\subset {\mathbb{R}}_{k+1}^n,0\le k\le t-1.$

Proof.

See Lemma 2 in [27].

The next lemma gives a lower bound for the norm of the gradient of $f_t(\cdot )$ on suitable points.

Lemma 6.5

Let k be an integer in the interval $[1,t-1),$ with $t+1\le n$. If $x\in {\mathbb{R}}_k^n,$ then $\parallel \mathrm{\nabla }{f}_t\left(x\right){\parallel }_{\ast }\ge \frac{1}{\sqrt{k+1}}$.

Proof.

In view of (99(99) $f_k\left(x\right)=\frac{1}{p+\nu }\left[\sum _{i=1}^{k-1}|x^{\left(i\right)}-x^{(i+1)}{|}^{p+\nu }+\sum _{i=k}^n|x^{\left(i\right)}{|}^{p+\nu }\right]-x^{\left(1\right)},2\le k\le n.$(99) ) we have (102) $f_k\left(x\right)={\eta }_{p+\nu }\left(A_{k}x\right)-⟨e_1,x⟩,$(102) where (103) ${\eta }_{p+\nu }\left(u\right)=\frac{1}{p+\nu }\sum _{i=1}^n|u^{\left(i\right)}{|}^{p+\nu },$(103) and (104) $A_k=\left(\begin{array}{cc}{U}_k& 0\\ 0& I_{n-k}\end{array}\right),\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}{U}_k=\left(\begin{array}{cccccc}1& -1& 0& \dots & 0& 0\\ 0& 1& -1& \dots & 0& 0\\ ⋮& ⋮& ⋮& & ⋮& ⋮\\ 0& 0& 0& \dots & 1& -1\\ 0& 0& 0& \dots & 0& 1\end{array}\right)\in {\mathbb{R}}^{k\times k}.$(104) By (104(104) $A_k=\left(\begin{array}{cc}{U}_k& 0\\ 0& I_{n-k}\end{array}\right),\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}{U}_k=\left(\begin{array}{cccccc}1& -1& 0& \dots & 0& 0\\ 0& 1& -1& \dots & 0& 0\\ ⋮& ⋮& ⋮& & ⋮& ⋮\\ 0& 0& 0& \dots & 1& -1\\ 0& 0& 0& \dots & 0& 1\end{array}\right)\in {\mathbb{R}}^{k\times k}.$(104) ) and (103(103) ${\eta }_{p+\nu }\left(u\right)=\frac{1}{p+\nu }\sum _{i=1}^n|u^{\left(i\right)}{|}^{p+\nu },$(103) ), we have ${\left(\mathrm{\nabla }{\eta }_{p+\nu }\left(A_{t}x\right)\right)}^{\left(i\right)}=\left\{\begin{array}{ll}|x^{\left(i\right)}-x^{(i+1)}{|}^{p+\nu -2}(x^{\left(i\right)}-x^{(i+1)}),& i=1,\dots ,t-1.\\ |x^{\left(i\right)}{|}^{p+\nu -2}\left(x^{\left(i\right)}\right),& i=t,\dots ,n.\end{array}\right.$ Since $x\in {\mathbb{R}}_k^n$, it follows that $x^{\left(i\right)}=0$ for i>k. Therefore, ${\left(\mathrm{\nabla }{\eta }_{p+\nu }\left(A_{t}x\right)\right)}^{\left(i\right)}=0,i=k+1,\dots ,n,$ which means that $\mathrm{\nabla }{\eta }_{p+\nu }\left(A_{t}x\right)\in {\mathbb{R}}_k^n$. Then, from (102(102) $f_k\left(x\right)={\eta }_{p+\nu }\left(A_{k}x\right)-⟨e_1,x⟩,$(102) ), we obtain (105) $\begin{array}{rl}\parallel \mathrm{\nabla }{f}_t\left(x\right){\parallel }_{\ast }^2& =\parallel A_t^T\mathrm{\nabla }{\eta }_{p+\nu }\left(A_{t}x\right)-e_1{\parallel }_{\ast }^2\ge \underset{y\in {\mathbb{R}}_k^n}{inf}\parallel A_t^{T}y-e_1{\parallel }_{\ast }^2\\ & =\underset{z\in {\mathbb{R}}^k}{inf}\parallel Bz-e_1{\parallel }_{\ast }^2\left[\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}B=A_t^T\left(\begin{array}{c}{I}_k\\ 0\end{array}\right)\right]\\ & =\parallel B(B^{T}B{)}^{-1}{B}^T{e}_1-e_1{\parallel }_{\ast }^2\\ & =\sum _{i=1}^n{\left({\left[B(B^{T}B{)}^{-1}{B}^T{e}_1\right]}^{\left(i\right)}-(e_1{)}^{\left(i\right)}\right)}^2.\end{array}$(105) By (104(104) $A_k=\left(\begin{array}{cc}{U}_k& 0\\ 0& I_{n-k}\end{array}\right),\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}{U}_k=\left(\begin{array}{cccccc}1& -1& 0& \dots & 0& 0\\ 0& 1& -1& \dots & 0& 0\\ ⋮& ⋮& ⋮& & ⋮& ⋮\\ 0& 0& 0& \dots & 1& -1\\ 0& 0& 0& \dots & 0& 1\end{array}\right)\in {\mathbb{R}}^{k\times k}.$(104) ), we have (106) $B=\left(\begin{array}{c}\tilde{U}\\ 0\end{array}\right)\in {\mathbb{R}}^{n\times k},\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\tilde{U}=\left(\begin{array}{cccccc}1& 0& 0& \dots & 0& 0\\ -1& 1& 0& \dots & 0& 0\\ 0& -1& 1& \dots & 0& 0\\ ⋮& ⋮& ⋮& & ⋮& ⋮\\ 0& 0& 0& \dots & -1& 1\\ 0& 0& 0& \dots & 0& 1\end{array}\right)\in {\mathbb{R}}^{(k+1)\times k}$(106) Consequently, (107) $B^T{e}_1=\left(\begin{array}{c}1\\ 0\\ ⋮\\ 0\end{array}\right)\in {\mathbb{R}}^k.$(107) and (108) $B^{T}B=\left(\begin{array}{cccccccc}2& -1& 0& 0& \dots & 0& 0& 0\\ -1& 2& -1& 0& \dots & 0& 0& 0\\ ⋮& ⋮& ⋮& ⋮& & ⋮& ⋮& ⋮\\ 0& 0& 0& 0& \dots & -1& 2& -1\\ 0& 0& 0& 0& \dots & 0& -1& 2\end{array}\right)\in {\mathbb{R}}^{k\times k}.$(108) From (108(108) $B^{T}B=\left(\begin{array}{cccccccc}2& -1& 0& 0& \dots & 0& 0& 0\\ -1& 2& -1& 0& \dots & 0& 0& 0\\ ⋮& ⋮& ⋮& ⋮& & ⋮& ⋮& ⋮\\ 0& 0& 0& 0& \dots & -1& 2& -1\\ 0& 0& 0& 0& \dots & 0& -1& 2\end{array}\right)\in {\mathbb{R}}^{k\times k}.$(108) ), it can be checked that (109) $(B^{T}B{)}^{-1}=\frac{1}{k+1}\tilde{B}\in {\mathbb{R}}^{k\times k},$(109) with (110) ${\tilde{B}}_{ij}=\left\{\begin{array}{ll}i\left[\right(k+1)-j],& \mathrm{i}\mathrm{f}j\ge i,\\ j\left[\right(k+1)-i],& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}.\end{array}\right.$(110) Now, combining (107(107) $B^T{e}_1=\left(\begin{array}{c}1\\ 0\\ ⋮\\ 0\end{array}\right)\in {\mathbb{R}}^k.$(107) ) and (108(108) $B^{T}B=\left(\begin{array}{cccccccc}2& -1& 0& 0& \dots & 0& 0& 0\\ -1& 2& -1& 0& \dots & 0& 0& 0\\ ⋮& ⋮& ⋮& ⋮& & ⋮& ⋮& ⋮\\ 0& 0& 0& 0& \dots & -1& 2& -1\\ 0& 0& 0& 0& \dots & 0& -1& 2\end{array}\right)\in {\mathbb{R}}^{k\times k}.$(108) )–(109(109) $(B^{T}B{)}^{-1}=\frac{1}{k+1}\tilde{B}\in {\mathbb{R}}^{k\times k},$(109) ), we get (111) ${\left[(B^{T}B{)}^{-1}{B}^T{e}_1\right]}^{\left(i\right)}=\frac{(k+1)-i}{k+1},i=1,\dots ,k.$(111) Then, it follows from (106(106) $B=\left(\begin{array}{c}\tilde{U}\\ 0\end{array}\right)\in {\mathbb{R}}^{n\times k},\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\tilde{U}=\left(\begin{array}{cccccc}1& 0& 0& \dots & 0& 0\\ -1& 1& 0& \dots & 0& 0\\ 0& -1& 1& \dots & 0& 0\\ ⋮& ⋮& ⋮& & ⋮& ⋮\\ 0& 0& 0& \dots & -1& 1\\ 0& 0& 0& \dots & 0& 1\end{array}\right)\in {\mathbb{R}}^{(k+1)\times k}$(106) ) and (111(111) ${\left[(B^{T}B{)}^{-1}{B}^T{e}_1\right]}^{\left(i\right)}=\frac{(k+1)-i}{k+1},i=1,\dots ,k.$(111) ) that (112) $\begin{array}{rl}{\left[B(B^{T}B{)}^{-1}{B}^T{e}_1\right]}^{\left(i\right)}& =\left\{\begin{array}{ll}\frac{k}{k+1},& i=1,\\ -\frac{(k+1)-(i-1)}{k+1}+\frac{(k+1)-i}{k+1},& i=2,\dots ,k,\\ -\frac{1}{k+1},& i=k+1,\\ 0,& i=k+2,\dots ,n.\end{array}\right.\\ & =\left\{\begin{array}{ll}\frac{k}{k+1},& i=1,\\ -\frac{1}{k+1},& i=2,\dots ,k+1,\\ 0,& i=k+2,\dots ,n.\end{array}\right.\end{array}$(112) Finally, by (105(105) $\begin{array}{rl}\parallel \mathrm{\nabla }{f}_t\left(x\right){\parallel }_{\ast }^2& =\parallel A_t^T\mathrm{\nabla }{\eta }_{p+\nu }\left(A_{t}x\right)-e_1{\parallel }_{\ast }^2\ge \underset{y\in {\mathbb{R}}_k^n}{inf}\parallel A_t^{T}y-e_1{\parallel }_{\ast }^2\\ & =\underset{z\in {\mathbb{R}}^k}{inf}\parallel Bz-e_1{\parallel }_{\ast }^2\left[\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}B=A_t^T\left(\begin{array}{c}{I}_k\\ 0\end{array}\right)\right]\\ & =\parallel B(B^{T}B{)}^{-1}{B}^T{e}_1-e_1{\parallel }_{\ast }^2\\ & =\sum _{i=1}^n{\left({\left[B(B^{T}B{)}^{-1}{B}^T{e}_1\right]}^{\left(i\right)}-(e_1{)}^{\left(i\right)}\right)}^2.\end{array}$(105) ) and (112(112) $\begin{array}{rl}{\left[B(B^{T}B{)}^{-1}{B}^T{e}_1\right]}^{\left(i\right)}& =\left\{\begin{array}{ll}\frac{k}{k+1},& i=1,\\ -\frac{(k+1)-(i-1)}{k+1}+\frac{(k+1)-i}{k+1},& i=2,\dots ,k,\\ -\frac{1}{k+1},& i=k+1,\\ 0,& i=k+2,\dots ,n.\end{array}\right.\\ & =\left\{\begin{array}{ll}\frac{k}{k+1},& i=1,\\ -\frac{1}{k+1},& i=2,\dots ,k+1,\\ 0,& i=k+2,\dots ,n.\end{array}\right.\end{array}$(112) ) we have $\begin{array}{rl}\parallel \mathrm{\nabla }{f}_t\left(x\right){\parallel }_{\ast }^2& \ge \sum _{i=1}^n{\left({\left[B(B^{T}B{)}^{-1}{B}^T{e}_1\right]}^{\left(i\right)}-(e_1{)}^{\left(i\right)}\right)}^2\\ & ={\left(-\frac{1}{k+1}\right)}^2+\sum _{i=2}^{k+1}{\left(-\frac{1}{k+1}\right)}^2=\sum _{i=1}^{k+1}\frac{1}{(k+1{)}^2}\\ & =\frac{1}{k+1},\end{array}$ and the proof is complete.

The next theorem establishes a lower bound for the rate of convergence of p-order tensor methods with respect to the initial functional residual $\left(f\right(x_0)-f^{\ast })$.

Theorem 6.6

Let $\mathcal{M}$ be a p-order tensor method satisfying Assumption 6.1. Assume that for any function f with $H_{f,p}\left(\nu \right)<+\mathrm{\infty }$ this method ensures the rate of convergence: (113) $\underset{1\le k\le t-1}{min}\parallel \mathrm{\nabla }f\left(x_k\right){\parallel }_{\ast }\le \frac{H_{f,p}\left(\nu {)}^{\frac{1}{p+\nu }}\right(f\left(x_0\right)-f^{\ast }{)}^{\frac{p+\nu -1}{p+\nu }}}{\kappa \left(t\right)},t\ge 2,$(113) where $\{x_k{\}}_{k\ge 0}$ is the sequence generated by method $\mathcal{M}$ and $f^{\ast }$ is the optimal value of f. Then, for all $t\ge 2$ such that $t+1\le n$ we have (114) $\kappa \left(t\right)\le D_{p,\nu }{t}^{\frac{3(p+\nu )-2}{2(p+\nu )}}\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}{D}_{p,\nu }={\left[2^{\frac{2+\nu }{2}}{\mathrm{\Pi }}_{i=1}^{p-1}(p+\nu -i)\right]}^{\frac{1}{p+\nu }}{\left[\frac{p+\nu -1}{p+\nu }\right]}^{\frac{p+\nu -1}{p+\nu }}.$(114)

Proof.

Suppose that method $\mathcal{M}$ is applied to minimize function $f_t(\cdot )$ with initial point $x_0=0$. By Lemma 6.4, we have $x_k\in {\mathbb{R}}_k^n$ for all k, $1\le k\le t-1$. Thus, from Lemma 6.5, it follows that (115) $\underset{1\le k\le t-1}{min}\parallel \mathrm{\nabla }{f}_t\left(x_k\right){\parallel }_{\ast }\ge \underset{1\le k\le t-1}{min}\frac{1}{\sqrt{k+1}}=\frac{1}{\sqrt{t}}.$(115) Then, combining (113(113) $\underset{1\le k\le t-1}{min}\parallel \mathrm{\nabla }f\left(x_k\right){\parallel }_{\ast }\le \frac{H_{f,p}\left(\nu {)}^{\frac{1}{p+\nu }}\right(f\left(x_0\right)-f^{\ast }{)}^{\frac{p+\nu -1}{p+\nu }}}{\kappa \left(t\right)},t\ge 2,$(113) ), (115(115) $\underset{1\le k\le t-1}{min}\parallel \mathrm{\nabla }{f}_t\left(x_k\right){\parallel }_{\ast }\ge \underset{1\le k\le t-1}{min}\frac{1}{\sqrt{k+1}}=\frac{1}{\sqrt{t}}.$(115) ), Lemma 6.1 and Lemma 6.2, we get $\begin{array}{rl}\kappa \left(t\right)& \le \frac{H_{f_t,p}\left(\nu {)}^{\frac{1}{p+\nu }}\right(f_t\left(x_0\right)-f_t^{\ast })}{\underset{1\le k\le t-1}{min}\parallel \mathrm{\nabla }{f}_t\left(x_k\right){\parallel }_{\ast }}\\ & \le {\left[2^{\frac{2+\nu }{2}}{\mathrm{\Pi }}_{i=1}^{p-1}(p+\nu -i)\right]}^{\frac{1}{p+\nu }}{\left[\frac{p+\nu -1}{p+\nu }\right]}^{\frac{p+\nu -1}{p+\nu }}{t}^{\frac{p+\nu -1}{p+\nu }}{t}^{\frac{1}{2}}\\ & \le D_{p,\nu }(t+1{)}^{\frac{3(p+\nu )-2}{2(p+\nu )}},\end{array}$ where constant $D_{p,\nu }$ is given in (114(114) $\kappa \left(t\right)\le D_{p,\nu }{t}^{\frac{3(p+\nu )-2}{2(p+\nu )}}\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}{D}_{p,\nu }={\left[2^{\frac{2+\nu }{2}}{\mathrm{\Pi }}_{i=1}^{p-1}(p+\nu -i)\right]}^{\frac{1}{p+\nu }}{\left[\frac{p+\nu -1}{p+\nu }\right]}^{\frac{p+\nu -1}{p+\nu }}.$(114) ).

Remark 6.1

Theorem 6.6 gives a lower bound of $\mathcal{O}\left(\right(\frac{1}{k}{)}^{\frac{3(p+\nu )-2}{2(p+\nu )}})$ for the rate of convergence of tensor methods with respect to the initial functional residual. For first-order methods in the Lipschitz case (i.e. $p=\nu =1$), we have $\mathcal{O}\left(\frac{1}{k}\right)$. This gives a lower complexity bound of $\mathcal{O}\left({ϵ}^{-1}\right)$ iterations for finding ε-stationary points of convex functions using first-order methods, which coincides with the lower bound (8a) in [6]. Moreover, in view of Corollary 5.8, Algorithm 6 is suboptimal in terms of the initial residual, with the complexity a complexity gap that increases as p grows.

Now, we obtain a lower bound for the rate of convergence of p-order tensor methods with respect to the distance $\parallel x_0-x^{\ast }\parallel$.

Theorem 6.7

Let $\mathcal{M}$ be a p-order tensor method satisfying Assumption 1. Assume that for any function f with $H_{f,p}\left(\nu \right)<+\mathrm{\infty }$ this method ensures the rate of convergence: (116) $\underset{1\le k\le t-1}{min}\parallel \mathrm{\nabla }f\left(x_k\right){\parallel }_{\ast }\le \frac{H_{f,p}\left(\nu \right)\parallel x_0-x^{\ast }{\parallel }^{p+\nu -1}}{\kappa \left(t\right)},t\ge 2,$(116) where $\{x_k{\}}_{k\ge 0}$ is the sequence generated by method $\mathcal{M}$ and $x^{\ast }$ is a global minimizer of f. Then, for all $t\ge 2$ such that $t+1\le n$ we have (117) $\kappa \left(t\right)\le L_{p,\nu }(t+1{)}^{\frac{3(p+\nu )-2}{2}}with{L}_{p,\nu }=2^{\frac{2+\nu }{2}}(3{)}^{-\frac{p+\nu -1}{2}}{\mathrm{\Pi }}_{i=0}^{p-1}(p+\nu -i).$(117)

Proof.

Let us apply method $\mathcal{M}$ for minimizing function $f_t(\cdot )$ starting from point $x_0=0$. By Lemma 6.4, we have $x_k\in {\mathbb{R}}_k^n$ for all k, $1\le k\le t-1$. Thus, from Lemma 6.5, it follows that (118) $\underset{1\le k\le t-1}{min}\parallel \mathrm{\nabla }{f}_t\left(x_k\right){\parallel }_{\ast }\ge \underset{1\le k\le t-1}{min}\frac{1}{\sqrt{k+1}}=\frac{1}{\sqrt{t}}.$(118) Then, combining (116(116) $\underset{1\le k\le t-1}{min}\parallel \mathrm{\nabla }f\left(x_k\right){\parallel }_{\ast }\le \frac{H_{f,p}\left(\nu \right)\parallel x_0-x^{\ast }{\parallel }^{p+\nu -1}}{\kappa \left(t\right)},t\ge 2,$(116) ), (118(118) $\underset{1\le k\le t-1}{min}\parallel \mathrm{\nabla }{f}_t\left(x_k\right){\parallel }_{\ast }\ge \underset{1\le k\le t-1}{min}\frac{1}{\sqrt{k+1}}=\frac{1}{\sqrt{t}}.$(118) ), Lemma 6.1 and Lemma 6.2 we get $\begin{array}{rl}\kappa \left(t\right)& \le \frac{H_{f_t,p}\left(\nu \right)\parallel x_0-x_{t+1}^{\ast }{\parallel }^{p+\nu -1}}{\underset{1\le k\le t-1}{min}\parallel \mathrm{\nabla }{f}_t\left(x_k\right){\parallel }_{\ast }}\le 2^{\frac{2+\nu }{2}}{\mathrm{\Pi }}_{i=1}^{p-1}(p+\nu -i)\parallel x_t^{\ast }{\parallel }^{p+\nu -1}{t}^{\frac{1}{2}}\\ & \le 2^{\frac{2+\nu }{2}}{\mathrm{\Pi }}_{i=1}^{p-1}(p+\nu -1){\left[\frac{(t+1{)}^{\frac{3}{2}}}{\sqrt{3}}\right]}^{p+\nu -1}(t+1{)}^{\frac{1}{2}}\le L_{p,\nu }(t+1{)}^{\frac{3(p+\nu )-2}{2}},\end{array}$ where constant $L_{p,\nu }$ is given in (117(117) $\kappa \left(t\right)\le L_{p,\nu }(t+1{)}^{\frac{3(p+\nu )-2}{2}}with{L}_{p,\nu }=2^{\frac{2+\nu }{2}}(3{)}^{-\frac{p+\nu -1}{2}}{\mathrm{\Pi }}_{i=0}^{p-1}(p+\nu -i).$(117) ).

Remark 6.2

Theorem 6.7 establishes that the lower bound for the rate of convergence of tensor methods in terms of the norm of the gradient is also of $\mathcal{O}\left(\right(\frac{1}{k}{)}^{\frac{3(p+\nu )-2}{2}})$. For first-order methods in the Lipschitz case (i.e. $p=\nu =1$), we have $\mathcal{O}\left(\frac{1}{k^2}\right)$. This gives a lower complexity bound of $\mathcal{O}\left({ϵ}^{-\frac{1}{2}}\right)$ for finding ε-stationary points of convex functions using first-order methods, which coincides with the lower bound (8b) in [6].

Remark 6.3

The rate of $\mathcal{O}\left(\right(\frac{1}{k}{)}^{\frac{3(p+\nu )-2}{2}})$ corresponds to a worst-case complexity bound of $\mathcal{O}\left({ϵ}^{-2/\left[3\right(p+\nu )-2]}\right)$ iterations necessary to ensure $\parallel \mathrm{\nabla }f\left(x_k\right){\parallel }_{\ast }\le ϵ$. Note that, for $ϵ\in (0,1)$, we have ${\left(\frac{1}{ϵ}\right)}^{\frac{p+\nu }{(p+\nu -1)(p+\nu +1)}}\le {\left(\frac{1}{ϵ}\right)}^{\frac{1}{p+\nu -1}}\le {\left(\frac{1}{ϵ}\right)}^{\frac{p+1}{(p-1)(3p-2)}}{\left(\frac{1}{ϵ}\right)}^{\frac{2}{3(p+\nu )-2}}.$ Thus, by increasing the power of the oracle (i.e. the order p), our non-universal schemes become nearly optimal. For example, if $ϵ={10}^{-6}$ and $p\ge 4$, we have $(\frac{1}{ϵ}{)}^{\frac{1}{p+\nu -1}}\le 10(\frac{1}{ϵ}{)}^{\frac{2}{3(p+\nu )-2}}$.

7. Conclusion

In this paper, we presented p-order methods that can find ε-approximate stationary points of convex functions that are p-times differentiable with ν-Hölder continuous pth derivatives. For the universal and the non-universal schemes without acceleration, we established iteration complexity bounds of $\mathcal{O}\left({ϵ}^{-1/(p+\nu -1)}\right)$ for finding $\overline{x}$ such that $\parallel \mathrm{\nabla }f\left(\overline{x}\right){\parallel }_{\ast }\le ϵ$. For the case in which ν is known, we obtain improved complexity bounds of $\mathcal{O}\left({ϵ}^{-(p+\nu )/\left[\right(p+\nu -1\left)\right(p+\nu +1\left)\right]}\right)$ and $\mathcal{O}(|\log (ϵ\left)|{ϵ}^{-1/(p+\nu )}\right)$ for the corresponding accelerated schemes. For the case in which ν is unknown, we obtained a bound of $\mathcal{O}\left({ϵ}^{-(p+1)/\left[\right(p+\nu -1\left)\right(p+2\left)\right]}\right)$ for a universal accelerated scheme. Similar bounds were also obtained for tensor schemes adapted to the minimization of composite convex functions. A lower complexity bound of $\mathcal{O}\left({ϵ}^{-2/\left[3\right(p+\nu )-2]}\right)$ was obtained for the referred problem class. Therefore, in practice, our non-universal schemes become nearly optimal as we increase the order p.

As an additional result, we showed that Algorithm 6 takes at most $\mathcal{O}(\log ({ϵ}^{-1}\left)\right)$ iterations to find ε-stationary points of uniformly convex functions of degree $p+\nu$ in the form (64(64) $F_{\delta }\left(x\right)=f\left(x\right)+\frac{\delta }{p+\nu }\parallel x-x_0{\parallel }^{p+\nu }.$(64) ). Notice that strongly convex functions are uniformly convex of degree 2. Thus, our result generalizes the known bound of $\mathcal{O}(\log ({ϵ}^{-1}\left)\right)$ obtained for first-order schemes (p = 1) applied to strongly convex functions with Lipschitz continuous gradients ($\nu =1$). At this point, it is not clear to us how p-order methods (with $p\ge 2$) behave when the objective functions are strongly convex with ν-Hölder continuous pth derivatives. Nevertheless, from the remarks done in [12, p. 6] for p = 2, it appears that in our case the class of uniformly convex functions of degree $p+\nu$ is the most suitable for p-order methods from a physical point of view.

Acknowledgements

The authors are very grateful to an anonymous referee, whose comments helped to improve the first version of this paper.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

G.N. Grapiglia was supported by the National Council for Scientific and Technological Development - Brazil [grant number 406269/2016-5] and by the European Research Council Advanced [grant number 788368]. Yurii Nesterov was supported by the European Research Council Advanced [grant number 788368].

Notes on contributors

G. N. Grapiglia

G. N. Grapiglia obtained his doctoral degree in Mathematics in 2014 at Universidade Federal do Paraná (UFPR), Brazil. Currently, he is an Assistant Professor at UFPR. His research cover the development, analysis and application of optimization methods.

Yurii Nesterov

Yurii Nesterov is a professor at the Center for Operations Research and Econometrics (CORE) in Catholic University of Louvain (UCL), Belgium. He received his Ph.D. degree (Applied Mathematics) in 1984 at the Institute of Control Sciences, Moscow. His research interests are related to complexity issues and efficient methods for solving various optimization problems. He has received several international prizes, among which are the Dantzig Prize from SIAM and Mathematical Programming society (2000), the John von Neumann Theory Prize from INFORMS (2009), the SIAM Outstanding Paper Award (2014), and the Euro Gold Medal from the Association of European Operations Research Societies (2016). In 2018, he also won an Advanced Grant from the European Research Council.

Notes

1 Conditions (47(47) ${\tilde{\mathrm{\Omega }}}_{x,p,H}^{\left(\nu \right)}\left(x^{+}\right)\le \tilde{f}\left(x\right)\mathrm{a}\mathrm{n}\mathrm{d}\parallel \mathrm{\nabla }{\mathrm{\Omega }}_{x,p,H}^{\left(\nu \right)}\left(x^{+}\right)+g_{\varphi }\left(x^{+}\right){\parallel }_{\ast }\le \theta \parallel x^{+}-x{\parallel }^{p+\nu -1},$(47) ) have already been used in [20] and are the composite analogue of the conditions proposed in [2]. It is worth to mention that, for p = 3 and $\nu =1$, the tensor model ${\mathrm{\Omega }}_{x,p,M}^{\left(\nu \right)}(\cdot )$ has very nice relative smoothness properties (see [27]) which allow the approximate solution of (44(44) $\underset{y\in \mathbb{E}}{min}{\tilde{\mathrm{\Omega }}}_{x,p,H}^{\left(\nu \right)}\left(y\right)$(44) ) by Bregman Proximal Gradient Algorithms [3,22].

Appendix. Accelerated scheme for composite minimization

To solve problem (41(41) $\underset{x\in \mathbb{E}}{min}\tilde{f}\left(x\right)\equiv f\left(x\right)+\varphi \left(x\right),$(41) ), we can apply the following modification of Algorithm 3 in [18]:

In order to establish a convergence rate for Algorithm A1, we will need the following result.

Lemma A.1

Suppose that H1 holds and let $x^{+}$ be an approximate solution to $\underset{y\in \mathbb{E}}{min}{\tilde{\mathrm{\Omega }}}_{x,p,H}^{\left(\nu \right)}\left(y\right)$ such that (A3) ${\tilde{\mathrm{\Omega }}}_{x,p,H}^{\left(\nu \right)}\left(x^{+}\right)\le \tilde{f}\left(x\right)\mathrm{a}\mathrm{n}\mathrm{d}\parallel \mathrm{\nabla }{\mathrm{\Omega }}_{x,p,H}^{\left(\nu \right)}\left(x^{+}\right)+g_{\varphi }\left(x^{+}\right)\parallel \le \theta \parallel x^{+}-x{\parallel }^{p+\nu -1},$(A3) for some $g_{\varphi }\left(x^{+}\right)\in \mathrm{\partial }\varphi \left(x^{+}\right)$. If $H\ge (p+\nu -1)\left(H_{f,p}\right(\nu )+\theta (p-1)!),$ then (A4) $⟨\mathrm{\nabla }\tilde{f}\left(x^{+}\right),x-x^{+}⟩\ge \frac{1}{3}{\left[\frac{(p-1)!}{H}\right]}^{\frac{1}{p+\nu -1}}\parallel \mathrm{\nabla }\tilde{f}\left(x^{+}\right){\parallel }_{\ast }^{\frac{p+\nu }{p+\nu -1}}.$(A4)

Proof.

Denote $r=\parallel x^{+}-x\parallel$. Then, $\begin{array}{rl}& \parallel \mathrm{\nabla }\tilde{f}\left(x^{+}\right)+\frac{H(p+\nu )}{p!}{r}^{p+\nu -2}B(x^{+}-x){\parallel }_{\ast }\\ & =\parallel \mathrm{\nabla }f\left(x^{+}\right)-\mathrm{\nabla }{\mathrm{\Phi }}_{x,p}\left(x^{+}\right)+\mathrm{\nabla }{\mathrm{\Omega }}_{x,p,H}^{\left(\nu \right)}\left(x^{+}\right)+g_{\varphi }\left(x^{+}\right){\parallel }_{\ast }\\ & \le \parallel \mathrm{\nabla }f\left(x^{+}\right)-\mathrm{\nabla }{\mathrm{\Phi }}_{x,p}\left(x^{+}\right){\parallel }_{\ast }+\parallel \mathrm{\nabla }{\mathrm{\Omega }}_{x,p,H}^{\left(\nu \right)}\left(x^{+}\right)+g_{\varphi }\left(x^{+}\right){\parallel }_{\ast }\\ & \le \left(\frac{H_{f,p}\left(\nu \right)}{(p-1)!}+\theta \right)r^{p+\nu -1},\end{array}$ which gives (A5) $\begin{array}{rl}\left(\frac{H_{f,p}\left(\nu \right)}{(p-1)!}+\theta \right)r^{2(p+\nu -1)}& \ge \parallel \mathrm{\nabla }\tilde{f}\left(x^{+}\right)+\frac{H(p+\nu )}{p!}{r}^{p+\nu -2}B(x^{+}-x){\parallel }_{\ast }^2\\ & =\parallel \mathrm{\nabla }\tilde{f}\left(x^{+}\right){\parallel }_{\ast }^2+\frac{2(p+\nu )}{p!}H{r}^{p+\nu -2}⟨\mathrm{\nabla }\tilde{f}\left(x^{+}\right),x^{+}-x⟩\\ & +\frac{H^2(p+\nu {)}^2}{(p!{)}^2}{r}^{2(p+\nu -1)}.\end{array}$(A5) From (A5(A5) $\begin{array}{rl}\left(\frac{H_{f,p}\left(\nu \right)}{(p-1)!}+\theta \right)r^{2(p+\nu -1)}& \ge \parallel \mathrm{\nabla }\tilde{f}\left(x^{+}\right)+\frac{H(p+\nu )}{p!}{r}^{p+\nu -2}B(x^{+}-x){\parallel }_{\ast }^2\\ & =\parallel \mathrm{\nabla }\tilde{f}\left(x^{+}\right){\parallel }_{\ast }^2+\frac{2(p+\nu )}{p!}H{r}^{p+\nu -2}⟨\mathrm{\nabla }\tilde{f}\left(x^{+}\right),x^{+}-x⟩\\ & +\frac{H^2(p+\nu {)}^2}{(p!{)}^2}{r}^{2(p+\nu -1)}.\end{array}$(A5) ), the rest of the proof follows exactly as in the proof of Lemma A.6 in [18].

Theorem A.2

Suppose that H1 holds and let the sequence $\{x_t{\}}_{t=0}^T$ be generated by Algorithm A1. Then, for $t=2,\dots ,T,$ (A6) $\tilde{f}\left(x_t\right)-\tilde{f}\left(x^{\ast }\right)\le \frac{2^{3p-1}M(p+\nu {)}^{p+\nu }\parallel x_0-x^{\ast }{\parallel }^{p+\nu }}{(p-1)!(t-1{)}^{p+\nu }}.$(A6)

Proof.

For all $t\ge 0$, we have (A7) ${\psi }_t\left(x\right)\le A_t\tilde{f}\left(x\right)+\frac{1}{p+\nu }\parallel x-x_0{\parallel }^{p+\nu },\mathrm{\forall }x\in \mathbb{E}.$(A7) Indeed, (A7(A7) ${\psi }_t\left(x\right)\le A_t\tilde{f}\left(x\right)+\frac{1}{p+\nu }\parallel x-x_0{\parallel }^{p+\nu },\mathrm{\forall }x\in \mathbb{E}.$(A7) ) is true for t = 0 because $A_0=0$ and ${\psi }_0\left(x\right)=\frac{1}{p+\nu }\parallel x-x_0{\parallel }^{p+\nu }$. Suppose that (A7(A7) ${\psi }_t\left(x\right)\le A_t\tilde{f}\left(x\right)+\frac{1}{p+\nu }\parallel x-x_0{\parallel }^{p+\nu },\mathrm{\forall }x\in \mathbb{E}.$(A7) ) is true for some $t\ge 0$. Then, $\begin{array}{rl}{\psi }_{t+1}\left(x\right)& ={\psi }_t\left(x\right)+a_t\left[f\left(x_{t+1}\right)+⟨\mathrm{\nabla }f\left(x_{t+1}\right),x-x_{t+1}⟩+\varphi \left(x\right)\right]\\ & \le A_t\tilde{f}\left(x\right)+a_t\tilde{f}\left(x\right)+\frac{1}{p+\nu }\parallel x-x_0{\parallel }^{p+\nu }=A_{t+1}\tilde{f}\left(x\right)+\frac{1}{p+\nu }\parallel x-x_0{\parallel }^{p+\nu }.\end{array}$ Thus, (A7(A7) ${\psi }_t\left(x\right)\le A_t\tilde{f}\left(x\right)+\frac{1}{p+\nu }\parallel x-x_0{\parallel }^{p+\nu },\mathrm{\forall }x\in \mathbb{E}.$(A7) ) follows by induction. Now, let us prove that (A8) $A_t\tilde{f}\left(x_t\right)\le {\psi }_t^{\ast }\equiv \underset{x\in \mathbb{E}}{min}{\psi }_t\left(x\right).$(A8) Again, using $A_0=0$, we see that (A8(A8) $A_t\tilde{f}\left(x_t\right)\le {\psi }_t^{\ast }\equiv \underset{x\in \mathbb{E}}{min}{\psi }_t\left(x\right).$(A8) ) is true for t = 0. Assume that (A8(A8) $A_t\tilde{f}\left(x_t\right)\le {\psi }_t^{\ast }\equiv \underset{x\in \mathbb{E}}{min}{\psi }_t\left(x\right).$(A8) ) is true for some $t\ge 0$. Note that ${\psi }_t(\cdot )$ is uniformly convex of degree $p+\nu$ with parameter $2^{-(p+\nu -2)}$. Thus, by the induction assumption ${\psi }_t\left(x\right)\ge {\psi }_t^{\ast }+\frac{2^{-(p+\nu -2)}}{p+\nu }\parallel x-v_t{\parallel }^{p+\nu }\ge A_t\tilde{f}\left(x_t\right)+\frac{2^{-(p+\nu -2)}}{p+\nu }\parallel x-v_t{\parallel }^{p+\nu }.$ Consequently, (A9) $\begin{array}{rl}{\psi }_{t+1}^{\ast }& =\underset{x\in \mathrm{d}\mathrm{o}\mathrm{m}\varphi }{min}\left\{{\psi }_t\left(x\right)+a_t\left[f\left(x_{t+1}\right)+⟨\mathrm{\nabla }f\left(x_{t+1}\right),x-x_{t+1}+\varphi \left(x\right)\right]\right\}\\ & \ge \underset{x\in \mathrm{d}\mathrm{o}\mathrm{m}\varphi }{min}\left\{A_t\tilde{f}\left(x_t\right)+\frac{2^{-(p+\nu -2)}}{p+\nu }\parallel x-v_t{\parallel }^{p+\nu }\right.\\ & \left.+a_t\left[f\left(x_{t+1}\right)+⟨\mathrm{\nabla }f\left(x_{t+1}\right),x-x_{t+1}⟩+\varphi \left(x\right)\right]\right\}.\end{array}$(A9) Since f is convex and differentiable and $g_{\varphi }\left(x_{t+1}\right)\in \mathrm{\partial }\varphi \left(x_{t+1}\right)$, we have (A10) $\tilde{f}\left(x_t\right)\ge \tilde{f}\left(x_{t+1}\right)+⟨\mathrm{\nabla }\tilde{f}\left(x_{t+1}\right),x_t-x_{t+1}⟩$(A10) and (A11) $\varphi \left(x\right)\ge \varphi \left(x_{t+1}\right)+⟨g_{\varphi }\left(x_{t+1}\right),x-x_{t+1}⟩.$(A11) Using (A10(A10) $\tilde{f}\left(x_t\right)\ge \tilde{f}\left(x_{t+1}\right)+⟨\mathrm{\nabla }\tilde{f}\left(x_{t+1}\right),x_t-x_{t+1}⟩$(A10) ) and (A11(A11) $\varphi \left(x\right)\ge \varphi \left(x_{t+1}\right)+⟨g_{\varphi }\left(x_{t+1}\right),x-x_{t+1}⟩.$(A11) ) in (A9(A9) $\begin{array}{rl}{\psi }_{t+1}^{\ast }& =\underset{x\in \mathrm{d}\mathrm{o}\mathrm{m}\varphi }{min}\left\{{\psi }_t\left(x\right)+a_t\left[f\left(x_{t+1}\right)+⟨\mathrm{\nabla }f\left(x_{t+1}\right),x-x_{t+1}+\varphi \left(x\right)\right]\right\}\\ & \ge \underset{x\in \mathrm{d}\mathrm{o}\mathrm{m}\varphi }{min}\left\{A_t\tilde{f}\left(x_t\right)+\frac{2^{-(p+\nu -2)}}{p+\nu }\parallel x-v_t{\parallel }^{p+\nu }\right.\\ & \left.+a_t\left[f\left(x_{t+1}\right)+⟨\mathrm{\nabla }f\left(x_{t+1}\right),x-x_{t+1}⟩+\varphi \left(x\right)\right]\right\}.\end{array}$(A9) ), it follows that (A12) $\begin{array}{rl}{\psi }_{t+1}^{\ast }& \ge \underset{x\in \mathrm{d}\mathrm{o}\mathrm{m}\varphi }{min}\left\{A_{t+1}\tilde{f}\left(x_{t+1}\right)+⟨\mathrm{\nabla }\tilde{f}\left(x_{t+1}\right),A_t{x}_t-A_t{x}_{t+1}⟩\right.\\ & \left.+a_t⟨\mathrm{\nabla }\tilde{f}\left(x_{t+1}\right),x-x_{t+1}⟩+\frac{2^{-(p+\nu -2)}}{p+\nu }\parallel x-v_t{\parallel }^{p+\nu }\right\}.\end{array}$(A12) Note that $A_t{x}_t=A_{t+1}{y}_t-a_t{v}_t$ and $A_{t+1}{x}_{t+1}=A_t{x}_{t+1}+a_t{x}_{t+1}$. Thus, combining (A12(A12) $\begin{array}{rl}{\psi }_{t+1}^{\ast }& \ge \underset{x\in \mathrm{d}\mathrm{o}\mathrm{m}\varphi }{min}\left\{A_{t+1}\tilde{f}\left(x_{t+1}\right)+⟨\mathrm{\nabla }\tilde{f}\left(x_{t+1}\right),A_t{x}_t-A_t{x}_{t+1}⟩\right.\\ & \left.+a_t⟨\mathrm{\nabla }\tilde{f}\left(x_{t+1}\right),x-x_{t+1}⟩+\frac{2^{-(p+\nu -2)}}{p+\nu }\parallel x-v_t{\parallel }^{p+\nu }\right\}.\end{array}$(A12) ) and Lemma A.1, we obtain $\begin{array}{rl}{\psi }_{t+1}^{\ast }& \ge A_{t+1}\tilde{f}\left(x_{t+1}\right)+\underset{x\in \mathrm{d}\mathrm{o}\mathrm{m}\varphi }{min}\left\{A_{t+1}\frac{1}{4}{\left[\frac{(p-1)!}{M}\right]}^{\frac{1}{p+\nu -1}}\parallel \mathrm{\nabla }\tilde{f}\left(x_{t+1}\right){\parallel }_{\ast }^{\frac{p+\nu }{p+\nu -1}}\right.\\ & \left.+a_t⟨\mathrm{\nabla }\tilde{f}\left(x_{t+1}\right),x-v_t⟩+\frac{2^{-(p+\nu -2)}}{p+\nu }\parallel x_t-v_t{\parallel }^{p+\nu }\right\}\ge A_{t+1}\tilde{f}\left(x_{t+1}\right),\end{array}$ where the last inequality follows from (A1) exactly as in the proof of Theorem 4.3 in [18]. Thus, (A8(A8) $A_t\tilde{f}\left(x_t\right)\le {\psi }_t^{\ast }\equiv \underset{x\in \mathbb{E}}{min}{\psi }_t\left(x\right).$(A8) ) also holds for t + 1, which completes the induction argument.

Now, combining (A7(A7) ${\psi }_t\left(x\right)\le A_t\tilde{f}\left(x\right)+\frac{1}{p+\nu }\parallel x-x_0{\parallel }^{p+\nu },\mathrm{\forall }x\in \mathbb{E}.$(A7) ) and (A8(A8) $A_t\tilde{f}\left(x_t\right)\le {\psi }_t^{\ast }\equiv \underset{x\in \mathbb{E}}{min}{\psi }_t\left(x\right).$(A8) ), we have (A13) $\tilde{f}\left(x_t\right)-\tilde{f}\left(x^{\ast }\right)\le \frac{1}{A_t}\left[\frac{1}{p+\nu }\parallel x_0-x^{+}{\parallel }^{p+\nu }\right].$(A13) Once again, as in the proof of Theorem 4.3 in [18], it follows from (A1) that (A14) $A_t\ge \frac{(p-1)!}{2^{3p-1}M}{\left[\frac{1}{p+\nu }{\left(\frac{1}{2}\right)}^{\frac{p+\nu -1}{p+\nu }}\right]}^{p+\nu }(t-1{)}^{p+\nu },\mathrm{\forall }t\ge 2.$(A14) Finally, (A6(A6) $\tilde{f}\left(x_t\right)-\tilde{f}\left(x^{\ast }\right)\le \frac{2^{3p-1}M(p+\nu {)}^{p+\nu }\parallel x_0-x^{\ast }{\parallel }^{p+\nu }}{(p-1)!(t-1{)}^{p+\nu }}.$(A6) ) follows directly from (A13(A13) $\tilde{f}\left(x_t\right)-\tilde{f}\left(x^{\ast }\right)\le \frac{1}{A_t}\left[\frac{1}{p+\nu }\parallel x_0-x^{+}{\parallel }^{p+\nu }\right].$(A13) ) and (A14(A14) $A_t\ge \frac{(p-1)!}{2^{3p-1}M}{\left[\frac{1}{p+\nu }{\left(\frac{1}{2}\right)}^{\frac{p+\nu -1}{p+\nu }}\right]}^{p+\nu }(t-1{)}^{p+\nu },\mathrm{\forall }t\ge 2.$(A14) ).