Examples Violating Golyshev’s Canonical Strip Hypotheses

Abstract

We give the first examples of smooth Fano and Calabi–Yau varieties violating the (narrow) canonical strip hypothesis, which concerns the location of the roots of Hilbert polynomials of polarized varieties. They are given by moduli spaces of rank 2 bundles with fixed odd-degree determinant on curves of sufficiently high genus, hence our Fano examples have Picard rank 1, index 2, are rational, and have moduli. The hypotheses also fail for several other closely related varieties.

Keywords:

• geography of Fano manifolds
• geography of Calabi-Yau manifolds
• roots of Hilbert polynomials
• Verlinde formula
• moduli spaces of vector bundles on algebraic curves; toric varieties

MSC codes:

• 14J45; 14J32; 14D20

1. The canonical strip hypotheses

Associated to a polarization of a smooth projective variety X we can consider its Hilbert polynomial. The complex roots of this polynomial satisfy a symmetry property induced by Serre duality. In [Golyshev 09] Golyshev introduced further constraints on these roots: the (narrow) canonical strip hypothesis. The motivation for these restrictions comes from Yau’s inequalities on characteristic numbers. At the end of this introduction we give a quick summary of the positive results regarding these hypotheses.

To state (and generalize) the canonical strip hypothesis we will use the following definition.

Definition 1.

A pair (X, H) of a normal variety X and an ample line bundle H is said to be monotone of index r if (1–1) $${\mathrm{c}}_1\left(X\right)=-{\mathrm{K}}_X\equiv \mathit{rH},$$(1–1) where the symbol $\equiv$ denotes numerical equivalence of divisors.

The case of $H=-{\mathrm{K}}_X$ (resp. $H={\mathrm{K}}_X$) as considered in [Golyshev 09] for a Fano variety (resp. variety with ${\mathrm{K}}_X$ ample) has index 1 (resp. −1). We will also consider polarized Calabi–Yau varieties, for which r = 0.

By Serre duality we have that (1–2) $$\chi \left(\mathit{nH}\right)={(-1)}^{\dim X}\chi (-(r+n\left)H\right).$$(1–2)

Hence the roots of the Hilbert polynomial are symmetric around the line $-r/2.$ Golyshev introduced the following further constraints on the real parts of the roots of the Hilbert polynomial.

Definition 2.

Let X be a smooth projective variety, and H an ample line bundle, such that (X, H) is monotone polarized of index r. Let ${\alpha }_1,\dots ,{\alpha }_{\dim X}$ be the real parts of the roots of the Hilbert polynomial associated to H. Then we say that X satisfies

• (CL) the canonical line hypothesis if

  (1–3) $${\alpha }_i=-\frac{r}{2},$$(1–3)

• (NCS) the narrow canonical strip hypothesis if (1–4) $${\alpha }_i\in \left[-r+\frac{r}{\dim X+1},-\frac{r}{\dim X+1}\right]$$(1–4)

  when $r\ge 0$

  (1–5) $${\alpha }_i\in \left[\frac{-r}{\dim X+1},-r+\frac{r}{\dim X+1}\right]$$(1–5)

  otherwise,

• (CS) the canonical strip hypothesis if

  (1–6) $${\alpha }_i\in [-r,0]$$(1–6)

  if

  (1–7) $${\alpha }_i\in [0,-r]$$(1–7)

  when r ≥ 0 otherwise,

  for all $i=1,\dots ,\dim X.$

  It is clear that (1–8) $$\left(\text{CL}\right)\Rightarrow \left(\text{NCS}\right)\Rightarrow \left(\text{CS}\right).$$(1–8)

If X is a Fano variety such that there exists a (normal) anticanonical divisor $Y-X,$ then we can consider the monotone polarized variety $(Y-{\mathrm{K}}_X{|}_Y).$ By [Golyshev 09, Theorem 4] we know that if $(X-{\mathrm{K}}_X)$ satisfies (CS) then $(Y-{\mathrm{K}}_X{|}_Y)$ satisfies (CL).

The goal of this paper is to give the first examples of

1. Fano varieties which violate the (narrow) canonical strip hypothesis;

2. embedded Calabi-Yau varieties which violate the (narrow) canonical strip hypothesis by

The question whether such varieties exist was raised by Golyshev in [Golyshev 09, §5.A]. The examples we give are moduli spaces ${\mathrm{M}}_C(2,\mathcal{L})$ of vector bundles of rank 2 with fixed determinant $\mathcal{L}$ of odd degree on a curve C of genus $g\gg 2.$

Theorem 3.

We have the following examples violating the (narrow) canonical strip hypothesis.

• Let $g\ge 8,$ then ${\mathrm{M}}_C(2,\mathcal{L})$ does not satisfy the narrow canonical strip hypothesis.

• Let $g\ge 10,$ then ${\mathrm{M}}_C(2,\mathcal{L})$ does not satisfy the canonical strip hypothesis.

• Let $g\ge 11$, then an anticanonical Calabi–Yau hypersurface inside ${\mathrm{M}}_C(2,\mathcal{L})$ does not satisfy the canonical line hypothesis.

Hence for g = 10 we have that ${\mathrm{M}}_C(2,\mathcal{L})$ violates the canonical strip hypothesis, yet an anticanonical Calabi–Yau hypersurface still satisfies the embedded canonical line hypothesis. See also Table 1 for more information.

Table 1. Maximum value of real parts of complex roots of Hilbert polynomial.

	Fano			Calabi–Yau
g	Fano^1	Fano^2	${\mathrm{M}}_C(2,\mathcal{L})$	CY^1	CY^2	CY^3	CY^4	CY^5	CY^6
2	–0.5	–0.5	–1	0	0	0	0	0	0
3	–0.5	–0.5	–0.7066405395	0	0	0	0	0	0
4	–0.5	–0.5	–0.4770019488	0	0	0	0	0	0
5	–0.2890507098	–0.3131727064	–0.3094989272	0	0	0	0	0	0
6	–0.1792056326	–0.2063905610	–0.1911961780	0	0	0	0	0	0
7	–0.1047144340	–0.1119844025	–0.1083536780	0	0	0	0	0	0
8	–0.0500408825	–0.0499879643	–0.0500409722	0	0	0	0	0	0
9	–0.0088875090	–0.0081356074	–0.0085094225	0	0	0	0	0	0
10	0.0213534238	0.0216201879	0.0214869361	0	0.0379539521	0.0381695630	0.0382767453	0.0383835172	0.0380619666
11	0.0434392549	0.0434699963	0.0434546003	0.0614369091	0	0	0	0	0
12	0.0597507064	0.0597412231	0.0597459652	0.0399471632	0.0731794361	0.0731745236	0.0731720669	0.0731696099	0.0731769800
13	0.0719600677	0.0719550941	0.0719575810	0.0801077393	0.0675677156	0.0675620782	0.0675592588	0.0675564391	0.0675648971
14	0.0811899396	0.0811890603	0.0811894999	0.0819305430	0.0845735173	0.0845730490	0.0845728148	0.0845725807	0.0845732831
15	0.0882121052	0.0882121423	0.0882121238	0.0879245273	0.0907743344	0.0907742826	0.0907742567	0.0907742308	0.0907743085
16	0.0935738073	0.0935738646	0.0935738359	0.0965258891	0.0911200604	0.0911201236	0.0911201551	0.0911201867	0.0911200920
17	0.0976711255	0.0976711387	0.0976711321	0.0946222779	0.1003675084	0.1003675211	0.1003675275	0.1003675339	0.1003675148
18	0.1007949361	0.1007949368	0.1007949365	0.1029737199	0.0981849016	0.0981849019	0.0981849020	0.0981849022	0.0981849018
19	0.1058859249	0.1058863358	0.1058861304	0.1051019381	0.1070028490	0.1070031860	0.1070033546	0.1070035231	0.1070030175
20	0.1146393484	0.1146393524	0.1146393504	0.1144075091	0.1150500957	0.1150501150	0.1150501247	0.1150501344	0.1150501053
21	0.1218850498	0.1218850164	0.1218850331	0.1225735595	0.1211992074	0.1211991712	0.1211991532	0.1211991351	0.1211991893
22	0.1278911325	0.1278911199	0.1278911262	0.1272829480	0.1284698807	0.1284698686	0.1284698625	0.1284698564	0.1284698747
23	0.1328722016	0.1328721997	0.1328722006	0.1332346075	0.1324975586	0.1324975566	0.1324975556	0.1324975546	0.1324975576
24	0.1370012165	0.1370012167	0.1370012166	0.1368306124	0.1371716714	0.1371716716	0.1371716717	0.1371716719	0.1371716715
25	0.1404184745	0.1404184747	0.1404184746	0.1404629798	0.1403761630	0.1403761632	0.1403761633	0.1403761634	0.1403761631
dim	3g–4	3g–3	3g–3	3g–4	3g–5	3g–3	3g–3	3g–3	3g–3

Observe that there exist smooth anticanonical hypersurfaces, by the very ampleness of Θ [Brivio and Verra 99] (which is the ample generator of ${\text{PicM}}_C(2,\mathcal{L}),$ as recalled in Section 2) and the Bertini theorem.

In Section 2 we give the proof of this theorem, and discuss related constructions, giving more families of examples violating Golyshev’s hypotheses. Before we do this we give an overview of the positive results in the literature. In [Golyshev 09] Golyshev explains how

1. the canonical line hypothesis holds for smooth projective curves (with the elliptic curve being embedded in ${\mathbb{P}}^2$);

2. the narrow canonical strip hypothesis holds for del Pezzo surfaces and surfaces of general type, and the canonical line hypothesis holds for embedded K3 surfaces;

3. the narrow canonical strip hypothesis holds for Fano 3-folds and minimal threefolds of general type.

Moreover it is explained how all Grassmannians (not just projective spaces) satisfy the narrow canonical strip hypothesis.

In [Manivel 09] Manivel shows that for G a simple affine algebraic group and P a maximal parabolic subgroup

1. G/P satisfies the tight¹ canonical strip hypothesis;

2. Fano complete intersections in G/P satisfy the tight canonical strip hypothesis;

3. general type complete intersections in G/P satisfy the canonical line hypothesis;

4. Calabi–Yau complete intersections in G/P satisfy the canonical line hypothesis.

Miyaoka’s celebrated pseudo-effectivity theorem [Miyaoka 87] implies that the embedded canonical line hypothesis holds for smooth Calabi–Yau threefolds, as well as for threefolds with numerically trivial canonical bundle, and terminal Gorenstein singularities that admit a crepant resolution.

Another case that can be checked is that of smooth toric Fano n-folds, for $n=4,\dots ,7.$ By [Cox et al. 11, Proposition 9.4.3] we have that the Hilbert polynomial for the anticanonical bundle is the Ehrhart polynomial of the moment polytope. In [Ehrhart Polynomials] we have computed these Ehrhart polynomials, based on the classification of the toric Fano polytopes up to dimension 7. It turns out there are no examples violating the canonical strip hypothesis. In other words, we can add the following proposition to the list of positive examples.

Proposition 4.

Let X be a smooth toric Fano variety of dimension at most 7. Then X satisfies the canonical strip hypothesis, but the narrow canonical strip hypothesis is violated starting in dimension 4.

In fact, the maximal value m_d of the real parts of the roots of the Hilbert polynomials for smooth toric Fano varieties of dimension d is given as (1–9) $$\begin{array}{cc}{m}_2\hfill & =-0.3333333333\dots \hfill \\ m_3\hfill & =-0.2500000000\dots \hfill \\ m_4\hfill & =-0.1394448724\dots \hfill \\ m_5\hfill & =-0.0868988066\dots \hfill \\ m_6\hfill & =-0.0566708554\dots \hfill \\ m_7\hfill & =-0.0354049073\dots \hfill \end{array}$$(1–9)

For Gorenstein toric Fano varieties hypothesis (CS) was shown to be true in dimensions up to 5 by [Hegedüs et al. 15, Theorem 1.7], but is violated in dimension 10 due to the example in [Hegedüs et al. 15, §7.3]. It is unknown whether hypothesis (CS) holds or not for Gorenstein toric Fano varieties of dimensions between 6 and 9. However for smooth toric Fanos hypothesis (CS) is also true in dimensions 6 and 7 by Proposition 4.

2. Examples violating the hypotheses

An interesting class of Fano varieties is given by moduli spaces of vector bundles on a curve. We will restrict ourselves to the case of rank 2. Let $\mathcal{L}$ be a line bundle of odd degree on a smooth projective curve C of genus g. Then the moduli space ${\mathrm{M}}_C(2,\mathcal{L})$ of rank 2 bundles with determinant $\mathcal{L}$ is a smooth projective variety of dimension $3g-3,$ of rank 1 and index 2, i.e. ${\text{PicM}}_C(2,\mathcal{L})\cong \mathbb{Z}\Theta ,$ and ${\omega }_{{\mathrm{M}}_C(2,\mathcal{L})}\cong {\Theta }^{\otimes -2},$ see [Drézet and Narasimhan 89].

To compute the Hilbert polynomial we can use the celebrated Verlinde formula, which gives an expression for $\dim {\mathrm{H}}^0({\mathrm{M}}_C(2,\mathcal{L}),{\Theta }^{\otimes k}),$ see [Beauville 95, Zagier 96] for a survey. It reads (2–10) $$\dim {\mathrm{H}}^0({\mathrm{M}}_C(2,\mathcal{L}),{\Theta }^{\otimes k})={(k+1)}^{g-1}\sum _{j=1}^{2k+1}\frac{{(-1)}^{j-1}}{{\hspace{0.17em}\text{sin}\hspace{0.17em}}^{2g-2}\frac{j\pi }{2k+2}}.$$(2–10)

Rather than this version of the Verlinde formula we will use an alternative form, taken from [Zagier 96]. Namely item (x) in Theorem 1 of op. cit. gives the formula (2–11) $$\dim {\mathrm{H}}^0({\mathrm{M}}_C(2,\mathcal{L}),{\Theta }^{\otimes k})=\frac{2^g\det M_{r,s}}{\prod _{j=1}^g\left(2j\right)!}$$(2–11) where the matrix ${(M_{r,s})}_{r,s=0,\dots ,g-1}$ is given by (2–12) $$M_{r,s}=\{\begin{array}{cc}1\hfill & r=0\hfill \\ {(k+1+r)}^{2s+2}-{(k+1-r)}^{2s+2}\hfill & r\ge 0\hfill \end{array}.$$(2–12)

The benefit of using this expression is that it can be computed in an exact fashion in computer algebra.

Using this formula one computes the first 3g coefficients of the Hilbert series, and from this we can obtain the Hilbert polynomial of ${\mathrm{M}}_C(2,\mathcal{L})$ with respect to Θ, i.e. we consider the monotone polarization given by $H=\Theta$ for ${\mathrm{M}}_C(2,\mathcal{L}).$ Two implementations of the computations (one in Pari/GP, another in Sage) can be found at [Canonical Strip Hypothesis]. The implementation computes the maximum of the real parts of the complex roots of the Hilbert polynomial, so we are interested in knowing when these are negative, but close to 0, or positive. From these computations we get Theorem 3 as in the introduction.

Remark 5.

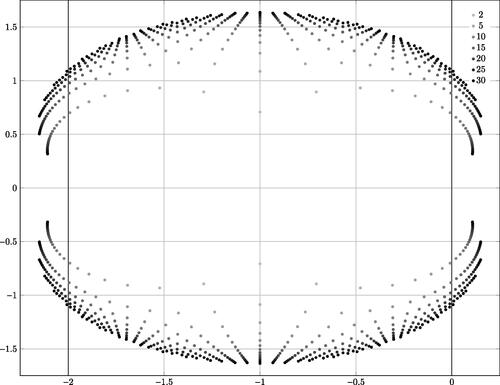
The values in the column labeled ${\mathrm{M}}_C(2,\mathcal{L})$ in Table 1 suggest an interesting convergence behavior for the maximum of the real part of the complex roots of the Hilbert polynomial. More generally one can compute that the collection of all roots of the Hilbert polynomial seems to exhibit a pattern where the limiting behavior involves the complex hull of the roots for increasing genera. A visualization of this is given in Figure 1. In the picture we have omitted the root at t = –1, which in all the examples we computed is of multiplicity g – 1, but we have no proof of this. We suggest these questions for future work.

Figure 1. Complex roots of Hilbert polynomials of ${\mathrm{M}}_C(2,\mathcal{L}),$ for $g=2,\dots ,30.$

2.1. Related constructions

Besides an anticanonical Calabi–Yau hypersurface constructed out of ${\mathrm{M}}_C(2,\mathcal{L})$ there are other Fano and Calabi–Yau varieties we can construct out of it. These are

• Fano¹ the $3g-4$—dimensional Fano variety given by a linear section;

• Fano² the $3g-3$—dimensional Fano variety given by a double cover branched in $2\Theta ;$

• CY² the $3g-5$—dimensional Calabi–Yau variety given by a linear section of codimension 2;

• CY³ the $3g-3$—dimensional Calabi–Yau variety given by a double cover branched in $4\Theta ;$

• CY⁴ the $3g-3$—dimensional Calabi–Yau variety given by the cone over the embedding given by Θ, intersected with a cubic hypersurface;

• CY⁵ the $3g-3$—dimensional Calabi–Yau variety given by the join with a line intersected with two quadric hypersurfaces;

• CY⁶ the $3g-3$—dimensional Calabi–Yau variety given by a smoothing of a linear section of a join with an elliptic curve of degree 1.

For all of these the canonical strip (resp. line) hypothesis eventually fails, as checked in [Canonical Strip Hypothesis]. In Table 1 we have collected the maximum over the real parts of the complex roots of the Hilbert polynomial, where the columns are labeled as in this remark. The Calabi–Yau variety denoted CY¹ is the anticanonical section of ${\mathrm{M}}_C(2,\mathcal{L})$ as considered in Theorem 3.

Remark 6.

The case Fano¹ was also used in [Castravet 07] to construct counterexamples to Pukhlikov’s conjecture that all smooth Fano varieties of dimension $\ge 4$ and index 1 are birationally rigid.

Remark 7.

The canonical line hypothesis can also be formulated for varieties with ample canonical bundle. One can construct new varieties of general type from ${\mathrm{M}}_C(2,\mathcal{L}),$ but we have not found examples of varieties violating the canonical line hypothesis by doing so.

Acknowledgments

The authors thank the referee for their comments.

Additional information

Funding

The first and third author were supported by the Max Planck Institute for Mathematics in Bonn. The second author was partially supported by the Hausdorff Center for Mathematics during the trimester program “Periods in Number Theory, Algebraic Geometry and Physics” and by the Laboratory of Mirror Symmetry NRU HSE, RF Government grant, ag. N. 14.641.31.0001.

Notes

1 A strengthening of the narrow canonical strip hypothesis for Fano varieties involving the index ${\iota }_X$ of X, i.e. with the notation of Definition 2 one asks for ${\alpha }_i\in [-1+1/{\iota }_X,-1/{\iota }_X],$ when $H=-{\mathrm{K}}_X.$