Simple Type Theory is not too Simple: Grothendieck’s Schemes Without Dependent Types

Abstract

Church’s simple type theory is often deemed too simple for elaborate mathematical constructions. In particular, doubts were raised whether schemes could be formalized in this setting and a challenge was issued. Schemes are sophisticated mathematical objects in algebraic geometry introduced by Alexander Grothendieck in 1960. In this article we report on a successful formalization of schemes in the simple type theory of the proof assistant Isabelle/HOL, and we discuss the design choices which make this work possible. We show in the particular case of schemes how the powerful dependent types of Coq or Lean can be traded for a minimalist apparatus called locales.

Keywords:

• Logic and verification
• higher order logic
• type theory
• algebraic geometry
• sheaves
• schemes

2010 MSC::

• 14A15
• 14-04
• 03B35
• 68V20

1 Introduction

1.1 A Challenge Accepted and Met

Proof assistants have made impressive progress on the formalization of algebra [14]. In 2003, Laurent Chicli, as the topic of his PhD thesis [7], formalized sheaves of rings and affine schemes in the proof assistant Coq [9], which is based on a powerful dependent type theory known as the Calculus of Inductive Constructions [10, 11]. However, Chicli’s Coq code certainly became deprecated long ago. More recently, in 2019 Grothendieck’s schemes [15] have been formalized by a group of six mathematicians led by Kevin Buzzard [6], with additional insights from Reid Barton and Mario Carneiro, using the brave new Lean theorem prover, which is based on a similar dependent type theory [12]. For the reader unfamiliar with schemes we will quote Kevin Buzzard.

Schemes are the fundamental objects of study in algebraic geometry. They were discovered (in their current form) by Grothendieck in the late 1950s and early 1960s and they revolutionised the theory of algebraic geometry.¹

and

A scheme is a mathematical object whose definition and basic properties are usually taught at MSc or early PhD level in a typical mathematics department.

Kevin Buzzard in 2017 proposed the formalization of schemes

as basically a challenge to see if Lean can handle such a complex definition.²

We should note that the Isabelle proof assistant is based on a much more minimalist type theory, known as simple type theory. As a consequence, many users of dependent type theories see Isabelle’s type theory as a far less expressive system for formalizing advanced mathematics. These doubts have been expressed by Kevin Buzzard on his blog:

What can Isabelle/HOL actually do before it breaks? Nobody knows. […] But do you people want to attract working mathematicians? Then where are the schemes? Can your system even do schemes? I don’t know. Does anyone know? If it cannot then this would be very valuable to know because it will help mathematician early adopters to make an informed decision about which system to use.³

Even the status of sheaves of rings, a prerequisite for schemes, was unclear:

I am not sure that it is even possible to write this code in Isabelle/HOL in such a way that it will run in finite time, […], and a sheaf is a dependent type, and your clever HOL workarounds will not let you use typeclasses […]⁴

In this article we present a formalization of sheaves of rings and schemes in Isabelle/HOL reaching the benchmark result set by [6]: an affine scheme is a scheme.

1.2 Toward a Discipline of Formalizing

To achieve this result, we tried to bridge the gap between set theory and type theory within the simple type theory of Isabelle/HOL, while forgoing the extension of Isabelle’s logic with a new rule for type definition as proposed by Kunčar and Popescu in their types-to-sets framework [19]. We avoided Isabelle’s type classes and type declarations whenever possible and relied on Isabelle’s module system called locales, whose modern incarnation appeared in 2006 [1]. Locales pervade our development and we exemplify their use in topology, abstract algebra and algebraic geometry. In particular, the present work makes a triple contribution to Isabelle/HOL: a first building block toward a new topology library, a new building block toward a library for abstract algebra and finally a formalization of schemes. The formalized material has a size of 7300 lines of code [5], including material in commutative algebra (prime and maximal ideals, localization of a ring) and our partial reconstruction of the topology library (down to the notion of a topological space). Our experiment meets the challenge of formalizing for the first time schemes in simple type theory and by doing so it demonstrates that intricate dependencies of mathematical structures can be managed in this formal logical system. In Section 4 the current limitations of locales are addressed and we point out possible improvements to make formal statements handled with locales more concise. Our approach through locales allows for intricate definitions as well as proofs where the efficient proof automation of Isabelle/HOL kicks in. We hope this work will help mathematicians interested in the formalization of mathematics to evaluate the formal systems available to them.

2 A World Without Dependent Types: Problems and solutions

2.1 Isabelle/HOL and Simple Type Theory

Isabelle/HOL [22] is a proof assistant for higher-order logic—Church’s simple type theory [8]—and is therefore based on the typed λ-calculus with Boolean and function types. A Boolean-valued function is a predicate, which yields a simple typed set theory that is expressive enough to express abstract mathematics, as we demonstrate below.

In Church’s original conception, the sole purpose of types is to prevent inconsistency, all collections being represented as sets. People today, influenced by programming languages, prefer to give types a more dominant role. They expect to have numeric types like int, nat, real, complex and for types to play a major role in logical reasoning. For example, an expression like x+y should be interpreted with respect to the types of x and y. Isabelle/HOL’s type classes [24] support this sort of type-based disambiguation in a strong sense, so that x+y refers to the correct instance of addition. Type classes work for such trivialities as the basic laws for addition and multiplication (with the help of type classes for groups and rings) and for more advanced topological properties [17]. A new type, once proved to be a topological space, instantly inherits such concepts as limits and continuity along with all theorems proved about them.

The drawback of type classes is simply that they refer to types. Mathematical constructions are generally too complex to formalize as types. Even the carrier of a group can be a complex object. Moving to a stronger type system, as done in Coq or Lean, brings issues of its own. Our solution is to define what we need using the naive set theory that comes with higher-order logic, through the mechanism of locales. ⁵

2.2 Locales

A locale [2] represents an Isabelle/HOL proof context. It can take parameters and instances of other locales. It can declare components constrained by assumptions. Thus they correspond directly to the mathematical practice of defining a monoid, say, as a tuple $(M,·,1)$ satisfying the obvious properties. A locale can inherit multiple instances, as when we define a monoid homomorphism with respect to two monoids.

Logically, a locale is nothing but a predicate; their power comes from Isabelle’s mechanisms for creating, managing and using locale hierarchies. If we work in a particular locale, we can refer to its components and assumptions. But we can also prove membership of a locale, which means to exhibit particular constructions—say a purported monoid carrier along with its multiplication and identity—and prove that they satisfy the locale’s assumptions. Sublocale declarations provide a means of proving inclusions between locales, for instance to prove once and for all that every submonoid is in particular a monoid. We found that locales handled the tangle of definitions building up to schemes faithfully.

However, the right way to formalize advanced algebra is not obvious. During the formal development the user has to decide how mathematical structures should be best organized in the proof assistant so that they can be used mechanically in an efficient way. It is well-known in the Isabelle community that the main algebra library needs to be rebuilt from scratch. In fact, there are many libraries for algebra in Isabelle: HOL-Algebra⁶ from the previous millennium (1999), the more recent HOL-Computational_Algebra⁷, and moreover some entries in the Archive of Formal Proofs⁸ like Groups, Rings and Modules [18] and Vector Spaces [21] among others. As a result, there is a lot of overlapping material, which makes the status of algebra confusing and unclear for the newcomer in the Isabelle world. And while these formalizations constitute an impressive body of work, parts of it are deprecated code not using locales or the Isar language, an additional layer of vernacular which allows for structured proofs making them more legible and easier to maintain. Despite these problems, there are noteworthy achievements like the formalization of the algebraic closure of a field [13].

Even using locales, we can still go wrong. The root of the problems in HOL-Algebra is the desire to refer to a structure such as a group with its components using a single variable, as a record data structure. The new (at the time) extensible records seemed perfect for the task. But they led to some peculiarities: notably, the locale abelian_group (in Theory Ring) which presents the odd twist of requiring a ring structure. The lack of multiple inheritance for records seems to have required the awkward use of the ring record for abelian groups. However, Clemens Ballarin recently conducted an experiment [3] showing that locales, without records, allow for a smooth handling of basic algebraic structures in Isabelle such as monoids, groups and rings. We decided to base our formal development on this experiment. In the next section we introduce schemes and their formal counterparts in simple type theory, replacing the dependent types of Buzzard et al. [6] by Isabelle’s locales.

3 Schemes in Isabelle/HOL

3.1 Elements of Topology

We seized the opportunity of formalizing schemes to build a new topology library despite the two existing formalizations of topology in Isabelle/HOL, namely HOL-Topological_Spaces.thy⁹ and HOL-Analysis/Abstract_Topology.¹⁰ Our new topology library is entirely built on locales without using type classes or type declarations (via the typedef command). In particular, our topological spaces have explicit carrier sets as part of their data instead of using UNIV, the set of all elements of some type, or having to define it later as the union of all the open sets.

locale topological_space =  fixes S:: "’a set" and is_open:: "’a set ⇒ bool"  assumes open_space [simp, intro]: "is_open S"   and open_empty [simp, intro]: "is_open {}"   and open_imp_subset: "is_open U ⇒ U ⊆ S"   and open_inter [intro]: "[[is_open U; is_open V]] ⇒ is_open (U ∩ V)"   and open_union [intro]:    "∧ F::(’a set) set. (∧ x. x ∈ F ⇒ is_open x)     ⇒ is_open (∪ x∈F. x)"

The token ’a set denotes the type of sets of elements of type ’a, this last type being the type of the elements of the carrier S of our topological space. Within the locale for topological spaces the axiom open_imp_subset enforces that an open is automatically a subset of the ambient space. This is a welcome addition, since it avoids having to add this assumption in every lemma mentioning an open set among its assumptions, making the economy of dozens of trivial assumptions.

Then we define the topology generated by a family of subsets of a given set,

inductive generated_topology:: "’a set ⇒ ’a set set ⇒ ’a set ⇒ bool"   for S:: "’a set" and B:: "’a set set"  where   UNIV: "generated_topology S B S" | Int: "generated_topology S B (U ∩ V)"   if "generated_topology S B U" and "generated_topology S B V" | UN: "generated_topology S B (∪ K)"   if "(∧ U. U ∈ K _⇒ generated_topology S B U)" | Basis: "generated_topology S B b" if "b ∈ B ∧ b ⊆ S"

where ’a set set denotes the type of sets of elements of type ’a set. The fact that the generated topology is indeed a topology is established as one of our first lemmas.

lemma generated_topology_is_topology:  fixes S:: "’a set" and B:: "’a set set"  shows "topological_space S (generated_topology S B)"

Covers in topology are an interesting example, since they illustrate how locales can be nested like matryoshka dolls.

locale cover_of_subset =  fixes X:: "’a set" and U:: "’a set"   and index:: "real set" and cover:: "real ⇒ ’a set" cover:: "real ⇒ ’a set"  assumes "U ⊆ X"   and "∧ i. i ∈ index ⇒ cover i ⊆ X"   and "U ⊆ (∪ i ∈ index. cover i)" locale open_cover_of_subset = topological_space X is_open    + cover_of_subset X U I C   for X and is_open and U and I and C +   assumes "∧ i. i∈I ⇒ is_open (C i)" locale open_cover_of_open_subset    = open_cover_of_subset X is_open U I C   for X and is_open and U and I and C +   assumes "is_open U"

Above, each locale builds on the previous one to define eventually an open cover of an open subset. The token “+” is used to declare a mathematical structure which was previously introduced and also to add possibly a list of assumptions. Our library includes also basic elements like homeomorphisms and the subspace topology induced on a subset.

3.2 Elements of Algebraic Geometry

Our presentation follows the classic graduate textbook of Hartshorne [16]. For the remainder of this text fix a ring R. The reader can safely assume that R is commutative.

3.2.1 The Zariski Topology

The definitions of a ring R and of an ideal of R were introduced in [3]. Note that in Isabelle we do not assume from the start that R is commutative, since we strive for generality. In formal mathematics, adding an axiom later is easier than removing one!

Definition 3.1

(ideal). An ideal $\mathfrak{a}$ of R is a subset of R which is an additive subgroup such that $R\mathfrak{a}=\mathfrak{a}$.

locale ideal = subgroup_of_additive_group_of_ring +  assumes ideal: "[[a ∈ R; b ∈ I]] ⇒ a b ∈ I"   "[[a ∈ R; b ∈ I]] ⇒ b a ∈ I"

The token subgroup_of_additive_group_of_ring is the way to introduce in Isabelle a ring R and an additive subgroup of R using Isabelle’s locale mechanism. Note that in the code above the ideal is denoted I while gothic letters are sometimes used for denoting ideals. In our code we use both depending on the situation. One easily checks that $\left\{0\right\}$ and R are ideals of R. In our formalization this translates as follows.

lemma (in comm_ring) ideal_R_R: "ideal R R (+) (・) 0 1" lemma (in comm_ring) ideal_0_R: "ideal {0} R (+) (・) 0 1"

The token “in comm_ring” allows to open a context where a commutative ring, here denoted R, has been previously declared in Isabelle. Given $\mathfrak{a}$ and $\mathfrak{b}$ two ideals of R, one defines $\mathfrak{a}\mathfrak{b}$ to be the ideal whose underlying set is $$\{a_1{b}_1+\dots +a_n{b}_n|a_i\in \mathfrak{a},b_i\in \mathfrak{b},n\in \mathbb{N}\}.$$

Actually, $\mathfrak{a}\mathfrak{b}$ is the smallest ideal generated by the set $$\left\{ab\right|a\in \mathfrak{a},b\in \mathfrak{b}\}.$$

definition (in comm_ring) ideal_gen_by_prod    :: "’a set ⇒ ’a set ⇒ ’a set"   where "ideal_gen_by_prod $\mathfrak{a}$ $\mathfrak{b}$ ≡ additive.subgroup_generated    {x. ∃a b. x = a b ∧ a ∈ $\mathfrak{a}$ ∧ b ∈ $\mathfrak{b}$}"

One easily checks $\mathfrak{a}\mathfrak{b}$ is an ideal.

lemma (in comm_ring) ideal_subgroup_generated:  assumes "ideal $\mathfrak{a}$ R (+) (・) 0 1" and "ideal $\mathfrak{b}$ R (+) (・) 0 1"  shows "ideal (ideal_gen_by_prod $\mathfrak{a}$ $\mathfrak{b}$) R (+) (・) 0 1"

This ideal can be characterized as the intersection of all ideals of R containing the set $$\left\{ab\right|a\in \mathfrak{a},b\in \mathfrak{b}\}.$$

lemma (in comm_ring) ideal_gen_by_prod_is_inter:  assumes "ideal $\mathfrak{a}$ R (+) (・) 0 1" and "ideal $\mathfrak{b}$ R (+) (・) 0 1"   shows "ideal_gen_by_prod $\mathfrak{a}$ $\mathfrak{b}$ = ∩ {I. ideal I R (+) (・) 0 1   ∧ {a ・b |a b. a ∈ $\mathfrak{a}$ ∧ b ∈ $\mathfrak{b}$} ⊆ I}"

Given $\left\{{\mathfrak{a}}_i\right\}$ a family of ideals of R indexed by an arbitrary set I, one defines the set $\sum _{i\in I}{\mathfrak{a}}_i$ to be the set $$\{a_1+\dots +a_n|n\in \mathbb{N},a_k\in {\mathfrak{a}}_{i_k}\}.$$of all finite sums of elements belonging to some ideals of the family. The set $\sum _{i\in I}{\mathfrak{a}}_i$, seen as an additive subgroup, is again an ideal of R.

The so-called prime ideals are an important class of ideals.

Definition 3.2

(prime ideal). A prime ideal is an ideal $\mathfrak{p}\ne R$ such that $xy\in \mathfrak{p}$ implies $x\in \mathfrak{p}$ or $y\in \mathfrak{p}$ for every elements x and y in R.

locale pr_ideal = comm:comm_ring R "(+)" "(・)" "0" "1"    + ideal I R "(+)" "(・)" "0" "1"   for R and I and addition (infixl "+" 65) and multiplication    (infixl "・" 70) and zero ("0") and unit ("1")  + assumes carrier_neq: "I ≠ R"     and absorbent: "[[x ∈ R; y ∈ R ⇒ (x ・ y ∈ I) ⇒ (x ∈ I ∨ y ∈ I)"

Our locale pr_ideal builds upon the locale ideal for ideals (introduced previously in [3]) which does not assume the commutativity of the ring R. As a consequence, in order to assume the commutativity of the ring, we have to declare afresh the parameters of the locale instead of simply writing

locale pr_ideal = ideal +  assumes carrier_neq: "I ≠ R"   and absorbent: "[[x ∈ R; y ∈ R]] ⇒ (x ・y ∈ I)    _⇒ (x ∈ I ∨ y ∈ I)"

as our locale, although this last locale would be syntactically correct.

Note that if $\mathfrak{p}$ is a prime ideal, then $1\notin \mathfrak{p}$.

lemma (in pr_ideal) not_1: "1 / ∉ I" proof  assume "1 ∈ I"  then have "∧ x. [[1 ∈ I; x ∈ R]] ⇒ x ∈ I"   by (metis ideal(1) comm.multiplicative.right_unit)  with 〈1 ∈ I〉 have "I = R"   by auto  then show False   using carrier_neq by blast qed

Let $\mathfrak{p}$ be a prime ideal and S be the complement of $\mathfrak{p}$ in R, we prove S is a multiplicative submonoid of R.

lemma (in pr_ideal) submonoid_notin:  assumes "S = {x ∈ R. x / ∉ I}"  shows "submonoid S R (・) 1"

If $\mathfrak{a}$ is an ideal of R, $V(\mathfrak{a})$ will denote the set of all prime ideals of R which contain $\mathfrak{a}$.

definition (in comm_ring) closed_subsets   :: "’a set ⇒ (’a set) set" ("ς_" [900] 900)  where "ς $\mathfrak{a}$ ≡ {I. pr_ideal R I (+) (・) 0 1 ∧ $\mathfrak{a}$ ⊆ I}"

Note that $V(R)=\varnothing$ and $V(\{0\})$ is the set of all prime ideals of R, abbreviated Spec in our code.

lemma (in comm_ring) closed_subsets_zero: "ς {0} = Spec" lemma (in comm_ring) closed_subsets_R: "ς R = {}"

Next, we define on the set of all primes ideals of R the so-called Zariski topology given by the subsets of the form $V(\mathfrak{a})$ as the closed subsets. We then prove in Isabelle that the set $\text{Spec}R$ together with its Zariski topology is a topological space.

definition (in comm_ring) is_zariski_open   :: "’a set set ⇒ bool" where  "is_zariski_open U ≡ generated_topology Spec    {U. (∃$\mathfrak{a}$. ideal $\mathfrak{a}$ R (+) (・) 0 1 ∧ U = Spec - ς$\mathfrak{a}$)} U" lemma (in comm_ring) zariski_is_topological_space:  "topological_space Spec is_zariski_open"

In the rest of this text $\text{Spec}R$ will denote the set of all prime ideals of R equipped with its Zariski topology.

3.2.2 Sheaves of Rings

We now teach Isabelle what presheaves of rings are.

Definition 3.3

(presheaf of rings). Let X be a topological space. A presheaf $\mathrm{F}$ of rings on X consists of the following data:

• for every open set U, a ring $\mathrm{F}(U)$

• for every inclusion $V\subseteq U$ of open subsets, a morphism of rings ${\rho }_{UV}:\mathrm{F}(U)\to \mathrm{F}(V)$

satisfying

1. $\mathrm{F}(\varnothing )=\left\{0\right\}$

2. ρ_UU is the identity map for every open subset U

3. If $W\subseteq V\subseteq U$ are three open subsets, then ${\rho }_{UW}={\rho }_{VW}°{\rho }_{UV}$.

locale presheaf_of_rings = topological_space  + fixes $\mathfrak{F}$:: "’a set ⇒ ’b set"  and ϱ:: "’a set ⇒ ’a set ⇒ (’b ⇒ ’b)" and b:: "’b"  and add_str:: "’a set ⇒ (’b ⇒ ’b ⇒ ’b)" ("+_")’b)" ("+_")  and mult_str:: "’a set ⇒ (’b ⇒ ’b ⇒ ’b)" ("・_")  and zero_str:: "’a set ⇒ ’b" ("0_")  and one_str:: "’a set ⇒ ’b" ("1_")  assumes is_ring_morphism:   "∧ U V. is_open U ⇒ is_open V ⇒ V ⊆ U    ⇒ ring_homomorphism (ϱ U V)     ($\mathfrak{F}$ U) (+U) (・U) ⁰U ¹U     ($\mathfrak{F}$ V) (+V) (・V) ⁰V ¹V" and ring_of_empty: "$\mathfrak{F}$ {} = {b}" and identity_map [simp]: "∧ U. is_open U    ⇒ (∧ x. x ∈ $\mathfrak{F}$ U ⇒ ϱ U U x = x)" and assoc_comp:  "∧ U V W x. [[is_open U; is_open V; is_open W;V ⊆ U;   W ⊆ V;x ∈ ($\mathfrak{F}$ U)]] ⇒ ϱ U W x = (ϱ V W ◦ ϱ U V) x"

Within the locale the sets $\mathrm{F}(U)$’s are endowed with ring structures using the functional add_str (resp. mult_str, zero_str, one_str) that takes an open subset U and outputs the addition (resp. the multiplication, the additive unit, the multiplicative unit) on the set $\mathrm{F}(U)$. Ring homomorphisms have been defined in [3] as follows.

locale ring_homomorphism =  map η R R’ + source: ring R "(+)" "(・)" 0 1  + target: ring R’ "(+’)" "(・’)" "0’" "1’"  + additive: group_homomorphism η R "(+)" 0 R’ "(+’)" "0’"  + multiplicative: monoid_homomorphism η R "(・)" 1 R’ "(・’)" "1’"  for η and R and addition (infixl "+" 65) and multiplication (infixl "・" 70)   and zero ("0") and unit ("1") and R’ and addition’ (infixl "+’’" 65)    and multiplication’ (infixl "・’’" 70) and zero’ ("0’’") and unit’ ("1’’")

As expected the source and target of a ring homomorphism are rings. As a consequence, the condition is_ring_morphism within the locale presheaf_of_rings, requiring ρ_UV to be a ring homomorphism, implies that $\mathrm{F}(U)$ together with its structure is a ring for every open subset U of the underlying topological space.

lemma (in presheaf_of_rings) is_ring_from_is_homomorphism:  fixes U:: "’a set"  assumes "is_open U"  shows "ring ($\mathfrak{F}$ U) (+U) (・U) ⁰U ¹U"

Notation 1. The elements of $\mathrm{F}(U)$ are sometimes called the sections of the presheaf $\mathrm{F}$ over U and given $s\in \mathrm{F}(U),s\mathrm{\upharpoonright }V$ denotes the element ${\rho }_{UV}(s)$.

Of course, we have the corresponding notion of morphisms.

Definition 3.4

(morphism of presheaves of rings). A morphism $\varphi :\mathrm{F}\to \mathrm{F}\prime$ of presheaves of rings on a topological space X is given by a morphism ${\varphi }_U:\mathrm{F}(U)\to \mathrm{F}\prime (U)$ for each open subset U of X such that the following diagram commutes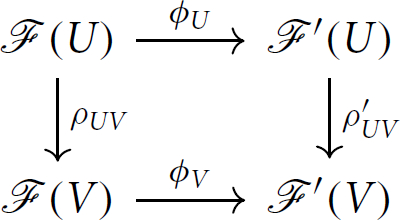for every inclusion $V\subseteq U$.

locale morphism_presheaves_of_rings =  source: presheaf_of_rings X is_open $\mathfrak{F}$ ϱ b add_str   mult_str zero_str one_str  + target: presheaf_of_rings X is_open $\mathfrak{F}$’ ϱ’ b’ add_str’   mult_str’ zero_str’ one_str’ for X and is_open   and $\mathfrak{F}$ and ϱ and b and add_str ("+_")   and mult_str ("・_") and zero_str ("0_")   and one_str ("1_") and $\mathfrak{F}$’ and ϱ’ and b’   and add_str’ ("+’’_") and mult_str’ ("・’’_")   and zero_str’ ("0’’_") and one_str’ ("1’’_") + fixes fam_morphisms:: "’a set ⇒ (’b ⇒ ’c)" assumes is_ring_morphism:  "∧ U. is_open U ⇒ ring_homomorphism (fam_morphisms U)   ($\mathfrak{F}$ U) (+U) (・U) ⁰U ¹U   ($\mathfrak{F}$’ U) (+’U) (・’U) ⁰’U ¹’U"   and comm_diagrams:  "∧ U V x. [[is_open U; is_open V; V ⊆ U;x ∈ $\mathfrak{F}$ U]]   ⇒ (ϱ’ U V ◦fam_morphisms U) x    = (fam_morphisms V ◦ϱ U V) x"

In the snippet of code above, we see the inheritance of locales in action. Indeed, the locale presheaf_of_rings inherits multiple instances, one for the source and one for the target of the notion of morphism being defined. The notion of composition for morphisms of presheaves is straightforward and we check in Isabelle without any difficulty that the composition is again a morphism between presheaves of rings.

Indeed, let $\varphi :\mathrm{F}\to \mathrm{G}$ (resp. $\psi :\mathrm{G}\to \mathrm{H}$) be a morphism of presheaves of rings on a topological space X. One defines the composition $\psi °\varphi$ from $\mathrm{F}$ to $\mathrm{H}$ as $${(\psi °\varphi )}_U:={\psi }_U°{\varphi }_U$$for every open subset U of X.

lemma comp_of_presheaves:  assumes "morphism_presheaves_of_rings X is_open $\mathfrak{F}$ ϱ b    add_str mult_str zero_str one_str $\mathfrak{F}$’ϱ ’ b’     add_str’ mult_str’ zero_str’ one_str’ ϕ"   and "morphism_presheaves_of_rings X is_open $\mathfrak{F}$’ϱ ’ b’    add_str’ mult_str’ zero_str’ one_str’ $\mathfrak{F}$’’ϱ ’’    b’’ add_str’’ mult_str’’ zero_str’’ one_str’’ ϕ’"  shows "morphism_presheaves_of_rings X is_open $\mathfrak{F}$ ϱ b add_str   mult_str zero_str one_str $\mathfrak{F}$’’ϱ ’’ b’’ add_str’’   mult_str’’ zero_str’’ one_str’’ (λU. (ϕ’ U ◦ ϕ U ↓ $\mathfrak{F}$ U))"

The syntax $g°f\downarrow D$, used in the last line of the above code, is simply some syntactic sugar for the definition of the composition $g°f$ of two maps f and g on the domain D.

Remark 3.5.

Given a presheaf $\mathrm{F}$ on X, let us define ${(1_{\mathrm{F}})}_U$ as the identity morphism of $\mathrm{F}(U)$ for every open subset U of X. The family $1_{\mathrm{F}}$ is obviously a morphism of presheaves from $\mathrm{F}$ to itself. A morphism $\varphi :\mathrm{F}\to \mathrm{G}$ of presheaves of rings is an isomorphism if and only if there exists a morphism $\psi :\mathrm{G}\to \mathrm{F}$ such that $\psi °\varphi =1_{\mathrm{F}}$ and $\varphi °\psi =1_{\mathrm{G}}$.locale iso_presheaves_of_rings

 = mor:morphism_presheaves_of_rings +   assumes is_inv: "∃ψ. morphism_presheaves_of_rings X is_open   $\mathfrak{F}$’ϱ’ b’ add_str’ mult_str’ zero_str’ one_str’ $\mathfrak{F}$ ϱ b    add_str mult_str zero_str one_str ψ ∧ (∀U. is_open U    → (∀x ∈ ($\mathfrak{F}$’ U). (fam_morphisms U ◦ ψ U) x = x)     ∧ (∀x ∈ ($\mathfrak{F}$ U). (ψ U ◦ fam_morphisms U) x = x))"

Now, we introduce the notion of a sheaf of rings.

Definition 3.6

(sheaf of rings). A sheaf of rings on a topological space X is a presheaf of rings on X that satisfies the following additional properties:

(locality)Given an open set U, $\left\{V_i\right\}$ an open covering of U and $s\in \mathrm{F}(U)$ such that $s\mathrm{\upharpoonright }{V}_i=0$ for all i, then one has s = 0.

(glueing)Given an open set U, $\left\{V_i\right\}$ an open covering of U and elements $s_i\in \mathrm{F}(V_i)$ satisfying the property $s_i\mathrm{\upharpoonright }{V}_i\cap V_j=s_j\mathrm{\upharpoonright }{V}_i\cap V_j$ for all i and j, then there exists an element $s\in \mathrm{F}(U)$ such that $s\mathrm{\upharpoonright }{V}_i=s_i$ for all i.

The resulting formalization of sheaves of rings in Isabelle is concise (10 lines), tidy and almost transparent with respect to the pen-and-paper definition.

locale sheaf_of_rings = presheaf_of_rings +  assumes locality: "∧ U I V s. open_cover_of_open_subset S     is_open U I V ⇒ (∧ i. i∈I ⇒ V i ⊆ U) ⇒ s ∈ $\mathfrak{F}$ U    ⇒ (∧ i. i∈I ⇒ ϱ U (V i) s = ⁰(V i)) ⇒ s = ⁰U"    and glueing:    "∧ U I V s. open_cover_of_open_subset S is_open U I V    ⇒ (∀i. i∈I → V i ⊆ U ∧ s i ∈ $\mathfrak{F}$ (V i))    ⇒ (∧ i j. i∈I ⇒ j∈I ⇒ ϱ (V i) (V i ∩ V j) (s i)    = ϱ (V j) (V i ∩ V j) (s j))    ⇒ (∃t. t ∈ $\mathfrak{F}$ U ∧ (∀i. i∈I → ϱ U (V i) t = s i))"

A morphism (resp. an isomorphism) of sheaves of rings is nothing but a morphism (resp. an isomorphism) of presheaves of rings, hence the following locale in Isabelle.

locale morphism_sheaves_of_rings = morphism_presheaves_of_rings

Let X be a topological space, $\mathrm{F}$ a sheaf of rings on X and U an open subset of X, one proves that the restriction of $\mathrm{F}$ to U, seen as a topological subspace with respect to the induced topology, is a sheaf of rings. In our formal development this sheaf is called the induced sheaf and shorten ind_sheaf. We encapsulate the relevant mathematical context (the “let be” part) in a dedicated locale and formalize within this locale the relevant definitions and we eventually prove the induced sheaf $\mathrm{F}{|}_U$ is indeed a sheaf of rings.

locale ind_sheaf = sheaf_of_rings +   fixes U:: "’a set"   assumes is_open_subset: "is_open U" begin interpretation it: ind_topology S is_open U definition ind_sheaf:: "’a set ⇒ ’b set"   where "ind_sheaf V ≡ $\mathfrak{F}$ (U ∩ V)" definition ind_ring_morphisms:: "’a set ⇒ ’a set ⇒ (’b ⇒ ’b)"   where "ind_ring_morphisms V W ≡ ϱ U ∩ V) (U ∩ W)" definition ind_add_str:: "’a set ⇒ (’b ⇒ ’b ⇒ ’b)"  where "ind_add_str V ≡ λx y. +(U ∩ V) x y" definition ind_mult_str:: "’a set ⇒ (’b ⇒ ’b ⇒ ’b)"  where "ind_mult_str V ≡ λx y. ・(U ∩ V) x y" definition ind_zero_str:: "’a set ⇒ ’b"  where "ind_zero_str V ≡ ⁰(U ∩V)" definition ind_one_str:: "’a set ⇒ ’b"  where "ind_one_str V ≡ ¹(U ∩V)" lemma ind_sheaf_is_sheaf:  "sheaf_of_rings U it.ind_is_open ind_sheaf ind_ring_morphisms   b ind_add_str ind_mult_str ind_zero_str ind_one_str" end

In the code above the interpretation mechanism for locales makes possible to instantiate the locale ind_topology, for the induced topology on a subset, with a list of arguments. Then it becomes possible to refer later to the induced topology on the open subset U with the abbreviation it.

We introduce a second construction that takes as input a given sheaf of rings and outputs a new sheaf of rings. Let $f:X\to Y$ be a continuous map between topological spaces and $\mathrm{F}$ a sheaf of rings on X. Given an open subset V of Y, define $(f_{*}\mathrm{F})(V)$ to be $\mathrm{F}(f^{-1}(V))$. We then prove that $f_{*}\mathrm{F}$, together with the obvious structure, is a sheaf of rings on the topological space Y. The sheaf $f_{*}\mathrm{F}$ is called the direct image of $\mathrm{F}$.

locale im_sheaf = sheaf_of_rings + continuous_map begin definition im_sheaf:: "’c set = > ’b set"  where "im_sheaf V ≡ $\mathfrak{F}$ (f⁻¹ S V)" definition im_sheaf_morphisms:: "’c set ⇒ ’c set ⇒ (’b ⇒ ’b)"  where "im_sheaf_morphisms U V ≡ ϱ (f⁻¹ S U) (f⁻¹ S V)" definition add_im_sheaf:: "’c set ⇒ ’b ⇒ ’b ⇒ ’b"  where "add_im_sheaf ≡ λV x y. +(f⁻¹ S V) x y" definition mult_im_sheaf:: "’c set ⇒ ’b ⇒ ’b ⇒ ’b"  where "mult_im_sheaf ≡ λV x y. ・(f⁻¹ S V) x y" definition zero_im_sheaf:: "’c set ⇒ ’b"  where "zero_im_sheaf ≡ λV. ⁰(f⁻¹ S V)" definition one_im_sheaf:: "’c set ⇒ ’b"  where "one_im_sheaf ≡ λV. ¹(f⁻¹ S V)" lemma im_sheaf_is_sheaf:  "sheaf_of_rings S’ is_open’ im_sheaf im_sheaf_morphisms b   add_im_sheaf mult_im_sheaf zero_im_sheaf one_im_sheaf" end

As can been seen in the snippet of code above, we encapsulate again the context of the construction in a dedicated locale and this lets us formalize the relevant definitions in this context and we eventually prove the direct image of a sheaf is again a sheaf.

3.2.3 Localizations of Rings

Next, we introduce the localization of commutative rings. Let S be a multiplicative submonoid of R. We consider pairs (r, s) with $r\in R$ and $s\in S$ and we define the following relation on them$(r,s)\sim (r\prime ,s\prime )$if and only if there exists $s_1\in S$ such that $s_1(s\prime r-sr\prime )=0$. One checks that the relation ∼ is an equivalence relation. The equivalence class of a pair (r, s) is denoted by r / s and the set of equivalence classes is denoted by $S^{-1}R$. We define the following addition on $S^{-1}R$.$\frac{r}{s}+\frac{r\prime }{s\prime }=\frac{rs\prime +r\prime s}{ss\prime }$

We also define the following multiplication on $S^{-1}R$.$\frac{r}{s}\times \frac{r\prime }{s\prime }=\frac{rr\prime }{ss\prime }$

One checks these operations are well-defined with $(S^{-1}R,0/1,+,1/1,\times )$ forming a ring. Following Serge Lang [20, II.4] we call the new ring $S^{-1}R$ the quotient ring of R by S¹¹. This construction translates into the following locale.

locale quotient_ring = comm:comm_ring R "(+)" "(・)" "0" "1"     + submonoid S R "(・)" "1"   for S and R and addition (infixl "+" 65)    and multiplication (infixl "・" 70) and zero ("0") and unit ("1") begin definition rel:: "(’a ×’a) ⇒ (’a ×’a) ⇒ bool" (infix "∼" 80)  where "x ∼ y ≡ ∃s1. s1 ∈ S ∧ s1 ・(snd y ・fst x - snd x ・fst y) = 0" interpretation rel: equivalence "R ×S" "{(x,y) ∈(R×S)×(R×S). x ∼y}" definition frac:: "’a ⇒ ’a ⇒ (’a ×’a) set" (infixl "’/" 75)  where "r / s ≡ rel.Class (r, s)" lemma add_rel_frac:  assumes "(r,s) ∈ R ×S" and "(r’,s’)∈ R ×S"  shows "add_rel (r/s) (r’/s’) = (r・s’ + r’・s) / (s・s’)" lemma mult_rel_frac:  assumes "(r,s) ∈ R ×S" and "(r’,s’)∈ R ×S"  shows "mult_rel (r/s) (r’/s’) = (r・r’) / (s・s’)" definition zero_rel::"(’a ×’a) set" where  "zero_rel = frac 0 1" definition one_rel::"(’a ×’a) set" where  "one_rel = frac 1 1" definition carrier_quotient_ring:: "(’a ×’a) set set"  where "carrier_quotient_ring ≡ rel.Partition" sublocale comm_ring carrier_quotient_ring add_rel mult_rel zero_rel one_rel end

The code above ends with a proof that the locale quotient_ring is a sublocale of the locale comm_ring, i.e., a proof that the quotient of a commutative ring by a multiplicative submonoid is a commutative ring. Remember that the complement of a prime ideal $\mathfrak{p}$ in R is a multiplicative submonoid, hence we can apply the previous construction with $S:=R-\mathfrak{p}$. The resulting ring $S^{-1}R$ is called the local ring of R at $\mathfrak{p}$.

context pr_ideal begin lemma submonoid_pr_ideal:  shows "submonoid (R \ I) R (・) 1" proof  show "a ・b ∈ R\I" if "a ∈ R\I" "b ∈ R\I" for a b   using that by (metis Diff_iff absorbent comm.multiplicative.composition_closed)  show "1 ∈ R\I"   using ideal.ideal(2) ideal_axioms pr_ideal.carrier_neq pr_ideal_axioms   by fastforce qed auto interpretation local:quotient_ring "(R\I)" R "(+)" "(・)" 0 1   apply intro_locales   by (meson submonoid_def submonoid_pr_ideal) definition carrier_local_ring_at:: "(’a × ’a) set set"  where "carrier_local_ring_at ≡(R \ I)⁻¹ R₍₊₎ (・) 0" definition add_local_ring_at:: "(’a × ’a) set ⇒(’a × ’a) set ⇒(’a × ’a) set"  where "add_local_ring_at ≡local.add_rel " definition mult_local_ring_at:: "(’a × ’a) set ⇒(’a × ’a) set ⇒(’a × ’a) set"  where "mult_local_ring_at ≡ local.mult_rel " definition uminus_local_ring_at:: "(’a × ’a) set ⇒ (’a × ’a) set"  where "uminus_local_ring_at ≡ local.uminus_rel " definition zero_local_ring_at:: "(’a × ’a) set"  where "zero_local_ring_at ≡ local.zero_rel" definition one_local_ring_at:: "(’a × ’a) set"  where "one_local_ring_at ≡ local.one_rel" end

This allows us to introduce the next construction.

3.2.4 The Spectrum of a Ring

Let U be an open subset of $\text{Spec}R$. We define ${\mathrm{O}}_{\text{Spec}\mathrm{ }R}(U)$ to be the set of all functions$s:U\to \coprod _{\mathfrak{p}\in U}{R}_{\mathfrak{p}}$such that $s(\mathfrak{p})\in R_{\mathfrak{p}}$ for every $\mathfrak{p}\in U$ and such that for every $\mathfrak{p}\in U$, there exist a neighborhood V of $\mathfrak{p}$, contained in U, and elements $r,f\in R$, such that for each $\mathfrak{q}\in V,f\notin \mathfrak{q}$ and $s(\mathfrak{q})=r/f$. We can prove that ${\mathrm{O}}_{\text{Spec}\mathrm{ }R}(U)$ is closed under the addition and multiplication of such functions and we take for the additive unit (resp. multiplicative unit) the function that maps each $\mathfrak{p}$ on the additive unit (resp. multiplicative unit) of $R_{\mathfrak{p}}$. Last, if $V\subseteq U$, then the morphism of rings ${\mathrm{O}}_{\text{Spec}\mathrm{ }R}(U)\to {\mathrm{O}}_{\text{Spec}\mathrm{ }R}(V)$ maps each $s\in {\mathrm{O}}_{\text{Spec}\mathrm{ }R}(U)$ on its restriction to V. One checks ${\mathrm{O}}_{\text{Spec}\mathrm{ }R}$ is a sheaf of rings on $\text{Spec}R$ and the pair $(\text{Spec}R,{\mathrm{O}}_{\text{Spec}\mathrm{ }R})$ is called the spectrum of the ring R. This last construction translates smoothly in Isabelle.

definition (in comm_ring)  is_locally_frac:: "(’a set ⇒(’a ×’a) set) ⇒’a set set ⇒ bool"  where "is_locally_frac s V ≡(∃r f. r ∈ R ∧ f ∈ R ∧ (∀ θ ∈ V.   f ∉ θ ∧ s θ = quotient_ring.frac (R \ θ) R (+) (・) 0 r f))" definition (in comm_ring) is_regular    :: "(’a set ⇒ (’a × ’a) set) ⇒’a set set ⇒ bool"  where "is_regular s U ≡ ∀π. π ∈ U →   (∃V. is_zariski_open V ∧ V ⊆ U ∧ π ∈ V ∧ (is_locally_frac s V))" definition (in comm_ring) sheaf_spec   :: "’a set set ⇒ (’a set ⇒ (’a × ’a) set) set" ("Ο_" [90] 90)  where "Ο U ≡ {s∈ (∏_E π ∈ U. (Rπ (+) (・) 0)). is_regular s U}" definition (in comm_ring) add_sheaf_spec   :: "(’a set) set ⇒ (’a set ⇒ (’a ×’a) set)    ⇒(’a set ⇒(’a × ’a) set) ⇒ (’a set ⇒ (’a × ’a) set)"   where "add_sheaf_spec U s s’ ≡    λπ∈U. quotient_ring.add_rel (R \ π) R (+) (・) 0 (s π) (s’ π)" definition (in comm_ring) mult_sheaf_spec   :: "(’a set) set ⇒ (’a set ⇒ (’a × ’a) set)    ⇒ (’a set ⇒ (’a × ’a) set) ⇒ (’a set ⇒ (’a × ’a) set)"   where "mult_sheaf_spec U s s’ ≡    λπ∈U. quotient_ring.mult_rel (R \ π) R (+) (・) 0 (s π) (s’ π)" definition (in comm_ring) zero_sheaf_spec   :: "’a set set ⇒ (’a set ⇒ (’a × ’a) set)"   where "zero_sheaf_spec U ≡    λπ∈U. quotient_ring.zero_rel (R \ π) R (+) (・) 0 1" definition (in comm_ring) one_sheaf_spec   :: "’a set set ⇒ (’a set ⇒ (’a × ’a) set)"   where "one_sheaf_spec U ≡    λπ∈U. quotient_ring.one_rel (R \ π) R (+) (・) 0 1" definition (in comm_ring) sheaf_spec_morphisms   :: "’a set set ⇒ ’a set set ⇒ ((’a set ⇒ (’a × ’a) set)    ⇒ (’a set ⇒ (’a × ’a) set))"   where "sheaf_spec_morphisms U V ≡ λs∈(Ο U). restrict s V" lemma (in comm_ring) sheaf_spec_is_sheaf:  shows "sheaf_of_rings Spec is_zariski_open sheaf_spec    sheaf_spec_morphisms Οb add_sheaf_spec mult_sheaf_spec     zero_sheaf_spec one_sheaf_spec"

Next, we introduce ringed spaces and their morphisms.

3.2.5 Ringed Spaces

Definition 3.7

(ringed space). A ringed space is a pair $(X,{\mathrm{O}}_X)$, where X is a topological space and ${\mathrm{O}}_X$ is a sheaf of rings on X.

locale ringed_space = sheaf_of_rings

Definition 3.8

(morphism of ringed spaces). A morphism of ringed spaces from $(X,{\mathrm{O}}_X)$ to $(Y,{\mathrm{O}}_Y)$ is a pair $(f,{\varphi }_f)$ consisting of a continuous map $f:X\to Y$ between topological spaces and a morphism ${\varphi }_f:{\mathrm{O}}_Y\to f_{*}{\mathrm{O}}_X$ of sheaves of rings.

locale morphism_ringed_spaces =   im_sheaf X is_open X Ο_X ϱ X b add_str_X mult_str_X zero_str_X one_str_X    Y is_open_Y f   + codom: ringed_space Y is_open_Y Ο_Y ϱ Y d add_str_Y mult_str_Y    zero_str_Y one_str_Y   for X and is_open_X and Ο_X and ϱ X and b and add_str_X and mult_str_X    and zero_str_X and one_str_X and Y and is_open_Y and Ο_Y and ϱ_Y    and d and add_str_Y and mult_str_Y and zero_str_Y and one_str_Y    and f   + fixes ϕf:: "’c set ⇒ (’d ⇒ ’b)"  assumes is_morphism_of_sheaves: "morphism_sheaves_of_rings Y     is_open_Y Ο_Y ϱ Y d add_str_Y mult_str_Y zero_str_Y one_str_Y     im_sheaf im_sheaf_morphisms b add_im_sheaf mult_im_sheaf     zero_im_sheaf one_im_sheaf ϕ_f"

A classic and ubiquitous notion in mathematics is the direct limit of a family of structured sets, here a family of rings.¹²

3.2.6 Direct Limit of a Presheaf of Rings

Let X be a topological space and $\mathrm{F}$ a presheaf of rings on X. The set I will denote a subset of the set of all open subsets of X such that for every U and V in I there exists W in I with $W\subseteq U\cap V$. Given $U,V\in I,s\in \mathrm{F}(U)$ and $t\in \mathrm{F}(V)$, we say that $s\sim t$ if and only if there exists $W\in I$ such that $W\subseteq U\cap V$ and $s\mathrm{\upharpoonright }W=t\mathrm{\upharpoonright }W$. One checks that ∼ is an equivalence relation. Now, we consider the quotient of the disjoint union of the $\mathrm{F}(U)$’s. $$\underset{I}{\underrightarrow{\lim }}\mathrm{F}:=\coprod _{U\in I}\mathrm{F}(U)/\sim$$

Last, we define the following binary operations on $\underset{I}{\underrightarrow{\lim }}\mathrm{F}$: $$\begin{array}{c}[(U,s)]+[(V,t)]=[(W,s\mathrm{\upharpoonright }W+t\mathrm{\upharpoonright }W)]\\ [(U,s)]\times [(V,t)]=[(W,s\mathrm{\upharpoonright }W\times t\mathrm{\upharpoonright }W)]\end{array}$$for some $W\in I$ such that $W\subseteq U\cap V$ and where the symbol $[\_]$ denotes the equivalence class of an element. These operations are well-defined, and assuming $V\in I$ one can prove that $$(\underset{I}{\underrightarrow{\lim }}\mathrm{F},[(V,0_V)],+,[(V,1_V)],\times )$$is a ring.

Definition 3.9

(direct limit of a presheaf of rings). Let X be a topological space, $\mathrm{F}$ a presheaf of rings on X and I a set of open subsets of X. The direct limit of $\mathrm{F}$ over I is the ring $\underset{I}{\underrightarrow{\lim }}\mathrm{F}$, denoted simply $\underrightarrow{\lim }\mathrm{F}$ if I is clear from the context.

The definition above, which could naively appear as a dependent type, gives rise to a smooth translation in Isabelle using the locale mechanism.

locale direct_lim = sheaf_of_rings +   fixes I:: "’a set set"   assumes subset_of_opens: "∧ U. U ∈I _⇒ is_open U"    and has_lower_bound: "∧ U V. [[U ∈I; V ∈I]] ⇒ ∃W ∈I. W ⊆ U ∩ V" begin definition rel:: "(’a set × ’b) ⇒ (’a set ×’b) ⇒ bool" (infix "∼" 80)   where "x ∼ y ≡ (fst x ∈ I ∧ fst y ∈ I) ∧ (snd x ∈ $\mathfrak{F}$ (fst x)   ∧ snd y ∈ $\mathfrak{F}$ (fst y)) ∧ (∃W. (W ∈ I)   ∧ (W ⊆ fst x ∩ fst y) ∧ ϱ (fst x) W (snd x)    = ϱ (fst y) W (snd y))" interpretation rel:equivalence "(Sigma I $\mathfrak{F}$)" "{(x, y). x ∼ y}" definition class_of:: "’a set ⇒ ’b ⇒ (’a set ×’b) set" (" _└(_,/ _)_┘")   where "_└ U,s _┘≡ rel.Class (U, s)" definition carrier_direct_lim:: "(’a set × ’b) set set"   where "carrier_direct_lim ≡ rel.Partition" definition get_lower_bound:: "’a set ⇒ ’a set ⇒ ’a set" where  "get_lower_bound U V = (SOME W. W ∈ I ∧ W ⊆ U ∧ W ⊆ V)" definition add_rel:: "(’a set × ’b) set ⇒ (’a set × ’b) set     ⇒ (’a set × ’b) set"   where "add_rel X Y ≡ let     x = (SOME x. x ∈ X);     y = (SOME y. y ∈ Y);     w = get_lower_bound (fst x) (fst y)   in    _└ w, add_str w (ϱ (fst x) w (snd x)) (ϱ (fst y) w (snd y)) _┘" definition mult_rel:: "(’a set × ’b) set ⇒ (’a set × ’b) set     ⇒ (’a set × ’b) set"   where "mult_rel X Y ≡ let     x = (SOME x. x ∈ X);     y = (SOME y. y ∈ Y);     w = get_lower_bound (fst x) (fst y)    in    _└ w, mult_str w (ϱ (fst x) w (snd x)) (ϱ (fst y) w (snd y))⌋ " lemma direct_lim_is_ring:   assumes "U ∈ I"   shows "ring carrier_direct_lim add_rel mult_rel ⌊ U, ⁰U _{⌋ ⌊} U, 1U ⌋" end

For every $U\in I$, there is a canonical map from $\mathrm{F}(U)$ to $\underrightarrow{\lim }\mathrm{F}$.

definition (in direct_lim)     canonical_fun:: "’a set ⇒ ’b ⇒ (’a set ×’b) set"    where "canonical_fun U x = ⌊ U, x ⌋"

The direct limit of a presheaf of rings satisfies a useful universal property. Indeed, for every ring A equipped with ring morphisms ${\psi }_U:\mathrm{F}(U)\to A$ for $U\in I$ satisfying ${\psi }_V°{\rho }_{UV}={\psi }_U$ for every inclusion $V\subseteq U$, there exists a unique ring morphism u making the following diagram commute.

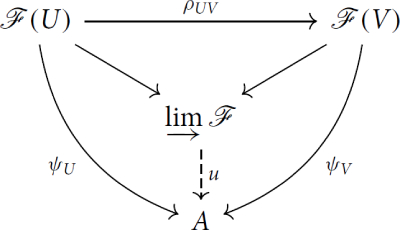
The counterpart in Isabelle is as follows.

proposition (in direct_lim) universal_property:   fixes A:: "’c set" and ψ:: "’a set ⇒ (’b ⇒ ’c)"    and add:: "’c ⇒ ’c ⇒ ’c" and mult:: "’c ⇒ ’c ⇒ ’c"    and zero:: "’c" and one:: "’c"   assumes "ring A add mult zero one"    and "∧ U. U ∈ I _⇒ ring_homomorphism (ψ U) ($\mathfrak{F}$ U) (+U)    (・U) ⁰U ¹U A add mult zero one"    and "∧ U V x. [[U ∈ I; V ∈ I; V ⊆ U; x ∈ ($\mathfrak{F}$ U)]]    ⇒ (ψ V ◦ϱ U V) x = ψ U x"   shows "∀V ∈I. ∃!u. ring_homomorphism u carrier_direct_lim add_rel     mult_rel ⌊V,⁰V⌋ ⌊V,¹V⌋ A add mult zero one    ∧ (∀ U ∈I. ∀x∈($\mathfrak{F}$ U). (u ◦canonical_fun U) x = ψ U x)"

One can instantiate direct limits in the following particular case.

3.2.7 Stalks of a Presheaf of Rings

Definition 3.10

(stalks of a presheaf). Let X be a topological space, $\mathrm{F}$ a presheaf of rings on X and x an element of X. The stalk ${\mathrm{F}}_x$ of $\mathrm{F}$ at x is the direct limit of $\mathrm{F}$ over the set of all the open neighborhoods of x.

locale stalk = direct_lim +   fixes x:: "’a"   assumes is_elem: "x ∈ S" and index: "I = {U. is_open U ∧ x ∈ U}" begin definition carrier_stalk:: "(’a set × ’b) set set"   where "carrier_stalk ≡ dlim $\mathfrak{F}$ ϱ (neighborhoods x)" definition add_stalk  :: "(’a set ×’b) set ⇒ (’a set × ’b) set ⇒ (’a set × ’b) set"   where "add_stalk ≡ add_rel" definition mult_stalk  :: "(’a set × ’b) set ⇒ (’a set ×’b) set ⇒ (’a set × ’b) set"   where "mult_stalk ≡ mult_rel" definition zero_stalk:: "’a set ⇒ (’a set × ’b) set"   where "zero_stalk V ≡ class_of V ⁰V" definition one_stalk:: "’a set ⇒ (’a set ×’b) set"   where "one_stalk V ≡ class_of V ¹V" end

One further step towards schemes consists in introducing local rings.

3.2.8 Local Rings

First, one needs to teach Isabelle simple facts about maximal ideals, starting with their definition.

Definition 3.11

(maximal ideal). Let $\mathfrak{m}$ be an ideal of R. The ideal $\mathfrak{m}$ is maximal if $\mathfrak{m}\ne R$ and there is no ideal $\mathfrak{a}\ne R$ such that $\mathfrak{m}\subset \mathfrak{a}$.

locale max_ideal = comm_ring R "(+)" "(・)" "0" "1"     + ideal I R "(+)" "(・)" "0" "1"   for R and I and addition (infixl "+" 65)    and multiplication (infixl "・" 70) and zero ("0") and unit ("1") +   assumes neq_ring: "I = R"    and is_max: "∧ $\mathfrak{a}$. [[ideal $\mathfrak{a}$ R (+) (・) 0 1; $\mathfrak{a}$ = R;I ⊆ $\mathfrak{a}$]] ⇒ I = $\mathfrak{a}$"

Classic facts about maximal ideals include the fact that every maximal ideal is prime.

proposition (in max_ideal) is_pr_ideal: "pr_ideal R I (+) (・) 0 1"

We then introduce the notion of a local ring.

Definition 3.12

(local ring). A ring is a local ring if it has a unique maximal left ideal.

locale local_ring = ring +   assumes is_unique: "∧ I J. max_lideal I R (+) (・) 0 1   ⇒ max_lideal J R (+) (・) 0 1 ⇒ I = J"   and has_max_lideal: "∃ω. max_lideal ω R (+) (・) 0 1"

Two remarks are in order. First, note that the property of being a local ring does not require the ring to be commutative. As a consequence, for generality, we do not assume the commutativity of the ring in the above definition and in its locale counterpart: hence the use of left ideals instead of two-sided ideals. Using right ideals would give rise to an equivalent definition. Second, we recall the following result which can be obtained using Zorn’s lemma. Let R be a unital ring, every proper ideal of R lies in a maximal ideal of R. As a corollary, every nonzero unital ring has a maximal ideal, hence, we could dispense with the property has_max_lideal in the locale local_ring, but only by adding the extra assumption that R is nonzero. Moreover, our formulation of this locale works as a convenient shortcut, avoiding the cost of formalizing the result recalled above.

We prove as expected that the local ring of R at $\mathfrak{p}$, previously denoted $R_{\mathfrak{p}}$, is a local ring.

lemma (in pr_ideal) local_ring_at_is_local:   shows "local_ring carrier_local_ring_at add_local_ring_at    mult_local_ring_at zero_local_ring_at one_local_ring_at"

Local rings have their corresponding notion of morphisms.

Definition 3.13

(local homomorphism). Let A and B be two local rings and ${\mathfrak{m}}_A,{\mathfrak{m}}_B$ their respective maximal ideals. A local homomorphism $f:A\to B$ is a morphism of rings such that ${\mathfrak{m}}_A\subseteq f^{-1}({\mathfrak{m}}_B)$.

Remark.

The inclusion ${\mathfrak{m}}_A\subseteq f^{-1}({\mathfrak{m}}_B)$ implies the equality $f^{-1}({\mathfrak{m}}_B)={\mathfrak{m}}_A$.

locale local_ring_morphism =     source: local_ring A "(+)" "(・)" 0 1    + target: local_ring B "(+’)" "(・’)" "0’" "1’"    + ring_homomorphism f A "(+)" "(・)" "0" "1" B "(+’)" "(・’)" "0’" "1’"   for f and A and addition (infixl "+" 65) and multiplication (infixl "・" 70)    and zero ("0") and unit ("1") and B and addition’ (infixl "+’’" 65)    and multiplication’ (infixl "・’’" 70) and zero’ ("0’’") and unit’ ("1’’")  + assumes preimage_of_max_lideal:   "∧ ωA ωB. max_lideal ωA A (+) (・) 0 1 ⇒ max_lideal ωB B (+’) (・’) 0’ 1’    ⇒ (f⁻¹ A ωB) = ωA"

Finally, we are able to introduce locally ringed spaces.

3.2.9 Locally Ringed Spaces

Definition 3.14

(locally ringed space). A locally ringed space is a ringed space $(X,{\mathrm{O}}_X)$ such that the stalk ${\mathrm{O}}_{X,x}$ at x is a local ring for every $x\in X$.

locale locally_ringed_space = ringed_space +   assumes stalks_are_local: "∧ x U. x ∈ U _ ⇒ is_open U ⇒ stalk.is_local    is_open $\mathfrak{F}$ ϱ add_str mult_str zero_str one_str (neighborhoods x) x U"

Moreover, one has the following result.

Proposition 3.15.

For every $\mathfrak{p}\in \text{Spec}R$, the stalk ${\mathrm{O}}_{\text{Spec}\mathrm{ }R,\mathfrak{p}}$ is isomorphic as a ring to $R_{\mathfrak{p}}$.

Proof.

See [16, Prop. 2.2.(a)]. □

locale key_map = comm_ring +   fixes π:: "’a set" assumes is_prime: "π ∈ Spec" begin interpretation pi:pr_ideal R π "(+)" "(・)" 0 1 interpretation st: stalk "Spec" is_zariski_open sheaf_spec sheaf_spec_morphisms   Οb add_sheaf_spec mult_sheaf_spec zero_sheaf_spec one_sheaf_spec   "{U. is_zariski_open U ∧ π∈U}" π lemma stalk_at_prime_is_iso_to_local_ring_at_prime:   assumes "is_zariski_open V" and "π ∈ V"   shows "∃ ϕ. ring_isomorphism ϕ st.carrier_stalk st.add_stalk st.mult_stalk   (st.zero_stalk V) (st.one_stalk V) (R π (+) (・) 0)   (pi.add_local_ring_at) (pi.mult_local_ring_at)   (pi.zero_local_ring_at) (pi.one_local_ring_at)" end

Now, it suffices to teach Isabelle that a ring which is isomorphic to a local ring is local.

lemma isomorphic_to_local_is_local:  assumes "local_ring B addB multB zeroB oneB"   and "ring_isomorphism f A addA multA zeroA oneA B addB multB zeroB oneB"  shows "local_ring A addA multA zeroA oneA"

Corollary 3.16.

$(\text{Spec}R,{\mathrm{O}}_{\text{Spec}\mathrm{ }R})$ is a locally ringed space.

As a sanity check for our formal definitions, we eventually prove in Isabelle that the spectrum of a commutative ring is indeed a locally ringed space, a result that required some amount of formal machinery, especially to prove the key proposition 3.15.

lemma (in comm_ring) spec_is_locally_ringed_space:   shows "locally_ringed_space Spec is_zariski_open sheaf_spec    sheaf_spec_morphisms Οb add_sheaf_spec mult_sheaf_spec     zero_sheaf_spec one_sheaf_spec"

The required formal machinery and our formalization as a whole benefited from the interpretation mechanism in order to prevent statements and proof scripts from becoming too unwieldy. Without this mechanism the terms involved in the statements and proof scripts of such an intricate hierarchy of nested algebraic structures would have to be fed with many arguments, cluttering these statements and proof scripts to the point where they would become unreadable and difficult to use. Fortunately, the interpretation mechanism that comes with locales allows for reasonably concise and manageable terms with many implicit arguments which are declared beforehand using the interpretation mechanism and its command interpretation.

Now, we introduce our last construction. Let $(X,{\mathrm{O}}_X),(Y,{\mathrm{O}}_Y)$ be two ringed spaces and $(f,{\varphi }_f)$ a morphism between them. Given $x\in X$, consider $$I:=\left\{V\right|V\text{is}\mathrm{ }\text{an}\mathrm{ }\text{open}\mathrm{ }\text{neighborhood}\mathrm{ }\text{of}f(x)\}.$$

Since we have a morphism ${\varphi }_f:{\mathrm{O}}_Y\to f_{*}{\mathrm{O}}_X$ of sheaves on Y, we get a map between the direct limits over I. $${\mathrm{O}}_{Y,f(x)}\to \underset{I}{\underrightarrow{\lim }}{f}_{*}{\mathrm{O}}_X$$

Last, there is a natural inclusion from $\underset{I}{\underrightarrow{\lim }}{f}_{*}{\mathrm{O}}_X$ to ${\mathrm{O}}_{X,x}$, since as V ranges over I, $f^{-1}(V)$ ranges over a subset of all the open neighborhoods of x. So, eventually we get an induced morphism of rings from ${\mathrm{O}}_{Y,f(x)}$ to ${\mathrm{O}}_{X,x}$ which we will denote ${\varphi }_{f,x}$. As usual we embed this construction into a dedicated locale in Isabelle.

locale ind_mor_btw_stalks = morphism_ringed_spaces +   fixes x::"’a"   assumes is_elem: "x ∈ X" begin interpretation stx:stalk X is_open_X Ο_X ϱ X b add_str_X mult_str_X zero_str_X   one_str_X "{U. is_open_X U ∧ x ∈ U}" "x" proof qed (auto simp: is_elem) interpretation stfx: stalk Y is_open_Y Ο_Y ϱ Y d add_str_Y mult_str_Y zero_str_Y   one_str_Y "{U. is_open_Y U ∧ (f x) ∈ U}" "f x" proof qed (auto simp: is_elem) definition induced_morphism:: "(’c set × ’d) set ⇒ (’a set × ’b) set"   where "induced_morphism ≡ λC ∈ stfx.carrier_stalk.    let r = (SOME r. r ∈ C) in     stx.class_of (f⁻¹ X (fst r)) (ϕ_f (fst r) (snd r))" end

This last construction is required to define morphisms between locally ringed spaces.

Definition 3.17

(morphism of locally ringed spaces). A morphism of locally ringed spaces from $(X,{\mathrm{O}}_X)$ to $(Y,{\mathrm{O}}_Y)$ is a morphism $(f,{\varphi }_f)$ between locally ringed spaces such that the induced map of local rings ${\varphi }_{f,x}:{\mathrm{O}}_{Y,f(x)}\to {\mathrm{O}}_{X,x}$ is a local homomorphism for every $x\in X$.

locale morphism_locally_ringed_spaces = morphism_ringed_spaces +   assumes are_local_morphisms:   "∧ x V. [[x ∈ X; is_open_Y V; f x ∈ V]] ⇒     ind_mor_btw_stalks.is_local X is_open_X Ο_X ϱ X add_str_X      mult_str_X zero_str_X one_str_X is_open_Y Ο_Y ϱ Y add_str_Y       mult_str_Y zero_str_Y one_str_Y f x V ϕX is_open_X Ο_X

Remark 3.18.

A morphism $(f,{\varphi }_f)$ between locally ringed spaces is an isomorphism if and only if f is an isomorphism between topological spaces, i.e., a homeomorphism, and ${\varphi }_f$ is an isomorphism between sheaves of rings.

locale iso_locally_ringed_spaces = morphism_locally_ringed_spaces +   assumes is_homeomorphism: "homeomorphism X is_open_X Y is_open_Y f"    and is_iso_of_sheaves: "iso_sheaves_of_rings Y is_open_Y Ο_Y ϱ Y d     add_str_Y mult_str_Y zero_str_Y one_str_Y im_sheaf im_sheaf_morphisms      b add_im_sheaf mult_im_sheaf zero_im_sheaf one_im_sheaf ϕ_f"

Ultimately, we reach our goal: teaching schemes to Isabelle.

3.2.10 Schemes

Definition 3.19

(affine scheme). An affine scheme is a locally ringed space $(X,{\mathrm{O}}_X)$ which is isomorphic (as a locally ringed space) to the spectrum $(\text{Spec}R,{\mathrm{O}}_{\text{Spec}\mathrm{ }R})$ for some commutative ring R.

locale affine_scheme = comm_ring  + locally_ringed_space X is_open Ο_X ϱ b add_str mult_str    zero_str one_str  + iso_locally_ringed_spaces X is_open Ο_X ϱ b add_str mult_str    zero_str one_str "Spec" is_zariski_open sheaf_spec     sheaf_spec_morphisms Οb "λU. add_sheaf_spec U"     "λU. mult_sheaf_spec U" "λU. zero_sheaf_spec U"      "λU. one_sheaf_spec U" f ϕ_f    for X is_open Ο_X ϱ b add_str mult_str zero_str one_str f ϕ_f

Of course, spectra of commutative rings being locally ringed spaces provide a class of affine schemes.

lemma (in comm_ring) spec_is_affine_scheme:   shows "affine_scheme R (+) (・) 0 1 Spec is_zariski_open sheaf_spec    sheaf_spec_morphisms Οb (λU. add_sheaf_spec U)    (λU. mult_sheaf_spec U) (λU. zero_sheaf_spec U)     (λU. one_sheaf_spec U) (identity Spec)      (λU. identity (Ο U))"

Definition 3.20

(scheme). A scheme is a locally ringed space $(X,{\mathrm{O}}_X)$ in which every point has an open neighborhood U such that the topological space U, together with the sheaf ${\mathrm{O}}_X{|}_U$, is an affine scheme.

locale scheme = locally_ringed_space X is_open Ο_X ϱ b      add_str mult_str zero_str one_str   for X is_open Ο_X ϱ b add_str mult_str zero_str one_str univ +   assumes are_affine_schemes: "∧ x. x ∈ X ⇒   (∃U. x∈U ∧ is_open U ∧ (∃R add mult zero one f ϕ_f.     R ⊆ univ ∧ comm_ring R add mult zero one ∧      affine_scheme R add mult zero one U      (ind_topology.ind_is_open X is_open U)      (ind_sheaf.ind_sheaf Ο_X U)      (ind_sheaf.ind_ring_morphisms ϱ U) b      (ind_sheaf.ind_add_str add_str U)      (ind_sheaf.ind_mult_str mult_str U)      (ind_sheaf.ind_zero_str zero_str U)      (ind_sheaf.ind_one_str one_str U) f ϕ_f))"

The only purpose of the variable univ in the locale scheme is to introduce properly a new type variable, in addition to the type variables from the carriers of X and of the rings ${\mathrm{O}}_X(U)$, to be used in the type of R, the carrier of the ring which is introduced by an existential quantification in the assumption are_affine_schemes once an open neighborhood U of a given element x in X has been fixed. As the name univ suggests, and as can be seen in the two lemmas below, this variable univ should be instantiated with UNIV, the set of all elements of a given type, while proving that a pair $(X,{\mathrm{O}}_X)$ is a scheme. The condition $R\subseteq \text{univ}$ in the locale scheme is then trivially satisfied and it introduces no additional constraint other than a type constraint on the carrier of the ring R as required by Isabelle type system.

To match what was achieved using Lean [6], we finally prove in Isabelle that an affine scheme is a scheme and we give the example of the empty scheme $(\varnothing ,{\mathrm{O}}_{\varnothing })$, where ${\mathrm{O}}_{\varnothing }(\varnothing )$ is the zero ring $\left\{0\right\}$.

lemma (in affine_scheme) affine_scheme_is_scheme:   shows "scheme X is_open Ο_X ϱ b add_str mult_str      zero_str one_str (UNIV::’a set)" lemma empty_scheme_is_scheme:   shows "scheme {} (λU. U = {}) (λU. {0})   (λU V. identity{0::nat}) 0 (λU x y. 0)    (λU x y. 0) (λU. 0) (λU. 0) (UNIV::nat set)"

4 Concluding Thoughts

4.1 Current Limitations of Locales

Our wish to avoid Isabelle’s records stemmed from their lack of multiple inheritance, as discussed above (Section 2.2). While locales possess multiple inheritance, locales without records make our formalization unnecessarily verbose in some places. The mechanism for locale interpretation is currently missing a convenient way to bundle up a list of arguments in order to prevent argument lists from becoming unwieldy. Such a bundling would ideally still allow easy access to any component of a list. However, these practical limitations are not fundamental; they are engineering issues that could be tackled in the near future.

4.2 The Song of the Sirens

It seems that our experience in Isabelle to formalize schemes was less tumultuous than the corresponding one in Lean, since Kevin Buzzard reported on his blog the difficulties he faced during his formalization in Lean:

The project is completely incompatible with modern Lean and mathlib, but if you compile it then you get a sorry-free proof that an affine scheme is a scheme. During our proof we ran into a huge problem because our blueprint, the Stacks Project, assumed that $R[1/f][1/g]=R[1/fg]$, and this turns out to be unprovable for Lean’s version of equality […]. The Lean community wrestled with this idea, and has ultimately come up with a beefed-up notion of equality for which the identity is now true.¹³

This difficulty basically comes from defining the sheaf structure of $\text{Spec}R$ first on the basis given by the so-called basic open sets before extending it to all open subsets. We did not meet this difficulty in Isabelle, since we did not follow this sheaf-on-a-basis approach and the sheaves in our library are always defined from the get-go on all open subsets instead. Also, Buzzard et al. mention another difficulty encountered when proving that an affine scheme is a scheme.

This means that rewriting the equality $\iota (U)=U$ can cause technical problems with data-carrying types such as ${\mathrm{O}}_X(\iota (U))$ which depends on $\iota (U)$ (although in our case they were surmountable). This is a technical issue with dependent type theory and can sometimes indicate that one is working with the wrong definitions. [6, 3.5]

where $\iota :\text{Spec}R\to \text{Spec}R$ is here simply the identity map. If, again, we gave a slightly different formulation for the definition of a scheme, following Hartshorne [16] instead of the Stacks project [23] as they did, it seems that this difficulty cannot possibly have a direct counterpart in Isabelle, since it arose from the difference between the so-called equality types, also known as identity types, and the definitional equality, a difference which is peculiar to dependent type theories. This difficulty was eventually overcome in Lean using a trick.

Fortunately, in our case, Reid Barton pointed out the following extraordinary trick to us: we can define the map ${\mathrm{O}}_X(\iota (U))\to {\mathrm{O}}_X(U)$ using restriction rather than trying to force it to be the identity! [6, 3.5.]

The gap between the type theories of Lean and Isabelle/HOL called for the very different approach of the present work. If our approach based on Isabelle’s locales required some craftsmanship, locales offered enough flexibility to avoid dead ends. While dependent types are expressive, expert users know they should be used with parsimony and some issues have been highlighted for instance in the context of formalizing analysis in the proof assistant Coq [4, p. 42]. Moreover, in the age of machine learning, one may expect there is a tradeoff between the expressiveness of a type theory and one’s ability to subject it to automation, for instance through SMT solvers and the so-called hammers embedded in some proof assistants. How deep one can go formalizing mathematics in simple type theory? This work provides a first hint at an answer that should not be ruled out: simple type theory is not too simple.

Acknowledgments

We thank Kevin Buzzard for his stimulating wit and his communicative energy and André Hirschowitz who commented on a draft of this document. We also thank the reviewers, one of whom noticed an inaccuracy (fortunately easy to correct) in the formal translation into Isabelle of Definition 3.21.

Additional information

Funding

This work was supported by the ERC Advanced Grant ALEXANDRIA (Project GA 742178).

Notes

1 https://github.com/leanprover-community/mathlib/issues/26

2 https://github.com/leanprover-community/mathlib/issues/26

3 https://xenaproject.wordpress.com/2020/02/09/where-is-the-fashionable-mathematics/

4 https://xenaproject.wordpress.com/2020/02/09/where-is-the-fashionable-mathematics/.SeethesectionentitledIsabelle/HOLusers.

5 Not to be confused with the locales of point-free topology!

6 https://isabelle.in.tum.de/dist/library/HOL/HOL-Algebra/

7 https://isabelle.in.tum.de/dist/library/HOL/HOL-Computational_Algebra/

8 https://www.isa-afp.org/

9 https://isabelle.in.tum.de/dist/library/HOL/HOL/Topological_Spaces.html

10 https://isabelle.in.tum.de/dist/library/HOL/HOL-Analysis/Abstract_Topology.html

11 It is also called the ring of fractions of R by S or the localization of R at S. No confusion with the factor ring should be possible, since S is not an ideal of R but a multiplicative submonoid.

12 In more modern parlance it is called a colimit.

13 https://xenaproject.wordpress.com/2020/06/05/the-sphere-eversion-project/