Confirming Brennan’s Conjecture Numerically on a Counterexample to Thurston’s K = 2 Conjecture

Abstract

It was shown by Bishop that if Thurston’s K = 2 conjecture holds for some planar domain, then Brennan’s conjecture holds for the Riemann map of that domain as well. In this paper we show numerically that the original counterexample to Thurston’s K = 2 conjecture given by Epstein, Marden and Marković is not a counterexample to Brennan’s conjecture.

KEYWORDS:

• Brennan’s conjecture
• Thurston’s K = 2 conjecture
• Riemann mapping
• complex earthquakes

1 Introduction

1.1 Thurston’s K = 2 conjecture

Let Ω be a simply connected proper subdomain of $\mathbb{C}\subset {\mathbb{S}}^2=\partial {\mathbb{H}}^3$ where ${\mathbb{H}}^3$ is the 3-dimensional hyperbolic space. Let $\tilde{\Omega }$ be the union of all hyperbolic half-spaces H such that $H\cap \partial {\mathbb{H}}^3\subseteq \Omega$. Then we define the dome of Ω to be $\text{Dome}(\Omega )=\partial \tilde{\Omega }\cap {\mathbb{H}}^3$. It is known (see the book by Epstein and Marden [7] for a detailed account) that $\text{Dome}(\Omega )$ with the path metric induced from ${\mathbb{H}}^3$ is isometric to the unit disk $\mathbb{D}$ with its hyperbolic metric. Using this isometry, we give $\text{Dome}(\Omega )$ a conformal structure.

Note that Ω and $\text{Dome}(\Omega )$ share the common boundary $\partial \Omega$, so we set$$\mathcal{F}=\left\{f:\Omega \to \text{Dome}(\Omega ):f(x)=x\mathrm{ }\text{for}\mathrm{ }\text{all}\mathrm{ }x\in \partial \Omega \mathrm{ }\text{and}\mathrm{ }f\mathrm{ }\text{is}\mathrm{ }\text{continuous}\right\}.$$

Let $\mathrm{M}ö\mathrm{b}(\Omega )$ be the set of all Möbius transformations that preserve Ω. Each such transformation extends to an isometry of ${\mathbb{H}}^3$ preserving $\text{Dome}(\Omega )$, so we define$${\mathcal{F}}_{\text{eq}}=\{f\in \mathcal{F}:f°\gamma =\gamma °f\mathrm{ }\text{for}\mathrm{ }\text{all}\mathrm{ }\gamma \in \mathrm{M}ö\mathrm{b}(\Omega )\}.$$

Definition 1.

Given a simply connected proper subdomain Ω of the plane, we define $$\begin{array}{c}K(\Omega )=\inf \{K>0:\text{there}\mathrm{ }\text{exists}\text{ a }K-\text{quasiconformal}\mathrm{ }\text{map}\mathrm{ }f\in \mathcal{F}\},\mathrm{ }\text{and}\mathrm{ }\\ K_{\text{eq}}(\Omega )=\inf \{K>0:\text{there}\mathrm{ }\text{exists}\text{ a }K-\text{quasiconformal}\mathrm{ }\text{map}\mathrm{ }f\in {\mathcal{F}}_{\text{eq}}\}.\end{array}$$

It was shown by Sullivan that $\underset{\Omega }{\sup }K(\Omega )<\infty$ in [13]. A more detailed proof of this result and a proof that $\underset{\Omega }{\sup }{K}_{\text{eq}}(\Omega )<\infty$ was given by Epstein and Marden in [7]. Thurston conjectured the following result.

Conjecture (Thurston’s K = 2 conjecture). For any simply connected proper subdomain $\Omega \subset \mathbb{C}$, we have $\underset{\Omega }{\sup }K(\Omega )=\underset{\Omega }{\sup }{K}_{\text{eq}}(\Omega )=2$.

Epstein, Marden and Marković constructed counterexamples for this conjecture in [8] for the equivariant case and in [10] for the general case. Komori and Matthews then constructed in [12] a more explicit counterexample for the equivariant case building on the ideas of [8].

1.2 Brennan’s conjecture

We remind the reader that given a simply connected proper subdomain $\Omega \subset \mathbb{C}$, by the Riemann mapping theorem there exists a conformal map $F:\Omega \to \mathbb{D}$. Brennan conjectured the following regarding the growth of $F\prime$ near $\partial \Omega$.

Conjecture (Brennan’s conjecture). Let Ω be a simply connected proper subdomain of $\mathbb{C}$, and let $F:\Omega \to \mathbb{D}$ be a conformal map. Then $F\prime \in L^p(\Omega )$ for all $\frac{4}{3}<p<4$.

Brennan’s conjecture in full generality is still open.

1.3 Bishop’s theorem

Bishop showed in [2] that if Thurston’s K = 2 conjecture holds for some domain, then Brennan’s conjecture holds for that domain as well.

Theorem 1.

Let Ω be a simply connected proper subdomain of the complex plane, and let $F:\Omega \to \mathbb{D}$ be a conformal map. Then $F\prime \in L^p(\Omega )$ for all $p<\frac{2K(\Omega )}{K(\Omega )-1}$. In particular if $K(\Omega )=2$, then Brennan’s conjecture holds for Ω.

It was shown by Epstein, Marden and Marković in [9] that Thurston’s K = 2 conjecture holds for domains in $\mathbb{C}$ that are convex (in the Euclidean sense), by Theorem 1 therefore proving Brennan’s conjecture in this case. Bishop showed in [3] that $K(\Omega )\le 7.82$ for all simply connected planar domains Ω, therefore giving a new proof that $F\prime \in L^{2.29}(\Omega )$ for conformal maps $F:\Omega \to \mathbb{D}$.

1.4 Our results

By Theorem 1, any counterexample to Brennan’s conjecture would also be a counterexample to Thurston’s K = 2 conjecture. In this paper we investigate if Brennan’s conjecture holds for a particular counterexample to Thurston’s K = 2 conjecture.

In this section we denote the counterexample to Thurston’s K = 2 conjecture from [12] by Ω. In [12] it was shown that $K(\Omega )=K_{\text{eq}}(\Omega )>2$. We show numerically that Brennan’s conjecture holds for Ω.

Main result. Let $F:\Omega \to \mathbb{D}$ be a conformal map and set $p_{\star }=\sup \{p>0:F\prime \in L^p(\Omega )\}$. We show numerically that $5.52<p_{\star }<5.54$. In particular $p_{\star }>4$ so Brennan’s conjecture holds for Ω.

The domain Ω is a connected component of the domain of discontinuity of an explicit Kleinian once-punctured torus group. Our results strongly suggest that Brennan’s conjecture holds for all domains constructed in this way. Equivalently, our results suggest that Brennan’s conjecture holds for all quasidisks invariant under a group of Möbius transformations, such that the quotient is a once-punctured torus.

1.5 General strategy

The domain Ω has an action by a Kleinian once-punctured torus group Γ. Write $F:\Omega \to \mathbb{D}$ for its Riemann mapping and $f=F^{-1}$ for its inverse. Let ${\Gamma }_0=F°\Gamma °F^{-1}$ be the once-punctured torus Fuchsian group obtained by conjugating Γ by F, and let $\rho :{\Gamma }_0\to \Gamma$ be the induced isomorphism. Let $\Phi$ be a fundamental domain for the action of ${\Gamma }_0$ on $\mathbb{D}$. Then $f(\Phi )$ is a fundamental domain for the action of Γ on Ω.

Since Ω and Γ are known, we can numerically compute the Riemann map $F:\Omega \to \mathbb{D}$ using Schwarz-Christoffel mappings and a polygonal approximation to Ω. The quality of this estimate deteriorates near the boundary $\partial \Omega$, making it imprecise to check if $F\prime \in L^p(\Omega )$ directly. However for $\gamma \in \Gamma$, the behavior of $F\prime$ on $\gamma f(\Phi )$ is controlled by γ and ${\rho }^{-1}(\gamma )$. Therefore $F\prime \in L^p(\Omega )$ if and only if a certain series over ${\Gamma }_0$ depending on $p,{\Gamma }_0$ and ρ converges.

We note that the estimates of F have higher accuracy away from $\partial \Omega$. We can hence still use them to reliably estimate ρ and ${\Gamma }_0$. Then we use these estimates to check numerically if the series mentioned in the previous paragraph converges.

1.6 A more detailed outline of the argument and the computation

The paper is divided into a theoretical Section 2, a brief section where we describe Ω and Γ in more detail Section 3, and a numerical methods and results Section 4.

In the theory part, we show that ${\int }_{\Omega }{\left|F\prime \right|}^{p}d\mathit{xdy}={\int }_{\mathbb{D}}{\left|f\prime \right|}^{2-p}d\mathit{xdy}$ is equal to a certain infinite series depending on ${\Gamma }_0$ and ρ, up to a bounded multiplicative error. We do this by decomposing $\mathbb{D}$ into $\gamma \Phi$, where $\Phi$ is a fundamental domain for the action of ${\Gamma }_0$ on $\mathbb{D}$. We express the integral ${\int }_{\gamma \Phi }{\left|f\prime \right|}^{2-p}d\mathit{xdy}$ in terms of γ and $\rho (\gamma )$, up to a bounded multiplicative error. We work in greater generality, considering Riemann maps $f:\mathbb{D}\to \Omega$ that conjugate a Fuchsian group Γ to a Kleinian group. We do this in Section 2, where the main result is Theorem 2.

In the proof of Theorem 2, issues arise since $\Phi$ is not assumed to be compact. This is handled by showing that on a horoball H, the derivative $\left|f\prime \right|$ achieves its minimum at the closest point of H to the origin, up to a bounded multiplicative error. This is Lemma 1 and is the most involved part of the proof of Theorem 2.

We now briefly describe how Ω is constructed in [12]. They start with a hyperplane in ${\mathbb{H}}^3$ along with a Fuchsian once-punctured torus group that preserves it. Fix a hyperbolic element in this group, and consider the orbit of its axis. This is a discrete set of geodesics, along which they bend the hyperplane. The resulting pleated plane intersects the boundary of ${\mathbb{H}}^3$ in a curve that bounds Ω. We give an equivalent form of their construction in Section 3 that does the bending in the complex plane, without mentioning ${\mathbb{H}}^3$.

This construction makes it easy to identify a point on the boundary of Ω, and to see that the orbit of any point on $\partial \Omega$ is dense in $\partial \Omega$. We use this observation to construct finite polygons that approximate Ω. These approximations are described in Section 4.1.

We use Schwarz-Christoffel mappings to numerically compute an approximation to the Riemann map $F:\Omega \to \mathbb{D}$. This approximation is used to (numerically) compute the generators of ${\Gamma }_0$. This is explained in Section 4.2.

We use estimates of ${\Gamma }_0$ and ρ to compute initial terms of the sum from Theorem 2. The terms appear to decay exponentially for p < 5.52 and to increase exponentially for p > 5.54. From this we conclude the Main result. This is done in Section 4.4.

2 Theoretical results

Throughout this section, we let Γ be a Fuchsian group such that $\mathbb{D}/\Gamma$ is a finite area hyperbolic surface. Let $f:\mathbb{D}\to \Omega$ be a conformal map, normalized so that $f(0)=0$ and $f\prime (0)=1$. Suppose that f conjugates Γ to a Kleinian group, and let $\rho :\Gamma \to \text{PSL}(2,\mathbb{C})$ be the induced homomorphism. Our main theoretical result is the following estimate.

Theorem 2.

Given q > 0, there exists a constant $C=C(\Gamma ,q)$ that depends only on Γ and q such that $$\frac{1}{C}\sum _{\gamma \in \Gamma }\frac{{\left|\gamma \prime (0)\right|}^{q+2}}{{\left|\rho (\gamma )\prime (0)\right|}^q}\le {\int }_{\mathbb{D}}\frac{1}{{\left|f\prime (z)\right|}^q}d\mathit{xdy}\le C\sum _{\gamma \in \Gamma }\frac{{\left|\gamma \prime (0)\right|}^{q+2}}{{\left|\rho (\gamma )\prime (0)\right|}^q}.$$

We now outline the proof of Theorem 2. The idea is to estimate the integral separately over $\mathcal{H}$ and $\mathbb{D}\setminus \mathcal{H}$, where $\mathcal{H}$ is the union of a certain Γ-invariant collection of horoballs based at fixed points of the parabolics in Γ. The proof consists of three steps.

1. For any horoball H in $\mathcal{H}$, we let z₀ be the closest point of H to the origin. We show the inequality $\left|f\prime (z)\right|\ge C\left|f\prime (z_0)\right|$ for $z\in H$, for some universal constant C. We will later use this to show that the integral from Theorem 2 over $\mathcal{H}$ is dominated by the integral over $\mathbb{D}\setminus \mathcal{H}$.

   We show $\left|f\prime (z)\right|\ge C\left|f\prime (z_0)\right|$ using the fact that f conjugates a parabolic element preserving H to a parabolic Möbius transformation. The core of the proof of this bound are estimates on the growth and derivative of a univalent map $g:\mathbb{H}\to \mathbb{C}$ satisfying $g(z+1)=g(z)+1$.

   We show the necessary bounds on g as Proposition 1 in Section 2.1. Then we derive $\left|f\prime (z)\right|\ge C\left|f\prime (z_0)\right|$ in Lemma 1 in Section 2.2.

   In Corollary 1, Section 2.2, using $\left|f\prime (z)\right|\ge C\left|f\prime (z_0)\right|$ we bound the integral of ${\int }_H{\left|f\prime (z)\right|}^{-q}d\mathit{xdy}$ in terms of $\left|f\prime (z_0)\right|$ and $1-\left|z_0\right|$.

2. In Section 2.3 we define $\mathcal{H}$ and construct a compact fundamental domain ${\Phi }^{*}$ for the action of Γ on $\mathbb{D}\setminus \mathcal{H}$. We show an estimate on ${\int }_{\gamma {\Phi }^{*}}{\left|f\prime (z)\right|}^{-q}d\mathit{xdy}$ as Proposition 3 in Section 2.4, making essential use of the compactness of ${\Phi }^{*}$. This estimate is in terms of the Euclidean distance of $\gamma {\Phi }^{*}$ to the boundary $\partial \mathbb{D}$ of the unit disk $\mathbb{D}$, and the absolute value of the derivative $\left|f\prime (\gamma (0))\right|$.

3. By equivariance of f, the derivative $f\prime (\gamma (z))$ is related to $\rho (\gamma )\prime (f(z))$ and $\gamma \prime (z)$. This allows us to replace $\left|f\prime \right|$ from the estimates in the first two steps with the derivatives $\left|\rho (\gamma )\prime \right|$ and $\left|\gamma \prime \right|$. For hyperbolic isometries γ of the disk, we relate $\left|\gamma (0)\right|$ and $\left|\gamma \prime (0)\right|$, so we also replace $\left|\gamma (0)\right|$ with $\left|\gamma \prime (0)\right|$ in the estimates in the first two steps. This is done in Section 2.5, and concludes the proof of Theorem 2.

Notation and conventions

We write $X{\lesssim }_{Z,W,\dots }Y$ if there exists a constant $C=C(Z,W,\dots )>0$ that depends only on the variables in the subscript, so that $X\le CY$. We analogously write $X{\gtrsim }_{Z,W,\dots }Y$ if $Y{\lesssim }_{Z,W,\dots }X$ and $X{\approx }_{Z,W,\dots }Y$ if $X{\lesssim }_{Z,W,\dots }Y$ and $Y{\lesssim }_{Z,W,\dots }X$.

We will use hyperbolic geometry in several places in this paper. We always use the metric of constant curvature –1. In particular on the unit disk $\mathbb{D}$ we have the metric $\frac{4{\left|dz\right|}^2}{{(1-{\left|z\right|}^2)}^2}$, and on the upper half-plane $\mathbb{H}$ we have the metric $\frac{{\left|dz\right|}^2}{\text{Im}{(z)}^2}$. Whenever we write $\text{dist}(·,·)$, we are referring to the distance coming from the hyperbolic metric on either $\mathbb{D}$ or $\mathbb{H}$.

2.1 Univalent maps and parabolic isometries

The main result of this subsection is concerned with the growth of univalent maps g defined on the upper half-plane $\mathbb{H}$ that commute with the parabolic γ given by $\gamma (z)=z+1$. By taking quotients $\mathbb{H}/〈\gamma 〉$ and $\mathbb{C}/〈\gamma 〉$, g descends to a univalent map $h:\mathbb{D}\setminus \left\{0\right\}\to \mathbb{C}$. The estimates we show on g come from the inequalities on h and its derivatives near 0, and follow from the general theory of univalent maps.

In Section 2.1.1 we recall some general results from the theory of univalent maps. The main result there is Claim 1. Then in Section 2.1.2 we state and prove the main result of this subsection.

2.1.1 General results on univalent maps

We recall some general theorems about univalent maps, that we later use in Section 2.1.2. We then show an estimate on how closely a univalent map h follows its linear approximation $h(0)+h\prime (0)z$ near 0. This is Claim 1.

Theorem (Koebe quarter theorem). Let $h:\mathbb{D}\to \mathbb{C}$ be a univalent function with $h(0)=0$ and $h\prime (0)=1$. Then $h(\mathbb{D})$ contains the disk of radius $\frac{1}{4}$ around 0.

Theorem (Koebe distortion theorem). Let $h:\mathbb{D}\to \mathbb{C}$ be a univalent function with $h(0)=0$ and $h\prime (0)=1$. Then $$\begin{array}{c}\frac{\left|z\right|}{{(1+\left|z\right|)}^2}\le \left|h(z)\right|\le \frac{\left|z\right|}{{(1-\left|z\right|)}^2},\\ \frac{1-\left|z\right|}{{(1+\left|z\right|)}^3}\le \left|h\prime (z)\right|\le \frac{1+\left|z\right|}{{(1-\left|z\right|)}^3},\\ \frac{1-\left|z\right|}{1+\left|z\right|}\le \left|z\frac{h\prime (z)}{h(z)}\right|\le \frac{1+\left|z\right|}{1-\left|z\right|}.\end{array}$$

Moreover, the second inequality implies that for any univalent function $f:\mathbb{D}\to \mathbb{C}$, we have for $z,w\in \mathbb{D}$, $$\frac{\left|f\prime (z)\right|(1-{\left|z\right|}^2)}{\left|f\prime (w)\right|(1-{\left|w\right|}^2)}\le e^{2\text{dist}(z,w)}.$$

The following Claim is the estimate we use to derive Proposition 1, the main result of this subsection.

Claim 1. Let $h:\mathbb{D}\to \mathbb{C}$ be a univalent map. Then whenever $\left|z\right|<\frac{1}{2}$, we have $$\left|h(z)-h(0)-h\prime (0)z\right|<100\left|h\prime (0)\right|{\left|z\right|}^2.$$

Remark 1.

The optimal constant in Claim 1 can easily be computed from de Branges’ theorem [4]. However since this is a fairly simple result, we choose to include a more elementary proof (with a non-optimal constant) below.

Proof

of Claim 1. Without loss of generality we can suppose $h(0)=0$ and $h\prime (0)=1$. Write$$h(z)=z+\sum _{n=2}^{\infty }{a}_n{z}^n.$$

Let γ be the circle of radius $\frac{2}{3}$ centered at the origin. Then$$\left|a_n\right|=\left|\frac{1}{2\pi i}{\int }_{\gamma }\frac{h(z)}{z^{n+1}}dz\right|\le \frac{1}{2\pi }{\left(\frac{3}{2}\right)}^n{\int }_0^{2\pi }\left|h\left(\frac{2}{3}{e}^{i\theta }\right)\right|d\theta .$$

By the Koebe distortion theorem, we have$$\left|h\left(\frac{2}{3}{e}^{i\theta }\right)\right|\le 6.$$

Therefore $\left|a_n\right|\le 6{(\frac{3}{2})}^n$. Therefore for $\left|z\right|<\frac{1}{2}$, we have$$\left|h(z)-z\right|\le 6\sum _{n=2}^{\infty }{\left(\frac{3}{2}\left|z\right|\right)}^n<6·\frac{9}{4}{\left|z\right|}^2\sum _{n=0}^{\infty }{\left(\frac{3}{4}\right)}^n<100{\left|z\right|}^2.$$□

2.1.2 Growth of univalent maps that commute with a parabolic Möbius transformation

We now state and prove the main result of this subsection, Proposition 1. As explained at the start of this subsection, starting with a map $g:\mathbb{H}\to \mathbb{C}$ that commutes with $\gamma (z)=z+1$, we construct a map $h:\mathbb{D}\setminus \left\{0\right\}\cong \mathbb{H}/〈\gamma 〉\to \mathbb{C}/〈\gamma 〉\cong \mathbb{C}\setminus \left\{0\right\}$. We show that it extends to 0 with $h(0)=0$ and then apply Claim 1 to h. This shows how h behaves near 0, and hence how g behaves near infinity. We also obtain some information on g from the Koebe distortion theorem and the Koebe quarter theorem applied to h.

Proposition 1.

There exists a universal constant C > 0 such that the following holds. Let $g:\mathbb{H}\to \mathbb{C}$ be a univalent holomorphic map with $g(z+1)=g(z)+1$. Then there exists a complex number $\alpha \in \mathbb{C}$ (depending on g) so that the following holds.

1. Whenever $\text{Im}(z)\ge C$, we have $\left|g(z)-z+\alpha \right|\le C{e}^{-2\pi \text{Im}(z)}$.

2. Whenever $\text{Im}(z)\ge C$, we have $\frac{1}{C}\le \left|g\prime (z)\right|\le C$.

3. When $\text{Im}(z)>\frac{\hspace{0.17em}\log \hspace{0.17em}2}{\pi }-\text{Im}(\alpha )$, we have $z\in g(\mathbb{H})$.

Proof.

Note that $\hspace{0.17em}\exp \hspace{0.17em}(2\pi ig(z))$ is 1-periodic, so there exists a holomorphic map $h:\mathbb{D}\setminus \left\{0\right\}\to \mathbb{C}$ defined by $h(\hspace{0.17em}\exp \hspace{0.17em}(2\pi iz))=\hspace{0.17em}\exp \hspace{0.17em}(2\pi ig(z))$. Since g is univalent, so is h. We first show that h extends to 0.

Claim 2. The map h has a removable singularity at 0 and can be extended holomorphically so that $h(0)=0$.

Proof.

Since h is univalent, it does not have an essential singularity at 0. We extend h to 0 so that it is a meromorphic function. Let $\gamma (t)=\hspace{0.17em}\exp \hspace{0.17em}(2\pi i(t+iR))$ for $t\in [0,1]$, and R > 0 large. Then $\frac{h\prime (\hspace{0.17em}\exp \hspace{0.17em}(2\pi iz))}{h(\hspace{0.17em}\exp \hspace{0.17em}(2\pi iz))}\exp \hspace{0.17em}(2\pi iz)=g\prime (z)$, and hence$$\frac{1}{2\pi i}{\int }_{\gamma }\frac{h\prime (z)}{h(z)}dz={\int }_0^{1}g\prime (t+iR)dt=1.$$

This shows that h has a simple zero at 0. Hence $h(0)=0$. □

We can now apply Claim 1 to get$$\left|h(z)-h\prime (0)z\right|<100\left|h\prime (0)\right|{\left|z\right|}^2,$$whenever $\left|z\right|<\frac{1}{2}$. We now set $C>\frac{\hspace{0.17em}\log \hspace{0.17em}2}{2\pi }$, so that when $\text{Im}(z)\ge C$, we have $\left|\hspace{0.17em}\exp \hspace{0.17em}(2\pi iz)\right|<\frac{1}{2}$, and hence$$\left|\frac{1}{h\prime (0)}\exp \hspace{0.17em}(2\pi ig(z))-\hspace{0.17em}\exp \hspace{0.17em}(2\pi iz)\right|<100e^{-4\pi \text{Im}(z)}.$$

Therefore$$\left|\hspace{0.17em}\exp \hspace{0.17em}(2\pi i(g(z)-z+\alpha ))-1\right|<100e^{-2\pi \text{Im}(z)},$$where $\alpha \in \mathbb{C}$ is such that $\hspace{0.17em}\exp \hspace{0.17em}(-2\pi i\alpha )=h\prime (0)$. For C large enough, whenever $\text{Im}(z)\ge C$, we will have $\left|g(z)-z+\alpha -m\right|\le \frac{1}{10}$ for some integer $m\in \mathbb{Z}$. We replace α with $\alpha -m$, so that $\left|g(z)-z+\alpha \right|\le \frac{1}{10}$. Since $\hspace{0.17em}\exp \hspace{0.17em}$ is bilipschitz on the disk centered at 0 of radius $\frac{1}{10}$, we see that$$\left|g(z)-z+\alpha \right|\lesssim e^{-2\pi \text{Im}(z)},$$ and (1) follows.

To show (2), we note that for $w=\hspace{0.17em}\exp \hspace{0.17em}(2\pi iz)$,$$g\prime (z)=w\frac{h\prime (w)}{h(w)}.$$

By the Koebe distortion theorem, since h is univalent on the unit disk, we have$$\frac{1-\left|w\right|}{1+\left|w\right|}\le \left|w\frac{h\prime (w)}{h(w)}\right|\le \frac{1+\left|w\right|}{1-\left|w\right|},$$so for any C > 0 fixed, $\left|w\right|=e^{-2\pi \text{Im}(z)}\le e^{-2\pi C}$, and we have $\left|g\prime (z)\right|=\left|w\frac{h\prime (w)}{h(w)}\right|\approx 1$.

We now turn to (3). Note that $\text{Im}(\alpha )=\frac{1}{2\pi }\text{Re}(-2\pi i\alpha )=\frac{1}{2\pi }\log \hspace{0.17em}\left|h\prime (0)\right|$. By the Koebe quarter theorem, the set $h(\mathbb{D})$ contains the disk D centered at 0 with radius $\frac{1}{4}\left|h\prime (0)\right|=\frac{1}{4}{e}^{2\pi \text{Im}(\alpha )}$. Note that $\hspace{0.17em}\exp \hspace{0.17em}(2\pi iz)\in D$ if and only if $\text{Im}(z)\ge -\text{Im}(\alpha )+\frac{1}{2\pi }\log \hspace{0.17em}4=\frac{\hspace{0.17em}\log \hspace{0.17em}2}{\pi }-\text{Im}(\alpha )$, so the final claim of the Proposition follows. □

2.2 Derivative bounds on a horoball

Here we give a lower bound on the derivative $\left|f\prime \right|$ of a univalent map $f:\mathbb{D}\to \mathbb{C}$ on a horoball, assuming that f conjugates a parabolic isometry of $\mathbb{D}$ that preserves that horoball to a parabolic Möbius transformation. The main result is Lemma 1. This lemma is used to bound the integral $\int {\left|f\prime \right|}^{-q}d\mathit{xdy}$ over a horoball in Corollary 1. This corollary is the result we use in the coming sections.

We first define the horoballs we will consider. All horoballs will be open. Given a horoball H, the horocycle $\partial H$ admits a natural orientation as follows. The vector v along $\partial H$ at $z\in \partial H$ is positive if (v, w) is a positively-oriented basis of $T_z\mathbb{D}$, where w is the vector at z tangent to the geodesic ray from z to the point at infinity of H.

Definition 2.

A horoball $H\subset \mathbb{D}$ is $\mathcal{l}$-adapted to a parabolic isometry $\gamma \in \text{Aut}(\mathbb{D})$ if the following conditions hold,

1. the parabolic γ preserves H,

2. the distance $\underset{z\in H}{\sup }\text{dist}(z,\gamma (z))=\mathcal{l}$,

3. the parabolic γ moves points on $\partial H$ in the positive direction.

When $0\notin H$, we define the anchor of H to be the point $z\in \partial H$ closest to the origin in the hyperbolic metric.

Definition 3.

We say that a parabolic $\gamma \in \text{Aut}(\mathbb{D})$ is positive if γ moves points on $\partial H$ in the positive direction, for some horoball H that is preserved by γ. We say that γ is negative if it is not positive.

We note that $\gamma \in \text{Aut}(\mathbb{D})$ is a positive parabolic if and only if ${\gamma }^{-1}$ is a negative parabolic. It is clear from the definitions that only positive parabolics in $\text{Aut}(\mathbb{D})$ can be adapted to horoballs.

Remark 2.

When $\gamma (z)=z+1$ in the upper half-plane model, the horoballs $\{z:\text{Im}(z)\ge C\}$ are $\text{dist}(iC,iC+1)$-adapted. The function $C\to \text{dist}(iC,iC+1)$ is decreasing, converges to infinity as $C\to 0$ and to 0 as $C\to \infty$, so by continuity $\mathcal{l}$-adapted horoballs exist and are unique for all $\mathcal{l}>0$. Any positive parabolic is conjugate to γ, so the analogous picture holds for an arbitrary positive parabolic.

Our main result is the following.

Lemma 1.

There exist universal constants $L,C>0$ such that the following holds. Let $f:\mathbb{D}\to \mathbb{C}$ be a univalent map, and let H be a horoball not containing 0 that is $\mathcal{l}$-adapted to a parabolic $\gamma \in \text{Aut}(\mathbb{D})$, with $\mathcal{l}<L$. Let the anchor of H be z₀. We assume that f conjugates γ to a parabolic Möbius transformation. Then for all $z\in H$, $$\left|f\prime (z)\right|\ge C\left|f\prime (z_0)\right|.$$

Remark 3.

It is crucial that $f(\mathbb{D})$ does not contain infinity in Lemma 1. Without this assumption, the Lemma does not hold. Note that we allow f to be unbounded, or equivalently $\infty \in \partial f(\mathbb{D})$.

Corollary 1.

Let $L,C,\mathcal{l}$ be as in Lemma 1. Let H be a horoball not containing 0 that is $\mathcal{l}$-adapted to a parabolic $\gamma \in \Gamma$, with anchor $z_0\in \partial H$. Then for any q > 0,$${\int }_H\frac{1}{{\left|f\prime (z)\right|}^q}d\mathit{xdy}\le \frac{\pi }{4C^q}\frac{{\left(1-{\left|z_0\right|}^2\right)}^2}{{\left|f\prime (z_0)\right|}^q}.$$

Proof.

It is standard that f conjugates γ to another parabolic $\rho (\gamma )$. From Lemma 1 we see that$$\begin{array}{c}{\int }_H\frac{1}{{\left|f\prime (z)\right|}^q}d\mathit{xdy}\le \frac{1}{C^q{\left|f\prime (z_0)\right|}^q}{\int }_{H}dxdy=\frac{1}{C^q{\left|f\prime (z_0)\right|}^q}\frac{\pi {(1-\left|z_0\right|)}^2}{4}\\ \le \frac{\pi }{4C^q}\frac{{\left(1-{\left|z_0\right|}^2\right)}^2}{{\left|f\prime (z_0)\right|}^q}.\end{array}$$□

Proof of Lemma 1.

The desired inequality will follow from the estimates in Proposition 1. We first need to conjugate f to a map $\mathbb{H}\to \mathbb{C}$ that commutes with $z\to z+1$.

Suppose without loss of generality that γ fixes 1. We will construct a commuting square

where A and B are Möbius transformations, and $g(z+1)=g(z)+1$.

We let $A(z)=\frac{z-\lambda i}{z+\lambda i}$ for $\lambda >0$ chosen such that $A^{-1}°\gamma °A(z)=z+1$. We choose B depending on finiteness of the fixed point of $f°\gamma °f^{-1}$.

We first give some preliminary observations that will be useful in both cases. The following Claim relates $f\prime$ and $g\prime$.

Claim 3. We have for all z, $$(f\prime °A)(z)=(B\prime °g)(z)g\prime (z)\frac{{(z+i\lambda )}^2}{2\lambda i}.$$

Proof.

We have $f=B°g°A^{-1}$, and $A^{-1}(z)=\lambda i\frac{1+z}{1-z}$. Therefore$$f\prime (A(z))=B\prime (g(z))g\prime (z)\left(A^{-1}\right)\prime (A(z)).$$

We have $(A^{-1})\prime (A(z))=\frac{2i\lambda }{{(1-\frac{z-\lambda i}{z+\lambda i})}^2}=\frac{{(z+\lambda i)}^2}{2\lambda i}$, and the result follows. □

For $z\in H$, we write $\mathbf{z}=A^{-1}(z)$. In particular ${\mathbf{z}}_0=A^{-1}(z_0)$.

Claim 4. We have $\text{Re}({\mathbf{z}}_0)=0$ and $\text{Im}(\mathbf{z})\ge \text{Im}({\mathbf{z}}_0)\ge \lambda$ for all $z\in H$.

Proof.

We have $A(\infty )=1$ and $A(\lambda i)=0$. Since the geodesic ray $[0,1)$ contains z₀, the geodesic ray $[\lambda i,\infty )$ contains ${\mathbf{z}}_0$. In particular $\text{Re}({\mathbf{z}}_0)=0$ and $\text{Im}({\mathbf{z}}_0)\ge \lambda$.

Since H is a horoball containing 1, the horoball $A^{-1}(H)$ contains infinity. Since ${\mathbf{z}}_0\in \partial A^{-1}(H)$, the second claim follows. □

Case 1 We first assume that $f°\gamma °f^{-1}$ fixes infinity. We let B(z) = az for $a\in \mathbb{C}\setminus \left\{0\right\}$ chosen so that $B^{-1}°(f°\gamma °f^{-1})°B(z)=z+1$. Since A and B are invertible, the commuting square exists by setting $g=B^{-1}°f°A$. Then $f°A$ conjugates $z\to z+1$ to $f°\gamma °f^{-1}$, and hence $B^{-1}°f°A=g$ conjugates $z\to z+1$ to itself. In particular $g(z+1)=g(z)+1$.

It follows from Claim 3 that$$\left|f\prime (z)\right|=\left|\frac{a}{2\lambda }\right|\left|g\prime (\mathbf{z})\right|{\left|\mathbf{z}+\lambda i\right|}^2.$$

By Claim 4, we have$$\frac{\left|f\prime (z)\right|}{\left|f\prime (z_0)\right|}=\frac{\left|g\prime (\mathbf{z})\right|}{\left|g\prime ({\mathbf{z}}_0)\right|}\frac{{\left|\mathbf{z}+\lambda i\right|}^2}{{\left|{\mathbf{z}}_0+\lambda i\right|}^2}\ge \frac{\left|g\prime (\mathbf{z})\right|}{\left|g\prime ({\mathbf{z}}_0)\right|}\approx 1,$$where we used Proposition 1 in the second estimate.

Case 2Assume now that $f°\gamma °f^{-1}$ fixes a point $a\in \mathbb{C}$. Set $B(z)=a+\frac{b}{z}$, where $b\in \mathbb{C}\setminus \left\{0\right\}$ is chosen so that $B^{-1}°(f°\gamma °f^{-1})°B(z)=z+1$. As in Case 1, both A and B are invertible so the commuting square exists, and $g(z+1)=g(z)+1$.

By Claim 3,$$\left|f\prime (A(z))\right|=\left|\frac{b}{2\lambda }\right|\frac{1}{{\left|g(z)\right|}^2}\left|g\prime (z)\right|{\left|z+\lambda i\right|}^2.$$

We have$$\frac{\left|f\prime (z)\right|}{\left|f\prime (z_0)\right|}={\left|\frac{g({\mathbf{z}}_0)}{g(\mathbf{z})}\right|}^2\left|\frac{g\prime (\mathbf{z})}{g\prime ({\mathbf{z}}_0)}\right|{\left|\frac{\mathbf{z}+\lambda i}{{\mathbf{z}}_0+\lambda i}\right|}^2.$$

By Proposition 1, $\left|\frac{g\prime (\mathbf{z})}{g\prime ({\mathbf{z}}_0)}\right|\approx 1$ and there exists $\alpha \in \mathbb{C}$ such that$$\left|g(\mathbf{z})-\mathbf{z}+\alpha \right|\lesssim e^{-2\pi \text{Im}(\mathbf{z})}.$$

Since infinity is not in the image of f, 0 is not in the image of g. In particular by Proposition 1, $\frac{\hspace{0.17em}\log \hspace{0.17em}2}{\pi }-\text{Im}(\alpha )\ge 0$. For $\mathcal{l}$ small enough, which corresponds to $\text{Im}({\mathbf{z}}_0)$ large enough, we have $\text{Im}(\mathbf{z}-\alpha )\ge \text{Im}({\mathbf{z}}_0)-\frac{\hspace{0.17em}\log \hspace{0.17em}2}{\pi }\gtrsim e^{-2\pi \text{Im}({\mathbf{z}}_0)}$, and hence $\left|g(\mathbf{z})\right|\approx \left|\mathbf{z}-\alpha \right|$. Therefore$$\frac{\left|f\prime (z)\right|}{\left|f\prime (z_0)\right|}={\left|\frac{{\mathbf{z}}_0-\alpha }{{\mathbf{z}}_0+\lambda i}\right|}^2/{\left|\frac{\mathbf{z}-\alpha }{\mathbf{z}+\lambda i}\right|}^2.$$

Let L be small enough so that for all $\mathbf{z}\in A^{-1}(H)$, we have $\text{Im}(\mathbf{z})\ge 1>10\frac{\hspace{0.17em}\log \hspace{0.17em}2}{\pi }>10\text{Im}(\alpha )$. Hence$${\left|\frac{\mathbf{z}-\alpha }{\mathbf{z}+\lambda i}\right|}^2\approx \frac{{(\text{Re}(\mathbf{z})-\text{Re}(\alpha ))}^2+\text{Im}{(\mathbf{z})}^2}{{\left|\mathbf{z}\right|}^2+{\lambda }^2}\lesssim \frac{{\left|\mathbf{z}\right|}^2+\text{Re}{(\alpha )}^2}{{\left|\mathbf{z}\right|}^2}.$$

Similarly we have$${\left|\frac{{\mathbf{z}}_0-\alpha }{{\mathbf{z}}_0+\lambda i}\right|}^2\approx \frac{\text{Re}{(\alpha )}^2+\text{Im}{({\mathbf{z}}_0)}^2}{\text{Im}{({\mathbf{z}}_0)}^2+{\lambda }^2}\approx \frac{\text{Re}{(\alpha )}^2+\text{Im}{({\mathbf{z}}_0)}^2}{\text{Im}{({\mathbf{z}}_0)}^2}\ge 1+\frac{\text{Re}{(\alpha )}^2}{{\left|\mathbf{z}\right|}^2}\gtrsim {\left|\frac{\mathbf{z}-\alpha }{\mathbf{z}+\lambda i}\right|}^2,$$where we used $\text{Im}({\mathbf{z}}_0)\ge \lambda >0$ in the second estimate and ${\left|\mathbf{z}\right|}^2\ge \text{Im}{(\mathbf{z})}^2\ge \text{Im}{({\mathbf{z}}_0)}^2$ in the third estimate. Therefore $\frac{\left|f\prime (z)\right|}{\left|f\prime (z_0)\right|}\gtrsim 1$, as desired.□

2.3 Dividing the disk into adapted horoballs and a cocompact subset

Recall that to show Theorem 2, we split the domain $\mathbb{D}$ into horoballs on which we use Lemma 1, and into the orbit of a compact set. We describe this splitting here, and how to estimate the integral from Theorem 2 over translates of a compact set in the next subsection.

Let L > 0 be the constant from Lemma 1. Choose $\mathcal{l}$ arbitrarily with $0<\mathcal{l}<\min (L,\underset{\gamma \in \Gamma }{\inf }\text{dist}(0,\gamma (0)))$. Let $\mathcal{H}$ be the union over all positive parabolic $\gamma \in \Gamma$ of the (open) horoball $H_{\gamma }$ that is $\mathcal{l}$-adapted to γ. We let $\Phi$ be the closed Dirichlet fundamental region for Γ centered at 0, and write ${\Phi }^{*}=\Phi \setminus \mathcal{H}$.

Proposition 2.

The set ${\Phi }^{*}$ is compact with 0 in its interior and is a fundamental domain for the action of Γ on $\mathbb{D}\setminus \mathcal{H}$.

Proof.

Implicit in the statement of the proposition is the claim that $\mathcal{H}$ is Γ-invariant. This follows from uniqueness of $\mathcal{l}$-adapted horoballs that was explained in Remark 2. The final claim follows from this and the fact that $\Phi$ is a fundamental domain for the action of Γ on $\mathbb{D}$.

Since $\mathbb{D}/\Gamma$ has finite area, by Siegel’s theorem the Dirichlet fundamental domain is a convex hyperbolic polygon [11, Theorem 4.1.1]. It is well known that any vertex at infinity $v\in \overline{\Phi }\cap {\mathbb{S}}^1$ of this polygon is a fixed point of a parabolic ${\gamma }_v\in \Gamma$ [1, Theorem 9.4.5 (4)]. By replacing γ_v with ${\gamma }_v^{-1}$ if necessary, we may assume that γ_v is positive. Therefore $\mathcal{H}$ contains horoballs $H^v:=H_{{\gamma }_v}$ that are $\mathcal{l}$-adapted to γ_v , and hence based at v, for each $v\in \overline{\Phi }\cap {\mathbb{S}}^1$. Therefore$${\Phi }^{*}=\Phi \setminus \mathcal{H}\subseteq \Phi \setminus \underset{v\in \overline{\Phi }\cap {\mathbb{S}}^1}{\cup }{H}^v$$is bounded, and thus compact.

For any positive parabolic $\gamma \in \Gamma$, since $\text{dist}(0,\gamma (0))>\mathcal{l}$, we have $0\notin H_{\gamma }$. Moreover since $\underset{\gamma \in \Gamma }{\inf }\text{dist}(0,\gamma (0))>\mathcal{l}$, we have$$\underset{\gamma \in \Gamma }{\inf }\text{dist}(0,H_{\gamma })>0.$$

Therefore 0 lies in the interior of ${\Phi }^{*}=\Phi \setminus \underset{\gamma }{\cup }{H}_{\gamma }$. □

2.4 Integral estimates on the lift of a compact part

Recall that one of the steps in the proof of Theorem 2 is bounding ${\int }_{\mathbb{D}\setminus \mathcal{H}}{\left|f\prime \right|}^{-q}d\mathit{xdy}$. We do this by splitting$${\int }_{\mathbb{D}\setminus \mathcal{H}}\frac{1}{{\left|f\prime (z)\right|}^q}d\mathit{xdy}=\sum _{\gamma \in \Gamma }{\int }_{\gamma {\Phi }^{*}}\frac{1}{{\left|f\prime (z)\right|}^q}d\mathit{xdy}.$$

Our goal in this subsection is to show how ${\int }_{\gamma {\Phi }^{*}}{\left|f\prime \right|}^{-q}d\mathit{xdy}$ depends on $\gamma \in \Gamma$. This follows from the Koebe distortion theorem that guarantees that $\left|f\prime \right|$ changes at most by a constant factor over $\gamma {\Phi }^{*}$.

Proposition 3.

For any q > 0 there exists a constant $C=C(\Gamma ,q)$ such that $$\frac{1}{C}\frac{{\left(1-{\left|\gamma (0)\right|}^2\right)}^2}{{\left|f\prime (\gamma (0))\right|}^q}\le {\int }_{\gamma {\Phi }^{*}}\frac{1}{{\left|f\prime (z)\right|}^q}d\mathit{xdy}\le C\frac{{\left(1-{\left|\gamma (0)\right|}^2\right)}^2}{{\left|f\prime (\gamma (0))\right|}^q}$$for all $\gamma \in \Gamma$.

Proof.

By Proposition 2, ${\Phi }^{*}$ is a compact set whose interior contains 0, so we can pick radii $r=r(\Gamma )<R=R(\Gamma )$ that depend only on Γ such that $B(0,r)\subseteq {\Phi }^{*}\subseteq B(0,R)$. Here we denote by B(z, C) the hyperbolic disk centered at z of radius C.

By the Koebe distortion theorem, we have for $z\in \gamma {\Phi }^{*}$,$$e^{-2R(\Gamma )}\le e^{-2\text{dist}(\gamma (0),z)}\le \left|\frac{f\prime (\gamma (0))(1-{\left|\gamma (0)\right|}^2)}{f\prime (z)(1-{\left|z\right|}^2)}\right|\le e^{2\text{dist}(\gamma (0),z)}\le e^{2R(\Gamma )}.$$

In particular, we have $\left|f\prime (z)\right|(1-{\left|z\right|}^2){\approx }_{\Gamma }\left|f\prime (\gamma (0))\right|(1-{\left|\gamma (0)\right|}^2)$.

Since $\gamma {\Phi }^{*}\subseteq B(\gamma (0),R)$, and the Euclidean diameter of the hyperbolic disk $B(\gamma (0),R)$ is $R(1-{\left|\gamma (0)\right|}^2)$ up to a bounded multiplicative error, on $\gamma {\Phi }^{*}$, we have $1-{\left|z\right|}^2\approx 1-{\left|\gamma (0)\right|}^2$. In particular, $\left|f\prime (z)\right|{\approx }_{\Gamma }\left|f\prime (\gamma (0))\right|$ for $z\in \gamma {\Phi }^{*}$.

Therefore$${\int }_{{\Phi }^{*}}\frac{1}{{\left|f\prime (z)\right|}^q}d\mathit{xdy}{\approx }_{\Gamma ,q}\frac{1}{{\left|f\prime (\gamma (0))\right|}^q}{\int }_{\gamma {\Phi }^{*}}dxdy.$$

The region $\gamma {\Phi }^{*}$ contains a hyperbolic disk of radius r, and hence a Euclidean disk of radius $r\prime \approx r(1-{\left|\gamma (0)\right|}^2)$. Therefore$$r^2{(1-{\left|\gamma (0)\right|}^2)}^2\lesssim {\int }_{\gamma {\Phi }^{*}}dxdy\lesssim R^2{(1-{\left|\gamma (0)\right|}^2)}^2,$$and hence ${\int }_{\gamma {\Phi }^{*}}dxdy{\approx }_{\Gamma }{(1-{\left|\gamma (0)\right|}^2)}^2$. Hence$${\int }_{{\Phi }^{*}}\frac{1}{{\left|f\prime (z)\right|}^q}d\mathit{xdy}{\approx }_{\Gamma ,q}\frac{{\left(1-{\left|\gamma (0)\right|}^2\right)}^2}{{\left|f\prime (\gamma (0))\right|}^q}.$$□

2.5 Proof of Theorem 2

We note that $f(\gamma (z))=\rho (\gamma )(f(z))$. Differentiating at 0, we see that $f\prime (\gamma (0))\gamma \prime (0)=\rho (\gamma )\prime (0)f\prime (0)$. Therefore(1) $$f\prime (\gamma (0))=f\prime (0)\frac{\rho (\gamma )\prime (0)}{\gamma \prime (0)}.$$(1)

Since γ is a Möbius transformation of the disk, we can write it as $\gamma (z)=\lambda \frac{z-a}{1-\overline{a}z}$, where $a\in \mathbb{D}$ and $\left|\lambda \right|=1$. Therefore(2) $$\left|\gamma \prime (0)\right|=1-{\left|a\right|}^2=1-{\left|\gamma (0)\right|}^2.$$(2)

Using (1), (2) and Proposition 3, we find that(3) $${\int }_{\mathbb{D}\setminus \mathcal{H}}\frac{1}{{\left|f\prime (z)\right|}^q}d\mathit{xdy}=\sum _{\gamma \in \Gamma }{\int }_{\gamma {\Phi }^{*}}\frac{1}{{\left|f\prime (z)\right|}^q}d\mathit{xdy}{\approx }_{\Gamma ,q}\sum _{\gamma \in \Gamma }\frac{{\left|\gamma \prime (0)\right|}^{q+2}}{{\left|\rho (\gamma )\prime (0)\right|}^q}.$$(3)

For any positive parabolic $\gamma \in \Gamma$, by Proposition 2 we have $0\notin H_{\gamma }$. Fix such a $\gamma \in \Gamma$, and let z₀ be the anchor of $H_{\gamma }$. Then $z_0\in \gamma {\Phi }^{*}$ for some $\gamma \in \Gamma$. Hence by Corollary 1 we have$${\int }_{H_{\gamma }}\frac{1}{{\left|f\prime (z)\right|}^q}d\mathit{xdy}{\lesssim }_q\frac{{\left(1-{\left|z_0\right|}^2\right)}^2}{{\left|f\prime (z_0)\right|}^q}.$$

Since $\gamma {\Phi }^{*}$ has hyperbolic diameter bounded over $\gamma \in \Gamma$, we have by the Koebe distortion theorem$$\left|\frac{f\prime (\gamma (0))(1-{\left|\gamma (0)\right|}^2)}{f\prime (z_0)(1-{\left|z_0\right|}^2)}\right|{\approx }_{\Gamma }1.$$

We also have as in the proof of Proposition 3,$$1-{\left|z_0\right|}^2{\approx }_{\Gamma }1-{\left|\gamma (0)\right|}^2.$$

Therefore$${\int }_{H_{\gamma }}\frac{1}{{\left|f\prime (z)\right|}^q}d\mathit{xdy}{\lesssim }_{\Gamma ,q}\frac{{\left(1-{\left|\gamma (0)\right|}^2\right)}^2}{{\left|f\prime (\gamma (0))\right|}^q}{\approx }_{\Gamma ,q}{\int }_{\gamma {\Phi }^{*}}\frac{1}{{\left|f\prime (z)\right|}^q}d\mathit{xdy}.$$

Since any fundamental region $\gamma {\Phi }^{*}$ intersects at most a bounded number of horoballs in $\mathcal{H}$, we see that(4) $${\int }_{\mathcal{H}}\frac{1}{{\left|f\prime (z)\right|}^q}d\mathit{xdy}{\lesssim }_{\Gamma ,q}{\int }_{\mathbb{D}\setminus \mathcal{H}}\frac{1}{{\left|f\prime (z)\right|}^q}d\mathit{xdy}.$$(4)

Combining (3) and (4), we see that$${\int }_{\mathbb{D}}\frac{1}{{\left|f\prime (z)\right|}^q}d\mathit{xdy}{\approx }_{\Gamma ,q}{\int }_{\mathbb{D}\setminus \mathcal{H}}\frac{1}{{\left|f\prime (z)\right|}^q}d\mathit{xdy}{\approx }_{\Gamma ,q}\sum _{\gamma \in \Gamma }\frac{{\left|\gamma \prime (0)\right|}^{q+2}}{{\left|\rho (\gamma )\prime (0)\right|}^q}.$$

3 Grafting a once-punctured torus

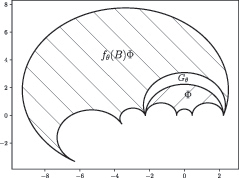
In this section and in the rest of the paper, denote by Ω the domain from [12], and by Γ the Kleinian once-punctured torus group that acts on Ω. Here we give a construction of Ω and Γ.

In [12], Ω is obtained by starting with a hyperplane in ${\mathbb{H}}^3$ and bending it along a certain discrete set of geodesics. The result of this is a set in ${\mathbb{H}}^3$ that disconnects $\partial {\mathbb{H}}^3={\mathbb{S}}^2$, and Ω is one of the resulting connected components. Since here we do not work with hyperbolic space ${\mathbb{H}}^3$, we give a concrete description of Ω as the union of regions in the complex plane bounded by 4 or 2 circular arcs.

In this section we work in the upper half-plane, closely following [12, §2]. We denote the Möbius transformations and subsets of $\mathbb{H}$ with a bar to distinguish them from their counterparts in the disk model.

We start with a once-punctured torus group generated by Möbius transformations$$\begin{array}{c}\overline{A}=\left(\begin{array}{cc}\cosh \frac{\lambda }{2}& \cosh \frac{\lambda }{2}+1\\ \cosh \frac{\lambda }{2}-1& \cosh \frac{\lambda }{2}\end{array}\right),\\ \overline{B}=\left(\begin{array}{cc}\cosh \frac{\tau }{2}\coth \frac{\lambda }{4}& -\sinh \frac{\tau }{2}\\ -\sinh \frac{\tau }{2}& \cosh \frac{\tau }{2}\tanh \frac{\lambda }{4}\end{array}\right).\end{array}$$

When λ and τ are real, the group $〈\overline{A},\overline{B}〉$ acts on $\mathbb{H}$ and $\frac{\mathbb{H}}{〈\overline{A},\overline{B}〉}$ is a once-punctured torus. We fix $\lambda =2{\cosh }^{-1}\frac{3}{2}$ throughout, and we let $\tau =\frac{\lambda }{2}+i\theta$ with θ a real parameter, to be set later. We denote by $\overline{B}(\theta )$ the Möbius transformation obtained by setting $\tau =\frac{\lambda }{2}+i\theta$ in the formula above, and set $\overline{\Gamma }(\theta )=〈\overline{A},\overline{B}(\theta )〉$. We write $\overline{\Gamma }=\overline{\Gamma }(0)$. Define a natural homomorphism ${\overline{f}}_{\theta }:\overline{\Gamma }\to \overline{\Gamma }(\theta )$ by ${\overline{f}}_{\theta }(\overline{A})=\overline{A},{\overline{f}}_{\theta }(\overline{B}(0))=\overline{B}(\theta )$.

Let $\Phi$ be the ideal quadrilateral with vertices $\pm \tanh \frac{\lambda }{4},\pm \coth \frac{\lambda }{4}$, so that $\Phi$ is a fundamental domain for the action of $\overline{\Gamma }$ on $\mathbb{H}$. Let Σ be the union of axes of all elements of $\overline{\Gamma }$. Then $\mathbb{H}\setminus \Sigma$ is a disjoint union of $\gamma \text{Int}(\Phi )$, where $\text{Int}$ denotes the topological interior.

Define a map ${\overline{\psi }}_{\theta }:\mathbb{H}\setminus \Sigma \to {\mathbb{S}}^2=\mathbb{C}\cup \left\{\infty \right\}$ by$${\overline{\psi }}_{\theta }(z)={\overline{f}}_{\theta }(\gamma )({\gamma }^{-1}z),$$where $\gamma \in \overline{\Gamma }$ is the unique element with the property that $z\in \gamma \text{Int}(\Phi )$.

For any hyperbolic element $\gamma \in \overline{\Gamma }$, the axis of γ is a boundary of exactly two (ideal) quadrilaterals ${\eta }_1\Phi ,{\eta }_2\Phi$ of the form $\eta \Phi$ for $\eta \in \overline{\Gamma }$. Order ${\eta }_1,{\eta }_2$ so that ${\eta }_1^{-1}{\eta }_2\in \{\overline{A},\overline{B}\}$. Then ${\overline{\psi }}_{\theta }({\eta }_2\Phi )={\overline{f}}_{\theta }({\eta }_1){\overline{f}}_{\theta }({\eta }_1^{-1}{\eta }_2)\Phi$ and ${\overline{\psi }}_{\theta }({\eta }_1\Phi )={\overline{f}}_{\theta }({\eta }_1)\Phi$. Since ${\overline{f}}_{\theta }(\overline{A})=\overline{A}$ we can extend ${\overline{\psi }}_{\theta }$ over all axes in Σ that separate ${\eta }_1\Phi$ and ${\eta }_1\overline{A}\Phi$. Denote the union of all other axes in Σ by Σ_B . For $\theta <0$ there is a region $G_{\theta }$ between $\Phi$ and ${\overline{f}}_{\theta }(B)\Phi$ bounded by two circular arcs (see Figure 1).$$\overline{\Omega }(\theta )={\overline{\psi }}_{\theta }(\mathbb{H}\setminus {\Sigma }_B)\cup \underset{\gamma \in \overline{\Gamma }(\theta )}{\cup }\gamma G_{\theta }.$$

Fig. 1 The gap $G_{\theta }$ between $\Phi ={\overline{f}}_{\theta }(\text{id})\Phi$ and ${\overline{f}}_{\theta }(B)\Phi$ in the image of ${\overline{\psi }}_{\theta }$.

Then $\overline{\Omega }(\theta )$ is simply connected and $\overline{\Gamma }(\theta )$-invariant.

Fix $\eta (z)=i\frac{1+z}{1-z}$ to be a Möbius transformation that maps $\mathbb{D}$ to $\mathbb{H}$. Set ${\theta }_0=\arccos \frac{1}{9}-\pi$.

Definition 4.

We define $\Omega ={\eta }^{-1}(\overline{\Omega }({\theta }_0))$, and $\Gamma ={\eta }^{-1}°\overline{\Gamma }({\theta }_0)°\eta$.

We also set $f(\gamma )={\eta }^{-1}°{\overline{f}}_{{\theta }_0}(\gamma )°\eta$ and $\psi ={\eta }^{-1}°{\overline{\psi }}_{{\theta }_0}$. A picture of Ω can be found in Figure 2.

Fig. 2 Domain Ω.

4 Numerical results

Let $F:\Omega \to \mathbb{D}$ be the Riemann map and $f=F^{-1}$ be its inverse. We denote by ${\Gamma }_0=F°\Gamma °F^{-1}$ and by $\rho :{\Gamma }_0\to \Gamma$ the homomorphism induced by f.

By a simple change of coordinates we see that(5) $${\int }_{\Omega }{\left|F\prime \right|}^{p}d\mathit{xdy}={\int }_{\mathbb{D}}{\left|f\prime \right|}^{2-p}d\mathit{xdy}.$$(5)

By Theorem 2 and (5), for p > 2 we have $F\prime \in L^p(\Omega )$ if and only if(6) $$\sum _{\gamma \in {\Gamma }_0}\frac{{\left|\gamma \prime (0)\right|}^p}{{\left|\rho (\gamma )\prime (0)\right|}^{p-2}}<\infty .$$(6)

In this section we describe how we estimate ρ and ${\Gamma }_0$, and how we estimate the range of values of p where the series (6) converges.

Since Γ is a free group of rank 2 generated by A and B (see Section 3), it suffices to estimate ${\rho }^{-1}(A)$ and ${\rho }^{-1}(B)$ for generators A and B of Γ. As explained in Section 3, the Möbius transformations A and B are given explicitly. To estimate ${\rho }^{-1}(A)=f^{-1}°A°f$ and ${\rho }^{-1}(B)=f^{-1}°B°f$, we estimate the Riemann mapping $f:\mathbb{D}\to \Omega$ using Driscoll’s Schwarz-Christoffel toolbox [5, 6], and then compute $f^{-1}°A°f$ and $f^{-1}°B°f$.

In Section 4.1 we describe how we get a polygon $\widehat{\Omega }$ that is an approximation to Ω. Then in Section 4.2 we explain how we get estimates of ${\rho }^{-1}(A)$ and ${\rho }^{-1}(B)$ using this polygon and the Schwarz-Christoffel toolbox. Finally in Section 4.4 we describe how we show numerically that the sum $\sum _{\gamma \in {\Gamma }_0}{\left|\gamma \prime (0)\right|}^p{\left|\rho (\gamma )\prime (0)\right|}^{2-p}$ converges for p = 4, and we check for which values of p it diverges.

4.1 Finite polygonal approximations

We first remind the reader of some notation from Section 3. Recall that we have a once-punctured torus group of Möbius transformations $\overline{\Gamma }$ acting on $\mathbb{H}$, a map $\psi :\mathbb{H}\to \Omega$, and a group isomorphism $f:\overline{\Gamma }\to \Gamma$, so that ψ is f-equivariant. Recall that $\eta =i\frac{1+z}{1-z}:\mathbb{H}\to \mathbb{D}$ is the Möbius transformation we use to move from the upper half-plane model to the disk model.

Since $\mathbb{D}/\overline{\Gamma }$ is a once-punctured torus, the limit set $\Lambda (\overline{\Gamma })$ of $\overline{\Gamma }$ is ${\mathbb{S}}^1$. Let $x_0=\eta \left(\coth \frac{\lambda }{4}\right)=i\frac{1+\coth \frac{\lambda }{4}}{1-\coth \frac{\lambda }{4}}=-i{e}^{\lambda /2}$ be the η-image of an ideal vertex of the fundamental domain $\Phi$ for the action of $\overline{\Gamma }$ on $\mathbb{H}$. It is easy to see that $\overline{\Gamma }{x}_0$ is dense in ${\mathbb{S}}^1$. From the construction of ψ, we see that it extends continuously to a surjection $\psi :{\mathbb{S}}^1\to \partial \Omega$. Therefore $\psi (\overline{\Gamma }{x}_0)$ is dense in $\partial \Omega$ and by equivariance $\psi (\overline{\Gamma }{x}_0)=\Gamma \psi (x_0)=\Gamma x_0$.

To obtain an approximation to $\partial \Omega$, we generate some number of random points $v_1,v_2,\dots ,v_n$ of the form $\gamma x_0$ where γ is a word in A and B of length at most some parameter $\mathcal{l}>0$. These points determine the boundary of a polygon $\widehat{\Omega }$ which is an approximation to Ω.

Our goal to use the Schwarz-Christoffel toolbox to compute the Riemann map of this polygon. For this we need the vertices v_i to be sorted, which will almost never happen. To sort them, we note that it suffices to sort ${\psi }^{-1}(v_i)$. If $v_i={\gamma }_i{x}_0$, then ${\psi }^{-1}(v_i)=f^{-1}({\gamma }_i)\left(\coth \frac{\lambda }{4}\right)\in \mathbb{R}$ by equivariance.This formula is used to compute ${\psi }^{-1}(v_i)\in \mathbb{R}$.

The content of this subsection is summarized in Procedure 1. In this procedure, we use the following additional piece of notation. For a word $w\in 〈a,b〉$ in the free group $〈a,b〉$ of rank 2, and elements $x,y\in G$ in some group G, denote by w(a, b) the element of G obtained by substituting x for a and y for b in w.

Procedure 1: Constructing finite polygonal approximations.

Input: The number of vertices n, and the maximum word length $\mathcal{l}$.

Output: The vertices $v_1,v_2,\dots ,v_n$ of a polygon.

1 Construct a list $W_1,W_2,\dots ,W_{2(3^{\mathcal{l}}-1)}$ of all words of length at most $\mathcal{l}$ in the free group $〈a,b〉$ of rank

2. Pick integers $1\le i_1<i_2<\dots <i_n\le 2(3^{\mathcal{l}}-1)$ uniformly at random.

3 Set ${\gamma }_k=W_{i_k}(A,B)$ and ${\overline{\gamma }}_k=W_{i_k}(\overline{A},\overline{B})$.

4 Reorder $i_1,i_2,\dots ,i_n$ so that ${\overline{\gamma }}_1\left(\coth \frac{\lambda }{4}\right)<{\overline{\gamma }}_2\left(\coth \frac{\lambda }{4}\right)<\dots <{\overline{\gamma }}_n\left(\coth \frac{\lambda }{4}\right)$.

5 Let $v_k={\gamma }_k(-i\hspace{0.17em}\exp \hspace{0.17em}(\lambda /2))$.

4.2 Procedure for estimating conjugated generators

Here we describe the method we use to estimate ${\rho }^{-1}(A)=f^{-1}°A°f$ and ${\rho }^{-1}(B)=f^{-1}°B°f$, assuming that we have an estimate of $f:\mathbb{D}\to \Omega$. We assume that we can compute f(z) and $f^{-1}(w)$ for any $z\in \mathbb{D},w\in \Omega$, which is the case for Riemann mappings computed using the Schwarz-Christoffel toolbox.

More generally, we describe how to estimate $f^{-1}°X°f$ for any Möbius transformation X preserving Ω. Since X preserves Ω, its conjugate $f^{-1}°X°f$ preserves the disk. It therefore takes the form$$f^{-1}°X°f=\lambda \frac{z-a}{1-\overline{a}z}.$$

Our methods estimate $\lambda \in {\mathbb{S}}^1$ and $a\in \mathbb{D}$. They are summarized in Procedure 2. Note that we can compute f and $f^{-1}$ at specific points. We generate some number n of points $z_1,z_2,\dots ,z_n\in \mathbb{D}$ and then compute $w_i=f^{-1}(X(f(z_i)))$. We estimate $\lambda ,a$ so that $\lambda \frac{z_i-a}{1-\overline{a}{z}_i}$ is as close as possible to w_i . Specifically, we use the sum-of-squares error$$\sum _{i=1}^n{\left|w_i-\lambda \frac{z_i-a}{1-\overline{a}{z}_i}\right|}^2.$$

In our implementation, we use MATLAB’s lsqcurvefit to do the optimization.

Procedure 2: Estimating $f^{-1}°X°f$ given the Riemann mapping $f:\mathbb{D}\to \Omega$ and a Möbius transformation X preserving Ω.

Input: The Riemann mapping $f:\mathbb{D}\to \Omega$, a Möbius transformation X preserving Ω, and the sample size n.

Output: Estimate $\widehat{X}$ of the Möbius transformation $f^{-1}°X°f$.

1 Generate n points $z_1,z_2,\dots ,z_n\in \mathbb{D}$ uniformly at random.

2 Compute $w_i=f^{-1}(X(f(z_i)))$.

3 Look for the minimizers $(\widehat{\lambda },\widehat{a})$ of$$\sum _{i=1}^n{\left|w_i-\lambda \frac{z_i-a}{1-\overline{a}{z}_i}\right|}^2$$over $(\lambda ,a)\in {\mathbb{S}}^1\times \mathbb{D}$.

4 Set $\widehat{X}=\widehat{\lambda }\frac{z-\widehat{a}}{1-\overline{\widehat{a}}z}$.

4.3 Estimates of the conjugated generators

To actually estimate generators of ${\Gamma }_0=f^{-1}°\Gamma °f$, we combine the procedures described in Section 4.1 and Section 4.2.

We first compute polygonal approximations to Ω using Procedure 1. We set the maximum word length $\mathcal{l}=12$. We construct the following approximations:

1. the main polygon, $\widehat{\Omega }$ that has n = 600 vertices, and

2. several smaller polygons, ${\widehat{\Omega }}_i^{\mathrm{s}}$ for $1\le i\le 20$, each with n = 100 vertices.

We will use $\widehat{\Omega }$ to obtain estimates of $f^{-1}°A°f$ and $f^{-1}°B°f$, and the smaller polygons ${\widehat{\Omega }}_i^{\mathrm{s}}$ to validate these estimates.

Using the Schwarz-Christoffel toolbox, we compute the Riemann mappings $f:\mathbb{D}\to \widehat{\Omega }$ and $f_i^{\mathrm{s}}:\mathbb{D}\to {\widehat{\Omega }}_i^{\mathrm{s}}$. We use Procedure 2 with f, and X = A and X = B. We denote the resulting estimates ${\lambda }^A,a^A$ and ${\lambda }^B,a^B$, and call them the main estimates in this subsection. These give the estimates of $f^{-1}°A°f$ and $f^{-1}°B°f$ that we will use in the rest of the paper.

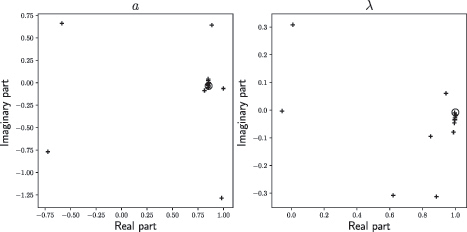
For validation, we also run Procedure 2 with ${\widehat{\Omega }}_i^{\mathrm{s}}$ for $i=1,2,\dots ,20$, and X = A and X = B. We call the resulting estimates ${\lambda }_i^A,a_i^A$ and ${\lambda }_i^B,a_i^B$. We plot these and the main estimates in Figures 3 and 4. We see that for each parameter, there is a clear cluster in the estimates obtained from ${\widehat{\Omega }}_i^{\mathrm{s}},i=1,2,\dots ,20$ centered approximately at the estimate obtained from $\widehat{\Omega }$. This suggests that ${\lambda }^A,a^A$ and ${\lambda }^B,a^B$ are accurate.

Fig. 3 The crosses represent values of parameters ${\lambda }_i^A,a_i^A$ of a disk automorphism estimated using smaller 100-point polygonal approximations ${\widehat{\Omega }}_i^{\mathrm{s}}$ to Ω. The circles are the estimates of λ^A and a^A obtained from $\widehat{\Omega }$.

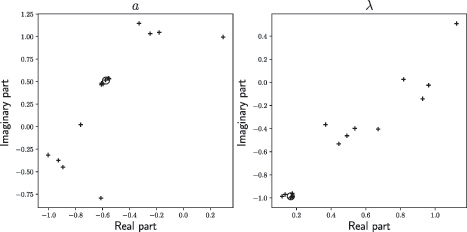
Fig. 4 The crosses represent values of parameters ${\lambda }_i^B,a_i^B$ of a disk automorphism estimated using smaller 100-point polygonal approximations ${\widehat{\Omega }}_i^{\mathrm{s}}$ to Ω. The circles are the estimates of λ^B and a^B obtained from $\widehat{\Omega }$.

Definition 5.

We set ${\widehat{\Gamma }}_0=〈\widehat{A},\widehat{B}〉$, where $$\widehat{A}(z)={\lambda }^A\frac{z-a^A}{1-\overline{a^A}z},$$and $$\widehat{B}(z)={\lambda }^B\frac{z-a^B}{1-\overline{a^B}z}.$$

We also define the homomorphism $\widehat{\rho }:{\widehat{\Gamma }}_0\to \Gamma$ by setting $\widehat{\rho }(\widehat{A})=A$ and $\widehat{\rho }(\widehat{B})=B$.

4.4 Values of p for which $F\prime \in L^p(\Omega )$

By Theorem 2 and (5), $F\prime \in L^p(\Omega )$ if and only if$$\sum _{\gamma \in {\Gamma }_0}{\left|\gamma \prime (0)\right|}^p{\left|\rho (\gamma )\prime (0)\right|}^{2-p}<\infty .$$

We are hence interested in values of p for which$$\sum _{\gamma \in {\widehat{\Gamma }}_0}\mathrm{ }|\gamma \prime (0){|}^p\mathrm{ }|\widehat{\rho }(\gamma )\prime (0){|}^2-p<\infty .$$

We define ${\widehat{\Gamma }}_0^n$ to be the set of all elements that have word length n in the generators $\widehat{A},\widehat{B}$ of ${\widehat{\Gamma }}_0$. We then split the above sum into$$\sum _{n\ge 0}{S}_n^{(p)}\mathrm{ }\text{where}\mathrm{ }{S}_n^{(p)}=\sum _{\gamma \in {\widehat{\Gamma }}_0^n}{\left|\gamma \prime (0)\right|}^p{\left|\widehat{\rho }(\gamma )\prime (0)\right|}^{2-p}.$$

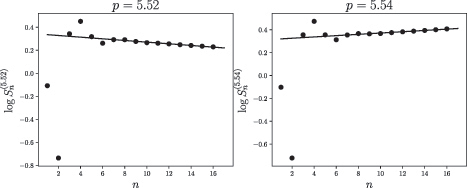
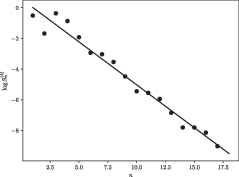
We numerically confirm that $S_n^{(4)}$ decays exponentially with n, see Figure 5.

Fig. 5 The plot of $\hspace{0.17em}\log \hspace{0.17em}{S}_n^{(4)}$ as a function of n for $n\le 17$. The solid line is the least-squares best linear fit to the shown data points.

Recall the definition of $p_{\star }$ from the Main result in Section 1.4, $p_{\star }=\sup \{p>0:F\prime \in L^p(\Omega )\}$. By Theorem 2 and (5), this is equal to$$p_{\star }=\sup \left\{p>0:\sum _{n\ge 0}{S}_n^{(p)}<\infty \right\}.$$

How close $p_{\star }$ is to 4 gives an indication of how close the domain Ω is to being a counterexample to Brennan’s conjecture. Numerical results show that $S_n^{(5.52)}$ decays exponentially with n and that $S_n^{(5.54)}$ grows exponentially with n, see Figure 6, meaning that $5.52<p_{\star }<5.54$, showing the Main result.

Fig. 6 The plots of $\hspace{0.17em}\log \hspace{0.17em}{S}_n^{(p)}$ as a function of n for $n\le 16$ and $p=5.52,5.54$. The solid lines are the least-squares best linear fits to the data points $(n,\hspace{0.17em}\log \hspace{0.17em}{S}_n^{(p)})$ for $n\ge 6$, for $p=5.52,5.54$.

Acknowledgments

I would like to thank Vladimir Marković for introducing me to this problem and for his advice while working on it, and in particular for his help on Lemma 1. I would also like to thank the reviewers for pointing out an error in an earlier draft of this paper, and for their helpful comments and suggestions.