Delayed Acceptance ABC-SMC

Abstract

Approximate Bayesian computation (ABC) is now an established technique for statistical inference used in cases where the likelihood function is computationally expensive or not available. It relies on the use of a model that is specified in the form of a simulator, and approximates the likelihood at a parameter value θ by simulating auxiliary data sets x and evaluating the distance of x from the true data y. However, ABC is not computationally feasible in cases where using the simulator for each θ is very expensive. This article investigates this situation in cases where a cheap, but approximate, simulator is available. The approach is to employ delayed acceptance Markov chain Monte Carlo within an ABC sequential Monte Carlo sampler to, in a first stage of the kernel, use the cheap simulator to rule out parts of the parameter space that are not worth exploring, so that the “true” simulator is only run (in the second stage of the kernel) where there is a reasonable chance of accepting proposed values of θ. We show that this approach can be used quite automatically, with few tuning parameters. Applications to stochastic differential equation models and latent doubly intractable distributions are presented. Supplementary materials for this article are available online.

KEYWORDS:

• Doubly intractable distributions
• Exponential random graph models
• Likelihood free inference
• Stochastic differential equations

1 Introduction

1.1 Motivation

Approximate Bayesian computation (ABC) is a technique for approximate Bayesian inference originally introduced in the population genetics literature (Pritchard et al. 1999; Beaumont, Zhang, and Balding 2002), but which is now used for a wide range of applications. It is suitable for situations in which a model $l(·|\theta )$ with parameters θ for data y is readily available in the form of a simulator, but where l as a function of θ (known as the likelihood) is intractable in that it cannot be evaluated pointwise. If θ is assigned prior distribution p, the object of inference is the posterior distribution $\pi (\theta |y)\propto p(\theta )l(y|\theta )$. ABC yields approximations to the posterior distribution through approximating the likelihood, in the simplest case using(1) $$\widehat{f_{ϵ}}\left(y|\theta \right)=\frac{1}{M}\sum _{m=1}^M{P}_{ϵ}\left(y|x^{(m)}\right),$$(1) where $P_{ϵ}$ is a kernel centered around $x^{(m)}$ and M points ${\left\{x^{(m)}\right\}}_{m=1}^M$ are sampled from $l(·|\theta )$. We may see Monte Carlo ABC algorithms as sampling from a joint distribution on θ and x proportional to $p(\theta )l(x|\theta )P_{ϵ}(y|x)$, where l is used as a proposal distribution for x.

In this article, we describe methods that are designed to be applicable in cases where the likelihood estimation is computationally costly because the model l is expensive to simulate from, for example when studying an ordinary differential equation (ODE) or stochastic differential equation (SDE) model (Picchini 2014) that requires a solver with a small step size, or when using an individual based model (van der Vaart et al. 2015) with a large number of individuals. This situation is not uncommon, since even if the model takes only a matter of seconds to simulate, this cost is prohibitive when it needs to be simulated a number of times due to estimating the likelihood at a large number of Monte Carlo points in θ-space. We note that this situation is exacerbated when θ is of moderate to high dimension, since in these cases (as in any Monte Carlo method) it is difficult to design a proposal that can efficiently make moves on all dimensions of θ simultaneously. Most commonly, each dimension of θ is updated using a single component move, and in the ABC context this means using M simulations from the likelihood when updating each dimension of θ.

1.2 Previous Work and Contributions

This article describes an ABC-sequential Monte Carlo (SMC) algorithm that uses a delayed acceptance (DA) ABC-Markov chain Monte Carlo (MCMC) move that aims to limit the number of θ points at which we need to perform an expensive simulation of the likelihood, while also attempting to maintain a good exploration of the target distribution. We begin in Section 2 with a review of the literature on ABC-SMC, focusing particularly on the case where a uniform ABC kernel is used. Then in Section 3.1.1, we describe DA ABC-MCMC for exploring θ-space, and use it as a method for discarding θ points that are unlikely to be in regions of high posterior density. DA decomposes an MCMC move into two stages. At the first stage a point is proposed and is accepted or rejected according to a posterior that is usually chosen to approximate the desired posterior. If accepted at the first stage, at the second stage an acceptance probability is used that “corrects” for the discrepancy between the approximate and the desired target. Thus, we may think of the first stage as screening for points to take through to the second stage. Compared to the previous work, this approach is most similar to the “early rejection” of Picchini and Forman (2016) who use the prior for this screening step. DA ABC-MCMC at the first stage makes use of an approximate, but computationally cheap, alternative to the full simulator. We will see that our approach is applicable in cases in which there is a cheap, approximate simulator is used independently of the full simulator, and also where the full simulator is a continuation of the initial cheap simulation. This latter situation is the same as that considered in “Lazy” ABC (Prangle 2016), in which is it possible to monitor a simulation as it is progressing, and to be able to assess before the full simulation whether the current θ point is likely to be in a region of high posterior density. We will see that using DA ABC-MCMC introduces an additional tuning parameter: the tolerance ϵ used for the cheap simulator. When using DA ABC-MCMC directly, it is not always straightforward to set this parameter. In Section 3.2.1, we embed DA ABC-MCMC in the ABC-SMC framework, since this is established as an effective method for guiding Monte Carlo points in θ-space to regions of high posterior density, and also since we see that it allows for automating the choice of the additional tuning parameter. The resultant algorithm is particularly useful for distributions for which it is difficult to design a useful proposal distribution. When our proposal has a poor acceptance rate, we may need to run the expensive simulator many times for a single acceptance. However, with delayed acceptance we may propose a very large number of points without the need to run the expensive simulator for a large number of them. The procedure is to evaluate whether the proposed points are in a high density region according to the cheap simulator—in the cases where they are, we run the expensive simulator. For points that lie in this region (i.e., that pass the first stage of DA), we must run the expensive simulator, and expect to accept a reasonable proportion of these (as long as the cheap simulator is close to the expensive simulator). Essentially, the first stage of the DA acts to give us a well-targeted proposal. Section 4 considers an application to SDEs, where we examine using cheap simulators with a large step size in the numerical solver. Section 5 considers applications to doubly intractable distributions: applying ABC to these models (and other Markov random fields) is complicated because no computationally feasible exact simulator is available. Instead an MCMC algorithm is commonly used as an approximate approach (Grelaud, Robert, and Marin 2009; Everitt 2012). In such approaches the burn in of this MCMC method determines the accuracy of the approach: for a small burn in the method is biased, with this bias being eliminated by a large burn in which may be computationally expensive. In the main article, we examine the case of latent Ising models previously studied in Everitt (2012), noting the potential advantage of ABC in these cases compared to methods such as the exchange algorithm. In the supplementary appendix, we also examine an application to a latent exponential random graph model (ERGM). We then conclude with a discussion in Section 6.

2 Background on ABC-SMC

2.1 SMC Samplers

An SMC sampler (Del Moral, Doucet, and Jasra 2006) is an importance sampling based Monte Carlo method for generating weighted points from a target distribution π through making use of a sequence of T target distributions that bridge between some initial proposal distribution π₀ from which we can simulate, and the final target ${\pi }_T=\pi$. Here we focus on the variant of the algorithm that uses an MCMC kernel, and provide a sketch of the main steps of the algorithm (further details may be found in Del Moral, Doucet, and Jasra (2006)). The algorithm begins by simulating N weighted “particles” from π₀ (initially with equal weights). Then the particles are moved from target π_t to ${\pi }_{t+1}$ through an importance sampling reweighting step, followed by a “move” step in which each particle is simulated from an MCMC kernel starting at its current value, and with target ${\pi }_{t+1}$. Let ${\theta }_t^{(i)}$ be the value taken by the ith particle after iteration t and $w_t^{(i)}$ be its (normalized) weight. The reweighting step then computes the (unnormalized) weight ${\tilde{w}}_{t+1}^{(i)}$ of the nth particle ${\theta }_t^{(i)}$ using(2) $${\tilde{w}}_{t+1}^{(i)}=w_t^{(i)}\frac{{\pi }_{t+1}\left({\theta }_t^{(i)}\right)}{{\pi }_t\left({\theta }_t^{(i)}\right)},$$(2) followed by a normalization step to find $w_{t+1}^{(i)}$. This algorithm yields an empirical approximation of π_t (3) $${\widehat{\pi }}_t^N=\sum _{i=1}^N{w}_t^{(i)}{\delta }_{{\theta }_t^{(i)}},$$(3)

where ${\delta }_{\theta }$ is a Dirac mass at θ, and an estimate of its normalizing constant(4) $$\widehat{Z_t}=\prod _{s=1}^t\sum _{i=1}^N{w}_s^{(i)}\frac{{\pi }_{s+1}\left({\theta }_s^{(i)}\right)}{{\pi }_s\left({\theta }_s^{(i)}\right)}.$$(4)

Usually the variance of the weights is monitored during the algorithm, and if this becomes too large (which would lead to high variance estimators if no intervention was made) a resampling step is performed after reweighting (in this article stratified resampling is used). The resampling step at iteration t + 1 simulates N particles from the empirical distribution ${\widehat{\pi }}_{t+1}^N$.

SMC outperforms importance sampling in cases where one needs many points to obtain low variance importance sampling estimates when directly using π₀ as a proposal for π, that is, when the distance between π₀ and π is too large. To ensure that SMC estimates have low variance, we require the distance between π_t and ${\pi }_{t+1}$ to be small for all t. a proxy for the distance between subsequent targets that may be estimated as the algorithm runs is given by the effective sample size (ESS) (Kong, Liu, and Wong 1994)(5) $$\text{ESS}={\left(\sum _{i=1}^N{\left(w_{t+1}^{(i)}\right)}^2\right)}^{-1}.$$(5)

A large ESS corresponds to a small distance between targets although, as referred to in the following section, a high ESS is necessary but not sufficient for achieving a low Monte Carlo variance.

2.2 ABC-SMC

Sisson, Fan, and Tanaka (2007, 2009) remarked that the ABC posterior ${\pi }_{ϵ}$ is a natural candidate for simulating from using SMC, in that a sequence of posteriors with a decreasing sequence of tolerances ϵ₁ to ${ϵ}_T=ϵ$ is a natural and useful choice as a sequence of distributions to use in SMC. We follow Del Moral, Doucet, and Jasra (2012a) in choosing the sequence of distributions(6) $${\pi }_t\left({\theta }_t,x_t|y\right)\propto p\left({\theta }_t\right)l\left(x_t|{\theta }_t\right)P_{{ϵ}_t}\left(y|x_t\right)$$(6) such that ${\theta }_t\sim {\pi }_{{ϵ}_t}$, with x_t being the corresponding auxiliary variable (as in Equation (1)(1) $$\widehat{f_{ϵ}}\left(y|\theta \right)=\frac{1}{M}\sum _{m=1}^M{P}_{ϵ}\left(y|x^{(m)}\right),$$(1) ) at iteration t. When an ABC-MCMC move is used for the “move” step, this leads to the following weight update when moving from target π_t to ${\pi }_{t+1}$ (7) $${\tilde{w}}_{t+1}^{(i)}=w_t^{(i)}\frac{P_{{ϵ}_{t+1}}\left(y|x_t^{(i)}\right)}{P_{{ϵ}_t}\left(y|x_t^{(i)}\right)}$$(7)

(a derivation may be found in the supplementary appendix). This weight update is computationally cheap and requires no simulation to produce $x_t^{(i)}$, which has been generated either in the initial step of the algorithm or as a part of a previous MCMC move. Additionally, it is cheap to compute for any choice of ${ϵ}_{t+1}$. This fact is used by Del Moral, Doucet, and Jasra (2012a) to devise an adaptive ABC-SMC algorithm that automatically determines the sequence $({ϵ}_t)$. At every SMC iteration a bisection method is used to determine the ${ϵ}_{t+1}$ that will result in an ESS that is some proportion (e.g., 90%) of N.

It is common practice in SMC algorithms to use the current set of particles to adaptively set the proposal for the MCMC kernels used in the “move” step (note that this introduces a small bias into estimates based on the SMC for the methods used in this article). The simplest scheme, from Robert et al. (2011), sets the proposal covariance to be some multiple of the empirical covariance of the particles (this choice being rooted in results on optimal proposals for some MCMC algorithms).

2.2.1 ABC-SMC With Indicator Potentials

In ABC a common choice for the kernel $P_{{ϵ}_t}$ is $P_{{ϵ}_t}(y|x_t)\propto \mathbb{I}(d(y,x_t)<{ϵ}_t)$, where d is a distance metric. This kernel is known to be sub-optimal (Li and Fearnhead 2018), but we restrict our attention to this case for the remainder of the article since it simplifies the presentation and interpretation of the algorithms we introduce. The first example of this simplification is that when used in the ABC-SMC method of Del Moral, Doucet, and Jasra (2012a), the particle weights are either zero (“dead”) or nonzero (“alive”) (this following from Equation (7)(7) $${\tilde{w}}_{t+1}^{(i)}=w_t^{(i)}\frac{P_{{ϵ}_{t+1}}\left(y|x_t^{(i)}\right)}{P_{{ϵ}_t}\left(y|x_t^{(i)}\right)}$$(7) ). This type of SMC algorithm is also studied in Cérou et al. (2012), Del Moral et al. (2015), and Prangle, Everitt, and Kypraios (2017). A further consequence that the ESS is equal to the number of “alive” particles with nonzero weight after the update, simplifying the interpretation of the adaptive approach to choosing ${ϵ}_{t+1}$ described above.

In this article, we use the revised scheme of Bernton et al. (2017). The revision addresses the issue that the acceptance rate of ABC-MCMC moves decreases as the ABC-SMC progresses (since the ABC tolerance decreases). When the MCMC moves have a poor acceptance rate, the ESS is not a good criterion for deciding on a new tolerance, since it is unaffected by the values taken by each particle: even if all particles take the same value, the ESS may be high. Therefore, Bernton et al. (2017) suggested instead to choose ${ϵ}_{t+1}$ such that some number U (with $0<U\le N$) of the N particles will be unique after resampling has been performed. Both this new scheme, and the original method that uses the ESS, introduce a small bias into estimates from the SMC (Cérou et al. 2012; Prangle, Everitt, and Kypraios 2017).

To simplify the presentation of our method, we perform resampling at every step of the algorithm. As a consequence, the denominator in Equation (7)(7) $${\tilde{w}}_{t+1}^{(i)}=w_t^{(i)}\frac{P_{{ϵ}_{t+1}}\left(y|x_t^{(i)}\right)}{P_{{ϵ}_t}\left(y|x_t^{(i)}\right)}$$(7) is positive and the same for every particle, thus in practice the reweighting step becomes$${\tilde{w}}_{t+1}^{(i)}=w_t^{(i)}\mathbb{I}\left(d\left(y,x_t^{(i)}\right)<{ϵ}_{t+1}\right),$$where for simplicity we have omitted the additional normalizing term for $\mathbb{I}(d(y,x_t)<{ϵ}_t)$, required to provide a correct marginal likelihood estimator—see Didelot et al. (2011) for details. Resampling at every step avoids propagating “dead” particles with zero weight, but is not an optimal strategy since it is possible that not all alive particles will be part of the resample (unless systematic resampling is used). A standard approach to deciding when to resample is to only do so when the ESS fall below a prespecified threshold (Del Moral, Doucet, and Jasra 2012b), but we do not consider such approaches in this article.

The ABC-SMC algorithm with the configuration described in this section is given in Algorithm 1. Note that although a final tolerance ${ϵ}_{\text{end}}$ is specified in this algorithm, in practice the method is run for as long as computational resources will allow; a standard approach would be to monitor the acceptance probability of the MCMC moves and to terminate when this is zero for a number of iterations. The early rejection method of Picchini and Forman (2016) may be employed for the ABC-MCMC moves when using an indicator kernel: this approach is precisely the same as standard ABC-MCMC, with the calculation reorganized to avoid unnecessary simulations from the likelihood (see the supplementary appendix for details).

Algorithm 1 ABC-SMC using early rejection.

Inputs: Number of particles N, desired number of unique particles U, prior p, simulator l, final tolerance ${ϵ}_{\text{end}}$.

Outputs: Particles ${\left\{({\theta }_t^{(i)},x_t^{(i)})\right\}}_{i=1}^N$ and weights ${\left\{w_t^{(i)}\right\}}_{i=1}^N$ for all t.

for $i=1:N$ do

$${\theta }_0^{(i)}\sim p(·)$$$$x_0^{(i)}\sim l\left(·|{\theta }_0^{(i)}\right)$$$$w_0^{(i)}=1/N$$

end for

${ϵ}_0={\max }_{i}d(y,x_0^{(i)})$, t = 0.while ${ϵ}_t>{ϵ}_{\text{end}}$ do

Simulate $v\sim \mathcal{U}{\left[0,1\right]}^N$, to be used in resampling.

Use bisection to choose ${ϵ}_{t+1}$ s.t. there will be U unique particles after reweighting and resampling (using random numbers v).for $i=1:N$ do $${\tilde{w}}_{t+1}^{(i)}=w_t^{(i)}\mathbb{I}\left(d\left(y,x_t^{(i)}\right)<{ϵ}_{t+1}\right)$$ end for

Normalize ${\left\{{\tilde{w}}_{t+1}\right\}}_{i=1}^N$ to give normalized weights ${\left\{w_{t+1}\right\}}_{i=1}^N$.

Perform resampling using random draws v.for $i=1:N$ do $${\theta }_{t+1}^{(i)}={\theta }_t^{(i)},x_{t+1}^{(i)}=x_t^{(i)}$$$${\left({\theta }_{t+1}^{(i)}\right)}^{*}\sim q\left(·|{\theta }_t^{(i)}\right)$$$$u\sim \mathcal{U}\left(0,1\right)$$ if $u<\frac{p({({\theta }_{t+1}^{(i)})}^{*})q({\theta }_t^{(i)}|{({\theta }_{t+1}^{(i)})}^{*})}{p({\theta }_{t+1}^{(i)})q({({\theta }_{t+1}^{(i)})}^{*}|{\theta }_t^{(i)})}$ then $${\left(x_{t+1}^{(i)}\right)}^{*}\sim l\left(·|{\left({\theta }_{t+1}^{(i)}\right)}^{*}\right)$$ if $d(y,{(x_{t+1}^{(i)})}^{*})<{ϵ}_{t+1}$ then $${\theta }_{t+1}^{(i)}={\left({\theta }_{t+1}^{(i)}\right)}^{*},x_{t+1}^{(i)}={\left(x_{t+1}^{(i)}\right)}^{*}$$ end if end if end for $$t=t+1$$ end while

3 Delayed Acceptance ABC-SMC

This section describes the algorithm that is introduced by this article: an ABC-SMC sampler that uses a DA ABC-MCMC kernel as its “move” step (instead of standard ABC-MCMC), with the DA move being tuned automatically using the population of particles. We begin by describing DA, then outline how it may be used in the ABC context, before describing an ABC-SMC sampler that makes use of it. Where they are omitted from the main article, full derivations are given in the supplementary appendix.

3.1 Delayed Acceptance

This section introduces DA (Christen and Fox 2005) as the algorithm that results when one Metropolis–Hastings kernel is used as a proposal within another. We note here the link with pseudo-marginal type algorithms that, as a special case, show how to use importance sampling or SMC within a Metropolis–Hastings algorithm. Let Metropolis–Hastings transition kernel K₁ have invariant distribution π₁ and suppose our aim is to use the distribution π₁ as the proposal distribution in another Metropolis–Hastings kernel K₂ with an invariant distribution π₂. It turns out that we can use a draw from K₁ as if it was a point drawn from π₁. That is, we apply K₁ to θ to obtain ${\theta }^{*}$, then accept ${\theta }^{*}$ with probability(8) $${\alpha }_2\left(\theta ,{\theta }^{*}\right)=\min \left\{1,\frac{{\pi }_2\left({\theta }^{*}\right){\pi }_1\left(\theta \right)}{{\pi }_2\left(\theta \right){\pi }_1\left({\theta }^{*}\right)}\right\}.$$(8)

A computational saving arises when a rejection occurs under K₁, since in this case ${\theta }^{*}=\theta$, giving ${\alpha }_2=1$ without needing to evaluate π₂. Verifying this acceptance probability is simple. Since ${\theta }^{*}$ is simulated from K₁, we have an acceptance probability for K₂ of(9) $${\alpha }_2\left(\theta ,{\theta }^{*}\right)=\min \left\{1,\frac{{\pi }_2\left({\theta }^{*}\right)K_1\left(\theta |{\theta }^{*}\right)}{{\pi }_2\left(\theta \right)K_1\left({\theta }^{*}|\theta \right)}\right\}.$$(9)

Now, K₁ satisfies the detailed balance equation with respect to π₁ (10) $${\pi }_1\left({\theta }^{*}\right)K_1\left(\theta |{\theta }^{*}\right)={\pi }_1\left(\theta \right)K_1\left({\theta }^{*}|\theta \right),$$(10) and substituting this into (9) we obtain the desired result of Equation (8)(8) $${\alpha }_2\left(\theta ,{\theta }^{*}\right)=\min \left\{1,\frac{{\pi }_2\left({\theta }^{*}\right){\pi }_1\left(\theta \right)}{{\pi }_2\left(\theta \right){\pi }_1\left({\theta }^{*}\right)}\right\}.$$(8) .

In the literature on DA, π₂ is chosen to be a desired target distribution that may be computationally expensive to evaluate, and π₁ is chosen to be a cheaper, approximate target distribution. Used in this way, the first stage of delayed acceptance (i.e., the result of applying K₁) provides a proposal that should be well suited for an MH algorithm with a target π₂, for example, Banterle, Grazian, and Robert (2014) used approximate likelihoods based on subsets of the data as the approximate targets. Strens (2004) used a very similar idea, that is, a hierarchical decomposition of the likelihood. Banterle, Grazian, and Robert (2014) noted that while a standard MH algorithm dominates DA in terms of the Peskun ordering, it is possible that a reduced computational cost in the first stage of DA can lead to more efficient algorithms in terms of the Monte Carlo error per computational time.

3.1.1 Delayed Acceptance With ABC-MCMC

This article makes use of DA in the ABC setting. Suppose that there exists a computationally cheap alternative l₁ to our “true” simulator $l_2=l$. We wish to perform the first stage of DA using points $x_1^{*}$ simulated from l₁, which are compared to data y₁ (which need not necessarily be the same as y) to determine the parameters at which we simulate points $x_2^{*}$ from l₂, from which we estimate the standard ABC likelihood. At the first stage of DA, we use an ABC-MCMC move with the simulator l₁, using a tolerance ϵ₁, giving an acceptance probability of(11) $${\alpha }_1=\min \left\{1,\frac{p\left({\theta }^{*}\right)P_{{ϵ}_1}\left(y_1|x_1^{*}\right)}{p\left(\theta \right)P_{{ϵ}_1}\left(y_1|x_1\right)}\frac{q\left(\theta |{\theta }^{*}\right)}{q\left({\theta }^{*}|\theta \right)}\right\}.$$(11)

The acceptance probability at the second stage is$${\alpha }_2=\min \left\{1,\frac{P_{{ϵ}_2}\left(y|x_1^{*},x_2^{*}\right)}{P_{{ϵ}_2}\left(y|x_1,x_2\right)}\frac{P_{{ϵ}_1}\left(y_1|x_1\right)}{P_{{ϵ}_1}\left(y_1|x_1^{*}\right)}\right\},$$where the marginal distribution of the target we have used is the ABC posterior with l₂, ϵ₂, and y. Note that we have included the conditioning on x₁ in $P_{{ϵ}_2}$ and l₂, which allows for the possibility that the “true” simulator is a composition of the simulators l₁ and l₂, with $x_1\sim l_1$ being a partial simulation. If the true simulator is simply l₂, we may drop this conditioning on x₁ from $P_{{ϵ}_2}$ and l₂.

3.2 Delayed Acceptance ABC-SMC

3.2.1 Use of DA-ABC-MCMC in ABC-SMC

We now examine the use of the DA-ABC-MCMC approach from the preceding section for the “move” step in the ABC-SMC algorithm of Del Moral, Doucet, and Jasra (2012a). The new SMC sampler operates on a sequence of target distributions where ϵ₂ decreases at each iteration, thus we use ${ϵ}_{2,t}$ to denote its value at the tth iteration. ϵ₁ and y₁ may also change between SMC iterations, and we denote their values at the tth iteration by ${ϵ}_{1,t}$ and $y_{1,t}$, respectively. In this case the weight update for each particle is given by(12) $${\tilde{w}}_{t+1}=w_t\frac{P_{{ϵ}_{2,,t+1}}\left(y|x_{1,t},x_{2,t}\right)}{P_{{ϵ}_{2,,t}}\left(y|x_{1,t},x_{2,t}\right)}.$$(12)

3.2.2 Adaptive DA Within ABC-SMC When Using the Indicator Kernel

In this section, we consider the implementation of the DA-ABC-MCMC move when $P_{{ϵ}_{1,t}}$ is chosen to be an indicator function; that is, $P_{{ϵ}_{1,t}}(y_{1,t}|x_{1,t}^{*})\propto \mathbb{I}(d(y_{1,t},x_{1,t}^{*})<={ϵ}_{1,t})$, where d is a distance metric. Following Section 3.1.1 we obtain, at the tth iteration of the SMC, an acceptance probabilities of(13) $${\alpha }_{1,t}=\{\begin{array}{cc}\min \left\{1,\frac{p\left({\theta }_t^{*}\right)}{p\left({\theta }_t\right)}\frac{q\left({\theta }_t|{\theta }_t^{*}\right)}{q\left({\theta }_t^{*}|{\theta }_t\right)}\right\}\hfill & \text{if}\mathrm{}d\left(y_{1,t},x_{1,t}^{*}\right),d\left(y_{1,t},x_{1,t}\right)\hfill \\ \hfill & \hspace{1em}<{ϵ}_{1,t}\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$(13)

and$${\alpha }_{2,t}=\{\begin{array}{cc}1\hfill & \text{if}\mathrm{}d\left(y,x_{2,t}^{*}\right)<{ϵ}_{2,t},\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}$$at the first and second stages of DA, respectively. The dependence in Equation (13)(13) $${\alpha }_{1,t}=\{\begin{array}{cc}\min \left\{1,\frac{p\left({\theta }_t^{*}\right)}{p\left({\theta }_t\right)}\frac{q\left({\theta }_t|{\theta }_t^{*}\right)}{q\left({\theta }_t^{*}|{\theta }_t\right)}\right\}\hfill & \text{if}\mathrm{}d\left(y_{1,t},x_{1,t}^{*}\right),d\left(y_{1,t},x_{1,t}\right)\hfill \\ \hfill & \hspace{1em}<{ϵ}_{1,t}\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$(13) on the condition $d(y_{1,t},x_{1,t})$ is maybe surprising, but is required since if it is not satisfied the denominator in the acceptance ratio is zero, and in this case the proposal should be rejected (Tierney 1998). The presence of this condition is due to the possibility that the sequence ${ϵ}_{1,t}$ is not always decreasing in t. Full details may be found in the supplementary appendix, along with details of how early rejection may be used in the first stage of DA.

Del Moral, Doucet, and Jasra (2012a) made use of a useful property of ABC to create an adaptive algorithm: once simulation of x has been performed for any θ, it is computationally cheap to estimate the ABC likelihood for any tolerance ϵ. Here we use this property, together with the fact that we have a population of particles available in the SMC algorithm, to automatically determine an appropriate value for ${ϵ}_{1,t}$ at every iteration. We choose ${ϵ}_{1,t}$ using the criterion that we desire to perform the second stage of the DA for a fixed proportion of the particles; we choose ${ϵ}_{1,t}$ such that A particles are accepted to move forward to the second stage, where $0<A\le N$ is chosen prior to running the SMC. This is achieved by choosing ${ϵ}_{1,t}$ such that A particles satisfy $d(y_{1,t},x_{1,t}),d(y_{1,t},x_{1,t}^{*})<{ϵ}_{1,t}$: a bisection method may be used to find such an ${ϵ}_{1,t}$. As with the bisection used in the adaptive approach of Del Moral, Doucet, and Jasra (2012a), in practice the bisection will not always give precisely A particles at the second stage of DA; if fewer than A particles pass early rejection due to the prior, ${ϵ}_{1,t}$ is chosen to let all these particles through to the second stage.

3.2.3 Discussion

This ABC-SMC algorithm, which we call DA-ABC-SMC, is described in full in Algorithm 2. In brief, we use this algorithm where we: adaptively choose the sequence $({ϵ}_{2,t})$ such that there are U unique particles after reweighting and resampling (Bernton et al. 2017); adaptively choose the variance of the (Gaussian) MCMC proposals to be the sample variance of the current particle set. The method requires us to specify: the number of particles N, the number of particles $0<A\le N$ that are allowed past the first stage of the DA and the number of unique particles $0<U\le N$. We now discuss how to choose each of these parameters.

• Number of unique particles: On terminating the algorithm, we effectively have a sample of size U from the final ABC posterior, thus U should be chosen to be the number of Monte Carlo points we wish to generate.

• Number of particles allowed past the first stage: A dictates the computational cost of each iteration, since it is the number of expensive simulations we will perform per SMC iteration.

• Total number of particles: To choose N we need to consider the factor F by which the cheap simulator is faster than the expensive simulator. For DA to be most effective, we require that the cost of running the cheap simulator is small compared to running the expensive simulator, that is, $N/F\ll A$.

If N is chosen to be much larger than A, we require a slightly nonstandard initial step in our SMC algorithm so that the computational expense of this step does not dominate the subsequent iterations. In a standard SMC sampler, the initial step would require initial values of x₁ and x₂ to be simulated for each of the N particles, which requires running the expensive simulator N times. Instead we simulate $(\theta ,x_1,x_2)A$ times from the initial distribution, and repeat these points N/A times (i.e., the vector of particles consists of stacked copies of these values) so that we have a sample of size N from the initial distribution. This sample contains only A unique points but, importantly, will result in N proposed points at every MCMC move in the SMC. The parameter N plays slightly different role to a standard SMC sampler, in which we might informally think of it as roughly the size of the Monte Carlo sample (in DA-ABC-SMC, U plays this role instead). In DA-ABC-SMC, N is one of four factors determining the “DA proposal” (i.e., the distribution of points that arrive at the second stage of DA), the remaining factors being: the choices of A and l₁, and the distribution of the particles from the previous iteration of the SMC. A useful DA proposal has similar characteristics to a good independent MCMC or importance sampling proposal: we wish it to be close to the target distribution, with wider tails. Since the DA proposal depends on the previous distribution of the particles, we observe empirically that it can to some extent automatically “track” the target distribution over SMC iterations, and provide a useful proposal distribution at each SMC iteration. The extent to which this is the case is investigated in Sections 4 and 5, where we illustrate the performance of our algorithm for different choices of the tuning parameters, which result in different sequences of DA proposals.

Algorithm 2 DA-ABC-SMC using early rejection.

Inputs: As algorithm 1, and the number of particles A to pass the first stage of DA.

Outputs: Particles ${\left\{({\theta }_t^{(i)},x_t^{(i)})\right\}}_{i=1}^N$ and weights ${\left\{w_t^{(i)}\right\}}_{i=1}^N$ for all t.

for $i=1:A$ do

$$w_0^{((i-1)N/A+1:iN/A)}=1/N,{\theta }_0^{((i-1)N/A+1:iN/A)}\sim p(·)$$$$x_{1,0}^{((i-1)N/A+1:iN/A)}\sim l_1\left(·|{\theta }_0^{(iN/A)}\right),x_{2,0}^{((i-1)N/A+1:iN/A)}\sim l_2\left(·|{\theta }_0^{(iN/A)},x_{1,0}^{((iN/A)}\right)$$

end for

${ϵ}_{1,0}={ϵ}_{1,\text{start}},{ϵ}_{2,0}={ϵ}_{2,\text{start}}$, t = 0.while ${ϵ}_{2,t}>{ϵ}_{2,\text{end}}$ do

Simulate $v\sim \mathcal{U}{\left[0,1\right]}^N$, to be used in resampling and use bisection to choose ${ϵ}_{2,t+1}$ s.t. there will be U unique particles after reweighting and resampling (using v).for $i=1:N$ do $${\tilde{w}}_{t+1}^{(i)}=w_t^{(i)}\mathbb{I}\left(d\left(y,x_{2,t}^{(i)}\right)<{ϵ}_{2,t+1}\right)$$ end for

Normalize ${\left\{{\tilde{w}}_{t+1}\right\}}_{i=1}^N$ to give normalized weights ${\left\{w_{t+1}\right\}}_{i=1}^N$, perform resampling using random numbers v, and let $I=\varnothing$.for $i=1:N$ do $${\theta }_{t+1}^{(i)}={\theta }_t^{(i)},x_{1,t+1}^{(i)}=x_{1,t}^{(i)},x_{2,t+1}^{(i)}=x_{2,t}^{(i)}$$$${\left({\theta }_{t+1}^{(i)}\right)}^{*}\sim q\left(·|{\theta }_t^{(i)}\right)$$$$u\sim \mathcal{U}\left(0,1\right)$$ if $u<\frac{p({({\theta }_{t+1}^{(i)})}^{*})q({\theta }_t^{(i)}|{({\theta }_{t+1}^{(i)})}^{*})}{p({\theta }_{t+1}^{(i)})q({({\theta }_{t+1}^{(i)})}^{*}|{\theta }_t^{(i)})}$ then $${\left(x_{1,t+1}^{(i)}\right)}^{*}\sim l_1\left(·|{\left({\theta }_{t+1}^{(i)}\right)}^{*}\right)$$ end if end for

Use bisection to choose ${ϵ}_{1,t+1}$ s.t. A particles satisfy $d(y_{1,t},x_{1,t}),d(y_{1,t},x_{1,t}^{*})<{ϵ}_{1,t}$.

Let I be the set of indices of the particles that pass the first stage of DA.for $i\in I$ do $${\left(x_{2,t+1}^{(i)}\right)}^{*}\sim l_1\left(·|{\left({\theta }_{2,t+1}^{(i)}\right)}^{*},{\left(x_{1,t+1}^{(i)}\right)}^{*}\right)$$ if $d(y,{(x_{2,t+1}^{(i)})}^{*})<{ϵ}_{2,t+1}$ then $${\theta }_{t+1}^{(i)}={\left({\theta }_{t+1}^{(i)}\right)}^{*},x_{1,t+1}^{(i)}={\left(x_{1,t+1}^{(i)}\right)}^{*},x_{2,t+1}^{(i)}={\left(x_{2,t+1}^{(i)}\right)}^{*}$$ end if end for $$t=t+1$$ end while

4 Application to SDEs

4.1 Lotka–Volterra Model

The Lotka–Volterra model is a stochastic Markov jump process that models the number of individuals in two populations of animals: predator and prey. It is a commonly used example in ABC since it is possible to simulate exactly from the model using the Gillespie algorithm (Gillespie 1977), but the likelihood is not available pointwise. We follow the model described in Wilkinson (2011), in which X represents the number of predators and Y the number of prey. The following reactions may take place: a prey may be born, with rate ${\theta }_{1}Y$, increasing Y by one; predator and prey may interact, with rate ${\theta }_{2}XY$, increasing X by one and decreasing Y by one; a predator may die, with rate ${\theta }_{3}X$, decreasing X by one. Papamakarios and Murray (2016) noted that for most parameters the size of one population quickly decreases to zero (in the case of the predators dying out, this results in the prey population growing exponentially). The relatively small region of parameter space that contains parameter values resulting in oscillating population sizes makes this a relatively challenging inference problem.

In this section, we use this example to demonstrate the use of DA-ABC-SMC for SDE models that need to be simulated numerically. To do this, we use the chemical Langevin equation approximation to the Markov jump process, as detailed in Golightly, Henderson, and Sherlock (2015). This results in two coupled nonlinear SDEs, which we simulate numerically using the Euler–Maruyama method.

4.2 Results

All of our empirical results were generated using R (R Core Team 2019), and the R packages ggplot2 (Wickham 2016), matlab (Roebuck 2014), and mvtnorm (Genz and Bretz 2009) were used. We study the data “LVPerfect” in the R package smfsb (Wilkinson 2018) (the numerical methods for simulating from the likelihood are also taken from this package). These data, which were generated using parameter values $({\theta }_1=1,{\theta }_2=0.05,{\theta }_3=0.6)$, have been previously studied in Wilkinson (2011), and we use the same priors and ABC approach as in this reference. We used DA-ABC-SMC with a variety of choices of U, A, and N, and two different choices of the Euler–Maruyama step size s in the cheap simulator s = 0.5 and s = 0.1, both of which result in very rough approximations of the dynamics. We compared these approaches with standard ABC-SMC, with N = 200 particles and a sequence of tolerances selected such that U = 100 unique particles are retained at each iteration, an SMC²-style approach (Duan and Fulop 2015) (that uses M particles when using a particle filter to estimate the likelihood) and also, as black horizontal lines, “ground truth” for the posterior expectation and standard deviation of the parameters found using a long run (10⁵ iterations) of ABC-MCMC. All algorithms we run 30 times, and measure computational cost, we counted the total number of steps S (taking the median $\overline{\mathbf{S}}$ over the 30 runs) simulated using Euler–Maruyama. The supplementary appendix contains the full details.

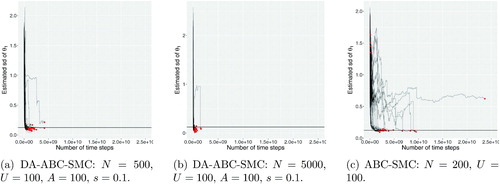
Figures 1 and 2 show, for every run of three methods, the evolution of the sample mean and standard deviation of the particles against the number of time steps of the numerical solver, with the final red dot indicating the estimate from the final distribution (where ${ϵ}_2=0.15$ was reached). The black line on each plots shows estimated ground truth values estimated using 20 runs of ABC-MCMC of length 5000 each. We only show the results for θ₁ here, since the results for the other parameters are comparable in terms of how they illustrate the properties of the algorithms. The method on the left is DA-ABC-SMC with N = 500 and $U=A=100$; in the middle is DA-ABC-SMC with N = 5000 and $U=A=100$; and on the right is ABC-SMC with N = 200 and U = 100. We observe that while ABC-SMC takes significantly more steps to converge to the target distribution, the estimates of the mean and standard deviation have a relatively low variance. The DA-ABC-SMC approaches converge much faster, but result in estimates that are usually further from the ground truth. In addition, both DA-ABC-SMC approaches appear to underestimate the posterior standard deviation, with this effect becoming more pronounced when N is larger. This result suggests that choosing N too large (resulting in A/N being small) can result in a DA proposal that is too concentrated compared to the target. To further elaborate on this important point, as the ratio A/N decreases, the first stage of the DA leads to a very poor proposal—this is because the particles that make it through to the second stage of the DA step are those that have simulations that result in the very smallest distance to the observed data. The effect is to make the DA proposal too concentrated around the mode of the posterior yielded by the fast approximation.

Fig. 1 The estimated posterior mean plotted against the total number of time steps used in Euler–Maruyama.

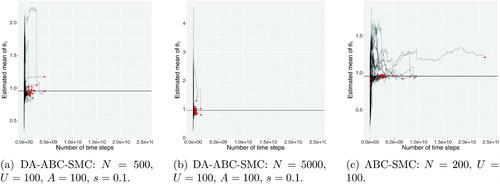
Fig. 2 The estimated posterior standard deviation plotted against the total number of time steps used in Euler–Maruyama.

Tables 1 and 2 summarize the properties of the estimates of the posterior mean and standard deviation from each method. The bias, standard deviation and root mean square error (RMSE) are reported, along with the $\text{RMSE}\times \sqrt{\overline{\mathbf{S}}}$, to help compare the errors of methods with different computational costs. The results for some configurations are heavily influenced by poor results from a single run, for example the case of DA-ABC-SMC with N = 1000, U = 100, A = 100, and s = 0.1. However, based on these tables and the plots of the estimated posterior mean and standard deviation in the supplementary appendix, there is evidence to make the following conclusions.

Table 1 Properties of estimators of the posterior mean of θ₁.

Method	Bias	SD	RMSE	$\text{RMSE}\times \sqrt{\overline{\mathbf{S}}}$
DA-ABC-SMC: N = 500, U = 100, A = 100, s = 0.1.	0.0033	0.0625	0.0626	2235
DA-ABC-SMC: N = 500, U = 100, A = 100, s = 0.5.	–0.0047	0.0439	0.0442	1449
DA-ABC-SMC: N = 1000, U = 100, A = 100, s = 0.1.	0.0659	0.2294	0.2387	6861
DA-ABC-SMC: N = 1000, U = 100, A = 100, s = 0.5.	–0.0003	0.0381	0.0381	1012
DA-ABC-SMC: N = 1000, U = 200, A = 100, s = 0.1.	0.0006	0.0559	0.0559	4320
DA-ABC-SMC: N = 1000, U = 50, A = 100, s = 0.1.	–0.0046	0.0754	0.0756	1232
DA-ABC-SMC: N = 5000, U = 100, A = 100, s = 0.1.	–0.0097	0.1094	0.1099	2401
DA-ABC-SMC: $N=10,000$, U = 100, A = 100, s = 0.1.	–0.0459	0.0703	0.0840	1960
SMC^2: N = 100, M = 100, $\alpha =0.9$, s = 0.1.	0.2929	1.2136	1.2485	35,065
SMC^2: N = 100, M = 100, $\alpha =0.99$, s = 0.1.	0.3261	1.0518	1.1012	55,438
SMC^2: N = 100, M = 1000, $\alpha =0.9$, s = 0.1.	0.9847	1.6379	1.9111	150,838
ABC-SMC: N = 200, U = 100.	–0.0092	0.0692	0.0698	3718
ABC-SMC${}^{\mathrm{a}}$: N = 200, U = 100.	0.0081	0.0583	0.0589	3136

${}^{\mathrm{a}}$The final line of the table refers to ABC-SMC where the runs that did not terminate are excluded from the calculation of the statistics.

Table 2 Properties of estimators of the posterior standard deviation of θ₁.

Method	Bias	SD	RMSE	$\text{RMSE}\times \sqrt{\overline{\mathbf{S}}}$
DA-ABC-SMC: N = 500, U = 100, A = 100, s = 0.1.	–0.0178	0.0299	0.0348	1242
DA-ABC-SMC: N = 500, U = 100, A = 100, s = 0.5.	–0.0403	0.0200	0.0450	1476
DA-ABC-SMC: N = 1000, U = 100, A = 100, s = 0.1.	0.0207	0.2368	0.2377	6833
DA-ABC-SMC: N = 1000, U = 100, A = 100, s = 0.5.	–0.0488	0.0194	0.0525	1393
DA-ABC-SMC: N = 1000, U = 200, A = 100, s = 0.1.	–0.0104	0.0275	0.0294	2273
DA-ABC-SMC: N = 1000, U = 50, A = 100, s = 0.1.	–0.0507	0.0277	0.0578	942
DA-ABC-SMC: N = 5000, U = 100, A = 100, s = 0.1.	–0.0568	0.0307	0.0645	1410
DA-ABC-SMC: $N=10,000$, U = 100, A = 100, s = 0.1.	–0.0621	0.0277	0.0680	1587
ABC-SMC: N = 200, U = 100.	0.2321	0.5136	0.5636	30,023
ABC-SMC${}^{\mathrm{a}}$: N = 200, U = 100.	0.0175	0.1105	0.1119	5961

${}^{\mathrm{a}}$The final line of the table refers to ABC-SMC where the runs that did not terminate are excluded from the calculation of the statistics.

• Choosing N too large (resulting in A/N being small) can result in a DA proposal that is too concentrated compared to the target, and leads to underestimating the posterior standard deviation.

• Even when N is not large, in this example often DA-ABC-SMC results in a sample that underestimates the standard deviation of the posterior distribution. The likely cause of this is that the DA proposal is too concentrated. This proposal easily generates unique points, thus the tolerance ϵ₂ is reduced too quickly, resulting in a poor quality sample. The results from DA-ABC-SMC when N = 1000, U = 200, A = 100, and s = 0.1, where 200 instead of 100 unique points are required when reducing the tolerance, suggests that when the SMC does not reduce the tolerance as fast (and hence more MCMC moves are made), the estimates of the posterior standard deviation are more accurate.

• DA-ABC-SMC can offer improved performance over ABC-SMC when measured by RMSE scaled by computational cost. This is largely due to its ability to quickly locate the region of highest posterior mass. However, it may not provide a representative sample from the posterior if the DA proposal is not tuned well. In contrast, compared to DA-ABC-SMC, standard ABC-SMC may be extremely slow in converging at all.

• The SMC² approaches tried here do not lead to an improvement over the ABC approaches, due to the low acceptance rate of the particle MCMC moves used in the move step of the SMC sampler (a consequence of the high variance likelihood estimates). In many cases no proposals were accepted at an SMC iteration, leading to a poor quality sample.

5 Applications to Doubly Intractable Distributions

5.1 Background

This section concerns the class of likelihoods that may not be evaluated pointwise due to the presence of an intractable normalizing constant, that is,$$l\left(y|\theta \right)=\frac{\gamma \left(y|\theta \right)}{Z\left(\theta \right)},$$where $\gamma (y|\theta )$ is tractable, but it is not computationally feasible to evaluate the normalizing constant $Z(\theta )$ (also known as the partition function). Such a distribution is known as doubly intractable (Murray, Ghahramani, and MacKay 2006) since it is not possible to directly use the Metropolis–Hastings algorithm to simulate from the posterior $\pi (\theta |y)$, due to the presence of $Z(·)$ in both the numerator and denominator of the acceptance ratio. The most common occurrence of these distributions occurs when l factorizes as a Markov random field. The most well-established approaches to inference for these models are the single and multiple auxiliary variable approaches (Møller et al. 2006; Murray, Ghahramani, and MacKay 2006) and the exchange algorithm (Murray, Ghahramani, and MacKay 2006), which, respectively, use importance sampling estimates of the likelihood and acceptance ratio to avoid the calculation of the normalizing constant. From here on we refer to these as “auxiliary variable methods.” ABC (Grelaud, Robert, and Marin 2009) and synthetic likelihood (Everitt, Johansen, et al. 2017) have also been used for inference in these models. See Stoehr (2017) for a recent, thorough review of the literature.

Previous work, for example, Friel (2013), suggests that auxiliary variable methods are more effective than ABC for simulating from the posterior $\pi (\theta |y)$ when l has an intractable normalizing constant. In the full data ABC case, Everitt, Prangle, et al. (2017) suggested that this is because the multiple auxiliary variable approach may be seen to be a carefully designed nonstandard ABC method. However, in this article we consider the situation in Everitt (2012), where our data y are indirect observations of a latent (hidden) field x^h, modeled with a joint distribution $p(\theta )l(x^h|\theta )g(y|x^h,\theta )$ with $l(x^h|\theta )$ having an intractable normalizing constant. In this case we might expect ABC to become more competitive, or even to outperform other approaches. The most obvious approach is to use data augmentation: using MCMC to simulate from the joint posterior $\pi (\theta ,x^h|y)$ by alternating simulation from the full conditionals of θ and x^h, with the exchange algorithm in the θ update. Everitt (2012) compared this approach with “exchange marginal particle MCMC,” in which an SMC algorithm is used to integrate out the x^h variables at every iteration of an MCMC and finds the particle MCMC approach to be preferable. However, to perform well, both of these approaches require efficient simulation from the conditional distribution $\pi (x^h|\theta ,y)$.

Now compare these “exact” approaches with ABC. In this case, for every θ we simulate $x^h\sim l(·|\theta )$ and $x\sim g(·|x^h,\theta )$, then use an ABC likelihood that compares $S(x)$ with $S(y)$. The x^h variables corresponding to a particular θ variable that are retained in the ABC sample are distributed according to an ABC approximation to $\pi (x^h|\theta ,S(y))$; indeed, that the ABC is at all efficient, there must be a reasonable probability that simulated x^h is in a region of high probability mass under this distribution. Compared to particle MCMC:

• Standard ABC has the disadvantage that the simulation of x^h is, in contrast to particle MCMC, not conditioned on y (although we note recent work in Prangle, Everitt, and Kypraios (2017) in which for some models we may also refine the ABC likelihood by conditioning on y).

• ABC has the advantage that a posteriori x^h is only conditioned on some statistic $S\left(y\right)$, rather than y as in particle MCMC. This condition is often considerably less stringent. For example, consider the Ising model example described below. When conditioning on y, the posterior $\pi \left(x^h|\theta ,y\right)$ is often restricted to relatively small regions of x^h-space: for individual pixel of x^h the posterior mass may be concentrated in a small region to match each individual data point. However, when conditioning on $S\left(y\right)$, the posterior $\pi (x^h|\theta ,S(y))$ may have nonnegligible mass in many regions of x^h-space: there are many different configurations of pixels that give rise to similar summary statistics.

In this article, we revisit using ABC on these models, examining the data previously studied in Everitt (2012), and show it is possible to make computational savings using DA-ABC-SMC. We now introduce the cheap simulator that makes this improvement possible. In Markov random field models, exact simulation from $l(·|\theta )$ is either very expensive or intractable. Grelaud, Robert, and Marin (2009) proposed to replace the exact simulator with taking the last point of a long MCMC run, and Everitt (2012) showed that, under certain ergodicity conditions, as the length of this “internal” MCMC goes to infinity, the bias in our ABC posterior sample due to this particular approximation also goes to zero (following ideas in Andrieu and Roberts (2009)). However, empirically one finds that often using only a single MCMC iteration is sufficient to yield a posterior close to the desired posterior. In this article, we propose to use an internal MCMC run of a single iteration as the cheap simulator, and to run the internal MCMC for many iterations (we use 1000) as the expensive simulator, where the final iteration of the cheap simulator is used as the first iteration of the expensive simulator. The next section presents an application to latent Ising models, with an application to ERGMs in the supplementary appendix.

5.2 Latent Ising Model

An Ising model is a pairwise Markov random field model on binary variables, each taking values in $\left\{-1,1\right\}$. Its distribution is given by$$l\left(x^h|{\theta }_x\right)\propto \hspace{0.17em}\text{exp}\hspace{0.17em}\left({\theta }_x\sum _{\left(i,j\right)\in \mathbf{N}}{x}_i^h{x}_j^h\right),$$where ${\theta }_x\in \mathbb{R},x_i^h$ denotes the ith random variable in x^h and N is a set defining pairs of nodes that are “neighbors.”We consider the case where the neighborhood structure is given by a regular two-dimensional grid. Our data y are noisy observations of this x^h field: the ith variable in y has distribution$$g\left(y_i|x_i^h,{\theta }_y\right)\propto \hspace{0.17em}\text{exp}\hspace{0.17em}\left({\theta }_y{y}_i{x}_i^h\right),$$ as in Everitt (2012) (with the normalizing constant being intractable). We used independent Gaussian priors on θ_x and θ_y, each with mean 0 and standard deviation 5. Our DA-ABC-SMC algorithm used $U=A=100$, and we examined different values of N. A single site Gibbs sampler was used to simulate from the likelihood, with the expensive simulator using the final point of 1000 sweeps of the Gibbs sampler. The MCMC proposal was taken to be a Gaussian distribution centered at the current particle, with covariance given by the sample covariance of the particles from the previous iteration. We used a single statistic in the ABC: the number of equivalently valued neighbors $S(y)=\sum _{(i,j)\in \mathbf{N}}{y}_i{y}_j$ (noting that this is not sufficient, but that the particle MCMC results in Everitt (2012) indicate that this does not have a large impact on the posterior). The distance metric used in ABC on the summary statistics was the absolute value of the difference.

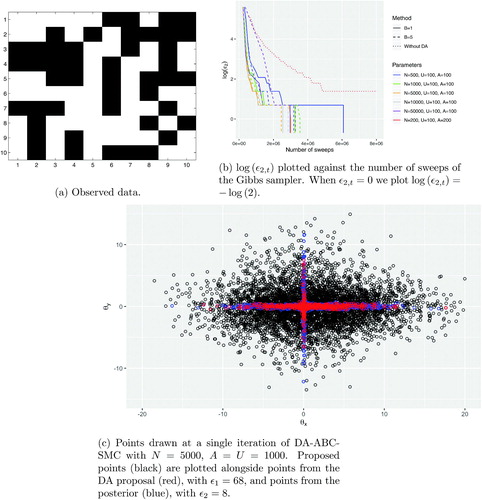
We used the same 10 × 10 grid of data as was studied in Everitt (2012), shown in Figure 3(a), which was generated from the model using ${\theta }_x={\theta }_y=0.1$. These parameter values represent a relatively weak interaction between neighboring pixels, and also quite noisy observations. On a grid of this size, there is ambiguity as to whether this data may have been generated with either one or both of θ_x and θ_y being small, giving a posterior distribution shaped like a cross, similar to that shown in Figure 3(c). Figure 3(c) gives an example of a DA proposal, that is, points that pass the first stage of the DA-MCMC, from the early stages of a run of DA-ABC-SMC. We observe how this distribution would be a suitable independent MCMC proposal for the posterior.

Fig. 3 DA-ABC-SMC applied to the latent Ising model.

All of our empirical results were generated using R (R Core Team 2019), and the R packages ggplot2 (Wickham 2016), matlab (Roebuck 2014), and mvtnorm (Genz and Bretz 2009) were used. We ran DA-ABC-SMC for several values of N, and compared the results with standard ABC-SMC using all of the same algorithmic choices, with N = 200 and U = 100. The standard ABC-SMC algorithm used the expensive simulator, that is, 1000 iterations of the internal Gibbs sampler. In algorithms we terminated the method when ${ϵ}_2=0$, or after 500 SMC iterations, whichever was sooner. We focus on studying the total computational effort expended in each algorithm, measured by the total number of sweeps S of the internal Gibbs sampler, and on the mean and standard deviation of the Euclidean distance ρ of the parameter vector $({\theta }_x,{\theta }_y)$ from the origin.

We ran the algorithm with several different values of N, and two different cheap simulators: the first where only a single sweep of the Gibbs sampler is used (B = 1); the second using the final point of 5 sweeps of the Gibbs sampler (B = 5). Each configuration was run 30 times. We chose N such that in most cases the computational cost was dominated by the expensive simulations in the second stage of the DA, although when $N=50,000$ and B = 5 the cost of the first stage dominated. Figure 3(b) shows gives an example showing the evolution of ϵ₂ against the total number of sweeps of the Gibbs sampler for several different configurations. We see that all configurations of the DA approach appear to have a significantly lower cost than standard ABC-SMC: in all cases the DA approach reaches ${ϵ}_2=0$ whereas the ABC-SMC reaches ${ϵ}_2=2$.

Table 3 shows properties of estimates of the mean and standard deviation posterior on ρ. The estimates from ABC-SMC are based on the output of the 500th iteration of the SMC, where in all runs ${ϵ}_2=2$. we observe that we obtain lower variance estimates from ABC-SMC than from DA-ABC-SMC, but at a higher cost. This cost may be significantly higher if we wish to reduce ϵ₂ to 0, as is achieved in all cases by DA-ABC-SMC. As in the previous section, we note that using a large value of N appears to lead to poor results; it appears likely that the standard deviation of the posterior is being underestimated.

Table 3 The mean and standard deviation of the estimated posterior mean (columns 2–4) and standard deviation (columns 5–7) of ρ, and the median number $\overline{\mathbf{S}}$ of sweeps of the Gibbs sampler $\overline{\mathbf{S}}$.

Method	Mean	SD	$\text{SD}\times \sqrt{\overline{\mathbf{S}}}$	Mean	SD	$\text{SD}\times \sqrt{\overline{\mathbf{S}}}$	$\overline{\mathbf{S}}$
DA N = 500, B = 1	3.3776	0.5517	11,579	2.5534	0.4121	8649	$4.41\times {10}^5$
DA N = 1000, B = 1	3.6168	1.2165	21,352	2.4516	0.7231	12,693	$3.08\times {10}^5$
DA N = 5000, B = 1	3.7702	1.6169	26,462	1.7376	0.9840	16,104	$2.68\times {10}^5$
DA $N=10,000$, B = 1	3.7532	2.0874	33,747	1.9016	0.8581	13,874	$2.61\times {10}^5$
DA $N=50,000$, B = 1	3.2808	2.4644	44,738	1.5644	1.0555	19,162	$3.30\times {10}^5$
DA N = 500, B = 5	3.8090	1.1143	22,445	2.7266	0.6132	12,353	$4.06\times {10}^5$
DA N = 1000, B = 5	3.4027	0.9633	16,572	2.3664	0.8668	14,911	$2.96\times {10}^5$
DA N = 5000, B = 5	3.5438	2.0486	35,046	1.8708	0.6549	11,205	$2.93\times {10}^5$
DA $N=10,000$, B = 5	3.6596	1.7692	31,444	1.7683	0.9247	16,435	$3.16\times {10}^5$
DA $N=50,000$, B = 5	3.8090	2.0645	43,305	1.4834	1.0414	21,845	$4.40\times {10}^5$
ABC-SMC N = 200	3.7580	0.3659	31,000	2.9472	0.2501	21,188	$7.18\times {10}^6$

NOTE: All rows refer to DA approaches, except the last, which is standard ABC-SMC.

6 Conclusions

In this article, we introduced DA-ABC-SMC as a means for reducing the computational cost of ABC-SMC in the case of an expensive simulator, through using a DA-ABC-MCMC move, in which a cheap simulator is used to “screen” the candidate values of proposed parameters so that less effort needs to be used running the expensive simulator. This cheap simulator may be completely independent of the expensive simulator, but preferably the expensive simulator may be conditioned on the output of the cheap simulator. The tolerance for the cheap simulator is chosen adaptively with DA-ABC-SMC, giving an algorithm that only has three relatively easy to choose tuning parameters. The key factor in the performance of the algorithm is the DA proposal, that is, the distribution of the particles that pass the first stage of DA. For this proposal to be useful, the cheap simulator needs to produce a posterior centered around the same values as the expensive simulator, and the total number of particles N in the DA-ABC-SMC needs to be chosen appropriately. The empirical results suggest that there is a trade-off in choosing the size of N: large values result in the largest computational saving, but can produce a DA proposal that is too concentrated which can result in a poor sample from the posterior. For smaller values of N the DA proposal is usually more suitable, and can result in computational savings compared to ABC-SMC.

Section 4 illustrates that DA-ABC-SMC shows promise for using ABC for inference in ODE or SDE models, where a numerical method is used to simulate from the model. Section 5 revisits the idea of using ABC for inference in latent Markov random field models, and suggests an approach that in some cases reduces the computational cost of ABC-SMC by using short runs of MCMC to simulate from the model. Future work might extend the approach to ABC methods that do not use an indicator kernel, use the adaptive tuning of the first stage of DA outside of the ABC context (along with an investigation of any bias this adaptation may introduce), or aim to improve the automation of the design of the DA proposal, which is often too concentrated.

Acknowledgments

Many thanks to Chris Drovandi for pointing out the method of Duan and Fulop (2015), and for discussions on using DA within SMC outside of the ABC setting.

Supplementary Materials

Appendix: Appendix containing full derivations of ABC-SMC and DA-ABC-SMC, additional results for the Lotka–Volterra model, and an application to ERGMs. (pdf)

Data and code: Data and R code implementing DA-ABC-SMC for the three applications. (zip)

Additional information

Funding

Richard Everitt’s work was supported by BBSRC grant BB/N00874X/1 and EPSRC grant EP/N023927/1, and Paulina Rowińska’s work was supported by EPSRC grant EP/L016613/1 (the Centre for Doctoral Training in the Mathematics of Planet Earth).