Flexible Variational Bayes Based on a Copula of a Mixture

Abstract

Variational Bayes methods approximate the posterior density by a family of tractable distributions whose parameters are estimated by optimization. Variational approximation is useful when exact inference is intractable or very costly. Our article develops a flexible variational approximation based on a copula of a mixture, which is implemented by combining boosting, natural gradient, and a variance reduction method. The efficacy of the approach is illustrated by using simulated and real datasets to approximate multimodal, skewed and heavy-tailed posterior distributions, including an application to Bayesian deep feedforward neural network regression models. Supplementary materials, including appendices and computer code for this article, are available online.

KEYWORDS:

• Multimodal
• Natural-gradient
• Non-Gaussian posterior
• Stochastic gradient
• Variance reduction

1 Introduction

Variational Bayes (VB) methods are increasingly used for Bayesian inference in a wide range of challenging statistical models (Ormerod and Wand 2010; Blei, Kucukelbir, and McAuliffe 2017). VB approximates the target posterior density as the solution of an optimization problem over a simpler and more tractable family of distributions; this family is usually selected to balance accuracy and computational cost. VB methods are particularly useful in estimating the posterior densities of the parameters of complex statistical models when exact inference is impossible or computationally expensive. They are usually computationally much cheaper than methods such as Markov chain Monte Carlo (MCMC) which produce exact draws from the posterior as the number of simulated draws goes to infinity. We call this property of MCMC estimators “simulation consistent,” and for the rest of the article, we refer to MCMC-type algorithms as “exact” methods.

Much of the current literature focuses on Gaussian variational approximation (GVA) for approximating the target posterior density (Challis and Barber 2013; Titsias and Lázaro-Gredilla 2014; Kucukelbir et al. 2017; Tan and Nott 2018; Ong, Nott, and Smith 2018). A major problem with Gaussian approximations is that many posterior distributions are skewed, multimodal, and heavy-tailed. This is true in particular for complex statistical models such as Bayesian deep feedforward neural network (DFNN) regression models (Izmailov et al. 2021; Jospin et al. 2022). Gaussian variational approximations for such models poorly approximate their posterior distributions; see Section 5.

There are a number of attempts to overcome the issue with Gaussian variational approximation including Smith, Loaiza-Maya, and Nott (2020) who propose Gaussian copula and skew Gaussian copula-based variational approximations; Guo et al. (2017) and Miller, Foti, and Adams (2017) who propose a mixture variational approximation; Rezende and Mohamed (2015) who propose normalizing planar and radial flows. Other types of normalizing flows for variational inference are also proposed in the literature and are reviewed by Papamakarios et al. (2021).

Our article makes a number of contributions. The first is to propose a flexible copula-based variational approximation by a mixture of Gaussians that builds on the Gaussian and skew-Gaussian copula approximations (Smith, Loaiza-Maya, and Nott 2020) and on the mixture of Gaussians variational approximations (Guo et al. 2017; Miller, Foti, and Adams 2017). We do not believe that such a variational mixture has been used before in the literature. The main idea of this part of our approach is to start by using a Gaussian or skew Gaussian copula-based approximation as the first component. This leads to a possible transformation of each parameter (marginal of the posterior) which may then make it easier to fit a joint distribution to the posterior of the transformed parameters. In our approach simpler Gaussian distributions are then used as the additional mixture components to make the optimization tractable while still improving the inference and prediction. Section 3 gives further details. The key insight is that of fitting a mixture after transforming each parameter, rather than using a simple multivariate family like the normal distribution. The proposed variational approximation allows fitting of multimodal, skewed, heavy tailed, and high-dimensional posterior distributions with complex dependence structures. We show in a number of examples that our approach gives more accurate inference and forecasts than the corresponding Gaussian copula and mixture of normals variational approximation. Although not proved in the article, it is not difficult to see that a version of an estimator based on a copula of a mixture will be a universal approximator of a multivariate distribution under reasonable assumptions because a mixture of normals is a universal approximator. It is interesting to note that a mixture of Gaussian copulas does not give a universal approximator of a multivariate distribution (Khaled and Kohn 2023).

Variational optimization of a copula-based mixture approximation is challenging in complex models with a large number of parameters because of the large number of variational parameters that need to be optimized. The boosting variational inference method in Guo et al. (2017), and Miller, Foti, and Adams (2017) is a promising recent approach to fit mixture type variational approximations. By adding a single mixture component at a time, the posterior approximation of the model parameters is refined iteratively. Miller, Foti, and Adams (2017) uses stochastic gradient ascent (SGA) optimization with the reparameterization trick to fit a mixture of Gaussian densities. They find that the use of the reparameterization trick in the boosting variational method still results in a large variance and it is necessary to use many samples to estimate the gradient of the variational lower bound. Guo et al. (2017), Locatello et al. (2018), and Campbell and Li (2019) consider similar variational boosting mixture approximations, although they use different approaches to optimize and specify the mixture components. Jerfel et al. (2021) consider boosting using the forward KL-divergence and combines variational inference and importance sampling.

Our second contribution is to build (see Section 4) on the variational boosting method by efficiently adding a single mixture component at a time using the natural gradient (Amari 1998) and the variance reduction method of Ranganath, Gerrish, and Blei (2014) to fit the flexible copula of the mixture. Previous literature on variational boosting optimization does not use the natural gradient. Many natural-gradient variational methods are available, for example, Hoffman et al. (2013), Khan and Lin (2017), and Lin, Khan, and Schmidt (2019). This literature shows that using natural gradients enables faster convergence than the traditional gradient-based methods because they exploit the information geometry of the variational approximation; Section 5.5 suggests that this is also true for our estimator.

Our third contribution (see Section 4.3) is to provide methods to initialize the variational parameters of the additional component in the mixtures.

The rest of the article is organized as follows. Section 2 gives the necessary background to the article; Section 3 discusses the copula of the mixture variational approximation; Section 4 discusses the variational optimization algorithm that fits the copula of a mixture variational approximation; Section 5 presents results from both simulated and real datasets; Section 6 concludes with a discussion of our approach and results. This article has an online supplement containing additional technical details and empirical results.

2 Variational Inference

Let $\theta \in \Theta$ be the vector of model parameters, and $y_{1:n}=(y_1,\dots ,y_n)$ the vector of observations. Bayesian inference about θ is based on the posterior distribution $$\pi \left(\theta \right)=p\left(\theta |y_{1:n}\right)=\frac{p\left(y_{1:n}|\theta \right)p\left(\theta \right)}{p\left(y_{1:n}\right)};$$

$p(\theta )$ is the prior, $p(y_{1:n}|\theta )$ is the likelihood function, and $p(y_{1:n})$ is the marginal likelihood. The posterior distribution $\pi (\theta )$ is unknown for most statistical models, making it challenging to carry out Bayesian inference. We consider variational inference methods, where a member $q_{\lambda }(\theta )$ of some family of tractable densities, indexed by the variational parameter $\lambda \in \Lambda$, is used to approximate the posterior $\pi (\theta )$. The optimal variational parameter λ is chosen by minimizing the Kullback-Leibler divergence between $q_{\lambda }(\theta )$ and $\pi (\theta )$, $$\begin{array}{c}\text{KL}\left(\lambda \right):=\int \hspace{0.17em}\log \hspace{0.17em}\left(\frac{q_{\lambda }\left(\theta \right)}{\pi \left(\theta \right)}\right)q_{\lambda }\left(\theta \right)d\theta .\\ =\int q_{\lambda }\left(\theta \right)\hspace{0.17em}\log \hspace{0.17em}\left(\frac{q_{\lambda }\left(\theta \right)}{p\left(y_{1:n}|\theta \right)p\left(\theta \right)}\right)d\theta +\hspace{0.17em}\log \hspace{0.17em}p\left(y_{1:n}\right)\\ =-\mathcal{L}\left(\lambda \right)+\hspace{0.17em}\log \hspace{0.17em}p\left(y_{1:n}\right),\end{array}$$where (1) $$\mathcal{L}\left(\lambda \right):=\int \hspace{0.17em}\log \hspace{0.17em}\left(\frac{p\left(y_{1:n}|\theta \right)p\left(\theta \right)}{q_{\lambda }\left(\theta \right)}\right)q_{\lambda }\left(\theta \right)d\theta ,$$(1) is a lower bound on the log of the marginal likelihood $\hspace{0.17em}\log \hspace{0.17em}p(y_{1:n})$. Therefore, minimizing the KL divergence between $q_{\lambda }(\theta )$ and $\pi (\theta )$ is equivalent to maximizing the Evidence Lower Bound (ELBO) given by (1). The ELBO can be used as a tool for model selection (Ong, Nott, and Smith 2018; Smith, Loaiza-Maya, and Nott 2020; Tran et al. 2020) although care is needed if the tightness of the lower bound varies significantly between the candidate models.

Although $\mathcal{L}(\lambda )$ is often an intractable integral with no closed form solution, we can write it as an expectation with respect to $q_{\lambda }(\theta )$, (2) $$\mathcal{L}\left(\lambda \right)=E_{q_{\lambda }}\left(\hspace{0.17em}\log \hspace{0.17em}g\left(\theta \right)-\hspace{0.17em}\log \hspace{0.17em}{q}_{\lambda }\left(\theta \right)\right),$$(2) where $g(\theta ):=p(y_{1:n}|\theta )p(\theta )$. This interpretation allows the use of stochastic gradient ascent (SGA) methods to maximize the variational lower bound $\mathcal{L}(\lambda )$. See, for example, Nott et al. (2012), Paisley, Blei, and Jordan (2012), Hoffman et al. (2013), Salimans and Knowles (2013), Kingma and Welling (2014), Titsias and Lázaro-Gredilla (2014), and Rezende, Mohamed, and Wierstra (2014). In SGA, an initial value ${\lambda }^{(0)}$ is updated according to the iterative scheme (3) $${\lambda }^{\left(t+1\right)}:={\lambda }^{\left(t\right)}+a_t°\widehat{{\nabla }_{\lambda }\mathcal{L}\left({\lambda }^{\left(t\right)}\right)},\text{for}t=0,1,2,\dots ;$$(3)

$°$ denotes the Hadamard (element by element) product of two random vectors; $a_t:={(a_{t1},\dots ,a_{tm})}^{\top }$ is a vector of step sizes, where m is the dimension of the variational parameters λ, and $\widehat{{\nabla }_{\lambda }\mathcal{L}({\lambda }^{(t)})}$ is an unbiased estimate of the gradient of the lower bound $\mathcal{L}(\lambda )$ at $\lambda ={\lambda }^{(t)}$. The learning rate sequence satisfies the Robbins-Monro conditions $\sum _t{a}_t=\infty$ and $\sum _t{a}_t^2<\infty$ (Robbins and Monro 1951), which ensures that the iterates ${\lambda }^{(t)}$ converge to a local optimum as $t\to \infty$ under suitable regularity conditions (Bottou 2010). Adaptive step sizes are often used in practice, and we employ the ADAM method of Kingma and Ba (2015), which uses bias-corrected estimates of the first and second moments of the stochastic gradients to compute adaptive learning rates. The update in (3) continues until a stopping criterion is satisfied.

To estimate the gradient, SGA methods often use the “log-derivative trick” (Kleijnen and Rubinstein 1996), $(E_{q_{\lambda }}({\nabla }_{\lambda }\hspace{0.17em}\log \hspace{0.17em}$ $q_{\lambda }(\theta ))=0)$, and it is straightforward to show that (4) $${\nabla }_{\lambda }\mathcal{L}\left(\lambda \right)=E_{q_{\lambda }}\left({\nabla }_{\lambda }\hspace{0.17em}\log \hspace{0.17em}{q}_{\lambda }\left(\theta \right)\left(\hspace{0.17em}\log \hspace{0.17em}g(\theta )-\hspace{0.17em}\log \hspace{0.17em}{q}_{\lambda }\left(\theta \right)\right)\right);$$(4)

$E_{q_{\lambda }}$ is the expectation with respect to $q_{\lambda }(\theta )$ in (4). Let $$g_{{\lambda }_i}:=\frac{1}{S}\sum _{s=1}^S\left(\hspace{0.17em}\log \hspace{0.17em}g({\theta }_s)-\hspace{0.17em}\log \hspace{0.17em}{q}_{\lambda }\left({\theta }_s\right)\right){\nabla }_{{\lambda }_i}\hspace{0.17em}\log \hspace{0.17em}{q}_{\lambda }\left({\theta }_s\right).$$

Then, ${(g_{{\lambda }_1},g_{{\lambda }_2},\dots ,g_{{\lambda }_m})}^{\top }$ is an unbiased estimate of ${\nabla }_{\lambda }\mathcal{L}(\lambda )$. However, this approach usually results in large fluctuations in the stochastic gradients (Ranganath, Gerrish, and Blei 2014). Section 4 discusses variance reduction and natural gradient methods, which are very important for fast convergence and stability.

3 Flexible Variational Approximation Based on a Copula of a Mixture

Smith, Loaiza-Maya, and Nott (2020) propose Gaussian and skew Gaussian copula based variational approximations, which are constructed using Gaussian or skew Gaussian distributions after element-wise transformations of the parameters. They consider the Yeo-Johnson (Yeo and Johnson 2000) and G&H families (Tukey 1977) for the element-wise transformations and use the sparse factor structure proposed by Ong, Nott, and Smith (2018) as the covariance matrix of the Gaussian distributions. This section discusses the flexible copula based mixture of Gaussians variational approximation that builds on Smith, Loaiza-Maya, and Nott (2020). The main idea is to use a flexible variational approximation, such as the Gaussian or skew Gaussian copulas of Smith, Loaiza-Maya, and Nott (2020) as the first component. This step also produces the transformed parameters we work with for the rest of the components. The rest of the components (second, third, etc.) are then chosen to be Gaussian distributions with a simple covariance structure making the optimization tractable, while still improving the inference and prediction.

Let $t_{\gamma }(\theta ):={(t_{{\gamma }_1}({\theta }_1),\dots ,t_{{\gamma }_m}({\theta }_m))}^{\top }$ be a family of one-to-one transformations with parameter vector γ. Each parameter θ_i is first transformed as ${\phi }_i:=t_{{\gamma }_i}({\theta }_i)$; the density of $\phi :={({\phi }_1,\dots ,{\phi }_m)}^{\top }$ is then modeled as a K component multivariate mixture of Gaussians. The variational approximation density for θ is then obtained by computing the Jacobian of the element-wise transformation from θ_i to ${\phi }_i$, for $i=1,\dots ,m$, so that (5) $$q_{\lambda }\left(\theta \right):=\sum _{k=1}^K{\pi }_{k}N\left(\phi |{\mu }_k,{\Sigma }_k\right)\prod _{i=1}^m{\dot{t}}_{{\gamma }_i}\left({\theta }_i\right);$$(5) the variational parameters are $$\begin{array}{cc}\lambda \hfill & =({\gamma }_1^{\top },\dots ,{\gamma }_m^{\top },\left({\mu }_1^{\top },\dots ,{\mu }_K^{\top }\right),\left({\pi }_1,\dots ,{\pi }_K\right),\hfill \\ \hfill & {\left(\text{vech}{({\Sigma }_1)}^{\top },\dots ,\text{vech}{({\Sigma }_K)}^{\top }\right))}^{\top };\hfill \end{array}$$¹

${\dot{t}}_{{\gamma }_i}({\theta }_i):=d{\phi }_i/d{\theta }_i$ and ${\sum }_{k=1}^K{\pi }_k=1$. The marginal densities of the approximation are (6) $$q_{{\lambda }_i}\left(\theta \right)=\sum _{k=1}^K{\pi }_{k}N\left({\phi }_i|{\mu }_{k,i},{\Sigma }_{k,i}\right)\prod _{i=1}^m{\dot{t}}_{{\gamma }_i}\left({\theta }_i\right),$$(6) for $i=1,\dots ,m$, with ${\lambda }_i=({\gamma }_i^{\top },{\left\{{\mu }_{k,i}^{\top },\text{vech}{({\Sigma }_{k,i})}^{\top }\right\}}_{k=1}^K$, ${\left\{{\pi }_k\right\}}_{k=1}^K{)}^{\top }$, a sub-vector of λ. As in Smith, Loaiza-Maya, and Nott (2020), the variational parameters λ are all identified in $q_{\lambda }(\theta )$ without additional constraints because they are also parameters of the margins given in (6). The variational approximation in (5) is called a copula of a mixture of Gaussians variational approximation (CMGVA). It can fit multimodal, skewed, heavy tailed, and high-dimensional posterior distributions with complex dependence structures; see Section 5.

When θ is high dimensional, we follow Ong, Nott, and Smith (2018) and adopt a factor structure for each Σ_k, $k=1,\dots ,K$. Let β_k be an $m\times r_k$ matrix, with $r_k\ll m$. For identifiability, we set the strict upper triangle of β_k to zero. Let $d_k={(d_{k,1},\dots ,d_{k,m})}^{\top }$ be a parameter vector with $d_{k,i}>0$, and denote by D_k the m × m diagonal matrix with entries d_k. We assume that $${\Sigma }_k:={\beta }_k{\beta }_k^{\top }+D_k^2,$$so that the number of parameters in Σ_k grows linearly with m if $r_k\ll m$ is kept fixed. Note that the number of factors r_k can be different for each component of the mixture for $k=1,\dots ,K$. We set the number of factors for the first component higher than for the other components in the mixture to make the variational approximation scalable. Section 5 discusses this further.

To draw S samples from the variational approximation given in (5), the indicator variables G_s, for $s=1,\dots ,S$, are first generated; each G_s selects the component of the mixture from which the sample is to be drawn, with $G_s=k$ with probability π_k. Then, $(z_{G_s,s},{\eta }_{G_s,s})\sim N(0,I)$ are generated, where $z_{G_s,s}$ is $r_{G_s}$-dimensional and ${\eta }_{G_s,s}$ is m-dimensional; ${\phi }_s={\mu }_{G_s}+{\beta }_{G_s}{z}_{G_s,s}+d_{G_s}°{\eta }_{G_s,s}$ are then calculated, where $°$ denotes the Hadamard product defined above. This representation shows that the latent variables z, which are low-dimensional, explain all the correlation between the transformed parameters ${\phi }_s$, and the parameter-specific idiosyncratic variance is captured by η. Finally, ${\theta }_{s,i}=t_{{\gamma }_i}^{-1}({\phi }_{s,i})$ is generated for $i=1,\dots ,m$ and $s=1,\dots ,S$. The Yeo-Johnson (YJ) transformation (Yeo and Johnson 2000) is used as $t_{{\gamma }_i}$ for all $i=1,\dots ,m$. If a parameter θ_i is constrained, it is first transformed to the real line; for example, a variance parameter is transformed to its logarithm. Smith, Loaiza-Maya, and Nott (2020) gives the inverses and derivatives of the Yeo-Johnson transformation. Both the Gaussian copula and the mixture of Gaussians variational approximations are special cases of the CMGVA. The mixture of Gaussians variational approximation is a special case of the CMGVA when the variational parameters γ_i, are set to 1 for $i=1,\dots ,m$. The Gaussian copula is a special case of the CMGVA when the number of components in the mixture is K = 1.

The variational approximation in (5) can be extended by including a skew Gaussian component as the first mixture component. It then becomes (7) $$q_{\lambda }\left(\theta \right):=\left({\pi }_{1}SN\left(\phi |{\mu }_1,{\Sigma }_1,{\tilde{\alpha }}_1\right)+\sum _{k=2}^K{\pi }_{k}N\left(\phi |{\mu }_k,{\Sigma }_k\right)\right)\prod _{i=1}^m{\dot{t}}_{{\gamma }_i}\left({\theta }_i\right),$$(7)

where $SN(\phi |{\mu }_1,{\Sigma }_1,{\tilde{\alpha }}_1)$ is a multivariate skew Gaussian distribution of Azzalini (1985) with density $$SN\left(\phi |{\mu }_1,{\Sigma }_1,{\tilde{\alpha }}_1\right)=2N\left(\phi |{\mu }_1,{\Sigma }_1\right){\Phi }_1\left({\tilde{\alpha }}_1^{⊺}{S}_1^{-1/2}\left(\phi -{\mu }_1\right)\right),$$

$S_1=\text{diag}({\sigma }_1^2,\dots ,{\sigma }_m^2)$, ${\sigma }_i^2$ is the ith diagonal element of ${\Sigma }_1$, and ${\tilde{\alpha }}_1={({\tilde{\alpha }}_{1,1},\dots ,{\tilde{\alpha }}_{1,m})}^{\top }$. The parameter ${\tilde{\alpha }}_{i,1}$ determines the level of skewness of the ith marginal of $\phi$. When ${\tilde{\alpha }}_{i,1}=0$ for $i=1,\dots ,m$, the distribution reduces to a multivariate Gaussian. The skew Gaussian copula is a special case of the variational approximation in (7) when the number of components in the mixture is K = 1.

4 Variational Methods

This section discusses the estimation method for the copula based mixture of Gaussians variational approximation in (5). We first describe how the first component of the mixture is fitted and then the process for adding an additional component to the existing mixture approximation. Extension to the variational approximation in (7) is straightforward.

4.1 Optimization Methods

The method starts by fitting an approximation to the posterior distribution $\pi (\theta )$ with a single mixture distribution, K = 1, using the variational optimization algorithm given in Smith, Loaiza-Maya, and Nott (2020); the optimal first component variational parameters are denoted as ${\lambda }_1^{*}:={({\mu }_1^{\top },{\beta }_1^{\top },d_1^{\top },{\pi }_1,{\gamma }^{\top })}^{\top }$, with the mixture weight π₁ set to 1. We do this by maximizing the first lower bound objective function $$\begin{array}{c}{\mathcal{L}}^{\left(1\right)}\left({\lambda }_1\right)=E_{q_{\lambda }}\left(\hspace{0.17em}\log \hspace{0.17em}g\left(\theta \right)-\hspace{0.17em}\log \hspace{0.17em}{q}_{{\lambda }_1}^{\left(1\right)}\left(\theta \right)\right),\\ {\lambda }_1^{*}=\underset{{\lambda }_1}{\text{argmax}}{\mathcal{L}}^{\left(1\right)}\left({\lambda }_1\right),\end{array}$$where $q_{{\lambda }_1}^{(1)}(\theta )=N(\phi ;{\mu }_1,{\beta }_1{\beta }_1^{\top }+D_1^2){\prod }_{i=1}^m{\dot{t}}_{{\gamma }_i}({\theta }_i)$. After the optimization algorithm converges, λ₁ is fixed as ${\lambda }_1^{*}$.

After iteration K, the current approximation to the posterior distribution $\pi (\theta )$ is a mixture distribution with K components $$q_{\lambda }^{\left(K\right)}\left(\theta \right)=\sum _{k=1}^K{\pi }_{k}N\left(\phi |{\mu }_k,{\beta }_k{\beta }_k^{\top }+D_k^2\right)\prod _{i=1}^m{\dot{t}}_{{\gamma }_i}\left({\theta }_i\right).$$

We can introduce a new mixture component with new component parameters, $({\mu }_{K+1},{\beta }_{K+1},d_{K+1})$, and a new mixing weight ${\pi }_{K+1}$. The weight ${\pi }_{K+1}\in \left[0,1\right]$ mixes between the new component and the existing approximation. The new approximating distribution is $$\begin{array}{c}{q}_{\lambda }^{\left(K+1\right)}\left(\theta \right):=(\mathrm{}\left(1-{\pi }_{K+1}\right)\mathrm{}\left(\sum _{k=1}^K{\pi }_{k}N\left(\phi |{\mu }_k,{\beta }_k{\beta }_k^{\top }+D_k^2\right)\mathrm{}\right)\mathrm{}\\ +{\pi }_{K+1}N\left(\phi |{\mu }_{K+1},{\beta }_{K+1}{\beta }_{K+1}^{\top }+D_{K+1}^2\right))\prod _{i=1}^m{\dot{t}}_{{\gamma }_i}\left({\theta }_i\right).\end{array}$$

The new lower bound objective function is $$\begin{array}{c}{\mathcal{L}}^{\left(K+1\right)}\left({\lambda }_{K+1}\right):=E_{q_{\lambda }}\left(\hspace{0.17em}\log \hspace{0.17em}g\left(\theta \right)-\hspace{0.17em}\log \hspace{0.17em}{q}_{\lambda }^{\left(K+1\right)}\left(\theta \right)\right),\\ {\lambda }_{K+1}^{*}:=\underset{{\lambda }_{K+1}}{\text{argmax}}{\mathcal{L}}^{\left(K+1\right)}\left({\lambda }_{K+1}\right).\end{array}$$

Note that with the copula transformation fixed, updating the mixture approximation parameters is the same as updating an ordinary mixture approximation in the transformed space of $\phi$. Since the existing variational approximation is also fixed, it is only necessary to optimize the new component parameters $({\mu }_{K+1},{\beta }_{K+1},d_{K+1})$, and the new mixing weight ${\pi }_{K+1}$, which reduces the dimension of the variational parameters to be optimized. Although the existing mixture components are fixed, their mixing weights can vary. It is possible to reoptimize the variational parameters γ_i for all $i=1,\dots ,m$ at each iteration of the algorithm. However, we obtained no substantial improvement with the increased computational cost. The γ_i, for all $i=1,\dots ,m,$ are kept fixed for iterations k > 1.

4.2 Updating the Variational Parameters

This section outlines the updating scheme for the variational parameters of the new component parameters $({\mu }_{K+1},{\beta }_{K+1},$ $D_{K+1})$ and the new mixing weight ${\pi }_{K+1}$ based on natural-gradient methods and control-variates for reducing the variance of the unbiased estimates of the gradient of the lower bound. Many natural-gradient methods for variational inference are available (Hoffman et al. 2013; Khan and Lin 2017); these show that natural-gradients produce faster convergence than traditional gradient-based methods.

The natural-gradient approach exploits the information geometry of the variational approximation $q_{\lambda }(\theta )$ to speed-up the convergence of the optimization. If the Fisher information matrix (FIM), denoted by $F_{\lambda }$, of the $q_{\lambda }(\theta )$ is positive-definite for all $\lambda \in \Lambda$, the natural-gradient update is (8) $${\lambda }^{\left(t+1\right)}={\lambda }^{\left(t\right)}+a_t°\left(F_{\lambda }^{-1}\widehat{{\nabla }_{\lambda }\mathcal{L}\left({\lambda }^{\left(t\right)}\right)}\right),\text{for}t=1,2,\dots$$(8)

Multiplying the estimated gradient of the lower bound by the inverse of the Fisher information matrix leads to a proper scaling of the gradient in each dimension and takes into account dependence between the variational parameters λ. In general, the natural-gradient update in (8) requires computing and inverting the FIM, which can be computationally expensive in high-dimensional problems. However, Khan and Nielsen (2018) shows that for exponential families (EF), the natural-gradient update can be much simpler than the traditional gradient-based methods. The standard EF variational approximation is $$q_{\lambda }\left(\theta \right)=h\left(\theta \right)\hspace{0.17em}\exp \hspace{0.17em}\left[〈\varphi \left(\theta \right),\lambda 〉-A\left(\lambda \right)\right],$$where $\varphi (\theta )$ is the sufficient statistic, $h(\theta )$ is the base measure, $A(\lambda )$ is the log-partition, and $〈·,·〉$ denotes an inner product. For such approximations, it is unnecessary to compute the Fisher information matrix (FIM) explicitly and the expectation parameter $m_{\theta }(\lambda )={\mathbb{E}}_q(\varphi (\theta ))$ can be used to compute natural-gradients, provided the FIM is invertible for all λ. The update for the natural-gradient method is now (9) $${\lambda }^{\left(t+1\right)}={\lambda }^{\left(t\right)}+a_t°\left(\widehat{{\nabla }_{m_{\theta }}\mathcal{L}\left({\lambda }^{\left(t\right)}\right)}\right),\text{for}t=1,2,\dots$$(9) where ${\nabla }_{m_{\theta }}$ denotes the gradient with respect to the expectation parameter $m_{\theta }$. The following is used to obtain (9): $${\nabla }_{\lambda }\mathcal{L}\left(\lambda \right)=\left[{\nabla }_{\lambda }{m}_{\theta }^{\top }\right]{\nabla }_{m_{\theta }}\mathcal{L}\left(\lambda \right)=\left[F_{\lambda }\right]{\nabla }_{m_{\theta }}\mathcal{L}\left(\lambda \right);$$ the first equality is obtained by using the chain rule and the second equality is obtained by noting ${\nabla }_{\lambda }{m}_{\theta }^{\top }={\nabla }_{\lambda }^{2}A(\lambda )=F_{\lambda }$; see Lin, Khan, and Schmidt (2019) for details.

Lin, Khan, and Schmidt (2019) derive natural gradient methods for a mixture of EF distributions in the conditional exponential family form (10) $$q_{\lambda }\left(\theta ,\underset{¯}{w}\right)=q_{\lambda }\left(\theta |\underset{¯}{w}\right)q_{\lambda }\left(\underset{¯}{w}\right),$$(10) with $q_{\lambda }(\theta |\underset{¯}{w})$ as the component and $q_{\lambda }(\underset{¯}{w})$ as the mixing distribution. A special case is the finite mixture of Gaussians, where the components in EF form are mixed using a multinomial distribution. They show that if the FIM, $F_{\lambda }(\theta ,\underset{¯}{w})$, of the joint distribution of θ and $\underset{¯}{w}$, is invertible, then it is possible to derive natural-gradient updates without explicitly computing the FIM. They use the update $${\lambda }^{\left(t+1\right)}:={\lambda }^{\left(t\right)}+a_t°\left(\widehat{{\nabla }_m\mathcal{L}\left({\lambda }^{\left(t\right)}\right)}\right),\text{for}t=1,2,\dots ,$$ with the expectation parameters $m:=(m_{\theta },m_{\underset{¯}{w}})$, where $m_{\theta }:=E_{q_{\lambda }(\theta |\underset{¯}{w})q_{\lambda }(\underset{¯}{w})}(\varphi (\theta ,\underset{¯}{w}))$, with $\varphi (\theta ,\underset{¯}{w}):=\{{\mathrm{I}}_k(\underset{¯}{w})\theta ,{\mathrm{I}}_k(\underset{¯}{w})$ $\theta {\theta }^{\top }{\}}_{k=1}^{K-1}$, and $m_{\underset{¯}{w}}:=E_{q_{\lambda }(\underset{¯}{w})}(\varphi (\underset{¯}{w}))$ with $\varphi (\underset{¯}{w})={\left\{{\mathrm{I}}_k(\underset{¯}{w})\right\}}_{k=1}^{K-1}$, and ${\mathrm{I}}_k(\underset{¯}{w})$ denotes the indicator function which is 1 if $\underset{¯}{w}=k$, and 0 otherwise. This results in simple natural-gradient updates for the mixture components and weights. Lin, Khan, and Schmidt (2019) apply their natural gradient methods for fitting a mixture of Gaussians variational approximation with a full covariance matrix for each component, which makes it less scalable for a large number of parameters. They also do not use the boosting approach for adding a mixture component one at a time. In this case, choosing good initial values for all variational parameters can be difficult.

As a factor structure is used for the covariance matrix, we adopt the natural-gradient updates of Lin, Khan, and Schmidt (2019) only for the new weight ${\pi }_{K+1}$ and the mixture means ${\mu }_{K+1}$. Denote ${\pi }_1^{\prime }:=(1-{\pi }_{K+1}){\sum }_{k=1}^K{\pi }_k$ and ${\pi }_2^{\prime }:={\pi }_{K+1},{\pi }_1^{\prime }+{\pi }_2^{\prime }=1$. The natural-gradient update for the new mixture weight, ${\pi }_{K+1}$ is (11) $$\begin{array}{c}\hspace{0.17em}\log \hspace{0.17em}{\left(\frac{{\pi }_1^{\prime }}{{\pi }_2^{\prime }}\right)}^{\left(t+1\right)}=\hspace{0.17em}\log \hspace{0.17em}{\left(\frac{{\pi }_1^{\prime }}{{\pi }_2^{\prime }}\right)}^{\left(t\right)}+a_t\left({\delta }_1-{\delta }_2\right)(\hspace{0.17em}\log \hspace{0.17em}\left(g\left(\theta \right)\right)\\ \mathrm{\hspace{1em}}\mathrm{\hspace{1em}}-\hspace{0.17em}\log \hspace{0.17em}{q}_{\lambda }^{\left(K+1\right)}\left(\theta \right)),\end{array}$$(11) where $q_{\lambda }^{(K+1)}(\theta )$ is given in (5) and the natural-gradient update for the new means ${\mu }_{K+1}$ is (12) $$\begin{array}{c}{\mu }_{K+1}^{\left(t+1\right)}={\mu }_{K+1}^{\left(t\right)}+a_t{\delta }_2\left({\beta }_{K+1}^{\left(t\right)}{\beta }_{K+1}^{{\left(t\right)}^{\top }}+D_{K+1}^{2\left(t\right)}\right)\\ \hspace{1em}\times \left({\nabla }_{\theta }\hspace{0.17em}\log \hspace{0.17em}\left(g\left(\theta \right)\right)-{\nabla }_{\theta }\hspace{0.17em}\log \hspace{0.17em}{q}_{\lambda }^{(K+1)}\left(\theta \right)\right);\end{array}$$(12) $$\begin{array}{c}{\delta }_1=\left(\sum _{k=1}^K{\pi }_{k}N\left(\phi |{\mu }_k,{\beta }_k{\beta }_k^{\top }+D_k^2\right)\right)/{\delta }_{\mathit{tot}},\\ {\delta }_2=\left(N\left(\phi |{\mu }_{K+1},{\beta }_{K+1}{\beta }_{K+1}^{\top }+D_{K+1}^2\right)\right)/{\delta }_{\mathit{tot}},\end{array}$$ where $$\begin{array}{c}{\delta }_{\mathit{tot}}=(\left(1-{\pi }_{K+1}\right)\left(\sum _{k=1}^K{\pi }_{k}N\left(\phi |{\mu }_k,{\beta }_k{\beta }_k^{\top }+D_k^2\right)\right)\\ \mathrm{\hspace{1em}}\mathrm{\hspace{1em}}+{\pi }_{K+1}N\left(\phi |{\mu }_{K+1},{\beta }_{K+1}{\beta }_{K+1}^{\top }+D_{K+1}^2\right)).\end{array}$$

Updating the variational parameters ${\beta }_{K+1}$ and $d_{K+1}$ is now discussed. There are two reasons why the reparameterization trick is not used to update the variational parameters ${\beta }_{K+1}$ and $d_{K+1}$. The first is that Miller, Foti, and Adams (2017) find that using the reparameterization trick in the boosting variational method still results in a large variance and it is necessary to use many samples to estimate the gradient of the variational lower bound. The second is that it may be impossible to use the reparameterization trick because of the copula transformation. An alternative method to update the variational parameters ${\beta }_{K+1}$ and $d_{K+1}$ is now discussed.

The gradients of the lower bound in (4) require the gradient ${\nabla }_{\lambda }\hspace{0.17em}\log \hspace{0.17em}{q}_{\lambda }(\theta )$. The gradient of $\hspace{0.17em}\log \hspace{0.17em}{q}_{\lambda }(\theta )$ with respect to ${\beta }_{K+1}$ is $$\begin{array}{c}{\nabla }_{\text{vech}\left({\beta }_{K+1}\right)}\hspace{0.17em}\log \hspace{0.17em}{q}_{\lambda }\left(\theta \right)=\frac{{\pi }_{K+1}N\left(\phi |{\mu }_{K+1},{\beta }_{K+1}{\beta }_{K+1}^{\top }+D_{K+1}^2\right)}{{\delta }_{\mathit{tot}}}\\ \text{vech}(-{\left({\beta }_{K+1}{\beta }_{K+1}^{\top }+D_{K+1}^2\right)}^{-1}{\beta }_{K+1}+\\ {\left({\beta }_{K+1}{\beta }_{K+1}^{\top }+D_{K+1}^2\right)}^{-1}\left(\phi -{\mu }_{K+1}\right){\left(\phi -{\mu }_{K+1}\right)}^{\top }\\ {\left({\beta }_{K+1}{\beta }_{K+1}^{\top }+D_{K+1}^2\right)}^{-1}{\beta }_{K+1}),\end{array}$$and the gradient of $\hspace{0.17em}\log \hspace{0.17em}{q}_{\lambda }(\theta )$ with respect to $d_{K+1}$ is $$\begin{array}{c}{\nabla }_{d_{K+1}}\hspace{0.17em}\log \hspace{0.17em}{q}_{\lambda }\left(\theta \right)=\frac{{\pi }_{K+1}N\left(\phi |{\mu }_{K+1},{\beta }_{K+1}{\beta }_{K+1}^{\top }+D_{K+1}^2\right)}{{\delta }_{\mathit{tot}}}\\ \text{diag}(-{\left({\beta }_{K+1}{\beta }_{K+1}^{\top }+D_{K+1}^2\right)}^{-1}{D}_{K+1}+\\ {\left({\beta }_{K+1}{\beta }_{K+1}^{\top }+D_{K+1}^2\right)}^{-1}\left(\phi -{\mu }_{K+1}\right){\left(\phi -{\mu }_{K+1}\right)}^{\top }\\ {\left({\beta }_{K+1}{\beta }_{K+1}^{\top }+D_{K+1}^2\right)}^{-1}{D}_{K+1}).\end{array}$$

We also employ control variates as in Ranganath, Gerrish, and Blei (2014) to reduce the variance of an unbiased estimate of gradient of the ${\nabla }_{\text{vech}({\beta }_{K+1})}\mathcal{L}(\lambda )$ and ${\nabla }_{d_{K+1}}\mathcal{L}(\lambda )$ and the efficient natural-gradient updates using the conjugate gradient methods given in Tran et al. (2020). To use a conjugate gradient linear solver to compute $F_{\lambda }^{-1}{\nabla }_{\lambda }\mathcal{L}(\lambda )$ it is only necessary to be able to quickly compute matrix vector products of the form $F_{\lambda }x$ for any vector x, without needing to store the elements of $F_{\lambda }$. When ${\beta }_{K+1}$ is a vector, the natural gradient can be computed efficiently as outlined in algorithm S1 in section S2 of the online supplement. Our updates for ${\beta }_{K+1}$ and $d_{K+1}$ are pre-conditioned gradient steps based on the natural gradient update for a Gaussian approximation in the added component, not the natural gradient in the mixture approximation.

Algorithm 1

Variational Algorithm

1. Initialize ${\lambda }_{K+1}^{(0)}=({\mu }_{K+1}^{\top (0)},\text{vech}{({\beta }_{K+1}^{(0)})}^{\top },d_{K+1}^{\top (0)},{\pi }_{K+1}^{(0)})$, set t = 0, and generate ${\theta }_s^{(t)}\sim q_{\lambda }^{(K+1)}(\theta )$ for $s=1,\dots ,S$. Let $m_{\beta }$, m_d, be the number of elements in $\text{vech}({\beta }_{K+1})$, and $d_{K+1}$.

   (b) Evaluate the control variates ${\varsigma }_{\text{vech}({\beta }_{K+1})}^{(t)}=({\varsigma }_{1,\text{vech}({\beta }_{K+1})}^{(t)}$ $,\dots ,{\varsigma }_{m_{\beta },\text{vech}({\beta }_{K+1})}^{(t)}{)}^{\top }$, ${\varsigma }_{d_{K+1}}^{(t)}={({\varsigma }_{1,d_{K+1}}^{(t)},\dots ,{\varsigma }_{m_d,d_{K+1}}^{(t)})}^{\top }$, with $$\text{}{\varsigma }_{i,d_{K+1}}^{\left(t\right)}$$

   $\text{}=\frac{\widehat{\text{cov}}(\left[\log \hspace{0.17em}(\pi (\theta ))-\hspace{0.17em}\log \hspace{0.17em}{q}_{\lambda }\mathrm{}(\theta )\right]{\nabla }_{{\lambda }_{i,d_{K+1}}}\hspace{0.17em}\log \hspace{0.17em}{q}_{\lambda }\mathrm{}(\theta ),{\nabla }_{{\lambda }_{i,d_{K+1}}}\mathrm{}\mathrm{}\hspace{0.17em}\log \hspace{0.17em}{q}_{\lambda }\mathrm{}(\theta ))}{\widehat{\mathbb{V}}({\nabla }_{{\lambda }_{i,d_{K+1}}}\hspace{0.17em}\log \hspace{0.17em}{q}_{\lambda }(\theta ))},$ (13)

   for $i=1,\dots ,m_d$, where $\widehat{\text{cov}}$ and $\widehat{\mathbb{V}}(·)$ are the sample estimates of covariance and variance based on S samples from step (1a). The ${\varsigma }_{\text{vech}({\beta }_{K+1})}^{(t)}$ are estimated similarly.

Repeat until the stopping rule is satisfied

• Update ${\beta }_{K+1},d_{K+1}$:

• Generate ${\theta }_s^{(t)}\sim q_{\lambda }^{(K+1)}(\theta )$ for $s=1,\dots ,S$.

• Compute $\widehat{{\nabla }_{\text{vech}({\beta }_{K+1})}\mathcal{L}({\lambda }^{(t)})}=(g_{1,\text{vech}({\beta }_{K+1})}^{(t)},\dots ,g_{m_{\beta },\text{vech}({\beta }_{K+1})}^{(t)})$, with

  $\begin{array}{c}{g}_{i,\text{vech}({\beta }_{K+1})}^{(t)}=\frac{1}{S}{\sum }_{s=1}^S[\log \hspace{0.17em}(g({\theta }_s^{(t)}))-\hspace{0.17em}\log \hspace{0.17em}{q}_{\lambda }({\theta }_s^{(t)})\\ -{\varsigma }_{i,\text{vech}({\beta }_{K+1})}^{(t-1)}]{\nabla }_{{\lambda }_{i,\text{vech}({\beta }_{K+1})}}\hspace{0.17em}\log \hspace{0.17em}{q}_{\lambda }({\theta }_s^{(t)})\end{array}$ (14)

• The gradient of the lower bound $\widehat{{\nabla }_{d_{K+1}}\mathcal{L}({\lambda }^{(t)})}=(g_{1,d_{K+1}}^{(t)},\dots ,g_{m_d,d_{K+1}}^{(t)})$ can be computed similarly as in (14).

• Compute the control variate ${\varsigma }_{\text{vech}({\beta }_{K+1})}^{(t)}$ and ${\varsigma }_{d_{K+1}}^{(t)}$ as in (13) and compute $g_{{\beta }_{K+1}}^{\text{nat}}$ and $g_{d_{K+1}}^{\text{nat}}$ using algorithm S1 in section S2 of the online supplement.

• Compute $△d_{K+1},△\text{vech}({\beta }_{K+1})$ using ADAM as described in section S1 of the online supplement. Then, set $d_{K+1}^{(t+1)}=d_{K+1}^{(t)}+△d_{K+1}$, $\text{vech}{({\beta }_{K+1})}^{(t+1)}=\text{vech}{({\beta }_{K+1})}^{(t)}+△\text{vech}$ $({\beta }_{K+1})$.

• Update ${\mu }_{K+1}$ and ${\pi }_{K+1}$

• Generate ${\theta }_s^{(t)}\sim q_{\lambda }^{(K+1)}(\theta )$ for $s=1,\dots ,S$.

• Use (11) to update ${\pi }_{K+1}$ and (12) to update ${\mu }_{K+1}$, respectively. Set $t=t+1$

However, we find this pre-conditioned gradient step improves efficiency compared to the ordinary gradient. Section 5.5 gives further details. Algorithm 1 presents the full variational algorithm.

4.3 Initializing a New Mixture Component

Introducing a new component requires setting the initial values for the new component parameters $({\mu }_{K+1},{\beta }_{K+1},D_{K+1})$ and the new mixing weight ${\pi }_{K+1}$. A good initial value for the new mixture component should be located in the region of the target posterior distribution $\pi (\theta )$ that is not well represented by the existing mixture approximation $q_{\lambda }^{(K)}(\theta )$. There are many ways to set the initial value. We now discuss some that work well in our examples. The elements in ${\beta }_{K+1}$ are initialized randomly by drawing from $N(0,{0.001}^2)$, the diagonal elements in $D_{K+1}$ are initialized by 0.001. These values ensure that the optimization algorithm is stable because generated values will be close to ${\mu }_{K+1}$ in the first few initial iterations. The mixture weight ${\pi }_{K+1}$ is initialized by 0.5. Algorithm 2 gives the initial value for ${\mu }_{K+1}={({\mu }_{1,K+1},\dots ,{\mu }_{m,K+1})}^{\top }$.

Algorithm 2

Initial values for ${\mu }_{K+1}$.

Input: ${\left\{{\pi }_k,{\mu }_k,{\beta }_k,d_k\right\}}_{k=1}^K$ and γ

Output: initial values for ${\mu }_{K+1}$

• For i = 1 to m

  • Construct a grid of S values of the ith transformed parameter ${\phi }_i$. One way to construct the grid of S values is to draw samples from the current approximation, and compute the minimum and maximum values $(\min ({\phi }_i),\max ({\phi }_i))$ for ${\phi }_i$. Let ${\phi }_s^{*}$ be a vector containing ${\phi }_{i,s}$ and other transformed parameters fixed at their means or some other reasonable values.

  • Compute ${\theta }_{j,s}^{*}=t_{\gamma }^{-1}({\phi }_{j,s}^{*})$ for $s=1,\dots ,S$ and $j=1,\dots ,m$.

  • Compute the $w_s^{*}=\frac{g({\theta }_s^{*})}{q_{\lambda }^{(K)}({\theta }_s^{*})}$ for $s=1,\dots ,S$.

  • Set ${\mu }_{i,K+1}={\phi }_{i,s}$ with a probability proportional to the weight $w_s^{*}$.

• Alternatively, when the dimension of the parameters is large,

  • Draw S samples from the current variational approximation $q_{\lambda }^{(K)}(\theta )$, and compute the weights $w_s^{*}=g({\theta }_s^{*})/q_{\lambda }^{(K)}({\theta }_s^{*})$ for $s=1,\dots ,S$. Then, set ${\mu }_{K+1}={\phi }_s^{*}$ with a probability proportional to the weight $w_s^{*}$.

5 Examples

To illustrate the performance of the proposed variational approximations described in Section 3, we employ them to approximate complex and high-dimensional distributions, where their greater flexibility may increase the accuracy of inference and prediction compared to simpler approximations.

The section has four examples. The first approximates a high dimensional, skewed, and heavy tailed distribution. The second example approximates a high dimensional multimodal distribution. The third example approximates the posterior distributions of the model parameters of a logistic regression model with a complex prior distribution. The fourth example fits a Bayesian deep neural network regression model. In all the examples, the following variational approximations are considered:

• (A1) A mixture of Gaussians variational approximation (MGVA). The Gaussian variational approximation is a special case with K = 1.

• (A2) The copula-based mixture of Gaussians variational approximation (CMGVA). The Gaussian copula variational approximation is a special case where K = 1.

• (A3) The mean-field mixture of Gaussians variational approximation (MGVA-MF). We use the terms mean-field variational approximation to refer to the case where the covariance matrix for each component in the mixture is diagonal.

• (A4) The mean-field copula-based mixture of Gaussians variational approximation (CMGVA-MF).

• (A5) The mixture of skew Gaussian variational approximation (MSGVA). This is a special case of the variational approximation described in (7) when the variational parameters ${\gamma }_i=1$ for all $i=1,\dots ,m$.

• (A6) The mixture of skew Gaussian copula-based variational approximation (CMSGVA) given in (7). For MSGVA and CMSGVA, only the first component is the skew Gaussian distribution. The other K – 1 components are Gaussian distributions.

All the examples are implemented in Matlab. The first three examples were run on a standard desktop computer. The fourth example was run on a 28 CPU-cores of a high performance computer cluster. Unless otherwise stated, we use the estimates of the variational lower bound to select the best variational approximations. In principle, making the variational family more flexible by adding new components should not reduce the variational lower bound; in practice, the difficulty of the optimization means that adding a new component may worsen the approximation. The variational approximation is useful when the exact MCMC method is impossible or computationally expensive. The boosting approach, where an existing approximation is improved by adding one new component at a time allows us to tune the accuracy/computational effort tradeoff, where we start with a rough fast approximation and keep improving until the computational budget is exhausted. All the variational parameters are initialized using the approach in Section 4.3.

5.1 Skewed and Heavy-Tailed High-Dimensional Distributions

This section investigates the ability of variational approximations (A1)–(A6) to approximate skewed, heavy-tailed, and high-dimensional target distributions. The true target distributions $\pi (\theta )$ are assumed to follow a multivariate t-copula, (15) $$\pi \left(\theta \right):=\pi \left(\zeta \right)\prod _{i=1}^m\left|\frac{d{\zeta }_i}{d{\theta }_i}\right|.$$(15)

The density $\pi (\zeta )$ is a multivariate t-distribution with zero mean, full-covariance matrix (ones on the diagonal and 0.8 on the off-diagonals), and degrees of freedom df = 4. The Yeo-Johnson (YJ) transformation with parameters set to 0.5 (Yeo and Johnson 2000) is used. The dimension of the parameters θ is set to m = 100. The number of factors r₁ is set to 4 for the first component and r_k = 1, for each additional mixture component for $k=2,\dots ,20$ for MGVA, CMGVA, MSGVA, and CMSGVA. We use S = 100 samples to estimate the lower bound and the gradients of the lower bound. The algorithm in Smith, Loaiza-Maya, and Nott (2020) is performed for 5000 iterations to obtain the optimal variational parameters for the first component of the mixture, and then Algorithm 1 is performed for 5000 iterations to obtain the optimal variational parameters for each additional component of the mixture for variational approximations (A1)–(A6).

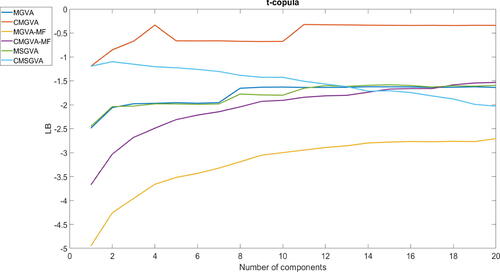
Figure 1 shows the average lower bound value over the last 500 steps of the optimization algorithm for variational approximations (A1)–(A6). The figure shows that the Gaussian and skew Gaussian copula-based estimators have similar lower bounds that are larger than the Gaussian, skew Gaussian, mean-field Gaussian copula-based approximations, and the mean-field Gaussian variational approximation. As expected, the mean-field Gaussian variational approximation has the lowest lower bound value because it does not capture the dependence structure of the θ posterior. The figure also shows that there is substantial improvement obtained by going from k = 2 to 8 components for most variational approximations, and there are no significant improvements thereafter. Interestingly, the lower bound values of the CMSGVA decrease when more components are added in the mixture. The Gaussian copula has greater lower bound than MGVA for any number of components for this example. The CMGVA with k = 4 components has a significantly higher lower bound compared to other variational approximations for this example.

Fig. 1 Plot of the average lower bound values over the last 500 steps for variational approximations (A1)–(A6) for the 100-dimensional multivariate t-copula example.

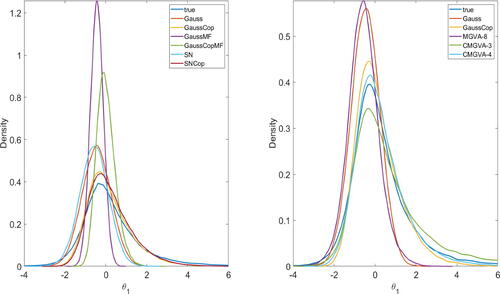
Figure 2 shows the kernel density estimates of the marginal densities of the parameter θ₁ estimated using the different variational approximations. The left panel of Figure 2 compares the performance of mean-field Gaussian, mean-field Gaussian copula, Gaussian, Gaussian copula, skew Gaussian, and skew Gaussian copula variational approximations. It shows that the mean-field Gaussian and mean-field Gaussian copula variational approximations significantly underestimate the posterior variances of the parameter θ₁. The Gaussian copula and skew Gaussian copula perform better than the Gaussian and skew Gaussian variational approximations. The right panel of Figure 2 shows that the CMGVA with k = 3 and k = 4 components captures both the skewness and the heavy tails of the marginal posteriors $\pi ({\theta }_1)$ better than the Gaussian copula and the mixture of the Gaussians variational approximations with k = 8 components.

Fig. 2 Left: Kernel density estimates of the marginal parameter θ₁ approximated by the mean-field Gaussian, Gaussian, skew Gaussian, Gaussian copula, mean-field Gaussian copula, skew Gaussian copula variational approximations. Right: Kernel density estimates of the marginal parameter θ₁ approximated by the Gaussian, Gaussian copula, 3-component CMGVA, 4-component CMGVA, and 8-component MGVA.

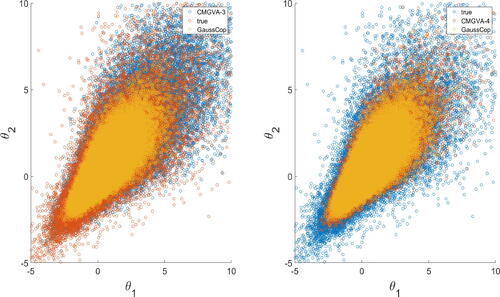
Figure 3 shows the scatterplot of the observations from the first and second margins generated from the true target densities, Gaussian copula variational approximation, the 3-component CMGVA, and the 4-component CMGVA. This suggests that the CMGVA is better at capturing the skewness and heavy-tailed properties of the true target densities compared to the Gaussian copula-based variational approximations.

Fig. 3 Left: Scatterplot of the observations from the first and second margins generated from true target density (red), Gaussian copula variational approximation (yellow), and 3-component CMGVA (blue). Right: Scatterplot of the observations from the first and second margins generated from true target density (blue), Gaussian copula variational approximation (yellow), and 4-component CMGVA (red).

We now compare the accuracy of the CMGVA to the densities estimated using the Hamiltonian Monte Carlo (HMC) method of Hoffman and Gelman (2014), called the No U-Turn Sampler (NUTS); this method is a popular MCMC algorithm for sampling high dimensional posterior distributions. For all examples, the NUTS tuning parameters, such as the number of leapfrog steps and the step size, are set to the default values as in the STAN reference manual ². We ran the HMC method for 1,005,000 iterations, discarding the initial 5000 iterations as warm-up. The remaining 1,000,000 MCMC samples are stored for further analysis. The inefficiency of the HMC method is measured using the integrated autocorrelation time (IACT) defined in section S3 of the online supplement.

Figure S2 in section S4 of the online supplement shows the IACT of the parameters θ estimated using the HMC method. The figure shows that the average IACT of the parameters is 391 with the average effective sample size of 2556.70. Figure S1 also shows that the Markov chain sometimes gets stuck, indicating that the HMC method performs quite inefficiently in this example. Figure 4 shows that the 3-component and 4-component CMGVA are more accurate than the HMC method for estimating the marginal density of the parameter θ₁. The same applies to other marginal densities. Again, this suggests that the CMGVA can capture the skewness and heavy-tailed properties of the true target densities.

Fig. 4 Kernel density estimates of the marginal parameter θ₁ estimated using the HMC method, 3-component CMGVA, and 4-component CMGVA for m = 100.

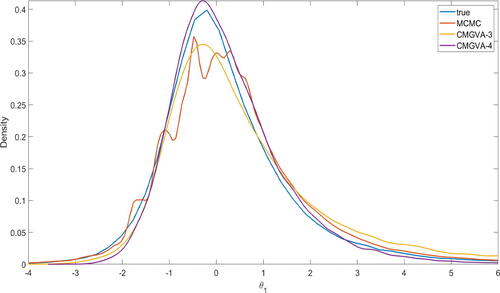
The CPU time for the HMC method is 167.5 min. The time taken for estimating the 3- and 4-component CMGVA are 36.15 min and 50.10 min.³ Therefore, the total CPU time for estimating the 3- and 4-component CMGVA are 4.63 and 3.34 times faster than the HMC method.

5.2 Multimodal High-Dimensional Distributions

This section investigates the ability of the proposed variational approximations (A1)–(A6) to approximate multimodal high-dimensional target distributions. The true target distribution is the multivariate mixture of normals, $\pi (\theta )={\sum }_{c=1}^3{w}_{c}N(\theta |u_c,{\Sigma }_c).$ The dimension of the parameters θ is set to 100. Each element $u_{i,c}$ is uniformly drawn from the interval $\left[-2,2\right]$ for $i=1,\dots ,100$ and $c=1,\dots ,3$. We set the full covariance matrix Σ_c with ones on the diagonal and the correlation coefficients $\rho =0.2$ and 0.8 in the off-diagonals for all components. The number of factors $r_1=4$ for the first component and r_k = 1, for each additional mixture component for $k=2,\dots ,20$ for variational approximations A1, A2, A5, and A6. Similarly to the previous example, we use S = 100 samples to estimate the lower bound values and the gradients of the lower bound. The algorithm in Smith, Loaiza-Maya, and Nott (2020) is performed for 5000 iterations to obtain the optimal variational parameters for the first component of the mixture and then Algorithm 1 is performed for 5000 iterations to obtain the optimal variational parameters for each additional component of the mixture. The step sizes are set to the values given in section S1 of the online supplement.

Figure S3 in section S5 of the online supplement shows the average lower bound values over the last 500 steps for the variational approximations (A1)–(A6) for the 100-dimensional mixture of normals example. The figure shows that the performances of the CMGVA, MGVA, MSGVA, and CMSGVA are comparable for the cases $\rho =0.2$ and $\rho =0.8$. Figure S4 in section S5 of the online supplement confirms that by showing that all the YJ-parameters are close to 1 for CMGVA and CMSGVA and all the $\tilde{\alpha }$ parameters in (7) are close to 0 for MSGVA and CMSGVA for the case $\rho =0.8$. Similar conclusions hold for the case $\rho =0.2$. The mixture of normals is a special case of CMGVA when all the YJ-parameters are equal to 1, are special cases of MSGVA when all the $\tilde{\alpha }$ parameters are close to 0, and are special cases of CMSGVA when all the YJ-parameters are close to 1 and all the $\tilde{\alpha }$ are close to 0. The MGVA, CMGVA, MSGVA, and CMSGVA are clearly much better than MGVA-MF and CMGVA-MF in this example.

The top panel of Figure 5 shows the kernel density estimates of some of the posterior densities of the marginal parameters of θ approximated with several of the variational approximations, together with the true marginal distributions and the marginal distributions estimated using the HMC method of Hoffman and Gelman (2014) for the case $\rho =0.8$. The HMC method ran for 1,005,000 iterations, with the initial 5000 iterations discarded as warm up. The remaining 1,000,000 iterations are used for further analysis. Figure S9 in section S5 of the online supplement shows the IACT of the parameters θ estimated using HMC. The figure shows that the average IACT of the parameters is 226.32 with the average effective sample size of 4418.52, indicating that the HMC method is also quite inefficient for this example.

Fig. 5 Kernel density estimates of some of the marginal parameters θ approximated with Gaussian, Gaussian Copula, skew Gaussian, skew Gaussian copula, and the optimal variational approximations (A1)–(A6) together with the true marginal distributions and the marginal distributions estimated using the HMC method for the mixture of normals example with $\rho =0.8$.

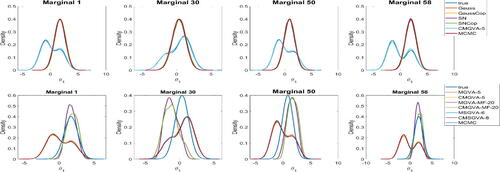
The bottom panel of Figure 5 shows the variational approximations (A1)–(A6), together with the true marginal distributions and the marginal distributions estimated using HMC for $\rho =0.8$. The top panel shows that the Gaussian, Gaussian copula, skew Gaussian, skew Gaussian copula, and HMC approaches are unable to approximate multimodal distributions. The bottom panel shows that the optimal MGVA, CMGVA, MSGVA, and CMSGVA perform much better than the optimal MGVA-MF and CMGVA-MF. Similar conclusions can be made from figure S5 in section S5 of the online supplement for the case $\rho =0.2$. The CPU time for the HMC method for this example is 83.75 min. The time taken to estimate the 5-component CMGVA is 37.25 min which is 2 and a quarter times faster than HMC.

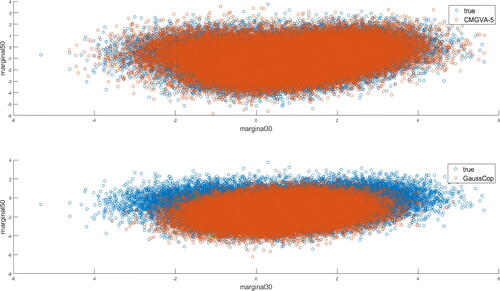
Finally, Figures 6 and S6 in section S5 of the online supplement show the scatterplots of the observations generated from the true density, the Gaussian copula variational approximation, and the optimal CMGVA for $\rho =0.8$ and 0.2, respectively. The figures confirm that the CMGVA can capture the bimodality and complex-shaped of the two dimensional distribution of the parameters.

Fig. 6 Top: Scatterplot of the observations generated from true target distribution (blue), and a 5-component CMGVA (orange) for the mixture of normals example with $\rho =0.8$; Bottom: Scatterplot of the observations generated from true target distribution (blue), and the Gaussian copula (orange) for the mixture of normals example with $\rho =0.8$.

We now show that the CMGVA does not overfit a Gaussian target distribution, which we take as a q-variate normal with zero mean and full covariance matrix with ones on the diagonal and correlation coefficients $\rho =0.8$ in the off-diagonals. Figure S7 in section S5 of the online supplement plots the average lower bound values over the last 500 steps for the CMGVA for this example and shows that no improvement is obtained by adding additional components in the mixture.

The two examples in Sections 5.1 and 5.2 suggest that: (a) The CMGVA can approximate heavy tails, multimodality, skewness and other complex properties of the high dimensional target distributions, outperforming the Gaussian copula and other variational approximations. Section 5.1 shows that the Gaussian copula outperforms MGVA, MGVA-MF, CMGVA-MF, MSGVA, and CMSGVA at approximating a skewed target distribution. The optimal variational approximations (A1)–(A6) are better than a Gaussian copula at approximating multimodal target distributions. (b) Adding a few components to the MGVA, CMGVA, MSGVA, and CMSGVA generally improves their ability to approximate complex target distributions. Therefore, the proposed approach can be considered as a refinement of the Gaussian copula and skew Gaussian copula variational approximations. (c) Adding additional components one at a time provides a practical method for constructing an increasingly complicated approximation and applies to a variety of multivariate target distributions. (d) The HMC method of Hoffman and Gelman (2014) fails to estimate the high dimensional, heavy tailed, and multimodal target distribution.

5.3 Bayesian Logistic Regression Models with Complex Prior Distributions

This section considers a logistic regression model $$p\left(y_i|x_i,b\right)=\frac{\hspace{0.17em}\exp \hspace{0.17em}\left(y_i{x}_i^{\top }b\right)}{1+\hspace{0.17em}\exp \hspace{0.17em}(x_i^{\top }b)},$$with the response $y_i\in \left\{0,1\right\}$, and with a complex prior distribution for the regression parameters $b={(b_0,b_1,\dots ,b_p)}^{\top }$. The prior for each regression parameter, except the intercept, is the two-component mixture of skew normals (16) $$\begin{array}{c}p\left(b_i|w,{\sigma }_1^2,{\sigma }_2^2,\alpha \right)=\mathit{wSN}\left(b_i;0,{\sigma }_1^2,\alpha \right)\\ \mathrm{\hspace{1em}}\mathrm{\hspace{1em}}+\left(1-w\right)SN\left(b_i;0,{\sigma }_2^2,\alpha \right),i=1,\dots ,p;\end{array}$$(16)

$SN(b_i;0,{\sigma }^2,\alpha )$ is the skew-normal distribution of Azzalini (1985) with density $\frac{2}{\sigma }\varphi \left(\frac{b_i}{\sigma }\right)\Phi \left(\alpha \frac{b_i}{\sigma }\right)$. We set w = 0.5, ${\sigma }_1^2=0.01,{\sigma }_2^2=100$, and $\alpha =-4$. This prior is motivated by a variable selection scenario, where some coefficients may be 0 and we would like to set these close to zero. The prior for the intercept term b₀ is N(0, 1)

We consider the spam, krkp, ionosphere, and mushroom data for the logistic regression model; they have sample sizes n = 4601, 351, 3196, and 8124, with 104, 111, 37, and 95 covariates, respectively and are also considered by Ong, Nott, and Smith (2018) and Smith, Loaiza-Maya, and Nott (2020); the data are available from the UCI Machine Learning Repository (Lichman 2013)⁴. In the results reported below, we include all covariates but only use the first 50 observations of each dataset. The small dataset size and the complex prior distribution for each regression parameter are chosen to create a complex posterior structure to evaluate the performance of variational approximations (A1)-(A6) when the posteriors are non-Gaussian.

Similarly to the previous example, we set the number of factors r₁ to 4 for the first component and r_k = 1, for each additional mixture component for $k=2,\dots ,20$ for variational approximations A1, A2, A5, and A6. We use S = 100 samples to estimate the lower bound values and the gradients of the lower bound. The algorithm in Smith, Loaiza-Maya, and Nott (2020) is performed for 5000 iterations to obtain the optimal variational parameters for the first component of the mixture and then Algorithm 1 is performed for 5000 iterations to obtain the optimal variational parameters for each additional component of the mixture.

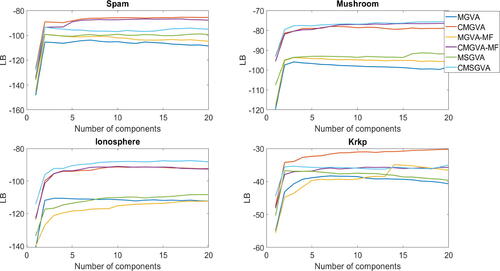
Figure 7 shows the average lower bound values over the last 500 steps of the optimization algorithm for the variational approximations (A1)–(A6) for the Bayesian logistic regression model for the four datasets. The Gaussian and skew Gaussian copula variational approximations outperform the Gaussian and skew Gaussian variational approximations. Interestingly, the mean-field Gaussian copula variational approximation is better than the skew Gaussian and the Gaussian variational approximation for the spam, mushroom, and ionosphere datasets. The figure also shows that adding a few components in the mixture for variational approximations (A1)–(A6) improves the lower bound values for all datasets. The optimal CMGVA performs the best for the spam and krkp datasets. The CMSGVA performs slightly better than CMGVA for the mushroom and ionosphere datasets.

Fig. 7 Plots of the average lower bound values over the last 500 steps for the variational approximations (A1)–(A6) for the Bayesian logistic regression model for the four datasets.

5.4 Flexible Bayesian Regression with a Deep Neural Network

Deep feedforward neural network (DFNN) models with binary and continuous response variables are widely used for classification and regression in the machine learning literature. The DFNN method can be viewed as a way to efficiently transform a vector of p raw covariates $X={(X_1,\dots ,X_p)}^{\top }$ into a new vector Z having the form (17) $$Z:=f_L\left(W_{L,}{f}_{L-1}\left(W_{L-1},\dots ,f_1\left(W_1,X\right)\right)\right).$$(17)

Each $Z_l=f_l(W_l,Z_{l-1}),l=1,\dots ,L$, is called a hidden layer, L is the number of hidden layers in the network, $W=(W_1,\dots ,W_L)$ is the set of weights and $Z_0=X$ by construction. The function $f_l(W_l,Z_{l-1})$ is assumed to be of the form $h_l(W_l{Z}_{l-1})$, where W_l is a matrix of weights that connect layer l – 1 to layer l, which includes weight coefficients attached to the input $Z_{l-1}$ and the constant terms, and $h_l(·)$ is a scalar activation function. Estimation in complex high dimensional models like DFNN regression models is challenging. This section studies the accuracy of posterior densities and the predictive performance of the variational approximations (A1)-(A6) for a DFNN regression model with continuous responses; see Goodfellow, Bengio, and Courville (2016, chap. 6, 9, and 10) for a comprehensive recent discussion of DFNNs and other types of neural networks.

Consider a dataset D with n observations, with y_i the scalar response and $x_i={(x_{i1},\dots ,x_{ip})}^{\top }$ the vector of p covariates. We consider a neural network structure with the input vector x and a scalar output. Denote $z_l:=f_l(x,w),l=1,\dots ,M$, the units in the last hidden layer, w is the vector of weights up to the last hidden layer, and $b={(b_0,b_1,\dots ,b_M)}^{\top }$ are the weights that connect the variable z_l, $l=1,\dots ,M$, to the output y. The model, with a continuous response y, can be written as (18) $${\tau }^2\sim \text{Gamma}\left(1,10\right),$$(18) (19) $$\begin{array}{c}{w}_i\sim 0.5SN\left(0,{\sigma }_1^2,\alpha \right)+0.5SN\left(0,{\sigma }_2^2,\alpha \right),\\ \text{for}i=1,\dots ,M_w,\end{array}$$(19) (20) $$\begin{array}{c}{b}_l\sim 0.5SN\left(0,{\sigma }_1^2,\alpha \right)+0.5SN\left(0,{\sigma }_2^2,\alpha \right),\\ \text{for}l=1,\dots ,M,\end{array}$$(20) (21) $$y|x,w,b,\tau \sim N\left(b_0+{\tilde{b}}^{\top }z,1/{\tau }^2\right),$$(21) where $z={(z_1,\dots ,z_M)}^{\top }$, $\tilde{b}={(b_1,\dots ,b_M)}^{\top }$, M_w is the number of weight parameters; $SN(B;0,{\sigma }^2,\alpha )$ is a skew-normal density of Azzalini (1985) defined in Section 5.3, and $\text{Gamma}(1,10)$ is the gamma distribution with shape parameter 1 and scale parameter 10. We set ${\sigma }_1^2=0.01,{\sigma }_2^2=100$, and $\alpha =-4$. Miller, Foti, and Adams (2017) uses similar priors for ${\tau }^2$. The priors for b_l for $l=1,\dots ,M$ and w_i for $i=1,\dots ,M_w$ will shrink some of the coefficients that may be 0 or very close to zero.

All the examples use the rectified linear unit (ReLU) $h(x):=\max (0,x)$ as an activation function, unless otherwise stated; ReLU is widely applied in the deep learning literature (Goodfellow, Bengio, and Courville 2016) because it is easy to use within optimization as it is quite similar to a linear function, except that it outputs zero for negative values of x.

We consider the auto and abalone datasets. The auto dataset, available from James et al. (2021), consists of 392 observations for different makes of cars, with the response being gas mileage in miles per gallon, with 7 additional covariates used here to predict the mileage. The abalone dataset, available on the UCI Machine Learning Repository, has 4177 observations. The response variable is the number of rings used to determine the age of the abalone. There are 9 covariates including sex, length, diameter, as well as other measurements of the abalone. We use 90% of the data for training and the rest for computing the log of the approximate predictive score in (24). Both datasets have continuous responses

Neural nets with (8,5,5,1), (8,10,10,1), and (8,20,20,1) structures are used for the auto dataset. For the (8,5,5,1) structure, the input layer has 8 variables, there are two hidden layers each having 5 units and there is a scalar output. The first layer has $8\times 5=40$ w parameters, the second layer has 6 × 5 = 30 w parameters (including the intercept term), and 6 b parameters (including the intercept term); this gives a total of 76 parameters. Similar calculations can be made for the (8,10,10,1) and (8,20,20,1) structures to give a total of 201 and 601 parameters, respectively. Neural nets with (9,5,5,1), (9,10,10,1), and (9,20,20,1) structures are used for the abalone dataset. Similar calculations can be done for them to give a total of 75, 211, and 621 parameters, respectively.

This section studies the accuracy of the inference and the predictive performance for variational approximations A1 and A2. For this example, variational approximations A5 and A6 are not implemented due to the numerical issues in estimating the skew normal and skew normal copula variational approximations. Sections 5.1–5.3 show that CMGVA is better than MSGVA and CMSGVA. We do not compare the posterior density of the parameters obtained from the variational approximations A1 and A2 to HMC, as it is difficult to obtain the exact posterior distribution for the parameters of the Bayesian neural network. Papamarkou et al. (2021) shows that the Markov chains generated by the Metropolis-Hastings and Hamiltonian Monte Carlo methods fail to converge for estimating the parameters of the Bayesian neural network model. To show the lack of convergence of the HMC method, we ran it for 1,005,000 iterations discarding the initial 5000 iterations as warm up for estimating neural nets with a (9,10,10,1) structure for the auto dataset. Figure S14 in section S8 of the online supplement shows the IACT of the parameters θ estimated using the HMC method. The figure shows that the average IACT of the parameters is 1904.08 with an average effective sample size of 525.19, indicating that HMC is very inefficient for this example. In addition, figure S13 in section S8 of the online supplement shows the trace plots of the parameters of the neural net with the (9,10,10,1) structure for the auto dataset. The figure shows that the parameters mix poorly. Computing time for a 10-component CMGVA is an order of magnitude less than for the HMC.

To evaluate the predictive accuracy of a DFNN regression model estimated by the variational approximations A1 and A2, we consider the posterior predictive density defined as (22) $$p\left(y|x,D\right)=\int p\left(y|x,\theta \right)p\left(\theta |D\right)d\theta .$$(22)

Given that we have the variational approximation of the posterior distribution, we can define the approximate predictive density (23) $$g\left(y|x,D\right)=\int p\left(y|x,\theta \right)q_{\lambda }\left(\theta \right)d\theta .$$(23)

Computing the approximate posterior predictive density in (23) is challenging because it involves high dimensional integrals that cannot be solved analytically. However, it can be estimated using Monte Carlo integration. The estimate of the log of the approximate posterior predictive score is (24) $$\hspace{0.17em}\log \hspace{0.17em} \widehat{g}\left(y|x,D\right)=\hspace{0.17em}\log \hspace{0.17em}\left(\frac{1}{R}\sum _{r=1}^{R}p\left(y|x,{\theta }^r\right)\right),{\theta }^r\sim q_{\lambda }\left(\theta \right).$$(24)

The higher the log of the approximate posterior predictive score, the more accurate the prediction.

In this example, the number of factors is set to 1 for all 20 components in the mixture; S = 200 samples are used to estimate the gradients of the lower bound; $R=10,000$ samples are used to estimate the log of the approximate posterior predictive score in (24); section S7 of the online supplement discusses the stopping criterion for the optimization algorithm.

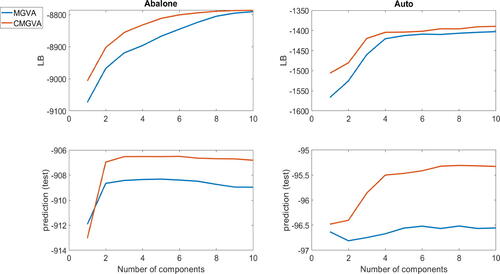
The top panels of figure S15 in section S8 of the online supplement show the average lower bound values over the last 100 steps of the optimization algorithm for the (8,5,5,1) neural net structure for the auto dataset and the (9,5,5,1) structure for the abalone dataset. The figure shows that adding components to the variational approximations A1 and A2 increases the lower bound significantly for both datasets. Clearly, CMGVA performs best for both datasets. The lower panels of figure S15 show the log of the estimated approximate posterior predictive scores evaluated for the test data. The figure also shows that adding more components to the variational approximations can improve the prediction accuracy significantly. Similar conclusions can be drawn from Figure 8 for the (8,10,10,1) neural net structure for the auto dataset and the (9,10,10,1) neural net structure for the abalone dataset and Figure 9 for the (8,20,20,1) neural net structure for the auto dataset and the (9,20,20,1) neural net structure for the abalone dataset. This suggests the usefulness of the proposed variational approximations for complex and high-dimensional Bayesian deep neural network regression models.

Fig. 8 Top panels: The plots of the average lower bound values over the last 100 steps for the variational approximations A1 and A2 for the (8,10,10,1) neural net structure for the auto dataset and the (9,10,10,1) neural net structure for the abalone dataset. Bottom panels: The plots of the log of the estimated approximate posterior predictive scores for the variational approximations A1 and A2 for the (8,10,10,1) neural net structure for the auto dataset and the (9,10,10,1) neural net structure for the abalone dataset.

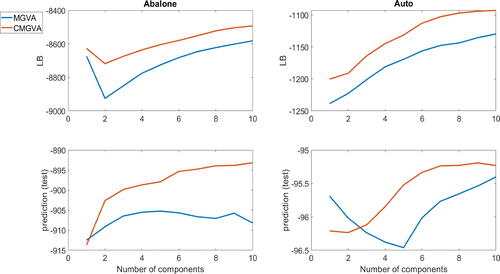
Fig. 9 Top panels: The plots of the average lower bound values over the last 100 steps for the variational approximations A1 and A2 for the (8,20,20,1) neural net structure for the auto dataset and the (9,20,20,1) neural net structure for the abalone dataset. Bottom panels: The plots of the log of the estimated approximate posterior predictive scores for the variational approximations A1 and A2 for the (8,20,20,1) neural net structure for the auto dataset and the (9,20,20,1) neural net structure for the abalone dataset.

We now compare the optimal CMGVA to the planar flows of Rezende and Mohamed (2015) with flow lengths of 10 transformations. Tanh is the non-linearity function with the initial distribution being Gaussian with mean μ and a diagonal covariance matrix; S = 1000 samples are used to accurately estimate the gradients of the lower bound. A similar stopping rule to that described in section S7 of the online supplement is used. Figures S11 and S12 in section S6 of the online supplement show that the lower bound of the planar flows for the two datasets for neural nets with different structures increase at the start and then converge. Table S1 in section S8 of the online supplement shows that the CMGVA has a higher lower bound and higher log of the approximate posterior predictive scores compared to the planar flows.

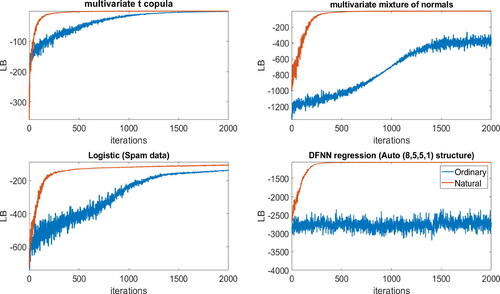
5.5 Efficiency of the Natural Gradient

This section compares the performance of the natural gradient and the ordinary gradient methods using the same initial values for the variational parameters for both methods. Figure 10 shows the lower bound values over iterations for both methods for the 2-component CMGVA for the multivariate t-copula, multivariate mixture of normals, logistic regression (spam dataset), and Bayesian DFNN regression (abalone dataset with neural net (9, 5, 5, 1) structure). The figure shows that the natural gradient is much less noisy and converges much faster than the ordinary gradient.

Fig. 10 The plot of the lower bound values over iterations for the ordinary and natural gradient methods for the 2-components CMGVA for the 100-dimensional multivariate t-copula, multivariate mixture of normals, Bayesian logistic regression model (spam data), and the DFNN regression model for the Abalone dataset with a (9,5,5,1) neural net structure examples.

6 Conclusion

The article proposes flexible variational approximations based on a copula of a mixture of normals and constructs the computational algorithms for estimating the approximation. An important part of the approach is the construction of appropriate transformations of the parameters to try and simplify the joint posterior which is then estimated by a mixture of normals.

The VB method is made efficient by using the natural gradient and control variates. Our approach of adding one component at a time provides a practical variational inference method that constructs an increasingly complicated posterior approximation and is an extension and refinement of state-of-the-art Gaussian and skew Gaussian copula variational approximations in Smith, Loaiza-Maya, and Nott (2020). The proposed variational approximations apply to a wide range of Bayesian models; we apply it to four complex examples, including Bayesian deep learning regression models, and show that it improves upon the Gaussian copula and mixture of normals variational approximations in terms of both inference and prediction. Our article uses a factor structure for the covariance matrix in our variational approximation, but it is straightforward to extend the variational approach to consider other sparse forms of the covariance structure, such as a sparse Cholesky factorization as in Tan, Bhaksaran, and Nott (2020).

We note that it is straightforward to use any other copula-based approximation as a first component in our approach, such as a t-copula. This may result in a simpler mixture approximation than using the Gaussian copula as a first component.

Supplementary Materials

CopMixJCGSSupp.pdf (pdf file) provides additional examples, results and technical details. Computer code to implement the methods for the examples of this article is available online.

Disclosure Statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

The research of Robert Kohn was partially supported by an ARC Center of Excellence grant CE140100049.

Notes

1 For an m × m matrix A, $\text{vec}(A)$ is the vector of length m² obtained by stacking the columns of A under each other from left to right; $\text{vech}(A)$ is the vector of length $m(m+1)/2$ obtained from $\text{vec}(A)$ by removing all the superdiagonal elements of the matrix A.

2 https://mc-stan.org

3 The CPU time for estimating the 3-component CMGVA is the total time taken for estimating 1 to 3-component CMGVA. Similar calculations are used for calculating the CPU time for the 4-component CMGVA.

4 see https://archive.ics.uci.edu/ml/datasets.phpforfurtherdetails.