Abstract
The aim of this work is to present a technique to identify elastic parameters of composite materials. The identification is based on model updating involving an optimization process in which the objective function is defined as the difference between analytical natural frequencies and their experimental counterparts. Such analytical natural frequencies are obtained by means of the finite element method while the experimental ones are obtained by standard modal tests. The optimization problem is solved by a genetic algorithm (GA), which does not require the cost function gradient avoiding the expensive eigenvectors computation presents in gradient methods. The proposed technique is assessed by a number of different tests.
Introduction
In order to obtain better engineering properties like stiffness, strength, weight reduction and thermal response composite materials have been used in many structural applications [Citation1]. In the design of sophisticated structures one should have a good estimate of physical properties and for composite materials this is not accomplished by conventional techniques. For instance, in [Citation2] the elastic constants were estimated by using simulated ultrasonic phase velocities. Genetic algorithms (GAs) are used in [Citation3] as a complementary technique to perform the initial estimation of the elastic parameters and then refining the solution by classical updating methods.
In the present work, the identification of elastic parameters yields in an inverse problem, which solution involves an optimization formulation. This problem relies on the comparison between experimental natural frequencies and their analytical counterparts. The experimental frequencies are obtained by means of modal tests that are performed on typical composite plates. The analytical frequencies are eigenfrequencies associated to finite element models of those structures. The novelty of the proposed approach is the use of a GA in the numerical solution of the optimization problem. It is worth mentioning that the use of this kind of algorithm avoids the expensive computation of gradients involving eigenvectors. Moreover, other advantages are recognized: for example, the choice of the initial guess required in the optimization process could be more flexible.
The experimental natural frequencies were obtained by tests that had been carried out on aluminum [Citation4] and on Glass–Epoxy plates [Citation5]. In order to stress the capacity of the approach, simulated experimental frequencies were obtained by numerical methods for aluminum, Kevlar–Epoxy and SCS-6–Ti-15-3. The stiffness properties of these materials were obtained from literature [Citation6]. The estimated properties obtained by using GA were compared with the available data.
Plate Theory
The kinematics of the classical plate theory [Citation7] which is adopted here is based on the following hypothesis: the vertical displacement vz is constant through the plate thickness (Eq. (Equation1(--1) )) and the straight lines normal to the xy-plane before deformation remain straight and normal to the midsurface after deformation (Eq. (Equation2
(--2) )). These assumptions correspond to neglecting both transverse shear and normal effects, i.e., the deformation is due entirely to bending and in-plane stretching.
(--1)
(--2)
where ∇ stands for the spatial gradient. Thus, the kinematics of the plate’s motion is expressed by means of three displacement fields defined over the middle surface.
The dynamics of the plate is governed by the virtual power principal [Citation7], which leads to the following variational equations:
(--3)
(--4)
(--5)
(--6)
The composite structures analyzed in this work consist in laminated plates formed by a matrix reinforced by perfectly aligned fibers. In Eq. (Equation6(--6) ), E1 is the elastic modulus in the fibrous direction, E2 is the elastic modulus in the transverse direction, ν12 and ν21 are the Poisson's ratio and G12 is the shear modulus.
Only four out of the five material constant for plane stress of an orthotropic material are independent. In this work, the choosen parameters are E1, E2, G12 and ν12. It is worth mentioning that, according to the reversible principle of elastic processes, the Poisson’s ratio ν21 is obtained as:
(--7)
Finite Element Modeling
In the finite element model, the plate is discretized by triangular elements with five degrees of freedom per node: two in-plane displacements, two rotations and the transversal deflection vz. Thus, the associate eigenvalue problem is represented by:
(--8)
where ωi is the ith natural frequency and φi is its associated vibration mode. M and K are, respectively, the mass and stiffness matrix of the finite element model.
It is important to remark that the stiffness matrix depends on the elastic parameters that are to be identified, i.e.
(--9)
The Genetic Algorithm
Genetic algorithms are search procedures based on the mechanics of natural selection. These techniques allow a population composed of many individuals to evolve, according to some prescribed rules, to a state that minimizes a cost function. Comparing with other random search techniques, the GAs are an intelligent way to find the global solution in the search space [Citation8].
In GAs, a finite number of candidate solutions, the chromosomes, are randomly created in order to form the initial population. A binary code [Citation9] was adopted here. Each chromosome represents a possible solution, divided in substrings that are decoded into their corresponding elastic constants. These chromosomes will create the new generation, by natural selection and reproduction procedures. As the cost function has to be minimized, only a few of the best chromosomes (the members with lower errors) will be kept for breeding.
The natural selection is a procedure that decides which individual should survive, forming the mating pool. Individuals with lowest cost reproduce more often than highest cost ones. When an overlapping population is permitted the offspring will replace the discarded chromosomes. Reproduction procedures consist in crossover and mutation. Two chromosomes, parent1 and parent2, are selected from the mating pool to produce two new offspring, child1 and child2. In order to form the children, a crossover point is randomly selected between the first and last bit of the parents, exchanging portions of their strings. This operation is performed with a probability pcross, that is normally a high value. Mutation operation change a bit from “1” to “0” or vice-versa, with a probability pmutation, normally a very low value. Increasing the number of mutations increases the algorithm's search outside the current region of parameter space. It also tends to distract the algorithm from converging on a solution. In order to propagate the best solution without changes, it is usual to keep the fittest chromosome without mutation.
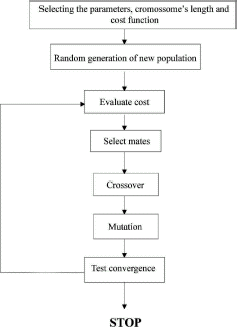
Eventually, the cost of the new generation is calculated and the described process is repeated, until a stopping criterion. The number of generations depends on whether an acceptable solution is reached or a certain number of iterations is exceeded (maxgen). shows the procedures of the present work.
FIGURE 1 Flow chart.
In the application of GA to the identification problem, the first choice relies in the way of representing the elastic parameters. A 40 bit chromosome was used: 16 bits for E1 and 8 bits for the others. All the elastic parameters are real numbers. The first eight bits of E1 are decoded to form the integer part and the others are decoded to form the decimal part. The other elastic parameters are calculated as a fractional part of the elasticity modulus E1. Therefore, the search space for each constant is defined as:
(--10)
In the optimization problem, the objective function is defined as the difference between natural frequencies and analytical ones [Citation10], stated as follows:
(--11)
where m is the number of used frequencies and θ is a vector which contains the elastic constants. After evaluating the fitness, the chromosomes are ranked from lowest to highest cost. Only the nbest chromosomes are kept to form the mating pool, while the others are discarded. In case of overlapping occurrence, the new generations are composed by the keep chromosomes and completed by the offspring which are created by crossover and mutation operations.
Parameters’ selection is different for each situation. Small population size ( popsize) should lead to premature convergence while a large one is commonly used to increase the variation within a population. However, the increase of the number of function evaluations results in increased computational costs.
Applications
The proposed approach is assessed by means of a number of applications. Both isotropic and orthotropic plates are explored. The former, although it does not constitute a composite structure, is used as far as it represents a test in which the detection of implementation errors is simpler and gaining some insight in the methodology is easier.
The elastic constants were identified for each specimen using the data from , where a and b define in-plane plate dimensions and h is plate thickness.
Table I Plate’s parameters
Aluminum Isotropic Plate
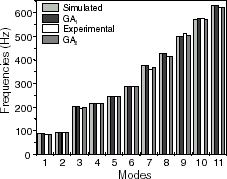
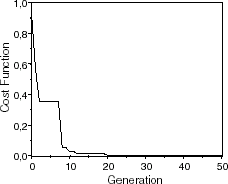
In order to enlarge the number of situations to be analyzed, some nonexperimental frequency values were introduced. They will be referred to as simulated frequencies, which are obtained with an a priori choice of the elastic parameters and the use of a finite element model of the plate. The simulated and experimental natural frequencies are shown in and . The two examples are labeled by GA1 and GA2, where the identification procedure were carried out for the former based upon the simulated frequencies and for the second one on the experimental values. The experimental frequencies along with its identified elastic parameters were obtained in [Citation4], where the authors adopted a different approach for estimating composite structures parameters. The deviation between the achieved results and the expected ones is presented in , reaffirming the good performance of the proposed method.
Table II Aluminum plate frequencies in Hz
FIGURE 2 Frequencies on aluminum plate.
FIGURE 3 Estimated elastic constants on aluminum plate.
For the aluminum plate, the following parameters of the GA were utilized.
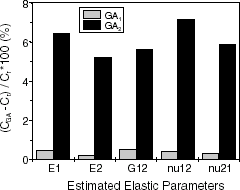
and show the estimated elastic constants attained by using four different initial guesses in the identification algorithm. The goal of doing such calculations is to assess the convergence characteristics of the proposed method. As it can easily be observed, the GA has reached stable values of the identified parameters even when noisy (experimental data) was used. It is interesting to remember that inverse problems are often ill-conditioned which entails a lot of difficulties in their numerical solution. The average value (μ) and the standard deviation (s) were also computed. Considering the literature values (), as the standard ones, it is noticeable that the elastic moduli are better estimated than the shear modulus and the Poisson’s ratio ().
Table III Estimated elastic constants for an aluminum plate – GA1
Table IV Estimated elastic constants for an aluminum plate – GA2
Orthotropic Plates
Kevlar–Epoxy
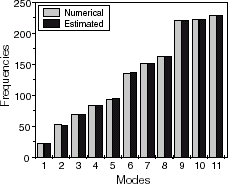
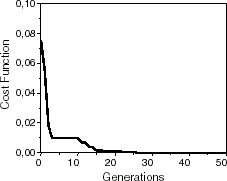
This plate is composed by four 1 mm thick plies and its dimensions are presented in . The simulated and estimated natural frequencies are shown in . As mentioned before, GAs are prone to handle common drawbacks present in inverse problems as the presence of multiple minima. This can be verified in the convergence curve of , where it is shown that along the iterative process the algorithm was able to escape from a local minimum towards a global one. The convergence was assured by comparing the obtained results with the available literature, which is summarized in .
Table V Estimated elastic constants for kevlar–epoxy
FIGURE 4 Frequencies on a kevlar–epoxy plate in Hz.
FIGURE 5 Cost function on a kevlar–epoxy plate.
For the Kevlar–Epoxy plate, the following parameters of the GA were utilized.
SCS-6–Ti-15-3
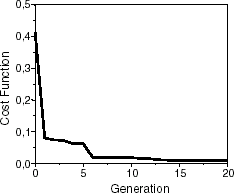
Geometrically, this plate is as the previous one but the plies material is SCS-6–Ti-15-3. The simulated and estimated natural frequencies are shown in . In this example, the algorithm also escaped from a local minimum (). In , the estimated elastic constants are compared to the literature values. Although the standard deviation presented high values, the estimated average values are very close to literature ones.
Table VI Estimated elastic constants for SCS-6–Ti-15-3
FIGURE 6 Frequencies on a SCS-6–Ti-15-3 plate in Hz.
FIGURE 7 Cost function on a SCS-6–Ti-15-3 plate.
For the SCS-6–Ti-15-3 plate, the following parameters of the GA were utilized.
Glass–Epoxy
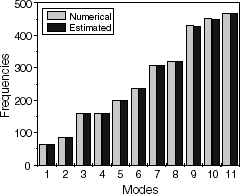
In this example, the natural frequencies were obtained by experimental tests that were carried out in [Citation5] and presented in . The plate consists of eight unidirectional layers with a layer stacking sequence [90/0/90/0]s. shows the results obtained by the identification procedure applied in [Citation5], comparing the elastic constants of the single layer of the cross-ply (CP) laminate with the properties obtained for the unidirectionally (UD) plate from the same material. shows the results obtained by the present approach. Unless the Poisson’s ratio, all the identified elastic constants have presented good adherence to those of [Citation5]. This discrepancy could be attributed to the low sensitivity of natural frequencies to the Poisson’s ratio, which is confirmed by observing . The frequencies computed using the identified parameters are very close to the experimental ones despite the uncertainty of the Poisson’s ratio value.
Table VII Frequencies on a glass–epoxy plate in Hz
Table VIII Elastic constants for glass–epoxy [5]
Table IX Estimated elastic constants for glass–epoxy
For the Glass–Epoxy plate, the following parameters of the GA were utilized.
The evolution of the cost function during the optimization process is depicted in .
FIGURE 8 Cost function on a glass–epoxy plate.
Conclusions
The proposed nondestructive method for identifying global elastic parameters in composite structures has shown to be promising as it was very effective in a number of real situations analyzed here. It is convenient to reinforce the simplicity of the methodology that relies on standard modal data.
It is clear from the examples that the GA was able to handle the usual drawbacks appearing in the solution of inverse problems, for instance, the presence of several minima and ill-conditioning. It has proved to be capable of skipping local minima and succeed even in the presence of noisy data coming from experiments.
Nomenclature
Additional information
Notes on contributors
Luís Alfredo Vidal De Carvalho
*E-mail: [email protected]
Notes
*E-mail: [email protected]
Related Research Data
- Reddy, JN, 1991. Mechanics of Laminated Composite Plates: Theory and Analysis, CRC Press. Boca Raton. 1991.
- Balasubramaniam, K, and Rao, NS, 1998. Inversion of composite material elastic constants from ultrasonic bulk wave phase velocity data using genetic algorithm, Composites: Part B 29B (1998), pp. 171–180.
- Cunha, J, Cogan, S, and Berthod, C, 1999. Application of genetic algorithms for the identification of elastic constants of composite materials from dynamic tests, International Journal for Numerical Method in Engineering 45 (1999), pp. 891–900.
- Bastos, SF, 2001. "Identification of elastic parameters by means of modal analysis". In: Department of Mechanical Engineering, Federal University of Rio de Janeiro – Brazil. 2001, Master Thesis (in Portuguese).
- Rikards, R, Chate, A, and Gailis, G, 2001. Identification of elastic constants of laminates based on experiment design, International Journal of Solids and Structures 38 (2001), pp. 5097–5115.
- Herakovich, CT, 1998. Mechanics of Fibbrous Composites, Jonh Wiley and Sons, Inc. New York. 1998.
- Shames, IH, and Dym, CL, 1973. Solid Mechanics: A Variational Approach, McGraw-Hill Int. Ed.. London. 1973.
- Haupt, RL, and Haupt, SE, 1998. Pratical Genetic Algorithms, John Wiley and Sons. New York. 1998.
- Goldberg, DE, 1998. Genetic Algorithms in Search, Optimization and Machine Learning, Addison-Wesley. Boston. 1998.
- Bledzki, AK, Kessler, A, Rikards, R, and Chate, A, 1999. Determination of elastic constants of glass/epoxy unidirectional laminates by the vibration testing of plates, Composite Science and Technology 59 (1999), pp. 2015–2024.