Response surface method for solution of structural identification problems

Abstract

The article is focused on the application of the Response surface method for the solution of structural identification problems. The approximating functions are obtained from the data of numerical experiments, which is performed in the sample points of experimental design. A Minimal mean squared distance Latin hypercube design is used in the present article. A local approximation method is employed for building the response surfaces. An example of the application of the response surface method and experimental design for the identification of elastic properties of a laminated composite material is discussed. The five elastic constants of carbon/epoxy laminate are determined employing experimentally measured eigenfrequencies of composite plates. The identification functional represents discrepancy between experimentally measured and numerically calculated frequencies, which are dependent on the variables to be identified. The identified elastic constants have been compared with the values obtained from an independent static test. A good agreement of the results is observed.

Keywords:

• Design of experiments
• Structural identification
• Local approximation
• Latin hypercube design

Introduction

In structural optimization and identification, some problems require excessive computational time when conventional methods of minimization are used. For example, it takes several hours of computer time for one variant of the finite element solution to be calculated. For complex optimum design problems it is necessary to perform calculations of several thousand variants. Similarly, the solution of some identification problems can also require large computational efforts. In order to reduce computational efforts, methods based on approximation concepts can be used. Nowadays these methods take a dominant position in structural optimization [1]. Approximation methods also are employed to solve identification problems [2]. The development of approximation functions has become a separate problem in optimum structural design. The approximating models can be built in different ways. Empirical model building theory is discussed in [3]. To construct a more general model of the original function, the method of experimental design [4,5] can be employed together with approximate model building [6–8]. A simplified model, called “metamodel”, is built using the results of a numerical experiment in the points of experimental design. Response analysis using the simplified model is computationally much less expensive than a solution using the original model. Although there is a wide literature present about experimental designs and the building of approximating functions, it should be noted that there are some special features present in the experimental design that are not present in the physical experiment. The main features are as follows.

1.

The results obtained in the numerical experiment are deterministic and without statistical errors. Repetition of the results is 100%. This means that there is no statistical dispersion of the model parameters. However, computer models produce numerical noise as a result of the incomplete convergence of iterative processes, round-off errors, and the discrete representation of continuous physical phenomena when a different number of calculation steps or a different finite element grid is generated [9]. In deterministic computer experiments, replication at a sample point is meaningless, therefore the points should be chosen to fill the design space.

2.

The mathematical model of the object is unknown, i.e., the form of the regression equation is not known. Therefore, well-known criteria for experimental design optimality, for example, D-optimality, cannot be used. Such criteria can be used only in the case when the form of the regression equation is known.

There is a wide literature present about the different methods of experimental design. Among the methods, the space filling designs can specifically be emphasized. The first space filling design for a computer experiment was proposed in [4]. In this work, designs in which the number of levels for each variable is equal to the total number of runs were first proposed. In [4], the space filling criterion based on a function similar to the function of the potential energy of gravity was first used. Later, the same kind of experimental designs was proposed as a Monte Carlo integration technique by McKay et al. [10], and the name “Latin hypercube samplings” was introduced. Numerous space filling experimental designs have since been developed in an effort to provide more efficient and effective means for sampling deterministic computer experiments based on Latin hypercubes. Different space filling criteria for Latin hypercube designs was proposed by many authors: Maximin Latin hypercubes [11], Minimal Integrated Mean Squared Error designs [12], Orthogonal array-based Latin hypercube designs [13], Orthogonal Latin hypercubes [14], Integrated Mean Squared Error (IMSE) optimal Latin hypercubes [15].

Good results for the problems based on numerical experiment can be obtained employing the approach of experimental design and approximation proposed by Eglais [4,6]. This approach based on global approximation was used in [2] for the solution of optimal design and identification problems. However, occasionally the results of the approximation are not satisfactory. Therefore, in the present article a Minimal Mean Squared Distance Latin hypercube (MMSDLH) design and local approximation method are employed to solve an identification problem similar to that described in [2]. Thus the accuracy of the solution can be improved.

In the past few years, the so-called non-parametric approximation methods have been widely used for the design and analysis of computer experiments: local polynomial approximation [16,17], Kriging [18]. Finally, other statistical techniques such as Multivariate Adaptive Regression Splines [19] and Radial Basis Functions [20–22] are beginning to draw the attention of many researchers. However, these methods are computationally expensive not only when used in metamodel building, but also when the metamodels are applied for prediction. In the present article, a local approximation method with weight functions is employed for the solution of the identification problem considered.

Experimental Frequencies

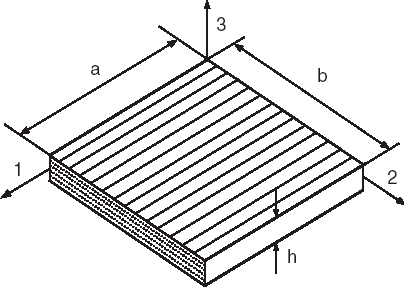
Experiments have been performed on unidirectional carbon/epoxy laminate (see Fig. 1). Plates were tested for vibrations in order to measure eigenfrequencies and corresponding modes. Experiments were performed with free–free boundary conditions on all edges of the plate, in order to exclude the influence of boundary conditions on the results of the identification. The plate dimensions are as follows: a = b = 207.5 mm; h = 2.0 mm. Density of the material ρ = 1535 kg/m³. Experimental eigenfrequencies are presented in the third column of Table I. As not all of the frequencies were observed experimentally, frequencies were arranged according to the finite element solution. In the second column, the frequencies obtained by FEM using the identified elastic constants (see the “Results and Verification” Section) are presented. Other quantities presented in Table I are explained in the “Results and Verification” Section.

FIGURE 1 Laminated composite plate.

TABLE I Experimental frequencies

No.	(Hz)	(Hz)	Δi (%)	Δfi (%)
1	97.9	97	+0.92	11.15
2	124.3	123	+1.06	6.94
3	235.7	237	−0.55	9.39
4	342.3	341	+0.38	6.89
5	455.3	458	−0.79	8.12
6	502.2	502	+0.04	1.43
7	539.4	541	−0.29	2.69
8	651.1	653	−0.29	5.07
9	676.5	–	–	–
10	779.7	–	–	–
11	860.8	–	–	–
12	1113	–	–	–
13	1169	1168	+0.08	7.96
14	1215	–	–	–
15	1376	1381	−0.36	1.52
16	1407	1413	−0.42	2.05
17	1503	1512	−0.59	3.04

It can be seen that in the range of the first 17 numerical frequencies only 12 experimental frequencies were observed. It should be noted that frequencies are identified through mode shapes, and the same modes were observed for numerical and experimental frequencies. These experimental frequencies were employed for identification.

Identification Functional and Approximation

The parameters x to be identified are five elastic constants of the transversally isotropic material of the plate (--1)

Here E₁ and E₂ are Young’s modulus in the fiber and transverse direction respectively, G₁₂ is the in-plane shear modulus, G₂₃ is the transverse shear modulus and ν₁₂ is the Poisson’s ratio. Directions of the material axes, which are also the plate axes, are denoted 1–2–3, where 1 is the fiber direction and 2, 3 are the transverse directions.

In [2] it was assumed that the values of five elastic constants (1), which give minimal differences between calculated and experimentally measured frequencies (eigenvalues), correspond to the material used in natural experiment. Therefore the functional to be minimized describes the discrepancy between the experimentally measured and the numerically calculated frequencies (--2) Here ε_i is the relative discrepancy or residual, and k_i are the weighting coefficients for the selected frequencies. In (2), the integer I is the total number of frequencies used in the analysis. It is possible to assign a non-negative weight to each residual. For simplicity, only unity values are used. The estimation can be based on any set of frequencies by assigning weights of zeros and ones as appropriate.

The numerical frequencies f_i(x) are functions of elastic constants. These functions are obtained as approximations of the finite element solution, which is performed in the sample points of the experimental design. The frequencies and the corresponding vibration modes (eigenvectors) are obtained by solving an eigenvalue equation (--3) Here K is the plate stiffness matrix, which depends on x, M is the mass matrix, U is the displacement vector (eigenvector) and is the eigenvalue and ω_i = 2πf_i is the circular frequency (rad/s).

For identification, the functional (2) can be used, but practical experience show that it is more appropriate to employ the eigenvalues instead of frequencies: (--4) The functionals (2) and (4) were employed for identification in [2], where, instead of the original functions , the approximating functions were used. Thus, in [2] the approximations were performed for each frequency. Employing the same functional (4), the procedure of identification can be modified so that the approximation can be performed for the whole functional Φ(x), rather than for each frequency separately. Thus, the function to be approximated and minimized is as follows: (--5) Here is the ith eigenvalue calculated by the finite element method in a sample point of a five-dimensional space of identification parameters, j is the number of the sample point (run) in the experimental design ( j = 1,2,…, N), N is the total number of sample points (number of runs) in the experimental design (see below), p = 1, 1/2, 1/4 or 1/8. The value of p is chosen in order to improve the quality of approximation. The best results were obtained (see below) with p = 1/2 and 1. Note that hereafter the upper index for the variable x denotes the number of point in the experimental design, while the lower index denotes the component of the variable x.

The functional Φ is minimized employing local approximation: (--6) In approximation (6), coefficients are calculated by (--7) where are coefficients of the local quadratic approximation (dependent on x), N_X is the set of numbers of the nearest neighbors of the point x. In the case when the Gaussian weight function is used in (7), all points of experimental design are considered as neighbors N_X = {1,2,…,N}. Here is the Euclidean distance between x and x ^j, and G is the coefficient of the Gaussian function. If G = 0, then the conventional least squares method is obtained (with all weighting coefficients equal to 1.0 in (5) and without division by Φ_j in (7)). Usually G = 0.75 was used.

Minimal Mean Squared Distance Design

For the computer experiment, the Minimal Mean Squared Distance (MMSD) experimental designs were employed. These designs were proposed in [23]. The MMSD designs are space filling designs that give minimal Mean Squared Distance (MSD) between the mesh points in design space R^m and the nearest point from experimental design D: (--8) where are points from a large sample in design space R^m (v = 1,..., n), N is the number of points of the experimental design and n is the number of mesh points. Approximately n = 1 000 000 equidistant mesh points for low dimensions (m = 2, 3) are employed, and a 100 000-point Latin hypercube sample for large-scale designs (m > 3) is used. These designs give points uniformly distributed in the design space and tend to minimize the expected mean squared error of the local quadratic approximation [23]. Fang and Wang [24] introduced a similar criterion, named Mean Squared Error. In [23], a quick search algorithm was proposed for the minimization of the MSD criterion for Latin hypercube designs in the unit cube [−1,1]^m, as well as for designs with unconstrained level values and numbers in unit cubes or m-dimensional spherical regions.

For the purpose of comparison with other designs, the distances and other characteristics of experimental designs are computed after the designs are scaled into the unit cube [0,1]^m, although the designs are mostly constructed in an m-dimensional cube [−1, 1]^m.

For comparison with other space filling designs, four additional criterions have been used:

1.	Eglais’ criterion [4], later proposed also by Morris and Mitchell [25] in a more general form: (--9)
2.	The MINDIST criterion, which seeks to maximize the minimum distance between any pair of points in the data collection plan [11]: (--10)
3.	The entropy criterion first proposed by Shewry and Wynn [26] and then adopted by Currin et al. [27]. The application of the entropy criterion for designs in unit cube [0,1] m is equivalent to the minimization of , where C is the N × N covariance matrix of the design with elements (--11) where i, j = 1,…, N. Throughout this article the value q = 2 is selected, so the correlation between two points is a function of their Euclidean distance L2, and Θ is set equal to 2.
4.	The discrepancy criterion, which averages the squared difference in the cumulative density function [28]: (--12) Table II shows a comparison of three 16-run designs of seven variables for all five criterions. MMSDLH stands for Minimal MSD Latin hypercube design; ULH stands for Uniform Design Based on Centered L2 Discrepancy Un (ns) [29] and MBLH is a Minimum Bias Latin hypercube [28]. It can be seen that the MMSDLH plan performs better than the others according to all five criterions.

TABLE II Comparison of 16-point designs for 7 variables

Design	MMSDLH	ULH	MBLH
MSD	0.3942	0.4006	0.3947
	9.5196	9.5449	9.5281
MINDIST	0.8869	0.8353	0.8000
Entropy	0.2900	0.3123	0.3147
DC	0.2464	0.2289	0.2468

For the identification problem formulated in the present article, an MMSDLH-type design with 101 runs and five factors is employed. For this design the values of criterions are as follows: MSD = 0.2051, = 89.0740, MINDIST = 0.3808, Entropy = 69.7806, DC = 0.0453.

Minimization

Unlike the parametric quadratic approximation commonly used in the response surface method, the minimization of a locally approximated function is more difficult. Generally, any method of nonlinear programming can be used. However, using the derivatives is not appropriate since the approximating function cannot be smooth enough and may have a lot of local extremes.

Two methods are employed in order to obtain a global minimum of the locally approximated function of interest.

The first method is iterations. A randomly selected point in the design space is chosen as the starting point. A local approximation is then built in this point, and the coefficients β are found according to (7). The minimum point of the approximating function is calculated with fixed values of coefficients β. This is a simple problem, which requires the solution of a system of only five linear algebraic equations. Afterwards a local approximation is built in this new point and the search is continued. It needs to be certain, however, that the true minimum has been found. In the case when the process converges (and converges to the same point from all starting points), there is a high probability that the actual minimum was found. From experience it can be concluded that in this case the physical parameters of the plate are correctly identified.

Unfortunately, two alternative cases are found to be more common. First, the process can converge to a point outside of the region in which the experimental design was planned. In this case, the center of the experimental design (for FEM calculations) should be moved or the bounds should be shifted.

In the worst case, when the iterative procedure diverges or gives a lot of local extremes, the second method, a global search, is used [30]. Approximately 100 000 points from the randomly selected Latin hypercube type sample are tested and the best point is selected. Then the search domain is reduced around this point and a new random search is performed until an acceptable accuracy of the extreme values is obtained.

This is a computationally more expensive method than the iterative search, since one calculation of the approximating function needs to solve the system of 21 linear equations (the Cholesky decomposition method has been used). The entire process requires about one to two minutes of calculation time on a Pentium 800 MHz processor, but compared with the time of the FEM simulation this time is negligible.

After the minimum of the approximating function of interest is found, N_a confirmation points near the optimal values should be calculated to verify the accuracy of identification. These points can be used as additional points and optimization may be recalculated employing N+N_a design points in order to improve the accuracy of the solution. (Note that when the optimum of the locally approximated function is found, the true value of the function is verified by FEM in any case.)

The minimum of the approximated objective function practically coincides with the minimum of the original function. This coincidence is tested and the area of variables is moved or reduced as necessary. The result of the minimization is always the same as in the case of direct minimization of objective function (5), approximation only reduces the computing time. One direct calculation of objective function requires FEM calculation of a rather large model and takes about 5 min of computing time. Minimization needs few thousand calculations of objective function, the authors have built metamodels with 101 calculations, sometimes the calculations are repeated in a reduced region.

Results and Verification

An MMSDLH type design with N = 101 sample points in five dimensions is used to build the local approximations. These sample points are distributed in the domain of interest, which is formed by the lower and upper bounds of variables. The initial guess values of these bounds can be chosen employing the elastic constants of a similar material. If the identified values are outside of the region, the bounds should be shifted and the procedure of identification should be repeated. Thus, the domain of interest is corrected in few stages of identification. For the present example, in the first stage the domain of interest was chosen as follows: (--13)

Here the Young’s modulus and shear modulus are given in GPa, but the Poisson’s ratio is a non-dimensional quantity. In sample points ( j = 1,2,…, N), the Eq. (3(--3) ) was solved and eigenvalues λ_i(x ^j) were obtained. These eigenvalues are treated as original functions. Approximations of the original function (5(--5) ) were obtained using the local approximation method described above.

Twelve experimentally measured frequencies, which are presented in Table I, can be used in identification in any combination. First, all 12 experimental frequencies were used in identification by minimizing the functional (5). Then, only the first six frequencies were employed in identification. In this case of minimizing the functional (5), the following elastic constants were obtained: (--14) Practically the same results were obtained employing all 12 experimental frequencies in minimization of the functional (5). It should be noted that employing the global approximations, the results (14) for the first four constants are approximately the same. The exception is Poisson’s ratio, which can be reliably determined only using the local approximations.

The verification of the results was performed by calculating with FEM the original function in the point of optimum (14). Then the numerical values were compared with the experimental frequencies. Residuals were calculated by the expression (--15) The results are shown in Table I. It can be seen that the differences between the experimental and the numerical frequencies are very small. Mostly the residuals do not exceed 1%, even for those six frequencies which were not used in identification (frequencies i = 7, 8, 13, 15, 16, 17). However, since higher frequencies are less sensitive to elastic constants than lower frequencies, in addition to the residuals ▵_i the range of each frequency in the space of the experimental design should be compared. In the last column of Table I the relative amplitude of each frequency ▵f_i in the experimental design space is presented. The relative amplitude is calculated by the expression (--16) Here (--17) In Table I it can be seen that lower frequencies are more sensitive to the elastic constants. However, the amplitude in the design space for the 8th and 13th frequency is also considerable.

In order to validate results, it is necessary to compare the properties obtained from the vibration tests through identification with those obtained from an independent test. Conventional static test was selected as the independent test. Static tests were performed according to ASTM guidelines (RTU-Riga Technical University and IAI-Israel Aircraft Industry LTD) and DIN standards (DLR-German Aerospace Center). Results are presented in Table III. The values obtained by the compression test are given in parenthesis. Generally, a good agreement of the results is observed.

TABLE III Comparison of elastic constants obtained from vibration and static tests

Elastic constant (GPa)	Vibration test	Static test
RTU	IAI	DLR
E1	170.7	176 (143)	165 (175)	192 (147)
E2	10.4	8.9 (9.6)	9.2 (11.8)	10.6 (9.7)
G12	6.2	5.2	5.4	6.1
G23	5.6	–	–	–
ν12	0.34	0.34	–	0.31 (0.34)

Analysis of Sensitivity

It is important to investigate the degree of accuracy of the acquired result, and the influence had on it by various factors. Concerning the identification of parameters of elasticity, there are two sources of errors. The first source is the experimentally measured frequencies, which can contain an error due to inaccuracy of measurement and due to errors made during calculations (fast Fourier transformation and others). These errors have bias and variance, and may have different characteristics for lower and higher frequencies. For statistical experiments we assume that errors are normally distributed with zero mean and standard deviation σ_i, proportional to frequency f_i.

The second source of error is the incomplete correspondence of the finite element model to the experiment (plate and fiber form errors, non-uniformity of material and others). It is known that in this case eigenfrequencies are weakly dependent on transverse shear modulus G₂₃ and Poisson’s ratio ν₁₂. This means that partial derivatives and are small or equal to zero. Therefore, the inverse calculation of G₂₃ and ν₁₂ for the given eigenfrequencies may be inaccurate or impossible altogether. To clarify this situation, a statistical test was performed. First, for the typical material with E₁ = 159.99, E₂ = 11.33, G₁₂ = 6.341, G₂₃ = 7.458, and ν₁₂ = 0.34, the eigenfrequencies (i = 1,…,30) are calculated using FEM. Experimental errors were modeled, adding to the known precise values the statistical error with normal distribution, zero mean and standard deviation, proportional to value of frequency. The results of the twelve numerical experiments are shown in Tables IV, V and VI, where errors of frequencies are presented.

TABLE IV Statistical experiment, uncorrelated errors of eigenfrequencies σ = 0.1%

Mean	Standard deviation	Standard deviation (%)
E1	160.0617	0.199	0.124
E2	11.3259	0.0191	0.169
G12	6.344	0.0143	0.226
G23	8.098	1.16	15.5
ν12	0.3327	0.02	5.95

TABLE V Statistical experiment, uncorrelated errors of eigenfrequencies σ = 0.5%

Mean	Standard deviation	Standard deviation (%)
E1	160.004	0.447	0.279
E2	11.3686	0.094	0.833
G12	6.354	0.054	0.86
G23	7.079	1.910	25.6
ν12	0.319	0.055	16.3

TABLE VI Statistical experiment, correlated errors of frequencies, correlation coefficient = 1, σ = 1%

Mean	Standard deviation	Standard deviation (%)
E1	159.79	2.757	1.7
E2	11.274	0.284	2.5
G12	6.334	0.123	1.9
G23	7.002	1.54	20
ν12	0.329	0.043	12.7

This means that for an adequate identification of Poisson’s ratio (the error less than 6%), the relative error of measured eigenfrequencies should be less than 0.1%. At the same time the identification error of transverse shear modulus G₂₃ may be relatively large.

Thus the relative error of E₁ is proportional (and even equal) to the relative frequency errors. The errors of E₂ and G₁₂ error is about two times greater but is also proportional to the frequency errors. For G₂₃ and ν₁₂, the dependency of the error on frequency errors is nonlinear.

It can be concluded that absolutely correlated errors (where all frequencies are measured with equal relative error) have a smaller influence on the determination of Poisson’s ratio ν₁₂ than uncorrelated errors. This means that Poisson’s ratio ν₁₂ is more dependent on the ratio of frequencies rather than their actual values.

Conclusions

The elastic constants of a unidirectionally reinforced laminate have been determined employing the identification procedure based on the experimental design and response surface method. For this purpose, MMSDLH designs and local approximations were used. It was shown that the elastic constants obtained from vibration tests through identification are in good agreement with the values obtained by conventional static tests.

Acknowledgements

Investigations concerning the development of identification methods for laminated composites are sponsored through Contract No. GRD-CT-1999-00103 by the Commission of European Union. We would also like to thank Dr. H. Abramovich (Israel Institute of Technology) for providing the vibration test data, Dr. Green (IAI – Israel Aircraft Industry LTD) and Dr. R. Zimmermann (DLR – German Aerospace Center) for providing the static test data.