Numerical Solution of an Applied Biophysics Inverse Problem

Abstract

The problem of reconstruction of the radionuclide intake dynamics using results of lifetime measurement of the ⁹⁰Sr incorporated in the enamel of human teeth is considered. This problem is a part of the system of dose reconstruction for the population exposed to ionizing radiation as a result of radioactive contamination of the environment. The approach to the solution of this task results in formulation of a mathematical inverse problem whose type depends on the biophysical properties of investigated radionuclide and the instrumental technique used for measurements. The problem results in two nonlinear integral equations with inexact known right parts. The basic method of research is linearization of this system and further regularization of linear integral equations. The main approach to solving these types of problems is based on minimization of the smoothing functional. Numerical procedure was carried out simultaneously by a direct minimization (method of Hook and Jeeves) and by a necessary condition analysis of extremum of the appropriate finite-dimensional problem. The solution obtained in such a way has biological and physical meaning and is in a good agreement with biological data.

Keywords:

• Radionuclide intake
• Integral equations
• Regularization

1. Introduction

One of the most important tasks in the field of radiation protection dosimetry is the reconstruction of radionuclide intake to the human body on the basis of the measurements of radionuclide incorporation in human organs and tissues. The approach to the solution of this problem usually results in formulation of a mathematical inverse problem, the type of which depends on the biophysical properties of investigated radionuclide and the instrumentation and technique used for measurements. In some cases, mathematical methods developed for numerical analysis of such problems could be applied to different engineering problems associated with the areas other than radiation protection dosimetry.

The problem considered here is a part of the system of dose reconstruction for the population exposed to ionizing radiation as a result of radioactive contamination of the environment that occurred half a century ago in the Southern Urals, Russia [1]. During 1949–1956 the plutonium production facility “Mayak” released liquid radioactive wastes into the Techa River that served as a source of drinking water for the residents of villages located downstream from the site of releases. As a result, villagers ingested a significant amount of fission products mainly with river water and milk. The main contributor to radiation exposure was long-lived strontium-90 (half-life is 29 years), which was accumulated in bones and teeth and retained for many years.

In 1959, a large-scale dosimetric investigations of the Techa River population were started using detectors registering surface-beta activity of ⁹⁰Sr (and its daughter ⁹⁰Y) incorporated in the front teeth (permanent incisors) [2]. The data were obtained using tooth-beta counter (TBC) developed that could be placed in the human mouth. The unit of TBC measurements is counts per minute (cpm), i.e., the TBC measurements give relative values of ⁹⁰Sr content in teeth. The TBC measurements were performed through 1995 and about 30 000 measurements for more than 15 000 persons were obtained in total. The analysis of these data showed that detectable levels of tooth-beta activity were registered only for the age groups for which the period of permanent teeth mineralization coincided with the period of ⁹⁰Sr intake [3]. Therefore, the teeth of these persons kept the information on ⁹⁰Sr ingested for a long time, because this radionuclide is incorporated in the mineral phase and the rate of elimination of ⁹⁰Sr from tooth enamel is very slow.

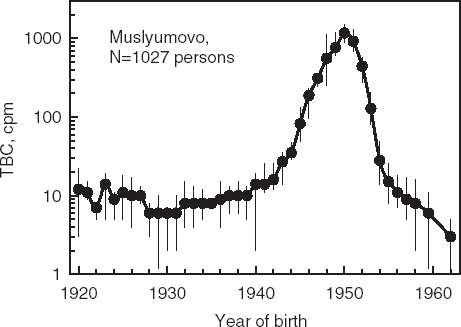
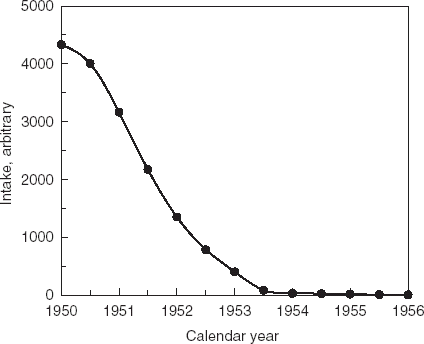
In 1970, Dr Igor Rasin expressed the pioneering idea of using TBC data for the purpose of reconstructing the intake of ⁹⁰Sr [4]. He was the first scientist formulating the task in the form of the basic integral equation which will be analyzed in detail in this article. According to his approach, an intake function can be reconstructed on the basis of the age-dependence of the TBC measurements and the ratio of ⁹⁰Sr intake by children of different ages-to-that by adults (this ratio is determined by the available data on age-dependencies of water and milk consumption as described by Kozheurov and Degteva [2] and verified by Tolstykh et al. [5]). In the framework of these estimations, reconstruction of ⁹⁰Sr intake was performed for a reference settlement on the Techa River, for which the most complete dosimetric information was available. Figure 1 demonstrates age-dependency of TBC values obtained for permanent residents of a reference settlement. These data are used in the analysis described here.

FIGURE 1 Age-dependent median-TBC values obtained for permanent residents of the referent settlement Muslyumovo on the Techa River during 1963–1971 (2231 measurements for 1027 persons). The year 1967 was assigned as an average-weighted value. Bars reflect quartile ranges.

2. Basic Equations

Tooth-beta counter measurements denoted here as Y(T, t_u) are available for date of birth, T, and for date of measurement, t_u, on the theoretical interval . The basic equation connecting the experimental data Y(T, t_u) with the decision variables x(t) and k(t − T), has the following form: (--1) Here, Y(T, t_u) is the TBC data for people who were born at time T and measured at time t_u; β is a scaling factor (number of indications that correspond to unit of activity in teeth); α(τ, t) is the ratio of ⁹⁰Sr intake for children of age τ at time t relative to intake for adults (τ = t − T); x(t) is the rate of ⁹⁰Sr intake at time t; k(τ) is the ⁹⁰Sr-transfer coefficient from the gastro-intestinal (GI) tract to enamel of permanent incisors at age τ; R(Δt) is the retention function, i.e. fraction of ⁹⁰Sr remaining in enamel of permanent incisors after the expiration of time ;

In addition, the following assumptions were used here:

t_u = 1967, a constant determined to be the weighted average for dates of TBC measurements, as described in [5]; assuming that the start of massive ⁹⁰Sr intake began in 1950 according to [1]; Here, λ is the rate of ⁹⁰Sr elimination from tooth enamel, for which the value λ = 0.043 y⁻¹ is evaluated according to [6]. here is a three-dimensional response surface with the range of variation [0.1; 1]; it is monotonic function of τ and t (see [5] for details).

2.1. The Domain of the Variables

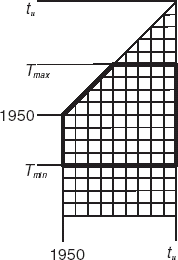
The domain D of the temporal variables (t, T) is described by the expression: This is also shown in Fig. 2.

FIGURE 2 The domain D of variables (t,T).

Now the initial point is changed by definition of t = t − 1950 and T = T − 1950 (i.e. the year 1950 is accepted as the zero point) and the integration variable is replaced in Eq. (1(--1) ) such that t = t − T. For considered boundary values of birth dates, and , the following notation is used:

Equation (1(--1) ) can be separated into

(--2) (--2-)

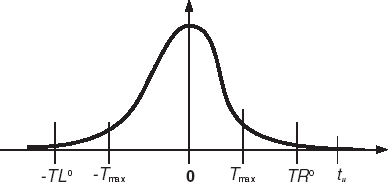
The measured values of Y(T, t_u) describe a rapidly decreasing function as . Figure 3 presents here the schematic analog of an experimental curve from Fig. 1.

FIGURE 3 Dynamics of the function Y(T). This is a schematic analog of the curve from Fig. 1.

This circumstance allows the specifications of two times, and , on the right and left of the figure, such that . But because the functions in Eq. (2(--2) ) are nonnegative, and the function Y(T, t_u) is monotonic, it follows that That is, intakes of ⁹⁰Sr fall to essentially zero at times greater than TR⁰, and the transfer from GI tract to tooth enamel is zero for times less than TL⁰. Therefore, integration of Eq. (2(--2) ) can be carried out from 0 to in the first equation and from T to in the second equation (Fig. 4).

FIGURE 4 Limited and actual domains of temporal variables.

2.2. Transformation of Equations

Considering the accuracy of the measurements of the function Y(T, t_u) (see Fig. 2), it is possible to set . Hence the domain of the temporal variables (t, T) may be described by expression (Fig. 3):

It is possible now to represent Eq. (2(--2) ) in the form (--3)

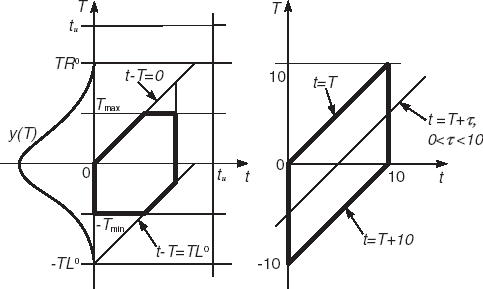
It will be convenient later to use yet another form for these equations taking into account the assumption of exponential retention of ⁹⁰Sr in teeth, and also that t_u is assumed to be a constant. Then, in the first equation of Eq. (3(--3) ), a new variable U is defined such that T + 10 = U. As then The modified equation takes the form

In the second equation, the integration variable may be replaced such that t = t−T. Then, V is defined as 10 − T, the equation becomes

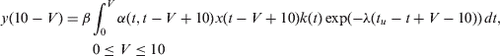
The set of the Eq. (3(--3) ) now takes the form (--4) (--4-)

Finally, the following designations are applied:

In this notation, the previous equations can be written in the form (--5) (--5-) which are considered as the final form.

3. Problem Definition: Linearization

As a summary of the above derivation, it is noted that the problem consists of definition of the nonlinear system of integral Eqs. (5(--5) ) and (5′(--5-) ); the unknown functions z(t) and k(t) for 0 ≤ t ≤ 10; and the unknown constant β.

If it is assumed that this task has at least one solution, then it is obvious that the set and will also be a solution for any nonzero constants c₁, c₂. In order to eliminate this marked ambiguity, a normalization is performed such that . Then, by setting , the following system is obtained: (--6) (--6-)

Representing the system of Eq. (6(--6) ) in operator form: (--7) where is a vector function (unknown), is the vector of the right parts (known – experimental data) of system (6), and is a nonlinear integral operator.

The iterative method of Newton–Kantorovich has been used to solve the problem represented by Eq. (7(--7) ). This method allows the linearization of the equations and their effective solution.

Let be some initial approximate solution, and f is real solution. Define and change from the nonlinear equation (7(--7) ) with unknown function f to the linear equation with unknown increment Δf: (--8) Here is a linear operator that is the derivative of the operator A. Actually, in this situation, Eq. (8(--8) ) represents a system of two linear integral equations with unknown components (Δk, Δz) of the increment Δf: (--9) (--9-) (--9-)

The process of solving the system of Eqs. (6(--6) )–(7(--7) ) is an iterative procedure beginning at some initial point f₀ and realized according to the rule . The increment Δf is defined at each step of procedure as the solution of the system of Eq. (9(--9) ).

4. Regularization of the Equations

It is well known (Ivanov et al. [7], Tikhonov et al. [8]) that a system of equations such as that of (9) is unstable in relation to uncertainties of the right-hand parts and is a so-called incorrectly-posed or ill-posed problem. Tikhonov's regularization procedure [7, 8] is used to solve this problem. This procedure allows changing from the problem of solving the system of Eq. (9(--9) ) to the problem of minimization of the smoothing function: (--10)

Here, is the mean square distance between and −A + Φ, and Ω is a stabilizer of the first order defined by the expression: and γ is a regularization parameter which should be found from equation (--10-)

In the last equation, Δf_γ is the solution of Eq. (10(--10) ) as a function of the regularization parameter γ, and δ is the uncertainty of the initial data Φ (δ is calculated as the pooled uncertainty of the TBC measurements presented in Fig. 1).

5. Design Equations

It is assumed that the numerical regularization procedure of Eqs. (8(--8) ) and (9(--9) ) on each step N of the iterative process uses the Ritz method of minimization of the system of Eq. (10(--10) ). This algorithm was used based on discrete approximation of the solution by piecewise-linear functions on an interval [0,10].

In greater detail, we shall set on an interval a grid with , and we shall define Λ_i(t) to be piecewise-linear functions that possess the value 1 at the nodal point with number i and the value zero at all another points. The functions are linearly independent and form the basis (Lagrange basis) of the piecewise-linear function's space on the given grid.

Assume that

Notice that the coefficients represent the value of the unknown functions at the nodal points of the grid.

The scalar form of the system of Eq. (10(--10) ) is

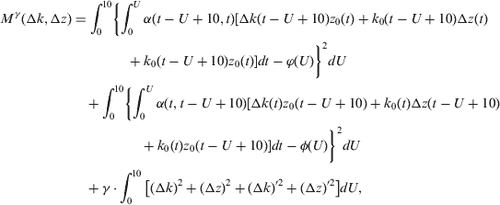
If the unknown functions are replaced by their discrete analogs, this function becomes the square-law function concerning unknowns (x,y): (--11) Here,

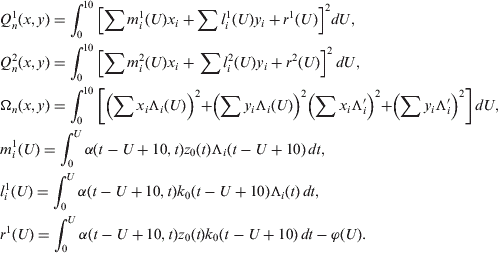
The coefficients , and r²(U) may be calculated as:

The necessary conditions for the minimum of the function (11) on the variable result in the equations:

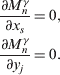
The first n of the specified equations are: 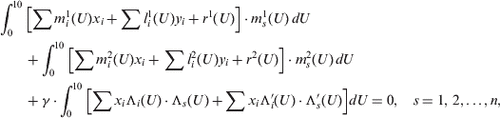Here, the summation on index i runs from 1 to n (i.e., it is taken into account that x₀ = 0).

Other n + 1 equations can be written in similar form:

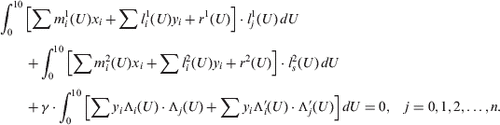
Thus, we come to a system of 2n + 1 linear equations concerning unknown x and y, which depend on the regularization parameter γ: (--12)

The factors of this system are given by the equations:

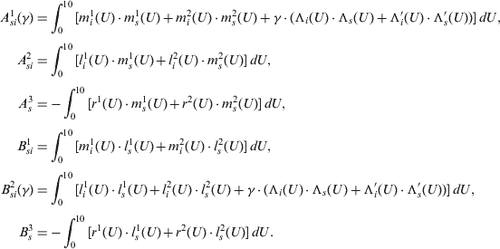
The solution of the minimization problem (11) is the solution of the system of Eq. (12(--12) ), corresponding to the regularization parameter γ determined from Eq. (10′(--10-) ):

6. Numerical Realization and Interpretation

The procedure of numerical realization of the algorithm described above was organized as follows: for each step N of iterative Newton–Kantorovich process, the domain of the variable was given discrete values on a grid for values of n equal to 10, 20 and 40, accordingly. For each of the chosen discrete values, the factors p, q, r and s of the stabilizer and of the level δ of uncertainty of the initial data, which together provided the indications of the small differences among the regularized solutions [i.e., solutions of the minimization problems (Eqs. 10(--10) , 10′(--10-) and 11(--11) )], were selected.

The minimization of the function in Eq. (10(--10) ) was carried out in parallel by method of Hook and Jeeves [9] and by solving the system of Eq. (12(--12) ). The iterative procedure stopped, if two adjacent iterations appeared to be within the limits of the given accuracy and residual of the system considered did not exceed uncertainty of the initial data. The number of iterations to obtain the desired results was about 20–30.

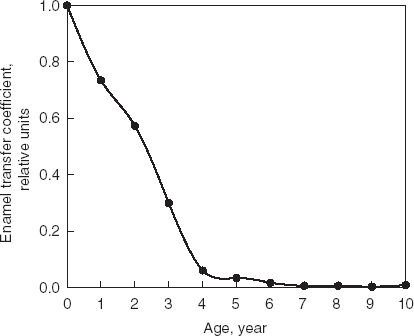
Solution of the problem is illustrated in Figs. 5 and 6. As seen from Fig. 5, the transfer coefficient for ⁹⁰Sr from GI tract to enamel is described by monotonic decreasing function. The values of this function become close to zero for ages more than 4–5 years. This is in accordance with biological data that indicate that the mineralization in the crown of front teeth is completed to this age [3]. The result of calculation of ⁹⁰Sr-intake function (Fig. 6) is in good agreement with the relative dynamics of the Techa River water contamination [5]. Therefore, the solution derived here has biological and physical meaning.

FIGURE 5 Solution: transfer coefficient from GI tract to enamel of permanent front teeth.

FIGURE 6 Solution: the rates of ⁹⁰Sr intake for the referent settlement.

7. Conclusion

A new mathematical approach was developed for the reconstruction of relative ⁹⁰Sr intake for the residents of the Techa River in the period of radioactive contamination. Numerical analysis described in this article allows us to obtain a unique and stable solution of the applied inverse problem. The obtained solution is in agreement with available biological data.

Acknowledgments

This work has been funded by the U.S. Department of Energy's Office of International Health Studies and by the Federal Department of the Ministry of Health of the Russian Federation. The authors would like to thank Vyacheslav Kozheurov and Evgenia Tolstykh from the Urals Research Center for Radiation Medicine, Russia and Lynn Anspaugh from the University of Utah, USA for helpful comments, suggestions and discussions.