Identification of Boundary Conditions using Natural Frequencies

Abstract

The present investigation concerns a disc of varying thickness of whose flexural stiffness D varies with the radius r according to the law , where D₀ and m are constants. The problem of finding boundary conditions for fastening this disc, which are inaccessible to direct observation, from the natural frequencies of its axisymmetric flexural oscillations is considered. The problem in question belongs to the class of inverse problems and is a completely natural problem of identification of boundary conditions. The search for the unknown conditions for fastening the disc is equivalent to finding the span of the vectors of unknown conditions coefficients. It is shown that this inverse problem is well posed.

Two theorems on the uniqueness and a theorem on stability of the solution of this problem are proved, and a method for establishing the unknown conditions for fastening the disc to the walls is indicated. An approximate formula for determining the unknown conditions is obtained using the first three natural frequencies. The method of approximate calculation of unknown boundary conditions is explained with the help of three examples of different cases for fastening the disc (rigid clamping, free support, elastic fixing).

Keywords:

• Boundary conditions
• A disc of varying thickness
• Inverse problem
• Plucker condition

1. Introduction

Discs are parts of turbines and other various devices (see [1–6]). If it is impossible to observe the disc directly, the only source of information about possible defects of its fastening can be the natural frequencies of its flexural vibrations. The question arises whether one would be able to detect damage in disc fastening by the natural frequencies of its symmetric flexural vibrations. This article gives and substantiates a positive answer to this question.

The problem in question belongs to the class of inverse problems and is a completely natural problem of identification of the boundary conditions.

Closely related formulations of the problem were proposed in [7,8]. Contrary to this, in this article it is not the form of the domain or size of an object which are sought for but the nature of fastening. The problem of determining a boundary condition has been considered in [9]. However, as data for finding the boundary conditions, we take a set of natural frequencies, but not condensation and inversion (as in [9]).

Similarly formulated problems also occur in the spectral theory of differential operators, where it is required to determine the coefficients of a differential equation and the boundary conditions using a set of eigenvalues (for more details, see [10–15]). However, as data for finding the boundary conditions, we take one spectrum but not several spectra or other additional spectral data (for example, the spectral function, the Weyl function or the so-called weighting numbers) that were used in [10–15]. Moreover, the principal aim was to determine the coefficients in the equation and not in the boundary conditions. The aim of this article is to determine the boundary conditions of the eigenvalue problem from its spectrum in the case of a known differential equation.

The problem of determining a boundary condition using a finite set of eigenvalues has been considered previously in [16–18]. In contrast to these article, we think it is necessary to determine not the type of fastening of a string, membrane or beam but the type of disc fastening of varying thickness.

2. Formulation of the direct problem

The problem of axisymmetric flexural oscillations of disc of varying thickness without a hole in the center is reduced to following differential equation [5] (--1) where w is the deflection at radius r, D is the flexural rigitiy, h is the thickness, ρ is the density and ν is Poisson's ratio.

If , where , and m are constants, the thickness h is given by . Then Eq. (1(--1) ) becomes

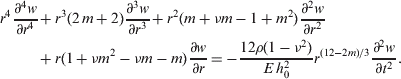
For vibrations, we write and hence obtain the following equation for u(r): (--2)

Although it is impossible to solve the problem for arbitrary m exactly, some particular solutions in terms of Bessel functions are found for a number of positive values of m and corresponding values of Poisson ratio ν in [19].

For the sake of being definite, we consider the particular case of Eq. (2(--2) ) with , Poisson ratio ν = 1/9, , and radius R = 1.

The problem of axisymmetric flexural oscillations of a disc of varying thickness without a hole in the center for this particular case is reduced to the following eigenvalue problem [19] (--3) (--4) (--5) Here is the eigenvalue parameter, E is the elasticity modulus, ω is the natural frequencies parameter, U₁(u), U₂(u) are the linear forms which characterize conditions for fastening the plate to the walls (rigid clamping, free support, free edge, floating fixing, elastic fixing), 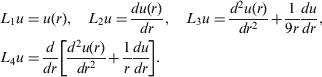The solution to (3) has form 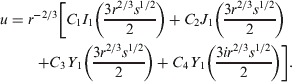[19] Here are the conventional notations for first-order Bessel functions of real and imaginary argument [20].

For a continuous plate (without a hole in the center), the constants .

Instead of the (4), (5), we can write the conditions (--6) where .

We shall now formulate the direct eigenvalue problem (3), (6): it is required to find the unknown natural frequencies of the oscillations of the plate from the linear forms U₁(u), U₂(u).

The natural frequencies ω_i are the corresponding positive eigenvalues of problem (3), (6) (see [6]). The nonzero eigenvalues of problem (3), (6) are the roots of the determinant where are linearly independent solutions of Eq. (3(--3) ); (--7) Thus, finding the three natural frequencies ω_i is equivalent to finding the three roots s_i of Δ(s).

For example, if boundary conditions (6) have the form (elastic clamping). For different c we have the different s_i. See Table I.

TABLE I Dependence c on s_i

	c = 10^−5	c = 1	c = 10	c = 10^2	c = 10^100
	0.085457	1.5178	2.6517	3.0663	3.0739
	3.1122	3.1145	3.1561	4.5575	5.1995
	5.4634	5.4651	5.4813	5.7412	7.3054

Thus, knowing c it is possible to find s_i by standard methods. The solution to this direct problem presents no difficulties. The question arises whether one would be able to do the reverse and find c knowing s_i. In a broader sense it may be stated as follows. Is it possible to derive unknown boundary conditions with a knowledge of s_i? The answer to this question is given in the next section.

3. Formulation of the inverse problem

The mathematical (direct) problem is an eigenvalue problem for a homogeneous linear fourth order equation, set up in the interval , accompanied by two linear homogeneous boundary conditions at r = 1; the sought solutions must be bounded for r = 0. The boundary conditions depend on 4 scalar coefficients (namely 3 because of the homogeneity).

Now we shall formulate the inverse of eigenvalue problem (3), (6): it is required to find the unknown linear forms U₁(u), U₂(u) from the natural frequencies of the disc oscillations.

We shall denote the matrix, consisting of the coefficients a_ij of the forms U₁(u) and U₂(u), by A and its minors by M_ij:

The search for the forms U₁(u) and U₂(u) is equivalent to finding the span of the vectors .

Hence, in terms of eigenvalue problem (3), (6), the inverse problem constructed above should be formulated as follows: the coefficients a_ij of the forms U₁(u) and U₂(u) of problem (3), (6) are unknown, the rank of the matrix A to make up these coefficients is equal to two, the nonzero natural frequencies s_k of problem (3), (6) are known and it is required to find the span of the vectors .

4. The uniqueness of the solution

Together with problem (3), (6), let us consider the following eigenvalue problem (--8) (--9) where .

We denote the matrix composed of the coefficients b_ij of the forms and by B and its minors by :

The span of the vectors is denoted by .

Theorem 1 (on the uniqueness of the solution of the inverse problem) Suppose the following conditions are satisfied (--10) If the nonzero eigenvalues {s_k} of problem (3), (6) and the nonzero eigenvalues of problem (8), (9) are identical, with account taken for their multiplicities, the spans and are also identical.

Proof The nonzero eigenvalues of problem (8), (9) are the roots of the determinant

In addition to the roots identical to the nonzero eigenvalues of the problems, the determinants Δ(s) and can also have the root s = 0 of finite multiplicity.

Since are entire functions in s of order 1/2, it follows from Hadamard's factorization theorem (see [21]) that determinants Δ(s) and are connected by the relation where k is a certain nonnegative integer and C is a certain nonzero constant. From this we obtain the identity (--11) Note that the number k in this identity is equal to zero. Actually, let us assume the opposite: k ≠ 0. Then the functions f_i(s) (i = 1, 2, 3, 4) and also the same functions multiplied by s^k are linearly independent.

Indeed, using MAPLE, we get ()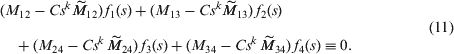 The determinant of the matrix 4 × 4 of the coefficients at sⁱ (i = 2, 4, 6, 8) in these representations of the functions f_j ( j = 1, 2, 3, 4) is not equal to 0. It now follows that eight functions f_j, s^k f_j ( j = 1, 2, 3, 4) are linearly independent for all k ≥ 8.

Further, the determinant of the matrix 8 × 8 of the coefficients at sⁱ() in the series expansion of the functions f_j, s^k f_j ( j = 1, 2, 3, 4) is not equal to 0 under k = 2, k = 4 or k = 6. This means that eight functions f_j (s), ( j = 1, 2, 3, 4) are linearly independent under k = 2, k = 4 or k = 6.

This completes the proof of linear independence of the functions f_j, s^k f_j ( j = 1, 2, 3, 4) for all k ≠ 0.

From this and identity (11) we obtain which, in combination with , contradict condition (10) of the theorem.

Hence, k = 0. From this and from identity (11), by virtue of the linearly independence of the corresponding functions, we obtain which is equivalent to the proportionality of the bivectors and .

It is well known [22] that there is a natural one-to-one correspondence between the classes of nonzero, proportional bivectors and the two-dimensional subspaces of a vector space. In this correspondence, a vector product of the vectors of its arbitrary basis x₁ and x₂ corresponds to each subspace and a subspace corresponds to each bivector . It, therefore, follows from the last equation that which it was required to prove.

5. Exact solution

It has been shown above that the problem of finding the unknown linear forms U₁(u) and U₂(u) from the natural frequencies of axisymmetric flexural oscillations of a disc of varying thickness has a unique solution (in the sense that the spans, composed of the coefficients of these linear forms, are uniquely defined). The next question is how this solution can be constructed.

This section deals with solving this problem and constructing exact solution by the first three natural frequencies ω_i.

Suppose s₁, s₂, s₃ are the values corresponding to the first three natural frequencies ω_i. We substitute the values s₁, s₂, s₃ into Δ(s) and obtain a system of three homogeneous algebraic equations in the four unknows (--12)

The resulting set of equations has an infinite number of solutions. If the resulting set has a rank of 3, the unknown minors can be found accurate to a coefficient. The unknown span and its basis are found from the minors using well-known methods of algebraic geometry [23]. We also note [17,24], in which detailed method for solution of this problem was given.

If the minors are found accurate to a constant then the unknown span and its basis are found from the minors using well-known methods of algebraic geometry [23]. We also note [17,24], in which a detailed method for solution of this problem was given.

For example, if M₁₂ = 1, then (--13) if M₁₃ = 1, then (--14)

These reasons prove

Theorem 2 (on the uniqueness of the solution of the inverse problem) If the matrix of system (12) has a rank of 3, the solution of the inverse problem of the reconstruction boundary conditions (4) and (5) is unique.

Remark Theorem 2 is stronger than Theorem 1. Theorem 2 uses only three natural frequencies for the reconstruction of boundary conditions and not all natural frequencies as in Theorem 1. It follows from the uniqueness Theorem 1 already proved that the unknown minors M₁₂, M₁₃, M₂₄, M₃₄ can be found accurate to a constant by all natural frequencies. To prove that the unknown minors M₁₂, M₁₃, M₂₄, M₃₄ can be found accurate to a constant by three natural frequencies is very easy problem in concrete cases. But in the common case to prove that set (12) has a rank of 3 has failed to do this. Yet our uniqueness Theorem 1 suggests this result in the common case.

6. Approximate solution

Since small errors are possible when measuring natural frequencies, the problem arises of finding an algorithm for the approximate determination of the type of fixing disc from the first three natural frequencies found with a certain error.

If the values s_i (i = 1, 2, 3) are approximately the same as the first three exact eigenvalues of problem (3), (6), and set (12) has a rank equal to 3, the unknown minors can be determined accurate to a coefficient. Further, the problem arises of finding the unknown span from the values M₁₂, M₁₃, M₂₄, M₃₄. However, the values M₁₂, M₁₃, M₂₄, M₃₄ cannot be minors of a matrix. So this problem is not trivial. We must find minors P₁₂, P₁₃, P₂₄, P₃₄ close to the values M₁₂, M₁₃, M₂₄, M₃₄. This problem is solved with the help of Lagrangian multiplier method and algebraic geometry.

It is known from algebraic geometry that the numbers P₁₂, P₁₃, P₁₄, P₂₃, P₂₄, P₃₄ are minors of some matrix, if and only if the following condition is satisfied This condition is called Plucker condition (see [22,23]).

Using , we get (--15)

By definition, put Using this definition, we get Plucker condition (--16) It characterizes a surface in the four-dimensional space.

By definition, put .

If Plucker condition for these numbers is realized, then M₁₂, M₃₄, M₁₃, M₂₄ are minors of some matrix and corresponding boundary conditions are found from the minors using the methods in Section 4.

If Plucker condition for numbers M₁₂, M₃₄, M₁₃, M₂₄ is not realized, the required minors P₁₂, P₁₃, P₂₄, P₃₄ are found with the help of Lagrangian multiplier method and algebraic geometry.

Indeed suppose is Lagrange function where 2p is the Lagrangian multiplier. If we find minimum of the function , then we obtain the minors P₁₂, P₁₃, P₂₄, P₃₄ most close to the values M₁₂, M₁₃, M₂₄, M₃₄.

The minimum of the function is found from equations (--17) (--18)

By definition, put

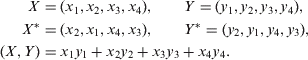
With the preceding notations Eqs. (17(--17) ) and (18(--18) ) are identical to the following equations (--19) (--20) It follows from (19) and (20) that the vector X* is orthogonal to the vector X, and the vector is on orthogonal projection of the vector on the surface (16).

Having solved (19) as set of linear equations with the unknowns , we get (--21) From (21) it is easy to get (--22)

Substituting (21) for X and (22) for X* in (20), we obtain

Notice that Therefore, This quadric equation has two roots If X is close to Y, then |p| ≪ 1 and thus we have (--23)

The vector X can be found using (21) and (23). The coordinates P₁₂, P₁₃, P₂₄, P₃₄ of X are minors of a matrix. This matrix and corresponding boundary conditions are found from the minors P₁₂, P₁₃, P₂₄, P₃₄ using the methods in Section 4.

7. Stability of the solution

In this section we study continuity of the solution of the inverse problem with respect to s_i. It is shown that small perturbations of eigenvalues s_i (i = 1, 2, 3) lead to small perturbations of the boundary conditions.

Let s_i (i = 1, 2, 3) be eigenvalues of problem (3), (6), and (i = 1, 2, 3) are such values that and R is such a number that

Theorem 3 Suppose that one of the third-order minors of the matrix is substantially non-zero. If then the boundary conditions of problem (8), (9) are close to the boundary conditions of problem (3), (6).

Proof By virtue of continuity of the functions (7), we have (--24) where .

First, let us prove that

Recall that one of the third-order minors of the matrix is substantially non-zero by the hypotheses of Theorem 3, and so (--25)

To be precise, assume that (--26) It follows from (24) that (--27)

It can be shown by direct calculations that set (12) has the solution (--28) Like previously, the set (--29) has solution (--30)

By definition, put

In the new notations, we have

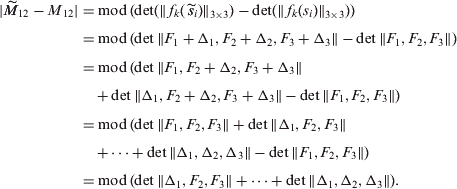
It follows from (24) that (--31) Calculating the determinant and using (31), we get Similarly, .

Arguing as above, we see that By definition, put . Then,

Continuing this line of reasoning, we see that

This implies that (--32) where By (26) and (27) this means that is close to Y.

Now let us prove that close to .

Combining (23) and (32), we see that 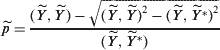close to p. This means that close to (21).

Finally, let us prove that the boundary conditions of problem (8), (9) are close to the boundary conditions of problem (3), (6), where ()

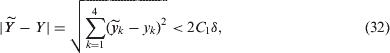
We know already (see [24]) that the coefficients of the boundary conditions are the minors of matrix A as in (13). This means that if is close to X, the boundary conditions of problem (8), (9) are close to the boundary conditions of problem (3), (6).

This completes the proof. ▪

Computer calculations confirm the stability of the solution of the inverse problem. The order of error is often hardly different from the error in the closeness of values of and λ_i and only in some cases can it be deteriorated by four orders of magnitude. So the measurement accuracy of instruments to measure natural frequencies must exceed accuracy to measure boundary conditions by four orders of magnitude.

It follows from Theorems 2 and 3 that the inverse problem is well posed, since its solution exists, is unique and continuous with respect to s_i (i = 1, 2, 3).

8. Examples

We use dimensionless variables in the numerical examples.

Example 1 If correspond to the first three natural frequencies ω_i determined using instruments for measuring the natural frequencies with an accuracy of 10⁻⁴, then the solution of set (12), accurate to a constant, has the form Using (21) and (23), we get

Suppose ; then from (13), we obtain

Note that the numbers presented above are almost the same as the first three exact values corresponding to rigid clamping. This means that the unknown disc fastening inaccessible to direct observation has been correctly determined.

Example 2 If correspond to the first three natural frequencies ω_i determined by a frequency meter with an accuracy of 10⁻⁴, then the solution of set (12), accurate to a constant, has the form Using (21) and (23), we get

Suppose ; then from (14), we obtain

Note that the numbers presented above are almost the same as the first three exact values corresponding to the free support. This means that the unknown disc fastening inaccessible to direct observation has been correctly determined.

Example 3 If correspond to the first three natural frequencies ω_i determined by means of instruments for measuring natural frequencies with an accuracy of 10⁻⁴, then the solution of set (12), accurate to a constant, has the form Using (21) and (23), we get

Suppose ; then from (13), we obtain

Note that the numbers presented above are almost the same as the first three exact values , which correspond to elastic fixing with matrix This means that the unknown disc fastening inaccessible to direct observation has been satisfactorily determined.

Thus, the form of the disc fastening of varying thickness can be determined from the first natural frequencies measured by special instruments.

Note that we choose such a particular variation law for the thickness of the disc to be precise. If the variation law for the thickness of the disc is different from that adopted in this study, then the mathematical formulation and the proposed procedures of solving of the direct and inverse problems remain valid. In this case we must substitute linearly independent solutions of corresponding differential equation for u₁ and u₂ in (7), whose are not singular at r = 0, and the corresponding linearly forms for L₁, L₂, L₃, L₄ in (6).

Direct problems on hydroelasticity and aeroelasticity are considered in [25,26]. Similar inverse problems can be solved by means of the method proposed in this article.

Acknowledgments

The authors are grateful to professor M.A. Ilgamov for useful discussions of engineering aspects.

This research was partially supported by the Russian Foundation for Basic Research (01-01-00996), Ministry of Education of Russia (E02-1.0-77), Emmy Noether Research Institute for Mathematics, the Minerva Foundation of Germany, the Excellency Center “Group Theoretic Methods in the Study of Algebraic Varieties” of the Israel Science Foundation, and by EAGER (European Network in Algebraic Geometry).

Additional information

Notes on contributors

A.V. Mouftakhov †

^†E-mail: [email protected]

Notes

^†E-mail: [email protected]