A wavelet multiscale method for the inverse problems of a two-dimensional wave equation

Abstract

This article considers the problem of estimating the velocity in a two-dimensional acoustic wave equation. The wavelet analysis is introduced and a wavelet multiscale method is constructed, based on the idea of hierarchical approximation. The inverse problem is decomposed into a sequence of inverse problems which rely on the scale variables and are solved successively according to the size of scale from the longest to the shortest. And in every inversion, at different scales, the regularized Gauss–Newton method is used, which is stable and fast, until the parameter of the primary inverse problem is found. The results of numerical simulations indicate that the method is a widely convergent optimization method (in some cases it may be global), and exhibits the advantages of conventional methods on computational efficiency and precision.

Keywords:

• Inverse problem of two-dimensional wave equation
• Parameter estimation
• Wavelet multiscale method
• Regularized Gauss–Newton method

1. Introduction

Inverse problems of wave equations have attracted much attention in the last three decades. Instances include pattern recognition, atmospheric test, quantum mechanics, image treatment, geophysical prospecting, etc. Many approaches have been proposed. Roughly speaking, they may fall into two kinds, namely linearized operator inversion and model iteration inversion. Linearized inversion only can be used when the geometric structure of the domain is simple or some fair priori knowledge on the background parameter field is known. Model iteration inversion belongs to the category of optimization inversion. The direct application of this kind of inversion to real and synthetic data has been disappointing because numerous local minima in the objective function prevent iterative optimization techniques from working effectively.

Multiscale inversion is a newly developed inversion strategy to accelerate convergence, enhance stability of inversion, overcome disturbance of local minima, and by which we can search out the global minimum. The main essence of multiscale inversion is to decompose the original problem into different scales or frequency bands, and to carry out inversion beginning at the longest scale, since at a longer scale, the objective function shows stronger convexity and has less minima, and therefore has a good chance of finding the global minimum. The global minimum of the longest scale is in the neighborhood of the global minimum for the problem at the second longest scale, and thus can be used as the initial guess for the second optimization problem. Successively fining upward in this way succeeds in finding the global minimum of the original fine scale problem.

For the one-dimensional inversion problem, scale decomposition was shown to be very effective [8]. Later, several ideas related to scale decomposition for the two-dimensional problem were published [9,10]. The multigrid method [7] is a family of techniques that are useful for solving large-scale linear and nonlinear problems. The method consists of decomposing a problem by scale, followed by the resolution of each scale component by a suitable relaxation operator. More recently, the multigrid method has been applied to distributed parameter estimation problems [1–3,14]. The results showed that iterative inversion methods performed much better when employed with a decomposition by scale.

Wavelet analysis is a kind of multiresolution method, and it has the properties of adaptability and localization. This allows the idea of wavelet multiresolution to be used for inverse problems. Jun Liu [11] numerically studied wavelet multiresolution method for distributed parameter estimation, and a simple elliptic problem was taken as a suitable model. Several authors have also used wavelet to analyze linear ill-posed problems [5,6,12,13]. All these works showed the effectiveness of wavelet on inverse problems.

The goal of this article is to develop a wavelet multiscale method for the parameter estimation problem of a two-dimensional acoustic wave equation in geophysical prospecting. The approach is based on the hierarchical approximation of wavelet, and combined with the regularized Gauss–Newton method [16], which is served as a basic iteration at every scale. This method turns out to be very robust (widely convergent or even globally convergent in some cases) and efficient (the computational cost is greatly reduced and the desired precision is guaranteed).

The article is organized as follows: in Section 2, we discuss two-dimensional wavelet multiresolution analysis (MRA), as background for later sections. Section 3 investigates the wavelet multiscale method for the inverse problem of acoustic wave equation. Section 4 presents some numerical results of two concrete examples. Finally, in Section 5, we give some conclusions.

2. Two-dimensional wavelet multiscale analysis

For notational purposes, a brief description of wavelet multiscale analysis follows. For more details, please refer to [4].

2.1. Wavelet and multiresolution analysis

Definition 2.1 A function ψ (x) in L² (R) is called a wavelet or mother wavelet, if it satisfies (---643--1) where R⁺ = R − { 0 }. Definition 2.2 For any function f(x) ∈ L² (R), its continuous wavelet transform is defined by (---643---1) Its inverse transform is (---643---2) If restricting (---643----1) with j, k ranging over Z, we obtain the discrete wavelet basis (---643---3) The discrete wavelet transform is (---643---4) Here we adopt a binary wavelet, namely a₀ = 2, b₀ = 1.

Definition 2.3 A MRA is a sequence of closed subspaces V_j in L² (R), called scaling spaces, satisfying

1.	Vj ⊂ Vj − 1 for all j∈ Z,
2.	Yj ∈ Z Vj is dense in L2 (R),
3.	(---643----2) ,
4.	f(x) ∈ Vj if and only if f(2j x) ∈V0 ∀ j ∈ Z,
5.	f(x) ∈ V0 if and only if f(x − k) ∈ V0, ∀ k ∈ Z,
6.	There exists ϕ ∈ V0 such that {ϕ0, k : k ∈ Z} is an orthonormal basis in V0, where (---643----3) for all j,k ∈ Z. The function is called the scaling function of the MRA.

It is easy to know from the definition of MRA that

1.	(---643----4) is an orthonormal basis for the space Vj.
2.	Suppose Pj is the orthogonal projection operator from L2 (R) onto Vj, then for any f(x) ∈ L2 (R), we have (---643----5) .

2.2. Multiscale decomposition and reconstruction

Let { V_j (x);j ∈ Z} be a one-dimensional MRA, its scale function is ϕ (x), the wavelet function is ψ (x). Then (---643----6) forms a two-dimensional MRA, its scale function is (---643--2) and the wavelet functions are (---643--3) (---643--4) (---643--5) Suppose a function(---643----7) , according to the principle of wavelet multiresolution decomposition, we have (---643--6) with (---643--7) (---643--8) and (---643--9) Let (---643----8) be infinite matrices, and let H_r and H_c denote the projections of H on the rank and column of matrix respectively; similarly G_r and G_c denote projections of G on the rank and column of matrix, respectively. Then (2.9)(---643--9) is simplified to (---643--10) Decompose successively until to a scale J₂, namely the decomposition is carried out for J₂ − J₁ step, then we obtain (---643--11) which is just the algorithm of two-dimensional wavelet multiscale decomposition.

From c_J2 and (---643----9) , we have the reconstruction algorithm (---643--12) where j = J₂ − 1, J₂ − 2, Λ Λ, J₁, and (---643----10) , are conjugate transpose operators of H_r, H_c, G_r, G_c, respectively.

In this article, the compact supported orthogonal wavelet basis – the “doub4,” constructed by I. Daubechies, is used to conduct two-dimensional multiscale decomposition and reconstruction.

2.3 Analysis on how two-dimensional multiscale analysis can increase resolution

From the principle of two-dimensional wavelet multiscale analysis, we know (---643---5) In fact, as any signal (or function) f(x, y) is received by physical instruments, it always has limited resolution. Therefore we can suppose f(x, y) ∈ V_J (x, y) (J is a definite integer). In addition, as { V_j (x, y);j ∈ Z} is an infinite space band on both sides, for simplicity, we suppose J = 0, and set f₀ (x, t) = f(x, t).

When j = 0, we have (---643---6)

When the problem is decomposed into the (j + 1)th scale from the jth scale, since the space V_j + 1 (x, y) only consists of the part of lower frequency of the space V_j (x, y), the inversed solution in the space V_j + 1 (x, y) should be an approximation to the original one, which does not contain the part of higher frequency; it is only a local trend near the parameter of the model. But since the subspace W_j + 1(x, y) of V_j (x, y) contains the part of higher frequency, we cannot get the information of higher frequency at smaller scale in the space V_j + 1 (x, y), but can obtain it through the inversion in the space V_j (x, y). Similarly, we cannot get the information of further higher frequency in the space V_j (x, y), but can obtain it through the inversion in the space V_j − 1 (x, y). This is just the principle of increasing resolution by two-dimensional wavelet multiscale analysis.

3. A wavelet multiscale method for the parameter estimation problem of a two-dimensional acoustic wave equation

3.1. Continuous mathematical model

The inverse problem of acoustic wave equation attempts to find the velocity model that minimizes the difference between observed and modeled data. The modeled data are generated by the acoustic wave equation (---643--13) with the boundary conditions (---643--14) (---643--15) and the initial conditions (---643--16) Here the wave field u and the source signal s are functions of the space variables x, z and the time variable t, and the velocity v is a function of x and z only. If the velocity v is known, (3.1)(---643--13) –(3.4)(---643--16) forms the direct problem for wave field simulations. But in practice, the velocity v is not known. What we know is merely some observed data of the wave field. We should reconstruct the velocity from (3.1)(---643--13) –(3.4)(---643--16) and the observed data. Then (3.1)(---643--13) –(3.4)(---643--16) , and the observed data form the model of inverse problem.

In general the observed data are available for some time interval t ∈ [0, T] and for some spatial interval x ∈ [0, L]. A measure of the difference between observed and modeled data can be obtained using the norm (---643--17) where f and (---643----11) are observed and modeled data, respectively. Actually (---643--18) which serves as the auxiliary condition of the inverse problem. The velocity field v, which minimizes Eq. (3.5)(---643--17) , is the desired solution to the inverse problem.

3.2. The discretized model and regularized gauss–newton method

We consider the situation of parallel incident wave, in this case, the Eq. (3.1)(---643--13) changes to (---643--19) where δ (x) is the δ-function, g(t) = 0, t < 0.

By using the classic second-order, finite-difference scheme, (3.1)′(---643--19) , (3.2)(---643--14) –(3.4)(---643--16) , and (3.6)(---643--18) can be discretized as (---643--20) where (---643----12) and h_z are the step sizes in x and z directions, respectively, τ is the step size of time, (---643----13) .

The difference Eq. (3.7)(---643--20) defines a vector-valued function A:V → F, where V and F denote vectors, which are composed of v_{i, j} and (---643----14) in a suitable sequence (---643---7) Let (---643----15) denote the observed data and form the vector (---643----16) in the some sequence as F, (---643---8) Then the problem of inversing V is reduced to a nonlinear operator equation (---643--21)

Tikhonov regularization [15] of such an ill-posed problem is achieved by replacing the operator (3.8)(---643--21) by the minimization problem (---643--22) where _M1 and M₂ are the second-order smooth matrices in the x-direction and in the z-direction, respectively, (---643---9) The regularized Gauss–Newton method (see [16]) can be used to find the minimum (---643--23) It is a stable and fast iterative method. But it is only a local convergent, namely the convergence to the global minimums relies highly on initial guesses.

3.3. Wavelet multiscale method

Theoretically, any iterative descent methods can be used to determine the optimum velocity model by globally minimizing the objective function. But the direct application of this inversion technique to real and synthetic data has been disappointing because numerous local minima in the objective function prevent iterative optimization techniques, such as the regularized Gauss–Newton method, from finding the global minimum unless the initial model for the velocity field is already in the neighborhood of the global solution.

The above discussion implies that the primary problem of inversion is the presence of local minima in the objective function. This leads to the idea of multiscale inversion that has explored the possibility of diminishing the problem of local minima by a decomposition of inversion problem by scale. Once the problem has been decomposed by scale the long scale components are solved first with the idea being that at long scales the number of local minima is greatly reduced and those that remain are further apart from each other. The application of an iterative descent method at a long scale of the problem is thus more likely (than at a short scale) to find the global minimum or at least a local minimum that is in the neighborhood of the global minimum. The solution found at the long scale of the problem is then recursively refined by using it as an initial solution at increasingly shorter scales.

In this article, we try to use wavelet to make decompositions, and at every scale, use the regularized Gauss–Newton method as the optimization algorithm. We call this inversion procedure a wavelet multiscale method. This method is more efficient and further reduces the computational burden of the inversion problem compared to that of the multigrid method, since there is no need to define restriction and injection operators, and fast wavelet decomposition and reconstruction algorithm can be used.

The object to be decomposed may be the source, the wave field, the velocity model, or a combination of the three. When carrying out the decomposition, there are two basic methods: the first one is to make wavelet transformation on all the velocity, the wave field and the source function. As the scale increases, the dimensions of the discretized inverse problems will be greatly reduced especially for high-dimensional continuous problems. But the problem to be faced is that the treatment on the boundary and the direct wave is troublesome, and demands high precision of the forward computation. The second one is to make wavelet transform only on the wave field and the source. This method is rather simple, and does not need high precision of the forward computation. Therefore we choose the second one in this article. The source and wave field are transformed by wavelets into different scales. Then accordingly the initial nonlinear minimization problem is decomposed into a sequence of nonlinear minimization problems at different scales. According to the idea of multiscale decomposition, the regularized Gauss–Newton method (3.10)(---643--23) is executed at the longest scale I until an approximation (---643----17) is obtained at this scale. It then proceeds at the second longest scale using (---643----18) as the initial guess. Successively fining upward in this way succeeds in finding the global minimum of the original fine scale problem.

The algorithm is summarized as follows:

1.	Step 1 For the model of two-dimensional wave equation, given the true velocity model V*, the source function s*, carry out forward computation in (3.7)(---643--20) to obtain the model data f*. Choose an initial velocity V0.
2.	Step 2 Use the compactly supported orthogonal wavelet “Doub4” and the two dimensional wavelet decomposition algorithm to conduct decompositions of s* and f* at different scales j(j = 0, 1, Λ, I), so as to obtain the smoother part (information of low frequency) (---643----19) of s* and f* at the longest scale I, and the coarser part (information of high frequency) (---643----20) at the scale sequence j (j = I, I − 1, Λ, 1).
3.	Step 3 At the longest scale I, taking the smoother part (---643----21) as the source and the wave field data, we obtain an approximation to the original inverse problem at scale I. Discretizing the inverse problem at scale I, similarly to (3.8)(---643--21) , we obtain an optimization problem. Use the regularized Gauss–Newton method to make correction on the initial velocity (---643----22) until the global minimum (---643----23) is obtained.
4.	Step 4 Reconstructing the smoother part (---643----24) and the coarser part (---643----25) at scale I by the two-dimensional wavelet reconstruction algorithm, we obtain the smoother part (---643----26) at scale I − 1. Taking (---643----27) as the source and the wave field data, we obtain an approximation to the original inverse problem at scale I − 1. Using the velocity (---643----28) as the initial velocity, we carry out the regularized Gauss–Newton iterations to obtain the global minimum (---643----29) at scale I − 1.
5.	Step 5 Proceed inductively until the global minimum of the original inverse problem (at scale 0) is obtained.

From the above inversion procedure we see that after conducting the decomposition of the source function and the wave field data, as scale increases, the complexity of the objective function is reduced. Its form further approaches the general trend of the waveform. In this situation, the number of local minima is greatly reduced and those that remain are further apart from each other. The reason lies in that by multiscale decomposition, we can give approximations to the original data in the sense of scale, therefore lots of local minima are degenerated to trivial points, thus the affections of local minima are reduced. In this case we can easily search out the global minimum by using the regularized Gauss–Newton method at long scale. As scale decreases, and the coarse parts of the source function and wave field data constantly are added, the coarse part of the objective function is gradually recovered. Since we have found the general trend of the objective function, the inversion procedure is conducted near the global minimum. Therefore it is easy to search out the “global minimum” at every scale. At last, when the scale is reduced to the original one (scale 0) of the source function and the wave field data, the velocity, which has been searched out to minimize the objective function, is just the optimal velocity in the sense of “global.”

4. Numerical simulations

In order to test the effectiveness of the wavelet multiscale method, we carry out numerical simulations for two concrete models in geophysical prospecting.

The source function is chosen as (---643----30) . At scale 0, we choose step sizes h_x = 1000 m h_z = 500 m τ = 0.1 s, therefore there are 10 grid points in the horizontal direction and 5 grid points in the vertical directions. The regularization parameters α₁ = α₂ = 10^− 6. The longest scale I of wavelet decomposition is 5. At every scale, the regularized Gauss–Newton method is terminated when the modification is equal to or less than 20 m/s.

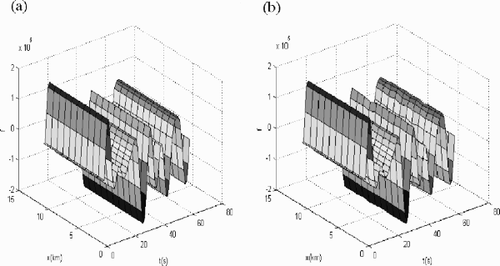
The first velocity model is depicted in Fig. 1(a). It is a model of leveled stratified medium, which has two interfaces. The forward seismic records (the observed data) of this velocity is shown in Fig. 2(a). The initial value v₀ (x, y) ≡ 2350 m/s. Figure 1(b) shows the inversion result at scale 0, it is the final approximation of the original inverse problem. Figure 2(b) gives the corresponding synthetic data (the modeled data). In this numerical example, if directly applying the regularized Gauss–Newton method, starting from the same initial value, the iteration is also convergent, but takes about 132.23% CPU time of the wavelet multiscale inversion method.

Figure 1. The velocity of model (I). (a) The true value of the velocity of model (I) and (b) the inversion result at 0-scale.

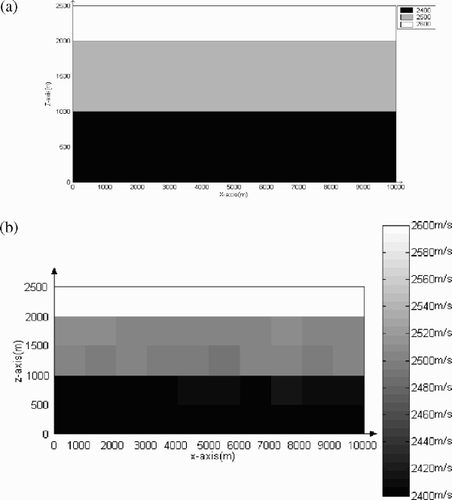
Figure 2. Comparison of seismic records of model (I). (a) The forward seismic records and (b) the synthetic data.

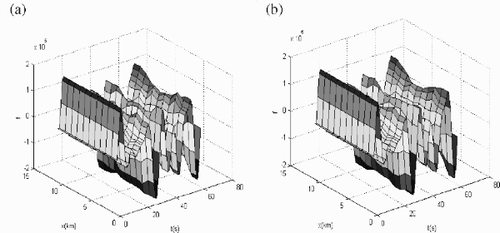
The second velocity model is depicted in Fig. 3(a). It is an inhomogeneous medium. The forward seismic records of this velocity is shown in Fig. 4(a). The initial value is also 2350 m/s. Figure 3(b) shows the inversion results at scale 0. Figure 4(b) gives the corresponding synthetic data. In this numerical example, if directly applying the regularized Gauss–Newton method, starting from the same initial value, the iteration is not convergent.

Figure 3. The velocity of model (II). (a) The true value of the velocity of model (II) and (b) the inversion result at 0-scale.

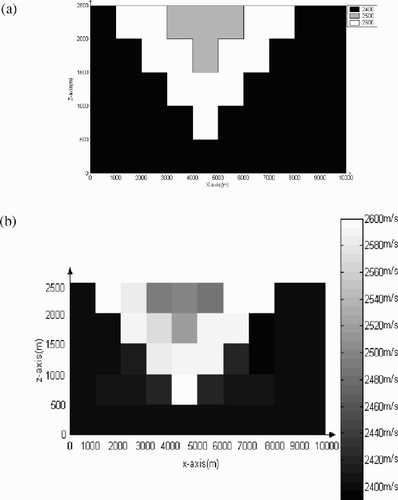
Figure 4. Comparison of seismic records of model (II). (a) The forward seismic records and (b) the synthetic data.

From the above numerical results we see that the wavelet multiscale inversion is really a widely convergent method, and reduces the computational burden of conventional inversion methods. Lots of other numerical tests have been made for different models, and in some cases, the wavelet multiscale method is global convergent.

5. Conclusion

Multigrid methods are successful for inverse problems at avoiding local minima, but must define restriction, relaxation, and injection operators. All these make the methods rather complicated. Multilevel methods must define prolongation operations. And computational precisions will be reduced, since there is no close connection between different levels. Wavelet multiscale inversion conducts analysis in a sequence of embedded spaces, fully utilizes the connections between different scales to guide search directions. Because there are ready-made fast algorithms of decomposition and reconstruction, the operation is simple, fast, and stable. Wavelet multiscale method can not only reduce the computational cost and improve precision of classical methods, but also overcome the problem of local convergence. It is an extremely promising strategy of inversion.

Acknowledgment

The work was supported by the National Science Foundation of China, under Grant No. 40374046.

Additional information

Notes on contributors

B. Han †

E-mail: [email protected]

Notes

E-mail: [email protected]