Abstract
In the conventional electrical impedance tomography (EIT), the internal impedivity distribution, that is mixture distribution, is reconstructed based on the physical relationship between the known sets of injected currents through the electrodes and induced voltages on the surface of the domain of interest under the assumpution that the domain is stationary during the measurements. This study considers a dynamic electrical impedance imaging to binary-mixture systems with known internal structures to which additional electrodes can be attached. We attempt the utilization of the additional electrodes to enhance the recontruction. Also, we assume the domain is undergoing rapid transient, so the resistivity distribution in the domain of interest changes rapidly within the time taken to acquire a full set of independent measurement data. The dynamic EIT problem is treated as the nonlinear state estimation problem and the unknown state (resistivity) is estimated with the aid of extended Kalman filter in a minimum mean square error sense. Computer simulations for the two-dimensional object with abrupt changing resistivity distribution are provided to illustrate the reconstruction performance of the proposed algorithm.
1. Introduction
Binary-mixture systems are frequently encountered in many engineering applications including heat exchangers, oil or natural gas pumping systems, fluidized beds, and so on. For the optimal operation as well as for the design and performance analysis, the knowledge on mixture distribution is of importance. Many imaging techniques using radiological, optical, sonic, or electromagnetic characteristics have been proposed and applied to visualize mixture systems. Among these, electrical impedance tomography (EIT), a relatively new imaging modality, is considered in this work.
Over the past few decades, EIT techniques have received much attention from both theoretical and experimental points of view since they can be used as an alternative imaging modality for monitoring tool in many engineering fields. This is mainly due to the relatively cheap electronic hardware requirements, noninvasive measurement sensing, and relatively good temporal resolution Citation[1–Citation3]. In EIT, the internal impedivity (inverse of admittivity) distribution corresponding to the mixture distribution is reconstructed with the known sets of injected currents through the electrodes and induced voltages on the surface of the domain of interest (the object) based on the relationship between electrical current and potential distribution. EIT includes both electrical capacitance tomography (ECT) and electrical resistance tomography (ERT). However, more frequently in EIT it is assumed that the resistive part of the impedivity dominates and only the resistivity (inverse of conductivity) distribution inside the object is estimated.
A basic idea of the conventional EIT is that the distribution of internal electrical properties is stationary during acquisition of a full set of EIT data required for the image reconstruction. However, the characteristic time of the systems under severe transient could be shorter than the time interval that would be required for the EIT measurement. We introduce a dynamic EIT imaging technique for the case where the resistivity distribution inside the object changes rapidly within the time taken to acquire a full set of independent measurement data. In this work, the inverse problem is treated as the nonlinear state estimation problem and the unknown state (resistivity) is estimated with the aid of extended Kalman filter in a minimum mean square error sense.
In particular, this study considers the systems with internal structures where internal electrodes could be attached. Such systems are often possible in heat exchangers with tube banks or mixers with rotors. Additional electrodes attached to the internal structure would be expected to enhance the reconstruction performance. Several simulated mixture distributions are reconstructed with and without internal electrodes and comparisons are made to illustrate the relative reconstruction performance. Several numerical results will be given to corroborate that the internal electrodes improve the spatial and temporal resolution of reconstructed images.
2. Mathematical model and dynamic EIT problems
2.1. Problem definition
In the present EIT problem, the quantity to be estimated is actually the resistivity distibution, which should satisfy the physical relationship between the internal resistivity distribution ρ and the potential distribution u expressed as a partial differential equation (Laplace equation) over the domain of interest Ω with appropriate boundary conditions:
(---471--1)
subject to
(---471--2-)
(---471--2-)
where Il denotes the injected current through the lth electrode el and L is the number of the electrodes mounted on the surface. Hence, the present problem is to find the resistivity distribution both satisfying the above constraints and minimizing the difference between the calculated bounday potential V and the measured boundary potential U:
(---471--3)
Owing to the complexity of this relationship, it is impossible to obtain a closed-form solution for arbitrary resistivity distribution. Hence, various reconstruction algorithms have been developed in the literature to estimate the internal resistivity distribution of the object. This work adopts the finite element method (FEM) to discretize the domain and to find the potential field induced by the applied currents in a predetermined manner. Also, as a solver to the present dynamic EIT problem the extended Kalman filter is introduced.
Most of the reconstruction algorithms presented so far are mainly focused on the case where the internal resistivity of the object is time-invariant within the time taken to acquire a full set of independent measurement data. As is well known, the conventional EIT imaging techniques such as backprojection or modified Newton–Raphson (mNR) algorithm use a full set of voltage measurements for each image Citation[4,Citation5]. However, in some real applications such as mixture fields in multi-phase heat transfer media and chemical process lines undergoing severe transient, this stationary approximation seems to be inadequate to obtain satisfactory temporal resolution for the reconstructed images due to the rapid changes in resistivity distribution.
More recently, dynamic imaging techniques have been developed to enhance the temporal resolution of the reconstructed images in the situations where the resistivity distribution inside the object changes rapidly in time. In most of these techniques, the inverse reconstruction problem is treated as a state estimation problem and the time-varying state is estimated with the aid of linearized Kalman filter (LKF) Citation[6–Citation10] or extended Kalman filter (EKF) Citation[11,Citation12].
Quite often in real situations there are partially known fixed internal structures inside the object. These internal structures can be, for example, an impeller drive shaft or a mixing paddle in process vessels and an assembly of fuel rods in nuclear reactor. The internal structures inside the object may results in difficulties in the image reconstruction by EIT especially when the high-resistive region is near the conductive internal structure or vice versa Citation[13,Citation14]. The so-called masking effect in the reconstructed image may be significant for the high-contrast case. There are two ways to get around these difficulties; one is to use the internal structure as additional electrodes Citation[13,Citation15,Citation16] and the other is to take it into account as a priori information in the inverse procedure Citation[14]. However, all of the above approaches are for the case where the resistivity distribution inside the object is time-invariant for one classical frame.
The purpose of the present work is to develop a dynamic EIT reconstruction algorithm for the visualization of transient binary-mixture systems whose internal structures are known a priori. For the utilization of the prior information as well as the enhancement of the image reconstruction, we consider the case where additional electrodes can be attached to the known internal structure.
The inverse problem is treated as the state estimation problem and the resistivity distribution is estimated with EKF. In order to deal with the well-known ill-posedness of the EIT inverse problem, a smoothness assumption is made and the generalized Tikhonov regularization technique is also introduced in the cost functional.
We carried out extensive computer simulations with synthetic data to illustrate the reconstruction performance, and to investigate the effects of additional internal electrodes on the spatial and temporal resolution of the reconstructed images.
2.2. Extended Kalman filter approach
In case where the resistivity distribution inside the object changes rapidly within the time taken to acquire a full set of independent measurement data, the conventional static imaging techniques which need a full set of voltage measurements for each image often fail to obtain satisfactory temporal information on the resistivity distribution. We consider the underlying inverse problem as a state estimation problem to estimate rapidly time-varying distribution of the resistivity. In the state estimation problem, we need so-called the dynamic model which consists of the state equation, i.e., for the temporal evolution of the resistivity and the observation equation, i.e., for the relationship between the resistivity and boundary voltage.
In general, the temporal evolution of the resistivity distribution ρk in the object Ω is related by the nonlinear mapping. Here, the state equation is assumed to be of the linear form, of which the modeling uncertainty is compensated by the process noise
(---471--4)
where Fk ∈ RN × N is the state transition matrix at time k and N is the number of finite elements in the FEM (finite element method). In particular, we take Fk = IN where IN ∈ RN × N is an identity matrix, to obtain the so-called random-walk model. It is assumed that the process error, wk is white Gaussian noise with the following covariance which determines the rate of changes in resistivity distribution
(---471--5)
Let Uk ∈ RL, defined as
(---471--6)
be the surface measurement voltages induced by the kth current pattern. Then the observation equation can be described as the following nonlinear mapping with measurement error
(---471--7)
where the measurement error vk is also assumed to be white Gaussian noise with covariance
(---471--8)
Linearizing EquationEq. (7)(---471--7) about the current predicted state ρk|k − 1 we obtain
(---471--9)
where HOTs represents the higher-order terms which will be considered as additional noise, and Jk(ρk|k − 1) ∈ RL × N is the Jacobian matrix defined by
(---471--10)
Define the pseudo-measurement as
(---471--11)
Then we obtain the linearized observation equation by considering the HOTs in Equation(9)
(---471--9) as additional noise
(---471--12)
where
(---471----1) is composed of measurement error and linearization error and also assumed to be white Gaussian noise with covariance as
(---471--13)
In Kalman filtering we estimate the state ρk based on all the measurements taken up to the time k. With the Gaussian assumptions the required estimate is obtained by minimizing the cost functional which is formulated based on the above state and observation EquationEqs. (4)(---471--4) and Equation(12)
(---471--12) , respectively. The cost functional for the conventional Kalman filter is of the form
(---471--14)
where Ck|k − 1 ∈ RN × N is the time-updated error covariance matrix, which is defined by
(---471--15)
In order to mitigate the inherent ill-conditioned nature of the EIT inverse problem, additional constraint is included in the cost functional
(---471--16)
where α is regularization parameter and R* is modified regularization matrix. There are two approaches for selecting regularization parameter α that have gained wide acceptance. One is composite residual and smoothing operator (CRESO) and the other is the L-curve approach Citation[17]. In this article, α is chosen a posteriori by simple trial-and-error method. One popular conventional method for the choice for the regularization matrix R* is a difference-type matrix on the basis of the generalized Tikhonov regularization technique Citation[6] by the smoothness assumptions in resistivity distributions. In this method, the resistivity distribution is parameterized such that
(---471--17)
where χn is the characteristic function of the nth finite element. Recalling that the problem domain is discretized into triangular elements, the ith row of R* is
(---471--18)
where 3 is located at the ith column and –1 is placed in the columns corresponding to elements having common edge with the ith element. Sometimes in real situations, there are partially known internal structures in which additional electrodes can be attached. This work considers the utilization of the prior information on the interior structure. In this case, the regularization matrix can be obtained from EquationEq. (18)
(---471--18) by removing the –1 that corresponds to element having common edge with the known internal structure. Also, the number 3 in EquationEq. (18)
(---471--18) should be replaced by 2 since the smoothness assumption is violated between the known element and background.
Define the augmented pseudo-measurement, (---471----2) and pseudo-measurement matrix, Hk ∈ R(L + N) × N as
(---471--19)
(---471--20)
Then the cost functional, EquationEq. (16)
(---471--16) can be rearranged as
(---471--21)
where the augmented covariance matrix, Γk ∈ R(L + N) × (L + N) is defined by
(---471--22)
Minimizing the cost functional, EquationEq. (21)(---471--21) , and solving for the updates of the associated covariance matrices we obtain the recursive extended Kalman filter algorithm which consists of the following two steps Citation[18]:
Measurement Updating Step (Filtering)
(---471--23)
(---471--24)
(---471--25)
Time Updating Step (Prediction)
(---471--26)
(---471--27)
3. Computer simulations
We carried out extensive computer simulations with synthetic data to evaluate the reconstruction performance of the proposed algorithm.
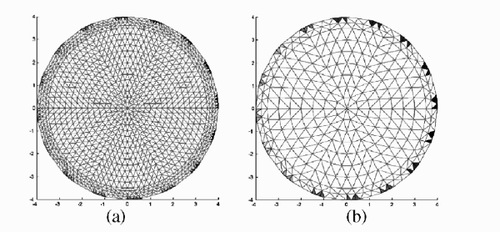
The FEM meshes without internal electrodes used for the forward and inverse solvers are shown in (a) and (b), respectively. In the forward computations we used the FEM with a mesh of 2400 elements and 1281 nodes. In the inverse computations, we used the FEM with a mesh of 600 elements and 341 nodes to reduce the computational burden. For the current injection and corresponding voltage measurement, traditional adjacent method Citation[1] was employed through 16 boundary electrodes (L) so that the total measurement voltage data were 256 (16 × 16).
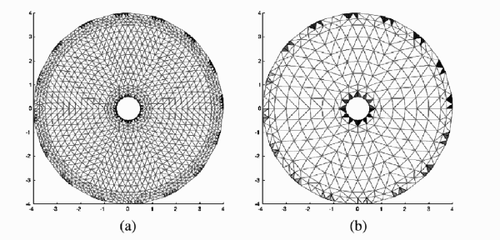
The FEM meshes with a single internal electrode used for the forward and inverse solvers are shown in (a) and (b), respectively. In the forward computations we used the FEM with a mesh of 2480 elements and 1336 nodes. In the inverse computations, we used the FEM with a mesh of 620 elements and 358 nodes. We injected electrical current between 16 boundary electrodes and the internal electrode and measured the corresponding voltage on the 17 electrodes (L) so that the total measurement voltage data were 272 (17 × 16).
To compare the reconstruction performance, we used the static algorithm based on the modified Newton–Raphson algorithm with internal electrodes (mNR-IE) Citation[16], dynamic algorithm based on the extended Kalman Filter (EKF) Citation[12], and the Extended Kalman Filter with internal electrodes (EKF-IE) described in this article. The parameters used for the three methods are as follows. The regularization parameter (α) is set to 0.5 in both simulations. The initial resistivity value is set to the same as the background value in all cases. For simplicity, it is assumed that the covariance matrices for all the EKFs are diagonal and time-invariant. The covariance matrix for process noise (---471----3) is 10 IN, the covariance matrix for measurement noise
(---471----4) is 0.0001IL and the initial value for the state error covariance matrix (C1|0) is IN in both simulations.
3.1. The first simulation
For the verification of the proposed model, we simulate binary-mixture distributions in a circular domain (8 cm in diameter). It is assumed that there is a known conductive circular structure (about 1 cm in diameter, 0.0001 Ω cm in resistivity), which is located at the center and is used as an internal electrode. This configuration could be found in many engineering applications like mixer with rotor, shell-and-tube type heat exchanger and so on.
Consider the following scenario of binary-mixture field undergoing transient. A single anomaly emerges and disappears. And then, three anomalies emerge and disappear. This transient is assumed to take place within the time interval required to measure a full set of EIT data (1 frame) in the context of the static EIT image reconstruction. The stationary approximation could not be effective over the entire time interval required for the injection of all the predetermined 16 current patterns and the measurement of the induced boundary potentials. Hence, we assume each transient stage to take the time interval equivalent to 4 current injections evenly. The background resistivity and the anomaly resistivity are set to 300 and 600 Ω cm, respectively. The simulated evolution of the mixture distribution is depicted in the first column of . In order to make the simulation more realistic, we assume that the measured boundary voltages are contaminated by the measurement error of 1%.
Figure 3 Reconstructed images for the first simulation: (a) true target, (b) reconstructions with EKF, (c) reconstructions with EKF-IE, and (d) reconstructions with mNR-IE.

The transient mixture field described above is visualized with different EIT algorithms; EKF, EKF-IE, and mNR-IE. Results from each algorithm are presented in (b), (c), and (d). As can be expected, (d) shows that mNR-IE totally fails to reconstruct the internal mixture field since the internal resistivity distribution is not stationary. The reproduced images by EKF without internal electrode seem to be rather vague although they are much better than the images by mNR-IE. However, the reconstructed images by EKF-IE in (c) show that the suggested algorithm gives significant improvement in the spatial resolution.
3.2. The second simulation
In the second simulation, we assume the same condition for the internal structure and the resistivity values as in the first simulation. In the measurement of boundary voltages, as in the first simulation, random error of 1% is included. However, a different evolution of mixture distribution is considered as shown in (a).
Figure 4 Reconstructed images for the second simulation: (a) true target, (b) reconstructions with EKF, (c) reconstructions with EKF-IE, and (d) reconstructions with mNR-IE.

In a similar manner to the results from the first simulation, mNR-IE cannot extract any useful information from the EIT image reconstruction. Even with EKF, the reconstruction seems to be more deteriorated compared to the first simulation. It should be noted that in this simulation we intentionally place two anomalies and the conductive internal structure close together. Then, resistive anomalies impede electrical current flowing to the conductive internal structure and the spatial resolution is expected to substantially worsen. However, the utilization of the internal electrode improves the spatial resolution in the binary-mixture field as can be seen in (c). Also, the temporal information for the abruptly changing mixture fields is severely lost in the reconstructed images by the conventional EKF.
3.3. Effects of the regularization parameter
In order to investigate how the regularization parameter affects the image reconstruction, we made EKF-IE reconstructions for the same scenario as the first and second simulation with different choices for α. The results are shown in and . As we can see from EquationEq. (16)(---471--16) , α is the weighting factor for the Tikhonov regularization. As we increase the value of α from 5 × 10−6 to 5 we get very homogeneous background images, but diminishing the sharpness for the moving target at the same time. Generally speaking, too small a value for α results in continued instability of the solution, whereas too large a value results in an overregularized solution that, while stable, has an unnecessarily large reconstruction error.
Figure 5 Reconstructed images for the first simulation with different values of α: (a) true target, (b) reconstruction with α = 5 × 10−6, (c) reconstruction with α = 0.05, (d) reconstruction with α = 0.3, (e) reconstruction with α = 0.5, (f) reconstruction with α = 1.0, and (g) reconstruction with α = 5.0.

Figure 6 Reconstructed images for the second simulation with different values of α: (a) true target, (b) reconstruction with α = 5 × 10−6, (c) reconstruction with α = 0.05, (d) reconstruction with α = 0.3, (e) reconstruction with α = 0.5, (f) reconstruction with α = 1.0, and (g) reconstruction with α = 5.0.
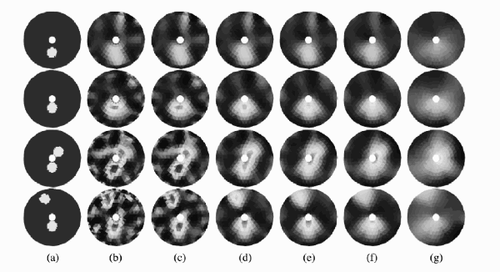
3.4. Effects of the measurement and linearization error
In order to see how the uncertainty (---471----5) in the measurement EquationEq. (12)
(---471--12) affects the image reconstruction, we chose the first simulation and made the EKF-IE reconstructions with different choices for the noise level. As can be seen from , the reconstruction performance of the EKF-IE deteriorate if we increase the level of the noise. As can be expected, too high a level of the uncertainty loses the targets completely as in the last column of .
4. Conclusions
In usual static EIT techniques, the internal resistivity distribution is assumed to be stationary during the measurement of the required full set of independent EIT data. Quite often in real situations, however, the object to be visualized may undergo severe transient. This study considers the application of the EIT technique to the visualization of binary-mixture systems under rapid transient. Also, we propose an EIT image reconstruction algorithm that utilizes the internal electrode attached to the known internal structure in addition to the external electrodes. Actually, in many engineering applications, there are known internal structures where the use of additional electrodes can be possible.
For the dynamic electrical impedance imaging, EIT inverse problem is formulated as a state estimation problem and the state (resistivity distribution) is estimated with the aid of the extended Kalman filter along with the inclusion of the internal electrode mounted on the known internal structure. Through the comparison with the dynamic algorithm using extended Kalman filter as well as the static algorithm like modified Newton–Raphson method, it is shown that the proposed method improves reconstruction performance significantly in the sense of the spatial and temporal resolution.
Acknowledgment
This work was supported by the Nuclear Academic Research Program of the Ministry of Science and Technology (MOST), Korea.
- Webster, JG, 1990. Electrical Impedance Tomography, Adam Hilger. Bristol. 1990.
- Williams, RA, and Beck, MS, 1995. Process Tomography: Principles, Techniques and Applications, Butterworth-Heinemann. Oxford. 1995.
- Beck, MS, and Williams, RA, 1996. Process tomography: a European innovation and its applications, Meas. Sci. Technol. 7 (1996), p. 215.
- Barber, DC, and Brown, BH, 1984. Applied potential tomography, J. Phys. E 17 (1984), p. 723.
- Yorkey, TJ, Webster, JG, and Tompkins, WJ, 1987. Comparing reconstruction algorithms for electrical resistance tomography, IEEE Trans. Biomed. Eng. 34 (1987), p. 843.
- Vauhkonen, M, Karjalainen, PA, and Kaipio, JP, 1998. A Kalman filter approach to track fast impedance changes in electrical impedance tomography, IEEE Trans. Biomed. Eng. 45 (1998), p. 486.
- Kaipio, JP, Karjalainen, PA, Somersalo, E, and Vauhkonen, M, 1999. State estimation in time-varying electrical impedance tomography, Ann. NY Acad. Sci. 873 (1999), p. 430.
- Vauhkonen, PJ, Vauhkonen, M, Mäkinen, T, Karjalainen, PA, and Kaipio, JP, 2000. Dynamic electrical impedance tomography – phantom studies, Inverse Prob. Eng. 8 (2000), p. 495.
- Vauhkonen, M, 1997. Electrical Impedance Tomography and Prior Information. 1997, Doctoral Dissertation, Dept. of Applied Physics, University Kuopio.
- Seppanen, A, Vauhkonen, M, Vauhkonen, PJ, Somersalo, E, and Kaipio, JP, 2001. State estimation with fluid dynamical evolution models in process tomography – an application with impedance tomography, Inverse Prob. 17 (2001), p. 467.
- Kim, KY, Kim, BS, Kim, MC, and Lee, YJ, 2001. On-line image reconstruction in dynamic electrical impedance tomography based on the extended Kalman filter, Proc. of Compumag-Evian IV (2001), p. pp. 70–71, France.
- Kim, KY, Kim, BS, Kim, MC, Lee, YJ, and Vauhkonen, M, 2001. Image reconstruction in time-varying electrical impedance tomography based on the extended Kalman filter, Meas. Sci. Technol. 12 (2001), p. 1032.
- Williams, RA, Jia, X, and McKee, SL, 1996. Development of slurry mixing models using resistance tomography, Powder Technol. 87 (1996), p. 21.
- Heikkinen, LM, Vauhkonen, M, Savolainen, T, Leinonen, K, and Kaipio, JP, 2001. Electrical process tomography with known internal structures and resistivities, Inverse Prob. Eng. 9 (2001), p. 431.
- Lyon, GM, and Oakley, JP, 1993. "A simulation study of sensitivity in stirred vessel electrical impedance tomography". In: Tomography Techniques for Process Design and Operation. Southampton, UK. 1993. p. pp. 137–146, In: M.S. Beck, E. Campogrande, M. Morris, R.A. Williams and R.C. Waterfall (Eds.).
- Heikkinen, LM, Vauhkonen, M, Savolainen, T, and Kaipio, JP, 2001. Modelling of internal structures and electrodes in electrical process tomography, Meas. Sci. Technol. 12 (2001), p. 1012.
- Johnston, PR, and Gulrajani, RM, 2000. Selecting the corner in the L-curve approach to Tikhonov regularization, IEEE Trans. Biomed. Eng. 47 (2000), p. 1293.
- Grewal, MS, and Andrews, AP, 1993. Kalman Filtering: Theory and Practice, Prentice Hall. Englewood Cliffs, New Jersey. 1993.