Abstract
Many elementary statistics textbooks recommend the sign test as an alternative to the t-test when the normality assumption is violated. This recommendation is not always warranted, as we demonstrate by extending previous studies of the effects of skewness, kurtosis, and shifting of the location parameter on the size and power of the t-and sign tests for the one-sample case. For skewed populations our simulations reveal that the power of the t-test can actually be higher than that of the t-test for a normal parent population when the location parameter is shifted in the opposite direction of the skewness of population. In that same instance, the power of the t-test is also significantly greater than that of the sign test. Furthermore, our simulations reveal that for low-kurtosis populations the power of the t-test is again greater than that of the sign test.
1. Introduction
The one-sample Student's t-test and the sign test are presented in most elementary statistics textbooks. The sign test is recommended as the alternative to the t-test when the normality assumption is violated. We extend previous studies to highlight situations in which the normality assumption is violated, but the t-test outperforms the sign test.
Many studies have been done to examine the effect of departures from normality on the significance level (size) and power of the t-test. CitationRhiel and Chaffin (1996) studied the power for the case of skewness in the direction of the rejection region tail as well as the significance level for both left- and right-tailed t-tests under right-skewed parent populations. CitationChaffin and Rhiel (1993) demonstrated that the significance level of the one-sample t-test is higher than the nominal level if the skewness of the parent population is in the opposite direction of the rejection region tail and is lower than nominal when the skewness of the parent population is in the same direction as the rejection region tail. We examine the significance level and power for shifts to both the left and right when the parent population is skewed.
It is well known that the distribution of the t-statistic inherits a skewness that is opposite of the parent population. CitationBoos and Hughes-Oliver (2000) clearly illustrate this fact and show that t-intervals constructed for right-skewed parent populations, for example, will have upper and lower bounds that are to the left of what they would be under a normally distributed parent, and vice-versa. In the context of hypothesis testing this translates into true tail probabilities that are higher than nominal in the upper tail, resulting in fewer rejections, and lower than nominal tail probabilities in the lower tail, resulting in more rejections than there would be under a normal parent for one-tailed tests.
In addition to studying the effects of skewness on the t-test, we compare the effects of not only skewness, but also kurtosis, shifting, and the direction of the test on the power of both the sign and t-tests. While it is true that the sign test requires no assumptions regarding the distribution of the parent population, skewness, shifting, and particularly kurtosis affect the power of the test. Simulations by CitationOtt and Longnecker (2001) show that the t-test is uniformly more powerful than the sign test for normal parent populations and that the sign test is more powerful in cases of heavily tailed or highly skewed parent populations. Our study is consistent with this for skewed parent populations when the shift is in the same direction as the skewness, but not when the shift is in the opposite direction. The power of the sign test is greatly diminished as kurtosis decreases. Simulations by CitationRandles and Wolfe (1979) showed that the power of the sign test is lower for low-kurtosis distributions than it is for high-kurtosis distributions. We also show that the power of the sign test decreases for low-kurtosis parent populations and provide insight as to why this is so.
2. Methodology
Computer simulations with a broad set of parent populations were performed using Matlab. We selected three skewed distributions from the chi-squared family with varying degrees of skewness (2, 4, and 8 degrees of freedom), three low-kurtosis distributions matching those used by CitationChaffin and Rhiel (1993), and three high-kurtosis distributions from the contaminated normal family (kurtosis 6, 9, and 12). Skewness and kurtosis are obtained using and
, respectively. For more information on contaminated normal distributions see CitationJohnson and Kotz (1970). Simulation results were also obtained for a normal parent population for the sake of comparison. Monte Carlo simulations of size 250,000 were run for each distribution using sample sizes 10, 20, 30, 60, and 100 and various significance levels. To make valid comparisons between the t and sign tests, we used levels of significance determined by sample size and the binomial table that were closest to 0.01, 0.025, 0.05, and 0.10 for both one- and two-tailed tests in the case of a skewed parent population and two-tailed tests for symmetric parent populations. Power was computed for shifts of the mean of the parent population from the hypothesized mean, in both directions, of 0.2σ to 2σ in increments of 0.2σ, where σ is the population standard deviation. The simulation errors for levels of significance .05 and 0.10 are 0.0004 and 0.0006, respectively, and the largest sampling error, associated with power 0.50, is 0.001.
3. Results
It is well known that under the null hypothesis the sampling distribution of the t-statistic , is negatively skewed when the parent population is positively skewed, and vice versa. This relationship is affected by shifts in the underlying population. shows the relationship between the skewness coefficient of the t-statistic and the size of the shift for the
parent population and samples of size 20. Monte Carlo simulations of size 1,000,000 for shifts from −1σ to 1.5σ in increments of 0.1σ show that a shift to the left causes even more negative skewness in t0 while a shift to the right will increase the skewness coefficient rather quickly even to the point of positive skewness.
Figure 1. The effect of the size and direction of the shift on skewness of the t-statistics when the parent population is for n = 20.
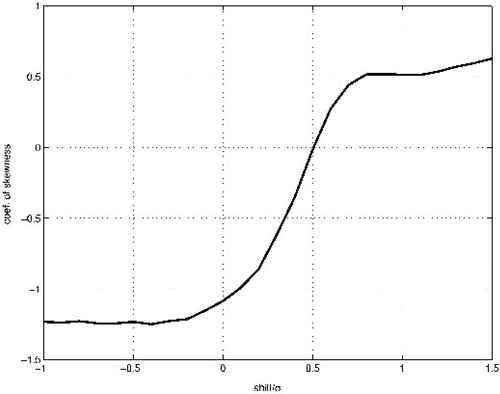
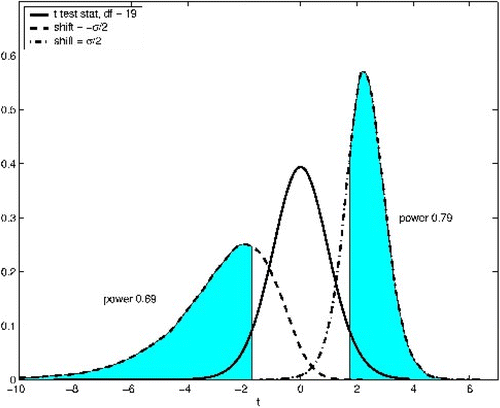
The direction of the shift is certain to be important when the parent population is skewed. In the case of right skewness, as with , the distribution of the t-statistic will be skewed to the right and the level of significance (size) of the test is higher than the nominal level for left-tailed tests and lower for right-tailed tests. illustrates the effect of the direction of the test on the power of the t-test in the case where there is a shift of size 0.5σ. It can be seen in that a shift to the right results in a higher skewness coefficient, yielding higher power, while a shift to the left decreases the skewness coefficient, resulting in lower power for the t-test. The skewness coefficients for the shifts to the left and right in are approximately −1.25 and 0, respectively.
Figure 2. Power of the left- and right-tailed t-tests for shifts of 0.5σ under a
parent population for n=20 and α = 0.05.
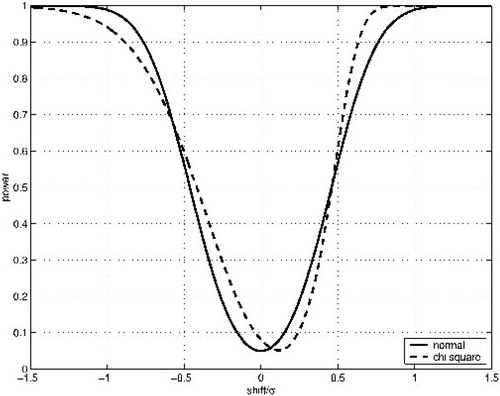
Two-tailed tests under positively skewed parents tend to have significance levels that are slightly higher than nominal due to the left skewness in the sampling distribution of the t-statistic. This is attributed to the fact that while the area under the sampling distribution curve of the t-statistic to the right of the usual critical value in the upper tail decreases, the area under the curve to the left of the usual critical value in the lower tail increases to an extent that the sum of the two areas exceeds the nominal level of significance. When there is a shift in the underlying parent population, the power of the t-test is not uniformly higher or lower for the skewed parent than for the normal parent population. A comparison of the power of the two-tailed t-test for normal and parent populations for samples of size 20 and α = 0.05 is plotted in . For shifts to the right less than 0.5σ, the power for the test when the parent is normal is higher than when the parent is
, but beyond shifts of 0.5σ the opposite is true. However, for shifts to the left the power for the
parent is higher until the shift is less than roughly −0.6σ.
Figure 3. The power of the two-tailed t-test is not uniformly higher or lower for the parent than for the normal parent population for n = 20 and α = 0.05.
Tables and show that for the right-skewed distribution , the level of significance is always higher than the nominal level for left-tailed tests (that is, when the direction of the test is opposite that of the skewness of the parent population). Conversely, the significance level is always lower than nominal when the direction of the test and the skewness of the parent population are the same. This is a result of the skewness in the sampling distribution of the t-statistic that occurs when the parent population is skewed. The relationship between the power of the t-test for normal parent populations and the power of the t-test for a
parent population for n = 20 and α=0.05 shown in is also evident for all of the sample sizes displayed in Tables and for α=0.05 and α=0.10. Specifically, the power of the right-tailed test starts out lower for the
parent than for the normal parent but then overtakes it as the shift increases. The larger the sample size, the smaller the shift required for the crossover to occur. The power of the left-tailed test starts out higher for the
parent than for the normal parent but then declines below it as the shift increases. Again, the larger the sample size, the smaller the shift required for the crossover to occur.
Table 1. Power of one-tailed t-test for various shifts and sample sizes under normal, , uniform, and contaminated normal (CN) parent populations, α = 0.05.
Table 2. Power of one-tailed t-test for various shifts and sample sizes under normal, , uniform, and contaminated normal (CN) parent populations, α = 0.10.
While there are no distributional assumptions necessary for the sign test, our simulations show that the power of the sign test is affected by skewness and kurtosis in the parent population. In the case of a skewed parent population, such as , the power of the sign test uniformly exceeds that of the t-test as long as the shift and direction of the test are the same as the direction of skewness of the parent population. However, and show that the t-test has superior power when the shift and direction of the test are in the opposite direction of the skewness of the parent population.
Figure 4 Power comparison for the two-tailed sign test versus the t-test when the parent population is for n=20 and α=0.0414.
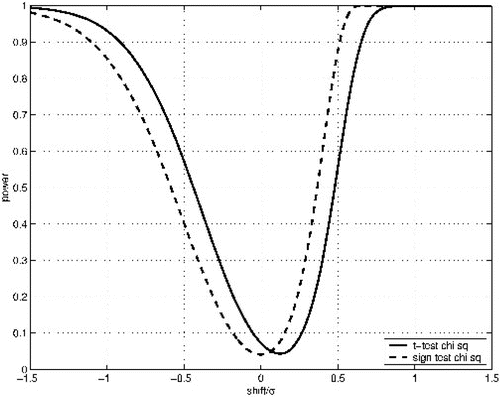
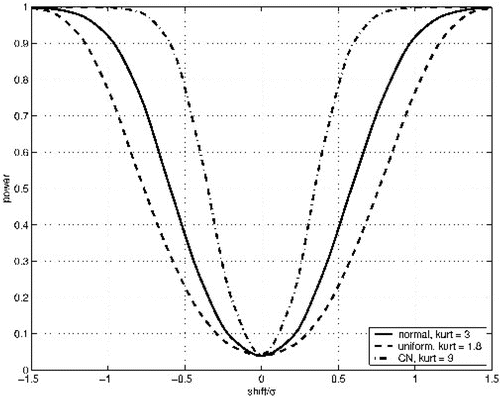
shows the large variation in the power of the sign test for three symmetric distributions with what we might consider low (k = 1.8), medium (k = 3), and high (k = 9) kurtosis. The power of the sign test is particularly sensitive to kurtosis for relatively small shifts, even among large sample sizes. It is evident that the power of the sign test for the high-kurtosis parent population is uniformly larger than the power of the tests for the medium- and low-kurtosis parent populations. Likewise, the power of the sign test under the medium-kurtosis parent is uniformly higher than the power for the low-kurtosis parent population. In other words, in the range of kurtosis from 1.8 to 9 the power of the sign test increases as kurtosis increases.
The reason for this is that samples from low-kurtosis populations have fewer observations in the center and more observations between, say, 1 and 2 standard deviations from the center than samples from high-kurtosis populations. As a result, small shifts do not result in very many observations “moved” to the other side of the median, so the sign test is not as likely to reject the null hypothesis, resulting in lower power. This idea can be taken to an extreme by considering a sample containing an equal number of two distinct values, say −1 and 1, for example. Such a population will have kurtosis equal to 1, the smallest value possible. In this case, any shift less than 1 will result in the power near the level of significance of the test, whereas any shift greater than 1 will result in nearly 100% power. On the other hand, samples from high-kurtosis populations have a higher concentration of observations near the center of the distribution by comparison, so even a small shift will result in a lot of observations being “moved” to the other side of the median, leading to more rejections of the null hypothesis, and hence greater power.
Figure 5 The power of the two-tailed sign test for low-, medium-, and high-kurtosis parent populations when n=20 and α = 0.0414.
In the power of one-tailed t and sign tests is given for the low-, medium- and high-kurtosis distributions. For levels of significance near 0.05, the significance level of each test is not affected by the choice of parent population, except for the t-test with a high-kurtosis parent at sample size 10, where it is slightly diminished. For the low-kurtosis parent population, the power of the t-test is uniformly higher than that of the sign test for each sample size and shift tested. While simulations by CitationOtt and Longnecker (2001) and CitationRandles and Wolfe (1979) show the superiority of the power of the sign test to the t-test for a symmetric high-kurtosis parent population, our simulation demonstrates that the power of the sign test is greatly reduced for a symmetric low-kurtosis parent population. That the t-test has higher power than the sign test under a normal parent population may have less to do with the fact that the t-test assumes normality and more to do with the kurtosis of the parent population.
Table 3. Power of one-tailed t and sign tests for normal and parent population.
Table 4. Power of one-tailed t and sign tests for low- (uniform), medium- (normal), and high-kurtosis (contaminated normal) parent populations.
4. Discussion
Skewness in the sampling distribution of the t-statistic depends on the size and direction of the shift as well as the skewness coefficient of the parent population. In the case of a right-skewed parent population, a shift to the left will decrease skewness in the sampling distribution of the t-statistic, whereas a shift to the right will increase the skewness coefficient of the sampling distribution of the t-statistic. The power of the t-test isn't necessarily diminished in the absence of normality. For example, the t-test with a normal parent has higher power than with a parent for small shifts to the right but lower power for larger shifts to the right. On the other hand, the t-test with a
parent has higher power than with a normal parent for small shifts to the left but lower power for larger shifts to the left.
The t-test is uniformly higher in power than the sign test in cases where the shift is in the opposite direction of the skewness in the parent population. We have shown the sensitivity of the sign test to changes in kurtosis for symmetric parent populations. For symmetric parent populations, the power of the sign test is low for parent populations with low kurtosis and high for parent populations with high kurtosis. In particular, the power of the sign test is less than the power of the t-test for a low-kurtosis parent population, especially for smaller shifts.
Acknowledgements
The authors are very grateful to two anonymous referees whose comments were very helpful in the editing of the paper.
References
- Boos, D. D., and Hughes-Oliver, J. M. (2000), “How Large Does n Haveto be for Z and t Intervals?” The American Statistician, 54(2), pp. 121–128.
- Chaffin, W. W., and Rhiel, G. S. (1993), “The Effect of Skewness andKurtosis on the One-Sample T Test and the Impact of Knowledge of the Population Standard Deviation,” Journal of Computation and Simulation, 46, pp. 79–90.
- Johnson, N., and Kotz, S. (1970), Continuous Univariate Distributions, New York: John Wiley & Sons, Inc.
- Ott, R. L., and Longnecker, M (2001), An Introduction to Statistical Methods and Data Analysis (5th ed.), Pacific Grove, CA: Duxbury.
- Randles, R. H., and Wolfe, D. A. (1979), Introduction to the Theory of Nonparametric Statistics, New York: John Wiley & Sons, Inc.
- Rhiel, G. S., and Chaffin, W. W. (1996), “An Investigation of the Large-Sample/Small-Sample Approach to the One-Sample Test for a Mean(Sigma Unknown),” Journal of Statistics Education [Online], 4(3).(ww2.amstat.org/publications/jse/v4n3/rhiel.html)