Developing PK-12 Preservice Teachers' Skills for Understanding Data-Driven Instruction Through Inquiry Learning

ABSTRACT

This article offers a description of how empirical experiences through the use of procedural knowledge can serve as the stage for the development of hypothetical concepts using the learning cycle, an inquiry teaching and learning method with a long history in science education. The learning cycle brings a unique epistemology by way of using procedural knowledge (“knowing how”) to enhance construction of declarative knowledge (“knowing that”). The goal of the learning experience was to use the learning cycle to explore “high tech” and “low tech” approaches to concept development within the context of statistics. After experiencing both, students recognized the value of high and low tech approaches to instruction. Given that statistical literacy is essential for engaging in PK-12 education, we argue that providing experiences that help preservice teachers understand statistical concepts while modeling effective pedagogical practices will help prepare them for planning instruction and teaching statistics concepts in PK-12 classrooms. This article provides an example of how to meaningfully incorporate statistics into a nonstatistics course for preservice teachers. Empirical experiences prior to introduction of mathematical and hypothetical concepts are necessary pedagogical practice.

KEYWORDS:

• Learning cycle
• Monte Carlo simulation
• Statistical literacy

1. Introduction

Data-driven instruction is one of the latest buzz terms in the realm of PK-12 education. Mathematics and science educators, however, have long known the importance of using data to guide instructional decisions (National Council of Teachers of Mathematics 1989, 1991, 2000; National Research Council 1996). Knowledge of assessment and statistics is necessary to support efforts to implement and continually improve instructional programs and student learning outcomes. Going beyond the idea of developing preservice teachers' statistics literacy for purposes of improving instruction in general, in their call for statistical education of preservice teachers, Franklin et al. (2015) assert that teachers must understand fundamental statistical concepts not only to guide instructional decisions but to also develop their students' knowledge of and problem solving skills with statistics (statistical literacy). Therefore, preservice teachers should engage in rich student-centered activities in ways that model effective pedagogy and emphasize statistical problem solving. Particularly, they should understand how fundamental statistical concepts connect to content understanding that is developed across curricula throughout PK-12 grades.

One solution that has been proposed for preservice teacher education is the creation of courses to explicitly address statistical literacy. For example, Green and Blankenship (2014) developed an introductory statistics course designed to help preservice teachers recognize the importance of statistics in the elementary curriculum and the integral role teachers play in their students' statistical education. Franklin et al. (2015) also recommended an entire course in statistics for elementary-school teachers, with more time and attention given to statistics in existing mathematics content courses, and a special section of an introductory statistics course geared specifically to content and instructional strategies. For middle school and high school levels, the number of recommended courses is greater. In an age where teacher education faculty are being asked to provide education programs with fewer credit hours, however, the addition of stand-alone courses may not be possible. In the absence of the option to create new courses, teacher education faculty may be obliged to find creative alternative paths to improving education majors' statistical literacy.

We do not have a specific statistics course for teachers in our preservice education programs. Consequently, we decided to investigate areas in our teacher education curriculum that could provide a context to introduce basic statistical concepts. We reasoned that data analysis and statistics instruction as part of a course on teaching and learning with technology would be a good starting point and address some of our needs. Below, we describe a learning cycle lesson enacted with approximately 24 undergraduate students within a course on technology in education. Students explored the idea of “low tech” versus “high tech” instructional tools to develop statistics concepts. During the learning cycle, they were introduced to fundamental knowledge types and guided inquiry instruction.

The learning cycle activities with preservice teachers presented below are Monte Carlo simulations on estimating the length of a straw (which we refer to as the shaker activity) and predicting voting results (polling) using a Flash movie simulation. The purpose of this article is to share an inquiry approach to developing statistical knowledge and skills with preservice teachers that emphasize statistical problem solving while modeling effective pedagogical practice. Our rationale for providing this instruction is to increase preservice teachers' knowledge and skills so that they have greater statistical literacy that may be applied when they plan and engage in teaching and learning with PK-12 students. We have organized discussion of our work in three parts: (a) a theoretical framework on knowledge and the learning cycle, (b) a description of how we used the learning cycle to explore and apply random sampling and sample size (standard error) and to generalize the use of discrete random observations to estimate population parameters in order to compare “high-tech” and “low-tech” approaches to instruction, and (c) an examination of preservice teachers' interactions during the activities and their subsequent responses to questions about the Monte Carlo simulations.

2. Knowledge and the Learning Cycle

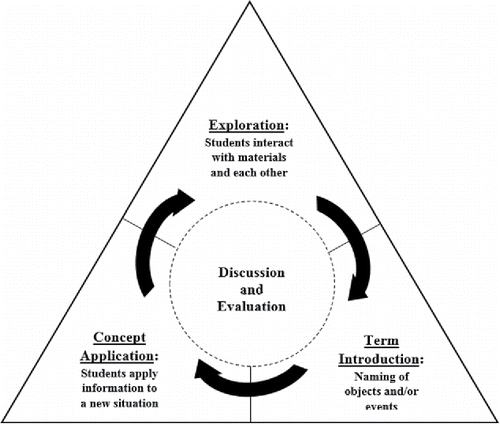
The learning cycle, an inquiry teaching and learning method with a long history, is still widely employed in science education. It brings a unique epistemology by way of using procedural ¹ knowledge (“knowing how”) to enhance construction of declarative knowledge (“knowing that”). As with many inquiry activities, the source of knowledge is the experience (see Figure 1). Facilitating student inquiry into statistical concepts through a learning cycle provides an excellent opportunity to improve preservice teachers' critical thinking and problem-solving skills at the same time as modeling pedagogical practices that can lead to deeper levels of conceptual understanding in all school content areas.

Figure 1. The learning cycle: three phases. Adapted from Barman (1989) and Lawson (1995).

Two fundamental types of knowledge are developed within the learning cycle: procedural and declarative. Procedural knowledge is “knowing how,” and declarative knowledge is basically “knowing that” (Lawson, Abraham, and Renner 1989). The acquisition of declarative knowledge is a constructive process that occurs through the use of procedural knowledge. Research has documented improvements in formal reasoning as a consequence of learning cycle instruction through the development of procedural knowledge (Lawson, Abraham, and Renner 1989). Examples of procedure knowledge might include questioning, controlling variables, analyzing data, and drawing conclusions.

Students can learn declarative knowledge through memorization, but such learning may be shallow and disconnected. For example, rote learning, which involves memorization and recall of factual knowledge, is often set in contrast to meaningful learning (Mayer 2002). Rote learning often occurs as a result of recitation or lecture-style classes where teachers present information to students who then study that information and are later tested on their ability to recall what was presented. With rote learning, new information may have no specific relevance to existing conceptual/propositional frameworks (Ausubel 1968). Moreover, rote learning can cause interference with previous similar learning, resulting in misassociations and difficulties with patterns of recall.

In contrast, “meaningful learning occurs when students build the knowledge and cognitive processes necessary for problem solving” (Mayer 2002). When using procedural knowledge to construct declarative knowledge, the learning becomes more meaningful and retention more likely. Meaningful learning, in turn, gives students tools for better understanding and the ability to approach explaining the world by generating and testing their own ideas.

The learning cycle is an inquiry-based approach to teaching and learning that encourages knowledge construction and meaningful learning. Lawson's (1995) three-phase model of the learning cycle consists of (1) exploration, (2) concept introduction or term introduction, and (3) application.

During the exploration phase of the learning cycle, “students learn from their own actions and reactions in a new situation” (Lawson 1995, p. 136). The instructor may provide an activity and describe and/or provide procedures for students to follow. The procedures guide students through data collection. Exploration begins with an observation and question. For example, an interesting question may arise or can be introduced by the teacher when observing a measurement activity with a jar of red and white beads. “Suppose you randomly selected beads from the jar. Could that information be used to determine the percentage of red and white beads in the jar?” These questions may lead to predictions. During the exploration phase, the instructor acts only as a facilitator who poses questions and assists in data collection. The students manipulate materials and collect and organize data. Exploration is typically done in small work groups where students negotiate the meaning of the activity through interactive discourse processes.

The second phase of the learning cycle is referred to as concept introduction or term introduction. Terms and concepts are used to refer to patterns observed during exploration. The key to success in the second phase is to allow sufficient exploration of the phenomenon prior to introducing terminology. Suppose during exploration a facilitator guided students to randomly select 10 beads from the jar 10 different times, asked them to repeat the procedure randomly selecting 10 beads from the jar, 20 different times, and so on. During this process, the students then compared data with each other or other groups. In this scenario, the teacher acts as a guide (facilitator) while the data are being analyzed. Students are encouraged to verbalize their understandings of the data and use the terms while working in small groups and engaging in whole-class discussion. Then, the teacher may choose to introduce definitions of the terms or interpretation of the data, if needed. This would only occur after students have had an opportunity to debate, argue, hypothesize, and discuss the meaning of the data and/or terms. In this hypothetical example, the concept of data parameters such as sample type, sample size, estimated values, and sampling error could be introduced.

The last phase of the learning cycle is referred to as concept application, where students organize the concept just learned with other related phenomena. The concepts learned through phases 1 and 2 are extended to new situations or contexts. Without a variety of applications, the meaning of a concept may remain restricted to the examples used at the time it was initially defined and discussed. For example, additional phenomena involving sample size and standard error, similar to estimating the number of beads in the jar by determining by the mass of beads in the jar, may be explored. In other words, students discuss the relationships between the original exploration and concept introduction and the new phenomenon. New concepts are neither introduced nor discussed during application. Without the application phase, students may fail either to abstract the concepts from its concrete examples or to generalize it to other situations (Lawson 1995; Odom and Settlage 1996; Bell and Odom 2012).

The power of the learning cycle comes from the sequencing of experiences to facilitate understanding of new concepts. With the learning cycle, empirical experiences through the use of procedural knowledge serve as the stage for the development of hypothetical concepts. For example, we used a Monte Carlo simulation to estimate the length of a straw (hypothetical concept) and compare the estimation to the length of the object as determined with a ruler (empirical experience). By running the simulation repeatedly, sample data can be used to estimate characteristics of a population, in this case the length of a straw.

Understanding population parameters involves the process of forming conclusions, judgments, and inferences from evidence. Further, it requires reasoning about hypothetical concepts and probabilistic reasoning. With probabilistic reasoning one must consider the likelihood of chance influencing phenomena (Batanero, Godino, and Roa 2004). Because researchers rarely have data on every person (or object) in a population, a parameter is a hypothetical concept requiring special treatment.

Virtually, all polls and surveys involve selecting a sample from a population, obtaining data from the sample, and making inferences about the population from the data. A survey item such as “For which of the two candidates running for office, A or B, will you vote?” is easily imagined and students would have little difficulty understanding data collected in response to the question. However, as survey data are collected, the survey item becomes more complex. It is no longer treated simply as the most popular candidate, but as data with parameters estimated via sample type, sample size, estimated values, and sampling error. Empirical experiences (a preference for Candidate A, for example) become hypothetical concepts (sampling error, etc.) requiring the interpretation of functional relationships in mathematical form.

3. Estimating Population Parameters Using the Learning Cycle

During the following activities, students were guided to estimate the length of a straw using a shaker (folded index card and piece of straw) to collect data, to plot the data in Excel, to graphically examine sample size and sampling error, and to apply the concepts of random sampling and sample size to estimate poll results with a Flash movie simulation.

3.1. Exploration Phase (30–45 min)

The shaker activity is as follows:

1. Students worked in pairs. After being told that they would use an index card to measure the length of a piece of coffee straw to a high degree of accuracy, they were asked to draw lines an equal distance apart, 1 inch, on a 3- by 5-inch index card and fold the index card in half lengthwise.

2. Next, they cut a piece of coffee straw and put it in the folded index card. (Other objects can be used, such as a toothpick.)

3. Students were directed to hold the folded index cards with two fingers at the fold and shake it back and forth for a couple of seconds.

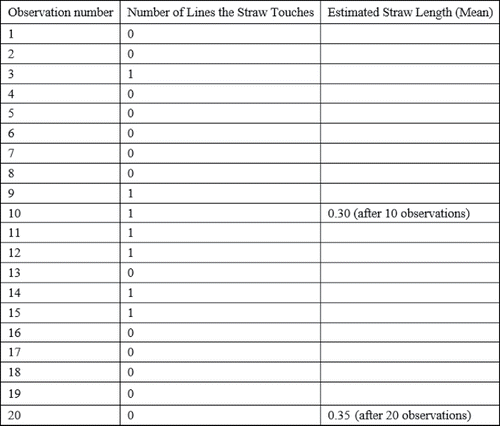
4. One student was the designated “shaker.” The other student counted and recorded the number of lines the straw was touching after each shaking event. This procedure was repeated 50 times. (To ensure random sampling, the shaker should not look at the index card and straw, and should try to avoid stopping the shaking action with the straw touching either finger.)

   A Monte Carlo experiment Flash movie (http://php2.umkc.edu/education/alodom/jse/montecarlo.swf) model is available to assist with preparation of this laboratory. The model is fully functional but should not be used to replace the lab (Odom and Settlage 1996; Bell and Odom 2012).

5. A running average of the number of lines touched by the straw after each shake was maintained as data were collected. (See Figure 2. In Figure 2, the straw that was used was less than one inch in length, thus, could not touch more than one line at a time. Each group of students could have a different length of straw depending on how they cut it.)

   Figure 2. Example student record (originally created in Excel).

   

6. After making 50 observations, students were asked to measure the length of the straw with a ruler. The observed straw length (determined with a ruler) and estimated length (as determined by the average of the “line hits”) were compared as the sample size increased. Students were asked to describe any trends among the estimated straw length, sample size, and observed straw length. (In Figure 2, the estimated straw length was 0.35 inches with lines drawn one inch apart on the index card.)

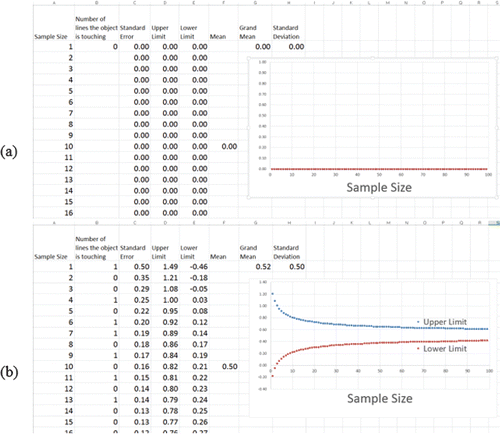
7. Next, students were asked to open an Excel file (shaker tab) preformatted with the equations for mean, standard deviation, standard error, and the upper and lower limit of the 95% confidence interval (see http://php2.umkc.edu/education/alodom/jse/shakererror.xlsx).

8. Students repeated the sampling activity, entering the number of lines the straw was touching in Column B (Figure 3a). The data were collected for 50–100 observations with a different straw segment. A graph, like the one in Figure 3b, was generated as data were collected. Again, students were asked to describe any trends among the estimated straw length, sample size, and observed straw length and speculate about the meaning of the graph generated during data collection.

   Figure 3. Example spreadsheet. Panel (b) illustrates a situation where students used a straw that was less than 1 inch in length. If the straw had been between 1 and 2 inches in length, the possible values for the number of lines the object is touching would be 1 and 2.

   

The possible student observations are as follows:

• As the sample size increases, the estimated length of the straw or sample mean changes.

• The estimated length or sample mean could increase or decrease in value with each iteration.

• The standard error (which is generated “automatically” in Excel in the given spreadsheet) decreases as sample size increases.

• The range of the upper and lower limits of the standard error also decreases as sample size increases.

• The estimated length becomes closer to the measured length as sample size increases (demonstrating the central limit theorem).

3.2. Term Introduction Phase (10–15 min)

1. Students began this phase by comparing the data in their Excel spreadsheets with each other and other groups. The teacher acted as a facilitator as the data were analyzed and challenged students with questions about the data: How were the straw length data generated? (randomly) How does the mean estimate of straw length change as the sample size increases? What happens to the upper and lower limit as sample size increases?

   Note: After students verbalize their data and terms, the teacher might choose to introduce a scientific definition, if needed, of the terms or an interpretation of the data. This would occur only after students have an opportunity to debate, argue, and discuss the meaning of the data and/or terms.

2. Students were given the following terms to incorporate into their data analysis: random sample, sample size, estimated mean, upper limit, lower limit, standard error, and population parameter. They were asked to write a general statement about each term based on the experiences with the shaker activity and then compare their statements to those below and discuss the comparisons.

   • A numerical characteristic of a population, such as mean or standard deviation, is a population parameter. Parameters do not change.

   • A samples value is determined by chance. The sample size is the number of observations or replicates.

   • The average values obtained from a large number of observations should be close to the expected value. The value will become closer as the number of observations increase.

   • Observations are used to calculate statistics. Statistics provide estimates of the population parameters.

   • The standard error of the sample is an estimate of how far the sample mean is likely to be from the population mean. Standard error can be used to determine confidence limits. The confidence limit is the estimated range (upper and lower limits) the sample mean is likely to be from the population.

Mathematical functions were not introduced. The goal was to establish initial conceptual understanding.

3.3. Application Phase (30–45 min)

The concepts of parameters, standard error, random sampling, and sample size were explored and verbalized during the previous two phases of the learning cycle. The goal of the application phase was to explore those concepts in a new context. We selected a hypothetical telephone survey similar to those used in political campaigns before elections. The notion of a telephone survey was familiar to many of our students, but few had explored the underlying statistical concepts. A Flash movie (http://php2.umkc.edu/education/alodom/jse/survey_poll.swf) and an Excel file were used to conduct a hypothetical telephone polling survey (recommended browser: Mozilla Firefox).

1. Students were asked to reopen the same Excel file used during the shaker activities at the survey tab (http://php2.umkc.edu/education/alodom/jse/shakererror.xlsx). The survey tab sheet was preformatted with the equations for mean, standard deviation, standard error, and the upper and lower limits of the 95% confidence interval.

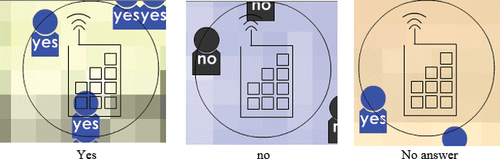
2. After opening the telephone survey Flash movie, the “add votes” button was selected (Figure 4), which populates the map with icons indicating “yes” and “no” votes. Students were encouraged to “play” with the Flash movie before recording any poll results. For example, they were guided to find the dial and hang-up buttons on the Flash movie, enter the last four digits of their phone number to the input box, and select dial to find out what would happen when selecting each of these features. Figure 5 shows three of many possible results of dialing a number.

   Figure 4. Example screenshot of telephone survey. URL: http://php2.umkc.edu/education/alodom/jse/survey_poll.swf; Password: abc123; up to 10,000 random yes/no votes generated.

   

   Figure 5. Identifying poll results.

   

   Technical note: The votes are randomly placed on the survey area grid which is a map of a hypothetical area. The last four digits of a phone number represent coordinates on the grid. Once a number is dialed, the movie zooms into the corresponding grid area. The phone numbers within Excel were generated with a random number function.

   While exploring the Flash movie application, the students were asked to determine the results of each voting sample item. Because some observations may not readily identified as having a “yes” or “no” result, we asked the students to develop a procedure for determining yes and no votes. (One of the constraints of the activity was that each phone call should result in a single yes vote, no vote, or the call was unanswered. Unanswered was defined as no voting icons or partial voting icons within the circle.) The procedures were shared and discussed with the whole class. Decisions on modifications in procedures were made before proceeding with the activity. Figure 5 illustrates one way a student may have decided to identify poll results.

3. Once all of the technical issues and constraints of the model were explored, students were asked to work in pairs to conduct a survey. Similar to the shaker activity, students recorded a yes or no vote after each observation (at least 50). In the Excel sheet, a yes vote was recorded as 1, a no vote was recorded as 0, and an unanswered phone call was not recorded. A running average was maintained as data were collected, just as in the shaker activity (see Figure 2).

   Note: Each time the Flash movie is used, the number of yes or no votes will randomly change. It's possible for one group to generate 4500 yes and 3500 no votes, while another group may generate 900 yes and 50 no votes. A password is provided to the user to determine the count, after collecting observations, of how many yes and no votes were generated. The teacher may choose not to have students check on the actual number of votes generated in the Flash movie, relying instead on estimations and other statistics from the activity.

4. After concluding the survey, student groups shared finding with each other. The concepts examined during the first two phases were reexamined and verbalized within the context of the telephone survey activity, thus completing the learning cycle.

4. Student-to-Student and Student-to-Instructor Social Interactions

The goal of the learning cycle lesson outlined above was for students to explore “high tech” and “low tech” approaches to concept development. After experiencing both, student recognized the value of high and low tech approaches to instruction. In other words, low tech solutions should not necessarily be dismissed in this current age of high tech options. The lesson lasted about 90 min.

Students' interactions, with each other and instructors, and their experiences with tangible objects during exploration (phase 1) facilitated understanding of hypothetical concepts and terminology (Abraham and Renner 1986). The exploration of statistical concepts was designed to support the evaluation of high-tech and low-tech approaches to instruction. In other words, students had to experience the processes of concept development in order to experience and evaluate “high tech” and “low tech” approaches to concept development. The class session was video recorded in order to study the development and effectiveness of this learning cycle lesson. Portions of the recording, transcribed verbatim, are provided and discussed below.

Early in the activity, students made observational comments that were relatively undeveloped—they reacted to the data collected early in the process with insufficient information to make strong conjectures about what was happening. For example, one pair of students noticed a number pattern emerge after the first several “shakes”:

Student 1: [Shaker results: … 1, 2, 1, 2] It's not, it's not random.

Student 2: [The straw then landed on 2 lines.] Now it's random.

Instructor 1: It's becoming more random?!

[Laughter.]

Instructions to students had included an emphasis on the “randomness” of where the straw lands in the crease of the index card after shaking, which may account for the students' concern over whether or not the outcomes were random. The instructor's question appears to have made the students realize the humor in their misuse of the term “random” in this exchange.

Another student reacted to the consistency of the data, and attributed the recognition of the consistency to “feeling”:

Student 3: One.

Student 4: One.

Student 3: I feel like all we are going to get is one.

Student 3 went on to express eagerness for more variety in the outcomes. “We are shaking it up, man. I really want it to land in between the lines so that it can be a zero.” This statement shows a somewhat emotional response to a process that is meant to be, ideally, logical and empirical—not controlled by desires for specific outcomes. It also conveys, however, understanding that there were only two possible outcomes.

Another student explained her completed dataset and the resulting average of slightly less than 1 by showing and telling:

Student 5: I just measured how many times it hit one line, and it is just barely short of the line; see? (See Figure 6.) So three times we got it like right in the middle. Zero.

Figure 6. Student demonstration of “Barely Short of the Line.”

The same student later described the difficulty of determining the number of lines the piece of straw was touching because of the “angular” cut on one end.

Instructor 2: How close was yours?

Student 5: It was pretty darned close. Ours was just about an inch. [Shows the piece of straw.] It's cut at an angle right there.

Instructor 2: So then you had to decide. Yeah, when I was cutting those [straws] I was thinking that. These are cutting at an angle.

Student 5: And [the piece of straw] would rotate. Then there were times when it wouldn't be able to hit [the lines].

Instructor 1: And yours is almost an inch exactly.

Student 5: I think it is, if you angle it right, yeah.

Instructor 1: So it is interesting that it still came so close. Did you ever count it as two?

Student 5: No. Never two. We got zero a couple of times. But we never got two.

This verbal exchange highlighted the need for the students to make determinations about the process of identifying outcomes and to be consistent with those determinations while engaging in this activity. They had to decide what would count as “hitting the line” and what would not. In the case of the shaker activity, the length of the straw could not be both 0 or 1 and 1 or 2. Although a similar dilemma could also occur while using computer simulations, manipulation of the concrete materials aided the student's explanation of her thinking processes.

Many students expressed amazement and excitement over the accuracy in measuring the length of the piece of straw in the shaker activity, as exemplified in the following exchange.

Instructor 1: So you measured [with a ruler], and it was what?

Student 6: One and a half [inches].

Instructor 1: And what was your average on there? [Pointing at the spreadsheet.]

Student 6: One and a half.

Student 7: We got pretty excited!

Student 6: … [Explains the process.] … We did that fifty times, and we took the average of all our attempts.

Instructor 1: And that gave you the length of the straw?

Student 6: Mm-hm. Yes. It did.

Instructor 1: Wow.

Student 6: I agree!

The excitement was also expressed in regard to being able to have a hands-on experience with concrete materials.

Student 8: [Holding the index card and straw; talking to another student.] This is like, actually touching.

Instructor 1: [Are you talking about] the ability to actually touch [the materials]?

Student 8: Yeah, because, like, this [computer simulation], I'm doing it, yeah. But this is like personal. [Indicating the index card and straw.]

The excitement over using concrete materials also showed up in students' postactivity survey responses, which are presented in the following section.

5. Students' Postactivity Reactions to the Monte Carlo Activities

In this exploratory learning cycle, students were guided to develop concepts associated with the activities but there was no direct instruction. Following engagement in the lesson, we asked our students (approximately 24 undergraduate students taking a course on teaching and learning with technology, in a computer lab) to share their impressions about learning through the Monte Carlo simulation. The computer lab setting allowed us to guide students through the comparison of “high tech” and “low tech” exploration of concepts. Collection of students' responses had occurred regularly as part of exploratory lessons in this course. Responses to questions about the activities were collected anonymously using the survey function of BlackBoard, which is a university system-wide web-based teaching resource. The questions were What did you learn from the activity? and Do you see any value in the activity?

We noticed two general categories of responses. The first was about using an inquiry approach to learn about statistics concepts, and the second was about the importance of sample size. Table 1 provides a representative sample of student comments about the Monte Carlo activities. It appears that inquiry learning, especially as related to understanding statistics, was a new and valuable experience for many students.

Table 1. Selected student responses to open-ended questions on the Monte Carlo activities.

Comment no.	Student comment
Inquiry and hands-on learning
1	In regards to inquiry based learning, I really see how students individually, through their own experiences and observation, can gain understanding at their own pace through their own mathematical thinking process through this activity.
2	Statistics can be hands on.
3	[I learned] how to create a hands-on experience for children to gain a deeper understanding about probability and chance. I also gained a deeper understanding about statistics and what not to do at the casino, ha ha.
4	I learned that actually doing the activity instead of using the computer module was more beneficial to my understanding. Statistics activities can be hands on.
5	I learned that it is possible for students to complete hands-on activities to learn how to talk about statistical data.
6	I liked how after doing the average on excel, a students is able to physically check the answer. It is a good mix of technology and doing it yourself.
7	I thought it was rather interesting how randomly shaking a stick can really get an accurate measurement. It was really cool.
Sample size
8	This activity showed me an interactive thing students can do that shows statistics. … It shows the need for a lot of samples, in order to get closer and closer to accuracy.
9	I learned that if you have a larger sample size of randomly generated numbers then you can get a relatively close answer with close to 100 percent confidence.
10	I learned that using this [concept of increasing] sample size, you get a more accurate reading than you would using other equipment to measure the length of the stick or straw.
11	I learned that the accuracy of measurement of something can be [obtained] through a large sample size. Statistics never lie.
12	I learned that the more samples you take when trying to find the probability, the closer you get to finding the actual probability.
13	I learned that larger sample sizes are needed in order to have more accurate statistics.
14	Sample size is important when taking surveys.
15	Sample size is important!

For students who may have had some previous understanding of the statistics concepts, the shaker and telephone survey activities deepened their understanding, as can be seen in comment 3—“I also gained a deeper understanding about statistics and what not to do at the casino, ha ha”—and possibly comment 9—“I learned that if you have a larger sample size of randomly generated numbers then you can get a relatively close answer with close to 100 percent confidence.” Some students' responses may indicate that they did not have previous knowledge of the statistical concepts experienced in these activities. For example, with comments 12–15, the students imply that previously they had been unaware of the benefits of large sample sizes. (A 95% confidence interval from the larger sample will be more precise—less width—than the 95% confidence interval from the smaller sample.) Two of the students' comments indicate positive affective responses to having engaged in the activities. Comment 6 is related to being able to measure the piece of straw with a ruler during the activity and seeing the relationship to the length obtained by averaging the numbers recorded in the spreadsheet. Comment 7 seems to express amazement with the accuracy of the measurement done through random sampling.

The two main categories that emerged from the students' comments warrant special note. The first, on inquiry and hands-on learning, is important because we were working with students who were either preeducation majors or recently accepted into a teacher preparation program. Courses provided for these students should, ideally, go beyond teaching specific content to include models of effective pedagogical practice that they will use in their future classes. We believe that the first eight comments convey our students' recognition of the relationship between pedagogical practices and the development of deep conceptual understanding. The science and statistics concepts were learned through engaging and motivating inquiry activities that provided authentic opportunities for development of understanding through social discourse.

The second category, on the insight gained related to the importance of sample size, indicates that many of our students did not have the types of experiences in previous classes or coursework that result in understanding how sampling techniques, such as conducting surveys, actually work. This knowledge is particularly important in a society that claims to value data-driven decision making, thus highlighting it as a critical component of PK-12 education.

Both the shaker and voting poll activities provided empirical experiences through use of procedural knowledge to direct the development of hypothetical concepts. In general, simple random sampling is a common method for sampling a population. Concrete experiences provided by the shaker activity allowed our students to see firsthand the power of random sampling and a context to develop specialized language including such terms as random sample, sample size, estimated mean, upper limit, lower limit, standard error, and population parameter. The activities provided opportunities to better understand basic statistics through generating and testing their own ideas. The concepts learned through the shaker activity were extended to the survey activity, providing a real-world type simulation of a telephone survey. Therefore, the voting poll application activity provided an opportunity to extend the knowledge into a new context.

6. Conclusion

The activities we provided for our students are a very small part of what might ideally be included in professional education programs for prospective teachers. In this article, we presented an example of empirical experiences gained through the use of procedural knowledge to set the stage for the development of hypothetical concepts while exploring pedagogical approaches to concept development. Current trends in PK-12 education demand that teachers understand fundamental statistical concepts, not only to guide instructional decisions but to also develop their students' knowledge of and problem solving skills with statistics (Franklin et al. 2015).

We believe that preservice teachers' authentic learning experiences that result in understanding of statistical concepts are prerequisite to understanding of how to guide instructional decisions. In our experience, many preservice teachers fear working with statistics. Therefore, they need to experience statistics in such a way that “takes out the fear factor.” In other words, our future teachers need to understand statistical concepts more deeply before they can use data to make informed decisions about instruction. Statistical concepts were introduced and explored in the activities described above, but making strong connections between the activities and using data to inform instruction would have to be a part of additional discussions and learning experiences that take place after the learning cycle we have described here. Additional experiences with statistics across preservice teacher education would be extremely beneficial.

We have not even come close to meeting the suggested course sequence provided by the American Statistical Association (Franklin et al. 2007, 2015) and other researchers (e.g., Green and Blankenship 2014). However, we have seen the power of engaging our students in the learning cycle to understand statistical concepts more deeply. While an ideal situation might be more fully realized in the creation of single or multiple courses in statistics, our work suggests that activities where students experience the power of statistics through the learning cycle could be integrated into other education courses as a starting point in working toward the ideal. Much more work remains to be done to reach the level of statistical literacy required of PK-12 teachers and informed citizens in a participatory democracy.

Notes

¹ Note that the term “procedural” is generally used differently in mathematics education. In the learning cycle, it refers to the procedures used to construct knowledge. In mathematics, it generally refers to applying algorithmic procedures.