The CASE Project: Evaluation of Case-Based Approaches to Learning and Teaching in Statistics Service Courses

ABSTRACT

The CASE project (Case-based Approaches to Statistics Education; see www.mas.ncl.ac.uk/∼nlf8/innovation) was established to investigate how the use of real-life, discipline-specific case study material in Statistics service courses could improve student engagement, motivation, and confidence. Ultimately, the project aims to promote deep learning of course material, with students from other disciplines being equipped with the skills to undertake independent quantitative analyses (for example, in their final year dissertations). In this article, I describe the case-based materials and associated activities, developed as part of this project, for first year Business undergraduates taking a compulsory course in quantitative methods. I also attempt to evaluate the success of the CASE project through a trial in which a randomly selected subgroup of students was exposed to case-based learning and teaching activities. After adjusting for nuisance factors, I found that students in this subgroup outperformed their peers who were not selected for case-based learning and teaching, in terms of their grades in both routine algorithmic homework exercises and more open-ended projects requiring problem-solving and interpretative skills.

KEYWORDS:

• Case-based learning and teaching
• Problem solving
• Statistics service courses

1. Introduction

Most faculty members in Mathematics and/or Statistics will be familiar with the difficulties that arise when teaching a Statistics course to nonspecialists. Statistics service teaching often occupies a considerable proportion of the overall departmental workload: undergraduates enrolled on programs in Business, Management, Biology, Psychology, Agriculture, Civil Engineering, Marine Science, and the Medical Sciences (to name but a few!) usually take compulsory courses in first year, and some in subsequent years. A typical first year introductory course in quantitative methods might cover the basics of descriptive statistics, probability, inference, and modeling, with courses in later years including ideas from multivariate statistics, nonparametric methods, time series analysis, and operations research. At the author's institution, class sizes in these courses can range from 30 to in excess of 400. I have found that, in such courses, it can be extremely difficult to motivate students. Some are surprised to find that such a course is a compulsory part of their curriculum, and some even resent having to study the subject. Some students often find it difficult to see the relevance of Statistics to their chosen degree programs, which also affects their motivation. A larger number lack confidence in undertaking anything vaguely quantitative. There can also be a huge ability range in a Statistics service course, which can make it very difficult for the teacher to find the right level at which to pitch the course. The large class sizes, and large curricula, do nothing to help these problems. Such difficulties are well known and well documented (for example, Pollock and Wilson 1976; Garfield 1995; Gelman and Nolan 2002; Kotecha 2012). The following are direct quotes taken from student module evaluations for a quantitative methods course for Business undergraduates, over the years 2006–2012 when I was the main teacher for this course:

I appreciate the teacher's efforts in the course but sadly they are wasted on me as there is no way I would ever be able to do this sort of maths.

I signed up to do a Marketing course so not sure why I'm being forced to take maths L

Good notes and resources but I feel like the lecturer speaks a different language to the rest of us… or at least most of us, I reckon only the best students in this class will get what he means.

The pace was far too slow—don't pitch the course at the bottom end of the class because most of us are now bored.

Such problems, in the author's experience, are often made worse by inadequate modes of assessment, which—at best—encourage only surface learning: a tacit acceptance of information, leading to a superficial retention of material. For example, in the author's experience of teaching the aforementioned quantitative methods course, in-course assessment was via a series of regular, short assessments using electronic tests and overly prescriptive written assignments based on unrealistic, “well behaved” and rather contrived datasets. Combined with similar types of examination questions, many students taking this course often received high overall grades—not necessarily a good indicator of their level of understanding.

Generally, case-based learning—in which relevant, thought-provoking, and often topical scenarios are used to stimulate interest in a particular area of a student's curriculum—is not a new concept (for example, Wassermann 1994; Edwards et al. 2001; Crosling and Webb 2002; Herreid 2007). According to the University of Michigan's Center for Research on Learning and Teaching (CRLT: http://www.crlt.umich.edu/), with case-based teaching, “…students develop skills in analytical thinking and reflective judgment by reading and discussing complex, real-life scenarios.” Further, a successful approach to case-based learning and teaching, says the CRLT, “…consists of carefully designed problems that challenge students to use problem-solving techniques, self-directed learning strategies, disciplinary knowledge and team participation skills.” Indeed, most authors agree that a case-based approach to learning and teaching should be learner-centered, with interaction between participants as they build their knowledge, working together as a group to examine the case material. Some even see the academic's role as a facilitator, while the students collaboratively address problems and resolve questions that might have no single right answer. Herreid (2007, p. 23) offers an 11-point checklist for the development of successful case material; see Figure 1.

Figure 1. Checklist for successful case-based learning (after Herreid, 2007).

In statistics, some have recognized the need for teaching statistical thinking rather than statistical recipes (Daisley 1979; Nolan and Speed 1999; Wild and Pfannkuch 1999). Lesser and Kephart (2011) provided a brief review of the Statistics education literature in which case-based and problem-solving approaches are considered: for example, Bransford, Brown and Cocking (1999) called for active learning in Statistics; the Guidelines for Assessment and Instruction in Statistics Education (GAISE) College Report (ASA 2016) recommend situating statistics learning activities in authentic, real-world problems and peer discussion of statistical reasoning; a study by Keeler and Steinhorst (1995) concluded that students in an introductory Statistics course selected for “co-operative learning” achieved higher overall course grades than those who were not; Brodie (2007) commented on the importance of discussion in inquiry-based mathematics teaching and how the teacher should take account of the “diversity of ideas that have been expressed.” However, to my knowledge, none have focused specifically on the benefits of case-based learning and teaching in Statistics service courses, and it could be argued—given my earlier discussion – that such innovations could be more appreciated by students in these courses (due to low levels of motivation, engagement, and confidence, for example) than those enrolled on degree courses in Mathematics and Statistics, perhaps leading to their greater success here.

Several institutions in the United Kingdom and United States have invested in providing resources for teachers, lecturers, and course facilitators wishing to implement a case-based approach to learning. For example, The Center for Teaching Excellence at the University of Medicine and Dentistry in New Jersey offers a wide variety of references, including 21 links to case repositories in the Health Sciences; the Teaching and Learning with Technology Center at Penn State offers an online handbook on using cases in teaching; the University of Birmingham in the United Kingdom has a webpage, with resources, dedicated to enquiry-based learning; and The National Center for Case Study Teaching in Science in the United States provides an award-winning library of over 410 cases and case materials while promoting the development and dissemination of innovative materials and sound educational practices for case teaching in the sciences. Lacking, however, are resources for case-based learning and teaching specific to Mathematics and Statistics, especially for the provision of service teaching in this area; the CASE project attempts to plug this gap.

I give careful attention to the development of (i) appropriate material, and (ii) suitable activities used to support the implementation of this material, for the successful roll-out of case-based learning and teaching. For example, in the development of my case material, I have acknowledged that the teacher of a Statistics service course is usually a nonspecialist in their students' chosen field. Thus, in a bid to develop genuinely interesting and relevant material to use in class (as points 2, 4, and 7 in Figure 1 suggest is important), the CASE project employs student interns from the “other” subjects to assist with the compilation of suitable case study material. As well as bearing in mind the other points in Figure 1 for producing successful case study material, I also use the existing literature to help develop appropriate delivery and assessment strategies that are compatible with a case-based approach to learning and teaching. This includes time for team work, a requirement for students to use their own disciplinary knowledge to help contextualize the Statistics involved in their work, and methods to assess students' performance in the case-based activities themselves and not just on the “final product” (i.e., report or write-up). Among others, I refer to McNaught et al. (2007) and Race (2000).

In this article, I discuss the development of materials and activities for case-based learning and teaching in a first year undergraduate Statistics service course for Business students enrolled on Bachelor's degrees in Accounting and Finance and Business Accounting & Finance, although the CASE project is currently developing similar materials and activities for students taking Statistics service courses from other disciplines. I also use appropriate techniques to evaluate the success of my case-based learning and teaching activities in this service course. Specifically, some students are randomly assigned to tutorial classes in which case study materials and activities are implemented; the other students have more standard tutorials in which more routine data-response questions, similar to those in lectures, are tackled. The grades for open-ended project work and more routine homework exercises are compared between the two groups, using a linear model to detect significant treatment effects (after adjusting for nuisance factors such as cohort (Accounting & Finance/Business Accounting & Finance) and gender).

This article is set out as follows. In Section 2, I discuss the development and implementation of my case-based activities, including (i) details about the targeted service course, (ii) the processes involved in designing the case materials and an outline of one of the case studies developed, (iii) how case study activities would be woven into the course, and (iv) initial student reception to the case-based activities. In Section 3, I attempt a more formal evaluation of my methods, including possible effects on student grades in project work and more routine in-course assessments. In Section 4, I reflect on my methods and evaluation, before finishing with some general conclusions and recommendations in Section 5.

2. Case-Based Activities: Development and Implementation

2.1. The Targeted Course – Syllabus, Structure, Assessment, and Composition

One of the courses targeted by the CASE project is a first year quantitative methods module taken by students enrolled on BA(hons) courses in Accounting & Finance and Business Accounting & Finance (henceforth AF and BAF, respectively) at Newcastle University in the United Kingdom. The module is compulsory and lasts the full academic year, which, at Newcastle, is split into two 12-week semesters. The case-based activities I develop would have to fit comfortably within this 24-week schedule, and around the syllabus for the module—which consists of a 3-week “mathematics primer” (giving students the opportunity to review simple but important techniques such as algebraic manipulation and working with simple linear functions), followed by “Types of data”; “Data collection methods”; “Graphical/numerical summaries of data”; “Introductory probability”; and “Discrete probability models” in the first semester, and then “Continuous probability models”; “Basic statistical modeling”; and “Inference for Normally distributed populations” in the second semester. As I discuss in Section 2.3, my activities could just as easily be integrated into 15-week semesters, as is traditional in most colleges in the United States. In each week of the first 12-week semester, the entire class attends a standard lecture in which material is delivered using slides and students are required to make notes (all students attend the same lecture with a single lecturer). Following the lecture, the students are split into eight small groups (A–H) for tutorial teaching, each tutorial group consisting of around 25 students. The structure of the second semester is similar, although the second half of this semester (roughly the last 6 weeks of the course) incorporates the Easter vacation and time for students to work on their projects. Overall assessment of the course consists of an end-of-year examination (70%) and in-course assessment (30%) which consists of individual project work and small homework exercises, some of which are computer-based (in fact, there are eight small assessed homework exercises; four written exercises and four exercises completed via the Numbas web-based e-assessment system¹ ). Each of these exercises is equally weighted.

In the academic year 2014/15, there were 198 students registered for this quantitative methods module. Of the 198 students, 113 were male and 85 female; 140 were registered on the AF degree and 58 on the BAF degree. The distinction between the AF/BAF degrees is important, as it is often the case that most students on the BAF degree have previously studied Mathematics/Statistics at a higher level than those on the AF degree. Students were randomly allocated to one of the eight small groups for tutorial teaching, giving similar proportions of male/female and AF/BAF students in each group as we observed across the full cohort. Students in groups A, B, and C (77 students in total) would experience case-based learning activities in their tutorial session, whereas the other students in groups D–H (121 students in total) would partake in “‘standard” tutorials in which they would be given the opportunity to work through practice questions which are routine in nature and directly linked to the lecture material. The same teaching staff were involved in all tutorials, although additional postgraduate support was necessary to run the case study tutorials.

2.2. Development of Case Material

As I discuss in Section 1, there are various online portals offering materials for case-based learning and teaching activities, although I found that none of these resources seemed to fit well with the syllabus of this quantitative methods module and the disciplinary interests of my AF/BAF students. I did find some relevant case material in Quantitative Methods text books; for example, Morris (2008), Swift and Piff (2014), and Waters (2011). However, the materials I found were too short, were often focussed on very narrow parts of the syllabus, usually came with worked solutions and did not lend themselves well to the teamwork activities I had in mind (e.g., group discussions, problem solving, and report writing). Thus, with guidance from academic staff in Accounting and Finance, the CASE project employed student interns to develop some bespoke case material to fit exactly the needs of my case-based approach to learning and teaching in this quantitative methods module. These student interns were final year undergraduates or postgraduates from Mathematics/Statistics and Accounting/Finance. I now describe one of the case studies developed. All case study materials can be viewed from my webpage.

Example case study: “The Beckham Effect: Football shirt sales at Paris Saint-Germain”

The student interns thought this case study would strike a chord with many students in the class, given the popularity of soccer and the celebrity status of David Beckham in the United Kingdom. The full case study handout, as presented to students, is shown in Figure A1 in the appendix, available in the online supplementary information. Elements of accounting and finance are brought in through linear functions for revenue, cost, and profit: the case study focuses on sales of replica team shirts the month before, and the month immediately after, the signing of David Beckham to French club Paris Saint-Germain. Students are required to use the information given in “the story” to construct general linear functions which link the number of shirts made/sold to the profit made by the club on these sales. This tests the students' mathematical—rather than statistical—reasoning, and their ability to translate written information into mathematical expressions.

The students are then asked to assess the suitability of their post-Beckham monthly linear profit function as a model for future profits from shirt sales: real data are presented on the number of shirts sold with the corresponding profit, per month, for the next 10 months. This provokes the comparison of a simple scatterplot of the data with the formulated profit function, as well as a comparison of the profit function with the estimated simple linear regression model obtained from the data. To do well in the case study report, not only should students be able to construct the profit functions and estimate the simple linear regression model from the data, but they should also be able to critique their work: there are clearly issues of extrapolation to consider, as well as a suggestion of nonlinearity in the scatterplot of the data. Given the material covered in class, the more astute students might also perform a hypothesis test on the slope of the regression model to assess whether there is evidence to suggest that it is significantly different from that first suggested. Students can also practice their data summary skills, including measures of average, spread, and correlation. Students can base their reports around responses to the “Possible ideas to investigate,” given at the end of the handout, but are told that they should by no means treat this list as exhaustive. I believe this case study qualifies for most of the criteria set out in Figure 1.

2.3. Accommodating Case-Based Activities

The example case study described in Section 2.2, and all other case studies I developed, were designed to occupy a six-week block in the timetable (in a more traditional 15-week semester, as observed in many U.S. colleges, I recommend extending this to a seven-week block, allowing more time for grading of case study written reports and perhaps a final week of reflection at the end of the semester; see Section 4). Given that in the last half of the second semester students would be allowed time to work on their individual projects, this would give each student in tutorial groups A, B, and C the chance to take part in three case studies—two in semester 1 and one in the first half of semester 2. Each 6-week block would include time in tutorials for teamwork; report-writing; assessment of case study activities (mainly focussing on students' contributions to staff-led discussions); submission of work; reflection; grading and return of work; and a feedback session. Some key decisions that were made are included in the answers to the following questions.

How can teamwork be facilitated? I believed group work was essential to the successful implementation of my case-based activities, with students perhaps learning more from each other than they would in a “standard” tutorial. Thus, in the first tutorial for groups A, B, and C, students would be asked to form small teams of about 4 to 5 students, giving around 5 or 6 small teams in each tutorial group. As Gross Davis (1993, p. 131) remarked, “Groups of 4–5 tend to balance well the needs for diversity, productivity, active participation, and cohesion.” I recognized that running case study tutorials would require more staff support and so postgraduate students would be employed to assist, these students being given training prior to the start of the course (all training documents are available to view from my webpage). As Hammond et al. (1999) discussed, “To the students, postgraduates as tutors may not be so daunting as lecturing staff.” Hammond et al. (1999) also pointed out that “…the staff time invested in training postgraduates is more than saved by teaching staff not running the tutorials.” I decided to let students form their own teams as I wanted them to feel comfortable with their fellow team mates. The case material developed (see Section 2.2) would be written to facilitate discussion, giving students “Possible ideas to investigate.”

How will students be assessed on their case study work? For students in tutorial groups A, B, and C, some of the assessed small homework exercises, mentioned in Section 2.1 as part of the standard requirements for in-course assessment, would be replaced with alternative assessments more compatible with case-based learning and teaching. Specifically, for each case study, students would be assessed via a mixture of standard summative assessment, in the form of a mark (out of 22) being awarded for an individual written report, and a mark (out of 3) for their contribution to small, staff-led group discussions taking place in the case study tutorials before the written work was submitted (giving a maximum mark of 25 for each case study). Students would be given an example case study, with example report write-up, so they would know exactly what was expected of them here (see webpage). In the group discussions, the teacher/postgraduate assistant would ask some thought-provoking questions from a list of such questions produced for each case study (see Figure A2a in the appendix); he/she would then observe the ensuing discussion, trying to make sure that quieter students would get their turn to speak. A mark would then be awarded for each student's contribution according to the criteria set out in Figure A2b (students would be given a copy of this document so they would know how marks could be attained). Given the nature of the case study work, up to half of the 22 marks available for the written report could be for interpretation and discussion, with up to 3 marks for “extras”—calculations or discussion showing independent research or an appreciation for the use of techniques beyond the scope of the course.

How will the case study tutorials actually run? In the first tutorial, each group would be given a case study handout comprising a scenario relevant to the world of Business, Accounting, and Finance (see Section 2.2), and the students would be given adequate time to read through and absorb the case material. Unlike in lectures and “standard” tutorial classes, I decided that no formal teaching would take place in the tutorials, and great care would be taken not to “teach to a solution.” Rather, the students would be encouraged to discuss the work with their group members and find their own paths. The teacher/postgraduate assistant should, of course, answer any generic questions, offer constructive criticism of students' approaches to the work, and take time to sit with each small group to discuss their progress and offer general advice. Assessed group discussions (see above) would take place in the fourth week of the 6-week cycle, and at any point until then verbal feedback on students' pre-submission write-ups would be given. Structured sessions on reflection and feedback would take place after the submission of the case study report. I would try to make sure the amount of work required of each case study would be manageable, largely in class time, within the four weeks from start to submission. In a more traditional 15-week semester, as observed in many U.S. colleges, I propose the same 4-week schedule, with the feedback process being completed in the seventh week rather than the sixth—allowing more time for the grading of written reports; see Section 4.

Should each team work on the same case study? It was initially decided that each team of 4–5 students would be given a different case study to work on. However, the length of time it took to compile material for each case study meant that by the start of term only two unique case studies for each 6-week cycle had been written. Thus, within each tutorial for groups A, B, and C, only two case studies would be in circulation, each small team of 4–5 students working on one of these two. During the fifth and sixth weeks, all students would see both case studies and be part of the reflection and feedback process for both, giving insight not only into their own case material but that for the other case study. Within each 6-week cycle, both case studies would cover exactly the same material from lectures and I would try to make sure that both were of equal difficulty.

2.4. Student Reception and Initial Evaluation

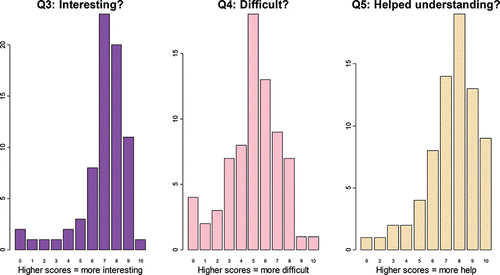
All students were asked to complete a questionnaire after the first six-week cycle to elicit their thoughts and opinions regarding the case studies. This questionnaire is shown in Figure A3 in the appendix. Student feedback was generally quite positive. Figure 2 shows the results of questions 3–5 of the questionnaire shown in Figure A3. There were 73 respondents out of 77 students in the three case study tutorial groups. Students completed the questionnaire in class, and there is a strict attendance policy in lectures and tutorials—hence the high completion rate achieved. As can be seen, although student responses are always variable, levels of interest in, and perceived usefulness of, the case studies were quite high; scores for perceived difficulty were somewhat more moderate. I was most pleased with responses to question 5: if the case studies had genuinely improved students' understanding of the course material, this was surely an indicator of success of the case-based activities! Interestingly, there was also a (significant) positive relationship between student responses to questions 3 and 4—that is, as the difficulty increased, so too did student interest in the material. In my experience, such an association is not common in student course evaluations, and I might interpret this as a positive finding from my work.

Figure 2. Student responses to questions 3, 4, and 5 in the CASE questionnaire.

In more open-ended comments and feedback, students were generally positive about their case-based learning experiences, although there were some reservations—as the comments below, taken directly from question 6 of the questionnaire, reveal:

Brought the ideas to life.

Gives the chance to apply maths in real situation.

Nice seeing a real world use of linear functions.

Took much time, and I think we need more help to solve problems.

Not sure the assessed discussions helped me.

Helped in depth understanding of the methods.

Although the evidence is rather anecdotal, I feel these comments go some way to show that the cases improved students' engagement and motivation.

Generally, I certainly feel as though students engaged with the case-based materials. After a rather slow start in the first case study, I found that students were quite willing to discuss their work in the case study tutorials and were keen to show me what they had done. I had anticipated the assessed group discussions would be quite painful, but this was not the case at all; students seemed relaxed and the atmosphere generally convivial. Comparing the attitude of students in groups A–C to that of students in groups D–H was also interesting: after an obvious settling-in period for students in the case study tutorials, there seemed to be a much more proactive attitude among many students involved with case study work than there was among the other students, and a willingness for the case study students to just “try things out” and not overly worry about making mistakes.

3. A More Formal Evaluation of My Case-Based Activities

I now attempt to evaluate my case-based activities in this Statistics service course more formally. Recall that there were 198 students taking this course in total, 77 of which were randomly allocated to case study tutorial groups A–C; the remaining 121 students were randomly allocated to tutorial groups D–H, in which “standard” tutorial activities took place, these mainly consisting of students working through nonassessed practice questions linked to the current lecture material, students having the opportunity to ask the tutorial leader questions about the work, should they wish. In all eight groups, there was a mixture of male and female students, as well as students enrolled on the AF/BAF degree programs. As discussed in Section 2.1, in-course assessment makes up 30% of the marks for this module, consisting of an individual project in the second half of the second semester and eight small homework exercises, four of which are written exercises and four of which are computer-based assessments (CBAs) using the Numbas e-assessment system. For students in tutorial groups A–C, undertaking case study work, three of the written exercises were replaced with written case study reports linked to the case material developed for the course; all students completed the same CBAs. In an attempt to formally evaluate the effectiveness of my case-based activities, I compare the project grades of students who took part in case study work to the grades of their peers who did not take part in case study work; I also compare the average CBA grades between the two sets of students. The CBA work consists of more routine, algorithmic style questions linked to the course material; see Figure 3. The project work requires students to analyze their own individual datasets in a way they deem appropriate, and write a report to discuss their findings; as such, this work is much less prescriptive than the CBA work, is more open-ended and tests students' interpretative skills. Given the nature of the case study activities for students in tutorial groups A–C, I hope that these students would be better prepared for this project and perhaps achieve higher grades here.

Figure 3. Screenshots taken from some of the Numbas tests used in the Statistics service course for Accounting and Finance students.

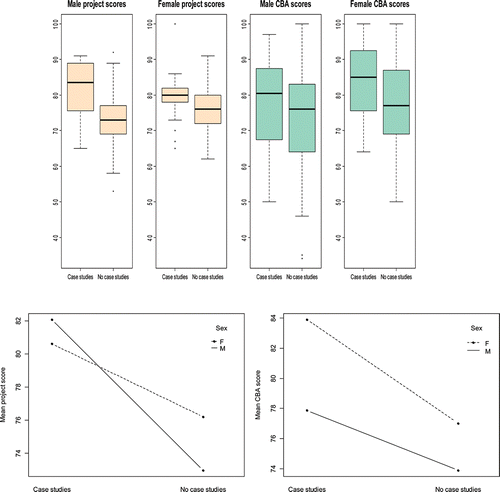
Figure 4 compares the project and CBA grades of students who took part in case-based activities to those who did not, broken down by male and female students. Both the project and CBA grades are generally higher for those students exposed to case-based activities, with female students consistently achieving higher grades, on average. Interestingly, the bottom row of plots in Figure 4 reveals that male students seem to be more receptive than female students to case-based learning and teaching activities, in terms of their in-course assessment grades – for their project work, at least. In a more formal assessment, I fit a linear model with project grades and CBA grades used separately as response variables, using indicators of treatment (case study exposure), gender, and cohort (AF/BAF degrees) as explanatory variables. For project grades, I found a significant difference between students who had, and had not, taken part in case-based activities, with the treatment indicator having a p-value of 0.00745. Similarly, the gender effect on project grades that we can see in Figure 4 is highly significant (p = 0.00699), with a significant interaction between gender and treatment (p = 0.04291). There was also a significant difference in CBA grades between the two groups, with the treatment indicator having a p-value of 0.01020. Differences between male and female students were only marginally significant here (p = 0.07765) but there was a significant cohort effect (p = 0.00154). There were no significant interactions here. In both models (project grades/CBA grades), the residuals were well behaved, being apparently normally distributed with constant variance.

Figure 4. Top row: boxplots showing student grades (out of 100) for the course project, and average student grades (out of 100) across the four computer-based assessments (CBAs). Bottom row: interaction plots showing mean project and CBA grades.

Also of interest is the performance of these students in the “Professional Skills” course they take alongside this Quantitative Methods module. In this course, students complete project work with some basic data analyses being required. Some of this project work requires individual student submissions, while some requires group submissions. Although not shown here, the grades of students in the individual elements of this course were significantly higher (p = 0.034) for those who had undertaken case-based work in the quantitative methods course, using a linear model with indicators of treatment, gender, and cohort as explanatory variables (as before). Similarly, groups who had at least two members of their team who had undertaken case-based work in my quantitative methods course obtained significantly higher group marks (p = 0.024) than those teams who did not have any members in my case study tutorials.

Other indicators of the success of my case-based activities include the following:

•	Every single student in tutorial groups A–C submitted a report for the first case study, compared to a submission rate of 95% for the corresponding standard written assignment set for students in groups D–H. For case study/written assignment 2 and 3, these submission figures were 99%/91% and 98%/87%, respectively. This could indicate that students involved in case-based activities were more engaged with the course material.
•	Recall that all students took part in my assessed CBA work. Again, submission rates were higher for students taking part in my case-based activities than for students who were not: 97% compared to 81% across all four CBA tests. Again, this could be indicative of higher student engagement in the case study group.
•	Grades for students' case study reports were generally lower than grades for the corresponding written assignments submitted by students who were not involved in case-based activities. However, I feel the standard written assignments were probably over-prescriptive (certainly relative to the case study work), quite algorithmic and so not a useful indicator of students' deep understanding of course material. In fact, my experience suggests that high marks in such written assignments often give students an overly optimistic view of their grasp of course material, leading to a heightened sense of disappointment with project marks (which are usually lower).

4. Reflection

The student responses discussed in Section 2.4 and my evaluation in Section 3 give me hope that at least some of my aims have been achieved with this project. However, the implementation of the case studies gave rise to some problems – some of which I anticipated, but others I did not. I now briefly discuss these so readers who are interested in trialing similar activities can learn by my mistakes!

Small group teaching with case studies required more staff input than my “standard” tutorials. Here, I made use of my postgraduate students from two disciplines—Mathematics/Statistics and Accounting/Finance—who relished the opportunity of teaching/demonstrating experience. However, generally I recognize that the increased staff demand could be problematic. Assessing each case study took much longer than assessing a standard written assignment. The assessed group discussions required one-to-one time between a staff member and each small team, and grading the individual case study reports was also very time expensive—the students were encouraged to “think outside the box” and were told that there might be several ways to tackle each case study, meaning that generic marking schemes were not always appropriate and individual work needed to be scrutinized carefully. Indeed, with submissions at the end of the fourth week there was less than two weeks for staff to grade all case study written reports, in order to return them to students in time for the feedback session in the sixth week. Although some students said they appreciated the individual written report for each case study, so they could personalize their work and include elements of their own research, some staff time could be saved by allowing group report submissions (and there might be reasons for preferring this with case study work). In my case, this would have reduced the number of reports to grade for each case study from 77 to just 15, significantly relieving the grading burden on staff within the 2-week postsubmission period. In a more traditional 15-week semester, submission of the written reports could still take place after four weeks, but in a seven-week case study block this would leave more time for grading the reports (and perhaps a “spare” week right at the end of the semester for reflection). An alternative would be to require submission at the end of the fifth week, with an extra week within the cycle for pre-submission feedback on draft work—this feature of my trial was especially popular with students. There were general, relatively expensive, set-up costs involved—in my case, these included sourcing the information for the case studies and compiling the case studies. However, I see such costs as “one-off”—once the material has been compiled, it is ready to use again with subsequent classes.

One issue which I had not anticipated—admittedly rather naively—was that I was under-prepared to teach problem solving. In principal, the idea of using real life, relevant source material to engage these students with Statistics has obvious appeal; in practice, and when I was faced with the first case study workshop of 25 students, I was not that sure exactly “how” to teach using the case studies! Of course, in the first class, the students needed time to digest the material they were presented with; in subsequent weeks, I faced a rather steep learning curve myself about how the case study workshops should be delivered. Perhaps the most difficult concept was to stand back and let the students think for themselves about how to tackle the problem: to act as facilitators, rather than teachers, as discussed in Section 1. However, standing back too much also caused problems: it was noted that a few students who were struggling with the work very quickly felt “marooned”—without any intervention from staff some of these students then drifted and became completely disconnected from the work. Interestingly, when such students were asked questions about the course material, it was clear that they could “turn the handle”—operating formulas etc.—suggesting that without suitable guidance in case study sessions the opportunity to convert this surface learning into deep learning of course material might be missed. As part of the ongoing CASE project, I intend to carefully examine texts, such as Pólya (1962), Schoenfeld (1994), Alcock and Simpson (2001), Hmelo-Silver et al. (2007), Mason et al. (2010), and Michalewicz and Michalewicz (2008), for the successful delivery of problem-solving and case-based activities. One idea I intend to implement soon is a “pop quiz” taken by all students at the start of each case study tutorial session. The quizzes would ask some very basic questions about the material in the case studies, and after just a few minutes the answers might be displayed on the projection screen at the front. This could capture students' attention and put them in a more receptive frame of mind for the rest of the case study tutorial.

In Section 3, I attempt to assess the effectiveness of my case-based activities by examining grades of students in in-course assessment exercises and project work. However, I acknowledge that there might be other ways of evaluating my methods, including an attempt at assessing the effects of case-based learning and teaching activities on students' general statistical literacy. Although this is, to some extent, covered in the open-ended project work students undertake, I could investigate the use of the ARTIST (Assessment Resource Tools for Improving Statistical Thinking) or CAOS (Comprehensive Assessment of Outcomes in a first Statistics course) suite of tests, as discussed in delMas et al. (2007). The very nature of my case-based efforts meant that students in tutorial groups A–C were “forced” to engage with material through activities, such as assessed group discussions, whereas my standard tutorials were more passive in nature, students generally only asking questions when they might be struggling with the material (or when they built up enough courage to ask questions!). Thus, higher grades in (for example) project work might be expected simply because students were more active in class and perhaps not because of the case materials themselves. I would argue that this might be difficult to measure (and difficult to separate from genuine treatment effects) and even if it is the active participation—rather than my case materials per se—which helped students achieve higher grades, then this is still a positive outcome!

5. Conclusions and Recommendations

The CASE project was set up to develop, and investigate the role of, case-based activities for learning and teaching in Statistics service courses. The current article describes, and evaluates, the merits of case-based tutorial activities for students taking a Statistics service course as part of their Accounting & Finance or Business Accounting & Finance degree. I believe there is evidence to suggest that students who were allocated to tutorials in which case-based activities were implemented benefited in terms of their ability to undertake independent inquiry-based statistical analyses, these students gaining significantly higher grades in their individual project work than students who were not involved in case-based work. This could be indicative of an increased level of confidence in these students, but perhaps even suggestive of a deeper understanding of course material. My analysis also suggests that—as far as their project work was concerned—male students were particularly receptive to the methods used in my case-based classes. Students exposed to case-based activities also gained significantly higher grades in the more routine, algorithmic in-course assessments. Further, students who had experienced case-based activities gained significantly higher grades than other students for inquiry-based work in the Professional Skills element of their degree.

There is some evidence of increased student engagement with the course material as a result of the case-based activities. Students in the case study tutorials were certainly more willing to discuss the work and ask questions, and I believe the nature of my case-based activities encouraged and fostered this attitude. Supporting this were significantly higher submission rates of in-course assessments among students taking part in case study tutorials compared to students who did not. The student questionnaires also support my claim of student engagement with, and enthusiasm for, the case-based activities, with generally positive feedback and favorable scores for their level of interest in the work and their perception of how the case studies helped them understand the course material. In terms of both students' ability and enthusiasm, I intend to follow-up the 2014/15 cohort of students to see if their experiences of case-based activities in this quantitative methods courses have helped them with other inquiry-based work in later years—in particular with any statistical analyses necessary as part of their final year dissertations.

I believe a case-based approach to learning requires group work, and I think my small groups of 4 to 5 students worked quite well. I also believe the entire case study process should make use of this group dynamic, including the submitted report. The increased demand on staff time as a result of incorporating case study material in 2014/15 was further exacerbated when I used individual submissions of case study reports, and so in future my intention is for each small team to submit a group report, perhaps incorporating some form of peer assessment using, for example, the WebPA system (www.webpa.ac.uk). Students should be given ample time to absorb the case study information, and certainly should not be taught in the case study tutorials. However, I believe that some structure to the classes, including some simple quiz questions posed at the start of each class, might help to capture students' attention and put them in a more receptive frame of mind for the rest of the class. The assessed group discussions just before the submission of the report also allowed me to assess students' in-class contributions and not just the final product of the report itself. I believe more time on the first case study, from start to submission to feedback, should be given, to allow students to acclimatize to a new way of learning.

Long term, the CASE project will provide teachers of Statistics service courses with a bank of case study materials which they can use in their own classrooms. I am currently developing some case-based activities for use in service courses for Business Management students and Psychology students. Interested readers should feel free to browse my materials at the CASE homepage (www.mas.ncl.ac.uk/∼nlf8/innovation) and leave me any comments or suggestions.

Supplementary Materials

Supplementary materials, including an example case study (“The Beckham Effect”), questions to promote team discussions in case study tutorials, marking forms/rubric for awarding marks in case study tutorial group discussions, and the student case study questionnaire, can be found in the online version of the article and on the author's dedicated webpage (www.mas.ncl.ac.uk/∼nlf8/innovation).

Acknowledgments

I thank the student interns—particularly Jack Aiston, Man Isha Kaur, Keith Newman, and Jamie Owen—for their assistance.

Funding

I would like to thank Newcastle University for funding the CASE project.

Notes

¹ Numbas is a web-based e-assessment system developed at Newcastle University, United Kingdom, and is currently used in Universities, schools, colleges, and hospitals in the United Kingdom, Norway, Australia, Denmark, Chile, Ireland, United States, Netherlands, and South Africa.