Classroom Investigations of Recent Research Concerning the Hot Hand Phenomenon

ABSTRACT

Many players and fans of basketball believe in the “hot hand” phenomenon, yet for years there has been little statistical evidence that such a phenomenon exists (hence the “hot hand fallacy”). However, recent research of Miller and Sanjurjo suggests that previous analyses of the hot hand have been subject to a bias, and after correcting for this bias, there is in fact evidence that the hot hand is real. Miller and Sanjurjo's analyses are based on permutation tests. In this work, we discuss the ideas behind the permutation test procedure, illustrate an online Shiny app we developed for conducting the test, and present related simulation-based inference activities for introductory statistics courses. Our examples are based on data from the NBA Three Point Contest, in which we do find evidence of an average hot hand effect. Furthermore, we discuss additional topics concerning the bias in previous hot hand studies which can be introduced in courses with a stronger emphasis on probability or mathematical statistics. In particular, we discuss a simple coin flipping problem with a surprising solution which has been the subject of much recent media coverage and debate.

KEYWORDS:

• Bias
• Conditional probability
• Expectation
• Hot hand in basketball
• Hot hand fallacy
• Permutation test
• Probability puzzles
• Shiny app
• Simulation-based inference

1. Introduction

Many basketball players and fans alike believe in the “hot hand” phenomenon: the idea that making several shots in a row increases a player's chances of making the next shot. However, the consensus conclusion of nearly 30 years of studies on the hot hand, beginning with the seminal study of Gilovich et al. (1985), has been that there is no statistical evidence that the hot hand in basketball is real. As a result, many statisticians regularly caution against the “hot hand fallacy”: the belief that the hot hand exists when, in reality, the degree of streaky behavior typically observed in sequential data is consistent with what would be expected simply by chance in independent trials. The belief is so pervasive that the Nobel prize-winning economist Daniel Kahneman has called the hot hand fallacy a “massive and widespread cognitive illusion” (Kahneman 2011).

However, recent research of Miller and Sanjurjo (2014, 2015, 2016b) suggests the hot hand fallacy is not a fallacy after all. The authors find strong evidence in favor of the hot hand effect in basketball shooting. Furthermore, the authors discover that previous studies on the hot hand in basketball, starting with Gilovich et al. (1985), have been subject to a bias. Using methods that correct for the bias, Miller and Sanjurjo reanalyze previous hot hand studies and find that the data used in those studies actually provide evidence in favor of the hot hand. Furthermore, they find evidence that not only is the hot hand effect real, its size can be quite substantial. The research of Miller and Sanjurjo has received a great deal of media attention (Cohen 2015; Ellenberg 2015; Johnson 2015; Remnick 2015) and has reignited debates on the hot hand.

Miller and Sanjurjo's analyses are based on permutation tests. In this work, we discuss the ideas behind the permutation test procedure, illustrate an online Shiny app (http://shiny.stat.calpoly.edu/Hothand/) we developed for conducting the test, and present related activities for introductory statistics courses in which students learn simulation-based inference (SBI) methods. Furthermore, we discuss additional topics concerning the bias in previous hot hand studies which can be introduced in courses with a stronger emphasis on probability or mathematical statistics.

Over the past decade simulation-based approaches to introducing concepts of statistical inference and for implementing inference techniques have gained in popularity and acceptance among statistics educators. There are now several widely used textbooks (Lock et al. 2012; Diez et al. 2014; Tintle et al. 2015) for teaching introductory statistics using an SBI approach. The merits of an SBI approach to teaching inference have been discussed in many publications; we do not attempt to provide a full literature review here. Our randomization-based analysis of the hot hand demonstrates two advantages of the SBI approach: it is readily adapted to the use of nontraditional statistics, and SBI methods are valid in many situations in which theory-based (normal) methods are not.

In Section 2, we present Miller and Sanjurjo's permutation test. The main idea behind the procedure should be natural to students familiar with SBI methods: Under the null hypothesis of no hot hand, the null distribution of a “streak statistic” is obtained by fixing the response values (success or failure) and shuffling the order of the observed outcomes. We also illustrate the corresponding Shiny app which functions like other popular SBI applets (e.g., Rossman/Chance, StatKey).

In Section 3, we use data, which we provide, from the 2013 through 2017 NBA Three-Point Contest to perform permutation tests and to estimate the size of the hot hand effect. Our example analysis does exhibit evidence of an average hot hand effect in the NBA Three-Point Contest, a conclusion consistent with Miller and Sanjurjo's (2015) claims.

Section 4 contains ideas for how research on the hot hand can be introduced in courses with a stronger emphasis on probability or mathematical statistics. We discuss a coin flipping problem introduced by Miller and Sanjurjo (2016b) to motivate the source of the bias in previous studies of the hot hand. While the problem is seemingly simple, its answer is unintuitive and demonstrates the importance of understanding fundamental concepts in probability. To demonstrate the ramifications of the bias, we reproduce an analysis of Miller and Sanjurjo (2016b), which finds, after correcting for bias, evidence of an average hot hand effect present in the original Gilovich et al. (1985) data.

Our work is strongly motivated by the recent papers of Miller and Sanjurjo (2014, 2015, 2016a, 2016b). Our main contributions include: a presentation of the permutation test which is accessible to introductory statistics educators and students; specific SBI activities which involve both tactile and technology-based simulation in a novel context; the Shiny app, which enables users to readily conduct hot hand analyses; the dataset and an example analysis of results from the 2013–2017 NBA Three Point Contests; and a discussion of how recent hot hand research can be incorporated in courses involving probability or mathematical statistics.

2. Randomization-Based Analysis of the Hot Hand Phenomenon

Here we describe Miller and Sanjurjo's (2014) randomization-based procedure that tests for hot hand behavior in a sequence of success/failure trials, such as the shot attempts of a basketball player. We also illustrate a Shiny app which implements the procedure. The procedure and the app are well suited for use in an introductory statistics course which covers simulation-based inference methods. In particular, the analysis we present can be adapted into transfer activities which enable students to employ simulation-based reasoning in a novel situation involving a data type (sequential trials) and statistics (subsample proportions, runs statistics) not commonly encountered in typical course topics.

2.1. Assumptions

The procedure is applicable when the data consist of the results of success/failure trials with the outcomes recorded in sequence. We focus on applications to basketball, in which each trial is a field goal attempt by a particular player. (Other applications in which hot hand type behavior is of interest include gambling, stock prices, and polling, as well as other sports.)

The test procedure relies on the following assumptions about the data-generating process.

1.	Each trial results in success (1) or failure (0).
2.	The number of trials is fixed. [While we assume throughout that the number of trials is fixed (not random), it is sufficient that the number of trials be independent of the outcomes of the trials.]
3.	The probability that a trial results in success is the same for all trials.

We will use the data in Table 1 throughout this section to illustrate the test procedure.

Table 1. Results for Stephen Curry in the first round of the 2016 NBA three-point contest.

Attempt #	1	2	3	4	5	6	7	8	9	10	11	12	13
Outcome	0	0	0	1	1	0	1	0	1	1	1	1	1
Attempt #	14	15	16	17	18	19	20	21	22	23	24	25
Outcome	1	1	1	1	1	1	0	0	0	0	1	1

2.2. Statistics Which Measure the Hot Hand Effect

While there is no consensus definition of what constitutes the hot hand, the term generally refers to a tendency for trials following streaks of successes to have an increased likelihood of resulting in success. Several statistics can be used to measure a hot hand effect; those included in the app are described below.

Helpful hint: Provide students with data like that in Table 1 and ask “How could we measure if this player had the hot hand?” Have students brainstorm various statistics and discuss their merits. (If desired, the source code of the app can be adapted to handle statistics other than the ones listed below.)

For statistics 1 through 4 below, the user must define the streak length: How many successes must be observed in a row in order to consider it a hot streak? Regarding the hot hand in basketball, 3 is commonly used for the streak length. (The app allows values between 1 and 7.)

In the app, the user can choose a streak statistic from the following.

1.	Proportion of S after streaks of S. The proportion of those trials that are immediately preceded by a streak of successes that result in success. For example, if the streak length is 3 and the sequence is 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, trials 5, 6, and 10 are preceded by a streak of 3 successes, and the proportion of successes on these trials is 2/3 = 0.6667. (This statistic is called the “hit streak momentum” by Miller and Sanjurjo [2014, 2015].)
2.	Difference in proportion of S (after streaks of S – other trials). The difference between statistic 1 and the proportion of the remaining trials that result in success. In the previous example, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, the value of the statistic is 2/3 – 6/7 = −0.1905.
3.	Difference in proportion of S (after streaks of S – after streaks of F). The difference between statistic 1 and the proportion of those trials that are immediately preceded by a streak of failures, of the same length, that result in success. In the previous example, this statistic cannot be computed since there are no trials which follow a streak of three failures. In the sequence 1, 0, 0, 0, 0, 1, 1, 1, 1, 1, with streak length 3, the value of the statistic is 2/2 – 1/2 = 0.5. (This statistic plays an important role in Gilovich et al. [1985].)
4.	Frequency of S streaks. The proportion of trials that are immediately preceded by a streak of successes. In the original example 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, the value of the statistic is 3/7 = 0.4286. With a streak length of 3 the first three trials are not counted in determining the frequency, and similarly for other streak lengths. (This statistic is called the “hit streak frequency” by Miller and Sanjurjo [2014, 2015].)
5.	Longest run of S. The largest number of successes in a row in the observed sequence. In the example 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, the value of the statistic is 4. (This statistic is called the “hit streak length” by Miller and Sanjurjo [2014, 2015].)
6.	Total number of runs. The total number of runs, of any length, of successes or failures. In the example 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, the value of the statistic is 4. (This is the usual “runs statistic,” and it is equivalent to the total number of “switches” or “alterations” between S and F if the first trial is counted as the first switch.)

Table 2 displays the values of these statistics, with a streak length of 3, for the data in Table 1. Nine trials (attempts 12 through 20) are each preceded by a streak of three successes, and eight of these trials result in success; while three trials (attempts 4, 23, and 24) are each preceded by a streak of three failures, and two of these trials result in success. The overall proportion of successes is 16/25 = 0.64.

Alternative application: See Section 3 of Miller and Sanjurjo (2015) for a more detailed discussion of the various statistics. The authors also consider a composite statistic which combines several of the streak statistics.

Using the app: In the app, data like that in Table 1 can be entered simply by copying the 0/1 values in order (separated by commas, e.g., 0, 0, 0, 1, 1, 0, 1). Alternatively, the user has the option to enter the following three values.

1.	Total number of trials;
2.	Total number of successes;
3.	Observed value of the streak statistic.

Table 2. Observed value of streak statistics, with a streak length of 3, for data in Table 1.

1	Proportion of S after streaks of S	8/9 = 0.8889
2	Difference in proportion of S (after streaks of S – other trials)	8/9 – 8/16 = 0.3889
3	Difference in proportion of S (after streaks of S – after streaks of F)	8/9 – 2/3 = 0.2222
4	Frequency of S streaks	9/22 = 0.4091
5	Longest run of S	11
6	Total number of runs	8

The second input method allows the user to analyze data from the hot hand literature, where tables of summary statistics are usually available but entire outcome sequences are not. (We use the summary statistics input option in Section 4.4.)

2.3. Permutation Test of the Hot Hand Effect

Miller and Sanjurjo (2014) introduced a permutation test for the hot hand effect. The test is based on concepts which should be natural to students familiar with simulation-based inference methods in an introductory statistics course. Furthermore, the permutation distribution of the streak statistic is often not well approximated by a normal distribution, even when the sample size is large, and so theory-based methods do not apply. (However, the nonnormal shape of the null distribution is not the most serious problem. The crucial issue with theory-based methods in this context is that a naïve application of the typical theory-based method assumes an incorrect mean of the null distribution, resulting in a bias which can be substantial. We discuss the issue of bias further in Section 4).

2.3.1. Simulating the Null Distribution

The null hypothesis is that the trials are independent, consistent with no hot hand effect. Recalling the assumptions in Section 2.1, if the null hypothesis is true then the trials are Bernoulli trials. Therefore, if the null hypothesis is true, the probability that n trials result in a particular ordered sequence of outcomes consisting of s successes is $p^s{\left(1-p\right)}^{n-s}$, where p is the probability of success in a single trial. While p is unknown, conditional on the observed number of successes s, each possible ordering of the s successes and n-s failures is equally likely under the null hypothesis (i.e., the trials are exchangeable). It follows that the exact null distribution of a streak statistic for a sequence of n trials with s successes can be constructed by computing the value of the streak statistic for each of the possible $\left(\begin{array}{l}n\\ s\end{array}\right)$ permutations of the s successes among the n trials. In practice, the null distribution can be approximated by simulating the value of the streak statistic for a large number of randomly generated permutations of the observed data.

Potential pitfall: An assumption is that the trials are identically distributed: the (unconditional, marginal) probability of success is assumed to be the same for all trials. The null hypothesis is that the trials are independent: the conditional probability of success given that the trial follows a streak of successes is equal to the unconditional probability of success. Students often confuse these two distinct notions—constant probability of success (i.e., identically distributed trials) versus independent trials—and this could be an opportunity for review or clarification.

Consider the data in Table 1 with 16 successes in 25 trials. The null distribution of a hot hand statistic can be simulated by randomly permuting the order of the 16 successes and 9 failures, computing the statistic for the resulting permutation, and repeating many times. The app implements this process; the following figures display examples of simulation output.

Helpful hint: Students should be able to identify that the null hypothesis is of no hot hand effect. For data like that in Table 1 ask students how they might simulate the null distribution of a streak statistic. Take advantage of students' familiarity with randomization-based tests for comparing groups. In that scenario, we fix the values of the response and rerandomize the groups to generate a hypothetical value from the null distribution under the null hypothesis of no difference between groups. In the hot hand procedure, we again fix the value of the response (success or failure) but now we rerandomize the order of the attempts to generate a hypothetical value from the null distribution.

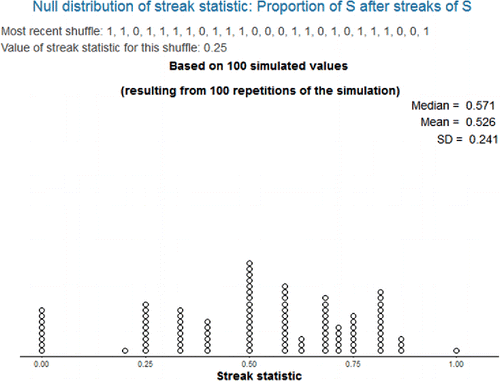
Helpful hint: Prior to using the app, have students work in small groups to perform a tactile simulation following these instructions. Obtain a set of index cards, one card for each trial in the observed data. Count the number of successes in the observed data and mark (with “1”) that many cards as successes and mark the others as failures (“0”). Shuffle the cards well and then deal them out one at a time, recording the outcomes in sequence (1, 1, 0, 1, and so on, like in Table 1). Compute the value of the streak statistic for this particular shuffle to obtain one hypothetical value of the statistic under the null hypothesis. [In the app, checking the box for “show most recent shuffle” will illustrate this process.] Have the groups repeat the process a few times to construct (e.g., on the blackboard) a null distribution like in Figure 1, which could then be used to obtain an initial approximation of the p-value.

Figure 1. One hundred simulated values of streak statistic 1 with streak length 3 when there are 16 successes out of 25 trials.

Using the app: Only the number of trials and the observed number of successes are needed to simulate the (null) permutation distribution. Thus, in addition to data analysis and inference, the app can be used to investigate some of the probabilistic concepts in Section 4. (See the “alternative application” at the end of Section 4.4.)

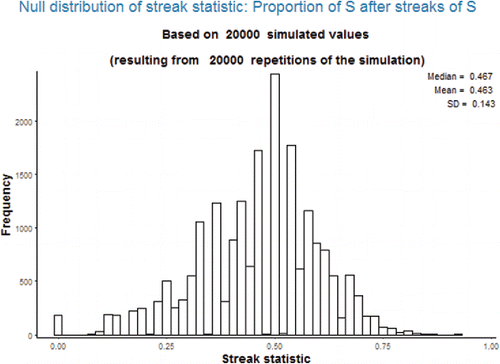
Figures 2 and 3 display the simulated null distribution for the data in Table 1 (16 successes in 25 trials) for streak statistics 1 and 2, respectively, with a streak length of 3. It should be apparent that the distributions do not have a nice or well-recognized shape.

Potential pitfall: One might expect the mean of the null distribution in Figure 2 to be 0.64, the overall proportion of successes; however, it is actually about 0.55. Similarly, one might expect the mean of the null distribution in Figure 3 to be 0, while it is about −0.10. See Section 4 for further discussion of related issues. (Of course, the value of the null mean is not needed to compute the simulation-based p-value.)

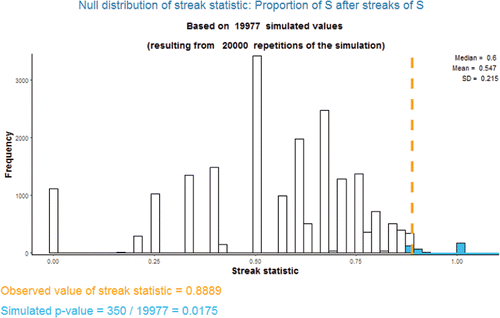
Using the app: As alluded to in the example for statistic 3 in Section 2.2, for streak statistics 1 through 4 the value of the statistic cannot be computed for a permutation in which there are no streaks of the specified length. Therefore, the app distinguishes between the number of repetitions performed and the number of simulated values of the statistic (e.g., 20,000 versus 19,977 in Figure 2). The latter value is the denominator of the simulated p-value.

Figure 2. Simulated null distribution of streak statistic 1 with streak length 3 when there are 16 successes in 25 trials.

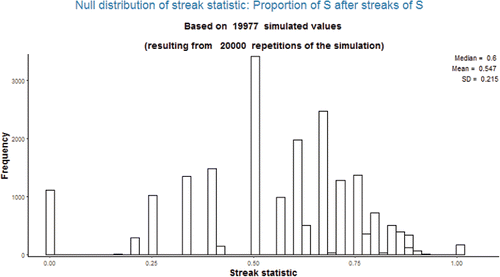
Figure 3. Simulated null distribution of streak statistic 2 with streak length 3 when there are 16 successes in 25 trials.

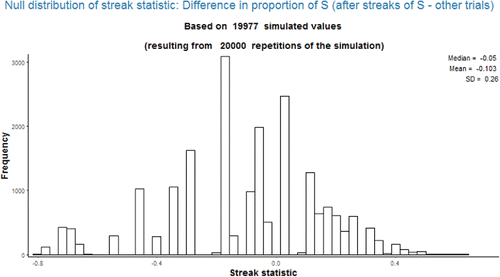
Students are likely familiar with checking conditions such “at least 10 successes and 10 failures” to assess validity of a normal approximation of a distribution of a sample proportion (or of a difference in proportions). However, the streak statistics involve subsample proportions: the proportion of trials which are immediately preceded by a streak of successes that result in success. The number of trials which are preceded by a streak can be relatively small, especially when the streak length is large. Thus, the effective sample size for the subsample proportion can be much smaller than the actual number of trials. Furthermore, even when the sample size is relatively large the permutation distribution of a streak statistic is often not well approximated by a normal distribution, as illustrated by Figure 4 which corresponds to 50 successes in 100 trials. Therefore, this hot hand analysis provides a scenario in which simulation-based methods are natural while theory-based methods often do not apply.

Figure 4. Null distribution of streak statistic 1 with streak length 3 when there are 50 successes in 100 trials.

2.3.2. Computing the p-Value

As usual, an approximate p-value is provided by the proportion of values in the simulated null distribution which are at least as extreme as the observed value of the statistic. (In the app the p-value is computed by checking the box for “Compute p-value.”) Since we are primarily interested in evidence against the null hypothesis of no hot hand in the direction of hot hand behavior, one-sided p-values are computed.

·	For the total number of runs (statistic 6 in Section 2.2), smaller values of the statistic are stronger evidence to reject the null hypothesis of no hot hand. (In hot hand behavior, we would expect longer, but fewer, runs of success.)
·	For all other streak statistics, larger values of the statistic are stronger evidence to reject the null hypothesis of no hot hand. For example, the larger the proportion of successes on trials preceded by streaks is than on other trials, the stronger the evidence of a hot hand effect.

Consider the data in Table 1. The observed value of the proportion of trials that are preceded by three successes which result in success is 0.8889, which yields a simulated p-value of about 0.02, as illustrated by Figure 5. Therefore in this particular sequence of shots there is some evidence of hot hand behavior as measured by this particular streak statistic.

Figure 5. Simulated p-value based on the null distribution in Figure 2 and an observed value of 0.8889.

3. Assessing Hot Hand Behavior across Multiple Basketball Players

In light of the assumptions in Section 2.1, the permutation test is not appropriate for in-game basketball data, as the number of attempts and probability of success on each attempt are influenced by a wide variety of factors (e.g., distance from the basket, performance of teammates or opponents, etc.). As a result, most previous research has focused on controlled shooting experiments in which players shoot a prespecified number of field goal attempts from fixed locations on the court (Jagacinski et al. 1979; Gilovich et al. 1985; Miller and Sanjurjo 2014).

Rather than conducting a shooting experiment, we follow the lead of several papers (Koehler and Conley 2003; Miller and Sanjurjo 2015) and study data from the NBA Three-Point Contest. In each round of the contest a participant has 60 sec to attempt a series of 25 three-point field goals, five attempts each at five fixed locations around the three-point line (two locations in each of the corners at a distance of 22 feet from the basket, and three locations at a distance of 23 feet 9 inches from the basket). Therefore, the number of attempts is fixed, and it is reasonable to assume that the probability of success is the same for all of a player's attempts. Furthermore, data on well-known NBA players participating in a real and popular contest is likely more interesting to students than data on anonymous players from a shooting experiment.

Alternative application: Students could design and conduct a controlled shooting experiment to collect data on themselves or local basketball teams.

3.1. Data Collection

The most comprehensive study to date of the hot hand in the NBA Three-Point Contest is Miller and Sanjurjo (2015) which uses data for the 1986 through 2015 contests; however, the dataset is not yet publicly available. We collected data from videos of the NBA Three-Point Contest from 2013 through 2017. (The 2016 and 2017 contests are not represented in Miller and Sanjurjo 2015). Each contest consisted of a first round and a championship round, and when necessary, tie break rounds. From 2014 through 2017, eight players participated in the first round; in 2013 six players participated in the first round. In 2015 through 2017, the three players with the highest first round scores competed in the championship round, while in 2013 and 2014 two players competed in the championship round.

The dataset consists of the sequence of results of the attempts for each of 58 player-rounds, a total of 1413 field goal attempts. A value of 1 represents a made field goal (success) and 0 represents a miss (failure). The following items describe a few details of the data collection.

·	In 2016, three players finished with the same first round score and competed in a 30 sec tie break round (labeled round 1.5). Due to the shorter length of the tie break round, two of the players attempted 14 shots, and the third attempted 13 shots.
·	In 2014 and 2017, the championship round initially ended in a tie, so there was an additional 60 sec round (round 2.5).
·	There were a few attempts in which the player made the shot but stepped on or over the three-point line before release. We counted these trials as successes even though the contest itself did not.
·	In a few rounds the player released his final shot just after time expired. In these cases, we counted made attempts as successes even though the contest did not. Recorded in this way, aside from the tie break round in 2016, there was only player-round in which the player did not complete all 25 attempts.
·	Attempts 1–5 and 21–25 are always in the corner locations, 6–10 and 16–20 on the wing locations, and 11–15 at the top of three-point line. However, we did not collect data on whether the player proceeded in a clockwise or counter-clockwise direction.
·	The only data recorded were the order and outcome of each attempt. In particular, we did not collect data on the time elapsed between attempts or whether the attempt was a “moneyball” (which in the contest is worth 2 points instead of 1).

Alternative application: The data can be analyzed to assess the validity of the assumption of constant probability of success across attempts or locations. Previous studies by Miller and Sanjurjo (2014, 2015) have found that players tend to perform relatively worse on their first two attempts than on the others, and students might consider omitting the first two attempts of each player-round. Miller and Sanjurjo's (2015) analysis concluded that, on average, players do not shoot significantly better or worse from any of the five locations (nor on the “moneyball” attempts).

Alternative application: Miller and Sanjurjo (2015) merge data from multiple rounds, and in some cases from multiple contests, to construct a player's shot sequence. Students might wish to debate the merits of this approach. Combining rounds enlarges the sample size for the player and hence increases the power of the test. (We will combine rounds for our analysis.) However, it could be argued that combining data from different contests violates the assumption of constant probability of success.

3.2. Significance at the Individual Player Level

Appendix A (available in the online supplementary material) summarizes the results of a permutation test for each of the players in the NBA Three-Point Contest data set. For this analysis, we pooled a player's results within each contest, but not between contests, performing a test for each player-year (37 in total). (We refer to “player-year” simply as “player” in what follows.) Statistic 2, the difference in proportions of successes between trials following streaks of three successes and all other trials, was used as the streak statistic for all tests.

Helpful hint: Each student or group could use the app to conduct the permutation test for different players. The results could then be collected to form a table like that in Appendix A.

At a significance level of 0.05, the null hypothesis of no hot hand is rejected in three of the tests (Stephen Curry 2016, Stephen Curry 2013, J.J. Redick 2015). Two of the tests, while not significant at a strict 0.05 level, yield p-values of about 0.06 (C.J. McCollum 2016, Stephen Curry 2015). Of course, we must consider the inflated probability of Type I error when conducting multiple tests. Assuming independence of tests, the probability that three or more of the 37 tests are significant at the 0.05 level is 0.28 if all 37 null hypotheses were true (0.28 = P(X ≥ 3) if X ∼ Binomial(37, 0.05), a calculation which could be performed with a “one proportion” applet (e.g., Rossman/Chance, StatKey)). Therefore, at strict level 0.05 the data do not provide convincing evidence in favor of the hot hand at the individual player level.

Unfortunately, the permutation test suffers from low power at the player level, especially for players who only participate in one round of 25 trials. Even when the number of trials is large, there will be relatively fewer trials which follow a streak of three successes, and so the measure of a player's success rate when in the “hot state” is highly variable. (For these reasons, controlled shooting experiments typically involve at least 100 shots per player).

Alternative application: We have included in the analysis all players with at least one streak. A stricter threshold for inclusion could improve power. Also, other streak statistics could be investigated as potentially more powerful alternatives to streak statistic 2.

3.3. Average Size of the Hot Hand Effect

Figure 6 displays the distribution of streak statistic 2, the difference in proportions of successes between trials following streaks of 3 successes and all other trials, for the 37 players in the dataset (Appendix A). For almost all of the individual players the permutation test is not significant at the 0.05 level. However, for the majority of players there is directional evidence of hot hand behavior: for 21 of the 37 players the observed value of the streak statistic is greater than the median of the corresponding null distribution. Furthermore, the mean difference between the observed streak statistic and the mean of the corresponding null distribution is about 7.5 percentage points, a substantial difference in the context of basketball field goal percentages. Therefore, while the test is ill powered to detect hot hand behavior at the individual player level, the data do provide some evidence of a general tendency toward hot hand behavior across many players.

Potential pitfall: Interpreting Figure 6, in particular its center, requires some care. In short, if there is no hot hand, the mean of the null distribution of streak statistic 2 is expected to be strictly less than 0. For the 37 players, the mean of the null distribution ranges from −0.20 to −0.03 with a mean of −0.12. (See Section 4 for further discussion of related issues.) For this reason, it is better to consider standardized values of the streak statistic, as we do below.

Figure 6. Values of streak statistic 2 with streak length 3 for the 37 players in Appendix A.

We use z-scores to measure the size of the hot hand effect. For each player, the z-score is computed by subtracting the mean and dividing by the standard deviation of the corresponding null distribution. Figure 7 displays the distribution of z-scores; the sample mean z-score is 0.340 standard deviations above the (null) mean, and the sample standard deviation is 0.906.

Figure 7. Values of z-score of streak statistic 2 with streak length 3 standardized with respect to the null distribution for the 37 players in Appendix A.

Figure 8. Values of the streak statistic and the bias-corrected values for the data in Appendix B.

If there is no hot hand effect, the 37 standardized values represent a sample from a distribution with a mean of 0 (and a standard deviation of 1). A one-sample t-test provides some evidence to conclude that the mean z-score is greater than 0 (t = 2.28, p-value = 0.014) which implies that, on average, NBA players do exhibit hot hand behavior in the Three Point Contest. Moreover, based on a one-sample t interval for the mean z-score, we estimate with 95% confidence that, on average, streak statistic 2 is between 0.038 and 0.642 standard deviations above what would be expected under the null hypothesis of no hot hand. While the standard deviation of the null distribution varies between players, the mean value is 0.254. Therefore, we can approximate that differences in proportion of successes between trials following streaks of three successes and all other trials are, on average, between 0.01 and 0.16 higher than what would be expected if the null hypothesis of no hot hand were true. While the range of the confidence interval does not rule out the possibility of a small average hot hand effect, a difference of even a few percentage points is of high practical importance in the context of basketball field goal percentages.

Alternative application: SBI methods could substitute for the t procedures above. For example, the StatKey confidence interval applet yields a bootstrap 95% confidence interval of [0.056, 0.625] for the mean z-score.

3.4. Pedagogical Outcomes

Our presentation in Sections 2 and 3 demonstrates how “simulation-based inference acts as a sandbox for students to explore more advanced statistical topics” (Tintle et al. 2015, p. 364). The activities we introduce enable introductory statistics students to employ simulation-based reasoning in a novel situation involving sequential trials and streak statistics. The analysis in Section 3 also provides opportunities to review or introduce topics of data collection, assumption checking, multiple testing, standardization, and effect size. The material in Sections 2 and 3 provides a strong foundation and many helpful suggestions for developing review or transfer activities for use in both introductory and subsequent statistics courses.

Our activities are well aligned with the six recommendations of the Guidelines for Assessment and Instruction in Statistics Education (GAISE) College Report (2016). The context—“can basketball players get a hot hand?”—requires little introduction and allows students to engage in statistical thinking throughout the investigative process: What data are appropriate for studying the hot hand? How do we measure how “hot” a player is? What would we expect if there were no hot hand? Our simulation-based activities place the focus on understanding of core concepts such as null distribution and p-value. The real data from the NBA Three Point Contest will be familiar to most students, and the context and purpose can be motivated via any of the recent articles on the hot hand (Cohen 2015; Ellenberg 2015; Johnson 2015; Remnick 2015). Our “Helpful Hints” provide suggestions for fostering active learning, including through both tactile and technology-based simulations. The app provides students with a user-friendly interactive technology to explore concepts of statistical inference and to analyze data to test for the hot hand. Finally, the hot hand activities can be used to evaluate student learning: How well can students transfer their knowledge of statistical inference to novel situations?

Furthermore, our work demonstrates the practical relevance of simulation-based inference. The hot hand research of Miller and Sanjurjo is evidence that simulation-based methods are becoming more mainstream in applied statistics (Tintle et al. 2015). While the details of various applications are numerous, the core principles are the same as those encountered in an SBI introductory statistics curriculum, as illustrated by the permutation test procedure in Section 2. Unfortunately, implementing randomization-based methods beyond scenarios encountered in introductory statistics typically requires significant computer programming. However, our app establishes a user-friendly interactive technology for conducting hot hand analyses. Thus, our app and related activities provide students opportunities to conduct simulation-based inference in a real, recent, and relevant research setting.

The methods in Sections 2 and 3 require only familiarity with the typical randomization-based procedures in an introductory statistics course. Section 4 introduces additional topics for further study in courses with a stronger emphasis on probability or mathematical statistics.

4. Using Probability and Expected Values to Investigate Recent Findings on the Hot Hand Effect

Careful inspection of the null distribution plots in Section 2 reveals something somewhat surprising. For the data in Table 1, if there is no hot hand we might expect the center of the null distribution of the proportion of successes on trials following streaks of success to be equal to 0.64, the overall proportion of successes. However, in Figure 2 the mean of the null distribution is about 0.55. Similarly, if there is no hot hand we might expect the center of the null distribution of the difference in proportions of successes between trials following streaks and all other trials to be 0; yet in Figure 3 the mean is about −0.10. In Figure 4, where the overall proportion of successes is 0.5, we find that the center of the null distribution is less than 0.5 even though the sample size is large.

Observations such as these illustrate a bias which has important implications for research on the hot hand. Miller and Sanjurjo (2016b) provide a thorough analysis of the bias and its implications. The authors motivate the source of the bias through a simple coin flipping problem which has a surprising answer. We present the problem and its solution, along with the most popular incorrect solution. The controversy surrounding the problem demonstrates the importance of understanding fundamental concepts in probability (e.g., random variables).

The coin flipping problem illustrates the source of the bias in previous hot hand studies. To demonstrate the implications of the bias, we reproduce an analysis of Miller and Sanjurjo (2016b) which uses data from the original Gilovich et al. (1985) study. We summarize the analysis and conclusions of Gilovich et al. (1985) and exhibit how they suffer from bias. We then reanalyze the data, using our Shiny app to correct for the bias, and consequently find evidence of an average hot hand effect present in the original Gilovich et al. (1985) data.

4.1. A Simple Coin Flip Problem (With a Surprising Answer)

The following seemingly simple problem was first presented in Miller and Sanjurjo (2016b) and has been the subject of much recent media coverage and debate, prompting the mathematician and author Jordan Ellenberg to call it “the Monty Hall problem of our time” (Ellenberg 2016).

Problem 1. Flip a fair coin four times and record the results in sequence. For the recorded sequence, compute the proportion of the trials immediately following H that result in H. What is the expected value of this proportion? If there are no trials which follow an H, i.e., the outcome is either TTTT or TTTH, discard the sequence and try again with four more flips.

We think that most people would expect the answer to Problem 1 to be 0.5. After all, the trials are independent, so it should not matter if a flip follows an H or not. But the surprising answer is that the proportion is expected to be less than 0.5! We now present a solution to Problem 1 based on first principles—considering the sample space of the coin flip process, defining appropriate random variables, and deriving their distributions.

After discarding TTTT and TTTH, there are 14 remaining equally likely outcomes. Let Z be the number of flips immediately following H and let Y be the number of flips immediately following H that result in H. Then the proportion of flips following H that result in H is the random variable X = Y/Z. Table 3 displays the sample space of possible coin flip sequences in Problem 1 and the corresponding values of the random variables X, Y, Z.

Table 3. The sample space for Problem 1. Flips that follow H are in boldface.

Outcome	Number of flips following H (Z)	Number of flips following H that result in H (Y)	Proportion of flips following H that result in H (X = Y/Z)
HHHH	3	3	1
HHHT	3	2	2/3
HHTH	2	1	1/2
HTHH	2	1	1/2
THHH	2	2	1
HHTT	2	1	1/2
HTHT	2	0	0
HTTH	1	0	0
THHT	2	1	1/2
THTH	1	0	0
TTHH	1	1	1
HTTT	1	0	0
THTT	1	0	0
TTHT	1	0	0
TTTH	These outcomes are discarded.
TTTT

Table 4 displays the marginal distribution of X. (All of the distributions in this section are conditional on $\left\{Z>0\right\}={\left\{\text{TTTH},\text{TTTT}\right\}}^c,$the event that there is at least one H in the first three flips. For simplicity, we have suppressed the conditioning from the notation.)

Table 4. The probability mass function of X, the proportion of flips following H that result in H in Problem 1.

X	0	1/2	2/3	1
P(X = x)	6/14	4/14	1/14	3/14

Table 5. The joint probability mass function, $p_{Y,Z}\left(y,z\right)=P\left(Y=y,Z=z\right)$, of Z, the number of flips immediately following H, and Y, the number of flips immediately following H that result in H, in Problem 1.

		z
		1	2	3
Y	0	5/14	1/14	0
	1	1/14	4/14	0
	2	0	1/14	1/14
	3	0	0	1/14

Table 6. Comparison of two-stage random processes.

	Problem 2 (restating Problem 1)	Problem 3
Stage 1	Flip a fair coin four times and record the results in sequence. If the outcome is TTTH or TTTT discard it and try again.	Flip a fair coin. If it lands T discard the trial and try again.
Stage 2	From the sequence observed in stage 1, select uniformly at random one of the flips which immediately follows an H, and record the result of the selected flip.	Flip the coin again and record the result.
P (Stage 2 results in H)	17/42	1/2

For example, over many repetitions of four flips of a fair coin with at least one H in the first three flips, in about 43% of the repetitions the proportion of flips following H that results in H would be 0, in about 29% of the repetitions it would be 0.5, etc.

To answer Problem 1, in a sequence of four flips of a fair coin with at least one H in the first three flips, the expected value of the proportion of flips following H that result in H is 0.405:$E\left(X\right)=\left(0\right)\left(6/14\right)+\left(1/2\right)\left(4/14\right)+\left(2/3\right)\left(1/14\right)+\left(1\right)\left(3/14\right)=17/42\approx \mathrm{0.405.}$

It is also instructive to consider the joint distribution of the count random variables Y and Z (again conditional on at least one H in the first three flips).

The proportion of flips following H that result in H is Y/Z, a function of Y and Z. Its expected value can be obtained from the joint distribution using the “law of the unconscious statistician”:$E\left(\frac{Y}{Z}\right)=\left(\frac{0}{1}\right)\left(\frac{5}{14}\right)+\left(\frac{0}{2}\right)\left(\frac{1}{14}\right)+\left(\frac{1}{1}\right)\left(\frac{1}{14}\right)+\left(\frac{1}{2}\right)\left(\frac{4}{14}\right)+\left(\frac{2}{2}\right)\left(\frac{1}{14}\right)+ \left(\frac{2}{3}\right)\left(\frac{1}{14}\right)+ \left(\frac{3}{3}\right)\left(\frac{1}{14}\right)=\frac{17}{42}$

From the marginal distribution of Y and Z, we obtain E(Y) = 12/14 and E(Z) = 24/14, and so E(Y)/E(Z) = 12/24 = 0.5. A common misconception is that E(Y/Z) is equal to E(Y)/E(Z). A similar “12/24 argument” will be discussed further in the next subsection.

Helpful hint: We suggest introducing a problem such as the following.

A toy store has a bin containing marbles which are identical except for their color. There are four blue marbles, one red marble, three green marbles, and six white marbles. Blue marbles are $0.50 each, red $0.67, green $1.00 each, and white marbles are free ($0). Let X be the price ($) of a randomly selected marble. Compute the expected value of X.

The random variable X has the same distribution and therefore the same expected value as the proportion of flips following H that result in H in Problem 1. While the marble problem is not interesting, it allows students to remove themselves from any penchant for disbelief due to preconceived notions about coin tossing. The marble problem is straightforward since its wording makes explicit the random variable involved and how its values are determined. In contrast, the difficulty in Problem 1 is that the appropriate random variables involved are not as apparent or as well behaved as intuition suggests.

4.2. Confusion Over the Coin Flip Problem

Problem 1 first appeared in Miller and Sanjurjo (2016b) and received widespread attention following a post on Andrew Gelman's blog (Gelman 2015). The problem has since been featured in the New York Times (Johnson 2015), The Wall Street Journal (Cohen 2015), The New Yorker (Remnick 2015), and Slate Magazine (Ellenberg 2015), among others. (Miller and Sanjurjo (2016a) and the authors' websites provide a more comprehensive account of media and online coverage.)

Unsurprisingly, the result of the coin flip problem (0.405 instead of 0.5) has been met with much skepticism. Miller and Sanjurjo (2016a) provide an interesting and comprehensive discussion of the problem and related probability puzzles, most of which is accessible to students in a first course in probability. We do not attempt to summarize all aspects of the issues involved. Instead we present now a popular alternative but incorrect solution to Problem 1 and discuss its crucial mistake, which involves a misunderstanding of the basic concept of a random variable.

Helpful hint: Problem 1 illustrates the importance of understanding fundamental concepts like random variables, proportion versus probability, and probability versus conditional probability. We emphasize in Sections 4.2 and 4.3 that care must be taken to not confuse the subtle probabilistic concepts involved.

A popular assertion for why the answer to Problem 1 should be 0.5 resembles the following, which we call the “12/24 argument”: “Among the outcomes in Table 3, (1) there are 24 flips that follow H of which 12 result in H, so (2) the expected value of the proportion of flips following H that result in H must be 12/24 = 0.5.”

While (1) is true, the incorrect “12/24 argument” forgets what a sampling distribution of a statistic is, or more generally, what the distribution of a random variable is (or even just what a random variable is). An outcome consists of four flips, rather than a single flip. Some of the 24 flips that follow H appear within the same outcome (e.g., HHTH contains 2 flips that follow H, HHHT contains 3, etc.). The 24 flips themselves are not distinct outcomes.

Imagine simulating the distribution of a random variable (or the sampling distribution of a statistic). The process is as follows.

1.	Simulate an outcome of the underlying random process (or a particular sample), for example, HHHT.
2.	Compute the value of the random variable for this particular outcome (or the value of the statistic for this particular sample), for example, 2/3.
3.	Repeat.

While the simulation process is eventually repeated many times, it is extremely important to remember that in a single repetition the simulated value of the random variable (or statistic) is computed based solely on the particular simulated outcome (or sample) for that repetition. The results of many repetitions can be aggregated to approximate probabilities or expected values; for example, the mean of many simulated values of the random variable approximates its expected value. However, computation of the values of the random variable itself proceeds outcome-by-outcome, repetition-by-repetition.

The object of interest in the coin flip problem is the proportion of flips which follow H that result in H. While this object might seem like a (conditional) probability, it is in fact a random variable (just as the usual sample proportion is a random variable). Thus, computation of values of the proportion must occur outcome by outcome. First, the value of the proportion is computed for each outcome (a set of four flips); then the values are aggregated (by averaging) to find the expected value. The first step is essential; however, the “12/24 argument” ignores it entirely and neglects to incorporate the primary random variable involved in Problem 1.

4.3. The Conditional Probability of H Following H

It is important to be clear about what the solution to Problem 1 does not imply. Problem 1 concerns the proportion of H in flips following H, a random variable, whose value varies outcome-to-outcome, which has expected value 0.405.

In contrast, the conditional probability of H on a flip following H is a single number, which of course is equal to 0.5. The “12/24 argument” essentially attempts to compute this conditional probability, but again the “12/24 argument” is wrong because the answer to Problem 1 does not concern a conditional probability but rather the expected value of a random variable.

Problem 2 in Table 6 restates Problem 1 as an equivalent problem involving a probability rather than an expected value. For comparison, Problem 3 presents a two-stage random process in which the probability that the second stage results in H represents the conditional probability of H following H.

In Problem 2, the conditional probability that the stage 2 selection results in H varies depending on the outcome of stage 1. For example, if the outcome of stage 1 is HHHH, then the conditional probability that the stage 2 selection results in H is 1; for HHHT it is 2/3; for HHTH it is 1/2, etc. The probability that stage 2 results in H in Problem 2—conditional on A = {TTTH, TTTT}^c, the event that the sequence is not discarded in stage 1—can be computed by the law of total probability.$\begin{array}{l}P\left(\text{stage}2\text{results}\text{in}\text{H}|A\right)\\ ={\displaystyle \sum P\left(\text{stage}2\text{results}\text{in}\text{H|stage}1\text{outcome},A\right)P\left(\text{stage}1\text{outcome}|A\right)}\\ =\left(1\right)\left(\frac{1}{14}\right)+\left(\frac{2}{3}\right)\left(\frac{1}{14}\right)+\left(\frac{1}{2}\right)\left(\frac{1}{14}\right)+\dots +\left(0\right)\left(\frac{1}{14}\right)=\frac{17}{42}.\end{array}$

The randomness in stage 2 in Problem 2 is due to sampling from the finite population determined by the result of stage 1. In contrast, the randomness in stage 2 in Problem 3 is due to a coin flip which is independent of the result of stage 1. In essence, in Problem 2 all the coin flips are performed at once and then the sequence is inspected, while in Problem 3 the inspection occurs after each individual flip. (We discuss some related issues in Section 5.)

The solution to Problem 1 also does not imply that coin flips are not independent. As always, each flip of the coin is independent of all other flips. However, independence involves the conditional probability of H following H, which we have already stressed is a different object than the proportion of H following H. What Problem 1 does imply is that in four independent fair coin flips the retrospective proportion of H following H is a biased estimator of the true conditional probability of H following H. This bias has important implications for research on the hot hand phenomenon.

4.4. Implications for Hot Hand Research

Beginning with the seminal paper of Gilovich et al. (1985) up until the work of Miller and Sanjurjo (2014, 2015, 2016b), the consensus conclusion of previous research had been that there is no evidence of a hot hand in basketball, hence the “hot hand fallacy.” The idea behind the conclusion resembles the following. Consider a player who attempts 100 shots and makes 50%. If there is no hot hand, then we would expect the player to make 50% of shots both on attempts that follow hit streaks and on other attempts. Therefore, a success rate of 50% on both sets of attempts provides no evidence of the hot hand.

However, Miller and Sanjurjo (2014, 2015, 2016b) discovered that the above reasoning is subject to a bias. If there is no hot hand, we would actually expect the player to have a shooting percentage of strictly less than 50% on attempts following streaks, and strictly greater than 50% on other attempts. Therefore, a success rate of 50% on both sets of attempts actually provides directional evidence in favor of the hot hand.

Problem 1 provides a concrete example of the source of the bias: in a fixed number of trials, the proportion of H on trials following H is expected to be less than the true probability of H, even though the trials are independent. The figures in Section 2 and the “null mean” column in Appendix A exhibit the magnitude of the bias encountered under the conditions of the NBA Three Point Contest. Intuiting the reason behind the bias is much more subtle. We refer the reader to the “primer” paper of Miller and Sanjurjo (2016a) which provides a detailed treatment of the issues involved. In particular, see Section 2.2 of Miller and Sanjurjo (2016a) for an explanation of the bias based on runs.

Helpful hint: Miller and Sanjurjo (2016a) contain many interesting examples and probability puzzles. Furthermore, the paper provides a fascinating account of the media coverage and response to Miller and Sanjurjo's work and the coin flipping problem (Problem 1). (Imagine the controversy over Marilyn vos Savant and the Monty Hall problem taking place today.) The paper is well worth discussing in undergraduate courses in probability.

To illustrate the ramifications of the bias in hot hand studies, we reproduce here an analysis of Miller and Sanjurjo (2016b, Section 3.2, Table 2), which itself is based on data from Gilovich et al. (1985, pp. 304–307, Table 4). Appendix B (available in the online supplementary material) provides a table of the data and some results. The data were taken from a controlled shooting experiment involving the 26 players on the men's and women's basketball teams at Cornell University; see Gilovich et al. (1985) for further details.

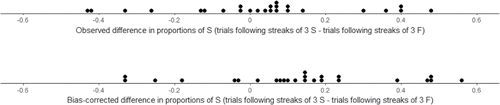
As in the previous studies, we use streak statistic 3, the difference in proportion of S (after streaks of S – after streaks of F) with streak length 3. (One player had no streaks of length 3 and was excluded from the analysis.) Figure 8 displays the data; the mean difference is 0.034 with a standard deviation of 0.240. Gilovich et al. (1985) concluded, based on a one-sample t-test, that the mean difference is not significantly greater than 0 (t = 0.7, p-value = 0.24), and so there is no evidence of the hot hand. However, this analysis assumes that the mean difference is expected to be 0 under the null hypothesis of no hot hand, which as we have discussed is incorrect. Therefore, the analysis of Gilovich et al. (1985) suffers from a bias which invalidates the conclusion.

The permutation test of Section 2 provides a mechanism for correcting for the bias. The mean of the permutation distribution is the expected value of the difference in success rates under the null hypothesis of no hot hand for a player with the specified number of successes. Therefore to assess evidence against the null hypothesis of no hot hand, an observed value of the difference in success rates should be judged relative to the mean of the corresponding permutation distribution, rather than 0. We compute a bias-corrected value for each player by subtracting the mean of the player's null distribution from the observed value of the streak statistic. (We follow the same procedure as Miller and Sanjurjo (2016b) but the null means are computed using our Shiny app with the “input summary statistics” option. Our results are consistent with theirs.) The bottom plot in Figure 8 displays the bias-corrected values. While the amount of bias correction varies among players, it is about 10 percentage points on average. (In some sense, using 0 as a reference value when comparing trials following streaks of success to trials following streaks of failures introduces a “double” bias: if there is no hot hand, the success rate on trials following streaks of successes is expected to be less than the overall success rate, while the success rate on trials following streaks of failures is expected to be greater than the overall success rate.)

The mean of the bias-corrected values is 0.126 with a standard deviation of 0.240. Under the null hypothesis of no hot hand, the bias-corrected values represent a sample from a distribution with a mean of 0, and thus the usual one-sample t-test applies. The t-test based on the bias-corrected values does in fact provide significant evidence to reject the null hypothesis of no hot hand at the player-average level (t = 2.62, p-value = 0.007), reversing the conclusion of the Gilovich et al. (1985) analysis. That is, after correcting for bias, the data in the seminal paper which gave rise to the phrase “hot hand fallacy” actually offer evidence in favor of the hot hand.

Helpful hint: Technically, the null standard deviations do vary from player to player, so adjusting via z-scores (as in Section 3.3) might be more appropriate. However, the variability of the null standard deviations for the Gilovich et al. (1985) data is small, in large part because almost all of the 25 players who were included in the analysis took 100 shots. The t-statistic based on z-scores is 2.61 (vs. 2.62) and the conclusion doesn't change. Therefore, we just subtract the means (1) to simplify, (2) to stay consistent with Miller and Sanjurjo (2016b), and (3) to emphasize that bias relates to the center of a distribution.

Alternative application: This section illustrates how correcting for bias affects the analysis of Gilovich et al. (1985), which was based on t procedures. Bootstrap procedures based on the bias-corrected values could be investigated as alternatives to the t procedures.

We present the above analysis merely as an illustration of how the bias impacts the analysis and conclusions of previous hot hand research. Miller and Sanjurjo (2014) provide a thorough examination of previous research on the hot hand in basketball, and upon correcting for bias they find “clear evidence of an average hot hand effect, across all extant controlled shooting studies.” (Miller and Sanjurjo 2014, p. 30).

Alternative application: Miller and Sanjurjo (2016b) can be adapted into simulation activities to investigate how the bias depends on the sample size, the probability of success, and the streak length. To reduce the amount of coding, students could be provided with the streak_stats.r function from the app to compute the streak statistics. Note that Miller and Sanjurjo (2016b) analyzed the sampling distribution of a streak statistic under the null, while our app simulates the permutation distribution. These two distributions are closely related (through the law of total probability), but there is an important distinction: the number of trials and the number of successes are fixed when simulating the permutation distribution, whereas for the sampling distribution, only the number of trials is fixed so the number of successes varies from sample to sample (like in Problem 1).

5. Conclusions

We have presented probability concepts underlying a bias in previous research on the hot hand in basketball, as well as a bias-corrected randomization-based procedure for testing for hot hand behavior. Our presentation demonstrates that simulation-based reasoning is an important component of statistical literacy. For example, the solution to the coin flip problem in Section 4 is, on the surface, counterintuitive and has caused some minor controversy. However, the correct solution quickly becomes apparent after some simulation-based thinking (as discussed in Sections 4.2 and 4.3). Simulation-based thinking involves considering questions such as: What does one repetition of the random process entail? What is being measured for an outcome? How can the results of many simulated repetitions be used to approximate the probabilistic objects of interest? Those with the facility to answer such questions are well equipped to reason probabilistically even if they are unfamiliar with terminology or mathematical concepts such as sample space, random variable, or expected value.

The hot hand analysis is a situation where the inherent “naïveté” of a simulation-based approach is beneficial. The idea of randomly permuting the order of sequential trials is a natural extension of randomization-based procedures for comparing groups. Therefore, someone familiar with SBI methods is well suited to carry out the unbiased analysis in Section 2, without any particular qualms or preconceived notions about what the center of the null distribution “should be.” After all, if the simulation properly incorporates the null hypothesis, the center of the simulated null distribution will be whatever it should be. Following a simulation-based approach avoids the mistake of Gilovich et al. (1985) of assuming a biased value for the center of the null distribution. (Of course, someone performing the hot hand permutation test might notice that the center of the null distribution seems “off” and question whether the simulation was performed properly. Such observations can motivate discussions relating to the topics in Section 4).

The hot hand analysis also demonstrates the essential role that the method of data collection plays in determining appropriate statistical methods and conclusions. Consider someone observing a sequence of independent fair coin flips. After some number of flips, the observer notices that among the flips which followed H a higher proportion resulted in T than in H. As discussed in Section 4, such a result is actually to be expected when retrospectively inspecting the outcomes of a sequence of independent trials. However, Gilovich et al. (1985) committed the “fallacy” of neglecting to recognize the truth in such an observation. Unfortunately, the bias in the methods of Gilovich et al. (1985) and other hot hand studies has gone unnoticed, so the resulting conclusions which promoted the “hot hand fallacy” have remained largely unchallenged for almost 30 years.

Now consider again the observer. Observing some number of flips and then retrospectively inspecting the sequence is a natural and valid way of collecting data. Furthermore, observing a higher proportion of T than H on flips following H is to be expected. The observer only commits a fallacy (the “gambler's fallacy”) when concluding that the observed result necessarily implies that the trials are not independent. It would be a fallacy to conclude based on the observed data that a future flip which follows H is more likely to result in T than in H, since the retrospective proportion of H following H is a biased estimator of the true conditional probability of H following H (as discussed in Section 4). However, this bias is so subtle that it has gone unnoticed, even by statisticians, until very recently.

Supplemental Material

Supplemental data for this article can be accessed on the publisher's website.

Acknowledgments

The author thanks the two anonymous reviewers and the editor of the Datasets and Stories section for many insightful comments that improved the article in general and Section 4 in particular. The author thanks Bradley Lubich for many helpful discussions which motivated the work in this article. Bradley also wrote the core of the streak_stats.r function used in the Shiny app, and he provided valuable feedback on previous versions of the app. The author also thanks participants at the 2016 Joint Statistical Meetings for feedback on a presentation of parts of this work.