“Should This Loan be Approved or Denied?”: A Large Dataset with Class Assignment Guidelines

ABSTRACT

In this article, a large and rich dataset from the U.S. Small Business Administration (SBA) and an accompanying assignment designed to teach statistics as an investigative process of decision making are presented. Guidelines for the assignment titled “Should This Loan Be Approved or Denied?,” along with a subset of the larger dataset, are provided. For this case-study assignment, students assume the role of loan officer at a bank and are asked to approve or deny a loan by assessing its risk of default using logistic regression. Since this assignment is designed for introductory business statistic courses, additional methods for more advanced data analysis courses are also suggested.

KEYWORDS:

• Case study
• Classification
• Decision rule
• Logistic regression
• Real data
• Risk indicator

1. Introduction

In the American Statistical Association's (ASA's) Guidelines for Assessment and Instruction in Statistics Education (GAISE) College Report (GAISE College Report ASA Revision Committee 2016), the following recommendations were made to teach introductory statistics:

(a)	Teach statistical thinking. Teach statistics as an investigative process of problem solving and decision making. Give students experience with multivariable thinking.
(b)	Focus on conceptual understanding.
(c)	Integrate real data with a context and purpose.
(d)	Foster active learning.
(e)	Use technology to explore concepts and analyze data.
(f)	Use assessments to improve and evaluate student learning.

In this article, we take into account these recommendations by providing a rich and large dataset which itself is a significant contribution, for it can be used by educators to create learning opportunities that are aligned with the 2016 GAISE recommendations. In conjunction with the dataset, a set of guidelines for a case-study assignment designed with the aforementioned recommendations in mind is also described.

The dataset accompanying this article is a real dataset from the U.S. Small Business Administration (SBA). The case-study assignment, titled “Should This Loan be Approved or Denied?” is designed to teach statistical thinking by focusing on how to use real data to make informed decisions for a particular purpose. For this assignment, students assume the role of a loan officer who is deciding whether to approve a loan to a small business.

By analyzing real data, students experience statistics as an investigative process of decision making, for the student is required to answer the following question: As a representative of the bank, should I grant a loan to a particular small business (Company X)? Why or why not? The student makes this decision by assessing a loan's risk.

The assessment is accomplished by estimating the loan's default probability through analyzing this historical dataset and then classifying the loan into one of two categories: (a) higher risk—likely to default on the loan (i.e., be charged off/failure to pay in full) or (b) lower risk—likely to pay off the loan in full. The process of making this determination requires students to conceptually understand the statistical concepts and how to apply them.

We have used an adapted version of this case-study assignment in data analysis courses for both undergraduate and graduate business students. These courses cover topics ranging from regression and analysis of variance in the undergraduate course to data mining in the graduate course. For all courses, logistic regression is included in the assignment while neural networks and support vector machines (SVMs) are introduced only in the graduate course.

For both courses, we initially present this as an in-class, interactive assignment. We spend two or three 75-min class periods in computer labs guiding students through specific steps in how to analyze this large dataset to help inform their decision making processes. To foster an active learning environment, we encourage discussion and questions during these class periods and typically break the students into groups to discuss certain steps and then ask them to present their ideas and rationale. To assess students’ statistical thinking, students are presented a similar case and required to write a report describing their loan decisions and rationale behind such decisions.

This assignment is ideal for data analysis courses for several reasons.

(a)	The case study incorporates all of the 2016 GAISE recommendations.
(b)	The topic itself captures students’ interest, for it is an application of actual data related to real-life financial decisions.
(c)	Students are exposed to managing a large dataset and understanding how historical data can be used to make informed decisions.
(d)	Critical thinking is promoted; analysis, synthesis, and decision making skills are used.
(e)	Students are introduced to logistic regression and other more advanced methods for classification.
(f)	The importance of identifying reasonable explanatory variables (e.g., risk indicators for loan default) to incorporate into statistical models provides lively and engaging discussions.

Moreover, business statistics instructors have reported that the use of case-study assignments has resulted in increased student motivation and participation, increased student awareness of the relevance of statistics to business decision making, and more positive classroom experiences for the instructor (e.g., Bryant 1999; Nolan and Speed 1999; Parr and Smith 1998; Smith and Bryant 2009). We have experienced similar benefits with this case-study assignment.

2. Background and Description of Datasets

The U.S. SBA was founded in 1953 on the principle of promoting and assisting small enterprises in the U.S. credit market (SBA Overview and History, US Small Business Administration (2015)). Small businesses have been a primary source of job creation in the United States; therefore, fostering small business formation and growth has social benefits by creating job opportunities and reducing unemployment. One way SBA assists these small business enterprises is through a loan guarantee program which is designed to encourage banks to grant loans to small businesses. SBA acts much like an insurance provider to reduce the risk for a bank by taking on some of the risk through guaranteeing a portion of the loan. In the case that a loan goes into default, SBA then covers the amount they guaranteed.

There have been many success stories of start-ups receiving SBA loan guarantees such as FedEx and Apple Computer. However, there have also been stories of small businesses and/or start-ups that have defaulted on their SBA-guaranteed loans. The rate of default on these loans has been a source of controversy for decades. Conservative economists believe that credit markets perform efficiently without government participation. Supporters of SBA-guaranteed loans argue that the social benefits of job creation by those small businesses receiving government-guaranteed loans far outweigh the costs incurred from defaulted loans.

Since SBA loans only guarantee a portion of the entire loan balance, banks will incur some losses if a small business defaults on its SBA-guaranteed loan. Therefore, banks are still faced with a difficult choice as to whether they should grant such a loan because of the high risk of default. One way to inform their decision making is through analyzing relevant historical data such as the datasets provided here.

Two datasets are provided: (a) “National SBA” dataset (named SBAnational.csv) from the U.S. SBA which includes historical data from 1987 through 2014 (899,164 observations)¹ and (b) “SBA Case” dataset (named SBAcase.csv) which is used in the assignment described in this paper (2102 observations). The “SBA Case” dataset is a subset of the “National SBA.”²

The variable name, the data type, and a brief description of each variable are provided for the 27 variables in the two datasets (see Table 1(a)). For the “SBA Case” dataset, an additional eight variables were generated by the authors as part of the assignment (see Table 1(b)) and described in Sections 4.1.4, 4.1.5, 4.1.6, 4.1.7, and 4.3.1. For most of the variables, the description is self-evident. The variables needing further explanation include: NAICS, NewExist, LowDoc, and MIS_Status and are described below.

Table 1(a). Description of 27 variables in both datasets.

Variable name	Data type	Description of variable
LoanNr_ChkDgt	Text	Identifier – Primary key
Name	Text	Borrower name
City	Text	Borrower city
State	Text	Borrower state
Zip	Text	Borrower zip code
Bank	Text	Bank name
BankState	Text	Bank state
NAICS	Text	North American industry classification system code
ApprovalDate	Date/Time	Date SBA commitment issued
ApprovalFY	Text	Fiscal year of commitment
Term	Number	Loan term in months
NoEmp	Number	Number of business employees
NewExist	Text	1 = Existing business, 2 = New business
CreateJob	Number	Number of jobs created
RetainedJob	Number	Number of jobs retained
FranchiseCode	Text	Franchise code, (00000 or 00001) = No franchise
UrbanRural	Text	1 = Urban, 2 = rural, 0 = undefined
RevLineCr	Text	Revolving line of credit: Y = Yes, N = No
LowDoc	Text	LowDoc Loan Program: Y = Yes, N = No
ChgOffDate	Date/Time	The date when a loan is declared to be in default
DisbursementDate	Date/Time	Disbursement date
DisbursementGross	Currency	Amount disbursed
BalanceGross	Currency	Gross amount outstanding
MIS_Status	Text	Loan status charged off = CHGOFF, Paid in full = PIF
ChgOffPrinGr	Currency	Charged-off amount
GrAppv	Currency	Gross amount of loan approved by bank
SBA_Appv	Currency	SBA's guaranteed amount of approved loan

Table 1(b). Description of additional 8 variables in SBA case dataset.

Variable name	Data type	Description of variable
New	Number	=1 if NewExist=2 (New Business), =0 if NewExist=1 (Existing Business)
Portion	Number	Proportion of gross amount guaranteed by SBA
RealEstate	Number	=1 if loan is backed by real estate, =0 otherwise
Recession	Number	=1 if loan is active during Great Recession, =0 otherwise
Selected	Number	=1 if the data are selected as training data to build model for assignment, =0 if the data are selected as testing data to validate model
Default	Number	=1 if MIS_Status=CHGOFF, =0 if MIS_Status=PIF
daysterm	Number	Extra variable generated when creating “Recession” in Section 4.1.6
xx	Number	Extra variable generated when creating “Recession” in Section 4.1.6

NAICS (North American Industry Classification System): This is a 2- through 6-digit hierarchical classification system used by Federal statistical agencies in classifying business establishments for the collection, analysis, and presentation of statistical data describing the U.S. economy. The first two digits of the NAICS classification represent the economic sector. Table 2 shows the 2-digit sectors and a corresponding description for each sector.

Table 2. Description of the first two digits of NAICS.

Sector	Description
11	Agriculture, forestry, fishing and hunting
21	Mining, quarrying, and oil and gas extraction
22	Utilities
23	Construction
31–33	Manufacturing
42	Wholesale trade
44–45	Retail trade
48–49	Transportation and warehousing
51	Information
52	Finance and insurance
53	Real estate and rental and leasing
54	Professional, scientific, and technical services
55	Management of companies and enterprises
56	Administrative and support and waste management and remediation services
61	Educational services
62	Health care and social assistance
71	Arts, entertainment, and recreation
72	Accommodation and food services
81	Other services (except public administration)
92	Public administration

Teaching Note: The table of two digit NAICS codes published by the U.S. Census Bureau (http://www.census.gov/cgi-bin/sssd/naics/naicsrch?chart=2012) merges a few sectors (see Manufacturing, Retail Trade, Transportation and Warehousing). To be consistent with the U.S. Census Bureau publication we also make the same mergers. However, instructors may wish to examine the individual sectors for Manufacturing, Retail Trade, Transportation and Warehousing.

NewExist (1 = Existing Business, 2 = New Business): This represents whether the business is an existing business (in existence for more than 2 years) or a new business (in existence for less than or equal to 2 years).

LowDoc (Y = Yes, N = No): In order to process more loans efficiently, a “LowDoc Loan” program was implemented where loans under $150,000 can be processed using a one-page application. “Yes” indicates loans with a one-page application, and “No” indicates loans with more information attached to the application. In this dataset, 87.31% are coded as N (No) and 12.31% as Y (Yes) for a total of 99.62%. It is worth noting that 0.38% have other values (0, 1, A, C, R, S); these are data entry errors. There are also 2582 missing values for this variable, excluded when calculating these proportions. We have chosen to leave these entries “as is” to provide students the opportunity to learn how to deal with datasets with such errors.

MIS_Status: This variable indicates the status of the loan: defaulted/charged off (CHGOFF) or have been successfully paid in full (PIF).

3. Pre-Assignment Creation Considerations

Prior to the assignment of the case study, it is suggested that educators consider: (a) developing learning objectives for the assignment; (b) using statistical analysis software packages that are easily accessible to the students for analysis; (c) determining a time period to be included in the analyses; and (d) deciding how to integrate the case-study assignment into a class and ways to assess learning.

3.1. Learning Objectives

Arguably, this is the most important step prior to assignment creation. A clear understanding and explanation of what the assignment is designed to teach is necessary. For the “Should This Loan Be Approved or Denied?” assignment, we want our students to:

1.	Analyze a large dataset to promote statistical thinking;
2.	Identify which explanatory variables may be good “predictors” or risk indicators of the level of risk associated with a loan;
3.	Work through the stages in model building and validation;
4.	Apply logistic regression (and other more advanced methods for graduate students) to classify a loan based on predicted risk of default; and
5.	Make a scenario-based decision informed by data analyses (i.e., whether to fund the loan).

3.2. Statistical Analysis Software Packages

The datasets are prepared for analysis in most available statistical analysis software packages. It is suggested that educators choose a software package that students can easily access and afford. We use Microsoft Excel, R, and SAS products (JMP, University Edition) because they are readily available to our students free of charge.

For our students, we export the data in the following formats: SAS permanent data (.sas7bdat) and Comma Separated Values (.csv). We have our undergraduate students use JMP to open the SAS data file to perform logistic regression and other analyses. JMP's user-friendly point-and-click interface is perfect for our undergraduate data analysis course. We have our MBA students use R to open the Comma Separated Values data file and perform analyses that include logistic regression, neural networks, and SVMs.

3.3. Time Period

Educators may also want to consider what time period to include in the analyses. For example, in our assignment, an emphasis is placed on the default rates of loans with a disbursement date through 2010.³ We chose this time period for two reasons. We want to account for variation due to the Great Recession (December 2007 to June 2009)⁴ ; so loans disbursed before, during, and after this time frame are needed. Secondly, we restrict the time frame to loans by excluding those disbursed after 2010 due to the fact the term of a loan is frequently 5 or more years.⁵

We believe that the inclusion of loans with disbursement dates after 2010 would provide greater weight to those loans that are charged off versus paid in full. More specifically, loans that are charged off will do so prior to the maturity date of the loan, while loans that will likely be paid in full will do so at the maturity date of loan (which would extend beyond the dataset ending in 2014). Since this dataset has been restricted to loans for which the outcome is known, there is a greater chance that those loans charged off prior to maturity date will be included in the dataset, while those that might be paid in full have been excluded. It is important to keep in mind that any time restriction on the loans included in the data analyses could introduce selection bias, particularly toward the end of time period. This may impact the performance of any predictive models based on these data.

3.4. Format of the Case-Study Assignment

This assignment can be adapted for in-class, hybrid, and online courses. While we describe how this assignment has been applied in our in-class courses, we encourage instructors to tailor the assignments to meet the needs of the students and the various modes of delivery.

For both the undergraduate and graduate courses, we initially present this as an in-class, interactive assignment. We spend two or three 75-min class periods to walk the students through the various steps described below. We encourage discussion and questions during these class periods. To promote active learning, we break the students into groups to discuss certain steps and then ask them to present their ideas and rationale. As instructors, we facilitate a larger class discussion after these presentations to ensure that students understand the various steps.

To assess student learning, we develop a graded case study assignment that is similar to the one presented in class. For the undergraduates, we let them complete the assignment in groups of three people. For the graduate courses, the students are required to complete the assignment as an individual.

4. Guidelines for “Should This Loan be Approved or Denied?” Case Study Assignment

This section is organized around the steps involved in the investigative process of analyzing these data to make an informed decision as to whether a loan should be approved or denied, one of the main learning objectives of this assignment. Students are guided through:

• Step 1: Identifying indicators of potential risk;

• Step 2: Understanding the case study;

• Step 3: Building the model, creating decision rules, and validating the logistic regression model; and

• Step 4: Using the model to make decisions.

4.1. Step 1: Identifying Explanatory Variables (Indicators or Predictors) of Potential Risk

In the first class period, we provide the students with the “National SBA” dataset, a background of the SBA, and the assignment with its learning objectives. Since economic models should be based on sound economic theory, we engage students in a discussion which requires them to identify which explanatory variables they think would be good indicators or predictors of the potential risk of a loan: likelihood of default (higher risk) versus paid in full (lower risk).

To meet the following learning objective, to identify which explanatory variables may be good predictors or risk indicators of the level of risk associated with a loan, we encourage students to consider default rates for a group which is represented by the percentage of loans that are classified as defaults. For a particular group of loans, the default rate is determined by using the “MIS_Status” variable and calculating the percent of the total number of loans (CHGOFF + PIF) that are classified as defaults (CHGOFF).

Teaching Note: We break the students into groups for discussion and ask them to provide written justification for each variable as to whether it would be a good risk indicator and have them briefly present these to the class. This activity reinforces the importance of having sound theory when constructing models and promotes active learning.

There are a number of variables that consistently emerge as indicators of risk that could explain the variation of loan default rates. Seven variables, along with some exploratory analysis, are discussed below including Location (State), Industry, Gross Disbursement, New versus Established Business, Loans Backed by Real Estate, Economic Recession, and SBA's Guaranteed Portion of Approved Loan. For a number of these indicators, dummy variables are created for analysis and are discussed in teaching notes.

4.1.1. Location (State)

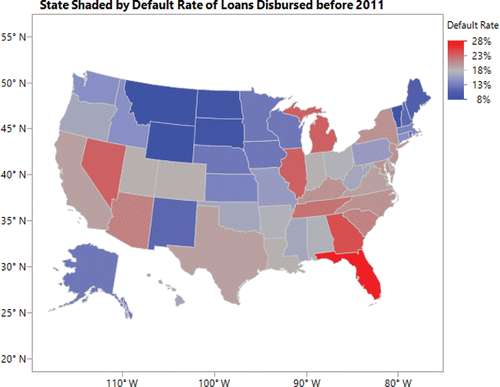
Location by State (represented as “State” in Table 1(a)) is one possible predictor that students identify in their discussions. They recognize that the 50 states and Washington DC have different economic environments in which they operate, resulting in different default rates. We display this heat map (Figure 1) in class to support this discussion.

Teaching Note: Students are encouraged to explore reasons for the differences in the default rates by states. For instance, during the Great Recession, Florida had a major decline in real estate prices which could contribute to high default rates; states such as Wyoming and North Dakota had stronger economies (due to their reliance on minerals and oil) which may explain their lower default rates. Since we operate in California, California relative to other states is highlighted, for it “brings home” the discussion. Instructors may choose to focus on states of interest to their students.

Figure 1. Heat map, default rates by state (Figure 1 was created using JMP).

4.1.2. Industry

Shown in Table 3, industry (first two digits of NAICS codes) is another risk indicator students consider due to the significant amount of variation in the default rates. At one end of the spectrum are industries with low default rates (8%–10%), such as: mining, oil and gas exploration (21), agriculture (11), security holding companies (55), and physicians and dentists (62). At the opposite end of the spectrum are industries with higher default rates (28%–29%), such as financial institutions like credit unions (52) and real estate agencies (53).

Table 3. Industry default rates (first two digit NAICS codes).

2 digit code	Description	Default rate (%)
21	Mining, quarrying, and oil and gas extraction	8
11	Agriculture, forestry, fishing and hunting	9
55	Management of companies and enterprises	10
62	Health care and social assistance	10
22	Utilities	14
92	Public administration	15
54	Professional, scientific, and technical services	19
42	Wholesale trade	19
31–33	Manufacturing	19, 16, 14
81	Other services (except public administration)	20
71	Arts, entertainment, and recreation	21
72	Accommodation and food services	22
44–45	Retail trade	22, 23
23	Construction	23
56	Administrative/support & waste management/remediation Service	24
61	Educational services	24
51	Information	25
48–49	Transportation and warehousing	27, 23
52	Finance and insurance	28
53	Real estate and rental and leasing	29

Variation in industry default rates is often due to the cyclical nature of the demand for products or services. For example, the construction industry (23) expands and contracts dramatically over a business cycle, while medical services industry (62) tends to be much more stable; consequently, revenue and net income are much less volatile for medical services than construction. Moreover, unlike construction, medical services have licensing requirements which create barriers that new businesses have to overcome. Since it is not easy to enter medical services, those entering this industry are very serious about their new venture and this further contributes to the medical industry's lower credit risk.

Like construction, another industry that has a higher default rate is the hotel accommodation and food service industry (i.e., hospitality) (72). Over time, hotel loan defaults tend to be high because hotels often overbuild new units when occupancy rates are high and then they may face low occupancy rates for a range of unexpected reasons. With regard to food service, the success of any new restaurant is highly unpredictable, and the continued success of existing restaurants is often threatened by new ventures.

Teaching Note: In our classes we tend to use the two digit codes shown in Table 3. However, one can have their students use additional digits in analysis. For example, physicians are coded as 6211 and dentists are 6212. The following link provides the coding scheme in greater detail than those provided in Table 3: http://www.census.gov/cgi-bin/sssd/naics/naicsrch?chart=2012. These definitions along with the detailed codes provided in the variable NAICS will enable students to analyze more specific industries.

4.1.3. Gross Disbursement

Gross disbursement (represented as “DisbursementGross” in the dataset) is another risk indicator that many students identify as a key variable to consider. The rationale behind selecting “DisbursementGross” is that the larger the loan size, the more likely the underlying business will be established and expanding (i.e., purchasing assets that have some resale value), thereby increasing the likelihood of paying off the loan. This rationale is confirmed by looking at the quartiles shown in Table 4.

Table 4. Quartiles of gross disbursement.

Quartiles	CHGOFF	PIF
100% maximum	$4,362,157	$11,446,325
75% quartile	$140,796	$255,000
50% median	$61,962.5	$100,000
25% quartile	$27,767	$49,034
Minimum	$4000	$4000

4.1.4. New versus Established Businesses

Whether a business is new or established (represented as “NewExist” in the dataset) is another potential risk indicator that students identify. Therefore, a dummy variable was created for the logistic regression: “New” = 1 if the business is less than or equal to 2 years old and “New” = 0 if the business is more than 2 years old.

Most students argue that new businesses fail at a higher rate than established businesses. Established businesses already have a proven track record of success and are requesting a loan to expand on what they already do successfully. Whereas, new businesses sometimes do not anticipate the obstacles they may face and may be unable to successfully overcome such challenges, resulting in defaulting on a loan.

However, when the default rates for loans to new businesses (less than or equal to 2 years) and established business (more than 2 years old) in this dataset are compared, there is a relatively negligible difference between them. The default rate for new businesses is 18.98%, and the rate for established businesses is 17.36%.

4.1.5. Loans Backed by Real Estate

Whether a loan is backed by real estate (possession of land) is another risk indicator that is discussed. The rationale for this indicator is that the value of the land is often large enough to cover the amount of any principal outstanding, thereby reducing the probability of default.

Since the term of the loan is a function of the expected lifetime of the assets, loans backed by real estate will have terms 20 years or greater (≥240 months) and are the only loans granted for such a long term, whereas loans not backed by real estate will have terms less than 20 years (<240 months). Therefore, the authors created a dummy variable, “RealEstate,” where “RealEstate” = 1 if “Term” ≥240 months and “RealEstate” = 0 if “Term” <240 months.

Shown in Table 5, loans backed by real estate have a significantly lower default rate (1.64%) than loans not backed by real estate (21.16%).

Table 5. Loans backed by real estate.

	Default	Paid in full
Loans Back by Real Estate (Term ≥240 months)	2472 (1.64%)	147,868 (98.36%)
Loans Not Backed by Real Estate (Term <240 months)	153,876 (21.16%)	573,212 (78.84%)

4.1.6. Economic Recession

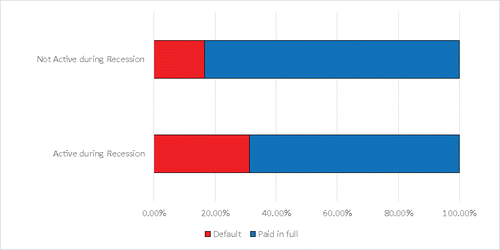
A risk indicator that consistently emerges in discussion is how the economy may impact default rates. Small business loans are affected by the economy in general, and more small business loans tend to default right before and during an economic recession. Therefore, the authors created a dummy variable, “Recession,” where “Recession” = 1 if the loans were active⁶ during the Great Recession (December 2007 to June 2009), and “Recession” = 0 for all other times.

Illustrated in a stacked bar chart (Figure 2), loans active during the Great Recession have a higher default rate (31.21%) than loans that were not active during the Recession (16.63%).

Figure 2. Status of the loans active or not active during the Great Recession.

4.1.7. SBA's Guaranteed Portion of Approved Loan

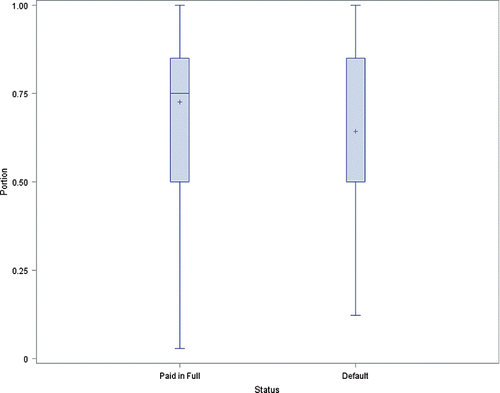
The portion which is the percentage of the loan that is guaranteed by SBA (represented as “Portion” in the dataset) is a final risk indicator that is discussed in our courses. This is one of the variables that the authors generated calculating the ratio of the amount of the loan SBA guarantees and the gross amount approved by the bank (SBA_Appv/GrAppv). Figure 3 shows the distribution of portion for paid-in-full loans and defaulted loans disbursed from 2002 to 2010. These two boxplots show that typically loans that are paid in full have a slightly higher SBA-guaranteed percentage, as indicated by the higher mean portion for paid-in-full loans.

Figure 3. SBA-guaranteed portions for paid-in-full and defaulted loans.

It is worth noting that the median is not displayed in the boxplots for defaulted loans because 54% of these loans have half of the loan amount guaranteed by SBA (portion = 0.5). As a result, there is no difference in the 1%, 5%, 10%, 25%, and 50% percentiles (all these percentiles are equal to 0.5).

Teaching Note: In addition to the variables in the dataset, we ask our students if there are any other variables that may be significant and should be considered. Students usually are unable to come up with any specific sources of variation. However, it should be noted that the dataset does not include any elements that directly represent credit risk. Within the past few years, SBA has collected and evaluated Fair Issac (FICO) credit scoring of guarantors and borrowers. If a borrower or guarantor is not a person, then a Dun and Bradstreet score is obtained. Many financial institutions now rely upon credit scores when making smaller loans. Unfortunately, this dataset does not include this information.

4.2. Step 2: Understanding the Case Study and Dataset

After identifying indicators of potential risk, a case study, where the student assumes the role of a loan officer who is required to determine whether to approve loans to two small businesses, is presented. We highlight the fact that banks attempt to minimize the risk of default (charged off) and only approve loans that are likely to be paid in full later.

Teaching Note: To account for two of the risk indictors, state and industry, we restrict the case study to one state and one industry (two-digit industry code). We suggest educators consider doing the same for three reasons: (a) it creates a more realistic decision making scenario; (b) inclusion of 50 States (plus Washington DC) and 20 industry classifications (2 digit NAICS) would result in a large number of binary variables and may create estimation problems; and (c) the dataset extracted from the larger dataset is more manageable for students. We describe this process and rationale to students in class.

For our courses, we have chosen to limit the case study to the State of California and the two-digit code 53: Real Estate and Rental and Leasing. We extract the relevant data from the larger dataset, “National SBA,” which produces a sample of 2102 observations and is included in the paper as the “SBA Case” data. We provide this dataset to the students to analyze in their roles as loan officers when deciding whether to approve or deny two loan applications.

Teaching Note: We restrict the scenario for the assignment to California because this is where we are located. Instructors may choose to focus on states of interest to their students. For the industry code, one may use any two digit codes or select a code using more than two digits.

California-Based Case Study: You, a loan officer for Bank of America, have received two loan applications from two small businesses: Carmichael Realty (a commercial real estate agency) and SV Consulting (a real estate consulting firm). Relevant application information is summarized below (see Table 6). As a loan officer, you need to determine if you should grant or deny these two loan applications and provide an explanation as to “why or why not.” To make this decision, you will need to assess the loan's risk by calculating the estimated probability of default using logistic regression. You will then want to classify this loan as either: “higher risk—more likely to default” or “lower risk—more likely to pay in full” when making your decision.

Teaching Note: We ask the students to provide a written summary of the business decision in question and the potential limitations of the dataset. We focus specifically on time frame and selection bias as discussed in Section 3.3.

Table 6. California-based case study: Information for two loan applications.

Loan	Name	City	Date	Loan amount requested	SBA portion guaranteed	Secured by real estate?
1	Carmichael Realty	Carmichael, CA	Current (not recession)	$1,000,000	$750,000	Yes
2	SV Consulting	San Leandro, CA	Current (not recession)	$100,000	$40,000	No

4.3. Step 3: Building the Model, Choosing a Decision Rule, and Validating the Logistic Regression Model

We guide our students through the process of building a logistic regression model to estimate the default probability of the various loan applications. To meet the learning objective, to understand the stages in model building and validation, we walk the students through a three-phase iterative model building process of specification, estimation, and evaluation and then validate the model.

To build the logistic regression model for the California-based case study, we randomly selected half of the data to be our “training” data (1051 of the original 2102 observations). In the “SBA Case” dataset, the variable “Selected” indicates which observations are the “training” data and which are the “testing” data (1 = training data to be used to build the model, 0 = testing data to validate the model).

Teaching Note: There are a number of possible classification techniques that can be used to model these data. Since our undergraduate business statistics course is a service course for the functional areas of business and a prerequisite for a number of courses such as finance and marketing, this course's learning objectives are aligned with our college's overall learning objectives and the objectives of other courses (which include an understanding of logistic regression). Therefore, in this paper, we present our coverage of basic logistic regression for our undergraduate business students. Students in more advanced statistical courses may be able to explore interactions in logistic regression, time-dependent covariates, as well as more advanced classification methods.

4.3.1. Model Specification and Estimation

When dealing with a binary response, as is the case here, logistic regression is a popular model choice to describe the relationship between the binary response and explanatory variables (predictors). Logistic regression models log odds as a linear combination of explanatory variables (predictors):$\log \left(\frac{P}{1-P}\right)={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+\cdots +{\beta }_K{X}_K.$

The probability of interest $P$ can then be obtained as$P=\frac{e^{{\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+\cdots +{\beta }_K{X}_K}}{1+e^{{\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+\cdots +{\beta }_K{X}_K}}=\frac{1}{1+e^{-\left({\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+\cdots +{\beta }_K{X}_K\right)}},$

where${\beta }_0+ {\beta }_1 X_1+ {\beta }_2 X_{2 }+···+ {\beta }_K{X}_K$ represents the coefficients and explanatory variables from the generalized linear regression model structure. The probability of interest $P$ can be predicted with the estimated coefficients.

In building the model, we point out to students that the dependent variable is a binary variable. In our analysis, the binary dependent variable is “Default” which is a dummy variable created from the “MIS_Status” variable. The value for “Default” = 1 if MIS_Status = CHGOFF, and “Default” = 0 if MIS_Status = PIF. Hence, the logistic regression model for this scenario predicts the probability of a loan defaulting.

We highlight why the logistic regression model is used, rather than ordinary linear regression, by discussing the assumptions of ordinary linear regression and violation of some of these assumptions had ordinary linear regression been applied to this dataset. Since we are dealing with a dichotomous outcome here (i.e., default or not) rather than a quantitative one, ordinary least squares regression is not appropriate. Instead we use logistic regression to predict odds ratios and probabilities.

For the possible explanatory variables, we revisit the outcomes of Step 1 where seven variables are identified as potential indicators of risk. Since “location (state)” and “industry” are already accounted for by restricting the analyses to one state and one industry, there are five variables that should be considered for inclusion in the model as explanatory variables: Economic Recession (“Recession”), New Business (“New”), Loans Backed by Real Estate (“RealEstate”), Gross Disbursement (“DisbursementGross”), and SBA's Guaranteed Portion of Approved Loan (“Portion”).

To illustrate the model-building process, we walk the students through two different versions of the model using the training data: (a) initial model with five explanatory variables (Table 7(a)), including the likelihood ratio test for partial effect obtained from a Type III analysis from SAS's PROC GENMOD (Table 7(b))⁷ ; and (b) re-specified model with three explanatory variables (Table 8). After the initial model is produced, a discussion about significant variables and p-values ensues. The students determine that the risk indicators “New” and “DisbursementGross” are not statistically significant, and they typically suggest re-specifying the model without these variables. Since the goal is prediction, the final model with the three explanatory variables “RealEstate,” “Portion,” and “Recession” will be used to classify the loans in the case study using the decision rules described in Section 4.3.2.

Table 7(a). California case study: Initial logistic regression model with five explanatory variables.

Parameter	DF	Estimate	Standard error	Wald Chi-Square	Pr > ChiSq
Intercept	1	1.3537	0.3229	17.5729	<0.0001
New	1	−0.0772	0.2101	0.1349	0.7134
RealEstate	1	−2.0331	0.3636	31.2663	<0.0001
DisbursementGross	1	−3.37E-7	3.52E-7	0.9173	0.3382
Portion	1	−2.8298	0.5594	25.5909	<0.0001
Recession	1	0.4971	0.2413	4.2441	0.0394

Table 7(b). Type III analysis.

Source	DF	Chi-Square	Pr > ChiSq
New	1	0.14	0.7130
RealEstate	1	39.96	<0.0001
DisbursementGross	1	0.97	0.3258
Portion	1	27.41	<0.0001
Recession	1	4.27	0.0389

Table 8. California-based case study: Re-specified model with three explanatory variables.

Parameter	DF	Estimate	Standard error	Wald Chi-Square	Pr > ChiSq
Intercept	1	1.3931	0.3216	18.7670	<0.0001
RealEstate	1	−2.1282	0.3450	38.0529	<0.0001
Portion	1	−2.9875	0.5393	30.6898	<0.0001
Recession	1	0.5041	0.2412	4.3679	0.0366

It is worth mentioning that: (a) the authors confirmed with an SBA employee with over 30 years of experience that it makes economic sense to drop “New” and “DisbursementGross” from the model and (b) there is almost no difference in the misclassification rates calculated for the test data, with or without the two variables “New” and “DisbursementGross.” While the model does not fit the data as well as one would hope, it gives reasonable predictive performance which is illustrated in the validation section (4.3.3) where the “testing data” is applied to the model.

As stated by George Box, “Essentially, all models are wrong, but some are useful” (Box and Draper 1987, p. 424). And, Seymour Geisser (1993) asserted that a model is useful as long as it gives good predictive performance.

Teaching Note: The variable “Selected” indicates which of the cases are training data versus testing data (1 for training and 0 for testing). This random sample was drawn in SAS using the SURVEYSELECT procedure: PROC SURVEYSELECT OUTALL OUT = dataca53 METHOD = SRS SAMPSIZE = 1051 SEED = 18467;

In addition to the discussion about p-values, how to interpret parameter estimates of the model with a focus on the odds of default is described. For example, since Real Estate is a dummy variable, we can interpret that coefficient as: ‘Given the same SBA backed portion and economic considerations (recession or not), the estimated odds ratio of default (backed by real estate vs. not backed by real estate) is e^−2.1282 = 0.12. So the odds of default when backed by real estate is only 12% the odds of default when not backed by real estate. Hence, as expected, there is a lower risk of default when the loan is backed by real estate.

We did consider other explanatory variables and interactions between dummy variables “RealEstate” and “Recession” and the continuous explanatory variable “Portion.” While no additional significant explanatory variables emerged, there were two significant interaction effects: “RealEstate*Portion” and “Recession*Portion”; this suggests that “Portion” had additional influence if the loan involved real estate or if it occurred during the recession. Since interaction in logistic regression is a complex concept to conceptualize in these introductory courses, we have decided not to include a discussion of these interaction effects in this article.

4.3.2. Choosing a Decision Rule

Next, the students are guided through the process of choosing a decision rule. We discuss how the estimated probability of default of a particular loan should be compared to a cutoff probability when making a decision, followed by a discussion as to what an appropriate cutoff probability might be. Students often suggest 0.5 as the cutoff, an obvious choice for many because it is equivalent to the odds (charged off vs. paid in full) of 1.

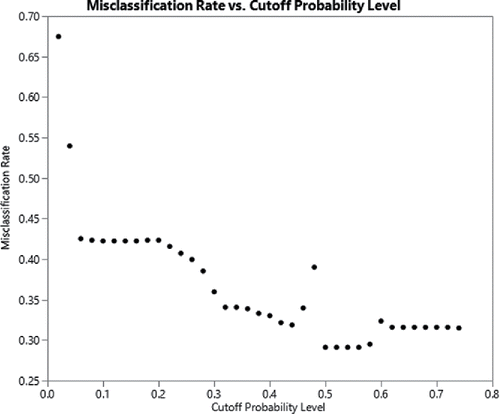
We have students calculate the misclassification rate using different levels of cutoff probability. The results are shown in Figure 4.

Figure 4. Misclassification rate versus cutoff probability level.

The cutoff probability level resulting in the lowest misclassification rate starts around 0.5. The misclassification rate starts to increase around a cutoff probability level of 0.6. Therefore, a cutoff probability level of 0.5 is a good choice. The following decisions rules are then adopted:

(i)	classify the loan application into the lower risk category and approve the loan when estimated probability of default ≤0.5, or
(ii)	classify the loan application into the higher risk category and deny the loan when estimated probability of default >0.5.

Teaching Note: In Section 3.3, the potential for selection bias due to the time period used in the analyses was discussed. It should be noted that there is another important source of selection bias here though. There is a critical mismatch between the data used to build the predictive model and the loans that will be evaluated using the model. Presumably only the loans which were perceived to have tolerably low risk were ever approved in the first place. That means all the loans represented in the data would have been perceived as “low” risk by someone. Those deemed to be of higher risk (and therefore, were not approved) don't appear in the data at all. Therefore, the in-sample default rate will likely be lower than the true default rate of all loan applications that were submitted in the first place.

4.3.3. Validation and Misclassification

We validate the final model by applying it to the other half of the data (the “testing” data which includes the remaining 1051 observations for California-based example) and gauge its performance by calculating the misclassification rate. To do this, students use the final logistic regression model to generate the estimated probability of default rate for each of the loans in the “test” data sample. Next, students are asked to classify the loans in the testing data as either “higher risk” or “lower risk” using the decision rules in Section 4.3.2.

Since the true outcomes of the loans in the test data are known (MIS_Status of charged off or paid in full), the rate of misclassification can be determined for the California-based scenario. In Table 9, the columns represent the reality of whether a loan was charged off or paid in full, and the rows represent the classification of the loan according to the decision rule (higher risk vs. lower risk). Shown below where the number of misclassifications is represented in bold font, 324 loans were misclassified as “lower risk” and 14 loans were misclassified as “higher risk.” The overall misclassification rate is 32.16% ((324 + 14)/1051).

Teaching Note: In class, we discuss how this process is part of evaluating the predictive performance of a model and that this particular model does give reasonable predictive performance.

Teaching Note: Since two different types of errors can be committed, misclassification of a loan as “higher risk” or as “lower risk,” we encourage students to discuss the consequences of committing either type of error and if treating the two types of errors the same is a wise business decision. Discussions typically revolve around the fact that the bank will lose both principal and interest if a loan is misclassified as a “lower risk” and then is charged off, while the bank will only incur opportunity cost in the amount of interest if a loan is misclassified as “higher risk.”

Teaching Note: In our graduate course, we also cover ROC (receiver operating characteristic) curve to describe classification accuracy by having students watch a short video tutorial at http://www.dataschool.io/roc-curves-and-auc-explained/. The ROC curve plots the true positive rate (on the y-axis) versus the false positive rate (on the x-axis) for every possible classification cutoff probability level while the misclassification rate is only for one cutoff probability level. The area under the curve (AUC) is the proportion of the box (the area of this box is 1) under this ROC curve. AUC is highest (over 0.75) for the most parsimonious model with three explanatory variables in Table 8, indicating acceptable classification performance (see Hosmer and Lemeshow 2000, p. 162).

Table 9. California-based scenario: Classification of loans.

	State of nature: Reality
Classification	Loans charged off	Loans paid in full	Total
Higher risk (more likely to be charged off)	31	14	45
Lower risk (more likely to be paid in full)	324	682	1006
Total	355	696	1051

4.4. Step 4: Using the Model to Make Decisions

To meet the learning objectives, to learn how to apply logistic regression to classify a loan based on default probability and to experience the investigative process of making a scenario-based decision informed by the data analyses, the final step in this assignment is to have students answer the initial question of whether to approve or deny a loan(s) by using: (a) the final logistic regression model generated to determine the estimated probability of default of a specific loan and (b) the decision rules to classify the loan. For the California-based example, the final model with the risk indicators in Table 8 is used to estimate the probability of default for the two loan applications; the estimated probability of default for Carmichael Realty (Loan 1) is 0.05 and SV Consulting (Loan 2) is 0.55. Applying the decision rules and cutoff probability of 0.5 from Section 4.3, Loan 1 is classified as “lower risk” and should be approved, and Loan 2 is classified as “higher risk” and should be denied (see Table 10).

Table 10. California-based scenario summary.

Loan	Name	Date	Loan amount requested	SBA portion guaranteed	Secured by real estate?	Estimated probability of default	Approve?
1	Carmichael Realty	Current (no recession)	$1,000,000	$750,000	Yes	0.05	Yes
2	SV Consulting	Current (no recession)	$100,000	$40,000	No	0.55	No

5. Assessment of Learning, Exploring More Advanced Classification Methods, and Concluding Remarks

5.1. Assessment of Learning

Previously mentioned, we assess student learning by developing a case study that is similar to the one presented in class and assign this to students for a letter grade. For the undergraduates, we let them complete the graded assignment in groups of three people. For the graduate courses, the students are required to complete the assignment as an individual.

For the graded assignments, students are required to submit a report explaining all of the steps they engaged in (which should mirror the steps described above) and a final recommendation as to whether the loan(s) should be approved or denied. We suggest the report to be three pages in length plus any tables, figures, and graphs that would help illustrate and support their recommendation. We allow students two weeks to complete the assignment after the in-class sessions. In assessing their learning, we use the grading rubric shown in Table 11.

Table 11. Grading rubric for assignment.

Step (Weight)	Doesn't meet expectations	Approaches expectations	Meets expectations	Exceeds expectations
1) Identifying indicators of potential risk (30%)	Identifies indicators of potential risk that do not make sense	Identifies indicators of potential risk, but fails to provide reasonable justification	Identifies indicators of potential risk and provides reasonable justification as why or why not variables should be considered	Identifies indicators of potential risk, provides reasonable justification as why or why not variables should be considered, and provides supporting evidence (analyses)
2) Understanding the case study (10%)	Understands the case study, but provides an inaccurate and/or confusing synopsis of the business decision in question	Understands the case study by providing a synopsis of the business decision in question, but does not include discussion of dataset limitations	Understands the case study by providing a synopsis of the business decision in question and includes discussion of limitations related to either time frame or selection bias	Understands the case study by providing a synopsis of the business decision in question and includes discussion of limitations related to time frame and selection bias
3) Building the model, creating decision rules, and validating the logistic regression model (50%)	Builds a model that does not make sense	Builds a model that makes sense, but does not create an appropriate decision rule or adequately validate the model	Builds a model that makes sense, creates an appropriate decision rule, but does not adequately validate the model	Builds a model that makes sense, creates an appropriate decision rule, and adequately validates the model
4) Using the model to make decisions (10%)	Derives an inaccurate estimated probability of default for both loans and makes poor decisions for both loans, using their model	Derives the correct estimated probability of default for one or both loans, but makes poor decisions for both loans, using their model	Derives the correct estimated probability of default for both loans and makes a good decision for one loan (but not the other), using their model	Derives the correct estimated probability of default for both loans and makes a good decision for both loans, using their model

5.2. Advanced Classification Methods for Graduate Students

While we focused on logistic regression in the “Should This Loan Be Approved or Denied?” assignment, other classification methods such as neural networks (see Odom and Sharda 1990; Tam and Kiang 1992; Lacher et al. 1995; Zhang et al. 1999) and SVMs (see Chen et al. 2010; Kim and Sohn 2010) could be taught using this dataset in more advanced graduate data analysis courses.

In our graduate data mining course, we emphasize to students that there are strict assumptions for traditional parametric models such as logistic regression. When these assumptions do not hold, the nonlinear nonparametric classification methods such as neural networks and SVMs are powerful alternatives. Neural networks (feed-forward) are flexible nonlinear regression models with many parameters, connecting inputs (explanatory variables or predictors) to outputs (the dependent variable) via hidden layers between inputs and outputs. The “activation function” of the hidden layer units is usually the logistic function (see Venables and Ripley 2002, sec. 8.10). Logistic regression is equivalent to the neural network with no hidden node (Zhang et al. 1999), and it is natural to compare the results from neural network to those from logistic regression. If the learning objective of an assignment is to separate loans from loans that are likely to default without needing the predicted probability of default, then neural networks and SVMs are good choices.

Teaching Note: We start our introduction of neural networks by demonstrating how to apply the neural networks function “nnet” in R to training and test data students had used before for logistic regression. Our students tried two neural network configurations: no hidden layer and a 5-unit hidden layer. We then move on to discuss some theoretical aspects of neural networks.

Teaching Note: Venables and Ripley (2002) provide a very readable short introduction with clear instructions for using the neural networks package “nnet” in R. We also ask students review the updated documentation for “nnet” with examples at http://cran.r-project.org/web/packages/nnet/nnet.pdf. Fitting such a neural network model can be easily accomplished by our graduate students with a few lines of code in R.

With the same assignment described above, graduate students were able to easily fit the neural networks model with the same explanatory variables and training data using R and obtain a slightly lower misclassification rate 31.97% ((324 + 12)/1051) for the test data. The R code is:

#Neural Networks

data <- read.csv(file = “C:/SBAcase.csv”, header = TRUE, sep = “,”)

summary(data)

attach(data)

x1 = RealEstate

x2 = (Portion-mean(Portion))/sqrt(var(Portion))

x3 = Recession

y = as.factor(MIS_Status)

dat = data.frame(x1,x2,x3,y)

library(nnet)

train = (Selected>0)

nnfit = nnet(y ∼., data = dat[train,], size = 5, skip = TRUE, rang = 0.02, decay = 1e-3, maxit = 10000)

summary(nnfit)

test = dat[!train,]

model_pred = predict(nnfit, test, type = “class”)

table(model_pred, test$y)

Another popular classification method for this binary classification problem (paid in full vs. charged off) is SVMs. SVM is an extension of the support vector classifier, which is closely related to logistic regression (see James et al. 2013, chap. 9.5). Thus, it is natural to ask students to compare SVM with logistic regression. In class, students can easily fit the SVM to the data using the function “SVM” in the R library e1071. The misclassification was found to be higher than those from logistic regression or neural networks.

5.3. Concluding Remarks

In conclusion, this rich dataset provides educators the opportunity to create meaningful assignments to teach a range of statistical concepts and highlight how data can be used to inform real business decisions. Aligned with the 2016 GAISE recommendations, “Should This Loan Be Approved or Denied?” case-study assignment is an excellent example of how to promote active learning and teach statistical thinking in a business context using real data.

We encourage others to think of creative ways to incorporate the data into alternative assignments. It is our hope that instructors will share their assignments with the statistical education community to enhance teaching effectiveness across the field of statistics.

Supplementary Material

Supplemental information for this article can be accessed on the publisher's website. This includes the “National SBA” and “SBA Case” data files and their corresponding documentation.

Notes

¹ Please note that the dataset we provide here is restricted to loans originating within the 50 United States and Washington DC (U.S. Territories were excluded) and for which the outcome (paid in full or charged off/default) is known; in order to teach logistic regression, a binary dependent variable is required.

² The SAS code used to create the data subset is found in the accompanying “SBA Case” data documentation file.

³ “DisbursementDate” is the variable used to determine this classification.

⁴ The dates as declared by The National Bureau of Economic Research (see http://money.cnn.com/2010/09/20/news/economy/recession_over/)

⁵ The distribution of the term of loans is such that the mode is 7 years (27% of loans are 7 years in duration) and 73% are greater than 5 years in duration. For those loans dispersed starting 2010, 66% have terms over 5 years.

⁶ The loans that were coded as “Recession=1” include those that were active for at least a month during the Great Recession time frame. This was calculated by adding the length of the loan term in days to the disbursement date of the loan. The coding in SAS for this is: Recession=0; daysterm=Term*30; xx=DisbursementDate+daysterm; if xx ge '1DEC2007′d AND xx le '30JUN2009′d then Recession=1.

⁷ Type III analysis tests the significance of each partial effect and the significance of an effect with all the other effects in the model.