Computer-Automated Approach for Scoring Short Essays in an Introductory Statistics Course

ABSTRACT

Over two semesters short essay prompts were developed for use with the Graphical Interface for Knowledge Structure (GIKS), an automated essay scoring system. Participants were students in an undergraduate-level online introductory statistics course. The GIKS compares students' writing samples with an expert's to produce keyword occurrence and links in common scores which can be used to construct a visual representation of an individual's knowledge structure. Each semester, students responded to the same two essay prompts during the first and last week of the course. All responses were scored by the GIKS and two instructors. Evidence for the validity of scores obtained using the GIKS was provided through the use of correlations with instructors' scores and final exam scores. Changes in scores from the beginning to end of the course were examined. Suggestions for writing open-ended prompts that work well with computer-automated scoring systems are given as well as suggestions for using the GIKS as a formative learning activity as opposed to summative assessment.

KEYWORDS:

• Automated essay scoring
• Introductory statistics
• Knowledge structure
• Statistics education

1. Introduction

Large-scale assessments, such as those often used in large introductory statistics courses or those that are nationally administered, tend to rely heavily on multiple-choice questions (e.g., CAOS, delMas, Garfield, Ooms, and Chance 2007; GOALS-2 [Sabbag and Zieffler 2015]; RPASS [Lane-Getaz 2013]). Although these assessments are quickly, easily, and objectively scored, there are a number of downsides to relying solely on multiple-choice assessments in both classroom and research settings.

Multiple-choice questions are typically scored dichotomously: correct or incorrect. When students get an item incorrect they receive no credit for that item and the only information that is available to the instructor or researcher as to why they got the item incorrect are the distractors (incorrect answers) that were selected. Students who give an incorrect response may hold a misconception, they may have misinterpreted the question, or they may have guessed. Writing high-quality multiple-choice questions that assess higher levels of understanding, such as the ability to organize knowledge or create a novel response, is difficult. Such learning objectives may be better assessed using a different assessment method (Rodriguez, 2007).

Multiple-choice tests have also been criticized for presenting students with incorrect information, which could lead to students learning the wrong answers. Roediger and Marsh (2005), for example, examined the impact of multiple-choice testing on a later cued-recall test. While they did find a positive effect for testing in that participants were more likely to correctly answer a question that they had previously seen in multiple-choice format, they also found that students learned incorrect information from the multiple-choice questions’ distractors, which they refer to as “lures.” When participants were instructed not to guess and to only answer questions that they thought they knew the answers to, compared to questions that they had not previously seen, students were more likely to attempt a question that they had seen in multiple choice format and get it incorrect. That is, they believed they were correct when in fact they were not. Thus, in addition to reinforcing correct information, students may also learn incorrect information. Though in a later study Marsh, Roediger, Bjork, and Bjork (2007) argued that the positive learning effects outweigh the negative, those negative effects may be avoided with the use of different question types.

The Guidelines for Assessment and Instruction in Statistics Education (GAISE) College Report suggests the use of writing assignments as they may “help students strengthen their knowledge of statistical concepts and practice good communication skills” (GAISE College Report ASA Revision Committee, 2016, p. 22). Open-response questions, such as short essays, give students the opportunity to practice communicating in the language of the discipline (Paxton 2000; Radke-Sharpe 1991). They can also provide rich data concerning students’ understandings, may greatly reduce variation related to guessing, and do not present students with incorrect information as multiple-choice questions do.

In an empirical study of undergraduate business statistics students, Smith, Miller, and Robertson (1992) compared students across several sections of a two-course series that either required ten writing assignments or none. Most students had favorable responses to the writing assignments and agreed that they were helpful in terms of their learning and communicating. Compared to students in the sections without writing assignments, greater improvements in attitudes toward statistics, value in learning statistics, and confidence were observed in students in the sections of the course with required writing assignments. Final exam scores were higher for students in the writing sections; however, these differences were not statistically significant when accounting for difference between instructors and students’ GPAs. There was, however, a statistically significant difference between the two groups in terms of the content quality and grammar of the essays on the final exam.

Parke (2008) described her experiences with incorporating activities emphasizing communication, both oral and written, into a graduate-level intermediate statistics course for education students. She emphasized the importance of these skills as her students need to not only understand statistical analyses themselves, but also to be able to communicate them to others. Qualitatively, Parke discussed how two students, one who began the course with “a lack of conceptual understanding and poor communication skills” (p. 15) and one who began at a more advanced level, both benefited from the communication emphasis. In a semester following her course, she compared writing samples from students who completed her course that emphasized communication to those who took the same course from a different instructor who did not emphasize communication in the same manner. Both groups of students were enrolled in a measurement course where they were given an assignment that involved conducting a statistical analysis and summarizing their results similar to what would be written in the results section of a journal article. When the two groups’ writing samples were blinded and scored by two raters using a 5-point holistic rubric, the mean score was higher, with a large effect size, for the students who completed the course emphasizing communication.

We agree with these authors above regarding the value of writing-to-learn in statistics courses. Instructors and researchers may avoid essay questions due to legitimate concerns with scoring. Reading even short essays written by all students in a large course can be very time consuming. Rater quality and rater drift are always present, if essays are graded over a period of time or by a team of teaching assistants, the consistency of scoring plus the cost in actual dollars and time are a real concern that should be continually addressed (Hunter and Docherty 2011). Further, the optimum learning benefit from writing-to-learn comes from specific and timely feedback for each essay, not just a numeric score. These are difficult issues for rater scored essays that are attainable with technology.

The use of a computer-automated scoring system could overcome scoring-related obstacles. A number of automated systems for scoring essays exist (e.g., LSA from ETS; EASE from EdX). These extant systems are proprietary, expensive, sometimes difficult to use, and typically only provide a numeric score with generic feedback. To address these issues, a team of education and information science researchers developed the Graphical Interface for Knowledge Structure (GIKS) system through a grant from the Center for Online Innovation in Learning (COIL) at The Pennsylvania State University. GIKS is free, it is totally web-based in a browser in html5 and can run on computers and tablets. It is fairly easy to use (requires about a 30-min training session to get a teacher up to speed) and since the teacher sets the writing prompt and the expert referent response it can be used for any domain normative content at any education level. The students’ essays are archived and teacher report functions can show the score on a prompt over time (to see improvement if it happens), and group averages to see where a class as a whole has missed the concepts and relations (for remediation and re-teaching).

This current investigation is an early effort to collect information to improve GIKS. It focuses on the concurrent validity of the underlying scoring algorithm which is critical to the overall approach. Future research (videotaped “think alouds” and post interviews) will address the specifics of how students use the system in order to improve it. GIKS is unique in that it can provide specific feedback in the form of a visual representation of knowledge structure inherent in the text's key concepts (i.e., identified keywords) and their proximity relationships (i.e., distance between keywords). It has user buttons that change the display of the network graph to show errors only, correct associations only, and both; and that provides a list of missing terms and missing links and prompts the student to revise and resubmit their essay (e.g., Clariana, Wolfe, and Kim 2014; Fesel, Segers, Clariana, and Verhoeven 2015; Kim and Clariana 2015).

2. Graphical Interface for Knowledge Structure (GIKS)

The GIKS converts students’ responses into two scores based on the presence of keywords and the order in which those keywords were used (i.e., “keyword occurrences” and “links in common,” calculations to be explained below) and can construct visual representations of the students’ knowledge structures (see Kim 2012 for GIKS algorithm). This is done by comparing each student's response to an expert response in which keywords and their synonyms are identified. Keywords can be single words or phrases and they can contain numbers or symbols. Keywords and their synonyms are ranked by word or phrase length. The keywords and synonyms with longer lengths are identified from the essay and removed to avoid duplication with shorter keywords and synonyms. Then, GIKS checks for keywords and synonyms with shorter lengths that remain in the essay. This process is repeated until all keywords and synonyms are checked and removed from the essay. The keyword occurrence score is a count of the number of keywords (or synonyms) that appear in the student's response. Each keyword may only be counted once toward this score. The links in common score compares the order of the keywords in the expert and student responses; a link is defined as two keywords appearing sequentially after all non-keywords are removed (see also Clariana, Wolfe, and Kim 2014).

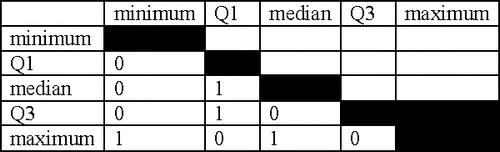
As a simple example, consider if learners are asked “What values are in the five number summary?” The expert answer could be “The five number summary consists of the minimum, Q1, median, Q3, and maximum values.” Five keywords may be identified as “minimum,” “Q1,” “median,” “Q3,” and “maximum.” In terms of synonyms, “first quartile” and “third quartile” are acceptable synonyms for the “Q1” and “Q3,” respectively, and “50th percentile” may be an acceptable synonym for “median.” The expert's response would reduce to “minimum – Q1 – median – Q3 – maximum” and would be converted to the matrix shown in Figure 1. Each student's submission would be converted into a matrix using the same keywords and compared to this expert matrix. Given that this is a short example with only five keywords and four correct links in the matrix, the maximum keyword occurrence score for this essay would be five and the maximum links in common score would be four.

Figure 1. Expert matrix example.

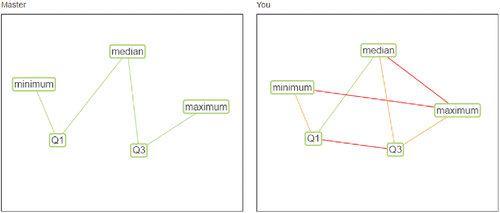
If a student submitted, “The five number summary contains a few statistics such as the minimum, maximum, median, Q1, and Q3.” That would reduce to “minimum – maximum – median – Q1 – Q3” for which the result would be the matrix in Figure 2. The student used all five keywords, so his or her keyword occurrence score would be five. The overlap in the expert and student matrices is the links in common score. Here, the student and expert overlap in one cell (Q1 – median); this student would earn a links in common score of one. Note that scores are not reduced for having unnecessary links.

Figure 2. Student matrix example.

The matrices shown in Figure 1 and Figure 2 could be converted to graphical representations by the GIKS. A screenshot of the students’ view after submitting this essay in the GIKS is shown in Figure 3. The links in this graphic are color coded with green representing correct links, yellow representing missing links, and red representing incorrect links.

Figure 3. Expert and student knowledge structures in the GIKS.

The GIKS has been designed to be used as a formative assessment activity in which students submit their essays, see their knowledge structures, see how their structures differ from an expert's structure, revise, and resubmit. In the future we intend to incorporate the formative assessment aspect into our use of the GIKS. First, however, it is necessary to learn more about the validity of the scores obtained using the GIKS which are used to construct the visual representations of students’ knowledge structures. The scores obtained using the GIKS should correlate with scores assigned by instructors and with final exam scores. We also need to learn more about what types of prompts work best with the GIKS in a statistics education setting. Two research studies were carried out in an undergraduate-level introductory statistics course in two consecutive semesters.

3. Context

In both studies, participants were enrolled in sections of an undergraduate-level introductory statistics course offered by the online campus of a large research-intensive university. This is a general education course that is required by a wide variety of majors. The online campus does not offer an undergraduate statistics or mathematics major, and while it is possible for students from physical campuses that do offer these majors to enroll in an online section of the course, this is rare.

In the first study the course was run in the course management system ANGEL and in the second study the course management system Canvas. Each week students had assigned readings in the online notes and textbook, a quiz that was completed in the course management system, and a written lab assignment that required the use of Minitab Express. The online notes included embedded example videos. Optional live peer tutoring sessions were available.

Prior to the first study, essays from a midterm exam in a previous semester were run through the GIKS. GIKS scores and the scores assigned by instructors were positively correlated serving as proof of concept. The correlations between the scores assigned by the GIKS and the instructors varied by instructor, bringing to attention the need for a common instructor scoring rubric. Both of the following studies were submitted to the university's institutional review board and given an exemption status. Only data from students who gave permission for their data to be used for research purposes are included in analyses. Data collected in the first study were used to inform data collection in the second study.

4. Study I

4.1. Methodology

Participants were students in two online sections of an undergraduate-level introductory statistics course in the summer 2016 semester. Summer semesters are 12 ½ weeks long and cover the same lessons as the 15 week fall and spring semesters. Of the 72 students enrolled in those two sections of the course at the beginning of the semester, 53 completed the pre-test during the first week of the course and gave permission for their data to be used for research purposes. Of those, 38 students also completed the post-test during the last week of the course before the final exam. There were also 6 students who gave permission for their data to be used for research purposes but only completed the post-test.

During the first week of the course all students were presented with an informed consent form and given the option of granting the researchers permission to use their course data for research purposes. All students were asked to complete a demographic survey and to respond to two essay prompts. Those prompts are presented in Appendix A. While data were collected from all students for instructional purposes, only data from the students who gave permission can be disseminated.

At the pre-test, for the first prompt there was one student who did not respond and two who wrote a sentence explaining that they could not answer the question. These were scored as zeros. For the second prompt at the pre-test, all participants attempted to provide a response. At the post-test, all participants submitted a response to both prompts.

The two course instructors manually scored all essays using an agreed upon point-based rubric. The maximum possible scores were 22 for the first prompt and 16 for the second prompt. Given that all ratings were whole numbers with a relatively limited range, and the underlying theoretically continuous distribution, polychoric correlations were computed between the two instructors’ as a measure of inter-rater reliability. Statistical significance was computed using a likelihood ratio test which computes a chi-square test statistic with one degree of freedom for a bivariate correlation (see SAS Institute Inc., n.d.). These statistics are presented in Table 1 for both prompts at pre- and post-test.

Table 1. Instructor inter-rater polychoric correlations.

	Pre-test (N = 53)				Post-test (N = 44)
	r	χ^2(1)	p-value		r	χ^2(1)	p-value
Prompt 1	0.871	62.093	< 0.001		0.888	60.266	< 0.001
Prompt 2	0.915	69.651	< 0.001		0.956	80.912	< 0.001

When the scores assigned by the two instructors varied by 2 points or less, the mean was used as the “manual score.” Raters agreed that when scores varied by more than 2 points, the essay would be reviewed by a third rater and the mean of the three raters’ scores was used as the “manual score.” A disagreement of more than 2 points was equivalent to disagreeing on one major aspect of the essay or more than 2 smaller aspects of the essay. At the pre-test there were two responses to the first prompt (3.8%) and two responses to the second prompt (3.8%) that the raters disagreed on by more than two points. At the post-test there were 11 responses to the first prompt (25%) and four responses to the second prompt (9.1%) that the raters disagreed on by more than two points. All essays were also scored by the GIKS.

At the end of the semester all students completed a final exam which consisted of 50 multiple-choice questions. Question banks were used and were organized by question type. For example, each student received one question from a question bank concerning classifying a study as observational or experimental. There were five questions in that question bank; each student received one randomly selected question from that bank. The same question banks and test blueprints were used across all online sections of the course. With each question worth 2 points, the maximum score on the final exam was 100 points. The exam was password protected and could only be accessed with a proctor who had been approved by the online campus.

4.2. Results

GIKS scores are discrete. Frequency distributions are presented in Table 2 and Table 3 displaying the GIKS scores on the first and second prompts, respectively. The manual scores assigned by individual instructors were also discrete, though the range of possible scores was wider and in cases where raters disagreed the average score was used. Descriptive statistics for the manual scores are presented in Table 4.

Table 2. Frequency distribution of scores on Prompt 1.

	Pre-test			Post-test
Links in common	N	Percent		N	Percent
0	17	44.74		6	15.79
1	12	31.58		8	21.05
2	7	18.42		13	34.21
3	2	5.26		5	13.16
4	0	0		6	15.79
	Pre-test			Post-test
Keyword occurrence	N	Percent		N	Percent
0	7	18.42		0	0
1	9	26.68		3	7.89
2	10	26.32		6	15.79
3	5	13.16		7	18.42
4	4	10.53		9	23.68
5	3	7.89		9	23.68
6	0	0		1	2.63
7	0	0		2	5.26
8	0	0		1	2.63

Table 3. Frequency distribution of scores on Prompt 2.

	Pre-test			Post-test
Links in common	N	Percent		N	Percent
0	24	63.16		2	5.26
1	6	15.79		12	31.58
2	7	18.42		10	26.32
3	1	2.63		7	18.42
4	0	0		5	13.16
5	0	0		1	2.63
6	0	0		1	2.63
	Pre-test			Post-test
Keyword Occurrence	N	Percent		N	Percent
0	0	0		0	0
1	7	18.42		0	0
2	16	42.11		2	5.26
3	5	13.16		8	21.05
4	8	21.05		13	34.21
5	2	5.26		10	26.32
6	0	0		3	7.89
7	0	0		1	2.63
8	0	0		0	0
9	0	0		1	2.63

Table 4. Descriptive statistics for manual scores.

	Pre-test					Post-test
	Mean	SD	Median	Skew.		Mean	SD	Median	Skew.
Prompt 1	2.724	1.830	2.500	1.923		7.171	3.664	6.750	0.314
Prompt 2	2.158	1.311	2.000	0.400		5.776	2.506	5.750	0.142

NOTE: N = 38

Students’ scores should increase from the pre- to post-test if the essay prompts are measuring content that was taught in the course. As evidence of this curricular validity, scores did increase from pre- to post-test on all measures for both prompts. Wilcoxon signed rank tests were used to evaluate the statistical significance of the increases. Data were paired by student and all changes were statistically significant. The signed rank test statistics (S) and unadjusted p-values are presented in Table 5 for both prompts.

Table 5. Change in scores with Wilcoxon signed rank tests.

	Change (post- pre)
	Q1	Median	Q3		S	Unadjusted p-value
Prompt 1
Links in common	0	1	2		142.0	< 0.0001
Keyword occurrence	0	2	3		192.5	<0.0001
Manual score	2	3	7		336.5	<0.0001
Prompt 2
Links in common	1	1	2		263.5	<0.0001
Keyword occurrence	1	2	3		257.5	<0.0001
Manual score	2	3.75	5		352.0	<0.0001

NOTE: N = 38.

Scores on the final exam, which was taken during the last week of the course, were approximately normally distributed. Out of a maximum of 100 points, the mean was 77.158 points with a standard deviation of 12.998 points. The median was 77.5 points.

Correlations between pre-test scores and final exam scores provide evidence of predictive validity, though these relations may be weaker than those between post-test scores and final exam scores which provide evidence of concurrent validity. Polychoric correlations were computed between all pre- and post-test scores as well as final exam scores for the two prompts separately. These are presented in Tables 6 and 7.

Table 6. Polychoric correlations for Prompt 1.

	1.	2.	3.	4.	5.	6.
1. Links in common, pre-test
2. Keyword occurrence, pre-test	0.871^**
3. Manual score, pre-test	0.553^*	0.779^**
4. Links in common, post-test	0.146	0.176	-0.008
5. Keyword occurrence, post-test	0.156	0.135	0.039	0.720^**
6. Manual score, post-test	0.114	0.128	0.107	0.361^*	0.714^**
7. Final exam score	0.044	0.337^*	0.523^*	0.380^*	0.328^*	0.359^*

NOTE: N = 38,

* p-value ≤ .05,

** p-value ≤ .001.

Table 7. Polychoric correlations for Prompt 2.

	1.	2.	3.	4.	5.	6.
1. Links in common, pre-test
2. Keyword occurrence, pre-test	0.984^**
3. Manual score, pre-test	0.862^**	0.749^**
4. Links in common, post-test	0.278	0.299	0.199
5. Keyword occurrence, post-test	0.384	0.433^*	0.160	0.833^**
6. Manual score, post-test	0.146	0.108	0.131	0.795^**	0.753^**
7. Final exam score	0.367	0.362^*	0.255	0.412^*	0.335^*	0.519^*

NOTE: N = 38,

* p-value ≤ 0.05,

** p-value ≤ 0.001.

4.3. Changes Following Study I

Given the results of the first study, a number of changes were made before the second study. Of primary interest were the relations between the manual scores and GIKS scores at each time point and the relations between the GIKS post-test scores and final exam scores. Instructors’ manual scores were significantly correlated with the GIKS scores for both prompts at both pre- and post-test, providing evidence of convergent validity. These relations were stronger for the second prompt compared to the first with the exception of the pre-test correlation with keyword occurrence which was only slightly stronger for the first prompt compared to the second. The correlations between the manual scores and links in commons scores for the first prompt were relatively low compared to the second prompt. The instructors suggested that for the first prompt students may have been able to take words from the output they were given and use them in their responses without fully understanding what they mean. For these reasons, in the second study this first prompt was not used.

A new prompt was written to replace the first prompt in the second study. It was developed taking into account that students should not be able to pull keywords directly from the prompt. The new prompt was also developed to address statistical inference from a more conceptual perspective as opposed to the applied perspective that was shared by both prompts used in the first study. Seven out of the twelve lessons in the course cover topics related to statistical inference.

Correlations between post-test GIKS scores and final exam scores were statistically significant but only weak to moderately strong. This may be because the prompts covered a limited amount of course content. The first prompt included a scatterplot and Pearson's r correlation output; this content is equivalent to half of one week's lesson. The second prompt covers more course content because it asks students to describe variables, select a graph, and select a statistical test. This content spans over three weeks’ content. This may partially explain why the relations with final exam scores were stronger for the second prompt compared to the first. The second prompt was used again in the second study.

5. Study II

5.1. Methodology

The data collection occurred during the fall 2016 semester which was approximately 15 weeks in length. There were 109 students enrolled in the two participating sections of the course at the beginning of the semester; 95 completed the pre-test during the first week of the course and gave permission for their data to be used for research purposes. For this semester, the course management system Canvas was used for the first time and the course was designed to require students to complete the survey containing the informed consent form before they could access other course materials, so there were no students who took the post-test without taking the pre-test. Of the 95 students who completed the pre-test and gave permission for their data to be used for research purposes, 75 also completed the post-test during the last week of the course before the final exam. There was one student who completed the pre- and post-test but did not complete the final exam, leaving complete data for 74 students.

The procedures in this second study were identical to those in the first study. One of the prompts was changed following the comments provided by the instructors after the first study. The prompts used in the second study are attached as Appendix B. The new prompt describes a sampling distribution and provides a probability distribution plot created using Minitab Express with the area representing the p-value shaded in. The prompt was designed to assess students’ levels of understandings about p-values and statistical significance.

At the pre-test, all participants submitted a response to the first prompt. For the second prompt, ten students did not provide a response and one wrote, “I have no idea.” At the post-test, all participants attempted to respond to the first prompt and only one did not respond to the second prompt.

Again, each essay was rated by two instructors using an agreed upon rubric and polychoric correlations were computed as a measure of inter-rater reliability, which are presented in Table 8. The maximum possible scores were 16 on the first prompt and 5 on the second prompt. When instructors’ scores varied by 2 points or less their mean was used as the “manual score.” When scores varied by more than 2 points, the essay was reviewed by a third rater and the mean of the three was used as the “manual score.” At the pre-test there was one response to the first prompt (1.1%) and no responses to the second prompt that the raters disagreed on by more than two points. At the post-test there were seven responses to the first prompt (9.3%) and no responses to the second prompt that the raters disagreed on by more than two points.

Table 8. Instructor inter-rater polychoric correlations.

	Pre-test (N = 95)				Post-test (N = 75)
	r	χ^2(1)	p-value		r	χ^2(1)	p-value
Prompt 1	0.983	143.502	< 0.001		0.909	111.938	< 0.001
Prompt 2	0.803	21.902	< 0.001		0.956	110.412	< 0.001

At the end of the semester all the students completed a final exam which consisted of 50 multiple-choice questions. Fifty question banks were used and were organized by question type. The same question banks and test blueprints were used across all online sections of the course. This test blueprint was modified between semesters. With each question worth 2 points, the maximum score on the final exam was 100 points. The exam was password protected and could only be accessed with a proctor who had been approved by the online campus or using the video proctoring service that was being piloted in one of the two participating sections.

5.2. Results

Frequency distributions are presented in Tables 9 and 10 displaying the GIKS scores on the first and second prompts, respectively. Descriptive statistics for the manual scores are presented in Table 11.

Table 9. Frequency distribution of scores on Prompt 1.

	Pre-test			Post-test
Links in common	N	Percent		N	Percent
0	64	86.49		15	20.27
1	4	5.41		22	29.73
2	2	2.70		18	24.32
3	2	2.70		10	13.51
4	1	1.35		5	6.76
5	1	1.35		2	2.70
6	0	0		1	1.35
7	0	0		1	1.35
	Pre-test			Post-test
Keyword occurrence	N	Percent		N	Percent
0	3	4.05		0	0
1	15	20.27		1	1.35
2	43	58.11		17	22.97
3	7	9.46		10	13.51
4	3	4.05		17	22.97
5	2	2.70		10	13.51
6	1	1.35		10	13.51
7	0	0		5	6.76
8	0	0		1	1.35
9	0	0		1	1.35
10	0	0		2	2.70

Table 10. Frequency distribution of scores on Prompt 2.

	Pre-test		Post-test
Links in common	N	Percent	N	Percent
0	48	64.86	26	35.14
1	18	24.32	24	32.43
2	8	10.81	14	18.92
3	0	0	5	6.76
4	0	0	5	6.76
	Pre-test		Post-test
Keyword occurrence	N	Percent	N	Percent
0	30	40.54	6	8.11
1	17	22.97	12	16.22
2	19	25.68	18	24.32
3	8	10.81	20	27.03
4	0	0	16	21.62
5	0	0	2	2.70

Table 11. Descriptive statistics for manual scores.

	Pre-test				Post-test
	Mean	SD	Median	Skew.	Mean	SD	Median	Skew.
Prompt 1	1.811	1.354	2.000	2.498	6.065	2.927	6.000	0.842
Prompt 2	0.297	0.421	0.000	1.741	1.318	1.318	1.000	0.898

NOTE: N = 74

For evidence of curricular validity, changes in scores were compared on both prompts from pre- to post- test. Scores increased on all measures for both prompts. Wilcoxon signed rank tests were used to evaluate the statistical significance of the increases. Data were paired by student and all changes were statistically significant. The signed rank test statistics (S) and unadjusted p-values are presented in Table 12 for both prompts.

Table 12. Change in scores with Wilcoxon signed rank tests.

	Change (post-pre)
	Q1	Median	Q3	S	Unadjusted p-value
Prompt 1
Links in common	0	1	2	827.5	<0.0001
Keyword occurrence	1	2	3	901	<0.0001
Manual score	2	4	6	1307.5	<0.0001
Prompt 2
Links in common	0	1	2	431	<0.0001
Keyword occurrence	0	1	2	713.5	<0.0001
Manual score	0	0.5	2	611.5	<0.0001

NOTE: N = 74

Scores on the final exam, which was taken during the last week of the course, were negatively skewed and leptokurtic. The mean score was 80.921 points with a standard deviation of 12.806 points. The median was 84 points. Polychoric correlations were computed between all pre- and post-test scores as well as final exam scores for the two prompts separately in Tables 13 and 14.

Table 13. Polychoric correlations for Prompt 1.

	1.	2.	3.	4.	5.	6.
1. Links in common, pre-test
2. Keyword occurrence, pre-test	0.986^**
3. Manual score, pre-test	0.938^**	0.628^**
4. Links in common, post-test	0.595^**	0.292^*	0.288^*
5. Keyword occurrence, post-test	0.435^*	0.253^*	0.296^*	0.790^**
6. Manual score, post-test	0.309	0.188	0.159	0.665^**	0.787^**
7. Final exam score	0.060	0.185	0.160	0.342^*	0.411^*	0.452^**

NOTE: N = 74,

* p-value ≤ 0.05,

** p-value ≤ 0.001.

Table 14. Polychoric correlations for Prompt 2.

	1.	2.	3.	4.	5.	6.
1. Links in common, pre-test
2. Keyword occurrence, pre-test	0.989^**
3. Manual score, pre-test	0.292	0.435^*
4. Links in common, post-test	0.240	0.195	0.161
5. Keyword occurrence, post-test	0.255	0.182	0.132	0.911^**
6. Manual score, post-test	0.115	0.087	0.092	0.579^**	0.655^**
7. Final exam score	0.060	0.187	0.046	0.276^*	0.226	0.286^*

NOTE: N = 74,

* p-value ≤ 0.05,

** p-value ≤ 0.001.

5.3. Changes Following Study II

The second prompt from the first study was reused as the first prompt in the second study. Correlations between GIKS scores and the manual scores assigned by instructors were strong at both the pre- and post-test for this prompt. Relations between post-test scores and final exam scores were again weak to moderately strong and positive. This prompt, or similar versions of it, will be used in the future. It seems to work well because it includes content across multiple lessons and it has clear correct and incorrect answers that can be detected by the GIKS system.

The second prompt referenced content covered in two weeks’ lessons: sampling distributions and hypothesis testing. The correlation between the GIKS links in common and keyword occurrence scores at the pre-test was very strong (r = 0.989). The range of scores obtained on both of these scales was limited. For the links in common measure, scores were limited to 0, 1, and 2. For the keyword occurrence measure, scores were limited to 0, 1, 2, and 3. Each student's keyword occurrences score had to be greater than his or her links in common score because the links were occurring between the identified keywords. The correlation between these two variables may have been very strong because they are relying on the presence of the same words in the writing samples and they have limited discrete ranges.

Relations between post-test scores on the second prompt and final exam scores were weaker than they were for the first prompt. The ranges of scores on the post-test for the second prompt were limited compared to those on the first prompt. For the first prompt, links in common scores ranged from 0 to 7 and keyword occurrence scores ranged from 1 to 10. For the second prompt, links in common scores ranged from 0 to 4 and keyword occurrence scores ranged from 0 to 5. The manual scores assigned by instructors were also significantly higher on the first prompt compared to the second prompt [mean difference = 4.740, s = 2.889, t (74) = 14.207, p < 0.001]. The second prompt may have been too difficult for students, particularly at the pre-test when 11 out of 95 (11.6%) students did not provide a response and 57 out of 95 (60%) students received a manual score of 0. At the post-test, 21 of the 75 (28%) students who submitted the assessment earned a manual score of 0. While this may not be ideal for research purposes, a difficult prompt, such as the second one in this study, may be appropriate if the GIKS is being used as a formative assessment activity.

6. Discussion

Two studies were conducted over consecutive semesters in an online introductory statistics course to accumulate evidence for the reliability and validity of scores on open-ended prompts obtained using the GIKS system. The prompt that was given as the second prompt in the first study and the first prompt in the second study had sufficiently strong correlations with the instructors’ manual scores. And, its post-test score correlations with final exam scores were positive and moderate in strength. This prompt worked well because it had a clear correct answer with a logical structure that could be measured by the GIKS. It was also a good prompt to use at the end of the semester because it required students to apply knowledge that was covered across three weeks’ lessons.

The first prompt that was used in the first study was not used again in the second study because instructors believed that students may have been able to take words from the prompt (i.e., the scatterplot and correlation output) and used them in their responses without fully understanding them. One of the advantages to using open-ended questions is that students should need to recall information as opposed to only recognizing it; this does not occur if keywords are featured in the prompt.

6.1. Limitations

A limitation of this study is that the GIKS was used as a summative assessment activity strictly for research purposes. A major benefit of the GIKS system is that if students enter their own responses directly into the system they will be shown a graphical representation of their knowledge structures. This did not occur in this study. Here, the reliability and validity of scores were examined in a research setting. While these studies provided valuable information about how to construct prompts that work well with the GIKS, it did not take full advantage of the abilities of the GIKS system. This will be addressed in future studies and will be discussed in Section 6.2.

Another possible limitation of the current study is that participants were all enrolled in an online course. The population of students who enroll in online courses is different from those that enroll in face-to-face courses. However, in the summer semesters about half of the students who enroll in online sections of this course are students who typically take face-to-face courses in the fall and spring semesters. A limitation of conducting this study with online students is that the knowledge structure activity was not proctored. Only the exams in this online course were proctored. Students could have looked up answers online or received help from another person. These integrity issues are not a primary concern, however, because students received full credit for submitting their responses regardless of their scores.

6.2. Future Plans for use as a Formative Assessment Activity

One of the major advantages of the GIKS system is that it may be used as a formative assessment activity. Students may enter their essays directly into the system and immediately see a graphical representation of their submission compared to that of the expert's structure. The students’ graphical representations are constructed using the links in common and keyword occurrence values that were examined in the two studies presented here. From these studies, we learned that essays that have a clear correct answer, and whose prompts do not contain the keywords, tend to work best with this system.

In the future, the GIKS will be used as a part of a learning activity in which students are given multiple attempts to edit their essay submissions. That is, after submitting their essay they will be shown their knowledge structures compared to the expert's and given the opportunity to edit their essays with the goal of getting their knowledge structure to match that of the expert.

Supplementary Material

The appendices for this article can be accessed as supplementary material on the publisher's website.