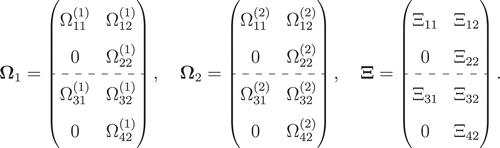A Marginal Maximum Likelihood Approach for Extended Quadratic Structural Equation Modeling with Ordinal Data

ABSTRACT

The literature on non-linear structural equation modeling is plentiful. Despite this fact, few studies consider interactions between exogenous and endogenous latent variables. Further, it is well known that treating ordinal data as continuous produces bias, a problem which is enhanced when non-linear relationships between latent variables are incorporated. A marginal maximum likelihood-based approach is proposed in order to fit a non-linear structural equation model including interactions between exogenous and endogenous latent variables in the presence of ordinal data. In this approach, the exact gradient of the approximated observed log-likelihood is calculated in order to attain the approximated maximum likelihood estimator. A simulation study shows that the proposed method provides estimates with low bias and accurate coverage probabilities.

KEYWORDS:

• Non-linear SEM
• interaction
• adaptive Gauss–Hermite approximation
• Laplace approximation

Introduction

Non-linear structural equation modeling (SEM) has been of great interest in the past few decades. Fruitful theories in psychology and business studies incorporate non-linear relations among latent variables. In the Theory of Planned Behavior, Ajzen (1991) emphasized the relevance of interaction between Motivation and Ability on Behavior. In a study focusing on the consumers’ loyalty, Agustin and Singh (2005) proposed a quadratic relationship between the latent constructs Satisfaction, Trust, Value, and Loyalty intentions in the framework of marketing sciences. In order to fit a non-linear SEM model, various methods have been proposed, which include but are not limited to the product indicator approaches (e.g., Kelava & Brandt, 2009; Marsh, Wen, & Hau, 2004; Wall & Amemiya, 2001; Yang-Jonsson, 1997), the method of moments (e.g., Mooijaart & Bentler, 2010; Wall & Amemiya, 2000), two-stage least squares (e.g., Bollen, 1995, 1996), the distributional analytic approaches (e.g., Klein & Moosbrugger, 2000; Klein & Muthén, 2007; Lee & Zhu, 2002), and the Bayesian methods (e.g., Lee & Song, 2004a; Zhu & Lee, 1999). The reader is directed to Brandt, Kelava, and Klein (2014) and Harring, Weiss, and Hsu (2012) for reviews and simulation studies comparing the aforementioned methods. Despite that the methods of fitting a non-linear SEM model are numerous, they are not flawless and do not always meet the needs of real data analysis.

First, most studies have focused on models with continuous indicators. In such cases, distributional assumptions are violated if indicators are ordinal. This has been investigated and observed extensively in linear models (e.g., Finney & DiStefano, 2006; Flora & Curran, 2004). Rhemtulla, Brosseau-Liard, and Savalei (2012) showed that ordinal data cannot be treated as continuous, unless the number of categories is large and the categories are equidistant. Due to the complexity of the non-linear model, we do not expect such methods to work well in a non-linear SEM model with ordinal data either. Lee and Zhu (2000) firstly considered a non-linear SEM model with the presence of polytomous indicators and proposed a Bayesian approach to estimate the parameters. Since then, various studies that directly handle the categorical nature emerge. Lee and Song (2003) extended the model in Lee and Zhu (2000) by incorporating covariates in the measurement and the structural model and proposed an MCEM algorithm (Wei & Tanner, 1990) to estimate the parameters. A similar algorithm was used by Song and Lee (2005) when the non-linear model has only dichotomous indicators. Lee and Song (2008) and Song and Lee (2006a) considered Bayesian estimation and comparison of non-linear models with a mixture of continuous, dichotomous, and ordinal indicators. Rizopoulos and Moustaki (2008) introduced non-linear terms of the latent variables to generalized latent variable models with covariates. When the non-linear model contains missing values, Lee and Song (2004a) proposed a Bayesian approach for a mixture of continuous and ordinal indicators, which is extended by Cai, Song, and Lee (2008) to model non-ignorable missing. Lee and Song (2007) proposed a unified maximum likelihood approach for non-linear models with different types of indicators and with or without missing values. Lee, Song, and Cai (2010) exemplified the use of the Bayesian approach in the non-linear models using dichotomous indicators as examples. Studies mentioned above are devoted to single group data analysis. It is further generalized by Song and Lee (2006b) to multigroup analysis and by Kelava and Brandt (2014), Lee and Song (2004b), Lee et al. (2009), and Song and Lee (2004) to multilevel analysis.

Second, in the Theory of Planned Behavior, Ajzen (1991) proposed that the effect of Intention (endogenous latent variable) on Behavior is affected by Perceived Behavioral Control (exogenous latent variable). Throughout the paper, an exogenous variable is a variable that is not caused by any other variables in the model and an endogenous variable is a variable that is caused by some variables in the model. Even though some methods can incorporate ordinal data into the model, they generally lack the interaction between endogenous latent variables and exogenous latent variables. In contrast, Agustin and Singh (2005) proposed an interaction effect between Consumer Trust (endogenous latent variable) and Satisfaction (exogenous latent variable). They treated ordinal data as continuous and used the two-step approach of Ping (1995). To our best knowledge, there are no contemporary methods that can estimate non-linear SEM models including interactions between exogenous and endogenous latent variables in the presence of ordinal indicators.

The main purpose of the current paper is to fit the non-linear SEM model with ordinal data in the presence of interactions between latent exogenous and latent endogenous variables. We propose a marginal maximum likelihood approach to estimate the fixed unknown parameters in the model. Instead of the commonly implemented expectation-maximization (EM, Dempster, Laird, & Rubin, 1977) algorithm, we propose to use direct maximization. As we shall explain in later sections, the direct maximum likelihood approach is based on the true gradient of the approximated observed log-likelihood, which makes the sandwich estimator of standard errors easier to obtain. In contrast, the sandwich estimator of standard errors is not directly available in the EM algorithm. Further, when the gradients in the M-step are approximated, the EM algorithm can be less accurate than the direct maximum likelihood approach with the same approximation method (Jin & Andersson, 2019a).

The article is organized as follows. The model is presented in the next section, which is followed by a description of the proposed method and an outline of the suggested procedure for directly maximizing the marginal likelihood. Next, a simulation study is conducted to investigate the small-sample performance of the proposed method. An empirical example is presented to illustrate the method, followed by a discussion with conclusions.

Non-linear structural equation model

Let $\mathit{\xi }$ (exogenous) and $\mathit{\eta }$ (endogenous) be latent random vectors with dimensions $K_{\xi }$ and $K_{\eta }$, respectively. The measurement model for $X_j$, the $j^{th}$ ordinal indicator of $\mathit{\xi }$, is:

(1) $g_j^{(x)}\left(P\left(X_j\le u_j|\mathit{\xi }\right)\right)={\alpha }_{x,j}^{(u_j)}-{\mathit{\beta }}_{x,j}^T\mathit{\xi },u_j\in \left\{1,...,U_j\right\},$(1)

where $U_j$ is the number of response categories for the ordinal indicator $X_j$, $g_j^{(x)}$ is the link function, ${\alpha }_{x,j}^{(u_j)}$ is the category-specific intercept for observing $u_j$, and ${\mathit{\beta }}_{x,j}$ is the factor loading vector for $X_j$. Such a setting is similar to the cumulative link model in the context of generalized linear model (Agresti, 2015, p. 213), but only with latent variables as explanatory variables. Likewise, the measurement model for $Y_j$, the $j^{th}$ ordinal indicator of $\mathit{\eta }$, is:

(2) $g_j^{(y)}\left(P\left(Y_j\le v_j|\mathit{\eta }\right)\right)={\alpha }_{y,j}^{(v_j)}-{\mathit{\beta }}_{y,j}^T\mathit{\eta },v_j\in \left\{1,...,V_j\right\},$(2)

where $V_j$ is the number of response categories for the ordinal indicator $Y_j$, $g_j^{(y)}$ is the link function, ${\alpha }_{y,j}^{(v_j)}$ is the category-specific intercept for observing $v_j$, and ${\mathit{\beta }}_{y,j}$ is the factor loading vector for $Y_j$. $\mathit{\xi }$ is assumed to have a $\mathbf{0}$ mean vector and a covariance matrix $\mathbf{\Phi }$. Further, partition $\mathit{\eta }$ into a $K_{{\eta }_1}\times 1$ vector ${\mathit{\eta }}_1$ and a $K_{{\eta }_2}\times 1$ vector ${\mathit{\eta }}_2$. The structural model of interest is:

(3) ${\mathit{\eta }}_1={\mathit{\tau }}_1+{\mathit{B}}_{11}{\mathit{\eta }}_1+{\mathit{B}}_{12}{\mathit{\eta }}_2+{\mathbf{\Gamma }}_1\mathit{\xi }+{\left({\mathit{I}}_{K_{{\eta }_1}}\otimes \mathit{\xi }\right)}^T{\mathbf{\Omega }}_1\mathit{\xi }+{\left({\mathit{I}}_{K_{{\eta }_1}}\otimes \mathit{\xi }\right)}^T\mathbf{\Pi }{\mathit{\eta }}_2+{\left({\mathit{I}}_{K_{{\eta }_1}}\otimes {\mathit{\eta }}_2\right)}^T\mathbf{\Xi }{\mathit{\eta }}_2+{\zeta }_1,$(3)

(4) ${\mathit{\eta }}_2={\mathit{\tau }}_2+{\mathit{B}}_{22}{\mathit{\eta }}_2+{\mathbf{\Gamma }}_2\mathit{\xi }+{\left({\mathbf{I}}_{K_{{\eta }_2}}\otimes \mathit{\xi }\right)}^T{\mathbf{\Omega }}_2\mathit{\xi }+{\zeta }_2,$(4)

where ${\mathit{I}}_a$ is an $a\times a$ identity matrix and $\otimes$ denotes the Kronecker product. The $\mathit{B}$ matrices represent linear effects among endogenous latent variables, where ${\mathbf{B}}_{11}$ and ${\mathbf{B}}_{22}$ are $K_{{\eta }_1}\times K_{{\eta }_1}$ and $K_{{\eta }_2}\times K_{{\eta }_2}$ matrices, respectively, with zero diagonal elements, and ${\mathit{B}}_{12}$ is a $K_{{\eta }_1}\times K_{{\eta }_2}$ matrix. The $\mathbf{\Omega }$ matrices represent non-linear effects of exogenous latent variables on the endogenous latent variables, where ${\mathbf{\Omega }}_1$ and ${\mathbf{\Omega }}_2$ are $K_{{\eta }_1}{K}_{\xi }\times K_{\xi }$ and $K_{{\eta }_2}{K}_{\xi }\times K_{\xi }$ matrices, respectively. $\mathrm{\Pi }$ is a $K_{{\eta }_1}{K}_{\xi }\times K_{{\eta }_2}$ matrix representing interaction effects between endogenous and exogenous latent variables, and $\mathbf{\Xi }$ is a $K_{{\eta }_1}{K}_{{\eta }_2}\times K_{{\eta }_2}$ matrix, representing non-linear effects among ${\mathit{\eta }}_2$ on ${\mathit{\eta }}_1$. The matrices ${\mathbf{\Omega }}_1$, $\mathbf{\Xi }$, and ${\mathbf{\Omega }}_2$ are block matrices stacking upper-triangular matrices on top of one another. For example, if $K_{{\eta }_1}=K_{{\eta }_2}=K_{\xi }=2$, ${\mathbf{\Omega }}_1$, ${\mathbf{\Omega }}_2$, and $\mathbf{\Xi }$ consist of two upper-triangular matrices each, i.e.

The diagonal elements of the upper-triangular matrices correspond to the quadratic effects, whereas the off-diagonal elements correspond to the interaction effects. The error terms ${\text{zetaa}}_1$ and ${\text{zetaa}}_2$ are assumed to have zero mean vectors and are independent of each other with $K_{{\eta }_1}\times K_{{\eta }_1}$ and $K_{{\eta }_2}\times K_{{\eta }_2}$ covariance matrices ${\mathbf{\Psi }}_{11}$ and ${\mathbf{\Psi }}_{22}$, respectively. ${\mathit{\tau }}_1$ and ${\mathit{\tau }}_2$ are the intercepts. The intercept ${\mathit{\tau }}_2$ is determined such that $E({\mathit{\eta }}_2)=\mathbf{0}$, that is, the $j^{th}$ element of ${\mathit{\tau }}_2$ is defined by:

${\tau }_{\mathit{2}\mathit{,}j}=-\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}\left({\mathbf{\Omega }}_j^{(2)}\mathbf{\Phi }\right),$

where ${\mathbf{\Omega }}_j^{(2)}$ is the $j^{th}$ upper-triangular matrix in ${\mathbf{\Omega }}_2$. For simplicity, we let ${\mathit{\tau }}_1=\mathbf{0}$. Thus, $E({\mathit{\eta }}_1)$ is not zero.

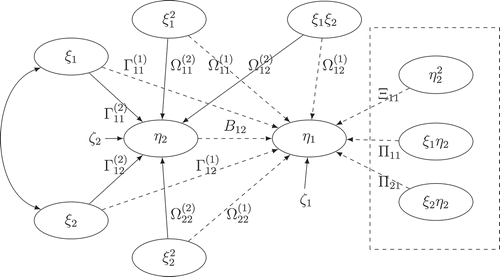
To our knowledge, the majority of studies on non-linear SEM overlooked Equation (3) and focused on Equation (4)(4) ${\mathit{\eta }}_2={\mathit{\tau }}_2+{\mathit{B}}_{22}{\mathit{\eta }}_2+{\mathbf{\Gamma }}_2\mathit{\xi }+{\left({\mathbf{I}}_{K_{{\eta }_2}}\otimes \mathit{\xi }\right)}^T{\mathbf{\Omega }}_2\mathit{\xi }+{\zeta }_2,$(4) . Take the path diagram of an extended quadratic structural model in Figure 1 as an example. If Equation (3) is ignored, the researchers are not able to model the paths in the dashed rectangle. As mentioned previously, the non-linear effects among endogenous and exogenous latent variables are commonly encountered in practice. Hence, it is of importance to include Equation (3) in the structural model.

Figure 1. The path diagram of the structural model of an extended quadratic structural equation model. The dashed paths correspond to the effects in Equation (3) and the solid paths correspond to the effects in Equation (4)(4) ${\mathit{\eta }}_2={\mathit{\tau }}_2+{\mathit{B}}_{22}{\mathit{\eta }}_2+{\mathbf{\Gamma }}_2\mathit{\xi }+{\left({\mathbf{I}}_{K_{{\eta }_2}}\otimes \mathit{\xi }\right)}^T{\mathbf{\Omega }}_2\mathit{\xi }+{\zeta }_2,$(4)

Marginal maximum likelihood estimation

Under the assumption of independent observations, the complete likelihood function is:

$\prod _{i=1}^{n}f({\mathit{y}}_i,{\mathit{x}}_i,{\mathit{\eta }}_i,{\mathit{\xi }}_i),$

where $n$ is the number of observations, and ${\mathit{y}}_i$ and ${\mathit{x}}_i$ are the $i^{th}$ observed ordinal vectors of indicators. Under the conditional independence assumption, the complete likelihood becomes:

(5) $\prod _{i=1}^{n}f({\mathit{y}}_i,{\mathit{x}}_i,{\mathit{\eta }}_i,{\mathit{\xi }}_i)=\prod _{i=1}^{n}f({\mathit{y}}_i|{\mathit{\eta }}_i)f({\mathit{x}}_i|{\mathit{\xi }}_i)f({\mathit{\eta }}_{1,i}|{\mathit{\eta }}_{2,i},{\mathit{\xi }}_i)f({\mathit{\eta }}_{2,i}|{\mathit{\xi }}_i)f({\mathit{\xi }}_i).$(5)

We assume that $\mathit{\xi }\sim N(\mathbf{0},\mathbf{\Phi })$, ${\zeta }_1\sim N(\mathbf{0},{\mathbf{\Psi }}_{11})$, and ${\zeta }_2\sim N(\mathbf{0},{\mathbf{\Psi }}_{22})$. Hence, ${\mathit{\eta }}_{1,i}|({\mathit{\eta }}_{2,i},{\mathit{\xi }}_i)$, ${\mathit{\eta }}_{2,i}|{\mathit{\xi }}_i$, and ${\mathit{\xi }}_i$ are multivariate normal. The expression of $f({\mathit{y}}_i,{\mathit{x}}_i,{\mathit{\eta }}_i,{\mathit{\xi }}_i)$ under these normal assumptions can be found in the appendix.

In practice, ${\mathit{\eta }}_1$ is often a scalar that has only one binary indicator. For example, $y_1=1$ if a behavior is conducted and 0 if not. If that is the case, further restrictions are needed for identification. One way is to let ${\mathbf{\Psi }}_{11}=0$ and ${\mathit{\beta }}_{y,1}=1$. This means that ${\mathbf{\Psi }}_{11}$ is singular and ${\mathit{\eta }}_{1,i}|\left({\mathit{\eta }}_{2,i},{\mathit{\xi }}_i\right)$ is a one-point distribution. Equivalently, ${\mathit{\eta }}_1$ is completely determined conditioned on $\mathit{\xi }$ and ${\mathit{\eta }}_2$.

Approximated observed log-likelihood

Let $\theta$ be the vector of parameters that includes the unconstrained elements in the structural matrices in ${\mathit{B}}_{11}$, ${\mathit{B}}_{12}$, ${\mathit{B}}_{22}$, ${\mathbf{\Gamma }}_1$, ${\mathbf{\Gamma }}_2$, ${\mathbf{\Omega }}_1$, ${\mathbf{\Omega }}_2$, $\mathrm{\Pi }$ and $\mathbf{\Xi }$, the unconstrained elements in the covariance matrices $\mathbf{\Phi }$, ${\mathbf{\Psi }}_{11}$, and ${\mathbf{\Psi }}_{22}$, and the unconstrained intercepts and factor loadings ${\alpha }_{y,j}^{(v_j)}$, ${\alpha }_{x,j}^{(u_j)}$, ${\mathit{\beta }}_{y,j}$, and ${\mathit{\beta }}_{x,j}$. In order to obtain the maximum likelihood estimator of $\theta$, the observed likelihood function is calculated by integrating out ${\mathrm{{\rm Y}}}_i=({\mathit{\eta }}_i^T,{\mathit{\xi }}_i^T{)}^T$ with ${\mathit{\eta }}_i=({\mathit{\eta }}_{1,i}^T,{\mathit{\eta }}_{2,i}^T{)}^T$ from Equation (5)(5) $\prod _{i=1}^{n}f({\mathit{y}}_i,{\mathit{x}}_i,{\mathit{\eta }}_i,{\mathit{\xi }}_i)=\prod _{i=1}^{n}f({\mathit{y}}_i|{\mathit{\eta }}_i)f({\mathit{x}}_i|{\mathit{\xi }}_i)f({\mathit{\eta }}_{1,i}|{\mathit{\eta }}_{2,i},{\mathit{\xi }}_i)f({\mathit{\eta }}_{2,i}|{\mathit{\xi }}_i)f({\mathit{\xi }}_i).$(5) , i.e.

(6) $\mathrm{\ell }(\theta )=\sum _{i=1}^{n}log\int f({\mathit{y}}_i,{\mathit{x}}_i,{\mathrm{{\rm Y}}}_i;\theta )d{\mathrm{{\rm Y}}}_i.$(6)

The integral in Equation (6)(6) $\mathrm{\ell }(\theta )=\sum _{i=1}^{n}log\int f({\mathit{y}}_i,{\mathit{x}}_i,{\mathrm{{\rm Y}}}_i;\theta )d{\mathrm{{\rm Y}}}_i.$(6) is intractable and approximations are needed. The approximated maximum likelihood estimator is obtained by maximizing the approximated observed log-likelihood function. Commonly used numerical approximation methods include the Laplace approximation (e.g., Huber, Ronchetti, & Victoria-Feser, 2004) and the Gauss–Hermitequadrature-based methods (e.g., Moustaki, 1996; Moustaki & Knott, 2000; Rabe-Hesketh & Skrondal, 2004; Rizopoulos & Moustaki, 2008). Alternatively, the observed gradient can be approximated by stochastic methods (e.g., Cai, 2010). In the present study, the second-order Laplace approximation (Shun & McCullagh, 1995) and the adaptive Gauss–Hermite quadrature (AGHQ) approximation of Liu and Pierce (1994) are implemented. The second-order Laplace approximation is second-order accurate and the accuracy of the AGHQ approximation depends on the number of quadrature points. A general introduction of these methods and the expressions of the approximations to Equation (6)(6) $\mathrm{\ell }(\theta )=\sum _{i=1}^{n}log\int f({\mathit{y}}_i,{\mathit{x}}_i,{\mathrm{{\rm Y}}}_i;\theta )d{\mathrm{{\rm Y}}}_i.$(6) can be found in the appendix.

Maximizing the approximated observed log-likelihood

A common approach in latent variable models is to employ the EM algorithm or its variants, where the latent variables are treated as missing values and the gradient of the conditional expectation in the E-step is approximated in the M-step. For example, the EM algorithm is used by Lee and Song (2004b), Lee, Song, and Lee (2003), and Lee and Zhu (2000) among others. The EM algorithm is known for its slow speed in many situations. When the integrals in the M-step are approximated, various studies (e.g., Bianconcini & Cagnone, 2012; Rizopoulos, Verbeke, & Lesaffre, 2009; Steele, 1996) argued that the fully exponential Laplace approximation (Tierney & Kadane, 1986; Tierney, Kass, & Kadane, 1989) is more accurate than the Laplace approximation. Jin and Andersson (2019a) proved that the estimator based on the EM algorithm with the fully exponential Laplace approximation is the same as the estimator that maximizes the Laplace approximated observed log-likelihood function, if implemented properly. Hence, we propose to directly maximize the approximated $\mathrm{\ell }(\theta )$, instead of the EM algorithm.

The gradients of the approximations can be readily obtained by the chain rule, explained in detail in the appendix. A quasi-Newton method (e.g., BFGS algorithm) can be used to find the maximizer of the approximated observed log-likelihood function. Since the approximations are subject to approximation error, the proposed approach can be interpreted as the quasi-maximum likelihood approach (Huber et al., 2004). If the approximated log-likelihood function is directly maximized, the gradient of the approximation is already available, which makes the standard errors easy to estimate (see Equation (10)(10) ${\left(\stackrel{ˆ}{\frac{{\mathrm{\partial }}^2\mathrm{\ell }\left(\theta \right)}{\mathrm{\partial }\theta \mathrm{\partial }{\theta }^T}}\right)}^{-1}\sum _{i=1}^n\left[\frac{\mathrm{\partial }{\mathrm{\ell }}_i\left(\hat{\theta }\right)}{\mathrm{\partial }\theta }\frac{\mathrm{\partial }{\mathrm{\ell }}_i\left(\hat{\theta }\right)}{\mathrm{\partial }{\theta }^T}\right]{\left(\stackrel{ˆ}{\frac{{\mathrm{\partial }}^2\mathrm{\ell }\left(\theta \right)}{\mathrm{\partial }\theta \mathrm{\partial }{\theta }^T}}\right)}^{-1},$(10) in the appendix). If the EM algorithm is used, the information matrix needed for standard errors is approximated afterward by, for example, the Louis method (Louis, 1982).

Simulation study

In order to investigate the performance of the suggested approach, a simulation study is conducted. The setup and result are presented in the following subsections.

Simulation design

In the simulation, a four-factor model is considered with two exogenous latent variables $\left\{{\xi }_1,{\xi }_2\right\}$ and two endogenous latent variables $\left\{{\eta }_1,{\eta }_2\right\}$. Each latent variable is associated with three ordinal indicators with five categories each. $\mathit{\xi }$, ${\zeta }_1$ and ${\zeta }_2$ are generated from multivariate normal distributions. The population parameters of the measurement model (Equations (1)(1) $g_j^{(x)}\left(P\left(X_j\le u_j|\mathit{\xi }\right)\right)={\alpha }_{x,j}^{(u_j)}-{\mathit{\beta }}_{x,j}^T\mathit{\xi },u_j\in \left\{1,...,U_j\right\},$(1) and (2(2) $g_j^{(y)}\left(P\left(Y_j\le v_j|\mathit{\eta }\right)\right)={\alpha }_{y,j}^{(v_j)}-{\mathit{\beta }}_{y,j}^T\mathit{\eta },v_j\in \left\{1,...,V_j\right\},$(2) )) are

$\begin{array}{c}{\mathit{\alpha }}_x^T=\left(\begin{array}{cccccc}-2.32& -2.13& -1.96& -2.32& -2.13& -1.96\\ 0.57& 0.52& 0.48& 0.57& 0.52& 0.48\\ 1.51& 1.39& 1.27& 1.51& 1.39& 1.27\\ 2.87& 2.64& 2.42& 2.87& 2.64& 2.42\\ \hspace{0.17em}& \hspace{0.17em}& \hspace{0.17em}& \hspace{0.17em}& \hspace{0.17em}& \hspace{0.17em}\end{array}\right)\\ {\mathit{\beta }}_x^T=\left(\begin{array}{cccccc}2.00& 1.80& 1.60& 0& 0& 0\\ 0& 0& 0& 2.00& 1.80& 1.60\\ \hspace{0.17em}& \hspace{0.17em}& \hspace{0.17em}& \hspace{0.17em}& \hspace{0.17em}& \hspace{0.17em}\end{array}\right)\\ {\mathit{\alpha }}_y^T=\left(\begin{array}{cccccc}-1.76& -1.70& -1.66& -2.20& -2.14& -2.08\\ -0.42& -0.40& -0.35& -0.91& -0.88& -0.87\\ 0.60& 0.56& 0.52& 0.00& 0.00& 0.00\\ 2.65& 2.60& 2.50& 1.79& 1.76& 1.72\\ \hspace{0.17em}& \hspace{0.17em}& \hspace{0.17em}& \hspace{0.17em}& \hspace{0.17em}& \hspace{0.17em}\end{array}\right)\\ {\mathit{\beta }}_y^T=\left(\begin{array}{cccccc}1.00& 0.95& 0.90& 0& 0& 0\\ 0& 0& 0& 1.00& 0.95& 0.90\end{array}\right),\\ \hspace{0.17em}\end{array}$

where zero elements are restricted to zero. Here the $(j,k{)}^{th}$ element in ${\mathit{\alpha }}_x$ is ${\alpha }_{x,j}^{(k)}$ and the $j^{th}$ row of ${\mathit{\beta }}_x$ is ${\mathit{\beta }}_{x,j}$ in Equation (1)(1) $g_j^{(x)}\left(P\left(X_j\le u_j|\mathit{\xi }\right)\right)={\alpha }_{x,j}^{(u_j)}-{\mathit{\beta }}_{x,j}^T\mathit{\xi },u_j\in \left\{1,...,U_j\right\},$(1) . Likewise, the $(j,k{)}^{th}$ element in ${\mathit{\alpha }}_y$ is ${\alpha }_{y,j}^{(k)}$ and the $j^{th}$ row of ${\mathit{\beta }}_y$ is ${\mathit{\beta }}_{y,j}$ in Equation (2)(2) $g_j^{(y)}\left(P\left(Y_j\le v_j|\mathit{\eta }\right)\right)={\alpha }_{y,j}^{(v_j)}-{\mathit{\beta }}_{y,j}^T\mathit{\eta },v_j\in \left\{1,...,V_j\right\},$(2) . The factor loadings only load on one latent variable giving this setup a simple structure for simplicity. ${\beta }_{y,11}$ and ${\beta }_{y,42}$ are fixed to $1$ for identification. The population covariance between the latent exogenous variables is 0.40 and the variances are fixed to 1 for identification. Ordinal observations are generated by the measurement model using the probit link function. Equations (3)(4) ${\mathit{\eta }}_2={\mathit{\tau }}_2+{\mathit{B}}_{22}{\mathit{\eta }}_2+{\mathbf{\Gamma }}_2\mathit{\xi }+{\left({\mathbf{I}}_{K_{{\eta }_2}}\otimes \mathit{\xi }\right)}^T{\mathbf{\Omega }}_2\mathit{\xi }+{\zeta }_2,$(4) and (4(5) $\prod _{i=1}^{n}f({\mathit{y}}_i,{\mathit{x}}_i,{\mathit{\eta }}_i,{\mathit{\xi }}_i)=\prod _{i=1}^{n}f({\mathit{y}}_i|{\mathit{\eta }}_i)f({\mathit{x}}_i|{\mathit{\xi }}_i)f({\mathit{\eta }}_{1,i}|{\mathit{\eta }}_{2,i},{\mathit{\xi }}_i)f({\mathit{\eta }}_{2,i}|{\mathit{\xi }}_i)f({\mathit{\xi }}_i).$(5) ) are set to be the same as Figure 1. The population values of the structural parameters are

$\begin{array}{rl}& B_{11}=0,B_{12}=0.15,{\mathbf{\Gamma }}_1=\left(\begin{array}{cc}0.15& 0.15\end{array}\right),\\ & {\mathbf{\Omega }}_1=\left(\begin{array}{cc}0.15& 0.20\\ 0& 0.15\end{array}\right),\mathrm{\Pi }=\left(\begin{array}{c}0.10\\ 0.10\end{array}\right),\mathbf{\Xi }=0.1,\end{array}$

$B_{22}=0,{\mathbf{\Gamma }}_2=\left(\begin{array}{cc}0.35& 0.35\end{array}\right),{\mathbf{\Omega }}_2=\left(\begin{array}{cc}0.20& 0.25\\ 0& 0.20\end{array}\right),$

where the zero elements are restricted to zero. The variances of the error terms are ${\mathbf{\Psi }}_{11}=2.00$ and ${\mathbf{\Psi }}_{22}=1.50$. Such population values are chosen to reflect common values in practice. The ${\mathit{\alpha }}_x$ and ${\mathit{\beta }}_x$ are chosen such that the reliabilities of the items range from 0.72 to 0.8 and the probabilities of observing each outcomes are 0.15, 0.45, 0.15, 0.15, and 0.1, respectively, for all items. The structural parameters are chosen such that the $R^2$‘s of the latent regression are approximately $0.43$ and $0.34$. The ${\mathit{\alpha }}_y$ and ${\mathit{\beta }}_y$ are chosen such that the reliabilities of the items range from 0.65 to 0.78 and the probabilities of observing each outcomes are approximately 0.10, 0.20, 0.20, 0.35, and 0.15 for all items. Four different sample sizes are considered, i.e., $n=\left\{400,600,800,1000\right\}$ and 2000 replications are generated for each sample size. Two second-order accurate approximation methods to the observed log-likelihood are considered in the simulation, namely, the second-order Laplace approximation, denoted by Lap(2nd), and the AGHQ with 5 quadrature points per latent variable, denoted by AGHQ(5p). We expect them to perform similarly in terms of bias. The approximated maximum likelihood estimator is obtained by maximizing the approximated observed log-likelihood using the direct maximum likelihood approach by the BFGS algorithm. The algorithm is stopped when the maximum absolute change in the parameter estimates of two consecutive iterations is less than ${10}^{-4}$. The code was written in R (R Core Team, 2018) by the aid of the package Rcpp (Eddelbuettel, 2013).

Simulation results

Replications which do not converge and those with nonpositive definite covariance matrices are excluded from the analysis. The percentage of excluded cases is reported in Table 1. The proportion of inadmissible cases is generally ignorable and decreases as the sample size increases.

Table 1. Percentage of inadmissible cases excluded from the analysis

	$n$
Method	400	600	800	1000
Lap(2nd)	$0.00$	$0.00$	$0.00$	$0.00$
AGHQ(5p)	$0.30$	$0.01$	$0.00$	$0.00$

Lap(2nd) refers to the second-order Laplace approximation and AGHQ(5p) refers to the adaptive Gauss–Hermite quadrature approximation with 5 quadrature points per latent dimension.

In order to investigate the performance of the methods the relative bias $\mathrm{R}{\mathrm{B}}_p=100R^{-1}{\sum }_{i=1}^R{\text{thetaa}}_p^{-1}({\widehat{\text{thetaa}}}_{p,i}-{\text{thetaa}}_p)$ and root mean squared error $\mathrm{R}\mathrm{M}\mathrm{S}{\mathrm{E}}_p=\sqrt{R^{-1}{\sum }_{i=1}^R{\left[{\widehat{\text{thetaa}}}_{p,i}-{\text{thetaa}}_p\right]}^2}$ are calculated for each structural parameter ${\text{thetaa}}_p$, where $R$ is the number of replications and ${\widehat{\text{thetaa}}}_{p,i}$ is the corresponding estimate at the $i^{th}$ replication. Table 2 shows the RB and RMSE for the structural parameters ${\mathit{B}}_{11}$, ${\mathit{B}}_{12}$, ${\mathit{B}}_{22}$, ${\mathbf{\Gamma }}_1$, ${\mathbf{\Gamma }}_2$, ${\mathbf{\Omega }}_1$, ${\mathbf{\Omega }}_2$, $\mathrm{\Pi }$ and $\mathbf{\Xi }$. Following the common practice in the SEM literature (e.g., Curran, West, & Finch, 1996; Flora & Curran, 2004), relative bias lower than $5$ is regarded as a low bias. Generally, the methods provide low biases for the sample sizes investigated. The RMSE decreases with sample size as expected. Lap(2nd) and AGHQ(5p) perform similarly in terms of RB and RMSE across parameters and sample sizes. In order to evaluate the performances of the calculated standard errors, coverage probabilities at the nominal level 95% are presented in Table 3. The coverage probabilities of covering the true values are generally close to the nominal level. Results not shown here indicate that the first-order Laplace approximation that is equivalent to the adaptive Gauss–Hermite quadrature approximation with 1 quadrature point can perform unacceptably poorly for non-linear terms.

Table 2. Relative bias and root mean squared error of the estimators of structural parameters in Equations (3)(4) ${\mathit{\eta }}_2={\mathit{\tau }}_2+{\mathit{B}}_{22}{\mathit{\eta }}_2+{\mathbf{\Gamma }}_2\mathit{\xi }+{\left({\mathbf{I}}_{K_{{\eta }_2}}\otimes \mathit{\xi }\right)}^T{\mathbf{\Omega }}_2\mathit{\xi }+{\zeta }_2,$(4) and (4(5) $\prod _{i=1}^{n}f({\mathit{y}}_i,{\mathit{x}}_i,{\mathit{\eta }}_i,{\mathit{\xi }}_i)=\prod _{i=1}^{n}f({\mathit{y}}_i|{\mathit{\eta }}_i)f({\mathit{x}}_i|{\mathit{\xi }}_i)f({\mathit{\eta }}_{1,i}|{\mathit{\eta }}_{2,i},{\mathit{\xi }}_i)f({\mathit{\eta }}_{2,i}|{\mathit{\xi }}_i)f({\mathit{\xi }}_i).$(5) )

		Parameter
$n$	Method	$B_{12}$	${\mathrm{\Gamma }}_{11}^{(1)}$	${\mathrm{\Gamma }}_{12}^{(1)}$	${\mathrm{\Omega }}_{11}^{(1)}$	${\mathrm{\Omega }}_{12}^{(1)}$	${\mathrm{\Omega }}_{22}^{(1)}$	${\mathrm{\Pi }}_{11}$	${\mathrm{\Pi }}_{21}$	${\mathrm{\Xi }}_{11}$	${\mathrm{\Gamma }}_{11}^{(2)}$	${\mathrm{\Gamma }}_{12}^{(2)}$	${\mathrm{\Omega }}_{11}^{(2)}$	${\mathrm{\Omega }}_{12}^{(2)}$	${\mathrm{\Omega }}_{22}^{(2)}$
Relative bias
400	Lap (2nd)	4.59	0.87	−0.08	−2.22	2.81	−2.16	1.65	−2.88	1.53	1.98	2.25	−0.89	3.12	−0.44
	AGHQ (5p)	2.09	3.03	2.24	0.86	4.69	1.03	2.66	−1.69	−2.23	1.33	1.63	0.29	1.54	0.77
600	Lap (2nd)	2.54	0.53	2.93	−1.27	0.07	0.30	−4.22	−2.80	2.01	1.93	1.81	0.22	2.99	−0.58
	AGHQ (5p)	0.26	2.51	4.79	1.36	2.23	2.83	−3.18	−1.63	−1.62	1.30	1.18	1.07	1.93	0.23
800	Lap (2nd)	2.05	−0.20	0.32	−2.34	1.33	−0.87	−1.45	−0.22	−0.13	0.82	1.44	0.30	0.28	0.48
	AGHQ (5p)	0.04	1.65	2.17	−0.02	3.65	1.57	−0.40	0.88	−3.53	0.22	0.82	0.95	−0.54	1.15
1000	Lap (2nd)	1.54	−0.57	−1.74	−0.40	−1.24	−0.32	2.47	−0.61	0.76	1.27	1.32	−0.31	1.84	−0.24
	AGHQ (5p)	−0.50	1.21	0.07	1.79	1.22	1.90	3.35	0.35	−2.66	0.65	0.71	0.23	1.08	0.30
Root mean squared error multiplied by $10$
400	Lap (2nd)	0.92	1.19	1.22	1.05	1.54	1.01	0.99	0.96	0.56	1.03	0.99	0.86	1.30	0.85
	AGHQ (5p)	0.91	1.19	1.21	1.07	1.53	1.03	0.98	0.95	0.55	1.02	0.99	0.87	1.30	0.87
600	Lap (2nd)	0.74	0.97	0.94	0.82	1.19	0.82	0.76	0.77	0.46	0.85	0.86	0.69	1.01	0.67
	AGHQ (5p)	0.74	0.97	0.94	0.84	1.18	0.85	0.76	0.77	0.45	0.84	0.86	0.71	1.02	0.69
800	Lap (2nd)	0.63	0.82	0.82	0.70	1.02	0.69	0.65	0.65	0.38	0.71	0.71	0.59	0.89	0.58
	AGHQ (5p)	0.63	0.82	0.82	0.72	1.02	0.70	0.65	0.64	0.38	0.71	0.71	0.60	0.90	0.60
1000	Lap (2nd)	0.56	0.72	0.72	0.62	0.89	0.64	0.58	0.58	0.34	0.65	0.63	0.54	0.78	0.53
	AGHQ (5p)	0.56	0.72	0.72	0.64	0.89	0.65	0.59	0.58	0.34	0.65	0.63	0.55	0.79	0.54

Lap(2nd) refers to the second-order Laplace approximation and AGHQ(5p) refers to the adaptive Gauss–Hermite quadrature approximation with 5 quadrature points per latent dimension. The superscript indicates to which $\mathit{\eta }$ the parameter belongs.

Table 3. Coverage probabilities (%) of the Wald confidence interval for structural parameters in Equations (3)(4) ${\mathit{\eta }}_2={\mathit{\tau }}_2+{\mathit{B}}_{22}{\mathit{\eta }}_2+{\mathbf{\Gamma }}_2\mathit{\xi }+{\left({\mathbf{I}}_{K_{{\eta }_2}}\otimes \mathit{\xi }\right)}^T{\mathbf{\Omega }}_2\mathit{\xi }+{\zeta }_2,$(4) and (4(5) $\prod _{i=1}^{n}f({\mathit{y}}_i,{\mathit{x}}_i,{\mathit{\eta }}_i,{\mathit{\xi }}_i)=\prod _{i=1}^{n}f({\mathit{y}}_i|{\mathit{\eta }}_i)f({\mathit{x}}_i|{\mathit{\xi }}_i)f({\mathit{\eta }}_{1,i}|{\mathit{\eta }}_{2,i},{\mathit{\xi }}_i)f({\mathit{\eta }}_{2,i}|{\mathit{\xi }}_i)f({\mathit{\xi }}_i).$(5) ) at the nominal level of 95%

		Parameter
$n$	Method	$B_{12}$	${\mathrm{\Gamma }}_{11}^{(1)}$	${\mathrm{\Gamma }}_{12}^{(1)}$	${\mathrm{\Omega }}_{11}^{(1)}$	${\mathrm{\Omega }}_{12}^{(1)}$	${\mathrm{\Omega }}_{22}^{(1)}$	${\mathrm{\Pi }}_{11}$	${\mathrm{\Pi }}_{21}$	${\mathrm{\Xi }}_{11}$	${\mathrm{\Gamma }}_{11}^{(2)}$	${\mathrm{\Gamma }}_{12}^{(2)}$	${\mathrm{\Omega }}_{11}^{(2)}$	${\mathrm{\Omega }}_{12}^{(2)}$	${\mathrm{\Omega }}_{22}^{(2)}$
400	Lap (2nd)	95.2	94.7	94.3	94.9	94.3	96.0	93.9	95.0	95.0	95.3	96.4	94.8	94.9	95.5
	AGHQ (5p)	95.3	94.4	94.3	94.8	94.4	95.9	94.1	94.8	94.9	95.6	96.4	94.5	95.1	95.3
600	Lap (2nd)	95.2	94.4	95.7	95.1	94.8	95.4	95.3	94.4	94.2	94.5	94.6	95.6	95.7	96.2
	AGHQ (5p)	95.6	94.5	95.9	94.8	95.3	95.1	95.6	94.4	93.6	94.8	94.6	95.0	95.9	95.7
800	Lap (2nd)	95.0	95.3	94.5	95.3	94.8	95.5	95.2	95.3	95.0	95.8	95.3	95.2	94.7	95.4
	AGHQ (5p)	95.1	95.2	95.0	95.0	95.0	95.3	95.3	95.4	94.2	96.0	95.6	95.2	95.0	95.4
1000	Lap (2nd)	95.4	95.6	95.5	95.5	96.1	94.8	95.4	95.2	95.3	95.0	95.9	94.8	95.2	95.0
	AGHQ (5p)	95.7	95.5	95.5	94.8	96.7	94.7	95.0	94.7	94.4	95.1	95.9	94.5	95.4	95.0

Lap(2nd) refers to the second-order Laplace approximation and AGHQ(5p) refers to the adaptive Gauss–Hermite- quadrature approximation with 5 quadrature points per latent dimension. The superscript indicates to which $\mathit{\eta }$ the parameter belongs.

The Laplace approximations are expected to be computationally more efficient than AGHQ approximations for similar error rates if the number of latent variables is large. However, a higher-order Laplace approximation requires calculations of higher-order derivatives which are not straightforward, whereas the AGHQ approximation provides the possibility of decreasing error rates by increasing the number of quadrature points with the drawback of being computationally heavier. In the current simulation, the average estimation time for the sample size $n=1000$ takes on average 90 s for AGHQ(5p) and 49 s for Lap(2nd). This relative difference is hypothesized to increase with increasing number of latent variables.

Empirical example

In order to demonstrate how the proposed method works in practice, an empirical example is considered in this section. The empirical example contains 707 complete responses of households in two Swedish municipalities Sollentuna and Saltjö-boo regarding their behavior of off-peak hour energy use (Bartusch, Juslin, Stitkvoort, Yang-Wallentin, & Öhrlund, 2019), in order to investigate the roles of the psychological factors, Attitude (${\xi }_1$), Belief (${\xi }_2$), Perceived Behavioral Control (${\xi }_3$) and Intentions (${\eta }_2$) in relation to the Behavior (${\eta }_1$) of shifting the energy use to off-peak hours. It is hypothesized that Behavior (${\eta }_1$) is affected by an interaction between Perceived Behavioral Control (${\xi }_3$) and Intentions (${\eta }_2$). ${\eta }_1$ has only one continuous indicator and it is dichotomized into a binary indicator. Other latent variables are associated with two indicators each, in the form of 7-point Likert scale items. The 7-point Likert scale items were aggregated into five categories in order to avoid categories with too few observations. For the purpose of modeling the interaction effects, we also include ${\xi }_3^2$ and ${\eta }_2^2$ in the model, as suggested by Kelava and Brandt (2009). The structural model of interest is then:

${\eta }_1=B_{12}{\eta }_2+\left(\begin{array}{ccc}0& 0& {\mathrm{\Gamma }}_{13}^{(1)}\end{array}\right)\mathit{\xi }+{\mathit{\xi }}^T\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& {\mathrm{\Omega }}_{33}^{(1)}\end{array}\right)\mathit{\xi }+{\mathit{\xi }}^T\left(\begin{array}{c}0\\ 0\\ {\mathrm{\Pi }}_{31}\end{array}\right){\eta }_2+{\mathrm{\Xi }}_{11}{\eta }_2^2,$

${\eta }_2={\tau }_2+\left(\begin{array}{ccc}{\mathrm{\Gamma }}_{11}^{(2)}& {\mathrm{\Gamma }}_{12}^{(2)}& {\mathrm{\Gamma }}_{13}^{(2)}\end{array}\right)\mathit{\xi }+{\mathit{\xi }}^T\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ \hspace{0.17em}& \hspace{0.17em}& \hspace{0.17em}\end{array}\right)\mathit{\xi }+{\zeta }_2.$

Table 4 shows the estimates and the 95% confidence intervals for the structural parameters using the AGHQ approximation with 5 quadrature points per latent variable and the second-order Laplace approximation. None of the non-linear parameters ${\mathrm{\Omega }}_{33}^{(1)}$, ${\text{⁋I}}_{31}$ and ${\mathrm{\Xi }}_{11}$ is significant at the 5% significance level. The linear effects of Attitude and Belief on Intention (${\mathrm{\Gamma }}_{11}^{(2)}$ and ${\mathrm{\Gamma }}_{12}^{(2)}$) are significant at the 5% significance level, whereas the linear effects of Perceived Behavioral Control on Intention and Behavior (${\mathrm{\Gamma }}_{13}^{(2)}$ and ${\mathrm{\Gamma }}_{13}^{(1)}$) and of Intention on Behavior ($B_{12}$), are not significant at the 5% significance level. Results not presented here, show that similar results are obtained when 7 quadrature points are used, which indicates that the approximation is stabilized.

Table 4. Point estimates and 95% confidence intervals for structural parameters in the empirical example corresponding to non-linear effects for the AGHQ approximation with 5-quadrature points, denoted by AGHQ(5p), and second-order Laplace approximation, denoted by Lap(2nd)

	Parameter
	$B_{12}$	${\mathrm{\Gamma }}_{13}^{(1)}$	${\mathrm{\Omega }}_{33}^{(1)}$	${\mathrm{\Pi }}_{31}$	${\mathrm{\Xi }}_{11}$	${\mathrm{\Gamma }}_{11}^{(2)}$	${\mathrm{\Gamma }}_{12}^{(2)}$	${\mathrm{\Gamma }}_{13}^{(2)}$
AGHQ (5p)
Point estimate	$-0.042$	$-0.046$	$-0.074$	$0.083$	$-0.008$	$1.802$	$0.636$	$0.069$
Lower bound	$-0.098$	$-0.230$	$-0.252$	$-0.010$	$-0.029$	$1.037$	$0.302$	$-0.324$
Upper bound	$0.014$	$0.138$	$0.104$	$0.177$	$0.012$	$2.568$	$0.971$	$0.463$
Lap (2nd)
Point estimate	$-0.045$	$-0.034$	$-0.088$	$0.083$	$-0.006$	$1.919$	$0.546$	$0.103$
Lower bound	$-0.105$	$-0.190$	$-0.327$	$-0.017$	$-0.033$	$1.153$	$0.140$	$-0.232$
Upper bound	$0.014$	$0.123$	$0.151$	$0.182$	$0.021$	$2.686$	$0.953$	$0.438$

Discussion and conclusion

In this article, a structural model with quadratic and interaction relations is considered in the presence of ordinal data. Structural models including interactions between exogenous and endogenous latent variables are rarely found in the literature. The current study provides the possibility to include such features. To this end, a marginal maximum likelihood approach is proposed, where the exact gradient of the approximated observed log-likelihood is computed and used to approximate the Hessian, providing the opportunity to obtain standard errors straightforwardly, which are not easily available using, for example, the EM algorithm.

Simulation results indicate that the second-order Laplace approximation and the AGHQ approximation with 5 quadrature points per latent variable provide accurate parameter estimators at finite sample sizes. On one hand, despite that only simply structures are considered in the current study, the proposed approach works for general loading structures, provided that the model is identified. On the other hand, more research is needed to provide a rule-of-thumb sample size requirement for non-linear models with interactions between endogenous and exogenous variables. We leave it as a future topic.

In this study, the Laplace approximation and the AGHQ approximation are used to approximate the log-likelihood function, where the quadrature nodes are chosen deterministically. Alternative approaches include the Monte Carlo-based maximum likelihood approaches (e.g., Lee & Song, 2003; Song & Lee, 2005) and the Bayesian approaches (e.g., Lee & Song, 2008; Lee & Zhu, 2000). To our knowledge, they are not yet implemented in the non-linear SEM model of our interest. This remains as a topic for future studies.

A drawback of the method is that it relies on normally distributed latent exogenous variables and error terms. It remains for future research to investigate the sensitivity against nonnormality and develop robust approaches. For example, non-normality in the latent exogenous variables could be modeled by mixtures of normals.

Acknowledgment

We thank the reviewers for useful comments that lead to an improved manuscript.

Additional information

Funding

The work was supported by the Swedish Research Council [contract number 2017-01175].

Appendix

Approximated Maximum Likelihood Estimator

In this section, the proposed maximum likelihood estimator is described in detail. For notational convenience, let the complete log-likelihood be:

$h_i({\mathrm{{\rm Y}}}_i;\theta )=logf({\mathit{y}}_i,{\mathit{x}}_i,{\mathrm{{\rm Y}}}_i;\theta ).$

Let $p_x$ and $p_y$ be the number of indicators associated with $\mathit{\xi }$ and $\mathit{\eta }$, respectively. Under the distributional assumptions $\mathit{\xi }\sim N(\mathbf{0},\mathbf{\Phi })$, ${\zeta }_1\sim N(\mathbf{0},{\mathbf{\Psi }}_{11})$ and ${\zeta }_2\sim N(\mathbf{0},{\mathbf{\Psi }}_{22})$,

$h_i({\mathrm{{\rm Y}}}_i;\theta )=logf({\mathit{y}}_i|{\mathit{\eta }}_i)+logf({\mathit{x}}_i|{\mathit{\xi }}_i)+logf({\mathit{\eta }}_{1,i}|{\mathit{\eta }}_{2,i},{\mathit{\xi }}_i)+logf({\mathit{\eta }}_{2,i}|{\mathit{\xi }}_i)+logf({\mathit{\xi }}_i),$

where

$logf({\mathit{y}}_i|{\mathit{\eta }}_i)=\sum _{j=1}^{p_y}logP\left(Y_{ij}=v_{ij}|{\mathit{\eta }}_i\right),$

$logf({\mathit{x}}_i|{\mathit{\xi }}_i)=\sum _{j=1}^{p_{\mathit{x}}}logP\left({\mathit{X}}_{ij}=u_{ij}|{\mathit{\xi }}_i\right),$

$logf({\mathit{\eta }}_{1,i}|{\mathit{\eta }}_{2,i},{\xi }_i)=-\frac{K_{{\eta }_1}}{2}log\left(2\pi \right)-\frac{1}{2}log\left[det\left({\mathbf{\Psi }}_{11}\right)\right]+log\left[det\left({\mathit{I}}_{K_{{\eta }_1}}-{\mathit{B}}_{11}\right)\right]$

$-\frac{1}{2}{\left(\left({\mathit{I}}_{K_{{\eta }_1}}-{\mathit{B}}_{11}\right)\left[{\mathit{\eta }}_{1,i}-E\left({\mathit{\eta }}_{1,i}|{\mathit{\eta }}_{2,i},{\mathit{\xi }}_i\right)\right]\right)}^T{\mathbf{\Psi }}_{11}^{-1}\left(\left({\mathit{I}}_{K_{{\eta }_1}}-{\mathit{B}}_{11}\right)\left[{\mathit{\eta }}_{1,i}-E\left({\mathit{\eta }}_{1,i}|{\mathit{\eta }}_{2,i},{\mathit{\xi }}_i\right)\right]\right),$

$logf({\mathit{\eta }}_{2,i}|{\mathit{\xi }}_i)=-\frac{K_{{\eta }_2}}{2}log\left(2\pi \right)-\frac{1}{2}log\left[det\left({\mathbf{\Psi }}_{22}\right)\right]+log\left[det\left({\mathit{I}}_{K_{{\eta }_2}}-{\mathit{B}}_{22}\right)\right]$

$-\frac{1}{2}{\left(\left({\mathit{I}}_{K_{{\eta }_2}}-B_{22}\right)\left[{\mathit{\eta }}_{2,i}-E\left({\mathit{\eta }}_{2,i}|{\xi }_i\right)\right]\right)}^T{\mathbf{\Psi }}_{22}^{-1}\left(\left({\mathit{I}}_{K_{{\eta }_2}}-{\mathit{B}}_{22}\right)\left[{\mathit{\eta }}_{2,i}-E\left({\mathit{\eta }}_{2,i}|{\mathit{\xi }}_i\right)\right]\right),$

$logf({\mathit{\xi }}_i)=-\frac{K_{\xi }}{2}log\left(2\pi \right)-\frac{1}{2}log\left|\mathbf{\Phi }\right|-\frac{1}{2}{\mathit{\xi }}_i^T{\mathbf{\Phi }}^{-1}{\mathit{\xi }}_i,$

with

$E\left({\mathit{\eta }}_{1,i}|{\mathit{\eta }}_{2,i},{\mathit{\xi }}_i\right)={\left({\mathit{I}}_{K_{{\eta }_1}}-{\mathit{B}}_{11}\right)}^{-1}\left[{\mathit{B}}_{12}{\mathit{\eta }}_{2,i}+{\mathbf{\Gamma }}_1{\mathit{\xi }}_i+\left({\mathit{I}}_{K_{{\eta }_1}}\otimes {\xi }_i^T\right){\mathbf{\Omega }}_1{\mathit{\xi }}_i+\left({\mathit{I}}_{K_{{\eta }_1}}\otimes {\mathit{\xi }}_i^T\right)\mathrm{\Pi }{\mathit{\eta }}_{2,i}+\left({\mathit{I}}_{K_{{\eta }_1}}\otimes {\mathit{\eta }}_{2,i}^T\right)\mathbf{\Xi }{\mathit{\eta }}_{2,i}\right],$

and

$E\left({\mathit{\eta }}_{2,i}|{\mathit{\xi }}_i\right)={\left({\mathit{I}}_{K_{{\eta }_2}}-{\mathit{B}}_{22}\right)}^{-1}\left[{\mathit{\tau }}_2+{\mathbf{\Gamma }}_2{\mathit{\xi }}_i+\left({\mathit{I}}_{K_{{\eta }_2}}\otimes {\mathit{\xi }}_i^T\right){\mathbf{\Omega }}_2{\mathit{\xi }}_i\right].$

Further, $P\left(Y_{ij}=v_{ij}|{\mathit{\eta }}_i\right)$ and $P\left(X_{ij}=u_{ij}|{\mathit{\xi }}_i\right)$ depend on the link function. For example, with the probit link,

$P\left(Y_{ij}=v_{ij}|{\mathit{\eta }}_i\right)=\left(\begin{array}{cc}\mathrm{\Phi }\left({\alpha }_{y,j}^{(1)}-{\mathit{\beta }}_{y,j}^T{\mathit{\eta }}_i\right),& v_{ij}=1,\\ 1-\mathrm{\Phi }\left({\alpha }_{y,j}^{(V_j-1)}-{\mathit{\beta }}_{y,j}^T{\mathit{\eta }}_i\right),& v_{ij}=V_j,\\ \mathrm{\Phi }\left({\alpha }_{y,j}^{(v_{ij})}-{\mathit{\beta }}_{y,j}^T{\mathit{\eta }}_i\right)-\mathrm{\Phi }\left({\alpha }_{y,j}^{(v_{ij}-1)}-{\mathit{\beta }}_{y,j}^T{\mathit{\eta }}_i\right),& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e},\end{array}\right.$

$P\left(X_{ij}=u_{ij}|{\mathit{\xi }}_i\right)=\left(\begin{array}{cc}\mathrm{\Phi }\left({\alpha }_{x,j}^{(1)}-{\mathit{\beta }}_{x,j}^T{\mathit{\xi }}_i\right),& u_{ij}=1,\\ 1-\mathrm{\Phi }\left({\alpha }_{x,j}^{(U_j-1)}-{\mathit{\beta }}_{x,j}^T{\mathit{\xi }}_i\right),& u_{ij}=U_j,\\ \mathrm{\Phi }\left({\alpha }_{x,j}^{(u_{ij})}-{\mathit{\beta }}_{x,j}^T{\mathit{\xi }}_i\right)-\mathrm{\Phi }\left({\alpha }_{x,j}^{(u_{ij}-1)}-{\mathit{\beta }}_{x,j}^T{\mathit{\xi }}_i\right),& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e},\end{array}\right.$

where $V_j$ is the number of response categories for the ordinal indicator $X_j$, $U_j$ is the number of response categories for the ordinal indicator $X_j$, and $\mathrm{\Phi }\left(\cdot \right)$ is the cumulative distribution function of a standard normal random variable. Then, the observed log-likelihood to be approximated is:

$\mathrm{\ell }(\theta )=\sum _{i=1}^{n}log\int f({\mathit{y}}_i,{\mathit{x}}_i,{\mathrm{{\rm Y}}}_i;\theta )d{\mathrm{{\rm Y}}}_i=\sum _{i=1}^{n}log\int exp\left\{h_i({\mathrm{{\rm Y}}}_i;\theta )\right\}d{\mathrm{{\rm Y}}}_i.$

If ${\mathit{\eta }}_1$ is a scalar that has only one binary indicator, we restrict ${\mathrm{\Psi }}_{11}=0$ and ${\mathit{\beta }}_{y,11}=1$. The modified complete log-likelihood is then:

$h_i({\mathrm{{\rm Y}}}_i;\theta )=logf({\mathit{y}}_i|{\mathit{\eta }}_i)+logf({\mathit{x}}_i|{\mathit{\xi }}_i)+logf({\mathit{\eta }}_{2,i}|{\mathit{\xi }}_i)+logf({\mathit{\xi }}_i),$

where

${\mathit{\eta }}_{1,i}={\left({\mathit{I}}_{K_{{\eta }_1}}-{\mathit{B}}_{11}\right)}^{-1}\left[{\mathit{B}}_{12}{\mathit{\eta }}_{2,i}+{\mathbf{\Gamma }}_1{\mathit{\xi }}_{\mathbf{i}}+\left({\mathit{I}}_{K_{{\eta }_1}}\otimes {\mathit{\xi }}_i^T\right){\mathbf{\Omega }}_1{\mathit{\xi }}_i+\left({\mathit{I}}_{K_{{\eta }_1}}\otimes {\mathit{\xi }}_i^T\right)\mathrm{\Pi }{\mathit{\eta }}_{2,i}+\left({\mathit{I}}_{K_{{\eta }_1}}\otimes {\mathit{\eta }}_{2,i}^T\right)\mathbf{\Xi }{\mathit{\eta }}_{2,i}\right].$

Accordingly, the vector of latent variables to be integrated out is ${\mathrm{{\rm Y}}}_i=({\mathit{\eta }}_{2,i}^T,{\mathit{\xi }}_i^T{)}^T$.

Laplace Approximation

In general, the first-order Laplace approximation (Barndorff-Nielsen & Cox, 1989) to the integral $\int exp\left\{g\left(\mathit{t}\right)\right\}d\mathit{t}$ is:

$(2\pi {)}^{K/2}{\left[det\left(-\frac{{\mathrm{\partial }}^{2}g\left(\hat{\mathit{t}}\right)}{\mathrm{\partial }\mathit{t}\mathrm{\partial }{\mathit{t}}^T}\right)\right]}^{-1/2}exp\left\{g\left(\hat{\mathit{t}}\right)\right\},$

where $\mathit{t}$ is a $K\times 1$ vector and $g\left(\mathit{t}\right)$ is a unimodal function with the mode $\hat{\mathit{t}}$. The approximation is essentially achieved by Taylor expanding $g\left(\mathit{t}\right)$ about its mode. Shun and McCullagh (1995) further derived the second-order Laplace approximation. The Laplace approximation of the observed log-likelihood is:

(7) ${\mathrm{\ell }}_{(Lap)}(\mathrm{{\rm Y}};\theta )=\sum _{i=1}^n\left[\frac{K}{2}log\left(2\pi \right)+h_i\left({\mathrm{{\rm Y}}}_i;\theta \right)-\frac{1}{2}logdet\left(-{\mathit{H}}_i\left({\mathrm{{\rm Y}}}_i;\theta \right)\right)+log\left(1+R_2\left({\mathrm{{\rm Y}}}_i;\theta \right)\right)\right],$(7)

where $K=K_{\xi }+K_{\eta }$ or $K=K_{\xi }+K_{{\eta }_2}$,

${\mathit{H}}_i\left({\mathrm{{\rm Y}}}_i;\theta \right)=\frac{{\mathrm{\partial }}^2{h}_i\left({\mathrm{{\rm Y}}}_i;\theta \right)}{\mathrm{\partial }{\mathrm{{\rm Y}}}_i\mathrm{\partial }{\mathrm{{\rm Y}}}_i^T},$

is the Hessian matrix, and ${\mathrm{{\rm Y}}}_i$ is evaluated at ${\widehat{\mathrm{{\rm Y}}}}_i$, the solution of

$\frac{\mathrm{\partial }{h}_i\left({\mathrm{{\rm Y}}}_i;\theta \right)}{\mathrm{\partial }{\mathrm{{\rm Y}}}_i}=\mathbf{0},$

with respect to ${\mathrm{{\rm Y}}}_i$ for a fixed $\theta$. In the first-order approximation, $R_2\left({\mathrm{{\rm Y}}}_i;\theta \right)=0$, for any $i$. In the second-order approximation,

$R_2\left({\mathrm{{\rm Y}}}_i;\theta \right)=-\frac{1}{2}\left[\frac{1}{4}\sum _{j,l,m,r=1}^K\left(-\frac{{\mathrm{\partial }}^4{h}_i\left({\mathrm{{\rm Y}}}_i;\theta \right)}{\mathrm{\partial }{\mathrm{{\rm Y}}}_j\mathrm{\partial }{\mathrm{{\rm Y}}}_l\mathrm{\partial }{\mathrm{{\rm Y}}}_m\mathrm{\partial }{\mathrm{{\rm Y}}}_r}{c}_{jm}{c}_{lr}\right)\right.$

$\left.-\sum _{j,l,m,r,s,t=1}^K\frac{{\mathrm{\partial }}^3{h}_i\left({\mathrm{{\rm Y}}}_i;\theta \right)}{\mathrm{\partial }{\mathrm{{\rm Y}}}_j\mathrm{\partial }{\mathrm{{\rm Y}}}_l\mathrm{\partial }{\mathrm{{\rm Y}}}_m}\frac{{\mathrm{\partial }}^3{h}_i\left({\mathrm{{\rm Y}}}_i;\theta \right)}{\mathrm{\partial }{\mathrm{{\rm Y}}}_r\mathrm{\partial }{\mathrm{{\rm Y}}}_s\mathrm{\partial }{\mathrm{{\rm Y}}}_t}\left(\frac{1}{4}{c}_{jl}{c}_{mr}{c}_{st}+\frac{1}{6}{c}_{jr}{c}_{ls}{c}_{mt}\right)\right],$

where $c_{j,m}$ is the $(j,m{)}^{th}$ element of the inverse of $-{\mathit{H}}_i\left({\mathrm{{\rm Y}}}_i;\theta \right)$ and the approximation is second-order accurate (Shun & McCullagh, 1995). The second-order Laplace approximation has been recommended by Lee and Nelder (2001) for generalized linear-mixed models and by Jin, Noh, and Lee (2018) for confirmatory factor analysis models with ordinal data.

Adaptive Gauss–Hermite Quadrature Approximation

The Gauss–Hermite-Hermite quadrature rule approximates the integral $\int exp\left\{g\left(\mathit{t}\right)\right\}d\mathit{t}$ by a weighted sum of function values evaluated at pre-specified quadrature points as:

$\sum _{k_1=1}^q\dots \sum _{k_k=1}^q{\omega }_{k_1{k}_2\dots k_k}^{\ast }exp\left\{g\left(z_{k_1},\dots ,z_{k_k}\right)\right\},$

where

$w_{k_1{k}_2\dots k_K}^{\ast }=\prod _{j=1}^K{w}_{k_j}exp\left\{z_{k_j}^2\right\},$

with $z_{k_j}$ being the Gauss–Hermite quadrature points, $w_{k_j}$ being the corresponding weights, and $q$ being the number of quadrature points per latent variable. Liu and Pierce (1994) proposed to translate and dilate the quadrature points in the weighted sum, known as the AGHQ approximation, to improve the approximation effectiveness when $g\left(\mathit{t}\right)$ is an unimodel function. The AGHQ approximated observed log-likelihood is:

(8) $\text{!!!!!!!!!!{ell \_{(AGHQ)}}(hat Upsilon ;theta) = sumlimits\_{i = 1}^n left({{K over 2}log left(2 right) - {1 over 2}log det left({ - {H\_i}left({{{hat Upsilon }\_i};theta } right)} right)} right.left. { + log sumlimits\_{{k\_1} = 1}^q cdots sumlimits\_{{k\_K} = 1}^q left{ {w\_{{k\_1}{k\_2}...{k\_K}}^*exp left[{{h\_i}left({{{widetilde Upsilon }\_i}left({{{bf{z}}\_{{k\_1}{k\_2} cdots {k\_K}}}} right);theta } right)} right]} right}} rightbig),}$(8)

where

${\widetilde{\mathrm{{\rm Y}}}}_i\left({\mathit{z}}_{k_1{k}_2\cdots k_K}\right)=\sqrt{2}{\mathit{L}}_i{\mathit{z}}_{k_1{k}_2\cdots k_K}+{\widehat{\mathrm{{\rm Y}}}}_i$

is the latent variable vector dilated and translated around the mode ${\widehat{\mathrm{{\rm Y}}}}_i$ with ${\mathit{L}}_i$ being the Cholesky decomposition of the inverse of the negative Hessian:

${\mathit{L}}_i{\mathit{L}}_i^T={\left(-{\mathit{H}}_i\left({\mathrm{{\rm Y}}}_i;\theta \right)\right)}^{-1},$

and ${\mathit{z}}_{k_1{k}_2\cdots k_K}$ being the vector containing the $k_1^{th}$, $k_2^{th}$,…, and the $k_K^{th}$ quadrature points. If only one quadrature point per latent variable is used, ${\mathrm{\ell }}_{(AGHQ)}({\widehat{\mathrm{{\rm Y}}}}_i;\theta )$ is the same as the first-order approximated ${\mathrm{\ell }}_{(Lap)}({\widehat{\mathrm{{\rm Y}}}}_i;\theta )$. Let ${\hat{\theta }}_{(AGHQ)}$ be the estimator of $\theta$ that maximizes (8). Following Bianconcini (2014), Jin and Andersson (2019b) showed that the error rate of the approximation is

$O\left({\left(p_x+p_y\right)}^{-⌊(q+2)/3⌋}\right),$

and that ${\hat{\theta }}_{(AGHQ)}$ satisfies

${\hat{\theta }}_{(AGHQ)}-{\theta }_0=O_p\left[max\left(n^{-1/2},{\left(p_x+p_y\right)}^{-⌊(q+2)/3⌋}\right)\right],$

where ${\theta }_0$ is the true parameter vector and $⌊\cdot ⌋$ takes the largest integer that is less than the enclosed value. Hence, using $5$ quadrature points per latent variable yields the same error rate as the second-order Laplace approximation.

Direct Maximum Likelihood

When maximizing functions such as (7) or (8) it is important to realize that the mode ${\widehat{\mathrm{{\rm Y}}}}_i$ depends on the parameter vector $\theta$. The gradient of the approximated observed log-likelihood (regardless of approximation method) is:

(9) $\frac{\mathrm{\partial }\mathrm{\ell }\left(\widehat{\mathrm{{\rm Y}}}\left(\theta \right);\theta \right)}{\mathrm{\partial }\theta }=\frac{\mathrm{\partial }\mathrm{\ell }\left(\theta \right)}{\mathrm{\partial }\theta }{|}_{\mathrm{{\rm Y}}=\widehat{\mathrm{{\rm Y}}}}+{\left(\frac{\mathrm{\partial }\widehat{\mathrm{{\rm Y}}}\left(\theta \right)}{\mathrm{\partial }{\theta }^T}\right)}^T\frac{\mathrm{\partial }\mathrm{\ell }\left(\mathrm{{\rm Y}}\right)}{\mathrm{\partial }\mathrm{{\rm Y}}}{|}_{\mathrm{{\rm Y}}=\widehat{\mathrm{{\rm Y}}}},$(9)

where $\mathrm{\partial }\mathrm{\ell }\left(\theta \right)/\mathrm{\partial }\theta$ is the derivative of the observed log-likelihood function with respect to $\theta$, treating the mode as constant. On the contrary, $\mathrm{\partial }\mathrm{\ell }\left(\mathrm{{\rm Y}}\right)/\mathrm{\partial }\mathrm{{\rm Y}}$ is the derivative of the observed log-likelihood function with respect to $\mathrm{{\rm Y}}$, treating $\theta$ as constant. Hence, the second term acknowledges that the mode is affected by $\theta$, by applying the chain rule. By the implicit function theorem,

$\frac{\mathrm{\partial }{\widehat{\mathrm{{\rm Y}}}}_i\left(\theta \right)}{\mathrm{\partial }{\theta }^T}=-{\left(\frac{{\mathrm{\partial }}^2{h}_i({\mathrm{{\rm Y}}}_i;\theta )}{\mathrm{\partial }{\mathrm{{\rm Y}}}_i\mathrm{\partial }{\mathrm{{\rm Y}}}_i^T}{|}_{{\mathrm{{\rm Y}}}_i={\widehat{\mathrm{{\rm Y}}}}_i}\right)}^{-1}\frac{{\mathrm{\partial }}^2{h}_i({\mathrm{{\rm Y}}}_i;\theta )}{\mathrm{\partial }{\mathrm{{\rm Y}}}_i\mathrm{\partial }{\theta }^T}{|}_{{\mathrm{{\rm Y}}}_i={\widehat{\mathrm{{\rm Y}}}}_i}.$

The sandwich estimator of standard errors can be calculated from:

(10) ${\left(\stackrel{ˆ}{\frac{{\mathrm{\partial }}^2\mathrm{\ell }\left(\theta \right)}{\mathrm{\partial }\theta \mathrm{\partial }{\theta }^T}}\right)}^{-1}\sum _{i=1}^n\left[\frac{\mathrm{\partial }{\mathrm{\ell }}_i\left(\hat{\theta }\right)}{\mathrm{\partial }\theta }\frac{\mathrm{\partial }{\mathrm{\ell }}_i\left(\hat{\theta }\right)}{\mathrm{\partial }{\theta }^T}\right]{\left(\stackrel{ˆ}{\frac{{\mathrm{\partial }}^2\mathrm{\ell }\left(\theta \right)}{\mathrm{\partial }\theta \mathrm{\partial }{\theta }^T}}\right)}^{-1},$(10)

where ${\mathrm{\ell }}_i$ is the $i^{th}$ term in Equation (7)(7) ${\mathrm{\ell }}_{(Lap)}(\mathrm{{\rm Y}};\theta )=\sum _{i=1}^n\left[\frac{K}{2}log\left(2\pi \right)+h_i\left({\mathrm{{\rm Y}}}_i;\theta \right)-\frac{1}{2}logdet\left(-{\mathit{H}}_i\left({\mathrm{{\rm Y}}}_i;\theta \right)\right)+log\left(1+R_2\left({\mathrm{{\rm Y}}}_i;\theta \right)\right)\right],$(7) or (8). In the BFGS algorithm, the inverse of the Hessian matrix of $\mathrm{\ell }\left(\widehat{\mathrm{{\rm Y}}}\left(\theta \right);\theta \right)$ is approximated and updated by low-rank approximations at every iteration. The Hessian matrix can also be approximated from the Louis (1982) method. Since the exact gradient of $\mathrm{\ell }\left(\widehat{\mathrm{{\rm Y}}}\left(\theta \right);\theta \right)$ is calculated by Equation (9)(9) $\frac{\mathrm{\partial }\mathrm{\ell }\left(\widehat{\mathrm{{\rm Y}}}\left(\theta \right);\theta \right)}{\mathrm{\partial }\theta }=\frac{\mathrm{\partial }\mathrm{\ell }\left(\theta \right)}{\mathrm{\partial }\theta }{|}_{\mathrm{{\rm Y}}=\widehat{\mathrm{{\rm Y}}}}+{\left(\frac{\mathrm{\partial }\widehat{\mathrm{{\rm Y}}}\left(\theta \right)}{\mathrm{\partial }{\theta }^T}\right)}^T\frac{\mathrm{\partial }\mathrm{\ell }\left(\mathrm{{\rm Y}}\right)}{\mathrm{\partial }\mathrm{{\rm Y}}}{|}_{\mathrm{{\rm Y}}=\widehat{\mathrm{{\rm Y}}}},$(9) , the sandwich estimator (10) of standard errors can be readily computed. In contrast, neither the gradient nor the Hessian matrix is the by-product in the EM algorithm and need to be computed afterward.