Teacher’s Corner: Evaluating Informative Hypotheses Using the Bayes Factor in Structural Equation Models

ABSTRACT

This Teacher’s Corner paper introduces Bayesian evaluation of informative hypotheses for structural equation models, using the free open-source R packages bain, for Bayesian informative hypothesis testing, and lavaan, a widely used SEM package. The introduction provides a brief non-technical explanation of informative hypotheses, the statistical underpinnings of Bayesian hypothesis evaluation, and the bain algorithm. Three tutorial examples demonstrate informative hypothesis evaluation in the context of common types of structural equation models: 1) confirmatory factor analysis, 2) latent variable regression, and 3) multiple group analysis. We discuss hypothesis formulation, the interpretation of Bayes factors and posterior model probabilities, and sensitivity analysis.

KEYWORDS:

• Bain
• bayes factor
• informative hypotheses
• structural equation modeling

Hypotheses play a central role in deductive, theory-driven research. A hypothesis allows a researcher to draw inferences about a population, based on data sampled from that population. In the context of structural equation modeling, there are two commonly used approaches to hypothesis evaluation. Firstly, researchers can construct a set of competing models, where each model represents several theoretically derived substantive hypotheses. Researchers can then use information criteria to select the best model in the set. Commonly used information criteria include Akaike’s information criterion (AIC, Akaike, 1974), the Bayesian information criterion (BIC, Schwarz, 1978), and the deviance information criterion (DIC, Spiegelhalter et al., 2002). Secondly, hypotheses about specific parameters within a model can be tested by comparing a null hypothesis against an alternative hypothesis using the likelihood ratio test (Wilks, 1938) or the Wald test (Buse, 1982).

A third approach is informative hypothesis evaluation (Hoijtink, 2011). Informative hypotheses are theoretically derived statements about directional differences and equality constraints between model parameters of interest. Informative hypotheses address an important limitation of classical null-hypothesis significance testing: The null-hypothesis that a parameter is equal to zero is often a straw man hypothesis. It holds little credibility and exists purely for the purpose of being rejected. The researcher’s actual theory, on the other hand, is subsumed under a very broad alternative hypothesis and is not directly tested. The paradox inherent in this approach is that rejecting the straw man null-hypothesis cannot be interpreted as evidence in support of the researcher’s theory, but merely as evidence against the null. Informative hypotheses overcome this counter-intuitive limitation, by explicitly testing a researcher’s theoretical beliefs.

Evaluating informative hypotheses is particularly straightforward from a Bayesian perspective. Bayesian inference is already widely applied in the context of multivariate normal linear models (see, for example: Van Well, Kolk, & Klugkist, 2008; Braeken et al., 2015; De Jong et al., 2017; Zondervan–Zwijnenburg et al., 2019). Methods for Bayesian hypothesis evaluation within the structural equation modeling framework are also available (Gu Hoijtink, Mulder, & Rosseel, 2019; Van De Schoot et al., 2012). However, they are less frequently applied (but see Van Lissa et al., 2016). This might be, in part, because user-friendly software was not available. In this Teacher’s Corner paper, we show how Bayesian tests of informative hypotheses about parameters in structural equation models can easily be conducted in R, using the bain package (Gu, Hoijtink, Mulder, & van Lissa, 2019, Gu et al. 2018; Hoijtink et al., 2019; Mulder, 2014) (https://informative-hypotheses.sites.uu.nl/software/bain/). From version 0.2.3 on, the package can evaluate informative hypotheses about structural equation models estimated with the free, open-source SEM-package lavaan (Loehlin & Beaujean, 2016; Rosseel, 2012) (www.lavaan.org). For tutorial and technical details, see Gu, Hoijtink, Mulder, & van Lissa (2019).

Formulating informative hypotheses

Informative hypotheses are formulated in terms of equality (=) and inequality (<, >) constraints between target parameters. For example, one might hypothesize that one regression coefficient is greater than the another, $H_1:{\beta }_1>{\beta }_2$, or that both are equal to a specific value, $H_2:({\beta }_1,{\beta }_2)=0.6$, or that one is greater than the other, which in turn is equal to zero, $H_3:{\beta }_1>{\beta }_2=0$. The bain package uses a simple syntax to specify such hypotheses, which is explained in detail in the package vignette. Here, we provide a brief overview of the syntactical elements that are relevant in the context of structural equation models:

• s1, …, s6: Refers to the target parameters s1 up to s6. Substitute these with the names of parameters in your model.

• s1 = c: An equality constraint, indicating that parameter s1 is equal to constant c

• s1 > c: An inequality constraint, indicating that parameter s1 is larger than constant c

• s1 = s2 = s3: Three parameters have equal values.

• (s1, s2, s3) > 0: Three parameters, grouped by parentheses, are greater than zero.

• c1 * s1 + c2 < c3 * s2 + c4: A linear transformation of s1 (where a constant is added to, or multiplied with, s1) is smaller than with a linear transformation of s2.

• … & … : Within one hypothesis, the ampersand connects two constraints.

• … ; … : The; separates two distinct informative hypotheses.

When writing informative hypotheses about parameters of a lavaan model, parameters can be referenced by name. These names should be (unique abbreviations of) the parameter names used by lavaan. For example, lavaan labels the factor loading of the indicator Ab on the latent variable A as A = A ~ b. This label, “A = ~Ab”, can be referenced verbatim in bain syntax, as in “A = ~Ab > .6.”

Note that comparing parameters (usually) makes sense only if they are on the same scale. For example, imagine that income is predicted by IQ and SES, where IQ is measured using a normed test ($M=100$, $SD=15$), and SES is rated on a 10-point ordinal scale which we treat as continuous. The regression coefficients for these predictors are ${\beta }_{IQ}$ and ${\beta }_{SES}$, respectively. Since IQ and SES are measured on different scales, the hypothesis that ${\beta }_{IQ}<{\beta }_{SES}$ is meaningless. The unstandardized coefficients reflect both the strength of the relation of the predictors with income and the scale with which the predictors were measured. The hypothesis does make sense with regard to the standardized model estimates, however. As a counterexample, if family income is predicted by maternal and paternal working hours, then the regression coefficients are on the same scale (dollars per hour of work) and can be directly compared. These examples illustrate that, except when comparing predictors measured on the same scale, or in other exceptional situations, it is usually safer to apply bain only to standardized model parameters.

Bayesian hypothesis evaluation

One of the key features of the Bayesian approach is that p-values, common to null-hypothesis significance testing, are dispensed with. Instead, hypotheses are evaluated using the Bayes factor (Kass & Raftery, 1995). The Bayes factor quantifies the relative support provided by the data for two competing hypotheses. For example, let $H_i$ be an informative hypothesis that describes some (in)equality constraints among model parameters. Let $H_u$ be an unconstrained hypothesis that places no constraints on these model parameters. The Bayes factor $\mathrm{B}{\mathrm{F}}_{iu}$, quantifies the support in favor of $H_i$ relative to $H_u$. If this Bayes factor $\mathrm{B}{\mathrm{F}}_{iu}$ is larger than 1, the data provide more support for $H_i$ than for $H_u$. If it is smaller than 1, the data provide more support for $H_u$ than for $H_i$. A Bayes factor near 1 is indecisive; both hypotheses are equally supported. The Bayes factor can be inverted to express support in favor of $H_u$, relative to $H_i$. To this end, one can compute $\mathrm{B}{\mathrm{F}}_{iu}$ as $1/\mathrm{B}{\mathrm{F}}_{ui}$. Thus, if $\mathrm{B}{\mathrm{F}}_{iu}=8.11$, then we can conclude that the data provide 8.11 times more support for $H_i$ than for $H_u$. Conversely, $\mathrm{B}{\mathrm{F}}_{ui}$ (note that the order of the indices has changed) would be $1/8.11=.12$.

Since the Bayes factor is a relative measure of support, it should not be compared to a threshold value. If, for example, $\mathrm{B}{\mathrm{F}}_{iu}=102.75$ it is clear that the data provide overwhelming support for $H_i$ over $H_u$. With smaller values, such as $\mathrm{B}{\mathrm{F}}_{iu}=7.34$, a preference for $H_i$ can still be defended, but other researchers might debate this preference, and with even smaller values, such as $\mathrm{B}{\mathrm{F}}_{iu}=3$, there is a preference for $H_i$, but $H_u$ is definitely not disqualified. Thus, the Bayes factor can, and should, be interpreted on a continuous scale. This also sets it apart from the dichotomous decision making imposed by the p-value. It is up to the scientific community to decide when enough evidence is obtained to completely rule out a hypothesis. For a more elaborate discussion of Bayesian hypothesis evaluation using bain, not specific to structural equation modeling, see the tutorial by (Hoijtink, Mulder et al., 2019).

Statistical underpinnings

The Bayes factor $\mathrm{B}{\mathrm{F}}_{iu}$ can be written as a ratio of two marginal likelihoods of the hypotheses given the data ($m$), or alternatively, as the ratio of fit ($f_i$) and complexity ($c_i$, Gu et al., 2018):

$B{F}_{iu}=\frac{m(H_i|data)}{m(H_u|data)}=\frac{f_i}{c_i}.$

The notion of fit reflects the extent to which the data is in agreement with the restrictions specified in the hypothesis, and its complexity reflects how specific the hypothesis is (Gu et al., 2018). This ratio of fit and complexity is a concept that is also reflected in information criteria such as the AIC (Akaike, 1974) and the DIC (Spiegelhalter et al., 2002).

The bain algorithm estimates fit and complexity based on normal approximations of the prior and posterior distributions for the target parameters of the hypothesis. These distributions have a known mean and covariance matrix (Gu et al., 2018; Hoijtink et al., 2019). The posterior is defined by the observed parameter estimate and their asymptotic covariance matrix. For hypotheses with only inequality constraints, the fit ($f_i$) is then given by the proportion of this posterior distribution that is in agreement with the hypothesis (Gu et al., 2018; Hoijtink et al., 2019). For hypotheses with equality constraints, the fit is defined in terms of the posterior density at the constraints.

The prior distribution is constructed to provide an adequate quantification of complexity (see Gu et al., 2018; Hoijtink et al., 2019). This is achieved by setting the prior mean along the boundary of the hypotheses under consideration. The prior covariance matrix is a scaling transformation of the posterior covariance matrix. Scaling increases the variances, leading to a flatter distribution. By default, bain scales the covariance matrix to be as flat as it would have been if it were based on the smallest possible sample required to estimate the target parameters. This is based on the concept of a minimal training sample (Berger & Pericchi, 2004; Mulder, 2014; O’Hagan, 1995). Thus, the prior covariance matrix is much flatter, and therefore less informative, than the posterior. The complexity ($c_i$) is given by the proportion (for inequality constrained hypotheses) or density (for equality constrained hypotheses) for the region of the prior distribution that is in agreement with the hypothesis.

Evaluating a single informative hypothesis

One way to evaluate a single informative hypothesis is to compare it with an unconstrained hypothesis, as in the preceding paragraphs. Let $H_i$ signify any informative hypothesis that describes some (in)equality constraints among model parameters, such as $H_i:{\beta }_1>{\beta }_2$, or $H_i:{\beta }_1>{\beta }_2=0.6$. The unconstrained hypothesis $H_u$ places no constraints on these model parameters: $H_u:{\beta }_1,{\beta }_2$. The Bayes factor $\mathrm{B}{\mathrm{F}}_{iu}$ then quantifies the relative support provided by the data in favor of the informative hypothesis, relative to the unconstrained hypothesis – or in other words, how likely is it that the specified parameter constraints are true, relative to any other ordering of parameters. Throughout this paper, we use the notation $\mathrm{B}{\mathrm{F}}_{.u}$ to refer to Bayes factors of this type in the general sense, where ${ }_{.}$ signifies any informative hypothesis.

A second way to evaluate support in favor of an informative hypothesis is to compare it to its complement. The complement is an alternative hypothesis that covers every ordering of parameter values that is not in line with the original hypothesis. If the informative hypothesis $H_i$ expresses the researcher’s theory, and $!$ represents logical negation (not), then the complement $H_c:!H_i$ means not the researcher’s theory. Comparing against the complement allows researchers to investigate whether their expectation is, or is not, supported by the data. Bayes factor of the type $\mathrm{B}{\mathrm{F}}_{.c}$ indicate whether the data provide more support in favor of, or against, an informative hypothesis. In principle, the complement is defined by reference to a specific informative hypothesis, such that the complement of $H_1$ is $!H_1$, and the complement of $H_2$ is $!H_2$. For hypotheses with at least one equality constraint, however, the unconstrained hypothesis and the complement are the same. Since version 0.2.4, bain reports both $\mathrm{B}{\mathrm{F}}_{.u}$ and $\mathrm{B}{\mathrm{F}}_{.c}$ by default.

It is worth pointing out that alternative, non-Bayesian methods exist that compare informative hypotheses against the null-hypothesis (Vanbrabant et al., 2017; Van De Schoot et al., 2010). When using bain, it is also possible to evaluate the null-hypothesis by specifying it as an informative hypothesis (i.e., a hypothesis that constrains all parameters to be equal to zero, or to be equal to one another), and comparing it with other informative hypotheses using the approach elaborated in the next paragraph.

Comparing two informative hypotheses

A second question researchers might want to address, is which of two informative hypotheses, $H_1$ and $H_2$, is most supported by the data. The Bayes factor $\mathrm{B}{\mathrm{F}}_{12}$ reflects the amount of support provided by the data in favor of $H_1$, relative to $H_2$. It is computed by taking a ratio of two other Bayes factors:

$B{F}_{12}=\frac{B{F}_{1u}}{B{F}_{2u}}$

This approach is valid because Bayes factors for any two informative hypotheses can be compared if both have the same denominator. In the previous section, we explained that it is not possible to compare Bayes factors of the type $\mathrm{B}{\mathrm{F}}_{.c}$, because the complement of $H_1$ is not the same as that of $H_2$. However, Bayes factors of the type $\mathrm{B}{\mathrm{F}}_{.u}$ are comparable, because the unconstrained hypothesis is identical for all informative hypotheses. Thus, $\mathrm{B}{\mathrm{F}}_{12}$ can be computed to contrast a pair of user-specified informative hypotheses.

By default, bain will compute Bayes factors to contrast all informative hypotheses. Thus, given three hypotheses, $H_1:\beta 1=\beta 2=\beta 3=0$, $H_2:\beta 1>0\mathrm{\&}\beta 2>0\mathrm{\&}\beta 3>0$, and $H_3:\beta 1>\beta 2>\beta 3>0$,bain will compute $\mathrm{B}{\mathrm{F}}_{12}$, $\mathrm{B}{\mathrm{F}}_{13}$, and $\mathrm{B}{\mathrm{F}}_{23}$. These Bayes factors are stored in the $BFmatrix element of the output.

Comparing more than two hypotheses

Any two informative hypotheses can be straightforwardly compared using the method outlined above. When there are more than two candidate hypotheses, however, comparing all of their mutual Bayes factors quickly becomes cumbersome. In this case, it is easier to compare the so-called posterior model probabilities for each hypothesis $H_i$, that is, $P(H_i|data)$. Each posterior model probability has a value between 0 and 1, and the posterior model probabilities for a set of hypotheses sum to 1.0. Under the assumption that a priori (before observing the data), each hypothesis is equally likely, the posterior model probabilities contain the same information as the Bayes factors upon which they are based. If, for example, $\mathrm{B}{\mathrm{F}}_{12}=3.5$, $\mathrm{B}{\mathrm{F}}_{13}=7.0$ and $\mathrm{B}{\mathrm{F}}_{23}=2.0$, the corresponding posterior model probabilities are $P(H_1|data)=.7$, $P(H_2|data)=.2$, and $P(H_3|data)=.1$, respectively. Note that, $\mathrm{B}{\mathrm{F}}_{12}=\frac{P(H_1|data)}{P(H_2|data)}=\frac{.7}{.2}=3.5$. Posterior model probabilities can also be interpreted as Bayesian error probabilities. If the set of hypotheses under consideration contains $H_1$, $H_2$, and $H_3$, and the corresponding posterior model probabilities are .7, .2, and .1, respectively, then the Bayesian error probability associated with a preference for $H_1$ is equal to .2 + .1 = .3.

A fail-safe hypothesis

It is important to emphasize that the posterior model probabilities only indicate which of the hypotheses in the set receives the most support from the data. Consequently, if all of the hypotheses in the set misrepresent the true relationship among parameters in the population, then researchers risk selecting the best of a set of bad hypotheses. Two approaches can be used to mitigate this risk. The first approach uses the unconstrained hypothesis $H_u$ as a fail-safe hypothesis. Recall that $H_u$ places no constraints on the parameters. If the best hypothesis in the set receives more support than the unconstrained hypothesis, we are reassured that it is not just the best of a set of bad hypotheses. This approach is currently implemented in bain. The second approach would be to include a hypothesis that is the complement of the union of all informative hypotheses in the set. A nice feature of this second approach is that, whereas $H_u$ overlaps with each of the hypotheses under consideration, the complement of the union does not. However, as to yet, this option is not implemented in bain.

Structural equation modeling using lavaan

In this paper, we present a subset of the (multiple group) structural equation models that can be specified using the lavaan function sem, and for which informative hypotheses can be formulated and processed with bain. The interested reader is advised to visit http://lavaan.org/, where mini-tutorials and examples are used to explain all the functions and options available in the lavaan package. For a general introduction to structural equation modeling, the interested reader is referred to Loehlin and Beaujean (2016). As will be elaborated upon in the discussion, it is relatively easy to use bain for the evaluation of hypotheses for all models that can be specified in lavaan.

When used in conjunction with lavaan, bain extracts the (standardized or unstandardized) target parameter estimates (per group), the covariance matrix of the estimates (per group) and the sample size (per group) from the lavaan output object. Target parameters are defined as model parameters about which informative hypotheses are formulated. By contrast, nuisance parameters are parameters not involved in the hypotheses of interest. Bain is validated for use with target parameters that are either 1) regression coefficients, 2) intercepts, or 3) factor loadings. Thus, by default, all (residual) (co)variances are treated as nuisance parameters, along with any remaining parameters not involved in the hypotheses.

A final note regarding assumptions: As explained earlier, bain constructs a default prior distribution for the target parameters (per group), and derives a normal approximation of the posterior. Asymptotically, the posterior distribution is indeed normal (see, for example, Gelman et al., 2013, Chapter 4). However, bain should only be used if approximate normality can be assumed, given the sample size. Rosseel (2020) provides references that validate the use of structural equation modeling when the sample size is at least 200. This approximate prior and posterior form the basis for the computation of Bayes factors for the informative hypotheses. A more detailed accessible introduction is presented in Gu, Hoijtink, Mulder, & van Lissa (2019), and the statistical underpinnings of the method are substantiated in Gu et al. (2018) and Hoijtink et al. (2019).

Tutorial examples

We present tutorial examples for three commonly used types of structural equation models: 1) confirmatory factor analysis, 2) latent variable regression, and 3) multiple group analysis. Each example follows a three-step workflow. In the first step, lavaan is used to estimate the parameters of a structural equation model. In the second step, one or more informative hypotheses are formulated. In the third step, the results of the lavaan analysis and the hypotheses are fed into bain, which renders a Bayesian evaluation of the hypotheses, returning Bayes factors and posterior model probabilities.

All examples use the synthetic data set sesamesim, which is included with the bain package. These data are generated to have similar distributional characteristics and covariances to the Sesame Street data provided by Stevens (2012). These data concern the effect of watching the tv-series Sesame Street for 1 year on the knowledge of numbers of 240 children aged between 34 and 69 months. We will use the following variables: Age in months (age), the Peabody test, which measures the mental age of children (peabody; score range 15 to 89), and sex, with boys coded as 1, and girls as 2. Several variables were measured both before- and after watching Sesame Street for 1 year: Knowledge of numbers (Bn: before, and An: after); knowledge of body parts (Bb and Ab, respectively), letters (Bl and Al), forms (Bf and Af), relationships (Br and Ar), and classifications (Bc and Ac). Models are fit using lavaan, and Figures are plotted using tidySEM (Van Lissa, 2020).

Example 1: Confirmatory factor analysis

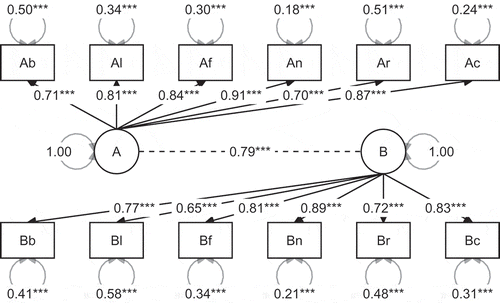
A two-factor confirmatory factor analysis is specified using the syntax below, in which the A(fter) measurements of all subtests load on factor A, and the B(efore) measurements load on the factor B (see Figure 1).

Figure 1. Confirmatory factor analysis

model1 <- ‘A = ~ Ab + Al + Af + An + Ar + Ac B = ~ Bb + Bl + Bf + Bn + Br + Bc’fit1 <- sem (model1, data = sesamesim, std.lv = TRUE)

The argument std.lv = TRUE implies that the model is identified by standardizing the latent variables B and A. This allows the formulation of informative hypotheses with respect to each of the factor loadings, including the first.

Specifying informative hypotheses

One plausible hypothesis for this confirmatory factor analysis might be that indicators are strongly related to the factors to which they are assigned. This is reflected by the following hypothesis, which states that all (standardized) factor loadings are larger than .6:

hypotheses1 <- “(A= ~Ab, A= ~Al, A= ~Af, A= ~An, A= ~Ar, A= ~Ac) >.6 & (B= ~Bb, B= ~Bl, B= ~Bf, B= ~Bn, B= ~Br, B= ~Bc) >.6”

This example consists of one hypothesis about two groups of parameters, enclosed by parentheses, which are chained by the ampersand symbol. Note that, although we could group all loadings between brackets, before and after are separated for clarity. In this example, the target parameters are factor loadings, the sample size is $N=240$, and therefore, we assume that the posterior distribution of the target parameters is approximately normal.

Evaluating hypotheses

Now, we will evaluate the informative hypotheses for this example using bain(). As input to the function, we use the lavaan output object fit1 and the hypotheses hypotheses1 that were specified above. The argument standardize = TRUE ensures that the hypotheses are evaluated in terms of standardized model parameters.

Before calling bain(), we set a seed for the random number generator using set.seed(). This is necessary to ensure computational replicability, because bain draws random samples from the prior and posterior distributions of the target parameters. If another seed is used, a different random sample will be drawn, which could lead to differences in the resulting Bayes factors and posterior model probabilities. These differences should be negligible, and it is good practice to conduct a sensitivity analysis for Monte Carlo error (the variability due to different random seeds) by changing the seed to ensure that the results are replicated.

set.seed (100) results1 <- bain (fit1, hypotheses1, standardize = TRUE) results1

The resulting bain() output is presented in Table 1. The Bayes factor $\mathrm{B}{\mathrm{F}}_{1c}$, which compares $H_1$ to its complement, is found on the row for $H_1$, in column BF.c. As can be seen, $\mathrm{B}{\mathrm{F}}_{1c}=93.33$, that is, the data offers overwhelming support in favor of $H_1$. This is not surprising when we examine the parameter estimates and their 95% central credible intervals using the summary() function (see Table 2).

Table 1. Bain output for the confirmatory factor analysis model

	Fit	Com	BF.u	BF.c	PMPa	PMPb
H1	0.88	0.01	93.33	762.05	1.00	0.99
Hu						0.01

PMP: Posterior model probabilities; PMPa excludes Hu; PMPb includes Hu.

Table 2. Standardized parameter estimates for the confirmatory factor analysis

Parameter	Estimate A	CI A	Estimate B	CI B
b	0.71	[0.64, 0.78]	0.77	[0.71, 0.82]
l	0.81	[0.76, 0.86]	0.65	[0.57, 0.73]
f	0.84	[0.79, 0.88]	0.81	[0.76, 0.86]
n	0.91	[0.88, 0.94]	0.89	[0.85, 0.92]
r	0.70	[0.63, 0.77]	0.72	[0.65, 0.79]
c	0.87	[0.84, 0.91]	0.83	[0.78, 0.87]

CI: Credible interval.

summary (results1)

In agreement with $H_1$, all observed standardized loadings are larger than .6. Note that, a preference for $H_1$ compared to $H_u$ comes with a Bayesian error probability of .01: A 1% probability that the choice for $H_1$ is incorrect, conditional on the set of models (see Table 1).

Example 2: Latent regression

A latent regression model is specified using the code below. The measurement model for the factors B and A is the same as in Example 1. In this example, however, the correlation from the preceding example is replaced by a regression coefficient. Moreover, age and peabody are included as observed covariates. This analysis thus allows us to investigate whether children’s knowledge after watching Sesame Street for a year is predicted by their knowledge 1 year before, as well as by their biological- and mental age.

model2 <- ‘A = ~ Ab + Al + Af + An + Ar + Ac B = ~ Bb + Bl + Bf + Bn + Br + Bc A ~ B + age + peabody’ fit2 <- sem (model2, data = sesamesim, std.lv = TRUE)

Specifying informative hypotheses

This example contains three hypotheses, separated by semicolons, regarding the relative importance of B, age, and peabody when predicting A:

hypotheses2 <- “A~B > A peabody = A~age = 0; A~B > A ~ peabody > A~age = 0; A~B > A ~ peabody > A~age > 0”

$H_1$ specifies that the regression coefficient of B on A is greater than zero, and that the coefficients of age and peabody on A are equal to zero. $H_2$ specifies that the regression coefficient of B on A is greater than that of peabody on A, which in turn is bigger than that of age on A, which is equal to zero. $H_3$ specifies that the coefficient of B on A is greater than that of peabody on A, which, in turn, is greater than that of age on A, which is greater than zero.

Evaluating hypotheses

The code below evaluates the hypotheses specified for the latent regression example:

set.seed (748) results2 <- bain (fit2, hypotheses2, standardize = TRUE)

The results are reported in Table 3. When $H_1$, $H_2$, and $H_3$ are compared to their respective complements, there is substantial support for $H_1$, somewhat less for $H_2$, and substantially less support for $H_3$. The posterior model probabilities, PMPb, help determine which of the three informative hypotheses is the best of the set, and whether the unconstrained hypothesis $H_u$ holds any credulity. Supported by a posterior model probability of .79, $H_1$ appears to be the best of the set of hypotheses. However, a choice for $H_1$ implies a Bayesian error probability of .17 + .03 + .01 = .21, that is, it would be unwise to ignore the possibility that another hypothesis (especially $H_2$) might also be a good candidate. It is clear that the regression coefficient of B is larger than zero, but maybe the regression coefficient of peabody is also larger than zero. We can see how these findings relate to the model parameters by calling summary() on the bain object (see Table 4).

Table 3. Bain output for the latent regression model

	Fit	Com	BF.u	BF.c	PMPa	PMPb
H1	69.90	0.46	150.87	150.87	0.80	0.79
H2	2.96	0.09	33.16	33.16	0.17	0.17
H3	0.07	0.01	5.64	6.01	0.03	0.03
Hu						0.01

PMP: Posterior model probabilities; PMPa excludes Hu; PMPb includes Hu.

Table 4. Standardized parameter estimates for latent regression

	Parameter	Estimate	CI
13	A ~ B	0.79	[0.73, 0.85]
14	A~ age	0.00	[−0.09, 0.09]
15	A~ peabody	−0.02	[−0.11, 0.08]

CI: Credible interval.

Example 3: Multiple group analysis

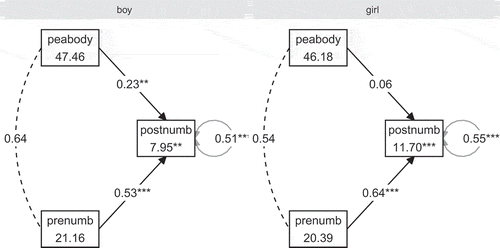
This example demonstrates how to evaluate informative hypotheses about freely estimated parameters across groups in a multi-group structural equation model. It is important to emphasize that the Bayes factor implemented in bain is only valid for multiple group models without any between-group parameter constraints. The reason is that bain requires a separate asymptotic covariance matrix for the parameters of each group. This is only possible when no between-group constraints are imposed, because then (and only then) is the asymptotic covariance matrix block-diagonal, and can we extract a covariance matrix per group. For more information, see Hoijtink et al. (2019). A multiple group model can be estimated by specifying a grouping variable in the call to sem. The code below runs an analysis in which the parameters of a regression model are estimated separately for boys and girls. The model predicts knowledge of numbers after watching Sesame Street for a year based on prior knowledge of numbers, and the peabody mental age test (see Figure 2).

Figure 2. Multiple group analysis

model3 <- ‘ postnumb ~ prenumb + peabody ‘ # Assign labels to the groups to be used when formulating hypotheses Sesamesim $sex$<-\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{o}\mathrm{r}$ ($\mathrm{s}\mathrm{e}\mathrm{s}\mathrm{a}\mathrm{m}\mathrm{e}\mathrm{s}\mathrm{i}\mathrm{m}$$sex, labels = c (“boy”, “girl”)) # Fit the multiple group structural equation model fit3 <- sem (model3, data = sesamesim, group = “sex”)

Specifying informative hypotheses

For the multiple group (boys versus girls) structural equation model, we evaluate two hypotheses: That standardized regression coefficients are equal for boys and girls ($H_1$), or that they are smaller for boys as compared to girls ($H_2$). In other words, are number knowledge before and the peabody test better predictors of number knowledge after for girls than for boys?

hypotheses3 <- “postnumb~prenumb.boy = postnumb~prenumb.girl & postnumb~peabody.boy = postnumb~peabody.girl; postnumb~prenumb.boy < postnumb~prenumb.girl & postnumb~peabody.boy < postnumb~peabody.girl”

Evaluating hypotheses

The results, displayed in Table 5, indicate that $H_1$ receives 41.20 times more support from the data than its complement. Conversely, $H_2$ received $1/.16=6.25$ times less support than its complement. These results indicate that the predictability of postnumb does not depend on gender. This is also reflected by the posterior model probabilities that show that a decision in favor of $H_1$ comes with a Bayesian error probability of only 0.02.

Table 5. Bain output for the latent regression model

	Fit	Com	BF.u	BF.c	PMPa	PMPb
H1	7.79	0.19	41.20	41.20	1.00	0.97
H2	0.02	0.11	0.18	0.16	0.00	0.00
Hu						0.02

PMP: Posterior model probabilities; PMPa excludes Hu; PMPb includes Hu.

set.seed (235) results3 <- bain (fit3, hypotheses3, standardize = TRUE)

This conclusion is corroborated by the model coefficients, obtained by running summary(results3). As seen in Table 6, the credible intervals for the regression coefficients for boys and girls show substantial overlap.

Table 6. Parameter estimates for the multiple group model

Parameter	Estimate boy	CI boy	Estimate girl	CI girl
postnumb~prenumb	0.53	[0.38, 0.68]	0.64	[0.52, 0.76]
postnumb~peabody	0.23	[0.07, 0.40]	0.06	[−0.09, 0.22]

CI: Credible interval.

Further extensions

Sensitivity analysis

Bayes factors for hypotheses containing at least one equality constraint are sensitive to the scaling factor used to construct the prior distribution. Recall that the default scaling factor in bain is based on the notion of a minimal training sample; the smallest sample size required to estimate the target parameters. This default scaling factor is set by the default argument fraction = 1 in the call to bain(). A default argument does not need to be specified, but can be changed manually by specifying a different value. The smallest possible scaling factor is the default, 1. Larger scaling factors increase confidence in the prior, making it more concentrated and less spread out. Thus, specifying fraction = 2 raises the scaling factor to twice the size of the minimal training sample, and fraction = 3 to thrice the size.

The reason hypotheses containing at least one equality constraint are sensitive to the scaling factor is that equality constraints are represented as a fixed-width slice of the parameter space around the constraint value (in technical terms, the point density at this value). If the width of the prior changes, the ratio of the fixed-width slice to the overall width of the prior changes. Hypotheses specified using only inequality constraints are not sensitive to the scaling factor, because these constraints divide the parameter space (like cutting the distribution into two halves). As the width of the prior changes, the space on both sides of the constraint decreases commensurately, so their ratio remains the same (see Hoijtink, Mulder, et al., 2019 for a full explanation).

It is possible to conduct a sensitivity analysis to examine how sensitive the Bayes factors are to the scaling factor. The convenience function bain_sensitivity() accepts a vector argument called fractions = …, and returns a list of bain objects. The summary() function for this sensitivity analysis accepts an argument which_stat, that can be used to request a sensitivity analysis table for a specific statistic (by default, this is the BF). Below, we demonstrate how to conduct a sensitivity analysis, based on Example 2:

set.seed (753) results_sens <- bain_sensitivity (fit2, hypotheses2, fractions = c (1, 2, 3), standardize = TRUE) summary (results_sens)

The results are presented in Table 7. It shows that the value of $\mathrm{B}{\mathrm{F}}_{3c}$ is invariant, whereas $\mathrm{B}{\mathrm{F}}_{1u}$ and $\mathrm{B}{\mathrm{F}}_{2u}$ decrease as the scaling factor increases. The posterior model probabilities change accordingly, as can be seen in Table 8.

Table 7. Sensitivity analysis for the Bayes factors (BF) of the latent regression model

Fraction	H1	H2	H3
1.00	150.87	36.69	6.84
2.00	75.44	25.94	6.84
3.00	50.29	21.18	6.84

Table 8. Sensitivity analysis for posterior model probabilities (PMPb) of the multiple group model

Fraction	H1	H2	H3	Hu
1.00	0.77	0.19	0.03	0.01
2.00	0.69	0.24	0.06	0.01
3.00	0.64	0.27	0.08	0.01

summary (results_sens, which_stat = “PMPb”)

The remaining question is how to deal with the sensitivity of the Bayes factor to the scale factor. There are three potential courses of action. Firstly, if all hypotheses under consideration are formulated using only inequality constraints, the Bayes factors are invariant, as can be seen from $\mathrm{B}{\mathrm{F}}_{3c}$ in Table 8. Secondly, if the hypotheses contain equality constraints, researchers can rely on the default scaling factor implemented in bain. The resulting Bayes factors tend to favor hypotheses with equality constraints over their complement. This approach ensures that the evidence in the data has to be compelling before it is concluded that the constraints do not hold. When applied to null-hypotheses (i.e., an equality constrained hypothesis stating that a parameter is equal to zero), this conservative approach curtails the false-positive rate. This is appropriate, especially in the context of the replication crisis (see, for example, Open Science Collaboration, 2015). Thirdly, researchers can execute a sensitivity analysis, as in the preceding example: Empirically investigate the sensitivity of the Bayes factors to the scaling factor, and report the results. In our experience, conclusions are usually robust with respect to different values of the scaling factor. This can also be seen in Table 7: Although the Bayes factor for $H_1$ decreases from 150.87 to 50.29, the conclusion remains that $H_1$ is substantially more supported than $H_c$. Furthermore, in terms of posterior model probabilities, the conclusion remains that $H_1$ is the best hypothesis, and that $H_2$ cannot be ruled out.

Experimental applications

The examples above all use the standard interface of the bain() function, which requires two arguments: A model object, and a hypothesis. This interface accepts all lavaan model objects generated by the functions cfa, sem, and growth. Within these models, parameters may be fixed, and data may be categorical, and hypotheses can be formulated with respect to intercepts, factor loadings, and regression coefficients. Some situations that cannot currently be handled by bain include multilevel models (specified using the cluster argument), and defined parameters, such as indirect effects in mediation models. If a researcher wishes to circumvent the standard user interface, bain() can be applied to a named vector of parameters, instead of one of the model types for which methods exist. This approach calls the default method of bain, which is less user-friendly, but more flexible than the model-specific interface. Section 4.i in the bain package vignette illustrates this approach and demonstrates how to manually extract the target parameter estimates and place them in a named vector, and how to obtain the parameter covariance matrix and sample size from a lavaan object. This vignette can be loaded by calling vignette (“bain_introduction”, package = “bain”). Note that nonstandard applications of bain that have not yet been validated should be identified as such, or substantiated with a simulation study.

Discussion

This Teacher’s Corner paper introduced Bayesian hypotheses evaluation for structural equation models using bain and lavaan. The combination of both R packages enables the free, open-source, and user-friendly evaluation of informative hypotheses for structural equation models. The approach elaborated in this paper uses Bayes factors, which are a measure of relative support for two hypotheses. The interpretation of Bayes factors is straightforward: It is a ratio of evidence in favor of one hypothesis, relative to evidence in favor of another hypothesis. Bayes factors can be indecisive; the closer Bayes factors get to one, the less differential support was found for either hypothesis. It is up to the scientific community to decide how much evidence is sufficient evidence.

The advocated approach allows users to evaluate support for a single informative hypothesis, either relative to its complement, or relative to an unconstrained hypothesis. The Bayes factor $\mathrm{B}{\mathrm{F}}_{.c}$ compares against the complement, and expresses how much evidence the data provide is in favor of the theory, as compared to not the theory. The Bayes factor $\mathrm{B}{\mathrm{F}}_{.u}$ compares against the unconstrained hypothesis, and expresses how much evidence the data provide is in favor of the theory, as compared to any ordering of parameters. Two informative hypotheses can be compared by computing their joint Bayes factor, which is a ratio of the two $\mathrm{B}{\mathrm{F}}_{.u}$s for these hypotheses.

When simultaneously evaluating more than two hypotheses, it is convenient to use the posterior model probabilities. These quantify the proportion of support for each hypothesis in a set, conditional on the data. This was illustrated in Example 2. Bayesian error probabilities additionally quantify the uncertainty of decisions about hypotheses. The probability that a preference for one hypothesis in the set is incorrect, is equal to the sum of posterior model probabilities for the other informative hypotheses. This is a conditional probability, that is, conditional on the available data and the hypotheses in the set.

Structural equation models are often estimated on data that contain missing values. Fortunately, the Bayes factor implemented in bain can also be computed if the data contain missing values (Gu, Hoijtink, Mulder, & Rosseel, 2019; Hoijtink, Gu, et al., 2019). Users can use multiple imputation (Van Buuren, 2018) to obtain estimates of the (standardized) target parameters, their covariance matrix, and the effective sample size, and once those are available, bain can be used for the evaluation of informative hypotheses. The interested reader is referred to the vignette included with the bain package, which includes an elaborate example.

Several potential limitations remain. One such limitation is the fact that bain utilizes normal approximations of the prior and posterior distribution. This could have implications for quantities whose sampling distribution is known to be non-normally distributed, such as indirect effects (MacKinnon et al., 2004). However, this problem is averted by the fact that users are currently prevented from using the lavaan interface to bain for derived parameters, which includes indirect effects. A second limitation is the fact that bain cannot handle multiple group models with between-group constraints. Substantial future research is required to overcome this issue. An implication of this limitation is that it is not possible to impose measurement invariance in multiple group latent variable models. One potential solution, that can already be applied, is to use linear transformations within the bain hypotheses to ensure that parameters are comparable across groups. However, this procedure is complicated and beyond the scope of this tutorial. Pending a future publication addressing measurement invariance, researchers can contact the authors to obtain support for such analyses.

In conclusion, bain enables user-friendly Bayesian evaluation of informative hypotheses for structural equation models estimated in lavaan. The method has been validated for regression coefficients, factor loadings, and intercepts, in a range of commonly specified structural equation models, such as factor analyses, latent regression analyses, multi-group models, and latent growth models. Its functionality will be further expanded in future updates, and the default method for named vectors offers the freedom to explore applications not currently covered by the standard interface.

Additional information

Funding

The first author is supported by an NWO Veni grant (NWO grant number VI.Veni.191G.090). The third author is supported by an NWO Vidi Grant (NWO grant number 452-17-006). The last author is supported by a fellowship from the Netherlands Institute for Advanced Studies in the Humanities and Social Sciences, and the Consortium on Individual Development (CID) which is funded through the Gravitation program of the Dutch Ministry of Education, Culture, and Science and the Netherlands Organization for Scientific Research (NWO grant number 024.001.003).