On the Differences between General Cross-Lagged Panel Model and Random-Intercept Cross-Lagged Panel Model: Interpretation of Cross-Lagged Parameters and Model Choice

ABSTRACT

Many methods have been developed to infer reciprocal relations between longitudinally observed variables. Among them, the general cross-lagged panel model (GCLM) is the most recent development as a variant of the cross-lagged panel model (CLPM), while the random-intercept CLPM (RI-CLPM) has rapidly become a popular approach. In this article, we describe how common factors and cross-lagged parameters included in these models can be interpreted, using a unified framework that was recently developed. Because common factors are modeled with lagged effects in the GCLM, they have both direct and indirect influences on observed scores, unlike stable trait factors included in the RI-CLPM. This indicates that the GCLM does not control for stable traits as the RI-CLPM does, and that there are interpretative differences in cross-lagged parameters between these models. We also explain that including such common factors as well as moving-average terms in the GCLM makes this interpretation very complicated.

Many researchers aim to uncover reciprocal (or, mutual or prospective) relations between longitudinally observed variables, and we have seen an increased number of such studies in the behavioral sciences. For example, during the past year more than 1,000 published psychology papers have dealt with this type of relation.¹ For this analytic purpose, the use of the cross-lagged panel model (CLPM) and estimation via structural equation modeling (SEM) have been a standard approach for decades in the behavioral sciences. In this model, a cross-lagged coefficient, which indicates a path from one variable measured at a time point $t-1$ to another measured at time point $t$, is a key parameter. Many alternatives to the CLPM have been proposed in various disciplines using SEM approaches (see Orth et al., in press; Usami, Murayama et al., 2019). Notably, in the last few years the random-intercept CLPM (RI-CLPM; Hamaker et al., 2015) has rapidly become a popular approach among psychologists, reaching more than 600 citations on Google Scholar as of August 2020. A major strength of this model is that it can account for stable trait factors that control for stable individual differences, allowing researchers to infer within-person relations between variables.

Usami, Murayama et al. (2019) proposed a unified framework to clarify the mathematical and conceptual similarities and differences among various longitudinal models. This framework revealed that existing SEM-based longitudinal models can be classified according to whether the model posits unique factors and/or (dynamic) residuals, and what types of common factors are used to model changes. They argued that the latter is essential to understanding how cross-lagged parameters can be interpreted in each model, and showed from the viewpoint of a potential outcome (or counterfactual) approach (the Rubin causal model; Rubin, 1974) that including stable trait factors as in the RI-CLPM is mathematically equivalent to controlling for latent (unobserved) time-invariant confounders.

Although longitudinal designs have numerous advantages over cross-sectional designs (e.g., McArdle & Nesselroade, 2014), the issue of causal inference becomes complicated and challenging in general for longitudinal studies, because researchers must effectively account for time-varying and time-invariant confounders. For this reason, efforts by researchers to devise a better methodology are continuing (e.g., Asparouhov et al., 2018; Hamaker et al., 2015; Imai & Ratkovic, 2015; Robins, 1999; Robins & Hernán, 2009; Zyphur et al., 2020a).

Among such methodologies, the general cross-lagged panel model (GCLM; Zyphur et al., 2020a, 2020b) is a recent variant of the CLPM. This model was not covered in the discussion of Usami, Murayama et al. (2019). The GCLM as a SEM-based approach assumes (time-varying) unit effects as well as moving average (MA) and cross-lagged moving average (CLMA) terms, aiming to increase the range of dynamic processes that can be modeled. Zyphur et al. (2020b) discuss the relation between the GCLM and other longitudinal models such as the latent growth model (LGM; Meredith & Tisak, 1984, 1990) and the autoregressive latent trajectory (ALT) model (Bollen & Curran, 2004, 2006; Curran & Bollen, 2001). Many researchers have shown interest in applying the GCLM, including more than 10 citations on Google Scholar as of August 2020 (e.g., Bollmann, Rouzinov, Berchtold, & Rossier, 2019; Oswald, 2019; Zhang et al., 2019).

This article aims to elucidate how common factors and cross-lagged parameters included in the GCLM can be interpreted using the unified framework, and to highlight conceptual and mathematical differences among the GCLM, the RI-CLPM, and other longitudinal models. Despite interpretative differences existing in cross-lagged parameters among models, it has long been common practice for researchers to run a single model (typically, the CLPM) and evaluate its cross-lagged relations without considering potential alternative models (Usami, Todo et al., 2019). This article should better reveal the strengths and potential weakness of the GCLM over other alternatives, helping researchers to seek better methodologies while minimizing risk of wrong conclusions regarding reciprocal effects.

Importantly, we show that the mathematical relation between the RI-CLPM and the GCLM as described in Zyphur et al. (2020b, p. 13) requires correction, and that there are interpretative differences in cross-lagged parameters and common factors in these models. Specifically, because common factors are modeled with lagged effects in the GCLM, they have both direct and indirect influences on observed scores, meaning that the GCLM does not control for stable traits as does the RI-CLPM. We will also show that including unit effects as well as moving average terms in the GCLM greatly complicates the interpretation of cross-lagged parameters.

In the next section, we provide a brief introduction for the GCLM after a brief overview of some existing models: the RI-CLPM, the LGM, and the ALT model. In the third section, we introduce the unified framework (Usami, Murayama et al., 2019). Readers who are already familiar with these models and the framework may skip these two sections. In the fourth section, we discuss how the GCLM can be characterized using the unified framework, showing interpretative differences in common factors and cross-lagged parameters from the RI-CLPM and other models. A conceptual diagram as well as path diagrams of models are also provided to further clarify relations between the models. The fifth section presents an empirical example to demonstrate how choice of the analysis model might lead to different conclusions about reciprocal relations. The sixth section briefly contrasts these SEM-based approaches with potential alternatives to effectively account for the influences of time-varying confounders. The final section presents our conclusions and some areas for future research.

Existing models

We first give an overview of the RI-CLPM, the LGM, and the ALT model, and then introduce the GCLM.

Random intercept cross-lagged panel model (RI-CLPM)

Throughout this article we assume that researchers are interested in reciprocal relations between two variables $X$ and $Y$. Let $x_{it}$ and $y_{it}$ be the measurements at time point $t$ ($1\dots t\dots T$) for person $i$ ($1\dots i\dots N$). In the RI-CLPM, $x_{it}$ and $y_{it}$ are first modeled as

(1) $\begin{array}{cc}{x}_{it}& ={\mu }_{xt}+I_{xi}+x_{it}^{\ast }\\ y_{it}& ={\mu }_{yt}+I_{yi}+y_{it}^{\ast }.\end{array}$(1)

Here, ${\mu }_{xt}$ and ${\mu }_{yt}$ are the temporal group means at time point $t$ (i.e., $E(x_{it})={\mu }_{xt}$, $E(y_{it})={\mu }_{yt}$). The terms $I_{xi}$ and $I_{yi}$ are (time-invariant) stable trait factors (alternatively, random intercepts) that represent a person’s trait-like deviations from the temporal group means. Trait factors $I_{xi}$ and $I_{yi}$ have means of 0 and a variance–covariance matrix. By accounting for stable trait factors for each person, $x_{it}^{\ast }$ and $y_{it}^{\ast }$ represent temporal deviations from the means of that person because they are subtracted from the expected scores of person $i$ (i.e., ${\mu }_{xit}={\mu }_{xt}+I_{xi}$ and ${\mu }_{yit}={\mu }_{yt}+I_{yi}$). Accordingly, in the RI-CLPM, the time series $x_{it}^{\ast }$ and $y_{it}^{\ast }$ can be considered as within-person fluctuation. Due to this statistical property in temporal deviations, at $t=1$ the initial deviation terms ($x_{i1}^{\ast }$ and $y_{i1}^{\ast }$) are assumed to be uncorrelated with stable trait factors. Using these within-person deviation terms, in the RI-CLPM the reciprocal relations are modeled for $t\ge 2$ as

(2) $\begin{array}{cc}{x}_{it}^{\ast }& ={\beta }_x{x}_{i(t-1)}^{\ast }+{\gamma }_x{y}_{i(t-1)}^{\ast }+d_{xit}\\ y_{it}^{\ast }& ={\beta }_y{y}_{i(t-1)}^{\ast }+{\gamma }_y{x}_{i(t-1)}^{\ast }+d_{yit},\end{array}$(2)

where ${\beta }_x$ and ${\beta }_y$ are autoregressive parameters. ${\gamma }_x$ and ${\gamma }_y$ are cross-lagged parameters, which are key for inferring reciprocal relations between the variables.² In $t=1$, the initial states $x_{i1}$ and $y_{i1}$ are modeled as exogenous variables (i.e., their variances and covariance are assumed). The residuals $d_{xit}$ and $d_{yit}$ are typically assumed to be normally distributed and correlated. If stable trait factors are omitted (i.e., if $I_{xi}=I_{yi}=0$), this version of the RI-CLPM is mathematically equivalent to the CLPM. The RI-CLPM is identified if two or more variables have been measured at three or more time points, whereas the CLPM requires only two time points (in which case it is saturated).

Because the RI-CLPM separates within-person fluctuations (temporal deviations) from stable between-person differences (stable trait factors) over time, cross-lagged relations in Equation 2(2) $\begin{array}{cc}{x}_{it}^{\ast }& ={\beta }_x{x}_{i(t-1)}^{\ast }+{\gamma }_x{y}_{i(t-1)}^{\ast }+d_{xit}\\ y_{it}^{\ast }& ={\beta }_y{y}_{i(t-1)}^{\ast }+{\gamma }_y{x}_{i(t-1)}^{\ast }+d_{yit},\end{array}$(2) can be considered as those pertaining to a process that takes place at the within-person level. Therefore, in the RI-CLPM, ${\gamma }_x$ and ${\gamma }_y$ can be interpreted as quantities that express the extent to which the two variables influence each other within persons. Hamaker et al. (2015) argued that parameter estimates in the CLPM conflate between-person and within-person processes, and that this model provides inaccurate estimates for within-person reciprocal effects as a consequence.

Equations (1(1) $\begin{array}{cc}{x}_{it}& ={\mu }_{xt}+I_{xi}+x_{it}^{\ast }\\ y_{it}& ={\mu }_{yt}+I_{yi}+y_{it}^{\ast }.\end{array}$(1) ) and (2(2) $\begin{array}{cc}{x}_{it}^{\ast }& ={\beta }_x{x}_{i(t-1)}^{\ast }+{\gamma }_x{y}_{i(t-1)}^{\ast }+d_{xit}\\ y_{it}^{\ast }& ={\beta }_y{y}_{i(t-1)}^{\ast }+{\gamma }_y{x}_{i(t-1)}^{\ast }+d_{yit},\end{array}$(2) ) are the formulation that were used in Hamaker et al. (2015). However, there is another formulation of the (RI-)CLPM if intercepts ($\alpha$) are included in the lagged regressions (Equation 2(2) $\begin{array}{cc}{x}_{it}^{\ast }& ={\beta }_x{x}_{i(t-1)}^{\ast }+{\gamma }_x{y}_{i(t-1)}^{\ast }+d_{xit}\\ y_{it}^{\ast }& ={\beta }_y{y}_{i(t-1)}^{\ast }+{\gamma }_y{x}_{i(t-1)}^{\ast }+d_{yit},\end{array}$(2) ) instead of excluding temporal group means ($\mu$) in Equation (1)(1) $\begin{array}{cc}{x}_{it}& ={\mu }_{xt}+I_{xi}+x_{it}^{\ast }\\ y_{it}& ={\mu }_{yt}+I_{yi}+y_{it}^{\ast }.\end{array}$(1) :

$x_{it}=I_{xi}+x_{it}^{\ast },y_{it}=I_{yi}+y_{it}^{\ast }$

(3) $x_{it}^{\ast }={\alpha }_{xt}+{\beta }_x{x}_{i(t-1)}^{\ast }+{\gamma }_x{y}_{i(t-1)}^{\ast }+d_{xit},y_{it}^{\ast }={\alpha }_{yt}+{\beta }_y{y}_{i(t-1)}^{\ast }+{\gamma }_y{x}_{i(t-1)}^{\ast }+d_{yit}.$(3)

$\alpha$ and $\mu$ are not mathematically identical unless $T=2$, because the former is modeled jointly with lagged effects and thus the influences of effects feed forward through the lagged relations. For example, expected values for $X$ and $Y$ at $t=3$ can be calculated by substituting the relations $x_{i2}^{\ast }={\alpha }_{x2}+{\beta }_x{x}_{i1}^{\ast }+{\gamma }_x{y}_{i1}^{\ast }+d_{xi2}$ and $y_{i2}^{\ast }={\alpha }_{y2}+{\beta }_y{y}_{i1}^{\ast }+{\gamma }_y{x}_{i1}^{\ast }+d_{yi2}$ into the equations $x_{i3}^{\ast }={\alpha }_{x3}+{\beta }_x{x}_{i2}^{\ast }+{\gamma }_x{y}_{i2}^{\ast }+d_{xi3}$ and $y_{i3}^{\ast }={\alpha }_{y3}+{\beta }_y{y}_{i2}^{\ast }+{\gamma }_y{x}_{i2}^{\ast }+d_{yi3}$. From this procedure, mathematical relations between $\alpha$ (in Equation (3))(3) $x_{it}^{\ast }={\alpha }_{xt}+{\beta }_x{x}_{i(t-1)}^{\ast }+{\gamma }_x{y}_{i(t-1)}^{\ast }+d_{xit},y_{it}^{\ast }={\alpha }_{yt}+{\beta }_y{y}_{i(t-1)}^{\ast }+{\gamma }_y{x}_{i(t-1)}^{\ast }+d_{yit}.$(3) and $\mu$ (in Equation (1))(1) $\begin{array}{cc}{x}_{it}& ={\mu }_{xt}+I_{xi}+x_{it}^{\ast }\\ y_{it}& ={\mu }_{yt}+I_{yi}+y_{it}^{\ast }.\end{array}$(1) can be expressed as

(4) $\begin{array}{c}E(x_{i3})={\mu }_{x3}={\alpha }_{x3}+{\beta }_x{\alpha }_{x2}+{\gamma }_x{\alpha }_{y2}\\ E(y_{i3})={\mu }_{y3}={\alpha }_{y3}+{\beta }_y{\alpha }_{y2}+{\gamma }_y{\alpha }_{x2}.\end{array}$(4)

By the same procedure, for $t=4$, we can derive the relations between $\alpha$ and $\mu$ as

(5) $\begin{array}{r}\begin{array}{c}E(x_{i4})={\mu }_{x4}={\alpha }_{x4}+{\beta }_x{\alpha }_{x3}+{\gamma }_x{\alpha }_{y3}+[{\beta }_x({\beta }_x{\alpha }_{x2}+{\gamma }_x{\alpha }_{y2})\\ +{\gamma }_x({\beta }_y{\alpha }_{y2}+{\gamma }_y{\alpha }_{x2})]\\ E(y_{i4})={\mu }_{y4}={\alpha }_{y4}+{\beta }_y{\alpha }_{y3}+{\gamma }_y{\alpha }_{x3}+[{\beta }_y({\beta }_y{\alpha }_{y2}+{\gamma }_y{\alpha }_{x2})\\ +{\gamma }_y({\beta }_x{\alpha }_{x2}+{\gamma }_x{\alpha }_{y2})].\end{array}\end{array}$(5)

Note that numbers of parameters are independent of the choice of $\alpha$ or $\mu$, and this choice does not influence the estimation results of other parameters, such as $\beta$ and $\gamma$.

Latent growth model (LGM)

A bivariate version of the (linear) LGM can be expressed as

(6) $\begin{array}{cc}{x}_{it}& =I_{xi}+(t-1)S_{xi}+{ϵ}_{xit}\\ y_{it}& =I_{yi}+(t-1)S_{yi}+{ϵ}_{yit}.\end{array}$(6)

Here, $I_{xi}$ and $I_{yi}$ are intercept factors and $S_{xi}$ and $S_{yi}$ are (linear) slope factors. The values ${ϵ}_{xit}$ and ${ϵ}_{yit}$ are unique factors (or measurement errors). In the LGM literature, $I$ and $S$ are often called growth factors, and nonzero factor means (as well as variances and covariances) are assumed.

The main difference between the LGM and the RI-CLPM is that while the LGM explicitly models mean growth trajectories via the intercept and slope factor means, this model instead assumes there are no lagged effects. In other words, in the RI-CLPM temporal group means ($\mu$) play a role in capturing mean growth trajectories without making an explicit modeling assumption (e.g., that growth trajectories are linear); instead, (within-person) reciprocal relations are modeled using lagged effects as well as stable trait factors.

Autoregressive latent trajectory (ALT) model

The ALT model was proposed by Curran and Bollen (2001), aiming to synthesize the traditions of the CLPM and the LGM. The bivariate (linear) ALT model can be expressed as

(7) $\begin{array}{cc}{x}_{it}& =A_{xi}+(t-1)B_{xi}+{\beta }_x{x}_{i(t-1)}+{\gamma }_x{y}_{i(t-1)}+d_{xit}\\ y_{it}& =A_{xi}+(t-1)B_{yi}+{\beta }_y{y}_{i(t-1)}+{\gamma }_y{x}_{i(t-1)}+d_{yit}.\end{array}$(7)

As in the LGM, temporal group means ($\mu$) are not included. Instead, common factors $A$ and $B$ play a role in describing growth trajectories (i.e., $A$ and $B$ have nonzero factor means). As before, ${\beta }_x$ and ${\beta }_y$ are autoregressive parameters, ${\gamma }_x$ and ${\gamma }_y$ are cross-lagged parameters, and $d_{xit}$ and $d_{yit}$ are residuals. The ALT is identified if two or more variables have been measured at four or more time-points when stationarity of parameters is assumed, while five or more time points are required under a non-stationarity assumption.

Obviously, the main difference between the ALT model and the LGM is that the former assumes lagged effects, as in the RI-CLPM. However, as we will see later, the presence of lagged effects causes the interpretations of common factors $A$ and $B$ in the ALT model to differ from those of growth factors $I$ and $S$ in the LGM.

General cross-lagged panel model (GCLM)

The GCLM was proposed as a generalization of the CLPM by including two aspects: (1) stable trait factors (i.e., unit effects), and (2) MA and CLMA terms (Zyphur et al., 2020a).³ The latter idea was motivated by vector autoregressive moving average (VARMA) models (Box et al., 2008; Browne & Nesselroade, 2005; as cited in Zyphur et al., 2020a), which helps to expand the range of dynamic processes that can be modeled.

For the former idea, Zyphur et al. (2020a) cited the work of Hamaker et al. (2015) and noted the necessity of accounting for stable trait factors from the view of causal inference: “[b]y failing to model stable factors, they will be confounded with the system dynamics that should be reflected by AR and CL terms” (p. 8). Specifically, Hamaker et al. (2015) argued that parameter estimates in the CLPM conflate between-person and within-person processes, while the RI-CLPM is an alternative model that can separate within-person processes from stable between-person differences. Therefore, inference of within-person reciprocal (as well as causal) effects by including stable trait factors, as in the RI-CLPM, was one of the central aims for Zyphur and colleagues in developing the GCLM.

Without loss of generality, here we can focus on a GCLM that assumes first-order lags for autoregressive and cross-lagged terms as well as for MA and CLMA terms. Zyphur et al. (2020a) called this version of the GCLM the AR(1)MA(1)CL(1)CLMA(1) model (the numbers in parentheses indicate lag orders), which can be expressed as⁴

(8) $\begin{array}{r}\begin{array}{c}{x}_{it}={\alpha }_{xt}+{\lambda }_{xt}{B}_{xi}+{\beta }_x{x}_{i(t-1)}+{\gamma }_x{y}_{i(t-1)}+{\delta }_x{d}_{xi(t-1)}\\ +{\zeta }_x{d}_{yi(t-1)}+d_{xit}\\ y_{it}={\alpha }_{yt}+{\lambda }_{yt}{B}_{yi}+{\beta }_y{y}_{i(t-1)}+{\gamma }_y{x}_{i(t-1)}+{\delta }_y{d}_{yi(t-1)}\\ +{\zeta }_y{d}_{xi(t-1)}+d_{yit},\end{array}\end{array}$(8)

for $t\ge 3$. The terms ${\alpha }_{xt}$ and ${\alpha }_{yt}$ are occasion-specific intercepts or occasion effects. As before, ${\beta }_x$ and ${\beta }_y$ are (first-order) autoregressive parameters, and ${\gamma }_x$ and ${\gamma }_y$ are (first-order) cross-lagged parameters. The terms $B_{xi}$ and $B_{yi}$ are (unit-specific) common factors, which Zyphur et al. (2020a, 2020b) called unit effects or stable (trait) factors. The means of these factors are set to zero. In addition, although not explicitly stated in Zyphur et al. (2020a, 2020b), these factors are assumed to be uncorrelated with the initial states ($x_{i1}$ and $y_{i1}$), though this assumption can be relaxed. ${\lambda }_{xt}$ and ${\lambda }_{yt}$ are weights or occasion-specific factors loadings, expressing changes in the effects of common factors over time. We will later discuss the meanings of the common factors (as well as cross-lagged parameters) in the GCLM.

The terms ${\delta }_x$ and ${\delta }_y$ indicate MA effects, and ${\zeta }_x$ and ${\zeta }_y$ are CLMA effects. They are included to make observations a direct function of past impulses (i.e., residuals $d_{(t-1)}$). In this version of GCLM, the short-run persistence for a variable becomes AR+MA, and the short-run effect of one variable on another becomes CL+CLMA. Zyphur et al. (2020a, p. 12) argued that past impulses $d_{yi(t-1)}$ and $d_{xi(t-1)}$ impact $x_{it}$ and $y_{it}$ via both CL and CLMA paths, respectively, because $d_{yi(t-1)}$ and $d_{xi(t-1)}$ are the components of $y_{i(t-1)}$ and $x_{i(t-1)}$. Therefore, this is akin to estimating an effect of $d_{yi(t-1)}$ and $d_{xi(t-1)}$ on $x_{it}$ and $y_{it}$ as the short-run effect by ${\gamma }_x+{\zeta }_x$ and ${\gamma }_y+{\zeta }_y$, again, respectively (Zyphur et al., 2020a, p. 12).

This version of the GCLM (the AR(1)MA(1)CL(1)CLMA(1) model) can be extended straightforwardly by including second- or higher-order terms. For example, we can include the additional terms ${\beta }_{x2}{x}_{i(t-2)}$ and ${\delta }_{x2}{d}_{xi(t-2)}$ for explaining $x_{it}$, and ${\beta }_{y2}{y}_{i(t-2)}$ and ${\delta }_{y2}{d}_{yi(t-2)}$ for explaining $y_{it}$. This version of the GCLM can be notated as AR(2)MA(2)CL(1)CLMA(1). The AR(1)MA(1)CL(1)CLMA(1) model fixing occasion-specific factor loadings as ${\lambda }_{xt}={\lambda }_{yt}=1$, which is applied in an empirical example below, is identified if two or more variables have been measured at three or more time-points when stationarity of parameters is assumed, while four or more time points are required under a non-stationarity assumption.

We can find mathematical relations between the GCLM and some of the longitudinal models we previously introduced. For example, if we set the weights of $B$ as ${\lambda }_{xt}={\lambda }_{yt}=t-1$ and exclude the intercepts (i.e., ${\alpha }_{xt}={\alpha }_{yt}=0$) as well as MA and CLMA terms (i.e., ${\delta }_x={\delta }_y={\zeta }_x={\zeta }_y=0$), and then include an additional common factor ($A$) whose weight is fixed to one, this version of the GCLM is mathematically equivalent to the ALT model. Likewise, by setting the weights of $B$ as ${\lambda }_{xt}={\lambda }_{yt}=t-1$ and excluding intercepts and all lagged effects (set the AR, CL, MA, and CLMA terms to zero), and then instead including one additional common factor whose weight is fixed to one, this version of the GCLM is mathematically equivalent to the LGM. In the latter comparison, because no lagged effects are assumed to be present, the common factor ($B$) in the GCLM plays a similar role as the growth factor ($S$). In the former comparison, because AR and CL effects are still present in the GCLM (or the ALT model), the common factor ($B$) does not play the role as the growth factor ($S$) in the LGM. This is why we use the notation $B$ (rather than $S$) to express common factors in the GCLM. This point is closely related to how we should interpret the common factors and cross-lagged parameters in each model. We revisit this issue later in more detail.

The relation between the CLPM and the GCLM is more obvious: excluding MA and CLMA terms as well as common factors (i.e., unit effects) from the GCLM reduces it to the CLPM. Therefore, the CLPM is a special case of the GCLM. This point might make us wonder whether the relation between the RI-CLPM and the GCLM is also simple. In fact, Zyphur et al. (2020b, p. 13) explain that a variant of the RI-CLPM (a special case of the RI-CLPM that assumes specific weights (time-varying effects) for stable trait factors $I$) is equivalent to the GCLM with MA and CLMA terms eliminated. However, because lagged effects (i.e., the AR and CL terms) are present and they are jointly modeled with common factors $B$ in the GCLM, even if we exclude MA and CLMA terms and fix the factor loadings to one, this version of the GCLM is not mathematically equivalent to the RI-CLPM, in which common factors (stable trait factors $I$) are separately (rather than jointly) modeled with lagged effects (i.e., Equations (1(1) $\begin{array}{cc}{x}_{it}& ={\mu }_{xt}+I_{xi}+x_{it}^{\ast }\\ y_{it}& ={\mu }_{yt}+I_{yi}+y_{it}^{\ast }.\end{array}$(1) ) and (2))(2) $\begin{array}{cc}{x}_{it}^{\ast }& ={\beta }_x{x}_{i(t-1)}^{\ast }+{\gamma }_x{y}_{i(t-1)}^{\ast }+d_{xit}\\ y_{it}^{\ast }& ={\beta }_y{y}_{i(t-1)}^{\ast }+{\gamma }_y{x}_{i(t-1)}^{\ast }+d_{yit},\end{array}$(2) . Therefore, common factors ($B$) included in the GCLM cannot be interpreted as the stable trait factors ($I$) in the RI-CLPM. We discuss this point in detail using the unified framework (Usami, Murayama et al., 2019) described in the next section.

Unified framework and specifications of existing longitudinal models

Unified framework

Usami, Murayama et al. (2019) provides a unified statistical framework that clarifies mathematical and conceptual relations among diverse SEM-based longitudinal models to examine reciprocal effects, which can be specified through this framework as particular cases. Formulation of the unified framework consists of three sets of equations, which Usami, Murayama et al. (2019) called measurement equations, decomposition equations, and dynamic equations.

Measurement equations. The first set of equations can be used to separate the latent true scores from unique factors (or measurement errors) as

(9) $\begin{array}{c}{x}_{it}=f_{xit}+{ϵ}_{xit}\\ y_{it}=f_{yit}+{ϵ}_{yit}.\end{array}$(9)

These unique factors are typically assumed to be normally distributed and possibly correlated. Among the models we have introduced, the LGM assumes unique factors. The GCLM as well as the (RI-)CLPM and the ALT model assume residuals $d$ in the lagged regressions, but they do not account for the presence of unique factors (or measurement errors) in their formulations. Some of the longitudinal models that include cross-lagged parameters (e.g., the stable trait autoregressive trait and state (STARTS) model; Kenny and Zautra (1995, 2001); and latent change score (LCS) model; Hamagami and McArdle (2001); McArdle and Hamagami (2001) assume unique factors.

Though the inclusion of unique factors is desirable on conceptual grounds, it can easily lead to estimation problems due to the strong dependency among the estimated parameters (Usami, Murayama et al., 2019). Notably, the STARTS model, in which both stable trait factors and unique factors are assumed, often suffers from improper solutions (e.g., Hamaker et al., 2015; Usami, Todo et al., 2019), and a potential solution using Bayesian estimation has been recently investigated (Lüdtke et al., 2018). Usami, Todo et al. (2019) provide a deeper discussion about improper solutions when applying the STARTS model through a simulation study that considers the presence of model misspecifications. Orth et al. (in press) also compared the behavior of several longitudinal models in ten datasets, empirically showing that CLPM and the RI-CLPM converged in every sample, whereas the other (ALT, LCS, and STARTS) models frequently failed to converge or did not converge properly.

Decomposition equations. The second set of equations allow for decomposition into an individual deterministic trend and a temporal deviation from this individual trend, denoted as $f_{xit}^{\ast }$ and $f_{yit}^{\ast }$. The individual deterministic trend can depend on the temporal group means ${\mu }_{xt}$ and ${\mu }_{yt}$ and/or on the random intercepts and (linear) slopes (i.e., $I_{xi}$, $I_{yi}$, $S_{xi}$, and $S_{yi}$). Thus, we have

(10) $\begin{array}{cc}{f}_{xit}& =[{\mu }_{xt}+\{I_{xi}+(t-1)S_{xi}\}]+f_{xit}^{\ast }\\ f_{yit}& =[{\mu }_{yt}+\{I_{yi}+(t-1)S_{yi}\}]+f_{yit}^{\ast }.\end{array}$(10)

Importantly, as we will show later, the common factors included in the decomposition equations (i.e., $I$ and $S$) have only direct effects on $f$, indicating these influences do not feed forward to later time points. Thus, these common factors can be characterized as stable trait (if $S$ is omitted as in the RI-CLPM) or growth factors (i.e., random intercepts and (linear) slope factors as in the LGM).

Dynamic equations. Finally, the dynamics of the processes are modeled with the dynamic equations, which include the lagged terms as autoregressive parameters ${\beta }_x$ and ${\beta }_y$ and cross-lagged parameters ${\gamma }_x$ and ${\gamma }_y$ along with the (dynamic) residuals $d_{xit}$ and $d_{yit}$. In addition, they also include the common factors $A$ and $B$, which are called accumulating factors in Usami, Murayama et al. (2019). This gives

(11) $\begin{array}{cc}{f}_{xit}^{\ast }& =\{A_{xi}+(t-1)B_{xi}\}+{\beta }_x{f}_{xi(t-1)}^{\ast }+{\gamma }_x{f}_{yi(t-1)}^{\ast }+d_{xit}\\ f_{yit}^{\ast }& =\{A_{yi}+(t-1)B_{yi}\}+{\beta }_y{f}_{yi(t-1)}^{\ast }+{\gamma }_y{f}_{xi(t-1)}^{\ast }+d_{yit}.\end{array}$(11)

Although these equations may look very similar to the ALT model (Equation (7)(7) $\begin{array}{cc}{x}_{it}& =A_{xi}+(t-1)B_{xi}+{\beta }_x{x}_{i(t-1)}+{\gamma }_x{y}_{i(t-1)}+d_{xit}\\ y_{it}& =A_{xi}+(t-1)B_{yi}+{\beta }_y{y}_{i(t-1)}+{\gamma }_y{x}_{i(t-1)}+d_{yit}.\end{array}$(7) ), dynamic equations are defined to explain temporal deviations $(f^{\ast })$ rather than observed scores. Because all terms in the dynamic equations contribute to the lagged predictors, their influences feed forward through the lagged relations and accumulate at later time points. This implies that the accumulating factors $A$ and $B$ as well as (dynamic) residuals $d$ have direct and indirect effects on $f^{\ast }$, and thus on the observed scores. In contrast, the effects of stable trait or growth factors ($I$ and $S$) are temporal and they have only direct effects on scores: their influences do not feed forward through the lagged relations and do not accumulate at later time points (Usami, Murayama et al., 2019). As we will discuss later, the choice to include accumulating factors ($A$ and/or $B$) or trait/growth factors ($I$ and/or $S$) in the model makes a difference in how we control (unobserved) confounders, resulting in different interpretations of the cross-lagged parameters in each model.

Note that we cannot apply this unified model to longitudinal data because it would be unidentified due to overparameterization. The aim of introducing this framework is to provide a general structure that helps to relate the many diverse modeling approaches (Usami, Murayama et al., 2019). Another important point is that in this framework MA and CLMA terms were not originally included, though extending the framework to include them is not difficult.

Specification of longitudinal models based on the unified framework

Using the unified framework presented above we can easily see that there are components that may or may not be included in the model. Here we explain how the longitudinal models we have introduced so far can be expressed using the unified framework.

First, the RI-CLPM can be expressed within the unified framework as

$x_{it}=f_{xit},y_{it}=f_{yit}$

(12) $f_{xit}={\mu }_{xt}+I_{xi}+f_{xit}^{\ast },f_{yit}={\mu }_{yt}+I_{yi}+f_{yit}^{\ast }$(12)

$f_{xit}^{\ast }={\beta }_x{f}_{xi(t-1)}^{\ast }+{\gamma }_x{f}_{yi(t-1)}^{\ast }+d_{xit},f_{yit}^{\ast }={\beta }_y{f}_{yi(t-1)}^{\ast }+{\gamma }_y{f}_{xi(t-1)}^{\ast }+d_{yit},$

by excluding unique factors $ϵ$, slope factors $S$, and accumulating factors $A$ and $B$ in the unified framework. As we have explained, because in the RI-CLPM the common factors (i.e., stable trait factors) are modeled separately (rather than jointly) from lagged effects (i.e., Equations (1(1) $\begin{array}{cc}{x}_{it}& ={\mu }_{xt}+I_{xi}+x_{it}^{\ast }\\ y_{it}& ={\mu }_{yt}+I_{yi}+y_{it}^{\ast }.\end{array}$(1) ) and (2(2) $\begin{array}{cc}{x}_{it}^{\ast }& ={\beta }_x{x}_{i(t-1)}^{\ast }+{\gamma }_x{y}_{i(t-1)}^{\ast }+d_{xit}\\ y_{it}^{\ast }& ={\beta }_y{y}_{i(t-1)}^{\ast }+{\gamma }_y{x}_{i(t-1)}^{\ast }+d_{yit},\end{array}$(2) )), they have only direct effects on observed scores.

The (linear) LGM can be expressed as

$x_{it}=f_{xit}+{ϵ}_{xit},y_{it}=f_{yit}+{ϵ}_{yit}$

(13) $f_{xit}=I_{xi}+(t-1)S_{xi}+f_{xit}^{\ast },f_{yit}=I_{yi}+(t-1)S_{yi}+f_{yit}^{\ast }$(13)

$f_{xit}^{\ast }=0,f_{yit}^{\ast }=0,$

by excluding temporal group means $\mu$, accumulating factors $A$ and $B$, lagged effects (i.e., setting ${\beta }_x={\beta }_y={\gamma }_x={\gamma }_y=0$) and (dynamic) residuals $d$ from the unified framework.

One feature of the LGM is that it does not include lagged effects, implying that the distinction between the dynamic equations and other equations becomes meaningless in this special case. Therefore, if we temporarily disregard the original definition that terms included in the dynamic equations are to be modeled by lagged effects, we can find another expression of the (linear) LGM using different symbols:

$x_{it}=f_{xit},y_{it}=f_{yit}$

(14) $f_{xit}=f_{xit}^{\ast },f_{yit}=f_{yit}^{\ast }$(14)

$f_{xit}^{\ast }=A_{xi}+(t-1)B_{xi}+d_{xit},f_{yit}^{\ast }=A_{yi}+(t-1)B_{yi}+d_{yit}.$

Conceptually, the common factors ($A$ and $B$) and $d$ included in this expression are to be interpreted as growth factors and unique factors, rather than as accumulating factors and (dynamic) residuals, respectively.

The ALT model can be expressed within the unified framework as

$x_{it}=f_{xit},y_{it}=f_{yit}$

(15) $f_{xit}=f_{xit}^{\ast },f_{yit}=f_{yit}^{\ast }$(15)

$f_{xit}^{\ast }=\{A_{xi}+(t-1)B_{xi}\}+{\beta }_x{f}_{xi(t-1)}^{\ast }+{\gamma }_x{f}_{yi(t-1)}^{\ast }+d_{xit}$

$f_{yit}^{\ast }=\{A_{yi}+(t-1)B_{yi}\}+{\beta }_y{f}_{yi(t-1)}^{\ast }+{\gamma }_y{f}_{xi(t-1)}^{\ast }+d_{yit},$

by excluding $ϵ$, $\mu$, and the growth factors $I$ and $S$. We provide path diagrams of the existing models (expressed using the unified framework) as well as the unified framework itself in Figure 1. This should better clarify the properties of trait/growth factors and accumulating factors: the former has only direct effects on observed scores and its influences are temporal, while the latter has both direct and indirect effects and influences feed forward through the lagged relations and accumulate at later time points.

Figure 1. Path diagrams of cross-lagged models. Notes. Residual covariances and covariances between common factors are omitted for clarity of presentation. In the LGM and the unified framework, unique factors (or measurement errors) are indicated by arrows only. Note that the means of common factors in the RI-CLPM and the GCLM are set to zero. In the GCLM, covariances between initial states and accumulating factors are not assumed

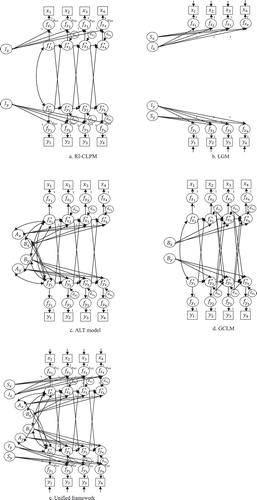
Contrasting the GCLM and the RI-CLPM

Specification of the GCLM from the unified framework

As we have observed, one important key to understanding the differences among the models is whether common factors included in the model are modeled with lagged effects, that is, whether common factors are included in either the decomposition equations (e.g., the RI-CLPM) or the dynamic equations (e.g., the ALT model).

With this point in mind, in this section we first show how the GCLM (i.e., Equation 8)(8) $\begin{array}{r}\begin{array}{c}{x}_{it}={\alpha }_{xt}+{\lambda }_{xt}{B}_{xi}+{\beta }_x{x}_{i(t-1)}+{\gamma }_x{y}_{i(t-1)}+{\delta }_x{d}_{xi(t-1)}\\ +{\zeta }_x{d}_{yi(t-1)}+d_{xit}\\ y_{it}={\alpha }_{yt}+{\lambda }_{yt}{B}_{yi}+{\beta }_y{y}_{i(t-1)}+{\gamma }_y{x}_{i(t-1)}+{\delta }_y{d}_{yi(t-1)}\\ +{\zeta }_y{d}_{xi(t-1)}+d_{yit},\end{array}\end{array}$(8) can be expressed within the unified framework. Then we discuss the interpretative differences of cross-lagged parameters between the GCLM and the RI-CLPM, which was overlooked in Zyphur et al. (2020a, 2020b). We also warn of the potential difficulty of its interpretation in the GCLM.

Like the (RI-)CLPM and the ALT model, the GCLM does not assume unique factors (or measurement errors), meaning $ϵ{}_{xit}=ϵ{}_{yit}=0$. Therefore, the expression in the measurement equations for the GCLM becomes

(16) $\begin{array}{cc}{x}_{it}& =f_{xit}\\ y_{it}& =f_{yit}.\end{array}$(16)

In the GCLM, the common factors ($B$) are modeled jointly with lagged effects to explain observed scores (see Equation (8)(8) $\begin{array}{r}\begin{array}{c}{x}_{it}={\alpha }_{xt}+{\lambda }_{xt}{B}_{xi}+{\beta }_x{x}_{i(t-1)}+{\gamma }_x{y}_{i(t-1)}+{\delta }_x{d}_{xi(t-1)}\\ +{\zeta }_x{d}_{yi(t-1)}+d_{xit}\\ y_{it}={\alpha }_{yt}+{\lambda }_{yt}{B}_{yi}+{\beta }_y{y}_{i(t-1)}+{\gamma }_y{x}_{i(t-1)}+{\delta }_y{d}_{yi(t-1)}\\ +{\zeta }_y{d}_{xi(t-1)}+d_{yit},\end{array}\end{array}$(8) ), indicating that common factors included in this model can be considered as accumulating factors rather than stable trait or growth factors. Therefore, growth factors ($I$ and $S$) in the decomposition equation can be excluded for the specification of the GCLM. Note that the original specification of the GCLM (Equation (8))(8) $\begin{array}{r}\begin{array}{c}{x}_{it}={\alpha }_{xt}+{\lambda }_{xt}{B}_{xi}+{\beta }_x{x}_{i(t-1)}+{\gamma }_x{y}_{i(t-1)}+{\delta }_x{d}_{xi(t-1)}\\ +{\zeta }_x{d}_{yi(t-1)}+d_{xit}\\ y_{it}={\alpha }_{yt}+{\lambda }_{yt}{B}_{yi}+{\beta }_y{y}_{i(t-1)}+{\gamma }_y{x}_{i(t-1)}+{\delta }_y{d}_{yi(t-1)}\\ +{\zeta }_y{d}_{xi(t-1)}+d_{yit},\end{array}\end{array}$(8) includes occasion-specific intercepts $\alpha$. Recall that the mean structure in the model can be expressed by modeling the temporal group means $\mu$ (rather than $\alpha$) as a function of $\alpha$ and lagged effects (Equations (4(4) $\begin{array}{c}E(x_{i3})={\mu }_{x3}={\alpha }_{x3}+{\beta }_x{\alpha }_{x2}+{\gamma }_x{\alpha }_{y2}\\ E(y_{i3})={\mu }_{y3}={\alpha }_{y3}+{\beta }_y{\alpha }_{y2}+{\gamma }_y{\alpha }_{x2}.\end{array}$(4) ) and (5))(5) $\begin{array}{r}\begin{array}{c}E(x_{i4})={\mu }_{x4}={\alpha }_{x4}+{\beta }_x{\alpha }_{x3}+{\gamma }_x{\alpha }_{y3}+[{\beta }_x({\beta }_x{\alpha }_{x2}+{\gamma }_x{\alpha }_{y2})\\ +{\gamma }_x({\beta }_y{\alpha }_{y2}+{\gamma }_y{\alpha }_{x2})]\\ E(y_{i4})={\mu }_{y4}={\alpha }_{y4}+{\beta }_y{\alpha }_{y3}+{\gamma }_y{\alpha }_{x3}+[{\beta }_y({\beta }_y{\alpha }_{y2}+{\gamma }_y{\alpha }_{x2})\\ +{\gamma }_y({\beta }_x{\alpha }_{x2}+{\gamma }_x{\alpha }_{y2})].\end{array}\end{array}$(5) . Therefore, we can express the decomposition equations for the GCLM using $\mu$ as

(17) $\begin{array}{cc}{f}_{xit}& ={\mu }_{xt}+f_{xit}^{\ast }\\ f_{yit}& ={\mu }_{yt}+f_{yit}^{\ast }.\end{array}$(17)

As we have observed, the GCLM includes MA and CLMA terms to explain observed scores. However, these terms were not originally included in the unified framework. For concision, suppose we slightly extend the unified framework to include these terms in the dynamic equations and assume the weights (i.e., factor loadings) of accumulating factors $B$ are fixed to $t-1$ in the GCLM. Then, the dynamic equations for the GCLM can be expressed as

(18) $\begin{array}{r}\begin{array}{c}{f}_{xit}^{\ast }=(t-1)B_{xi}+{\beta }_x{f}_{xi(t-1)}^{\ast }+{\gamma }_x{f}_{yi(t-1)}^{\ast }+{\delta }_x{d}_{xi(t-1)}\\ +{\zeta }_x{d}_{yi(t-1)}+d_{xit}\\ f_{yit}^{\ast }=(t-1)B_{yi}+{\beta }_y{f}_{yi(t-1)}^{\ast }+{\gamma }_y{f}_{xi(t-1)}^{\ast }+{\delta }_y{d}_{yi(t-1)}\\ +{\zeta }_y{d}_{xi(t-1)}+d_{yit},\end{array}\end{array}$(18)

by excluding accumulating factors $A$. Note that the occasion-specific intercepts $\alpha$, which are included in the original specifications of the GCLM (Equation (8)(8) $\begin{array}{r}\begin{array}{c}{x}_{it}={\alpha }_{xt}+{\lambda }_{xt}{B}_{xi}+{\beta }_x{x}_{i(t-1)}+{\gamma }_x{y}_{i(t-1)}+{\delta }_x{d}_{xi(t-1)}\\ +{\zeta }_x{d}_{yi(t-1)}+d_{xit}\\ y_{it}={\alpha }_{yt}+{\lambda }_{yt}{B}_{yi}+{\beta }_y{y}_{i(t-1)}+{\gamma }_y{x}_{i(t-1)}+{\delta }_y{d}_{yi(t-1)}\\ +{\zeta }_y{d}_{xi(t-1)}+d_{yit},\end{array}\end{array}$(8) ), are not modeled here because temporal group means $\mu$ in the decomposition equations already account for the mean structure. A path diagram of the GCLM within the unified framework is provided in Figure 1.

To better clarify the relations among models including the GCLM, a conceptual diagram is provided in Figure 2, which is an extension of the figure provided in Usami, Murayama et al. (2019). Note that we assumed time-invariant autoregressive and cross-lagged parameters in all the models here, though this assumption can be relaxed.

Figure 2. Conceptual diagram clarifying relations among cross-lagged models as an extension of Usami, Murayama et al. (2019). Notes. Single-headed arrows indicate nested relations, with dotted lines indicating relations that can be conditionally satisfied. Double-headed dotted lines indicate that models are statistically equivalent under particular circumstances. Note that we suppose time-invariant autoregressive and cross-lagged parameters in all models. Hamaker (2005) compared the ALT model and the LCM-SR, and McArdle (2009) explained that the LGM (or, latent curve model: LCM) is a special version of the LCS model. Usami, Hayes & McArdle (2015) showed that the factor CLPM (i.e., CLPM that includes measurement errors) is a special version of the TCS model (i.e., LCS model that assumes time-varying factor loadings for accumulating factors). GCLM: general cross-lagged panel model; CLPM: cross-lagged panel model; RI-CLPM: random-intercepts CLPM; STARTS: stable trait autoregressive trait and state; LCM-SR: latent curve model with structured residuals; ALT: autoregressive latent trajectory; LCS: latent change score; TCS: triple change score

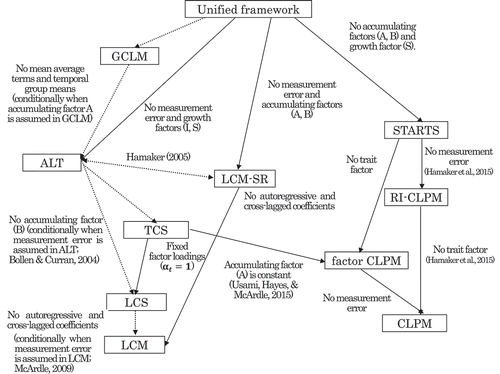
As we have observed, the GCLM and the ALT model commonly include accumulating factors, and a special case of the GCLM (in which weights are set to $\lambda =t-1$, intercepts as well as MA and CLMA terms are excluded as zero, and one additional common factor $A$ is included instead) is mathematically equivalent to the ALT model. Thus, we express the (conditionally) nested relations between these two models in the diagram.

In sum, the GCLM can be viewed as a model in which all terms (excepts for temporal group means $\mu$) are posited in the dynamic equations, as in the ALT model. Thus, it is again obvious that the common factors included in the GCLM can be viewed as accumulating factors rather than as stable trait or growth factors. Therefore, one important conclusion of this article is that the common factors (unit effects) included in the GCLM cannot be interpreted as the stable trait factors used in the RI-CLPM, and that the GCLM does not control for the stable traits as in the RI-CLPM. In addition, the description that compares the RI-CLPM and the GCLM in Zyphur et al. (2020b, p. 13) is incorrect, because a variant of the RI-CLPM (i.e., a special case of the RI-CLPM that assumes specific weights for stable trait factors $I$) is not mathematically equivalent to the GCLM with MA and CLMA terms eliminated.

Mathematical definition of stable traits and illustration of what the GCLM and the RI-CLPM control for

Psychometricians have used the terms “(stable) traits” and “within-person relations” in ambiguous ways when describing SEM-based longitudinal models, despite mathematical and interpretative differences existing between them. Common factors that play a role as accumulating factors have been called by different names. The unified framework helps to resolve this problem and facilitate comparison of different models. In this subsection we provide a mathematical definition of stable traits, and mathematically sketch what the GCLM and the RI-CLPM control for through common factors.

Inspired by the formulation of the RI-CLPM and the unified framework, Usami (2020) defined a stable trait factor (say, for variable $Y$) for person $i$ as the difference between expected value for an observation (the true score) of this person at time $t$ (expressed as ${\mu }_{yit}$) and the temporal group mean at time $t$ (${\mu }_{yt}$) that are invariant over time as

(19) $I_{yi}={\mu }_{yit}-{\mu }_{yt},$(19)

where $-\mathrm{\infty }<{\mu }_{yit}<\mathrm{\infty }$ and $-\mathrm{\infty }<{\mu }_{it}<\mathrm{\infty }$. Note that $E(I_{yi})=E({\mu }_{yit}-{\mu }_{yt})={\mu }_{yt}-{\mu }_{yt}=0$. Then, the within-person variability score $y_{it}^{\ast }$ is also defined as the temporal deviation of person $i$ at time $t$ (i.e., the difference between an observation and its expected value) as

(20) $y_{it}^{\ast }=y_{it}-{\mu }_{yit}=y_{it}-({\mu }_{yt}+I_{yi}),$(20)

assuming that $E(y_{it}^{\ast })$=0 and $Cov({\mu }_{yit},y_{it}^{\ast })=0$ (i.e., expected values of observations and within-person variability scores are uncorrelated). Then, Usami (2020) proposed a general procedure for estimating causal effects of time-varying treatments or predictors on outcomes using within-person variability scores that are estimated by a factor analysis model.

As we have argued, the role of common factors critically depends on whether they are separated from lagged relations in the model. Because accumulating factors included in dynamic equations are not separated from the lagged relations in the model, they do not satisfy the relation in Equation (19)(19) $I_{yi}={\mu }_{yit}-{\mu }_{yt},$(19) (i.e., the difference between the expected value of observation (true score) for person $i$ and the temporal group mean is not invariant over time). To illustrate this point, we dig into the observed score of variable $Y$ at time $t$ ($y_{it}$) in the RI-CLPM and the GCLM. In the RI-CLPM, $y_{it}$ can be re-expressed using Equations (1(1) $\begin{array}{cc}{x}_{it}& ={\mu }_{xt}+I_{xi}+x_{it}^{\ast }\\ y_{it}& ={\mu }_{yt}+I_{yi}+y_{it}^{\ast }.\end{array}$(1) ) and (2(2) $\begin{array}{cc}{x}_{it}^{\ast }& ={\beta }_x{x}_{i(t-1)}^{\ast }+{\gamma }_x{y}_{i(t-1)}^{\ast }+d_{xit}\\ y_{it}^{\ast }& ={\beta }_y{y}_{i(t-1)}^{\ast }+{\gamma }_y{x}_{i(t-1)}^{\ast }+d_{yit},\end{array}$(2) ) as

$y_{it}={\mu }_{yt}+I_{yi}+y_{it}^{\ast }$

$={\mu }_{yt}+I_{yi}+{\beta }_{yt}{y}_{i(t-1)}^{\ast }+{\gamma }_{yt}{x}_{i(t-1)}^{\ast }+d_{yit}$

$={\mu }_{yt}+I_{yi}+{\beta }_{yt}({\beta }_{y(t-1)}{y}_{i(t-2)}^{\ast }+{\gamma }_{y(t-1)}{x}_{i(t-2)}^{\ast }+d_{yi(t-1)})$

(21) $+{\gamma }_{yt}({\beta }_{x(t-1)}{x}_{i(t-2)}^{\ast }+{\gamma }_{x(t-1)}{y}_{i(t-2)}^{\ast }+d_{xi(t-1)})+d_{yit}.$(21)

This expression shows that stable trait factor $I_{yi}$ has a direct effect on $y_{it}$, since it does not show up in the lagged terms in Equation (21)(21) $+{\gamma }_{yt}({\beta }_{x(t-1)}{x}_{i(t-2)}^{\ast }+{\gamma }_{x(t-1)}{y}_{i(t-2)}^{\ast }+d_{xi(t-1)})+d_{yit}.$(21) . As a result, the expected score for person $i$ at $t$ is ${\mu }_{yit}={\mu }_{yt}+I_{yi}$. Thus, ${\mu }_{yit}-{\mu }_{yt}=({\mu }_{yt}+I_{yi})-{\mu }_{yt}=I_{yi}$, indicating that the stable trait factor in the RI-CLPM satisfies the definition in Equation (19)(19) $I_{yi}={\mu }_{yit}-{\mu }_{yt},$(19) .

In contrast, in the GCLM, it can be shown that accumulating factor $B_{yi}$ has both direct and indirect effects on $y_{it}$. Using Equation (8)(8) $\begin{array}{r}\begin{array}{c}{x}_{it}={\alpha }_{xt}+{\lambda }_{xt}{B}_{xi}+{\beta }_x{x}_{i(t-1)}+{\gamma }_x{y}_{i(t-1)}+{\delta }_x{d}_{xi(t-1)}\\ +{\zeta }_x{d}_{yi(t-1)}+d_{xit}\\ y_{it}={\alpha }_{yt}+{\lambda }_{yt}{B}_{yi}+{\beta }_y{y}_{i(t-1)}+{\gamma }_y{x}_{i(t-1)}+{\delta }_y{d}_{yi(t-1)}\\ +{\zeta }_y{d}_{xi(t-1)}+d_{yit},\end{array}\end{array}$(8) , we can re-express $y_{it}$ in the GCLM as

$\begin{array}{l}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}{y}_{it}={\alpha }_{yt}+{\lambda }_{yt}{B}_{yi}+{\beta }_y{y}_{i(t-1)}+{\gamma }_y{x}_{i(t-1)}\\ +{\delta }_y{d}_{yi(t-1)}+{\zeta }_y{d}_{xi(t-1)}+d_{yit}\\ ={\alpha }_{yt}+{\lambda }_{yt}{B}_{yi}+{\beta }_y({\alpha }_{y(t-1)}+{\lambda }_{y(t-1)}{B}_{yi}+{\beta }_y{y}_{i(t-2)}\\ +{\gamma }_y{x}_{i(t-2)}+{\delta }_y{d}_{yi(t-2)}+{\zeta }_y{d}_{xi(t-2)}+d_{yi(t-1)})\\ +{\gamma }_y({\alpha }_{x(t-1)}+{\lambda }_{x(t-1)}{B}_{xi}+{\beta }_x{x}_{i(t-2)}+{\gamma }_x{y}_{i(t-2)}\\ +{\delta }_x{d}_{xi(t-2)}+{\zeta }_x{d}_{yi(t-2)}+d_{xi(t-1)})+{\delta }_y{d}_{yi(t-1)}\\ +{\zeta }_y{d}_{xi(t-1)}+d_{yit}\end{array}$

(22) $={\alpha }_{yt}+({\lambda }_{yt}+{\beta }_y{\lambda }_{y(t-1)})B_{yi}+{\gamma }_y{\lambda }_{x(t-1)}{B}_{xi}+{\beta }_y({\alpha }_{y(t-1)}\text{break}+{\beta }_y{y}_{i(t-2)}+{\gamma }_y{x}_{i(t-2)}+{\delta }_y{d}_{yi(t-2)}+{\zeta }_y{d}_{xi(t-2)}\text{break}+d_{yi(t-1)})+{\delta }_y{d}_{yi(t-1)}+{\zeta }_y{d}_{xi(t-1)}+d_{yit}.$(22)

This shows that the effect of the common factor $B_{yi}$ is different at each time point, and its function becomes increasingly more complex at later time points. In the first line, where $y_{it}$ and $y_{i(t-1)}$ are contrasted, the effect of the accumulating factor appears as ${\lambda }_{yt}{B}_{yi}$. However, in the third line, where $y_{it}$ and $y_{i(t-2)}$ are contrasted, the effect becomes $({\lambda }_{yt}+{\beta }_y{\lambda }_{y(t-1)})B_{yi}$, which reflects both a direct effect and an indirect effect of $B_{yi}$. $B_{xi}$ also impacts $y_{it}$ (${\gamma }_y{\lambda }_{x(t-1)}{B}_{xi}$). Furthermore, the third line also suggests that the expected score for person $i$ on variable $Y$ at $t(\ge 3)$ is a function of a) occasion-specific intercepts $\alpha$, b) occasion-specific factor loadings $\lambda$, c) the common factors $B$, d) the lagged parameters $\beta$ and $\gamma$, and e) the initial states $y_{i1}$ and $x_{i1}$. These suggest that the difference between the expected value of observation (true score) for person $i$ and the temporal group mean is not equal to $B_{yi}$ and not invariant over time. Namely, the accumulating factor in the GCLM (or the ALT model) does not satisfy the definition in Equation (19)(19) $I_{yi}={\mu }_{yit}-{\mu }_{yt},$(19) . Zyphur et al. (2020a, p. 9) gave reasons for allowing the effect of accumulating factor $B$ to vary over time (${\lambda }_t\ne \lambda$), and the definition of stable trait factors Equation (19)(19) $I_{yi}={\mu }_{yit}-{\mu }_{yt},$(19) might be expanded to allow such time-varying effects. Regardless of how we define stable traits, however, this observation reveals that mathematical roles differ between stable trait factors in the RI-CLPM and the accumulating factors in the GCLM (or the ALT model), and that the GCLM (or the ALT model) does not control for stable traits as in the RI-CLPM.

Interpretation of cross-lagged parameters in the GCLM

Given the above, how can the cross-lagged parameters in the GCLM be interpreted, and how is this different from other models, such as the RI-CLPM? Zyphur et al. (2020a) explained how the range of dynamic processes that can be modeled increases by including MA and CLMA terms, and also discussed two threats to causal inference (trends and regime changes). However, they did not provide a clear explanation of how to interpret cross-lagged parameters in the GCLM. Below we discuss the potential difficulty of interpreting cross-lagged parameters in the GCLM from two aspects: including the accumulating factors, and the MA and CLMA terms. Here we partly refer to Usami, Murayama et al. (2019) for the former point.

Accumulating factors. As we have argued, the accumulating factors have both a direct effect and an indirect effect on outcomes Equation (22)(22) $={\alpha }_{yt}+({\lambda }_{yt}+{\beta }_y{\lambda }_{y(t-1)})B_{yi}+{\gamma }_y{\lambda }_{x(t-1)}{B}_{xi}+{\beta }_y({\alpha }_{y(t-1)}\text{break}+{\beta }_y{y}_{i(t-2)}+{\gamma }_y{x}_{i(t-2)}+{\delta }_y{d}_{yi(t-2)}+{\zeta }_y{d}_{xi(t-2)}\text{break}+d_{yi(t-1)})+{\delta }_y{d}_{yi(t-1)}+{\zeta }_y{d}_{xi(t-1)}+d_{yit}.$(22) , and the same is true even if occasion-specific factor loadings are fixed to 1 ($\lambda =1$). Therefore, the GCLM (or the ALT model) does not control for stable traits as in the RI-CLPM. Because accumulating factor $B$ correlates with observations and its effect differs at each time point, one could say that the GCLM (or the ALT model) implicitly controls for unobserved time-varying confounders, and that those influences feed forward through lagged relations. However, one potential risk of the GCLM is that estimates of cross-lagged parameters are biased and cannot be interpreted as causal estimates unless influences of time-varying confounders are precisely expressed by the complex function of $B$ and $\lambda$, as well as $\beta$ and $\gamma$ Equation (22)(22) $={\alpha }_{yt}+({\lambda }_{yt}+{\beta }_y{\lambda }_{y(t-1)})B_{yi}+{\gamma }_y{\lambda }_{x(t-1)}{B}_{xi}+{\beta }_y({\alpha }_{y(t-1)}\text{break}+{\beta }_y{y}_{i(t-2)}+{\gamma }_y{x}_{i(t-2)}+{\delta }_y{d}_{yi(t-2)}+{\zeta }_y{d}_{xi(t-2)}\text{break}+d_{yi(t-1)})+{\delta }_y{d}_{yi(t-1)}+{\zeta }_y{d}_{xi(t-1)}+d_{yit}.$(22) . Correct specification of a highly structured model such as the GCLM might be a strong assumption in general, and even minor model misspecifications can cause severely biased estimates of cross-lagged parameters.

Even if no model misspecification occurs, the assumption that the GCLM (or the ALT model) controls for unobserved time-varying confounders may be inappropriate for some instances, potentially leading to erroneous conclusions. Specifically, if individual differences in growth captured by accumulating factors in one of the observed variables is actually (in part) the result of growth in another observed variable, then using this model, which might cause unnecessary adjustment (i.e., overadjustment⁵) of growth, is likely to result in biased estimates of reciprocal (as well as causal) effects (Usami, Murayama et al., 2019). Namely, there is a great risk that accumulating factors wrongly account for individual differences in growth, resulting in biased estimates of reciprocal effects if such individual differences are considered to be constituent components of these effects.⁶ More importantly, it is very difficult in general for researchers to precisely know what the accumulating factor $B$ as a time-varying latent variable actually represents, causing interpretative difficulty of the cross-lagged parameters if this is included in the model.

In contrast, the RI-CLPM allows for a group-level trajectory (expressed as ${\mu }_t$) that can take on any shape, and each person deviates from this trajectory by a constant distance (i.e., $I$). The reciprocal effects are then modeled between the residuals, that is, the deviations from the expected scores, without controlling for persons’ growths by slope ($S$) or accumulating factors ($A$ and $B$). Hence, in this approach, stable trait factors can be clearly interpreted, and (time-varying) individual differences in growth remain in the reciprocal parts of the model, unlike in the GCLM (or the ALT model). However, if individual differences in growth are actually caused by unobserved time-varying confounders, failing to include them in the model may also cause biased estimates of cross-lagged parameters (Usami, Murayama et al., 2019).

In other words, the critical point of model selection and interpretation of cross-lagged parameters lies in what aspects are considered critical components of reciprocal or causal effects. If (time-varying) individual differences in growth trajectories are considered a critical component of these effects, then the RI-CLPM might be an appropriate choice (Usami, Murayama et al., 2019). On the other hand, if researchers assume that the influences of unobserved time-varying confounders can be perfectly captured by accumulating factors, then the GCLM (or the ALT model) might be a better choice. However, in many cases one can see that growth aspects are considered to be a critical component of reciprocal or causal effects rather than mere unobserved time-varying confounders, so choosing the GCLM (or the ALT model) might not be appropriate. This point implies that two primary analytic purposes of applying longitudinal models that include reciprocal relations-namely, inferring reciprocal effects between variables and modeling individual differences in growth trajectories by common factors-are intertwined (Usami, Murayama et al., 2019).

MA and CLMA terms. We have discussed the potential limitation of interpreting cross-lagged coefficients if accumulating factors are modeled as in the GCLM. However, this problem becomes more complicated in the GCLM because it assumes MA and CLMA terms in addition to accumulating factors.

(CL)MA terms are composed by (dynamic) residuals. The residuals mean that the components of the observed scores that cannot be explained by lagged effects (i.e., deviations of observed scores from temporal group means in the previous time point) as well as accumulating factors (i.e., unit effects). Considering also that the role of the residuals in general is to account for all sources of variation unexplained by the fitted model (e.g., possible model misspecification, unobserved confounders and (dynamic) errors), it is not surprepsilong that the exact meanings of (CL)MA terms (or residuals) are obscure and their interpretations are very difficult in general. This point makes interpretation of cross-lagged parameters much more difficult in the GCLM, and can also cause biased estimates because of overadjustment.

A critical point is that (dynamic) residuals in the CLMA terms are already accounted for as one component of temporal deviations in the CL term. Specifically, say $d_{y(t-1)}$, which is a component of $y_{t-1}$ in the CL term to explain $x_t$, is also accounted for by the CLMA term. This implies that in the GCLM, the same residual $d$ is accounted for twice. Likewise, in the unified framework expression for the GCLM (Figure 1d), $f_{xt}^{\ast }$ is expressed by (i) the direct effect of $d_{y(t-1)}$ (a path $d_{y(t-1)}\to f_{xt}^{\ast }$) and (ii) an indirect effect of $d_{y(t-1)}$ (a path trace $d_{y(t-1)}\to f_{y(t-1)}^{\ast }\to f_{xt}^{\ast }$). This redundancy can cause high correlation between the CL term ($y_{t-1}$) and the CLMA term ($d_{y(t-1)}$). As a result, not only biases in cross-lagged parameter estimates but also multicollinearity (inflated standard errors) might arise.

In sum, accumulating factors and (CL)MA terms included in the GCLM increase the risks of bias, multicollinearity (inflated standard errors), and interpretative difficulty in cross-lagged parameters to estimate reciprocal or causal effects, even if no model misspecification occurs. Although the RI-CLPM is not a perfect procedure for every situation, if the model can be correctly specified and if time-varying confounders can be appropriately controlled for, this choice better infers reciprocal or causal effects occurring at the within-person level. We revisit the issue of time-varying confounders from the view of causal inference later in this article.

Our goal in this article is not to suggest that researchers completely avoid using the model. The GCLM might be a good choice for researchers interested in building a useful linear model to predict observed scores, because this model can increase the range of dynamic processes that can be modeled. However, if the interpretation of cross-lagged parameters (inferring reciprocal effects) or controlling for stable traits (like in the RI-CLPM) is key in the application, applying the GCLM cannot be recommended.

An example using empirical data

This section presents an example using empirical data to show how estimates of reciprocal effects differ depending on model choice. Specifically, we focus on the GCLM and the RI-CLPM to illustrate (i) how differences in common factors included in the models, and (ii) how inclusion of (CL)MA terms in the GCLM influence estimates of reciprocal effects. In this example we investigate the reciprocal relation between adolescents’ exposure to smoking in movies ($X$) and their smoking intensity ($Y$), using data from the Minnesota Adolescent Community Cohort (MACC) Study 2000–2013. The MACC Study is a prospective cohort study designed to expand understanding of the transitional process from nonsmoking to smoking during adolescence and to examine the effect of state- and local-level tobacco prevention and control programs for youth in Minnesota (Choi, Forster, Erickson, Lazovich, & Southwell, 2012). For illustrative purposes we used a sample of 4,671 adolescents aged 15 to 20 years who were surveyed from every six months in most years of the survey. When participants responded to two surveys in a year, only response data from the first survey were used to construct the dataset of $T=6$. More detailed information about the study design and population in the MACC study is available in Choi et al. (2012) and from the website of the Inter-university Consortium for Political and Social Research.⁷ Usami, Murayama et al. (2019) used the same dataset to compare estimates of reciprocal effects among various models, though they did not include the GCLM in this comparison. In this example we newly fit the GCLM to the dataset for illustrative purposes.

Exposure to smoking in movies and smoking intensity were assessed during each round of data collection. Participants were asked to report how often they saw actors and actresses smoking when they watched movies, with four response options: most of the time (4), some of the time (3), hardly ever (2) and never (1). The data also included an index for six levels of smoking intensity, which was created by five measures (see Choi et al., 2012, for details). There were two sources of missing data, those missing by design and those by attrition. We used all available data when estimating parameters of the models, but we removed data for one participant with missing data for all variables at all time points. All analyses were conducted using the lavaan package (Rosseel, 2012) in R with the full information maximum likelihood estimation method. The lavaan source code used in this example is available in the Online Supplemental Materials.

To clarify the comparison between the models, in this example occasion-specific factor loadings are all fixed to 1 (${\lambda }_{xt}=1$ and ${\lambda }_{yt}=1$), and covariances between the first states ($x_{i1}$ and $y_{i1}$) and accumulating factors $B$ were not assumed in the GCLM. We then fit two kinds of first-order GCLMs to the dataset: AR(1)MA(1)CL(1)CLMA(1) and AR(1)CL(1). Comparison between these two GCLMs illustrates how inclusion of the (CL)MA terms affects estimates of cross-lagged parameters in the GCLM. Because the number of parameters is the same and the kind of common factor included is the only difference between AR(1)CL(1) and the RI-CLPM, comparing estimates from these two models illustrates how choice of common factors included in the model affects estimates of cross-lagged parameters. In both the GCLMs and the RI-CLPM, we assume stationarity of parameters (e.g., equality of AR, CL, and CL(MA) effects and residual (co)variances over time). However, because the AR(1)MA(1)CL(1)CLMA(1) model resulted in an improper solution, we assumed non-stationarity of parameters for residual variances of $X$ and residual covariances in this model.

Table 1 shows parameter estimates and fit indices from the RI-CLPM and the two GCLMs. The RI-CLPM showed nonsignificant estimates for both cross-lagged parameters (exposure to smoking in movies $X$ did not predict later smoking intensity $Y$, and vice versa), while the two GCLMs showed significant estimates. The AR(1)MA(1)CL(1)CLMA(1) fit better than did the other models, and resulted in significant estimates for both cross-lagged parameters. Note that this model also showed relatively larger standard errors, implying the influence of multicollinearity caused by correlations among accumulating factors ($B$), (lagged) observations ($x_{i(t-1)}$ and $y_{i(t-1)}$), and (lagged) residuals ($d_{xi(t-1)}$ and $d_{yi(t-1)}$).

Table 1. Parameter estimates and model fit indices from different longitudinal models (N = 4,670)

Parameters and model fit indices	RI-CLPM			GCLM
				AR(1)MA(1)CL(1)CLMA(1)			AR(1)CL(1)
	Est.	SE	p	Est.	SE	p	Est.	SE	p
βy	0.700	0.012	0.000	0.708	0.028	0.000	0.525	0.016	0.000
γy	−0.005	0.022	0.824	−0.181	0.044	0.000	−0.031	0.020	0.122
βx	0.166	0.011	0.000	0.273	0.025	0.000	0.142	0.010	0.000
γx	−0.008	0.007	0.250	−0.083	0.013	0.000	−0.021	0.007	0.001
CFI	0.959			0.975			0.962
AIC	72224.166			72000.100			72181.582
BIC	72385.389			72238.710			72342.805
RMSEA [95% CI]	0.045 [0.042, 0.048]			0.039 [0.036, 0.043]			0.043 [0.040, 0.047]
SRMR	0.066			0.054			0.068
Degrees of freedom	65			53			65
Number of parameters	25			37			25

Note. Analysis result of the RI-CLPM is the same from Usami, Murayama et al. (2019). In the GCLM occasion-specific factors loadings were all fixed to 1, and covariances between the initial states and accumulating factor were not assumed. Because the AR(1)MA(1)CL(1)CLMA(1) model showed the improper solutions, the stationarity assumption was relaxed for residual variance of X and residual covariance. RI-CLPM random-intercept cross-lagged panel model; GCLM; general cross-lagged panel model; CFI comparative fit index; AIC Akaike information criterion; BIC Bayesian information criterion; RMSEA root mean square error of approximation; CI confidence interval; SRMR standardized root mean square residual.

This example clearly demonstrates the risk of drawing different conclusions based on the cross-lagged parameters from different models. Focusing on model fit, the AR(1)MA(1)CL(1)CLMA(1) model would be the most appropriate for these data. Moreover, since model fits of the two GCLMs were much better than that of the RI-CLPM, it seems safe to conclude that there are omitted time-varying confounders affecting both observed variables.

As we have argued, however, cross-lagged parameters in the AR(1)MA(1)CL(1)CLMA(1) model are very difficult to interpret and also pose greater risks of bias in its estimates due to inclusion of (CL)MA terms and accumulating factors. If researchers are interested in estimating reciprocal or causal effects and can reasonably expect that influences of unobserved time-varying confounders can be perfectly expressed as accumulating factor $B$, choosing the estimation results from the AR(1)CL(1) model should be more reasonable than use of the AR(1)MA(1)CL(1)CLMA(1) model. In most cases, however, researchers are uncertain regarding how the impacts of unobserved time-varying confounders shift over time. If longitudinal changes in smoking intensity and exposure to smoking in movies are considered critical components of reciprocal effects, AR(1)CL(1) is an inappropriate option, and the RI-CLPM could be an option. In this case, it would be reasonable to conclude that there are no significant reciprocal effects between these variables. However, from the view of causal inference, we need to consider that their estimates of reciprocal effects in the RI-CLPM might be biased due to omitted time-varying confounders. To mitigate this risk, including observed time-varying confounders in this model should be a useful strategy, and this is discussed further in the next section.

Estimating causal effects by the RI-CLPM and recent potential outcome approaches

As we have argued, including accumulating factors and (CL)MA terms as in the GCLM should increase risk of bias in reciprocal or causal effect estimates. The RI-CLPM, which does not include these components, separates within-person fluctuations (temporal deviations) from stable between-person differences (stable trait factors) over time, and cross-lagged relations in Equation (2)(2) $\begin{array}{cc}{x}_{it}^{\ast }& ={\beta }_x{x}_{i(t-1)}^{\ast }+{\gamma }_x{y}_{i(t-1)}^{\ast }+d_{xit}\\ y_{it}^{\ast }& ={\beta }_y{y}_{i(t-1)}^{\ast }+{\gamma }_y{x}_{i(t-1)}^{\ast }+d_{yit},\end{array}$(2) can be considered as those pertaining to a process that takes place at the within-person level. From the view of the potential outcome approach, which is currently the standard framework for defining causal effects, within-person reciprocal effects estimated in the RI-CLPM can represent causal effects under assumption of no model errors and no unobserved confounders (see Usami, Murayama et al., 2019; Usami, 2020 for more details). If measurement errors (violation of the consistency assumption) are expected to be present, using the STARTS model, which is a simple extension of the RI-CLPM to allow measurement errors, might be an option. However, see Usami, Todo et al. (2019) and Orth et al. (in press) for further discussion about improper solutions frequently appearing in the STARTS model.

Regardless of which model we take, estimates of cross-lagged parameters are biased if there are omitted unobserved confounders. When time-varying observed confounders are available, a typical approach is to directly include them into the model like an analysis of covariance (ANCOVA). This approach requires assumptions of linearity and additivity of relations between outcomes and confounders. Namely, even if observed confounders are included when applying the RI-CLPM (or the STARTS model), it requires correctly specified linear regressions to connect variables at the within-person level. However, the linearity that is typically assumed in path modeling and SEM has often been criticized in the causal inference literature (e.g., Hong, 2015).

To mitigate this problem, non-SEM approaches such as marginal structural models (MSMs; Robins, 1998, 1999; Robins et al., 2000) or structural nested mean models (SNMMs; e.g., Robins, 1994, 1999) with $G$-estimators are useful. They have been applied in epidemiology to estimate the causal effects of sequences of time-varying treatments or predictors $A_{(t-1)}={(A_{(t-1)},A_{(t-2)},\dots ,A_1)}^{\text{t}}$ on outcomes $Y_t$. Although these methods originally considered the situation where one is interested in evaluating a unidirectional relation (the effect of a treatment on an outcome) rather than reciprocal relations, they can be extended in a straightforward manner.

In MSMs, researchers specify a treatment assignment model $f(A_{(t-1)}|{\mathit{L}}_{(\mathit{t}-\mathbf{1})})$ at time point $t-1$ (and previous time points) to express the probability that one receives a certain level of treatment or predictors $A_{(t-1)}=a_{(t-1)}$ using the history of observed confounders ${\mathit{L}}_{{ }_{(\mathit{t}-\mathbf{1})}}=(L_{(t-1)},L_{(t-2)},\dots ,L_1{)}^t$. Next, the inverse probability weights (IPW) required for estimating an outcome model $f(Y_t|{\mathit{A}}_{{ }_{(\mathit{t}-\mathbf{1})}})$ are calculated using information of inverse probability $1/\hat{f}(A_{(t-1)}|{\mathit{L}}_{(t-1)})$ at time point $t-1$ (and previous time points) under the assumption of no unobserved confounders or sequential ignorability. Causal effects are then estimated by fitting a weighted outcome model with an IPW estimator. Unlike ANCOVA, MSMs do not demand that researchers model the relation between outcomes and observed confounders. In general, MSMs can be easily understood and fit with standard, off-the-shelf software that allows for weights (Vansteelandt & Joffe, 2014). However, it is also well-known that MSMs can be highly sensitive to misspecification of the treatment assignment model, even when there is a moderate number of time points (e.g., Hong, 2015; Lefebvre et al., 2008). Imai and Ratkovic (2015) proposed a covariate balancing propensity score methodology for robust IPW estimation.

Although actual applications have been relatively infrequent, mainly due to a lack of the off-the-shelf software (however, see Wallace et al., 2017 as an exception), SNMMs with $G$-estimators are a better approach for handling violation of assumption of no unobserved confounders or sequential ignorability (Vansteelandt & Joffe, 2014). Specifically, by solving estimating equations constructed based on this assumption, consistent estimates of causal parameters can be obtained when either a treatment assignment model or a model for outcome that would be observed if the treatment were stopped from a specific time can be correctly specified (the doubly robust property; see Vansteelandt & Joffe, 2014; Usami, 2020 for details). In addition, SNMMs can allow direct modeling of the interactions and moderation effects of treatments or predictors with observed confounders. Another advantage of SNMMs is that the variance of locally efficient IPW estimators in MSMs exceeds that of $G$-estimators in SNMMs, unless treatments or predictors and observed confounders are independent.

Note that observed confounders are typically included in applications of MSMs and SNMMs. That is, they do not often explicitly include latent variables or common factors like the stable trait factors. This implies that stable individual differences might not be adequately controlled for in usual applications of MSMs and SNMMs. Usami (2020) proposes a two-step analysis method for within-person variability scores-based causal inference to estimate joint effects of time-varying treatments or predictors by controlling for stable traits as time-invariant unobserved confounders. In this method, within-person variability scores for each person Equation (20)(20) $y_{it}^{\ast }=y_{it}-{\mu }_{yit}=y_{it}-({\mu }_{yt}+I_{yi}),$(20) , which are disaggregated from stable traits of that person, are first calculated through a factor analysis model. Causal parameters are then estimated via a potential outcome approach, either MSMs or SNMMs, using calculated within-person variability scores. Through simulation and empirical application, it was shown that the proposed method can recover causal parameters well and that causal estimates might be severely biased if one does not properly account for stable traits. It should be beneficial for researchers to take such non-SEM-based approaches as possible alternatives in future research, especially if they aim to effectively and flexibly control for time-varying confounders.

Conclusion

We discussed how common factors and cross-lagged parameters included in the GCLM can be interpreted using a unified framework, highlighting the conceptual and mathematical differences among the GCLM, the RI-CLPM, and other longitudinal models. Our conclusions can be summarized as follows: (1) Common factors included in the GCLM are not stable trait factors (as included in the RI-CLPM), but are accumulating ones (as included in the ALT model), which have both direct and indirect influences on observed scores, meaning that the GCLM does not control for stable traits of persons as does the RI-CLPM. (2) Including accumulating factors as well as (CL)MA terms, which are main features of the GCLM, makes the interpretation of cross-lagged parameters very complicated in general. (3) Even if no model misspecification occurs, seriously biased estimates of cross-lagged parameters (and inflated standard errors) might be obtained in the GCLM when (time-varying) individual differences in the growth trajectories accounted for by accumulating factors are critical components of reciprocal or causal effects. (4) Although the GCLM might be an option if one is especially interested in predicting outcomes, applying this approach entails great risk if uncovering reciprocal or causal effects is the primary focus. (5) Although the RI-CLPM (and the STARTS model) is not a perfect procedure for every situation, if the model can be correctly specified and if time-varying confounders can be appropriately controlled for, this choice is better to infer reciprocal or causal effects that occur at a within-person level. Finally, (6) If one aims to effectively and flexibly control for time-varying confounders, the RI-CLPM (or the STARTS model) with ANCOVA approach is not the only option, and it is beneficial to take non SEM-based approaches such as MSMs and SNMMs as possible alternatives. Table 2 summarizes our discussion of each model.

Table 2. Summary of methods

Method	Minimum T required for identification in stationarity (non-stationarity)assumption	Common factor controlled for	Can control for stable traits (Equation 19(19) $I_{yi}={\mu }_{yit}-{\mu }_{yt},$(19) ) as unobserved time-invariant confounders	Can control for unobserved time-varying confounders by common factors (has also a risk that factors wrongly account for critical components [individual differences of growth] in reciprocal or causal effects)	Has interpretative difficulty of cross-lagged parameters due to MA terms	Is SEM-based approach (also requires correctly specified [linear] regression models between [observed] time-varying confounders and outcomes)
CLPM	2 (2)	No factor	No	No	No	Yes
RI-CLPM	3 (3)	Stable trait factor	Yes	No	No	Yes
ALT	4 (5)	Accumulating factor	No	Yes	No	Yes
GCLMAR(1)MA(1)CL(1)CLMA(1)AR(1)CL(1)	3* (4*)	Accumulating factor	No	Yes	Yes	Yes
	3* (3*)	Accumulating factor	No	Yes	No	Yes
Within-person variability scores based method with MSMs and SNMMs (Usami, 2020)	3	Stable trait factor	Yes	No	No	No

Note. The assumption of stationarity indicates that autoregressive parameters, cross-lagged parameters, moving-average parameters and residual (co)variances are time invariant, whereas non-stationarity indicates time-varying. *In the GCLM, time-varying loadings from accumulating factors B were assumed to be prespecified as λt = 1, and covariances between the initial states and accumulating factor were not assumed. CLPM cross-lagged panel model; RI-CLPM random-intercept CLPM; ALT autoregressive latent trajectory model; GCLM general cross-lagged panel model; MSMs marginal structural models; SNMMs structural nested mean models

Notably, regarding the last point, SNMMs with $G$-estimators are a better approach for handling violation of assumption of no unobserved confounders or sequential ignorability, because of their doubly robust property. However, MSMs and SNMMs originate from epidemiology and thus have not been broadly used in the behavioral sciences. In future studies, we plan to contrast these methods with various longitudinal models from both conceptual and mathematical viewpoints, and to introduce the within-person variability scores-based causal inference approach (Usami, 2020). Because estimation performance of these methods has not been exhaustively compared with the RI-CLPM (with an ANCOVA approach), this point should be investigated in future studies. We hope this corner and related future studies will help researchers choose better methodologies when aiming to uncover reciprocal or causal effects with minimal risk of obtaining wrong conclusions.

Correction Statement

This article has been republished with minor changes. These changes do not impact the academic content of the article.

Additional information

Funding

This work was supported by the Japan Society for the Promotion of Science [19K14378].

Notes

¹ Based on a literature search using the UTokyo REsource Explorer (TREE; http://tokyo.summon.serialssolutions.com/) search engine on Oct 28, 2019. TREE aggregates information from many major databases, including Web of Science, PubMed, PsycINFO, Engineering Village, ERIC, and JSTOR, as well as electronic journals under contract with the University of Tokyo. We used the keyword “cross-lagged,” searching papers published in English from Oct 2018 to Oct 2019. We limited our search to only peer-reviewed papers, resulting in 1,065 papers found. Most were applied research, though some were research reviews or theoretical/methodological studies.

² Note that the original introduction in Hamaker et al. (2015) assumed time-varying autoregressive and cross-lagged parameters, but we assume here, without loss of generality, time-invariant parameters to keep the discussion concise.

³ Zyphur et al. (2020a) used the term “stable factors” rather than “stable trait factors.”

⁴ For consistency between expressions of the introduced models, and to clarify the meanings of parameters and common factors, here we use symbols different from those in Zyphur et al. (2020ab). Specifically, in this article we use symbols ${\lambda }_{xt}$, $B_{xi}$, ${\gamma }_x$, ${\zeta }_x$, and $d_{xit}$, instead of using ${\lambda }_t^{(x)}$, ${\eta }_i^{(x)}$, ${\beta }_y^{(x)}$, ${\delta }_y^{(x)}$, and $u_{it}^{(x)}$, respectively.

⁵ We use the terms unnecessary adjustment or overadjustment to describe a variable that increases net bias and/or decreases precision, while some researchers use these to indicate only the latter meaning. See Schisterman et al. (2009) regarding this point.

⁶ As a variant of the ALT model, we have seen the recent development of a latent variable-autoregressive latent trajectory (LV-ALT) model (Bianconcini & Bollen, 2018), which aims to provide a framework for comparing different longitudinal models and allows researchers to explore alternative structures to best model their longitudinal data. One may wish to apply the bivariate version of this model to evaluate reciprocal effects between variables. However, the risk that accumulating factors wrongly account for (time-varying) individual differences in growth remains in this model.

⁷ https://www.icpsr.umich.edu/icpsrweb/ICPSR/studies/36282