Specification Search in Structural Equation Modeling (SEM): How Gradient Component-wise Boosting can Contribute

ABSTRACT

Although structural equation model (SEM) is a powerful and widely applied tool particularly in social sciences, few studies have explored how SEM and statistical learning methods can be combined. The purpose of this paper is to explore how gradient component-wise boosting (GCB) can contribute to item selection. We ran 200 regressions with different farmer psychological variables collected to explain variation in an animal welfare indicator (AWI). The most frequently selected variables from the regressions were selected to build a SEM to explain variation in the AWI. The results show that boosting selects relevant items for a SEM.

KEYWORDS:

• Specification search
• SEM
• boosting
• statistical learning

Introduction

Structural equation models (SEMs) capture hypotheses about multivariate data by specifying relations among observed entities and hypothesized latent constructs. Generally, specifying a SEM based on substantive theory begins by defining the latent variables and then constructing items to measure them. Sometimes, however, a more exploratory approach is needed. When the substantive theory is weak and a set of variables/items exists but the exact number or meaning of the factors is unknown, specifying a SEM often starts with exploring item correlations and exploratory factor analysis (EFA). Which factors to extract and the number of factors are important steps in EFA, often followed by a confirmatory factor analysis (CFA). In datasets where there is weak correlation between an observed dependent variable and the available explanatory variables or items, it can be challenging to specify factors. Given ever richer datasets, extracting the relevant variables or items to specify factors becomes even more laborious. Commonly applied tools like EFA and CFA work well to extract factors. However, these methods offer little help when one also wants to use the factors to explain variation in a dependent variable because they do not relate the items directly to the variable they are supposed to predict. Thus, we agree with Jacobucci et al. (2019) that there is an increasing need for efficient item selection when constructing a SEM.

Maybe the newcomer ESEM (Exploratory structural equation modeling; Asparouhov and Muthén (2009)), where an EFA measurement model with rotation can be used in a SEM has the potential to help select items.

A commonly used phrase to describe these activities within SEM is conducting a specification search (Long, 1983). The basic idea behind conducting a specification search is to find a better fitting model after comparing distinct SEM models using a chi-square difference test or other selected fit indices (Marcoulides & Falk, 2018). Rudimentary forms of specification searches in SEM may consist of manually fitting alternative models and comparing fit, with model changes based on substantive theory: modification indices to determine which parameters to free; Wald-based tests to determine which parameters to fix; or some synthesis of these approaches (Marcoulides & Falk, 2018).

In parallel with the search for better specification methods in SEM, statistical learning methods (SL) are increasingly used to analyze or find patterns in very large data sets. Hence, there is a need for statistical techniques to select the most informative features or items out of a large set of predictor variables. SL refers to a vast set of tools for modeling and understanding data (James et al., 2017). Thus, SL is concerned with model validity, accurate estimation of model parameters and inference from the model (Fawcett & Hardin, 2017). In the field of SL, a key issue is the development of algorithms for model building and variable selection (Hastie et al., 2009). Much attention has been dedicated to the topic of how predictors can be optimally selected when little or no prior knowledge exists. Boosting algorithms represent one of the most promising methodological approaches for data analysis developed in the last two decades (Mayr et al., 2014). Originally developed in the machine learning community (Freund & Schapire, 1996; Schapire, 1990) primarily to handle classification problems, boosting has been successfully translated into the statistical field (Breiman, 1998; Friedman et al., 2000). In recent years, its use has been extended to many statistical problems. Because boosting fits an additive model or an ensemble in a forward-stagewise manner, some similarities with forward stepwise regression exist. In boosting, however, at each iteration a weak learner, or a learner that performs only slightly better than random, is introduced to compensate for the “shortcomings” of existing weak learners. Gradient component-wise boosting (GCB) (Breiman, 2000; Friedman, 2001), is an example of an innovation that enjoys good predictive performance, e.g., in regressions. GCB performs well in variable selection because it discards the least important ones, and also ranks variables or items by decreasing importance (Efron & Hastie, 2016), both important factors in specifying a SEM. The aim of this paper is to show how GCB can be applied to select relevant items for inclusion in a SEM with only one observed dependent variable.

To more efficiently specify a SEM, recent research has suggested integrating regularization techniques like the Lasso, Ridge and elastic net and SEM (Jacobucci et al., 2019). Various methods for identifying group differences (Frick et al., 2015; Kim & von Oertzen, 2018; Tutz & Schauberger, 2015) together with combinations of SEM and decision trees (Brandmaier et al., 2013) and forests (Brandmaier et al., 2016) have also been suggested. However, few proponents of SEM have explored the merits of boosting in variable selection. Our goal in this paper is to present an example of how boosting, specifically GCB, can help to answer the question: “What subset of items is most predictive for my outcome variable and at the same time gives rise to a reasonable measurement model? “. To answer this question, we use a dataset from dairy farming where an observed continuous outcome variable, an animal welfare indicator (AWI), is only weakly correlated with all items applied (Hansen & Österås, 2019).

To arrive at the SEM suggested in Hansen and Österås (2019), (see Table A1 in the Appendix for an overview), the authors first followed the traditional procedure and started with an EFA to extract factors. Although they managed to extract meaningful factors representing underlying theoretical constructs, the extracted factors showed only weak relationships with AWI, the dependent variable. The problem is that neither the EFA nor the frequently applied principal component analysis (PCA) selects subsets of the predictors or items based on their association with the outcome. Item selection is based solely on the associations among them. Therefore, selecting the relevant items to include in a SEM required significant trial and error. Hansen and Österås (2019) experiences inspired the authors of this paper to use the same dataset as an example of how the specification process can be more streamlined. Our strategy was to combine GCB, CFA and SEM. A similar procedure has been used in other studies to select the most relevant variables to feed a Gaussian Process regression model (Friederich et al., 2020). To provide a contrast, we also included an ESEM. Because the aim of this study was not to compare Boosting and ESEM, the ESEM results are reported in the appendix and only briefly described in the results section. The remainder of the paper is organized as follows: First we introduce the example context with material and methods, and thereafter results, discussion and conclusion. An on-line appendix with R-code and an anonymized and masked data set are also included.

Example and analysis

Hansen and Österås (2019):” Animal welfare is a term used to express ethical concerns about the quality of life experienced by animals, particularly animals that are used by human beings in production agriculture (Duncan & Fraser, 1997; Fraser & Weary, 2004; Tannenbaum, 1991). The characteristics of farmers that may influence the animal welfare standards include knowing and being skilled at the techniques they use, job motivation and satisfaction, and attitudes (Hemsworth & Coleman, 2009)”. Hansen and Österås (2019) showed that a relationship exists between farmers’ occupational well-being and stress, and an animal welfare indicator. In as SEM, ibid. reported a significant positive relationship between the AWI and farmer occupational well-being (FOW), and a negative relationship between AWI and and farmer stress (FS). in a SEM. FOW included the items 3, 7, 8 and 12 reported in this study, and FS included items 14, 15 and 18, see Table 1. For a thorough description of the context, we refer to Hansen and Österås (2019).

Table 1. The items in Hansen and Österås (2019), except one item that was removed due to little relevance, with median values. All items range from 1 to 11, and items 10, 11 and 12 to 18 are reverse-coded

Item	Median score
1. I have a flexible working day	8
2. I have an optimistic view about the future	8
3. I have sufficient time for family life	6
4. I have sufficient time for friends	5
5. I have good physical health	9
6. I have an income I can live well of	7
7. I’m satisfied with my working day	9
8. I’m satisfied with my work safety	9
9. I’m satisfied with my work environment	9
10. As a farmer I work too much during weekends	3
11. I feel little appreciated as a farmer	6
12. I feel I do not have enough time off the farm	4
13. I’ve often been stressed due to work	4
14. I’ve often felt lonely as a farmer	6
15. I’ve often been concerned about the debt	7
16. I’ve often been concerned about my health	8
17. I’ve often felt weary	4
18. I’ve often felt I do not cover all I should have done	3

The dataset used in Hansen and Österås (2019) was collected for a larger study about automatic milking systems (AMS), also called milking robots. The aim of the study was to explore how farmers perceive their quality of life, their working situation and mental health, the future of their farm, work division among family members, income, etc. To compare farmers with and without AMS, their questionnaire was distributed to all 1700 farmers registered with an AMS autumn 2017, and to 1700 randomly selected dairy farmers with conventional milking systems. Hansen and Österås (2019) merged the 1288 answers from the web-survey with the participant’s AWI. Because not all 1288 farmers had an AWI available when the study was conducted, the final sample included 914 dairy farmers.

Table

The AWI was developed using variables listed in The World Organization for Animal Health, OIE (2016) standard. In the Norwegian Animal Registry (NAR) farmers and veterinarians report herd data monthly on production, animal health and so on. All variables included in AWI were collected from the NAR, where in 2017 97.1% of the dairy herds were members. All variables included in AWI were available from the NAR, where farmers and veterinarians report monthly herd data on production, animal health, etc. In 2017, 97.1% of dairy herds were included in the NAR. The mean AWI in 2017 was 104.181, with standard deviation of 11.244, ranging from 72 to 132, with higher values indicating better animal welfare. The variables included in the AWI are shown in Appendix Table A2. In this paper only data from 2017 was used. The total AWI is the sum of all the indicators presented in Table A2. A more comprehensive description of the AWI is available in Hansen and Österås (2019).

The items used to collect data on dairy farmer’s quality of life (items 1 to 7), working situation (items 8 to 12) and mental health (items 13 to 18) are shown in Table 1. All items were coded on an 11-point Likert scale ranging from to a smaller degree to a larger degree (Items 1–7), strongly agree/strongly disagree (Items 8–12), and very often/very seldom (Items 13–18). The items were treated as ordinal variables, and the negatively phrased items 10, 11 and 12 to 18 were reverse-coded to avoid negative factor loadings.

Boosting and modeling

In this section, we first give a brief overview of gradient component-wise boosting and the package ‘mboost’ in the statistical software R (CRAN, 2020). Then we describe the specification of the CFA and the SEM. Our point of departure is that several explanatory variables are needed to explain the relationship between farmer welfare and animal welfare. Therefore, we think SEM is a good tool to model this relationship. By using the CFA approach, as a measurement model, on the “right-hand side” of the equation one can benefit from minimizing bias in the regression parameter estimates, since we control for the measurement error. This is one of many strengths – and a very important one—of SEM relative to e.g., OLS regression. However, specifying a SEM item selection is crucial, and this is where boosting is particularly useful.

Gradient component-wise boosting and the R-package mboost

While several variants of boosting exist, here we focus on gradient component-wise boosting. To select relevant variables to include in a SEM, the task is to model the relationship between the AWI ($y$) and a vector consisting of the different items $x$= ${\left(x_1,\dots ..,x_p\right)}^T$depicted in Table 1, to obtain an “optimal” prediction of $y$ given $x$. This is accomplished by minimizing a loss function over a prediction function (depending on $x$). Here the loss function corresponds to the least squares objective function and $f$is a linear function of $x$. If we use squared error loss, the negative gradient vector scaled by 1/2 equals the residuals. Gradient boosting tries to find the direction in space with the largest decrease in the squared error loss function $L\left(y,f\left(x\right)\right)$, i.e. to find the negative gradient $-\frac{\mathrm{\partial }L\left(y,f\left(x\right)\right)}{\mathrm{\partial }f\left(x\right)}$. Component-wise boosting means that the model calculates updates for each dimension $p$, and selects the best update among them. The following algorithm based on Hofner et al. (2014) is used to minimize the loss function over $f$:

1. Initialize the function estimate ${\hat{f}}^{\left[0\right]}$ with offset values. ${\hat{f}}^{\left[0\right]}$is a vector of length n. Let the vector of function estimates at iteration m be ${\hat{f}}^{\left[m\right]}.$

2. Specify a set of base-learners. Base-learners are simple regression estimators with a fixed set of input variables and a univariate response. The sets of input variables may differ among the base-learners. Usually, the input variables of the base-learners are small sets of the predictor variables. In the simplest case like in this paper, there is exactly one base-learner for each predictor variable, and the base-learners are just simple linear models using the predictor variables as input variables. Each base-learner represents a modeling alternative for the statistical model. We denote the number of base-learners, P, and set m = 0.

3. Increase m by 1, where m is the number of iterations.

4. a) Compute the negative gradient $-\frac{\mathrm{\partial }L\left(y,f\left(x\right)\right)}{\mathrm{\partial }f\left(x\right)}$ of the loss function and evaluate it at ${\hat{f}}^{\left[m-1\right]}$($x_i^T$), $i=1,\dots ,n$ (i.e. at the estimate of the previous iteration). This yields the negative gradient vector

$u^{\left[m\right]}$= ${\left(u_i^{\left[m\right]}\right)}_{i=1,\dots ,n}$:= ${\left(-\frac{\mathrm{\partial }L\left(y,f\left(x\right)\right)}{\mathrm{\partial }f\left(x\right)}(y_i,{\hat{f}}^{\left[m-1\right]}\left(x_i^T\right)\right)}_{i=1,\dots ,n}$

b) Fit each of the P-base-learners to the negative gradient vector, i.e. use each of the regression estimators specified in step 2 separately to fit the negative gradient. The resulting P regression fits yield P vectors of predicted values, where each vector is an estimate of the negative gradient vector $u^{\left[m\right]}.$

c) Select the base-learner that fits $u^{\left[m\right]}$best according to the residual sum of squares criterion and set ${\hat{u}}^{\left[m\right]}$equal to the fitted values of the best-fitting base-learner.

d) Update the current estimate by setting ${\hat{f}}^{\left[m\right]}$= ${\hat{f}}^{\left[m-1\right]}$ + $\nu {\hat{u}}^{\left[m\right]}$, where 0 $<\nu <1$is a real-valued step length factor.

• (5) Iterate steps 3 and 4 until the stopping criterion $m_{stop}$ is reached.

From 4c and 4d we can see that the algorithm sequentially carries out variable selection and model choice, as only one base-learner is selected for updating ${\hat{f}}^{\left[m\right]}$ in each iteration. Boosting is a way of fitting an additive expansion in a set of elementary “basis” functions. The final boosting iteration has similarities to the additive predictor of a generalized additive model

$\hat{f}$ = ${\hat{f}}_1$+ … … .+ ${\hat{f}}_p$, where ${\hat{f}}_1$, … ., ${\hat{f}}_p$ correspond to the functions specified by the base-learners. Consequently, ${\hat{f}}_1$, … ., ${\hat{f}}_p$ depend on the predictor variables that were used as input variables of the respective base-learners. A base-learner can be selected multiple times. In contrast to the choice of the stopping iteration, the choice of the step length factor $\nu$has been shown to be of minor importance for the predictive performance of a boosting algorithm. The only requirement is that the value of $\nu$ is small, e.g., $\nu$ = 0.1 as applied in this paper (see Schmid & Hothorn, 2008b).

The R package mboost offers an easy entry into the world of boosting. It implements a model-based boosting approach that results in interpretable structured additive models in a form that will feel familiar for most researchers. The interfaces of fitting functions are quite similar to standard implementations like lm() or glm() and are hence relatively easy to use (Hofner et al., 2014). Because of its user-friendly formula interface, mboost can be used in a manner similar to classical functions for statistical modeling in R (Hofner et al., 2014). In the linear model applied in this paper the regression coefficients can be interpreted similarly to ordinary least squares coefficients. In addition to linear effects, the package also offers possibilities for modeling non-linear or interaction effects with other predictor variables. The structural assumption is given as a formula using base-learners. The mboost package also offers high flexibility when it comes to the type of risk function to be optimized. The loss function, as specified by the family argument is independent of the estimation of the base-learners. As one can see in the GCB algorithm, the loss function is used to compute the negative gradient in each boosting step only. The predictors are then related to these values by penalized ordinary least-squares estimation, irrespective of the loss function. The function glmboost() provides an interface to fit (generalized) linear models. The resulting models from glmboost() can essentially be interpreted the same way as models that are derived from glm(). The only difference is that the boosted generalized linear model additionally performs variable selection (Hofner et al., 2014).

To load mboost in R write library(mboost). It contains the function glmboost with the following interface:

model<−glmboost (formula, data = list(), weights = NULL, center = TRUE, control = boost_control(), …). The model is specified using a formula as in glm() of the form response ~ predictor1 + predictor2, and the data set is provided as a data.frame via the data argument. Optionally, weights can be given for weighted regression estimation. The argument center is specific for glmboost(). It controls whether the data is internally centered. Centering of predictors is of great importance as this allows much faster “convergence” of the algorithm or even ensures that the algorithm converges in the direction of the true value at all. The second boosting-specific argument, control, allows to define the hyper-parameters of the boosting algorithm. This is done using the function boost_control(). For example, one may specify:

boost_control(mstop = 200, # Initial number of boosting #iterations. default: 100

+ nu = 0.05), # step length, default: 0.1. Finally, the user is allowed to specify the distributional assumption via a family, which is “hidden” in the ‘ … ’ argument (see ?mboost_fit for details and other possible parameters). The default family is gaussian(), which is applied in this study. In the following example-script we set y equal to the AWI, and define X as a matrix containing all the items in Table 1:

model <− glmboost (y=AWI, x=X, family = gaussian(), control=boost_control, center=TRUE)

Cross-validation is crucial to determine the optimal number of iterations mstop. The following procedure invokes a ten-fold cross-validation:

cv <− cvrisk (model, folds = cv(model.weights(model), type = “kfold”, B = 10))

mstop(cv) # shows the optimal number of boosting iterations

Finally, summary yields the coefficients and the items selected in the final model:

summary(model[mstop(cv)]).

We regressed the AWI on all 18 items with the function glmboost and ordinary least squares base-learners. To rank items according to importance in the regressions we used the “selection frequency” reported in the mboost-package, which reflects point 4 c) that a base learner can be choosen several times during the fitting process.

Structural equation modeling (SEM) and Confirmatory Factor analysis (CFA)

Like SEM, CFA is a well-established research tool in social science and business. For a thorough mathematical description, we refer to Bollen (1989) and Jöreskog et al. (2016). A CFA was used to estimate and test a model of the latent variables. It begins by defining the latent variables one would like to measure, based on substantive theory and/or previous knowledge (Jöreskog et al., 2016). The CFA was built on the most frequently selected items from the GCB and tested for goodness of fit. Finally, a GCB-SEM was specified with the factors from the CFA as predictors of the dependent variable animal welfare. The CFA and the GCB-SEM were modeled using the lavaan package in R (CRAN, 2020).

The analysis of the dataset was done as follows:

1. We randomly divided the whole dataset into two equal-sized parts.

2. Then, one of these parts was used to run a GCB regression to select items associated with the AWI. This was done to avoid using exactly the same dataset for boosting and for SEM, and to make the task more difficult for the boosting algorithm.

3. Procedures 1) and 2) were repeated 200 times. For each GCB regression, we registered which items the GCB selected, and their relative importance.

4. Finally, the remaining part of the data set and the most frequently selected items from the GCB regressions were used to specify a CFA and a SEM to explain the variation in the AWI.

Results

The coefficients of the Spearman rank correlation are shown in Table 2.

Table 2. Spearman rank correlation correlations between the AWI and the items and between items (N = 914)

AWI Item	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
AWI	.04	−.09	.15	.01	.01	−.02	.09	.08	.05	.10	.02	.09	−.03	−.03	.07	−.02	.04	.01
1		.06	.37	.40	.39	.22	.28	.46	.22	.34	.16	.12	.14	.17	.18	.11	.20	.24
2			−.08	.02	−.01	.21	−.03	.05	.10	.03	−.16	−.14	−.20	−.08	−.12	.02	.03	−.07
3				.41	.40	.28	.42	.57	.28	.45	.22	.38	.22	.23	.38	.18	.23	.33
4					.72	.24	.34	.47	.24	.36	.35	.21	.33	.36	.26	.23	.18	.38
5						.21	.37	.42	.17	.29	.35	.22	.38	.33	.24	.21	.19	.40
6							.21	.32	.18	.26	.10	.20	.04	.17	.12	.23	.55	.34
7								.35	.18	.25	.16	.30	.23	.21	.21	.38	.19	.26
8									.44	.61	.28	.27	.22	.30	.35	.19	.30	.38
9										.62	.05	.11	.12	.18	.20	.12	.16	.16
10											.14	.18	.19	.23	.31	.14	.22	.27
11												.31	.34	.29	.29	.16	.19	.31
12													.19	.21	.32	.24	.16	.23
13														.44	.33	.20	.12	.39
14															.44	.36	.32	.57
15																.31	.34	.44
16																	.37	.35
17																		.50

We observe that the correlations between the AWI and the different items are weak, in particular for items related to mental health (items 13 to 18). We also notice that the correlation between these items are moderate or strong (Shortell, 2001). The low correlations with the dependent variable suggests that it will be challenging to select relevant items and specify reliable factors. The results from the 200 GCB-regressions are shown in Table 3.

Table 3. How often each item was selected in the 200 GCB regressions on the AWI together with relative importance of the different items in each regression. The items are ranked after decreasing frequency of selection. For each regression, the GCB shows the relative importance of each variable

Item	How often each item was selected by the GCB	Relative importance in each of the 200 GCB-regressions (median)	Items used to specify the CFA and the GCB-SEM
2	196	2	✓
6	151	4	✓
5	150	3
11	143	5	✓
12	135	5	✓
9	124	4
13	120	5	✓
16	95	5
15	89	6
3	67	6
14	63	6
10	59	8	✓
4	59	6
18	48	8
1	46	8
8	42	7
7	41	7
17	27	7

In Table 3 we can see that the items differ significantly in how often they are selected by the GCB. A group of seven items stand out as the most important ones; items 2, 6, 5, 11, 12, 9 and 13. We expect these to be the most relevant ones to include in a CFA and a SEM. Contrary, items 17, 7, 8, 18, 1, 4, 10 and 14 appear to be of little relevance in explaining variation in the AWI. Thus, we have managed to exclude a group of eight items with a weak relationship to the AWI. The remaining items appear to be of medium importance. In each run of 200 regressions, the GCB ranks the items by decreasing importance, and the median importance for all items over the 200 GCB-runs are shown in column 3 of Table 3. The numbers in this column mirror how often the items are selected. Thus, the items most often selected; 2, 6, 5, 11, 12, 9 and 13, are all ranked the five most important ones. Conversely, items 17, 7, 8, 18, 1, 4, 10 and 14 are all ranked between six and eight. Therefore, they are of little interest. To summarize, the 200 GCB regressions have reduced the number of relevant items to less than half of the original items, indicating that boosting has contributed to both item selection and item ranking.

To specify a CFA we started at the top of the list with the most frequently selected items in Table 3, and decided to use items 2, 6, 11, 12, 13 and 10. The first five items are among the seven most frequently selected, while item 10 is ranked 12. Item 10 was chosen in spite of its low ranking in the 200 regressions in order to include at least three items per factor. It appeared that item 10 functioned well with the items 12 and 13 in a factor denoted farmer stress, see Figure 1. Thus, item 10 was needed to create a coherent factor including three items.

Figure 1. The CFA with two factors, farmer occupational well-being FOW and farmer stress (FS). The dotted lines and box to the right illustrates how the CFA extends to the GCB-SEM (An arrow for the disturbance term is not included).

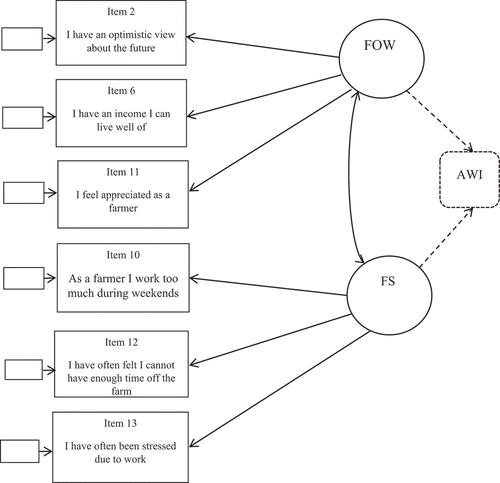
In the CFA, all standardized factor loadings are significantly different from zero and within the interval [0.483, 0.680] (see Table 4). FOW includes items related to working situation and quality of life, while FS includes two items related to mental health and one related to quality of life. Cronbach’s alpha is calculated as 0.682 and average composite reliability is 0.611.

Table 4. Items and standardized factor loadings in CFA and SEM with standard errors

CFA			SEM
Factor	Items	Factor loading	SE factor loading	Factor loading	SE factor loading
FOW	Item 2	0.680***	0.060	0.699***	0.060
FOW	Item 6	0.483***	0.050	0.488***	0.049
FOW	Item 11	0.627***	0.056	0.608***	0.053
FS	Item 10	0.559***	0.054	0.558***	0.054
FS	Item 12	0.590***	0.057	0.591***	0.056
FS	Item 13	0.571***	0.055	0.571***	0.055

Finally, we specified the CFA and the GCB-SEM, both of which are shown in Figure 1. The dotted part (dotted lines and the box AWI) extend the CFA to a SEM with a single observed dependent variable.

In the SEM, the estimated regression coefficient for FOW on AWI was 0.377*** (0.105), and the regression coefficient for FS on the AWI was −0.291***(0.107). The correlation between FOW and FS was 0.611.

FOW is positively associated with the AWI, while FS is negatively associated, and the signs are as expected. FS contributes negatively to animal welfare, while occupational wellbeing contributes positively to animal welfare. Both factors yield moderate relationships with the AWI. The theoretical models provide a good fit to the observed data (See Table 5).

Table 5. Goodness of fit measures and degrees of freedom (df) for the CFA and the GCB-SEM

	CFA	GCB-SEM
Chi-square	14.391 (p = .072)	16.732 (p = .160)
RMSEA	0.042	0.029
SRMR	0.040	0.040
NFI	0.967	0.964
CFI df	0.985 11	0.989 12

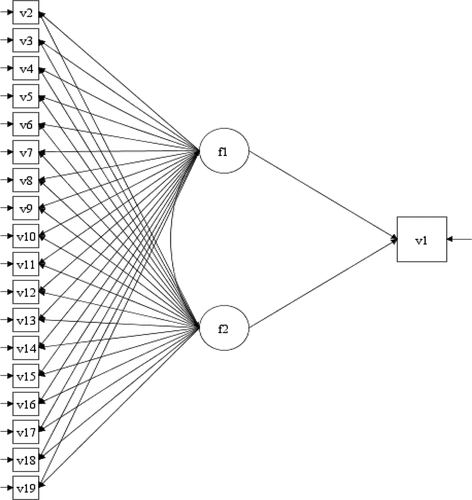
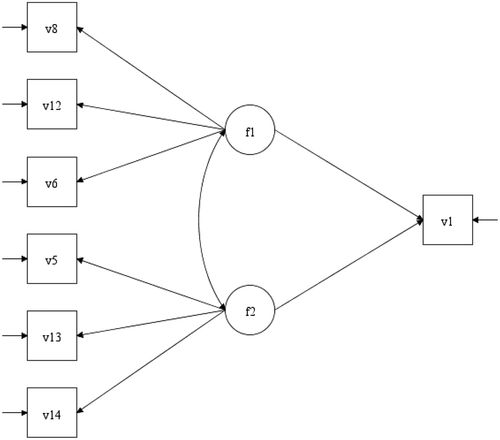
In the appendix, the section “ESEM vs Boosting” compares a SEM derived from using ESEM and the GCB-SEM derived from Boosting. As mentioned earlier, the intention of this paper is not to compare these two methods. The focus is to show how Boosting can be applied to select relevant items. Given the objective of ESEM (Asparouhov & Muthén, 2009) we were tempted to use ESEM on the same data set with the same goal, to build a SEM. So, we conducted a quick ESEM analysis, using Mplus 8.3: 1) In Figure A1, the original ESEM is depicted, with all 18 items for two common factors. 2) In Figure A2 and A3 we can see the SEMs where all items with factor loadings <0.4 and <0.5, respectively, are deleted. We ended up with two distinct factors with no cross loading. This is an interesting finding. The “final” model (SEM2) depicted in Figure A3 was re-estimated in laavan by using the whole sample (N = 914). The same was done with the GCB-SEM (SEM3) derived from Boosting, but now including the whole sample. The results are in Tables A4 and A5 respectively. As we can see for SEM 3 (3 items per factor), the fit is good (Chi sq. =19.389 (12) p =.08)), the factor loadings are in the interval 0.560 to 0.705, and the regression parameters are 0.326 and −0.226, respectively. However, for SEM2 (four items per factor), the fit is not as good (Chi sq. = 54.292 (25) p = .001), the factor loadings are in the interval 0.534 to 0.866, and the regression parameters are 0.169 and −0.076, respectively. The results are interesting, however, in factor 2, three items that reflect stress due to lack of time and work overload (items 13,17 and 18) are mixed with an item reflecting stress due to health worries (item 16). Overall, the results in SEM2 are probably as one should expect, given the different “philosophy” of the two approaches. A thorough simulation study that compares the two approaches could provide more specific information.

Discussion and conclusion

This paper and the R-code provided demonstrate an example of how boosting with R can be used as a tool to facilitate a SEM specification search. That is, boosting is not used to choose among different SEM-models, but to select possible items to include in a SEM. At the outset of this study we had 18 items, and with three items per factor, there are 816 possible combinations. The GCB reduced the number of relevant items to eight, which reduces the number of possible combinations to 56. Our example, therefore, demonstrates how GCB can contribute to item selection, and thus to SEM specification. At the very least, the GCB algorithm can be effective as an initial exploratory tool that can be used in modeling complex behavioral, educational, and social phenomena. In this study, GCB selects and ranks the items and simultaneously ensures that there is a relationship between the items and the dependent variable. Compared to the SEM in Hansen and Österås (2019, p. 6), the GCB-SEM in this study exhibits a stronger relationship between FOW, FS and the AWI (see Table A1). This is as expected, since the GCB was trained in a regression with the AWI as the dependent variable, the item selection in Hansen and Österås (2019) was based on a trial and error approach involving all 18 items. It is noteworthy that the GCB-SEM includes only four of the seven items used in Hansen and Österås (2019) (see Table A1). This finding suggests that not all items in Hansen and Österås (2019) were the optimal ones to explain the variation in the AWI, and boosting has improved item selection. Taken together, our example shows that GCB has the potential to streamline the task of selecting items and specifying a SEM when the task is to explain the variation in an observed variable. That being said, we acknowledge that settings might exist where boosting is not necessarily the best tool to facilitate a SEM- specification search.

What can be considered a reliable factor loading remains a topic for discussion. For example, the software package SPSS uses 0.4 as the cutoff criteria. However, all factor loadings in this paper are above this value. The strength of the relationships between FOW, FS and the AWI in Figure 2, while moderate, are within the range frequently found in studies of job satisfaction and stress versus job performance (Judge et al., 2001). How farmers thrive at work is pivotal to productivity and to to keep up dairy farming. Our findings show that there is a positive relationship between FOW and the AWI, and a negative relationship between FS and the AWI (Figure 2). Thus, a relationship exists between farmers’ occupational well-being and stress on one side, and how well they take care of their animals on the other, which supports the findings in Hansen and Österås (2019) (see Table A1).

It is important to recognize that results from a computerized specification search like the one applied in this paper, may reflect an element of chance. Therefore, without a theoretical background related to the question being examined or preliminary research conducted in the field, there is no way one can distinguish between different ways to determine relationships among variables (Tarka, 2018). Furthermore, our example shows that when specifying factors there is some degree of subjectivity involved in determining the number and interpretation of the factors. Thus, we had to include item 10, ranked as number 12 by the GCB, to specify a meaningful factor. The GCB algorithm is developed for supervised statistical learning, and does not group items based on their degree of association. This task is left, instead, to the researcher. An ideal solution would be to end up with sets of highly ranked grouped items ready to include in factors. To achieve this, one possible strategy could be to integrate the GCB algorithm in the SEM framework. However, considering the complexity involved in merging the two algorithms, the authors have some doubt about whether this is the right path to follow. A more practical approach is, perhaps, to run an EFA including the items from the GCB to extract factors before one specifies a SEM. The reduced set of items would significantly facilitate both the interpretation of the EFA, and the specification of factors. Furthermore, a procedure that generates 200 GCB regressions and produces a list of items ranked by importance could easily be implemented in R, and could prove a valuable tool.

In conclusion, the example analyzed in this study demonstrates that GCB can contribute significantly to simplifying the specification search in SEM. The findings suggest that boosting, and in particular GCB, has a potential to facilitate the task of selecting items to specify a SEM when the correlation between the dependent manifest variable(s) and the items is low. More research is needed, however, to determine the full merits of employing boosting in specifying a SEM.

Acknowledgments

Ruralis-Institute for rural and regional research and Renate Butlie Hårstad are acknowledged for facilitating the data set. Professor Ingrid Kristine Glad at the University of Oslo is also acknowledged for valuable comments.

Appendix

Table A1. The main results from the SEM in Hansen and Österås (2019) with the two factors FOW and FS, the corresponding items and the regression coefficients between the factors and the AWI

Items	Factor	Factor loading	SE factor loading	Regression coeff. with AWI	SE regression coeff.with AWI
Item 2	FOW FOW FOW FOW	0.677***	0.044	0.352***
Item 6		0.502***	0.033
Item 7		0.654***	0.038		0.101
Item 11		0.524***	0.028
Item 13	FS FS FS	0.568***	0.035	−0.233***	0.102
Item 14		0.719***	0.033
Item 17		0.656***	0.036

*** p ≤ 0.001

Table A2. Goodness of fit measures for the SEM in Hansen and Österås (2019)

	SEM
Chi-square	11.241 (p = .667)
RMSEA	0.000
SRMR	0.018
NFI	0.992
CFI	1.000

Table A3. Overview over variables used to calculate the AWI, reprinted from Hansen and Österås (2019)

Variable	Used mean value	Used STD	Calculations	Chosen values^c
Milk yield indicator
305 days milk yield in 2^nd parity minus 1^st parity	980	990	NSTDcont^a	−3;3
305 days milk yield in 3^rd parity minus 2^nd parity	515	1015	NSTDcont^a	−3;3
305 days milk yield in 3^rd parity minus 1^st parity	1491	1059	NSTDcont^a	−3;3
Life indicator
Proportion of cows culled the first 14 days in milk	0.064		NSTDpoi^b	−3;3
Culled cows between 84 and 290 days in diagnosed pregnant cows	0.100		NSTDpoi^b	−3;3
Culled inseminated/mated cows between 84 and 290 days without pregnancy test^d	0.110		NSTDpoi^b	−3;3
Replacement rate (proportion of 1^st parity cows)	0.360	0.133	NSTDcont^a	−3;3
Length of life for cows after 2^nd parturition (days)	680	283	NSTDcont^a	−3;3
Metabolic indicator
Number of milk fever after 2^nd parity	0.078		NSTDpoi^b	−3;3
Number of ketosis of all cows	0.037		NSTDpoi^b	−3;3
Number of thin cows (BCS < 2.75)	0.043		NSTDpoi^b	−3;3
Number of thick cows (BCS > 3.75)	0.175		NSTDpoi^b	−3;3
Variation of BCS (STD)	0.419	0.123	NSTDcont^a	−3;3
Carcass weight cows in kg	269	30	NSTDcont^a	−3;3
Meat classification young cows			See Table 2
Meat classification cows			See Table 2
Carcass weight young cows	254	28	NSTDcont^a	−3;3
Fat classification young cows			See Table 2
Fat classification cows			See Table 2
Udder health indicator
Number of cow cell counts > 200,000 pr. ml	0.201		NSTDpoi^b	−3;3^e
Cases of clinical mastitis	0.224		NSTDpoi^b	−3;3^e
Number of cows culled due to bad udder health	0.025		NSTDpoi^b	−3;3
Fertility indicator
Number of days from average last insemination till first insemination for each cow	27.5	24.2	NSTDcont^a	−3;3
Average calving interval in months	12.7	1.37	NSTDcont^a	−3;3
Number of cows culled due to bad fertility	0.134		NSTDpoi^b	−3;3
Young stock indicator
Number of dead young stock	0.017		NSTDpoi^b	−3;3
Number of emergency-slaughtered young stock	0.002		NSTDpoi^b	−3;3
Number of euthanized young stock	0.004		NSTDpoi^b	−3;3
Number of treated young stock	0.022		NSTDpoi^b	−3;3
Carcass weight heifers, kg	218	38	NSTDcont^a	−3;3
Growth rate heifers (gram per day)	342	57	NSTDcont^a	−3;3
Carcass weight young bull kg	297	46	NSTDcont^a	−3;3
Growth rate young bull (gram per day)	523	81	NSTDcont^a	−3;3
Carcass weight young cow kg	254	28	NSTDcont^a	−3;3
Growth rate young cow (gram per day)	214	31	NSTDcont^a	−3;3
Age in months at first calving	25.8	2.234	NSTDcont^a	−3;3
Dehorning indicator
Number of dehorning after 42 days of life	0.350		NSTDpoi^b	−3;3
Number of dehorning after 70 days of life	0.100		NSTDpoi^b	−3;3
Number of calves with horn	0.760		NSTDpoi^b	−3;3
Dead cow indicator
Dead cows	0.025		NSTDpoi^b	−3;3
Cows emergency slaughtered	0.010		NSTDpoi^b	−3;3
Cows euthanized	0.007		NSTDpoi^b	−3;3
Calves indicator (until 180 days in life)
Dead calves	0.080		NSTDpoi^b	−3;3^f
Treated calves	0.064		NSTDpoi^b	−3;3^f
Claw indicator
Number of claw diagnosis with pain^g	0.120		NSTDpoi^b	−3;3
Professionality of claw trimming^h				−3;3
Number of trimmed cows	0.670		NSTDpoi^b	−3;3

^aNormalized standard deviation for continuous variables = (observed value – mean value)/STD

^bNormalized standard deviation for Poisson distributed variables = (possible numbers x 0.064 minus observed numbers)/(possible numbers x 0.064)^0.5

^cIf NSTDcont or NSTDpoi > 3 then set to 3; if NSTDcont or NSTDpoi<-3 then set to −3

^dThis variable is weighted by 0.5

^eIf NSTDpoi for cases of clinical mastitis > 0 and NSTDpoi for number of cow cell count > 200,000 per ml <0 then NSTDpoi for mastitis is multiplied with −1.

^fIf NSTDpoi for dead calves < 0 and STDpoi for treated calves > 0 then STDpoi for treated calves are multiplied with −1.

^gDiagnosis with pain is defined as: Digital dermatitis, Lameness, Sole ulcers, White line fissure and White line abscess.

^hSum of proportion of claw trimmed by professional claw trimmer x 0.3 and proportion of claw trimmed by uncertified claw trimmer x 0.2 and proportion of claw trimmed by owner x 0.1 all divided by 10.

The R-code for boosting

library(mboost)

set.seed(123) # To get repeatable solutions

model <- glmboost(y = y.train, x = X.train, family = Gaussian(),control = boost_control(),center = TRUE)

# This is the model specification with linear base-learners. family specifies the distribution of the

#dependent variable while control is to specify the hyperparameters in the model, see boost_control in

#the package vignette for detailed info. Here one can adjust e.g., the penalizing parameter, the initial

#number of boosting iterations etc., center = TRUE is a logical indicating whether the predictor

#variables should be centered before fitting or not.

summary(model)

cv <- cvrisk(model, folds = cv(model.weights(model), type = “kfold”, B = 10))

# Cross-validation to #find the optimal number of boosting iterations.

mstop(cv)

# the optimal number of boosting iterations selected

summary(model[mstop(cv)])

# A summary of the model

round(coefficients(model[mstop(cv)]), 3)

#Rounding the coefficients to three digits

Here y.train is the AWI for half of the dataset, and X.train is a matrix containing all items and half of the observations in the dataset.

Then a simple lavaan-code with AWI as the dependent variable, and the most frequently chosen items by the GCB grouped in the two factors were run.

ESEM vs BOOSTING

Variable names: v1 = AWI; v2 = item 7; v3 = item 8; v4 = item 9; v5 = item 10, v6 = item 11; v7 = item 1;

V8 = item 2; v9 = item 3; v10 = item 4; v11 = item 5; v12 = item 6; v13 = item 12; v14 = item 13;

V15 = item14; v16 = item 15; v 17 = item 16; v18 = item 17 and v19 = item 18. Sample size = 914.

Figure A1. ESEM with 18 items and two common factors.

Figure A2. SEM1 based on ESEM and deleting all items where standardized factor loading < 0.4, absolute value.

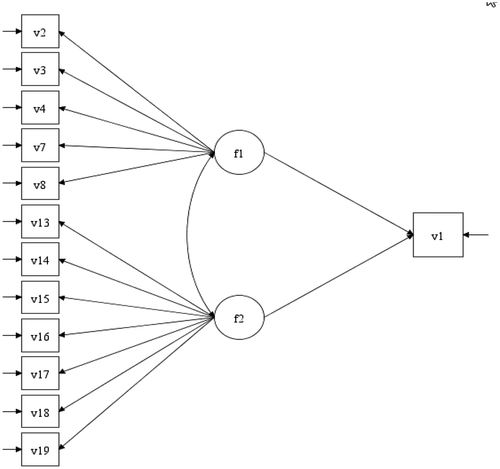
Figure A3. SEM2 based on ESEM and deleting all items where standardized factor loading < 0.5, absolute value.

Figure A4. SEM3 based on boosting (Model in the main text, but now estimated for the whole sample).

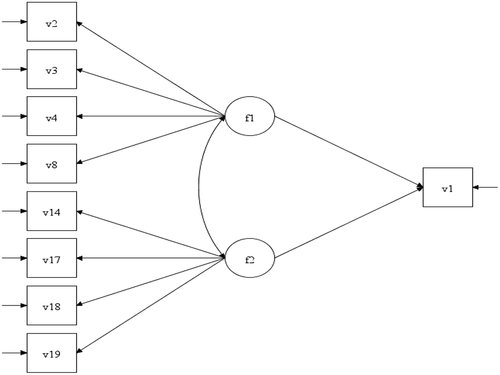
Table A4. SEM 2 depicted in Figure A3. Estimator DWLS

Items/variables	Factor loading	Regression parameter	p-value
Item 7/v2	(f1) 0.859		0.000
Item 8/v3	(f1) 0.534		0.000
Item 9/v4	(f1) 0.748		0.000
Item 2/v8	(f1) 0.661		0.000
Item 13/v14	(f2) 0.652		0.000
Item 16/v17	(f2) 0.558		0.000
Item 17/v18	(f2) 0.866		0.000
Item18/v19	(f2) 0.698		0.000
f1→AWI		0.169	0.000
f2→AWI		−0.076	0.039
Cor(f1,f2) = 0.512			0.000
Fit Statistics	Chi.sq = 54.292 (25) p = .001	RMSEA = 0.036

Table A5. SEM 3 depicted in Figure A4. Estimator DWLS

Items/variables	Factor loading	Regression parameter	p-value
Item 2/v8	(f1) 0.560		0.000
Item 6/v12	(f1) 0.677		0.000
Item 11/6	(f1) 0.660		0.000
Item 10/v5	(f2) 0.705		0.000
Item 12/v13	(f2) 0.614		0.000
Item13/v14	(f2) 0.651		0.000
f1→AWI		0.326	0.000
f2→AWI		−0.226	0.000
Cor(f1,f2) = 0.616			0.000
Fit Statistics	Chi.sq = 19.389 (12) p = .08	RMSEA = 0.026