Prior Predictive Checks for the Method of Covariances in Bayesian Mediation Analysis

ABSTRACT

Bayesian mediation analysis using the method of covariances requires specifying a prior for the covariance matrix of the independent variable, mediator, and outcome. Using a conjugate inverse-Wishart prior has been the norm, even though this choice assumes equal levels of informativeness for all elements in the covariance matrix. This paper describes separation strategy priors for the single mediator model, develops a Prior Predictive Check (PrPC) for inverse-Wishart and separation strategy priors, and implements the PrPC in a Shiny app. An empirical example illustrates the possibilities in the app. Guidelines are provided for selecting the optimal prior specification for the prior knowledge researchers wish to encode.

KEYWORDS:

• Prior Predictive Check
• Bayesian Mediation Analysis
• Method of Covariances
• Separation Strategy
• Shiny app

Bayesian methods are gaining popularity in psychology and related fields (van de Schoot et al., 2017). Recent years have seen a number of articles on procedures for fitting commonly used statistical models in the Bayesian framework (e.g., Wang & Preacher, 2015; Yuan & MacKinnon, 2009; Zhang et al., 2007), and comparisons between statistical properties of Bayesian summaries and frequentist estimates (e.g., Depaoli, 2013; Lee & Song, 2004; Lee et al., 2010). Software implementations of Bayesian methods have been on the rise as well (e.g., SAS Institute Inc, 2017; Stan Development Team, 2020; Merkle & Rosseel, 2018; Muthén & Muthén, 1998–2017; StataCorp, 2019). Despite the increased use of Bayesian statistics in the social sciences, prior distributions remain a controversial and problematic element in the application of Bayesian methods. In the absence of prior knowledge, researchers can specify diffuse priors, and the numerical results are often identical to those obtained using frequentist methods. Discussions of what constitutes a diffuse prior for different models and sample sizes have been published elsewhere, and are not the focus of this paper (e.g., Miočević et al., 2020; Smid et al., 2020; van Erp et al., 2018). This paper focuses on informative priors in mediation analysis. More specifically, we outline a procedure for specifying informative priors based on published articles that contain summary statistics (means, variances, covariances, correlations, and/or standard deviations) for some or all variables in the mediation model of interest.

The topic of encoding existing information in prior distributions is sometimes touched on in textbooks (e.g., Kaplan, 2014) and articles (e.g., Smid et al., 2020). However, with certain prior specifications, researchers need an explicit check of whether selected priors indeed reflect their beliefs and imply realistic distributions of the variables in the model. Prior Predictive Checks (abbreviated PrPC to distinguish them from Posterior Predictive Checking, which is abbreviated as PPC) are a very helpful tool for refining prior specifications to reflect the researcher’s intended representation of prior knowledge (Levy, 2011). However, despite the existence of tutorials on PrPC for social sciences researchers (van de Schoot et al., 2020), PrPC are not the norm in psychology and there is a lack of implementations of prior predictive checks in software for Bayesian analysis. This paper describes a PrPC procedure for Bayesian mediation analysis using the method of covariances. The PrPC procedure is implemented in a freely available, user-friendly Shiny app. We show steps in conducting PrPC for an inverse-Wishart prior and the Separation Strategy (Barnard et al., 2000) when these priors are informative and based on published summary statistics for variables in the single mediator model. Subsequent paragraphs describe Bayesian mediation analysis, the general purpose of PrPC, and candidate prior specifications for Bayesian mediation analysis using the method of covariances. The procedure and implementation of the PrPC for Bayesian mediation analysis using the method of covariances in the app are illustrated using an example from the educational psychology literature.

Bayesian mediation analysis

Mediation analysis is used to investigate the role of intermediate variables in the relationship between the independent and dependent variables (MacKinnon, 2008). In the single mediator model with a continuous mediator and outcome, the total effect of $X$ on $Y$ can be decomposed into the direct effect ($c^{\prime }$) and the indirect effect of $X$ on $Y$ through the mediator $M$. The equations describing the single mediator model are:

(1) $M_i=b_{0M}+a{X}_i+e_{Mi}$(1)

(2) $Y_i=b_{0Y}+b{M}_i+c^{\prime }{X}_i+e_{Yi}$(2)

where M_i and Y_i denote the values of the mediator and the outcome for participant i, $b_{0M}$ and $b_{0Y}$ represent the intercepts for the mediator and outcome, a represents the effect of $X$ on $M$, b represents the effect of $M$ on $Y$ controlling for $X$, and c’ represents the effect of $X$ on $Y$ controlling for $M$. The residuals e_Mi and e_Yi are assumed to follow normal distributions with means of 0 and variances of ${\sigma }_{eM}^2$ and ${\sigma }_{eY}^2$, respectively.

In the frequentist framework, it is recommended to test the significance of the indirect effect using interval estimators based on critical values from the distribution of the product (MacKinnon et al., 2002) or using methods such as the bootstrap that make no distributional assumptions about the indirect effect (MacKinnon et al., 2004; Shrout & Bolger, 2002).

Bayesian mediation analysis has been described for both manifest and latent variable mediation models (Enders et al., 2013; Miočević, 2019; Yuan & MacKinnon, 2009). In the Bayesian framework, the posterior distribution is obtained by updating the prior distribution with observed data and inferences are made by summarizing the posterior distribution of the parameters (Lynch, 2007). Due to space constraints, we do not describe Bayesian methods in detail, but we invite readers who are new to Bayesian methods to consult introductions by van de Schoot et al. (2014) and van de Schoot and Depaoli (2014). For readers interested in an introduction to Bayesian mediation analysis, we suggest papers by Yuan and MacKinnon (2009) and Enders et al. (2013).

Bayesian mediation analysis can be conducted using the method of coefficients (Yuan & MacKinnon, 2009) or the method of covariances (Enders et al., 2013). The method of coefficients requires prior specifications for the parameters in Equations 1(1) $M_i=b_{0M}+a{X}_i+e_{Mi}$(1) and 2(2) $Y_i=b_{0Y}+b{M}_i+c^{\prime }{X}_i+e_{Yi}$(2) : the intercepts $b_{0M}$ and $b_{0Y}$, regression coefficients a, b, and c’, and the residual variances ${\sigma }_{eM}^2$ and ${\sigma }_{eY}^2$. The method of covariances assigns priors to the vector of means of $X$, $M$, and $Y$ denoted by $\mu$ and the variance-covariance matrix of $X$, $M$, and $Y$ denoted by $\mathrm{\Sigma }$. Scores on X, M, and Y are assumed to follow a multivariate normal distribution with means μ and covariance matrix Σ. The indirect effect can then be computed using the elements in Σ:

(3) $ab=\frac{{\sigma }_{XM}}{{\sigma }_X^2}\frac{\left({\sigma }_{MY}{\sigma }_X^2-{\sigma }_{XM}{\sigma }_{XY}\right)}{\left({\sigma }_X^2{\sigma }_M^2-{\sigma }_{XM}^2\right)}$(3)

Findings from simulation studies show that with diffuse priors, the method of coefficients, and the method of covariances yield intervals for the mediated effect with comparable statistical properties to those of the best frequentist methods. With accurate priors, the method of coefficients and the method of covariances have adequate power to detect the indirect effect with up to half of the sample size required by frequentist methods (Miočević et al., 2017). The possibility of including prior information in the analysis to increase power and sequentially accumulate knowledge are important reasons for opting for Bayesian over frequentist methods. In practice, however, researchers often struggle to identify appropriate sources of prior information (Miočević et al., 2020) and to translate published findings into priors for analyses of new data. With the method of coefficients, the task of specifying informative prior distributions is somewhat easier because researchers express their knowledge and beliefs about a and b by assigning priors for these two coefficients directly. However, applied researchers in psychology are more likely to find published papers that include summary statistics (means, standard deviations, covariance matrices, and/or correlation matrices) than published papers that report findings from a mediation model that has exactly the same independent variable, mediator, and outcome and controls for all relevant covariates as the current study. Thus, the method of covariances might be more useful for specifying informative priors based on published articles. With the method of covariances, priors for the a and b paths are implied by the prior chosen for Σ. PrPC can be used to determine whether the chosen prior distribution truly represents the researcher’s beliefs based on the previous literature. We dedicate the remainder of the introduction to describing PrPC in general and specifically for the method of covariances.

Prior predictive checks

Before describing PrPC, it is helpful to revisit the concept of PPC, especially its logic as described by Levy (2011). PPC essentially evaluates how well the model accounts for a particular characteristic of the data referred to as the test statistic. PPC is conducted by first fitting the model to the data, using each Markov Chain Monte Carlo (MCMC) draws from the posterior to generate posterior predictive data, computing the test statistic for each posterior predicted data set, and comparing the posterior predictive test statistic to the test statistic from the observed data. Large discrepancies between the test statistic in the posterior predictive data and the test statistic in the observed data are indicative of the model’s poor ability to account for a particular characteristic of the data.

Similarly, PrPC consists of generating prior predictive distributions of the data that are then evaluated on their ability to account for a particular characteristic of the data. Unlike PPC, in PrC the model is not fit to the data. Instead, PrPC is concerned with how well the chosen prior distribution accounts for the characteristics of the data. There could be different features of the data that researchers aim to recover with their choice of prior distribution, which translates to different criteria in PrPC. We describe the distributional forms recommended for Bayesian mediation analysis using the method of covariances and the criteria we implement in PrPC for this analytic method.

Prior distributions for the method of covariances

As previously described, the method of covariances requires specifying priors for the vector of means of $X$, $M$, and $Y$ ($\mu )$ and the covariance matrix of $X$, $M$, and $Y$ (Σ). Prior information about $\mu$ can be specified in the form of a multivariate normal distribution for the vector of means or using univariate priors for individual means. In our PrPC procedure we allow users to specify univariate normal prior distributions for ${\mu }_X$, ${\mu }_M$, and ${\mu }_Y$. The mean hyperparameters of the normal priors represent the best guesses for the corresponding means, and the standard deviation hyperparameters quantify the uncertainty about this best guess. The inverse-Wishart distribution is a conjugate prior for covariance matrices, and it is described using the scale parameter Sc and the degrees of freedom parameter df (Equation 4(4) $\mathrm{\Sigma }\sim IW\left(Sc,df\right)$(4) ). $Sc$ must be a positive definite matrix often chosen to equal the sum of squares and cross products matrix (Enders et al., 2013). For the inverse-Wishart to be proper it is necessary that $df$ > m, where m represents the dimensions of the covariance matrix. For the single mediator model with three variables, m = 3.

(4) $\mathrm{\Sigma }\sim IW\left(Sc,df\right)$(4)

The expectation of the inverse-Wishart function is computed as $\frac{Sc}{df-m-1}$ (Gelman et al., 2004). If a proper inverse-Wishart prior is specified for Σ, the implied value of the indirect effect can be computed analytically using Equation 3(3) $ab=\frac{{\sigma }_{XM}}{{\sigma }_X^2}\frac{\left({\sigma }_{MY}{\sigma }_X^2-{\sigma }_{XM}{\sigma }_{XY}\right)}{\left({\sigma }_X^2{\sigma }_M^2-{\sigma }_{XM}^2\right)}$(3) .

Even though the inverse-Wishart distribution is commonly used as a prior for covariance matrices, having a single degree of freedom parameter is a limitation in situations where researchers have prior information about some elements of the covariance matrix (e.g., variances) because specifying informative priors for only a subset of elements of the covariance matrix is not possible. Furthermore, eliciting prior information about elements of the covariance matrix of $X$, $M$, and $Y$ may be more challenging than eliciting prior information about the standard deviations of and correlations between $X$, $M$, and $Y$.

An alternative to the inverse-Wishart prior for the covariance matrix is the Separation Strategy (Barnard et al., 2000). The covariance matrix can be computed using the correlation matrix (R) and the vector of standard deviations (S) of $X$, $M$, and $Y$ as $\mathrm{\Sigma }=diag(S)Rdiag(S)$. In the Separation Strategy, the prior for the covariance matrix of $X$, $M$, and $Y$ is implied by priors that are specified for R and S. Each element in $R$ and $S$ can be assigned univariate priors (assuming implied $R$ is positive definite), so it is possible to encode as little or as much prior certainty about a given relationship between variables and/or variability of scores on $X$, $M$, and $Y$.

Priors for the correlation matrix R

In this paper, we consider two possible prior distribution specifications for the correlation matrix $R$, namely the truncated normal univariate priors for individual correlations in R, and the LKJ prior for the correlation matrix (Lewandowski et al., 2009). The truncated normal distributions for $r_{XM}$, $r_{XY}$, and $r_{XM}$ are specified with limits of −1 and 1 to avoid impossible values. The mean hyperparameter of the truncated normal priors represents the best guess for a given correlation, and the standard deviation hyperparameter encodes the certainty about this best guess. A detailed explanation of how correlations are generated from a truncated normal distribution can be found in Robert (1995), but it is important to know that the limits are determined by a uniform distribution. Possible values of the correlation between $M$ and $Y$ for a positively definite correlation matrix are bounded by the values of the correlations between $X$ and $M$ and $X$ and $Y$ (Budden et al., 2007) so specifying univariate priors for the three correlations may result in a non-positive definite correlation matrix. Thus, when defining separate priors for the three correlations between $X$, $M$, and $Y$, the prior for the last of the three correlations being specified should have the following bounds (as shown by Stanley & Wang, 1969):

(5) ${\rho }_{MY}U[{\rho }_{XM}{\rho }_{XY}-\sqrt{(1-{\rho }_{XM}^2)(1-{\rho }_{XY}^2)},{\rho }_{XM}{\rho }_{XY}+\sqrt{(1-{\rho }_{XM}^2)(1-{\rho }_{XY}^2)}].$(5)

Another possible prior for the correlation matrix is the LKJ distribution (Lewandowski et al., 2009). The LKJ prior is a multivariate prior with a single hyperparameter, $\eta$ which must be greater than 0. For a 3 by 3 correlation matrices, $\eta$ = 0.5 corresponds to a $U\left[-1,1\right]$ distribution for the individual correlations (Joe, 2006). Smaller values of $\eta$ result in a trough-shaped distribution, while larger $\eta$ results in an increasingly sharp peak in the density around 0. In the case of the single mediator model, the LKJ prior is an appropriate choice if there is no prior knowledge about correlations between X, M, and Y and/or it is safe to assume that the correlations are not large.

Priors for the vector of standard deviations S

There are numerous distributional forms that can be used as prior distributions for standard deviations. In this paper, we will discuss and evaluate three prior specifications for standard deviations of $X$, $M$, and $Y$: half-Cauchy, lognormal, and the inverse-gamma distribution for the corresponding variance.

Half-Cauchy

The half-Cauchy distribution is characterized by a broad peak at zero and a gentle slope in the tails, making it a relatively uninformative prior distribution for standard deviations (Polson & Scott, 2012). The half-Cauchy distribution has no analytical solution for the mean or standard deviation. It is specified using the mean and scale (A) hyperparameters. The interquartile range is equal to 2$A$. Therefore, a half-Cauchy distribution is usually specified with a mean hyperparameter of 0 and a scale parameter ($A$) that reflects the median and the interquartile range of the standard deviation.

Lognormal

Hyperparameters of the lognormal distribution are the mea (usually denoted by $\mu$; however, we use the symbol ${\mu }_{LN}$ to avoid confusing the hyperparameters of the lognormal prior with the vectors of means of X, M, and Y) and the standard deviation ($\sigma )$. The mean of the lognormal distribution is equal to$exp({\mu }_{LN}+\frac{{\sigma }^2}{2})$, the mode is equal to$exp({\mu }_{LN}-{\sigma }^2)$, and the median is equal to $exp({\mu }_{LN})$(Barnard et al., 2000; Zellner, 1971). Ideally, ${\mu }_{LN}$ should reflect a reasonable estimate for the value of the corresponding standard deviation parameter. The variance of the lognormal distribution (denoted lN) is determined by both ${\mu }_{LN}$ and $\sigma$, $var(lN)=exp(2{\mu }_{LN}+{\sigma }^2)(exp({\sigma }^2)-1).$

Inverse-gamma

The inverse-gamma distribution is a conjugate prior distribution for variance parameters (Gelman, 2006), and it is described using the shape ($\alpha$) and scale ($\beta )$ parameters. An inverse-gamma prior with α = β = 0.001 is considered uninformative for variance parameters in most settings except for multilevel models with very few level-2 units (Gelman, 2006) and structural equation models with small samples (van Erp et al., 2018). In this context, the inverse-gamma priors are specified for the variances of $X$, $M$, and $Y$, thus implying priors for the standard deviations of these three variables. Selecting values of α and β that yield an implied prior for the standard deviation with the bulk of the density around the researcher’s best guess for this parameter may not be intuitive; however, we still include this prior specification because of its frequent use.

Prior Predictive Check (PrPC) for Bayesian mediation analysis using the method of covariances

Unlike in the method of coefficients, prior specifications in the method of covariances inherently encode beliefs about the distributions of scores on $X$, $M$, and $Y$ through chosen priors for μ and Σ. The PrPC consists of generating values of $X$, $M$, and $Y$ based on user-specified prior distributions and evaluating how well these priors match the expected characteristics of the data (Levy, 2011). If a lot of “impossible” scores of $X$, $M$, and $Y$ are generated, this signals that the prior specifications may be unrealistic.

We focus on five ways of assessing whether the chosen priors lead to (un)realistic data: 1) by visually inspecting the distribution of scores of $X$, $M$, and $Y$; 2) by generating a distribution of implied values of the indirect effect; 3) by computing the proportion of observations in generated¹ data sets that are outside the range of possible scores on continuous $X$, $M$, and $Y$; 4) by running t-tests to compare the means of continuous X, M, and Y for each generated sample based on the chosen prior and the observed mean values in the prior data set; and 5) by running F-tests to compare the variances of continuous X, M, and Y for each generated sample based on the chosen prior and the user-specified (observed) variance values in the prior data set.

Empirical example

We present an empirical example from the educational psychology literature to illustrate how the Shiny app (https://bayesianmed-lab.shinyapps.io/Prior-Predictive-Checks-Bayesian-Mediation-Analysis/) can be used to specify informative priors that reflect the researcher’s beliefs about the data in the context of a Bayesian mediation analysis of a hypothetical new study. Numerous studies have focused on how collaboration, i.e., positive interdependence between partners, affects learning outcomes (e.g., Nokes-Malach et al., 2015; Summers et al., 2005; van Boxtel et al., 2000). Positive social interdependence refers to the belief that individuals can reach their goals only once other group members also reach their goals (Johnson et al., 1979; van Blankenstein et al., 2018), resulting in higher achievement, helping behavior, and positive peer relationships (Roseth et al., 2008). Previous research evaluated elaboration during the collaborative process as a potential mediator between positive interdependence and the higher learning outcomes (Figure 1). Elaboration in collaboration is defined as situations where someone must explain, argue, and summarize their understanding to their partner(s). Elaboration leads to deeper understanding and improved learning (Denessen et al., 2008).

Figure 1. Single mediator model depicting the indirect effect of positive interdependence (X) on learning achievement (Y) through elaboration (M). Residual variances are omitted from the figure but estimated in the model

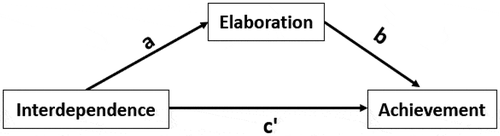
We use two published studies as sources of prior information based on historical data (Chang & Hwang, 2017; Hooper & Hannafin, 1991) to show how to evaluate prior specifications based on existing information. The study by Hooper and Hannafin (1991) reports summary statistics that allow for computing all correlations between and standard deviations of $X,M$, and $Y$, which can then be used as input for the inverse-Wishart distribution. The study by Chang and Hwang (2017) reports standard deviations of $X,M$, and $Y$, and correlations between $X$ and $M$($r_{XM}$) and $X$ and $Y$ ($r_{XY}$), but not $r_{MY}$. In this situation, researchers may wish to specify an uninformative multivariate LKJ prior for the correlation matrix of $X,M$, and $Y$ or informative priors for $r_{XM}$ and $r_{XY}$ but a diffuse prior for $r_{MY}$; we illustrate the PrPC conclusions for both choices. Note that the two historical studies use different measures of learning outcomes and elaborative utterances during collaboration; in an applied setting, researchers would select the study that used identical definitions and scales for all variables in the model as the source of prior information for their study (Miočević et al., 2020). Here, we focus on illustrating how information from published studies can be used to specify priors based on available summary statistics, and we discuss the implications of selected priors. Visuals from the Shiny app and all the code for the empirical example can be found at https://osf.io/jgtpb/?view_only =b41dda8984fa48b098a23da058567408.

Methods

This Shiny app (accessible at https://bayesianmed-lab.shinyapps.io/Prior-Predictive-Checks-Bayesian-Mediation-Analysis/) contains separate tabs for the inverse-Wishart and the Separation Strategy specifications. Both tabs require the user to specify the sample size, whether $X$ is binary, and hyperparameters of the univariate normal priors for the means of $X$ (only if $X$ is continuous), $M$, and $Y$. Both studies defined positive interdependence as a binary variable (either there was a setting eliciting positive interdependence or there was not); thus, the user needs to input only the variance of $X$, and the mean and plausible scores on $X$ are not evaluated as part of the PrPC. In each tab, we set the sample size (N) equal to the number of participants in the study, and the means of $M$ and $Y$ to the reported values from each study. The sample size was N = 125 in Hooper and Hannafin (1991; denoted by HH in subsequent paragraphs) and N = 65 in Chang and Hwang (2017; denoted by CH in subsequent paragraphs). Mean hyperparameters of normal univariate priors for the means of $M$ and $Y$ were equal to observed means in a given study, and standard deviation hyperparameters were set equal to observed standard errors of the means. The symbol p() denotes a prior distribution, and N denotes a normal prior. Unless specified otherwise, the second hyperparameter in normal priors is the standard deviation. In HH, p(μ_M) ~ N(10.48, 0.76), p(μ_Y) ~ N(70.20, 2.54); in CH, p(μ_M) ~ N(26.20, 1.45), p(μ_Y) ~ N(68.78, 2.47).

Inverse-Wishart

The degrees of freedom hyperparameter (df) of the inverse-Wishart prior is equal to the sample size (N) of the observed data set minus one. For HH, df = 124 and the scale matrix is set to equal the sum of squares and cross products matrix in the observed data; SS_X = 30.89, SS_M = 2234.53, SS_Y = 24,597.56, SP_XM = 94.47, SP_XY = 133.48, and SPMY = 2203.74. The IW prior was not evaluated for the CH study due to missing information about $r_{MY}$. If the user-specified values do not satisfy a check for positive definiteness of the prior expectation for the covariance matrix, an error message will appear at the top of the main panel (Expectation for the Covariance Matrix) of the Inverse-Wishart tab. If df = 4, all entries in the expectation for the covariance matrix are equal to infinity, and it is impossible to compute the implied value of ab in the subtab Indirect Effect.

Separation strategy

In HH, the observed standard deviations for $X,M$, and Y are equal to 0.50, 4.25, and 14.08, respectively. The observed Pearson correlations are $r_{XM}$ = 0.36, $r_{MY}$ = 0.15, and $r_{XY}$ = 0.30. In CH, observed standard deviations of $X,M,$ and $Y$are equal to 0.49, 11.70, and 19.80, respectively. The observed Pearson correlations are $r_{XM}$ = 0.82, $r_{XY}$ = 0.50, and the correlation $r_{MY}$ is not reported. For the sake of space, we present prior specifications for R and S based on values from HH; however, the procedure was identical for CH. Analyses were run for all possible pairs of specifications (e.g., the LKJ prior for R and lognormal priors for standard deviations of $M$, and $Y$). Since X is a dichotomous variable, the default setting for the variance of X was used (using an informative inverse-gamma distribution).

Truncated normal priors for the correlations

The mean hyperparameters of truncated normal priors are set to equal the observed correlations between $X,M,$ and $Y$. In our example, we set the standard deviation hyperparameters in our example equal to the standard deviations of the correlations $r_{XM}$, $r_{XY}$, and $r_{MY}$ over the four groups in HH, which are 0.11 0.15, and 0.27 (respectively). In CH, we set the standard deviation hyperparameters of truncated normal priors for $r_{XM}$ and $r_{XY}$ equal to the standard errors of the observed correlations, which equaled 0.07 and 0.11, respectively. In CH, the unobserved correlation $r_{MY}$ was assigned a truncated normal prior that approximates a uniform prior on the possible range of $r_{MY}$, tN(0, 10).

LKJ prior for the correlation matrix

We set η = 0.5 for the LKJ prior to illustrate a scenario where researchers do not have any prior information about correlations between $X,M,$and $Y$. For a model with three variables, η = 0.5 implies uniform priors for marginal correlations ranging from −1 to 1 (Joe, 2006).

Lognormal priors for standard deviations

The mean hyperparameters for $M$ and $Y$ are set equal to the natural logarithms of the observed standard deviation of each of the three variables in the data set, i.e., 1.45, and 2.65, respectively. The choice of the standard deviation hyperparameter of the lognormal prior is subjective; lower values of this hyperparameter encode more certainty about the chosen mean hyperparameters. We visualized lognormal priors with three choices of standard deviation hyperparameter values (1, 2, and 3) for standard deviations of $M$ and $Y$. We chose a standard deviation hyperparameter of 1 based on a comparison of values in the 95^th percentile range for the three values of the standard deviation hyperparameter; the standard deviation hyperparameter of 1 led to more realistic ranges of standard deviation values than higher values of the standard deviation hyperparameter. When the hyperparameter values are entered into the Shiny app, the measures of the central tendency of the prior distributions for standard deviations of $M$ and $Y$ are computed using the following equations: mean = exp(μ_LN +${\sigma }^2$/2), median = exp(μ_LN), and mode = exp(μ_LN-${\sigma }^2$).

Half-Cauchy priors for the standard deviations

There is no arithmetic solution for the mean, mode, or variance of the half-Cauchy distribution. The mean equals 0, and the interquartile range (25–75%) is equal to the scale parameter times two. We set the median hyperparameters for half-Cauchy priors equal to the observed standard deviations of $M$ and $Y$.

Inverse-gamma priors for the variances

Following the recommendation by Gelman et al. (2004) for selecting hyperparameters for inverse-gamma priors, we set α equal to the sample size divided by 2 and β equal to the observed variance of the variable in the prior data set times the sample size divided by 2. For HH, α = 125/2 = 62.5 for all variables, and β hyperparameters are equal to 15.625 for the variance of $X$, 1126.28 for the variance of $M$, and 12,397.96 for the variance of $Y$. The Shiny app computes the measures of the central tendency of the prior distributions for variances of $M$ and $Y$ using the following equations: mean = β/(α – 1) and mode = β/(α + 1). The median is computed as the 50% quantile of the inverse-gamma distribution in the extraDistr package (Wolodźko, 2019)

Prior predictive check

In both the inverse-Wishart and the Separation Strategy tabs, the Lower Percentile and Upper Percentile inputs represent the percentile of scores on a given variable ($X,M,$and $Y$) in each generated data set for which the proportions of impossible scores will be computed in the Prior Predictive Check. As such, the Lower and Upper Percentiles capture the researcher’s desired level of conservativeness for this check. For example, specifying 0.5 as the Lower and Upper Percentiles will compute the percentages of data sets with median values below the lower limit of the scale and median values above the upper limit of the scale. Thus, selecting 0.01 as the Lower Percentile would be a stricter criterion than specifying 0.45 as the Lower Percentile because it leads to higher percentages of “impossible” data sets. Conversely, selecting 0.99 as the Upper Percentile would lead to a stricter criterion than selecting 0.55 as the Upper Percentile because a higher percentage of data sets would be labeled as “impossible.” Plots and tables in the app display the proportion of data sets with impossible scores below the Lower Limit and above the Upper Limit separately for each variable. For our example, we selected a Lower Percentile of 0.25 and an Upper Percentile of 0.75.

Realistic ranges for continuous $X,M,$and $Y$ represent the range of possible values of each variable. Once all inputs are filled, the data generation is initiated by pressing the Simulate button. The 10,000 prior predictive data sets with scores on continuous $X,M,$and $Y$ are generated using the R packages extraDistr (Wolodźko, 2019), MASS (Venables & Ripley, 2002), and MCMCpack (Martin et al., 2011).

Results

For the sake of space, we do not present any of the plots produced by the Shiny App, but interested readers can find them in the Supplemental Materials available at https://osf.io/jgtpb/?view_only =b41dda8984fa48b098a23da058567408. We present the findings from the PrPC for the two historical studies separately.

PrPC for Hooper and Hannafin (1991)

The sample size of HH was 125, and participants were distributed across 4 different groups based on ability. The variance of binary $X$ (positive interdependence) was 0.25. Elaboration was a measure of average instances of cooperation over a period of 5 minutes; reasonable minimum and maximum values would be 0 and 50, respectively. Achievement was measured on a scale ranging from 1 to 100. In Table 1 we can see how often the prior specification resulted in large proportions of values outside these realistic ranges. Notably, the inverse-Wishart and inverse-gamma prior specifications had the lowest proportions of values outside realistic ranges of elaboration ($M$) and achievement ($Y$).

Table 1. PrPC results for realistic ranges of M and Y are in the study by Hooper and Hannafin (1991)

	Proportion of lower percentiles below lower limit		Proportion of upper percentiles above upper limit
	M	Y	M	Y
IW	<.001	<.001	<.001	<.001
HC & LKJ	.216	.098	.058	.224
HC & TN	.217	.102	.057	.231
IG & LKJ	<.001	<.001	<.001	<.001
IG & TN	<.001	<.001	<.001	<.001
LN & LKJ	.144	.038	.008	.176
LN & TN	.139	.038	.007	.176

Italicized values indicate the lowest value in the column. IW denotes an inverse-Wishart prior, HC denotes a half-Cauchy prior, LKJ denotes the Lewandowski et al. (2009) prior, TN denotes a truncated normal prior, IG denotes an inverse-gamma prior, and LN denotes a lognormal prior.

The comparison of user-specified means and means generated by the prior specification shows that on average, the generated means by all priors were unbiased relative to user-specified means in the data (see column “Absolute Difference between Proportion lower and higher” in Table 2). The half-Cauchy and the truncated normal prior specifications had both the lowest proportion of significant differences and the highest symmetry between whether the user-specified means were overestimated or underestimated. With respect to generated means these two prior specifications may be the best representation of the available (observed) prior information; however, almost all prior specifications led to generated values of ${\mu }_M$ and ${\mu }_Y$ close to observed (user-specified) values.

Table 2. PrPC results for the mean difference for Hooper and Hannafin (1991)

	Proportion of data sets where generated means are significantly lower than the observed mean		Proportion of data sets where generated means are significantly higher than the observed mean		Absolute Difference between Proportion lower and higher
	M	Y	M	Y	M	Y
IW	0.149	0.144	0.143	0.143	.006	.001
HC & LKJ	0.132	0.146	0.139	0.150	.007	.004
HC & TN	0.137	0.142	0.137	0.142	<.001	<.001
IG & LKJ	0.152	0.148	0.146	0.146	.006	.002
IG & TN	0.150	0.151	0.153	0.144	.003	.007
LN & LKJ	0.143	0.144	0.141	0.133	.002	.011
LN & TN	0.144	0.140	0.141	0.134	.003	.006

Italicized values indicate the lowest value in the column. IW denotes an inverse-Wishart prior, HC denotes a half-Cauchy prior, LKJ denotes the Lewandowski et al. (2009) prior, TN denotes a truncated normal prior, IG denotes an inverse-gamma prior, and LN denotes a lognormal prior.

Observed variances of positive interdependence ($X$), elaboration ($M$), and achievement ($Y$) were 0.25, 18.78, and 179.95 (respectively). The inverse-Wishart and inverse-gamma prior specifications had the lowest proportions of significant differences between the user-specified variances and the variances in the generated data sets (Table 3). The LKJ and truncated normal specifications seem to result in a smaller systematic difference between the variances of the generated data and the user-specified variances. In this case, the inverse-Wishart prior leads to underestimation of the user-specified variances in the generated data set more often than overestimation. Using inverse-gamma priors with either the LKJ prior or truncated normal priors for the correlations may be preferred if researchers are more concerned with underestimation than overestimation of the variances of $X,M,$and $Y$.

Table 3. PrPC results for the variance difference for Hooper and Hannafin (1991)

	Proportion of generated data sets with significantly lower variance than the observed variance			Proportion of generated data sets with significantly higher variance than the observed variance
	X	M	Y	X	M	Y
IW	.042	.061	.061	.060	.044	.042
HC & LKJ	.050	.451	.459	.051	.454	.449
HC & TN	.048	.458	.448	.045	.450	.458
IG & LKJ	.053	.054	.046	.052	.043	.049
IG & TN	.054	.055	.052	.049	.046	.048
LN & LKJ	.048	.453	.437	.050	.436	.444
LN & TN	.048	.439	.437	.050	.439	.448

Bolded values indicate high proportions. Italicized values indicate the lowest proportion in the column. IW denotes an inverse-Wishart prior, HC denotes a half-Cauchy prior, LKJ denotes the Lewandowski et al. (2009) prior, TN denotes a truncated normal prior, IG denotes an inverse-gamma prior, and LN denotes a lognormal prior.

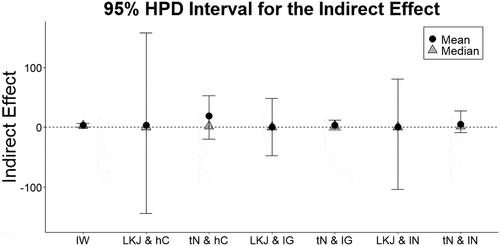
The inverse-Wishart distribution resulted in the narrowest intervals for the implied indirect effect, and the LKJ prior for correlations (particularly combined with the half-Cauchy priors for standard deviations) resulted in the widest intervals (Figure 2). The range of the dependent variable is 1–100, and the width of the intervals for the indirect effect produced by the LKJ prior encompasses values greater than 100 in absolute value. Unless researchers are interested in a fairly diffuse implied prior for the indirect effect, the LKJ prior is a less appealing alternative than the inverse-Wishart prior according to this check.

Figure 2. 95% HPD intervals for the indirect effects when specifying the different priors based on Hooper & Hannafin (1991). The dotted line indicates the indirect effect estimate of 0. IW denotes an inverse-Wishart prior, tN denotes a truncated normal prior, lN denotes a log normal prior, IG denotes an inverse-gamma prior, and hC denotes a half-Cauchy prior

PrPC for Chang and Hwang (2017)

In CH, 65 elementary school students participated in a digital learning task. Positive interdependence was elicited by taking a peer-assistance approach in the learning task in the experimental group, which had the goal of both improving learning outcomes and increasing positive peer interactions. Students were distributed in two groups (experimental group N₁ = 34 and control group N₂ = 31). The variance for positive interdependence ($X$) was 0.25. Elaboration was measured as the number of instances of elaboration in 180 interactions; thus, the maximum for this variable was 180. The theoretical range of the achievement test was from 1 to 100. Since the relationship between Elaboration and Achievement was not reported in this article, the inverse-Wishart prior specification was not pursued.

The inverse-gamma prior resulted in generated data that were most in line with possible values of M and Y (Table 4). The next best prior specification according to this criterion was the combination of the lognormal and LKJ distributions, but even this prior specification often leads to high proportions of generated scores above the upper limit of achievement ($Y$).

Table 4. PrPC results for a realistic range for Chang and Hwang (2017)

	Proportion of lower percentiles below lower limit		Proportion of upper percentiles above upper limit
	M	Y	M	Y
HC & LKJ	.220	.152	.041	.309
HC & TN	.222	.140	.040	.299
IG & LKJ	<.001	<.001	<.001	.002
IG & TN	<.001	<.001	<.001	<.001
LN & LKJ	.157	.076	.002	.258
LN & TN	.168	.084	.003	.257

Italicized values indicate the lowest value in the column. HC denotes a half-Cauchy prior, LKJ denotes the Lewandowski et al. (2009) prior, TN denotes a truncated normal prior, IG denotes an inverse-gamma prior, and LN denotes a lognormal prior.

The results of the prior predictive check that compared user-specified means to the means generated by the prior specification show that the priors do not differ in the proportions of significant mean differences (Table 5). Also, both the inverse-gamma prior specification and the lognormal specification seemed to result in an appropriate symmetry between underestimation of means and overestimation of means.

Table 5. PrPC results for the mean difference for Chang and Hwang (2017)

	Proportion of data sets where generated means are significantly lower than the observed mean		Proportion of data sets where generated means are significantly higher than the observed mean		Absolute Difference between Proportion lower and higher
	M	Y	M	Y	M	Y
HC & LKJ	.050	.050	.050	.046	<.001	.004
HC & TN	.046	.047	.050	.048	.004	.001
IG & LKJ	.048	.050	.047	.049	.001	.001
IG & TN	.052	.049	.050	.049	.002	<.001
LN & LKJ	.049	.050	.051	.048	.002	.002
LN & TN	.048	.048	.050	.048	.002	<.001

Italicized values indicate the lowest value in the column. HC denotes a half-Cauchy prior, LKJ denotes the Lewandowski et al. (2009) prior, TN denotes a truncated normal prior, IG denotes an inverse-gamma prior, and LN denotes a lognormal prior.

The observed variances of positive interdependence ($X$), elaboration ($M$), and achievement ($Y$) were 0.25, 136.90, and 392.22, respectively. The half-Cauchy and the lognormal specifications led to frequent over- and underestimation of the variances (Table 6). The inverse-gamma specification did not result in notable overestimation or underestimation, regardless of the prior for correlations (LKJ or truncated normal).

Table 6. PrPC results for variance difference for Chang and Hwang (2017)

	Proportion of generated data sets with significantly lower variance than the observed variance			Proportion of generated data sets with significantly higher variance than the observed variance
	X	M	Y	X	M	Y
HC & LKJ	.048	.440	.436	.050	.425	.437
HC & TN	.050	.435	.440	.047	.436	.430
IG & LKJ	.047	.048	.051	.050	.049	.045
IG & TN	.051	.055	.053	.050	.046	.046
LN & LKJ	.051	.421	.419	.050	.411	.419
LN & TN	.050	.415	.428	.051	.417	.410

Bolded values indicate high proportions. Italicized values indicate the lowest proportion in the column. HC denotes a half-Cauchy prior, LKJ denotes the Lewandowski et al. (2009) prior, TN denotes a truncated normal prior, IG denotes an inverse-gamma prior, and LN denotes a lognormal prior.

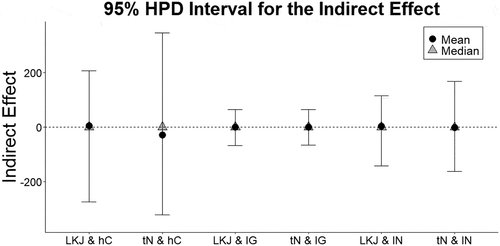
Finally, we evaluate the implied indirect effect estimates in Figure 3 to choose between prior specifications. Remembering that the realistic range of Achievement is 1–100, the only prior specifications with reasonable Highest Posterior Density (HPD) intervals for the indirect effect are the inverse-gamma with LKJ or the inverse-gamma with the truncated normal distribution. Based on all prior predictive checks, the inverse-gamma with either the LKJ or truncated normal priors for correlations yield the best representations of summary statistics in CH.

Figure 3. 95% HPD intervals for the indirect effects when specifying the different priors based on Chang & Hwang (2017). The dotted line indicates the indirect effect estimate of 0. IW denotes an inverse-Wishart prior, tN denotes a truncated normal prior, lN denotes a log normal prior, IG denotes an inverse-gamma prior, and hC denotes a half-Cauchy prior

Conclusion

Specifying priors for Bayesian mediation analysis using the method of covariances can be challenging because of the lack of intuition about the implications of hyperparameter choices for the encoded prior beliefs about the mediated effect and distributions of scores. The goal of this paper was to illustrate PrPC for the methods of covariances in Bayesian mediation analysis and to guide researchers through the process of selecting hyperparameters for different prior distributions based on available data. In the study by Hooper and Hannafin (1991), the same amount of prior information was available for all elements of the covariance matrix of $X,M,$and $Y$ which made the inverse-Wishart prior an appropriate choice. Still, the PrPC showed that the separation strategy prior using the inverse-gamma specification performed similarly to the inverse-Wishart, and even performed a bit better when the goal was to avoid underestimating the variances of $X,M,$and $Y$ . Given that the study by Chang and Hwang (2017) did not report $r_{MY}$, we compared six different prior specifications using the separation strategy and found that the half-Cauchy and lognormal prior specifications resulted in large instances of unrealistic generated data and many differences between user-specified and generated variances. These priors encode more uncertainty about the variance relative to inverse-gamma priors, which may be an attractive feature when the researcher wants to specify a weakly informative prior based on the published study. The optimal prior specification based on the published study depends on the researcher’s confidence that data from the published study are exchangeable with data from the current study, which they wish to analyze using Bayesian mediation analysis with informative priors. The proposed procedure and Shiny app are useful tools for comparing possible prior specifications based on available summary statistics in published articles.

This paper describes the first proposed PrPC for Bayesian mediation analysis for the method of covariances, and the first illustration of the use of the Separation Strategy for Bayesian mediation models. Informative priors in Bayesian analysis yield important advantages relative to methods that do not use prior information (e.g., Miočević et al., 2017), but come with a risk of severely biasing the results if the information is inaccurate (e.g., Depaoli, 2014). The consensus in the methodological literature is that Bayesian methods are most useful with thoughtfully chosen priors (Smid et al., 2020), and we hope the proposed PrPC facilitates the specification of such priors for mediation analysis. Future research should outline PrPC procedures for other types of commonly used statistical models in psychology, such as CFA, longitudinal growth models, and mixture models.

Correction Statement

This article has been republished with minor changes. These changes do not impact the academic content of the article.

Additional information

Funding

This work was supported by the Natural Sciences & Engineering Research Council (NSERC) [Discovery Grant] awarded to Dr. Milica Miočević.

Notes

¹ We use the term “generated data set” or “generated sample” to refer to values of X, M, and Y generated from the user-specified hyperparameters for different prior distributions. If the user-specified hyperparameter values correspond to summary statistics from a published study, we use the terms “observed” and “user-specified” interchangeably.