Variable Selection for Mediators under a Bayesian Mediation Model

Abstract

This study proposes a Bayesian variable selection approach to select mediators and quantify their respective posterior probabilities in exploratory mediation analysis. Monte Carlo simulation studies demonstrate that the proposed method has high statistical power in selecting mediating effects and low Type I error rate in excluding null effects. By estimating the probability of a given mediating effect via the posterior distribution, the proposed method quantifies the variable’s influence on a continuum scale. This is an attractive and unique gain that neither conventional p-value-based mediation methods nor the regularization-based LASSO method for exploratory mediation possess. We offer four decision rules to assist in selecting mediators and excluding null effects to minimize a common problem (i.e., elevated type I errors) in the exploratory context, as well as provide an empirical example to illustrate the proposed method’s application and interpretation. We end with a discussion of the work and directions for future work.

Keywords:

• Bayesian variable selection
• decision rules
• exploratory mediation analysis
• Gibbs sampling
• model uncertainty

Mediation analysis is a popular statistical technique that remains an active topic in both methodological (e.g., MacKinnon & Fairchild, 2009; Tofighi & Kelley, 2020; Miočević & Golchi, 2022; Miočević et al., 2021) and substantive (e.g., Chalder et al., 2015; Vuorre & Bolger, 2018; Wiedermann & Sebastian, 2020) research. Mediation analysis explains the process of an independent variable (X) transmitting an effect on a dependent variable (Y) via a third intervening variable, called a mediator (M). Exploring relational chains among variables in the model is common in psychological, behavioral, and social science research. Mediation analysis provides a possible mechanism to explain these relations.

A typical mediation model can be represented with the following set of linear equations (1) $$Y_i=I_1+c{X}_i+e_{1i}$$(1) (2) $$\begin{array}{c}{Y}_i=I_2+c\prime X_i+{\Sigma }_{k=1}^K{\mu }_k{M}_{ik}+e_{2i}\\ M_{ik}=I_{k+2}+{\nu }_k{X}_i+e_{k+2,i}\end{array}$$(2) where $I_1,I_2,I_{k+2}$ are the intercepts, X_i is the independent variable, Y_i is the dependent variable, and M_ik is the mediator for an ith individual and the kth mediator. Equation (1)(1) $$Y_i=I_1+c{X}_i+e_{1i}$$(1) represents the total effect, and Equation (2)(2) $$\begin{array}{c}{Y}_i=I_2+c\prime X_i+{\Sigma }_{k=1}^K{\mu }_k{M}_{ik}+e_{2i}\\ M_{ik}=I_{k+2}+{\nu }_k{X}_i+e_{k+2,i}\end{array}$$(2) parses the total effect model into direct and indirect components, allowing for K mediators, $k=1,\dots ,K$ (Bollen, 1987), and thus K indirect effects. The total mediated effect is the sum of all these indirect effects, one for each mediator, represented as ${\Sigma }_{k=1}^K{\nu }_k{\mu }_k$ (MacKinnon et al., 2007). The total mediated effect ${\Sigma }_{k=1}^K{\nu }_k{\mu }_k$ is defined using parameters from Equation (2)(2) $$\begin{array}{c}{Y}_i=I_2+c\prime X_i+{\Sigma }_{k=1}^K{\mu }_k{M}_{ik}+e_{2i}\\ M_{ik}=I_{k+2}+{\nu }_k{X}_i+e_{k+2,i}\end{array}$$(2) and is equivalent to the total effect of c from Equation (1)(1) $$Y_i=I_1+c{X}_i+e_{1i}$$(1) in linear models. 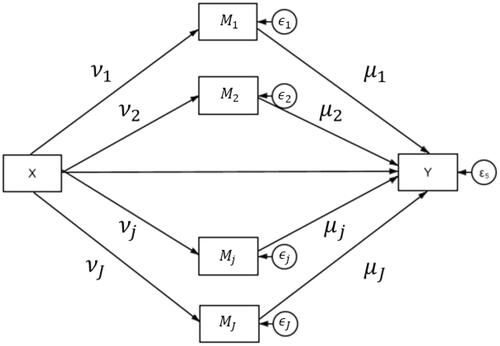The corresponding path diagrams for Equations (1(1) $$Y_i=I_1+c{X}_i+e_{1i}$$(1) ) and (2(2) $$\begin{array}{c}{Y}_i=I_2+c\prime X_i+{\Sigma }_{k=1}^K{\mu }_k{M}_{ik}+e_{2i}\\ M_{ik}=I_{k+2}+{\nu }_k{X}_i+e_{k+2,i}\end{array}$$(2) ) are shown in the path diagrams in Figures 1 and 2, respectively.

Figure 1. The total effect model.

Figure 2. The multiple mediator model.

Many key research questions and theories often involve multiple mediators, rather than single mediator models (e.g., VanderWeele & Vansteelandt, 2014). Consider the case of a health promotion program that targets multiple mechanisms of behavioral change, such as the PHLAME intervention trial that aimed to improve the physical wellness of firefighters (e.g., Ranby et al., 2011). The single mediator model is a special case of the multiple mediator model (MacKinnon, 2000; MacKinnon & Fairchild, 2009). To claim that M_ik is a significant mediator, indirect effects, ${\nu }_k\times {\mu }_k,$ must be statistically significant.

Mediator models can be estimated using ordinary least squares (OLS) regression¹ or fitted in the structural equation modeling (SEM) framework (e.g., Preacher, 2015; Preacher & Hayes, 2008). For detailed steps to establishing mediation relations, please see MacKinnon et al. (2007). While the indirect effects of a, b, as illustrated in Figure 2, can be fitted through OLS or SEM, the standard errors of the indirect effects (${\nu }_k\times {\mu }_k$) and the associated joint significance need special treatment. Early approaches to examining mediation used standard error estimators based on the multivariate delta method (e.g., Sobel, 1982) to test the significance of indirect effects. These normal theory standard error estimators are conservative, however, as they assume symmetrical normal approximations, whereas the sampling distribution of the product of two random variables (such as the mediated effect) is nonnormal (Meeker et al., 1981). A more popular method is to use nonparametric bootstrapping for estimating the standard errors of indirect effects (Bollen & Stine, 1990; Shrout and Bolger, 2002), which uses the empirical distribution to construct confidence intervals for the indirect effects (MacKinnon et al., 2007; Preacher & Hayes, 2004). This approach leads to smaller Type I error rates and higher power relative to conventional methods. The percentile bootstrap in particular has been shown to have good performance across a range of simulated parameter combinations that emulate those typically seen in empirical research (MacKinnon et al., 2004; Williams & MacKinnon, 2008).

The approaches discussed above are confirmatory based models that implicitly require strong theory. In this traditional approach, models are first constructed based on theory and then empirically tested with predefined hypotheses about specific mediating variables. Mediation analysis may also be driven by data and can be exploratory (Farbmacher et al., 2022; Jan van Kesteren & Oberski, 2019); this possibly has garnered enhanced focus given an increased application of high-dimensional data (e.g., gene sequencing, fMRI). For example, researchers may be interested in studying the impact of genetic variants on pathological behaviors through neuroimaging phenotypes (Bi et al., 2017); or the influence of single nucleotide polymorphisms on fractional amplitude of low-frequency fluctuations mediated by grey matter volume alterations (Luo et al., 2018). Thus, exploratory approaches may be useful in at least two situations. First, one may consider exploratory methods for mediation when the available theoretical information is weak or underexplored in practice, precluding the development of clear hypotheses and/or the inclusion of a specific mediating effect. Second, it may also be useful to consider exploratory mediation approaches when the parameter space of candidate mediators for a relationship of interest is high dimensional and would benefit from data reduction techniques (Blum et al., 2020). For instance, the mediating effects of the gut microbiome are often interesting to microbiome researchers, in which the host gene expression leads to a given clinical/health outcome through the gut microbiome (Kurilshikov et al., 2017; Rooks & Garrett, 2016). Carter et al. (2020) are particularly interested in how microbial taxa may mediate the effect of gene expression on clinical outcomes but find it challenging with high dimensional omics data. Detecting potential mediators in an exploratory approach can assist in identifying plausible mediator variables to examine in future research via confirmatory methods (e.g., Farbmacher et al., 2022), but appropriate methods must be in place to facilitate these analyses.

Recently, Serang et al. (2017) developed an initial framework for exploratory mediation analysis via regularization. Their approach explores and determines potential mediators using regularization techniques instead of specifying mediators in a model a priori based on previous knowledge, expanding one’s potential to examine mediation effects in exploratory, data-driven contexts. These authors adopted a two-step approach to identify potential mediators in the modeling process. First, all potential mediators are fitted into a multiple mediator model where the least absolute shrinkage and selection operator (LASSO) penalty is added. The LASSO singles out a subset of mediators that are potentially influential in the process, while zeroing out the remaining variables that are less impactful as mediators. In the second step of Serang et al.’s method, the most influential variables from the first stage are then used as mediators to refit a regular multiple mediator model to obtain parameter estimates. This regularization approach puts constraints on the sizes of the coefficients associated with variables to compare and identify the most potentially influential mediators among all variables in the process, and as such may be viewed as a variable selection problem. Rather than determining mediators theoretically, the exploratory mediation approach is data-driven. Despite having a clear value in situations where theory may be scarce (yielding increased sensitivity to identifying true mediators relative to conventional methods), it is important to note that the increased power of the regularization method may come at the expense of elevated Type 1 error rates (see results in Serang et al. (2017)).

While classic variable selection approaches such as regularization or stepwise regression help identify possible mediator variables in an exploratory context, they have several limitations. First, the decision to retain variables in a model is binary; variables are either kept or dropped based on statistical significance alone. Focusing on null hypothesis significance testing in this way, rather than using a continuous metric like effect size or posterior probability, may encourage the identification of potential mediators by chance characteristics that would not replicate in other studies (Lu et al., 2016). Second, as pointed out by Wagenmakers et al. (2017), failing to reject the null hypothesis does not mean that the null hypothesis is true. In other words, because the LASSO yields only one explanation does not mean it provides the only explanation nor indicates that other explanations are false (Epskamp et al., 2017). In an exploratory context, it might be more useful to produce results that offer comparative insights into candidate mediator variables (rather than absolute inclusion or exclusion based on statistical significance). Lastly, traditional stepwise procedures may lead to inflated parameter estimates and biased standard error estimates (Mundry & Nunn, 2009; Altman and Andersen, 1999). Wasserstein and Lazar (2016) stressed the importance of measuring model uncertainty. Failure to account for model uncertainty will result in underestimated standard errors and model overfitting (e.g., Hoeting et al., 1999; Lu et al., 2016; Wasserstein and Lazar, 2016), distorting statistical inference and eventually misleading interpretations.

Building on previous work, this study proposes an alternative Bayesian variable selection approach to identify potential mediators in exploratory mediation that attends to the aforementioned limitations of other methods. By selecting the potentially most influential mediators among a potential set, the proposed method overcomes the challenges of pure binary decision from classic significance-based or regularization-based methods. By estimating the probability of a given mediating effect via the posterior distribution, the proposed method quantifies the variable’s influence on a continuum scale. We evaluate the proposed Bayesian variable selection approach in a Monte Carlo simulation study that mirrors the study design of Serang et al. (2017) to facilitate comparison of the approaches. Results show that the proposed exploratory method had comparable performance to Serang et al. 2017’s regularization-based exploratory mediation analysis, while conveying an additional advantage of quantifying the magnitude of each mediating effect in the model, compared to a pure dichotomized “to drop or to retain a variable” decision.

The remainder of the paper is structured as follows. We first briefly review Bayesian variable selection methods, particularly the Gibbs variable selection approach that underlies our work, to set the context for our proposed model. We then introduce the exploratory Bayesian mediation model, which uses a Bayesian variable selection (BVS) approach to identify potential mediators and to discuss model-related issues, including prior choices and model estimation. Next, we investigate the performance of the proposed technique and compare it with Serang et al. (2017)’s regularization-based exploratory mediation model. We follow with a real data example to illustrate the effects and application of the proposed BVS technique and conclude with recommendations and directions for future work.

1. Bayesian Variable Selection Methods

Variable selection has been a vital component in statistical inference. Classic approaches develop various search algorithms or use model selection criteria to select appropriate variables. On the one hand, traditional likelihood ratio tests such as stepwise regression, forward selection, and backward elimination select variables by searching the model space. They tend to select complicated models for a large sample size. On the other hand, model selection criteria such as Akaike Information Criterion (AIC, Akaike, 1974) and Bayesian Information Criterion (BIC, Schwarz, 1978) are commonly used to compare candidate models and select variables. These criteria face computational burdens when the number of competing models is sizeable. Recent advances in machine learning techniques, such as regularization-based methods, add another methodological dimension for variable selection. By carefully focusing on tuning parameters, the regularization-based methods penalize the model flexibility and avoid the risk of overfitting. Different from the least squares models, regularization reduces the variance of the model without substantially increasing its bias and improves predictive accuracy (e.g., Tibshirani, 1996).

Variable selection using Bayesian methods has been actively studied in the statistical literature. Bayesian models combine the likelihood of the observed data with prior distributions for the model parameters to obtain posterior distributions and make statistical inferences. Bayesian variable selection (BVS) methods have multiple lines of strategies to select variables. One line focuses on approximating the parameter shapes and quantifying the prior uncertainties via probabilities to calculate the posterior model probabilities (e.g., Chen et al., 2008). Specifically the adaptive shrinkage priors such as the Laplacian prior (Figueiredo, 2003) or Jeffrey’s prior (Hobert & Casella, 1996) are developed to approximate the parameter shape in the prior information and shrink estimation of variances. This is also viewed as a Bayesian regularization method to select variables. Other BVS methods consider the variable selection problem as part of model comparisons. Studies have used DIC (DIC, Spiegelhalter et al., 2002), Bayes Factor (Berger & Pericchi, 1996), or Bayesian Model Averaging (Draper, 1995) to compare models and thus select variables (Fortes Tondello et al., 2018; Van Der Linde, 2005).

This study, which applies another school of BVS strategy, transforms variable selection into a parameter estimation problem. In this study, we utilize an indicator model selection approach (O'Hara & Sillanpää, 2009) to select the most influential mediators in the Bayesian mediation model. The idea of the approach is to consider models containing all possible combinations of variables as submodels, estimate the submodels using Bayesian methods, obtain the posterior probabilities of including a variable, and select the final model based on the posterior probabilities of variables to be selected. In this line, multiple research strategies were developed and advanced, including developing Gibbs samplers via MCMC methods (Carlin & Chib, 1995) and modifying Gibbs samplers to sample from a joint distribution with only conditional distributions (Dellaportas & Smith, 1993). In particular, Kuo and Mallick (1998) proposed an indicator variable strategy with unconditional priors to select variables without tuning. In the absence of tuning, the coefficient has an exact probability of being zero (e.g., Han & Brynjarsdottir, 2017). The approach creates an indicator variable with a slab-and-spike prior for each covariate in the model. Independence is assumed between the indicators and the covariates on the outcome variables. The strategy estimates the posterior probabilities of the indicators, keeps variables who has high corresponding posterior probabilities for the indicators, and transforms the task of selecting variables into estimating parameters. This variable selection strategy has since seen methodological developments and substantive applications in various studies.

Following Kuo and Mallick (1998)’s initial development of the work in general linear models, Dellaportas et al. (2000) compared the performance of the indicator model selection method with two other Gibbs sampler based BVS approaches (stochastic search variable selection (SSVS; George & McCulloch, 1993) and Gibbs variable selection (GVS; Carlin & Chib, 1995; Dellaportas & Smith, 1993)) in generalized linear models. The study concluded that BVS techniques that are based on the Gibbs samplers are easy to apply and computationally convenient and fast. The findings lay the groundwork for building and advancing the Gibbs sampler based BVS techniques. Applying a stochastic search Gibbs sampler algorithm, Kinney and Dunson (2007) advanced the method to select the fixed and random effects in the mixed effects models for correlated data. Paroli and Spezia (2007) proposed a “Metropolization” of the algorithm of Kuo and Mallick (1998) to select variables with high model complexity and strong correlations between exogenous variables in Markov mixture models. A variation of the method was developed by (Kim et al., 2009) that imposed hyperpriors for the indicator variables for a Bayesian mixed hierarchical spatial model. In substantive fields, this approach has been used to map linked quantitative trait loci in genetics (Uimari & Hoeschele, 1997) and spatial epidemiology in hierarchical modeling (Lawson, 2018).

2. Exploratory Bayesian Mediation Modeling

This study proposes an exploratory Bayesian mediation (EBMed) model that uses a Bayesian variable selection approach to select potential mediators. The EBMed model, in essence, transforms the task of selecting variables into estimating the marginal posterior probability that a variable should be included in the model.

Let X_i be a vector of independent variables, Y_i be a vector of dependent variables, and M_ik be a vector of mediators for the ith individual at the kth mediator in the EBMed model. The EBMed model can be written as (3) $$Y_i=c\prime X_i+{\tau }_k{\mu }_k{M}_{ik}+{ϵ}_{1i}$$(3) (4) $$M_{ik}={\gamma }_k{\nu }_k{X}_i+{ϵ}_{2i},$$(4) where $c\prime$ represents the direct effects of X_i on Y_i after controlling for M_ik. In Equation (3)(3) $$Y_i=c\prime X_i+{\tau }_k{\mu }_k{M}_{ik}+{ϵ}_{1i}$$(3) , the coefficient μ_k denotes the direct effects of M_ik on Y_i for the ith individual at the kth mediator. To induce sparsity, we introduce a latent indicator variable, τ_k, for each mediator to the EBMed model, where ${\tau }_k=0$ means that M_ik pertains to a fixed value but is not related to Y_i and ${\tau }_k=1$ means that M_ik and Y_i are dependent. Estimating the posterior probabilities of each τ_k in the model is equivalent to obtaining the probabilities or weights that the corresponding variable should be included in the model. This technique assumes the independence between the indicators and the mediating effects, which is in line with Kuo & Mallick, 1998’s indicator model selection technique. Other Gibbs-sampling based BVS methods, such as SSVS (George & McCulloch, 1993) and GVS (Dellaportas & Smith, 1993) require the indicators to be dependent on the modeling effect to overcome potential sampling issues. These latter BVS approaches need additional tuning steps and are beyond the scope of the current study. The model residual ${ϵ}_{1i}$ is the residual for estimating the effects of M_ik on Y_i for the ith individual. In Equation 4(4) $$M_{ik}={\gamma }_k{\nu }_k{X}_i+{ϵ}_{2i},$$(4) , the coefficient ν_k denotes the effect of X_i on each mediator M_ik, and ${ϵ}_{2i}$ is the model residual that is typically assumed to be normally distributed. A second set of indicators for each independent variable, γ_k, is put into the model to estimate the effects of X_i on M_ik. Both μ_k and ν_k must demonstrate significant effects in order to claim the corresponding mediating effects M_k. Note that the parameters μ_k and ν_k were developed particularly for the EBMed model to estimate the posterior probabilities under the Bayesian framework and are not part of a standard mediation model estimated in the frequentist approach.

The EBMed model incorporates indicator variables into the model and estimates the posterior probabilities of those latent indicators. By building zeros into the coefficients to induce model sparsity, we can define various submodels with varying combinations of candidate variables (Kuo & Mallick, 1998) and measure their corresponding likelihood to guide the selection of a final mediation model. Because the indicator variables are supported at the values of one or zero, we assign Bernoulli prior distributions to the indicator variables, as ${\tau }_k\sim \mathit{Bernoulli}(\theta )$ and ${\gamma }_k\sim \mathit{Bernoulli}(\theta ),$ where θ are the hyperparameters for the indicators and denote the probability that a random indicator takes on the value of one or zero. Rather than giving a fixed value to the hyperparameter θ, we assign a prior to θ to allow the flexibility for incorporating more information. Specifically, we assign $\theta \sim \mathit{Beta}({\alpha }_{\theta },{\beta }_{\theta }),$ where the shape of the hyperparameter depends on how informative one is about the mediating effects. For example, specifying ${\alpha }_{\theta }>{\beta }_{\theta }$ indicates that one believes that less than half of the candidate variables are true mediators (e.g., there are less than 5 mediators among 10 candidate variables), thus forming a postively skewed distribution for the hyperprior; whereas if over half candidate variables are believed to be mediators, a negatively skewed distribution with the hyperprior being ${\alpha }_{\theta }<{\beta }_{\theta }$ is reasonable. Suppose one has limited or no prior relevant information about the mediating effects as in many exploratory settings, setting the hyperpriors equal to each other $({\alpha }_{\theta }={\beta }_{\theta })$ guarantees that the potential mediating effects (i.e., μ_k and ν_k) are equally likely to be significant or nonsignificant in the model. The direct effect of c’ in Equation (3)(3) $$Y_i=c\prime X_i+{\tau }_k{\mu }_k{M}_{ik}+{ϵ}_{1i}$$(3) is given a noninformative prior as $c\prime \sim N(0,1E+6).$ The coefficients μ_k and ν_k are given typical normal prior distributions as ${\mu }_k\sim N(0,{\sigma }_{\mu })$ and ${\nu }_k\sim N(0,{\sigma }_{\nu }).$ Because model residuals are typically assumed to be normally distributed, normal prior distributions are given as ${ϵ}_{1i}\sim N(0,\varphi )$ and ${ϵ}_{2i}\sim N(0,\psi ).$ All together formulate the model as $$\begin{array}{c}{\tau }_k\sim \mathit{Bernoulli}(\theta ),{\mu }_k\sim N(0,{\sigma }_{\mu })\\ Y_i|{\tau }_k,{\mu }_k,M_{ik}\sim N(〈\tau \odot \mu ,M_{ik}〉,\varphi )\end{array}$$ in correspondance to Equation (3)(3) $$Y_i=c\prime X_i+{\tau }_k{\mu }_k{M}_{ik}+{ϵ}_{1i}$$(3) , and $$\begin{array}{c}{\gamma }_k\sim \mathit{Bernoulli}(\theta ),{\nu }_k\sim N(0,{\sigma }_{\nu })\\ M_{ik}|{\gamma }_k,{\nu }_k,X_{ik}\sim N(〈\gamma \odot \nu ,X_{ik}〉,\psi )\end{array}$$ corresponding to Equation (4)(4) $$M_{ik}={\gamma }_k{\nu }_k{X}_i+{ϵ}_{2i},$$(4) , where $\odot$ denotes the Hadamard product. The posterior distributions for μ_k, τ_k and ν_k, γ_k follow $$p({\tau }_k,{\mu }_k|{\mathcal{D}}_{\mathcal{Y}})=\frac{1}{p({\mathcal{D}}_{\mathcal{Y}})}p({\tau }_k)p({\mu }_k)\prod _{i=1}^{N}p(y_i|{\tau }_k,{\mu }_k,M_{ik})$$ and $$p({\gamma }_k,{\nu }_k|{\mathcal{D}}_{\mathcal{M}})=\frac{1}{p({\mathcal{D}}_{\mathcal{M}})}p({\gamma }_k)p({\nu }_k)\prod _{i=1}^{N}p(M_{ik}|{\gamma }_k,{\nu }_k,X_i),$$ respectively, where $$p({\mathcal{D}}_{\mathcal{Y}})=\int p(\tau )p(\mu )\prod _{i=1}^{N}p(y_i|\tau ,\mu ,M_i)\mathit{\text{dτdμ}}$$

and $$p({\mathcal{D}}_{\mathcal{M}})=\int p(\gamma )p(\nu )\prod _{i=1}^{N}p(M_i|\gamma ,\nu ,X_i)\mathit{\text{dγdν}}$$ are the likelihood and $i=1,\dots ,N$ denotes the sample size. We employ the Gibbs sampling algorithm to approximate the inference for the posterior distributions. For each iteration, each indicator variable has an estimated value of one or zero. For Equation (3)(3) $$Y_i=c\prime X_i+{\tau }_k{\mu }_k{M}_{ik}+{ϵ}_{1i}$$(3) , we start with initial values ${\tau }^{(0)}$ and ${\mu }^{(0)};$ assume at the jth iteration, we have ${\tau }^{(j)}$ and ${\mu }^{(j)},$ and then iterate $$\begin{array}{c}{\tau }_1^{(j+1)}\sim p({\tau }_1|{\tau }_{2:k}^{(j)},{\mu }^{(j)},{\mathcal{D}}_{\mathcal{Y}});\\ {\tau }_2^{(j+1)}\sim p({\tau }_2|{\tau }_1^{(j+1)},{\tau }_{3:k}^{(j)},{\mu }^{(j)},{\mathcal{D}}_{\mathcal{Y}});\\ ⋮⋮\\ {\tau }_k^{(j+1)}\sim p({\tau }_k|{\tau }_{1:(k-1)}^{(j+1)},{\mu }^{(j)},{\mathcal{D}}_{\mathcal{Y}});\\ {\mu }^{(j+1)}\sim p(\mu |{\tau }^{(j+1)},{\mathcal{D}}_{\mathcal{Y}}).\end{array}$$

For large enough J iterations, we yield samples from the joint posterior distribution. Whereas an estimated value of one for the indicator variable denotes a significant mediating effect, an estimated indicator value of zero shows that the corresponding effects of μ_k or ν_k are nonsignificant. The posterior probabilities of the indicators summarize the probabilities or the weights that a corresponding mediator should be included in the model. Furthermore, we advance the EBMed over traditional BVS method in that, all the precision hyperparameters, including ${\sigma }_{\mu },$ ${\sigma }_{\nu },{ϵ}_{1i},$ and ${ϵ}_{2i}$ are given random effects. Specifically, we assign noninformative hyperpriors to the precision parameters for the mediating effects μ and ν and model residuals ϵ₁ and ϵ₂, as ${\sigma }_{\mu }\sim \Gamma (1,1E+3),$ ${\sigma }_{\nu }\sim \Gamma (1,1E+3),\varphi \sim \Gamma (1,1E+3),$ and $\psi \sim \Gamma (1,1E+3),$ respectively. The Gibbs sampler is desirable in the EBMed model as it quickly finds the conditional distribution for each parameter rather than locating the joint posterior probability. The indicator variables take on the value of 1 if the posterior distribution is sampled from a subset of candidate mediators; when the indicator takes on the value of 0, the coefficient estimate is updated from the full conditional distribution, which is the prior distribution for the coefficient. Patterns of the sampled values of the coefficients will quickly emerge in Gibbs samplers, but rarely flip between situations where the indicators are slabbed or spiked (e.g., Kuo & Mallick, 1998). The proposed EBMed method can handle from a small handful to hundreds of potential mediators in a model. Although computational burdens may appear to be a concern, they are not in the current study since the Bayesian indicator-based model selection approach can quickly navigate submodels with promising predictors (Dellaportas et al., 2000; O'Hara & Sillanpää, 2009). Through simulations, Kuo and Mallick (1998) found that favorable predictors showed high frequencies in the Gibbs samplers, whereas less promising variables rarely appear in the Gibbs algorithm. The Gibbs sampler estimates the posterior probabilities of the indicators τ_k and γ_k. The posterior inclusion probability, or the posterior probability of a variable being in the model, is computed as the mean of the posterior samples of τ_k and γ_k. The posterior inclusion probability not only selects significant mediators but quantifies the likelihood of potential mediating effects. By selecting submodels with the highest joint posterior probabilities of the indicators τ_k and γ_k, the final model is determined based on the marginal posterior probabilities of including the mediators of interest. The final estimated mediating effects are then computed as the product of μ_k and ν_k, or a given mediation effect.

2.1. Decision Rules (DR)

To address a common limitation of exploratory methods (i.e., elevated Type I error rate), we formulate a series of decision making strategies (i.e., decision rules) to retain selected mediators in the EBMed modeling framework. We outline each decision making strategy below and describe their respective advantages and disadvantages.

2.2. DR1

This approach considers and compares the joint posterior inclusive probabilities of the indicators $\widehat{{\gamma }_k}\times \widehat{{\tau }_k}$ to include mediators and exclude null effects. The approach rank orders the joint posterior inclusive probabilities for the indicators, and then selects a pre-determined number of mediators associated with the highest posterior inclusive probabilities. This approach requires knowledge of prior substantive theory to pre-determine the number of mediating effects in the model. For instance, the current simulation study uses three as the pre-determined number of mediators to be in the model, based on prior knowledge (i.e., true data generating process). Accordingly, we select three most influential mediators that are associated with the largest joint posterior inclusive probabilities. While this approach is straightforward to comprehend and easy to implement, researchers need to have a strong prior theory to know in advance how many mediators one wants to include. Thus, in some sense, this approach may appear to be incompatible with a purely exploratory approach.

2.3. DR2

Rather than relying on substantive theory, EBMed DR2 determines the number of mediators by directly computing the estimated posterior mean of the hyperparameter from the model. Let K be the total number of candidate mediators and q be the posterior mean of the hyperparameter for the indicators, θ. Given known K and q, the desired number of mediators k is computed as $k=K\times q,$ as the posterior mean of θ controls the probability of keeping a particular candidate mediator in the model. After rounding k, the whole number is the sought-after number of mediators selected in the model. The approach then selects k mediators associated with the highest joint posterior inclusive probabilities for the corresponding indicators. In the simulation study, for example, the total number of candidate variables, K, is 5; one simulation replication produces an estimated posterior mean of 0.57 for the indicator’s hyperparameter, denoted as q; the information together determines the desired number of mediators to be 3 $(k=K\times q\simeq 5\times 0.57).$ The approach then picks out the largest three joint posterior inclusive probabilities for the indicators and retains their corresponding mediators.

2.4. DR3

EBMed DR3 adopts the same algorithm as EBMed DR2 to determine the number of mediators to be included in the model by using the estimated posterior mean of the hyperparameter for the indicators θ. After determining the optimal number, EBMed DR3 keeps mediators whose corresponding indicators have the joint posterior inclusive probabilities being larger than 0.5. Rather than sticking to a pre-determined number of mediators, this approach avoids selecting spurious relations by erring on the side of caution. Therefore, EBMed DR3 can be more conservative in making fewer Type I errors and gives researchers more flexibility to select the final mediators in the model.

2.5. DR4

EBMed DR4 shares the same decision rules as EBMed DR3 but implements the process in an opposite direction. EBMed DR4 first includes all mediators whose corresponding joint posterior inclusive probabilities are larger than 0.5. The approach then calculates the optimal number of mediators in the model and excludes mediators who fail in either criterion. EBMed DR4 is a reversed selection process of EBMed DR3. It is expected to perform similarly to EBMed DR3 and can be conservative.

3. A Simulation Study

3.1. Simulation Design

We evaluated the performance of the EBMed model and the associated DRs via a Monte Carlo simulation study. The goal was to assess how accurate the proposed technique selected true mediators as well as excluded null mediating effects. We generated data following the study by Serang et al. (2017), using regularization-based techniques to select mediators. Applying the data in an identical setting allowed us to better understand the performance of the EBMed model, in comparison with other established techniques. 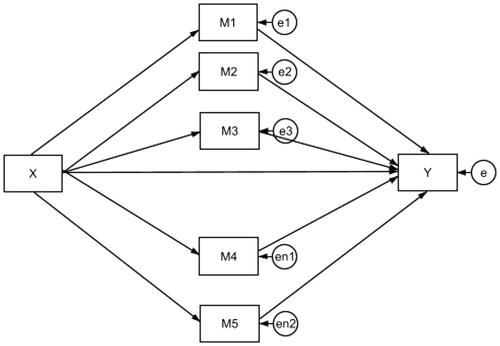Raw data were generated from a multiple mediator model shown in Equations from (5) to (10) and Figure 3 (5) $$Y_i={\Sigma }_{k=1}^k{\mu }_k{M}_{ik}+e_i,$$(5) (6) $$M_{i1}={\nu }_1{X}_i+e_{1,i},$$(6) (7) $$M_{i2}={\nu }_2{X}_i+e_{2,i},$$(7) (8) $$M_{i3}={\nu }_3{X}_i+e_{3,i},$$(8) (9) $$M_{i4}={\nu }_4{X}_i+e_{4,i},$$(9) (10) $$M_{i5}={\nu }_5{X}_i+e_{5,i},$$(10) where the multiple mediator model had one dependent variable Y_i, one independent variable X_i, and five potential mediators $M_{i1},\dots ,M_{i5}$ for the ith individual. Among the five mediators, three of them $M_{i1}, M_{i2}, M_{i3}$ had true mediating effects and two $M_{i4}$ and $M_{i5}$ were variables that had null effects but were difficult to control in the design. The three true mediators $M_{i1}, M_{i2}, M_{i3}$ had large (0.59), medium (0.36), and small (0.11) effect sizes, respectively, based on altering the population values of the ν_k and μ_k $(k=1,\dots ,5)$ path in the model. The choice of the population values was consistent with the existing literature in mediation analysis (i.e., Serang et al., 2017). Additionally, the two null effects $M_{i4}$ and $M_{i5}$ were designed to assess the performance of the EBMed model with respect to Type I error rate. We manipulated the factor of sample sizes of $N=$50, 100, 200, 500, 1000, and 2000 to determine if the selection rates varied by sample size.

Figure 3. Population model.

We applied two analytic methods to compare the performance of the mediator selection techniques in the multiple mediator model. The first method was the proposed EBMed model discussed above in Equations (3)(3) $$Y_i=c\prime X_i+{\tau }_k{\mu }_k{M}_{ik}+{ϵ}_{1i}$$(3) and (4)(4) $$M_{ik}={\gamma }_k{\nu }_k{X}_i+{ϵ}_{2i},$$(4) . We assigned a normally-distributed hyperprior to the indicator hyperparameter θ, as ${\tau }_k\sim \mathit{Bernoulli}(\theta ),{\gamma }_k\sim \mathit{Bernoulli}(\theta ),$ and $\theta \sim \mathit{Beta}(3,3),$ where the hyperprior $\theta \sim \mathit{Beta}(3,3)$ approximated a normal distribution with the mean centered around 1/2, ensuring an equal probability of (non)significant mediating effects for μ_k and ν_k, respectively. The second method was the regularization-based mediator model by Serang et al. (2017). In the previous literature, Serang et al. (2017) compared the regularization-based technique to other traditional classic mediation methods that calculated standard errors using the multivariate delta method (Casella and Berger, 2021) and bootstrapping (Bollen & Stine, 1990). We directly reported results of these two traditional approaches from Serang et al. (2017) to align with prior work and will focus on the comparison of the exploratory regularization-based method by Serang et al. (2017).

All data generation process and analyses were conducted in R (R Core Team, 2021) and JAGS (Plummer, 2003). Bayesian estimation was used for the proposed EBMed technique. We ran a total of 10,000 iterations for the MCMC chains, with the first 1,000 iterations as the burn-in period. Each condition was replicated 1,000 times.

3.2. Evaluation Criteria

To assess the performance of the proposed technique, we investigate the sensitivity and the Type I error rate for selecting mediators under all conditions. Sensitivity measures the proportion of the true positives being correctly detected. It can also be understood as the true positive rate or the statistical power. Type I error rate is the incorrect rejection of a true null effect. In this study, sensitivity is the percentage of the true mediators being selected, and Type I error rate is the percentage of selecting the null mediators or the false positives.

Because Bayesian methods transform the task of variable selection to parameter estimation, we estimate two sets of parameters/hyperparameters in the EBMed model (Equations (3)(3) $$Y_i=c\prime X_i+{\tau }_k{\mu }_k{M}_{ik}+{ϵ}_{1i}$$(3) and (4)(4) $$M_{ik}={\gamma }_k{\nu }_k{X}_i+{ϵ}_{2i},$$(4) ) to achieve the goal. The first set of the parameters is the posterior joint estimates of the indicators γ_k and τ_k. The second set is the posterior mean of the hyperparameter for the indicators, θ, which controls the probability of retaining or removing a particular candidate mediator in the model. Specifically, the joint estimate of the indicators is denoted as $\widehat{{\gamma }_k}\times \widehat{{\tau }_k},$ which reads as the posterior mean or the joint posterior inclusion probability of the indicator variables. The joint posterior mean can be understood to be the posterior probability of including an associated variable in the model (Kuo & Mallick, 1998). That is, the joint posterior mean of the indicators is the quantified effect of a corresponding mediator. For example, for an estimated value of 0.84, $\widehat{{\gamma }_k}\times \widehat{{\tau }_k}$ shows that the joint effect of ν_k and μ_k from the mediator M_k, which intervenes the relations between X and Y, is estimated to be 0.84. The posterior mean of the indicator hyperparameter θ determines the posterior probability that an associated mediator should be kept or dropped. For example, the posterior mean of θ being 0.5 means that there is an equal probability of retaining or dropping a particular mediator.

4. Results

4.1. Variable Selection

To determine the performance of the methods in correctly identifying true mediators, we computed the proportion of replications for selecting the true and null mediating effects by applying the four Decision Rules described above. Table 1 presented results from the EBMed model, the LASSO regularization mediation model (LASSO hereafter), mediation models using the multivariate delta method (Delta hereafter), and mediation models using the percentile bootstrap (bootstrap hereafter). We first compare the EBMed model with other methods, and then examine four Decision Rules applied to the EBMed model. Because mediators M1–M3 represent true mediating effects, the proportion of replications for selecting mediators M1–M3 from Columns 1–3 in Table 1 illustrates sensitivity or statistical power. Conversely, because variables M4 and M5 reflect spurious effects, the proportion of replications for selecting mediators M4 and M5 in the last two columns demonstrates a Type I error rate. All models reached full convergence.

Table 1. Power and type I error rates.

N		M1	M2	M3	M4	M5	N		M1	M2	M3	M4	M5
50	BmedDR1	1	0.978	0.496	0.252	0.274	100	BmedDR1	1	0.999	0.596	0.207	0.198
	BmedDR2	0.995	0.928	0.436	0.3	0.292		BmedDR2	0.998	0.957	0.525	0.261	0.236
	BmedDR3	0.957	0.686	0.112	0.017	0.001		BmedDR3	1	0.928	0.126	0.01	0
	BmedDR4	0.948	0.678	0.086	0.036	0.025		BmedDR4	0.998	0.922	0.109	0.013	0.022
	LASSO	0.995	0.885	0.46	0.375	0.345		LASSO	1	0.995	0.42	0.155	0.155
	Delta	0.905	0.285	0	0	0		Delta	1	0.83	0.005	0	0
	Bootstrap	0.94	0.215	0	0	0		Bootstrap	1	0.755	0.005	0	0
N		M1	M2	M3	M4	M5	N		M1	M2	M3	M4	M5
200	BmedDR1	1	1	0.776	0.121	0.103	500	BmedDR1	1	1	0.961	0.018	0.021
	BmedDR2	1	0.972	0.616	0.221	0.17		BmedDR2	1	0.975	0.737	0.131	0.142
	BmedDR3	1	0.972	0.172	0.004	0		BmedDR3	1	0.975	0.41	0.002	0
	BmedDR4	1	0.97	0.165	0.007	0.006		BmedDR4	1	0.975	0.407	0.002	0.003
	LASSO	1	1	0.54	0.22	0.19		LASSO	1	1	0.79	0.16	0.195
	Delta	1	1	0.005	0	0		Delta	1	1	0.31	0	0
	Bootstrap	1	1	0.005	0	0		Bootstrap	1	1	0.26	0	0
N		M1	M2	M3	M4	M5	N		M1	M2	M3	M4	M5
1000	BmedDR1	1	1	0.998	0	0.002	2000	BmedDR1	1	1	1	0	0
	BmedDR2	1	0.989	0.773	0.132	0.126		BmedDR2	1	1	1	0.001	0
	BmedDR3	1	0.989	0.68	0.004	0		BmedDR3	1	1	1	0.001	0
	BmedDR4	1	0.989	0.68	0.002	0.002		BmedDR4	1	1	1	0.001	0
	LASSO	1	1	0.98	0.115	0.12		LASSO	1	1	1	0.105	0.085
	Delta	1	1	0.77	0	0		Delta	1	1	1	0	0
	Bootstrap	1	1	0.76	0	0		Bootstrap	1	1	1	0	0

The four Bayesian selection EBMed models (EBMed DR1, EBMed DR2, EBMed DR3, and EBMed DR4) had comparable performance to all other three mediation methods in selecting the true mediating effects and excluding the null effects. In very large sample conditions (e.g., N = 2000), the sensitivity and Type I error rate for all the four EBMed models and the other three mediation models were similar. This means that the seven mediation models (four EBMed models, LASSO mediation model, mediation model using Delta, and mediation using bootstrap) performed similarly with very large samples. Depending on the choice of the decision rules discussed above, the Bayesian EBMed approach may produce the highest sensitivity and the lowest Type I error rate in selecting mediators among all competing mediation models when the sample sizes were medium to small (i.e., N < 500). Results from the seven models across sample sizes were presented in Table 1. The EBMed DR1 had the overall best performance in terms of high statistical power and low Type I error rates among all the competing mediation models. The EBMed DR1 outperformed all other competing models as it can accommodate prior information (in the form of knowing the number of true mediating effects in advance). The EBMed DR2, on the other hand, did not rely on priors but estimated the information from the model, and thus was the closest comparison to LASSO mediation approach. The EBMed DR2 and LASSO approaches performed similarly, with comparable power and Type I error rates across sample and effect sizes. The EBMed DR3 and EBMed DR4 approaches better controlled the Type I error rates but at the expense of power. They were thus best compared to the mediation models with Delta or bootstrap standard errors. With uniformly high power, the EBMed DR3 and EBmed DR4 models were tenable and strong exploratory tools in the initial stage that prepare for further confirmatory analyses.

While the seven mediation models were asymptotically similar in selecting mediators and excluding null effects, the four Bayesian EBMed models had outperformed other methods in small sample and small effect-size conditions. For example, the EBMed DR1, which incorporated prior information, had higher power and better control of Type I error rates across medium to small sample sizes (i.e., $N\le 500$). The EBMed DR2 had a strong overall balance of high statistical power in detecting medium to small effect sizes and low Type I error rates for null effects when the sample size was small. Compared to the LASSO mediation method, the EBMed DR2 yielded a much higher power for a medium effect sized mediator and a lower Type I error rate for null effects when N = 50. Their performance was comparable as sample sizes increased to N = 500 and were almost identical when N = 2000.

Each decision rule developed for the EBMed model differentially balanced statistical power and Type I error when selecting mediators. EBMed DR1 had the best overall performance in terms of high statistical power and low Type I error rate. The EBMed DR1 model yielded the highest power among all other competing mediation models in selecting true mediating effects. This was consistent across all sample conditions. Using the same decision making rule, the power was as high as 100% for selecting all large mediating effects and most medium-sized mediators. The power remained the largest among all competing mediation models when selecting small-sized mediators. The EBMed DR1 model had low Type I error rates when excluding null mediators in the model across most sample conditions. The only exception was when N = 100, where the LASSO method yielded slightly lower Type I error rate than the EBMed DR1 method. In sum, applying the EBMed DR1 to select mediators and null effects in EBMed model guaranteed the best overall performance among all suggested decision making approaches and all competing mediation methods. The trade-off, however, was that EBMed DR1 relied on substantive theory to pre-determine the number of mediators to be selected, being disqualified as a pure exploratory approach.

The EBMed DR2, on the other hand, was purely exploratory and yielded a balanced trade-off between high statistical power and low Type I error rate when selecting mediators and excluding null effects. EBMed DR2 did not rely on prior information but estimated the number of mediators to be selected from the model, and thus was most comparable to the LASSO mediation approach. Overall, these two methods performed similarly and the EBMed DR2 slightly outperformed when in small-sampled and small effect-size conditions. Compare the EBMed DR2 model to the LASSO mediation method, the EBMed DR2 model produced similar power but lower Type I error rate when N = 50. When the sample size increased to N = 100, the EBMed DR2 method had higher Type I error rate but also higher power in detecting small mediation effects. As the sample size increased, the EBMed DR2 method had similar results to the LASSO method. In sum, results from the EBMed DR2 method represented a good balance between statistical power and Type I error rate.

The remaining two decision rules, the EBMed DR3 and EBMed DR4 models were particularly advantageous in retaining low Type I error rates. When the EBMed DR3 or EBMed DR4 was applied, they yielded low Type I error rates while retaining decent statistical power. This advantage was particularly notable in small to medium sampled conditions, in which other competing mediation methods were challenged with either low statistical power or high Type I error rate. For instance, when N = 100, while the LASSO led to the Type I error rates of 15.5% for both null effects, the EBMed using DR3 had error rates of 1% and 0%, respectively, for null effects. The EBMed technique allowed for a decision making strategy that could minimize a common problem in exploratory contexts – the elevated type 1 errors. This was benefit over other exploratory approaches (e.g., Serang et al., 2017).

4.2. Posterior Probability

As discussed, the proposed Bayesian EBMed method had an additional advantage of reporting the probability of selecting a particular mediator. By utilizing this quantitative metric, the EBMed method selected mediators on a continuum scale and offered in-depth insights into the variable selection. This is an attractive and unique gain that neither the traditional p-value based methods nor the regularization-based LASSO method possess. This metric also provided the basis for formulating different DRs, which facilitates the identification of mediators while minimizing Type I error rate for some decision making strategies. The posterior probability was calculated as the summary of all converged posterior samples. Table 2 presented the posterior probability of selecting a corresponding mediator across all sample conditions. When N = 200, for example, by averaging the posterior probabilities across all 1000 replications, the Bayesian EBMed model presented a posterior probability of 100% for including a large mediating effect, a posterior probability of 98.9% for having a medium size effect, and a posterior probability of 32.8% for having a small mediating effect in the model. Additionally, the model reported the posterior probabilities of 15.9% and 15.7%, respectively, for the presence of the null mediating effects. This numerical summary provided additional valuable information regarding the probabilities of including and excluding certain mediators.

Table 2. Posterior probabilities for selecting mediators.

N	M1	M2	M3	M4	M5
50	0.778	0.599	0.336	0.298	0.296
100	0.989	0.868	0.318	0.231	0.227
200	1.000	0.989	0.328	0.159	0.157
500	1.000	1.000	0.508	0.096	0.098
1000	1.000	1.000	0.792	0.068	0.067
2000	1.000	1.000	0.978	0.045	0.044

5. An Empirical Example

We apply the Bayesian EBMed model to an empirical example to illustrate the implementation of the proposed mediation selection method. To mimic findings and compare results from the exploratory LASSO mediation analysis, we use the same college admission data as in Serang et al. (2017)’s study. Serang et al. (2017) examined whether the number of new students enrolled in college can be predicted by the number of applications accepted by a school, mediated by six potential variables: Outstate (out-of-state tuition), Room.Board (room and board costs), Books (estimated book costs), Personal (estimated personal spending), S.F.Ratio (student to faculty ratio), and Expend (instructional expenditure per student). While in our opinion, these potential variables are more likely confounders than mediators, we still apply the example for pedagogical and direct comparison purposes.

The data consist of statistics from 777 US colleges from the 1995 issue of US News and World Report. The dataset is available from the ISLR package in the R environment (James et al., 2013). Serang et al. (2017) examined the relationship between college acceptance and college enrollment on a subsample of N = 212 public schools of the data. They used the regularization-based LASSO mediation method to select mediators among the six above-mentioned potential mediators. In this example, we fit the Bayesian EBMed model to the same subset of college data. We aim to re-select the mediators using the Bayesian EBMed model and compare the results with those from the regularization-based LASSO approach as well as p-value-based Delta and Bootstrap methods. The Bayesian EBMed approach selects mediators and additionally provides the posterior probability of selecting a particular mediator among all the potential candidates.

Bayesian EBMed model was fitted to the data. The model assigned a Bernoulli prior distribution to the indicators. The hyperparameter of the Bernoulli prior distribution was assigned with a noninformative Beta prior to allow for estimation flexibility. The indirect and direct effects in the mediation model were assigned with noninformative normal priors. All the precision hyperparameters for the direct effects were given random effects. The model ran 10,000 iterations, with the first 1,000 as the burn-in phase. The Geweke test was used to assess model convergence and showed that the fitted Bayesian EBMed model was converged. Table 3 presented the posterior probability of selecting a particular mediator from the Bayesian EBMed model. Ranging from the highest to the lowest, each candidate mediator had a posterior probability of being selected from the model. The candidate Room.Board, representing room and board costs, had the largest probability of being selected as the mediator for the analysis. The second most likely candidate mediator was Expend, the instructional expenditure per student, which had the second largest posterior probability of presenting the mediating effect as 82.9%. Next, Personal, one’s estimated personal spending, was the third most likely mediator to be selected in the model, with a posterior probability of being selected to be 69.7%. The variable, Outstate, representing the out-of-state tuition, had 53.9% probability of being included in the model, and was ranked the fourth as a likely mediator in the model. The remaining two variables, S.F.Ratio and Books, meaning student to faculty ratio and the estimated book costs had less than 40% probability of being selected, and were therefore unlikely to be true mediators. Additionally, the posterior mean of the indicator hyperparameter, θ, was estimated to be $\widehat{\theta }=0.68.$ This information was useful for selecting mediators following the four selection approaches proposed above.

Table 3. Posterior probability and mediator selection for the college data example.

	Outstate	Room.board	Books	Personal	S.F. ratio	Expend
	Posterior probability
Bmed (%)	53.86	98.93	39.71	69.65	23.96	82.90
	Mediator selection
Bmed DR1	No	Yes	No	Yes	No	Yes
Bmed DR2	Yes	Yes	No	Yes	No	Yes
Bmed DR3	Yes	Yes	No	Yes	No	Yes
Bmed DR4	Yes	Yes	No	Yes	No	Yes
LASSO	No	Yes	No	Yes	No	Yes
Delta	No	Yes	No	No	No	Yes
Bootstrap	No	Yes	No	No	No	Yes

We apply the above-mentioned four DRs to discuss mediator selections under each DR scenario. Results are compared with those from the regularization-based and p-value based mediation methods (Table 3). DR1 relies on substantive theory to predetermine the number of mediating effects. We use information from Serang et al. 2017’s study and pre-determine that there will be three true mediating effects in the model. We then use EBMed DR1 to pick out the three mediators that have the highest joint posterior inclusion probabilities for the corresponding indicators. Accordingly, DR1 selects Room.Board (room and board costs), Expend (instructional expenditure per student), and Personal (estimated personal spending). Different from DR1, DR2 uses the estimated hyperparameter $\widehat{\theta }$ to compute the number of optimal mediators in the model, which is 4 ($\simeq 6\times 0.681),$ where 6 is the total number candidate variables and 0.681 is the estimated hyperparameter $\widehat{\theta }.$ DR2 then selects mediators that have the highest four joint posterior inclusion probabilities, which are Room.Board (room and board costs), Expend (instructional expenditure per student), Personal (estimated personal spending), and Outstate (out-of-state tuition). The same algorithm using the posterior hyperparameter mean is applied to DR3 and DR4 to determine the number of mediators in the model. DR3 computes the number of mediators in the model first and then selects mediators whose posterior inclusive probabilities for the corresponding indicators are larger than 0.5. In this example, DR3 selects Room.Board (room and board costs), Expend (instructional expenditure per student), Personal (estimated personal spending), and Outstate (out-of-state tuition). DR4 takes on a reversed selection approach compared to DR3. Specifically, DR4 includes all mediators whose corresponding indicators have a larger-than-0.5 posterior inclusive probability and then computes the number of mediators in the model. In the example, DR4 selects the variables Room.Board (room and board costs), Expend (instructional expenditure per student), Personal (estimated personal spending), and Outstate (out-of-state tuition). Comparing results across all mediation models, the Bayesian EBMed model using DR1 and the regularization-based LASSO select the same three mediators Room.Board, Expend, and Personal. The other three DRs from the Bayesian EBMed model select one additional mediator Outstate, on top of the three same mediators selected by DR1 and LASSO. The p-value-based Delta and Bootstrap methods select the same Room.Board and Expend variables as two mediators as other methods, but not a third or fourth mediator.

In sum, all four decision rules from the Bayesian EBMed model perform at least equally well in selecting mediators as other mediation models. The Bayesian EBMed model additionally quantifies the probabilities for selecting the mediators. Room.Board has the highest probability of 98.9% as a mediator. The following two variables Expend and Personal have the probabilities of 82.9 and 69.7%, respectively, to be the mediators. Using the other three DRs, the Bayesian EBMed model picks out a fourth variable, Outstate, and reports its posterior probability of being a potential mediating effect, as 53.9%. No other methods produce this extra quantifying information. While the p-value-based approaches conservatively select only two mediators, the Bayesian EBMed method picks out three or four mediators, keeping low Type I error rates based on the Monte Carlo simulation finding. The Bayesian EBMed method demonstrates that Personal and Outstate have a medium posterior probabilities to be mediators, lower than those of Room.Board and Expend, but higher than S.F.Ratio and Books. This also explains why these two variables are selected by neither the Delta nor Bootstrap method, but are selected by more liberal approaches such as LASSO or Bayesian EBMed model using DR1.

The proposed EBMed technique serves as a methodological tool in the exploratory stage to examine potential mediating effects. In line with Serang et al. 2017’s recommendation for including as many potential mediators in the exploratory stage to allow for future confirmatory opportunities, the Bayesian EBMed approach not only includes potential mediators, but provides information as to why a certain mediators are unselected from the model. After screening the mediators in the exploratory stage, it is essential to use human judgment following the initial identification to see if the variables are theoretically sensible. This is particularly important given that researchers cannot empirically distinguish confounding from mediating effects, as shown in this empirical example.

6. Discussion

In this study, we proposed a Bayesian approach for selecting and quantifying mediation effects in exploratory mediation analysis. The proposed approach transforms the task of selecting mediators into estimating parameters within a Bayesian context. The method, termed the exploratory Bayesian Mediation (EBMed) model, considered models with all possible variable combinations as submodels, introduced the concept of indicator variables to the Gibbs sampling process, estimated submodels, and obtained the posterior probabilities of including certain mediating effects. The study further developed four decision rules to assist the mediation selection process. The proposed method has access to two pieces of useful information that current mediation methods rarely provide simultaneous information. First, the EBMed model effectively selects mediators among all candidate mediating effects in a model. Second, the EBMed model quantifies the probability of including a certain mediator in the model.

A Monte Carlo simulation study was designed and implemented to investigate the performance of the proposed Bayesian method. The Bayesian EBMed model was evaluated in terms of sensitivity and Type I error rates, and compared to the regularization-based exploratory mediation analysis developed by Serang et al. (2017). While all competing mediation models were asymptotically identical in selecting mediators, the Bayesian EBMed model outperformed other methods in detecting small-effect mediators across sample size, the outperformance of which became more notable as the sample size got smaller (e.g., N = 50). With an appropriate choice of the decision rules developed in the study, the EBMed model had a pronounced high sensitivity and low Type I error in small to medium samples (i.e., N < 500). The EBMed model provided additional numerical information to quantify the posterior probability of including a particular mediating effect in the model. This extra quantifying information was valuable for researchers to make decisions on a continuous scale rather than relying on a pure significance-based binary decision. Based on the continuous posterior probabilities, the study developed four decision rules to facilitate using the model in practice. Each decision rule emphasized different perspectives regarding statistical power and Type I error rate. EBMed DR3 and DR4 effectively mitigate the risk of elevated Type I error rates, a common problem in exploratory studies, while retaining a decent statistical power in selecting true mediators. The EBMed model using DR1 had the best overall performance regarding high statistical power and low Type I error rate. This decision rule, however, requires a pre-specified number of mediators in the model from existing theory, and was thus not purely exploratory in this sense. EBMed DR2 kept: a balanced trade-off between high statistical power and low Type I error rate when selecting mediating effects and excluding null effects. Under the premise that no prior knowledge of true mediating effects is present, we recommend using EBMed DR2 as it is in the most balanced position of being neither too liberal like LASSO nor too conservative. None of DR2, DR3, or DR4 required the specification of number of mediators a priori in the model, and was therefore, purely exploratory.

The proposed Bayesian EBmed model is not a solution to test mediation without theory. Instead, EBmed is a tool to explore mediating effects and to offer a starting point to examine mediation in situations where theory is limited or scientific justification is sparse. The EBmed method also serves as a tool to expand, refine, and/or test the existing theory. The importance of importing human judgment on the viability of a selective variable as a potential mediator in this context cannot be overstated, given that confounders are not empirically distinguishable (MacKinnon et al., 2000).

The exploratory mediation analysis may be most useful when used in a multistep process. Rather than estimating causal effects from the outset, exploratory mediation analysis can focus on building the body of research for a particular phenomenon, in line with the basic philosophy of science. Exploratory methods can identify what potential mediators to test in theory-limited or high-dimensional data situations by offering insight into potential mediator selection from an empirical vantage. Exploring potential mediating effects in high-dimensional data is not uncommon. For example, high-dimensional biological and medical data have increased considerably in recent years (e.g., genomic biomarkers or signatures). These genetic studies typically have high-dimensional pools of candidate variables that require dimension reduction techniques (Eguchi et al., 2013). Researchers typically need to pare down a parameter space to facilitate the development of models that can inform future intervention work. The EBMed model can be useful in high-dimensional settings by helping reduce the pool of candidate variables so that researchers focus on ones that may be the most critical. Second, post-hoc application of theory to validate identified variables as possible mediators in a causal chain is essential in this context, as confounding effects cannot be empirically differentiated from mediation effects (MacKinnon et al., 2000). By applying a theoretical lens after the empirical identification, as researchers can exclude nonsensical mediators that are potentially identified in exploratory settings. Doing so facilitates the retention of variables that can sensibly be possible outcomes of the independent variables, as well as predictors of the outcome variables. Third, researchers can consider using confirmatory methods to test the retained mediators. For instance, one could set up a “mediation by design” study to assess how changes in the empirically identified mediators affect subsequent changes of the outcomes, to provide more confidence in the variable’s true role as a mediator.

Using the Bayesian approach to explore and select potential mediating effects has several advantages. First, the Bayesian approach offers a probabilistic view of the parameters, allowing the assessment of uncertainties. This perspective attends to the concern in the frequentist-based exploratory mediation approach, which is based strictly on statistical significance. That is, using classic statistical significance testing as the criterion to select mediators is at odds with the basic premise of an exploratory approach, since the concept derives from a confirmatory setting. Second, the EBMed approach can enhance the ability to identify mediators in the exploratory context by using adjacent theory (or meta-analysis) to provide priors when expanding to a new field. Incorporating prior knowledge is analogous to having additional data in the form of priors, and may be helpful, particularly in small samples. Third, the inclusion of posterior probability estimates quantifies the selection metric on a continuum scale, which may guide the selection of mediators in resource-constrained environments. For example, the EBMed model may help select a subset of mediators with the highest posterior probabilities, if there are not enough resources to examine or incorporate all potential mediators into a study or program of interest. Furthermore, the availability of the posterior estimates allows for the decision rules to mitigate the elevated Type 1 error rates, which is typically a problem in the exploratory mediation context.

The study develops and discusses Bayesian methods in exploratory mediation modeling and has promising future directions to pursue. By investigating initial model structures and data patterns, the exploratory process sheds light on further confirmatory analyses. Initial knowledge at the exploratory stage could be sparse, but it still provides information. Knowing nothing about a parameter in question still shows something we know (Gelman et al., 2003). Bayesian methods incorporate this information to the modeling process by placing Bayesian priors to the model. Depending on the knowledge level and exposure, researchers may apply noninformative, weakly informative, or strong informative priors to the modeling process (e.g., Chung et al., 2015). In situations where prior knowledge is untenable and difficult to form informative knowledge, researchers may consider using data dependent priors (DDP; McNeish, 2016). DDP applies techniques such as maximum likelihood estimation to obtain parameter estimates from the data and then sees the estimates as hyperpriors for the Bayesian model. The DDP approach has shown to effectively aid in obtaining hyperprior information and have been used in Bayesian mixed-effects models (Serang et al., 2015) and Bayesian growth curve models (Shi & Tong, 2017). In this proposed Bayesian exploratory mediation analysis, one may use the exploratory LASSO mediation approach (Serang et al., 2017) to explore and determine the mediating effects in the model. The estimated mediating effects can then be used to inform the DDP for the EBMed model in the study, which is essentially the EBMed DR1 model. As illustrated in the simulation findings, the EBMed DR1 method produces the highest power and best controls Type I error rates, given known prior information. In sum, borrowing the information estimated from LASSO to form a DDP and using them in the EBMed model has the potential to equally perform or outperform the current mediator selection process and be an encouraging future direction.

Moreover, the proposed Bayesian mediation selection approach can accommodate the prior knowledge of the mediating effects by flexibly specifying the hyperpriors for the indicator variables. The current study assumes an equal probability for all candidate variables to be mediators in the model. It, therefore, assigns Beta(3, 3) hyperpriors for the indicator variables, which approximates a bell-curved shape with a mean of 0.5. In real-world applications, substantive researchers may adjust hyperprior specifications to meet their theoretical needs. For example, suppose there is convincing evidence for a particular mediating effect in the model; a Beta prior for the corresponding indicator with high first shape hyperparameter but low second shape hyperparameter (e.g., Beta(6, 2)) could be specified to reflect the high probability and strong belief for a mediating effect. Conversely, for a mediating effect with weak existing evidence, a low first shape hyperparameter but high second shape hyperparameter in the Beta distribution (e.g., Beta(2, 8)) could be considered to echo this belief. Note that hyperprior assignments are independent for each candidate variable, and can therefore be tailored to the theoretical view of the individual variable. Future directions may study the sensitivity of the hyperpriors and their impact on selecting mediators.

Finally, future research may consider extending the EBMed approach to study dichotomous outcomes, including binary dependent variables and mediators. Preliminary studies showed consistent findings and promising implications in this realm (e.g., Serang & Jacobucci, 2020).

Acknowledgements

Dr. Dingjing Shi gratefully acknowledges the support of the Office of the Vice President for Research and Partnerships from the University of Oklahoma through the Junior Faculty Fellowship, which was instrumental in carrying out the research presented in this paper.

Dr. Amanda J. Fairchild would like to gratefully acknowledge the sabbatical leave granted to her by the University of South Carolina, which provided the time to help make this research possible.

We are grateful to the editor, Dr. George A. Marcoulides, and the anonymous reviewers for their careful reviews and insightful comments that greatly improved the manuscript.

Notes

1 There are methods to handle models with categorical outcomes and/or mediators, but those aren’t discussed here.