Beneficial Effects of Freezing Rate Determined by Indirect Thermophysical Calculation on Cell Viability in Cryopreserved Tissues

Abstract

Many types of mammalian cells, such as sperm, blood, embryos, etc., have been successfully cryopreserved for the last few decades, while no optimal method for the cryopreservation of mammalian tissues or organs has been established, showing a poor survival after thawing with a low recovery of function. In this study, the freezing rate was determined by indirect thermodynamic calculation, and its potential effect on the cryoprotection of human saphenous veins and tissue-engineered bones was investigated. The vein segments were frozen according to the calculated freezing rate, using rate-controlled freezing devices, with a freezing solution composed of 10% dimethylsulphoxide and 20% fetal bovine serum in RPMI 1640 media. The efficacy of indirect calculation was assessed by the cell viability measured using fluorescence double-staining methods. The results indicated that the freezing rate determined by indirect calculation significantly (P < 0.05) maintained the post-thaw cellular viability of the blood vessel, particularly in terms of the endothelial cells. However, it exerted relatively less protective effect on the osteoblastic cell-cultured scaffolds. These results suggest that freezing-induced injuries may occur in tissues, and the freezing rate determined by indirect thermophysical calculation can be used for the optimization of tissue cryopreservation by minimizing the injuries.

Keywords:

• Freezing rate
• Indirect thermodynamic calculation
• Cryopreservation
• Cell viability
• Human saphenous veins

INTRODUCTION

Cryopreserved cells and tissues are increasingly used for stem cell transplantation and tissue engineering, but their storage and thawing are associated with severe damage, suggesting the need for better cryopreservation methods [[1]]. Cryopreservation has many immunological advantages for clinical cell transplantation from multiple donors, but optimized rate-controlled freezing should be defined and then applied to the cryopreservation of various tissues. An important issue for successful freezing protocols is the prevention of intracellular ice formation, which is considered to be one reason for cellular damage. Intracellular ice formation might be prevented by freezing the tissue sufficiently slowly to allow cells to lose water in response to an increase in solute concentration in the extracellular medium. In this way, cells become dehydrated with no or minimal intracellular ice crystal formation [[2]]. On the other hand, intracellular ice formation may be avoided when cells are frozen very quickly in the presence of high concentrations of cryoprotectant, leading to vitrification of the tissue. High concentrations of cryoprotectant, however, are potentially toxic, and the cooling rates needed for complete vitrification might not be achievable in multicellular tissue [[3]]. Therefore, the use of cryoprotectants, such as glycerol and dimethylsulphoxide (DMSO), allows both the structure and viability to be retained almost indefinitely by reducing electrolyte concentration in the residual unfrozen solution in and around a cell at any given temperature, with carefully controlled rates of freezing and thawing [[4-7]].

In the present study, two different thermodynamic calculations were investigated in order to find the optimal freezing rates for human saphenous veins (HSV) and tissue-engineered bones (TEB) and to see whether they give enhanced protection in terms of cellular viability. One was the direct calculation method, where many parameters, such as the thermophysical characteristics of all components, latent heat of fusion, area, density and volume, etc., should be considered. Because this kind of calculation was very sophisticated, some variables could not be determined. The other was the indirect calculation method, where HSV and TEB were frozen using a previously constructed freezing rate, and then the actual freezing rates of both tissues were determined. Finally, the freezing rate was modified by several calculation steps, including polynomial regression analysis and time constant, thermal response and inverse chamber temperature calculations.

MATERIALS AND METHODS

Preparations of Human Saphenous Vein

Using the methods described previously [[8-10]], HSV segments were harvested from 20 patients undergoing arterial bypass graft surgery. The segments containing the branches were excluded from the testing, as it was impossible to achieve a precise cell viability measurement as well as homogeneous freezing.

Cell Cultures and Conditions

The mouse pre-osteoblasts (MC3T3-E1) were obtained from the RIKEN Cell Bank (Tsukuba Sciences City, Japan). The normal rat osteoblasts (NROs) were isolated from neonatal (< 1 day old) Sprague-Dawley rat calvariae, which were used between passages 5 to 10. The MC3T3-E1 cells were cultured in minimum essential medium alpha modification (Sigma, St. Louis, MO), supplemented with 10% (v/v) fetal bovine serum (FBS; Sigma) and a 1% (v/v) antibiotic antimycotic solution (including 10,000 units penicillin, 10 mg streptomycin and 25 µg amphotericin B per ml, Sigma). The NROs were grown in Dulbecco's modified Eagle's medium (Sigma), supplemented with 10% FBS and 1% penicillin-streptomycin (Sigma). These cells were routinely maintained at 37°C in a 5% CO₂ humid environment.

Fabrication of Tissue-Engineered Bones

Porous poly(DL-lactic-co-glycolic acid, 65:35) (PLGA; Aldrich, Milwaukee, WI) scaffolds (12 mm diameter and 3 mm thickness) were prepared by a salt-leaching method, as described previously [[11]]. Initially, a 0.1 g/mL viscous polymer solution was prepared by dissolving the polymer in chloroform (Sigma). The solution was precipitated in cold ethanol and homogenated with sodium chloride salt particles followed by freeze-drying. The MC3T3-E1 cells were seeded at the initial density of 2 × 10⁵ cells/scaffold and then cultured into the PLGA scaffolds for 5 to 7 days prior to freezing.

Using the previously described method [[12], [13]], a composite of 980°C-heated carbonate apatite (CAp), produced by a solution-precipitation method, and type I atelocollagen (AtCol), extracted from bovine tail skins, were grafted onto poly-L-lactic acid (PLLA; Polysciences Inc., Warrington, PA) scaffolds (12 mm diameter and 3 mm thickness). To increase the collagen fibrillar cross-links, the fabricated scaffolds were irradiated by ultraviolet rays (wave length 254 nm) at 4°C for 4 h. The NROs (initial seeding density, 1 × 10⁵ cells/scaffold) were cultured onto the CAp-AtCol-PLLA scaffolds for 7 days prior to freezing.

Thermophysical Modeling and Calculation

Lumped Thermal Capacity Model

If a system undergoing a transient thermal response to a heat transfer process has a nearly uniform temperature, small differences of temperature within the system can be ignored. Changes in the internal energy of the system can then be specified in terms of the changes in the assumed uniform temperature of the system. This approximation is called the lumped thermal capacity model [[14]]. This model was adopted for the numerical modeling of the cooling process of tissue samples. Although the model is only applicable to a small sample able to be considered as having a uniform temperature, it enables a first-order ordinary differential equation for the sample temperature, T_s, as a function of time, t, to be obtained. This equation is:where T_f is the freezing chamber temperature, t_c = ρVc/h_cA [s] is the time constant of the process, where ρ is the sample density, V the sample volume, c the sample specific heat, and h_c the heat transfer coefficient averaged over the sample surface area, A.

Direct Thermophysical Calculation

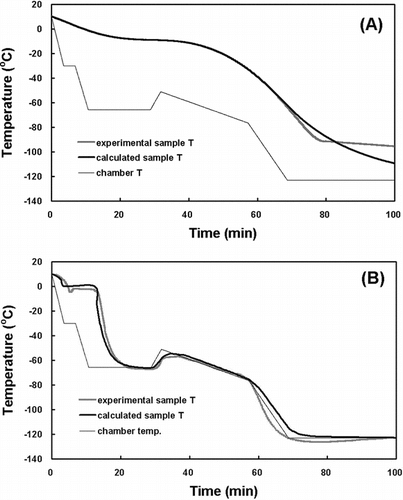
At first, the direct thermophysical calculation was employed to find the optimal freezing rate. This method consists of the following five steps: (a) inputting thermophysical properties of a tissue sample whose ideal freezing rate is being sought; (b) inputting the freezing chamber temperature profile, where the change in the sample temperature will be simulated; (c) calculating T_s using the lumped thermal capacity model during the cooling process before the freezing process; (d) calculating T_s during the freezing process; and (e) calculating T_s using the lumped thermal capacity model during the cooling process after the freezing process. Difficulty in obtaining the exact thermophysical properties of each sample, however, renders the direct thermophysical calculation inefficient. Most of all, the exact thermophysical properties are essential for step (d). Figure 1 shows the comparison between the experimental freezing rates and the calculated freezing rates using the direct thermophysical calculation for the HSV (A) and TEB (B).

Figure 1 The comparison between the experimental freezing rate and the calculated freezing rate using the direct thermophysical calculation for the HSV (A) and TEB (B).

Indirect Thermophysical Calculation

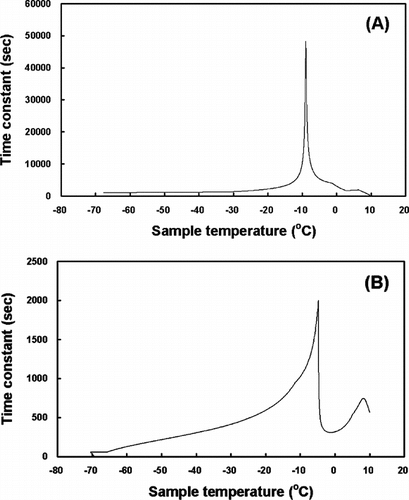
To make up for the shortcoming of the direct thermophysical calculation, and thus calculate the ideal freezing rate without inputting the respective thermophysical properties of each sample, the indirect thermophysical calculation was employed in this study. This was derived from the idea that t_c can be regarded as a function of T_s in a particular freezing chamber. Given the t_c − T_s diagram calculated and organized from a freezing experiment on a tissue sample, the various thermal responses of the sample to diverse freezing rates in the chamber can be simulated without knowing the respective thermophysical properties of the sample.

The algorithm of the indirect thermophysical calculation is described, with the demonstration of the calculation method on HSV and TEB, as follows. First, experimentally freezing the tissue samples for which the ideal freezing rate is being sought. Second, reading the (T_s, t) and (T_f, t) coordinates from the experimental result at 1.0-second intervals of t, using a polynomial regression analysis. Third, calculating t_c by substituting the coordinates values obtained from the previous step into the above Eq. (1) and constructing the t_c − T_s diagram, as shown in Figure 2. The freezing process within the sample can be understood indirectly by analyzing the diagram, even though the complex thermophysical aspect of the freezing process is not considered in the indirect thermophysical calculation. For example, the freezing point of the sample can be inferred from the fact that the phase change in the sample happens most actively at the sample temperature where the time constant is a maximum. Fourth, inputting the chamber temperature profile, where the change in the sample temperature will be simulated. Fifth, calculating the thermal response of the sample using the lumped thermal capacity model from the t_c − T_s diagram.

Figure 2 The t_c − T_s diagrams of the chamber temperature for the HSV (A) and the TEB (B).

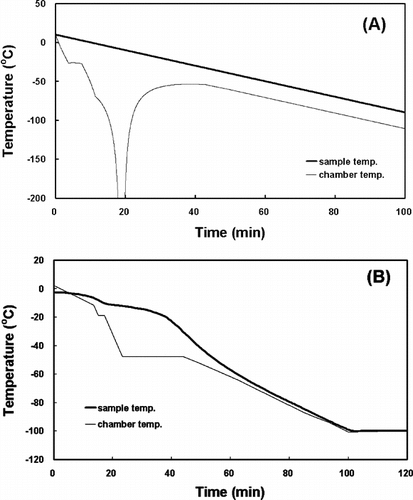
Along with its simplicity in simulating the thermal response of the sample, the inverse calculation of the chamber temperature is another advantage of the indirect thermophysical calculation. The indirect thermophysical calculation can simulate the chamber temperature profile that makes the temperature of a tissue sample change as intended, by inputting the intended sample temperature profile in the fourth step above (Figs. 3 and 4).

Figure 3 The freezing rate (A), theoretically obtained but practically not existing, and the inverse calculation (B) of the chamber temperature for the HSV in a 180 ml freezing bag.

Figure 4 The inverse calculations of the chamber temperature for PLGA with MC3T3-E1 cells (A) and CAp-AtCol+PLLA with NROs (B) in a 3.6 ml cryogenic vial.

Freezing and Thawing

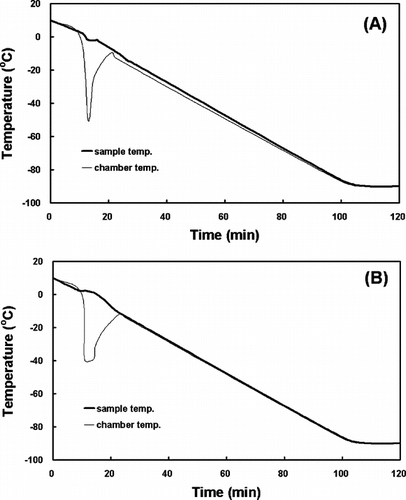
The rate-controlled freezing protocol determined by the indirect thermophysical calculation was applied to the vein segments, as shown in Figure 3(B). By inserting a stopcock into a lumen, an extremity of the vessel was closed and tied. In a freezing solution composed of 10% DMSO (Sigma) and 20% FBS in RPMI 1640 media (Gibco BRL, Grand Island, NY), the segments were distended at 14.7 mmHg to prevent shrinkage. After absolutely filling the lumen with the freezing solution, the opposite extremity was also tied. The tied vein segments were placed in a commercial freezing bag, with a 180 ml final volume, and then slowly frozen in a computer-controlled programmable freezer (SY-LAB Geräte GmbH, Neupurkersdorf, Austria), using a cooling rate of 1°C/min down to −20°C, followed by 10°C/min down to −50°C and then 1°C/min down to −100°C. Finally, the bag was stored in the liquid phase of liquid N₂ (−196°C). This technique allows for good and reproducible control of the freezing process, including the possibility of preventing a temperature rise due to crystallization. For comparison, the vein segments packed in the freezing bag were frozen down to −100°C according to the freezing rate determined by the direct calculation [Fig. 1(A)]. After 2 weeks of storage, both the freezing bags were thawed in a water bath at 70±10°C, and then stepwise diluted with thawing media (RPMI 1640 + 10% FBS + 5 M manitol and RPMI 1640 + 10% DMSO) until the bag-temperature reached 37°C. The thawing rate was 2.5°C/min.

The cell-cultured scaffolds were also frozen using the freezing rates shown in Figures 1(B) and 4. The final volume, including medium, serum, DMSO and scaffolds, was 3.6 ml. Cryogenic vials (Corning Costar Corp., Cambridge, MA) were used for freezing. After 1 week of storage, the vials were removed from the liquid N₂ and thawed quickly in a water bath at 37°C.

Cell Viability Measurement

The fluorescence double-staining method, combined with flow cytometry (FCM; FACSCalibur, BD Biosciences Immunocytometry Systems, San Jose, CA) was used to determine the cellular viability of the cryopreserved vein segments. By enzymatic digestion with solution containing collagenase 1A (250 units/ml; Sigma) and trypsin (2.5 mg/ml; Sigma) mixed 2:1 by volume, all vascular cells, including endothelial cells (ECs), were obtained. As described in previous studies [[8-10]], 0.004% Griffonia simplicifolia agglutinin-fluorescein isothiocyanate (GSA-FITC; MP Biomedicals, Aurora, OH), mixed with 2 mM CaCl₂ and 2 mM MgCl₂ in phosphate-buffered saline (PBS, pH 7.4) and 20 µM propidium iodide (PI; Sigma), were added to a dissociated cell suspension containing 1 × 10⁵ cells/ml. The GSA-FITC/PI double-stained cells were detected by FCM, and the unstained dissociated cells were regarded as the non-frozen control. The data obtained were analyzed with CellQuest software, written in MacApp (BD Biosciences Immunocytometry Systems), and plotted as dot plots and histograms.

Similarly, the cell-cultured scaffolds were washed twice with PBS and trypsinized. The cell precipitates were obtained by centrifugation at 200 × g and then re-suspended in PBS. As described previously [[15]], 2 µM 5(6)-carboxyfluorescein diacetate (cFDA; Sigma) and 20 µM PI (Sigma) were added to the suspension containing 1 × 10⁵ cells/ml and analyzed by the above-mentioned FCM.

Statistical Analysis

All variables were tested in three independent cultures for each experiment, and each experiment was repeated twice (n = 6). The student's t-test was used to detect the influence of the freezing rate, as determined by the indirect thermodynamic calculation, on the cellular viability, and compared with the direct calculation. Results are reported as means±standard deviation, and differences were considered statistically significant if the P value was less than 0.05.

RESULTS

Freezing Rates Determined by Direct Thermophysical Calculation

For the HSV [Fig. 1(A)] and TES [Fig. 1(B)], the experimental freezing rates and the calculated freezing rates using the direct thermophysical calculation could be respectively obtained. Although both the rates would appear to be clearly similar to each other in their shapes, there were found to be subtle differences attributed to many hypotheses and limits to exact thermophysical calculation in the direct calculation methods.

Freezing Rates Determined by Indirect Thermophysical Calculation

Figure 2 showed the inverse operation of the time constant by the indirect thermophysical calculation. The phase changes in the HSV (A) and the TEB (B) in the freezing process occurred at about −7.9°C and −4.8°C, respectively. These results suggest that the time constants from experimental data may be different according to the size (volume) and the thermal properties of the samples. Moreover, the inverse calculation of the chamber temperature allowed the temperature of a sample to change as intended. As shown in Figure 3(A), however, the rate of the chamber temperature change should be infinitely large in order to obtain the linear temperature response of the sample. This phenomenon might be impossible to happen in nature and, if possible, it would take infinite time to do so. The freezing rate for the HSV in a 180 ml freezing bag was determined by the inverse calculation as shown in Figure 3(B) and that for the TEB in a 3.6 ml cryogenic vial was shown in Figure 4.

Cryoprotection of HSV and TEB Using Freezing Rates Determined by Thermodynamic Calculations

Freezing the HSV according to the freezing rate determined by direct thermophysical calculation resulted in a significant (P < 0.05) decrease in cellular viabilities [Fig. 5(A)]. After thawing, approximate 30% and 35% loss was observed in total vascular cell and EC viability, respectively. When the veins were frozen using the freezing rate determined by the indirect calculation, the vascular cell viability was significantly maintained up to about 88% including over 85% of viable EC, suggesting that the freezing rate can suppress freezing-induced cell injury.

Figure 5 The cellular viability of the cryopreserved HSV (A) and TEB (B), according to the freezing rates determined by direct or indirect thermophysical calculations.

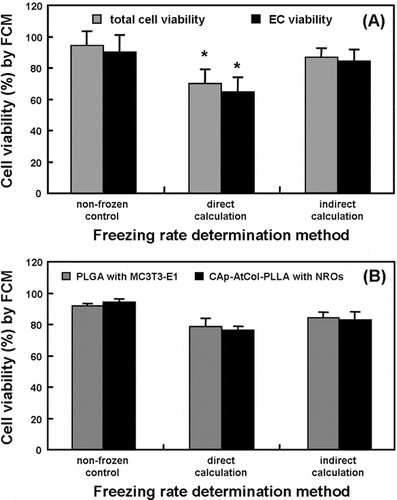
The effects of the indirect calculation on post-thaw cell viability were also investigated using artificially fabricated tissues, TEB including PLGA scaffolds with MC3T3-E1 cells and CAp-AtCol-PLLA scaffolds with NROs. It was revealed that the TEB frozen using the freezing rate determined by the direct calculation showed an appreciable decrease in cell viability compared with the non-frozen control [Fig. 5(B)]. About 22% and 27% decreases in the cell viability of PLGA scaffolds with MC3T3-E1 cells and CAp-AtCol-PLLA scaffolds with NROs were respectively observed after freezing by direct calculation, while the cell viabilities of both the osteoblastic cells after freezing by indirect calculation were respectively 83% and 82%. However, there was no significant (P < 0.05) difference between direct and indirect calculations. These results might be attributed to the small volume of the cellular component-contained scaffolds.

DISCUSSION

The ultra-low-temperature storage of cells, embryos and some human tissues for banking purposes is now a common practice. Freezing is an insult to cells, where physical disruption leads to chemical changes taking place. The rate at which cells are cooled and the concentration of cryoprotectant are two of the main factors governing the survival of frozen cells [[16]]. The use of various freezing devices allows for better control of the cooling rate and protects the cells during the critical freezing stages. The freezing rate during the critical temperature range, defined as the range when ice crystal formation and consequent cell dehydration occurs, is of considerable importance [[17]]. In this range (approximately −5 to −50°C), the freezing rate determines whether the cells remain in equilibrium with their extracellular environment or become progressively supercooled, with the increasing possibility of intracellular ice formation. In the present study, those ranges were respectively about −7.9°C and −4.8°C for the HSV and the TEB when the freezing rate were determined by indirect thermophysical calculation (Fig. 3).

One proposed hypothesis of injury during hypothermia and freezing is the formation of oxygen-free radicals [[18-20]]. Whiteley et al. [[21]] showed a rise in the malondialdehyde levels of rat liver homogenates stored at high subzero temperatures. Thus, free radical damage has been implicated as one of the causes of cell viability loss during or just after freezing [[22]]. Though DMSO is a known hydroxyl-free radical scavenger [[23]], it has been reported to be ineffective in protecting V-79 Chinese hamster cells exposed to hypothermia [[24]]. Furthermore, the use of very low temperatures for storage of human allografts can lead to significant damage to cells and the extracellular matrix, especially during the freeze–thaw cycle [[25]]. This can potentially alter the graft elastic properties, which were positively correlated with the graft patency [[26], [27]]. In order to preserve the viability of all the cellular components, various cryopreservation techniques have been employed that have utilized glycerol, chondroitin sulphate or DMSO [[28]]. Extensive research on animal models has shown that, with the appropriate freezing procedures, the vein cellular components responsible for their elastic properties are well maintained after cryopreservation [[29]]. These include the smooth-muscle cell morphology, the contractility and the structure of the elastic lamina.

Whatever the tissue or cell type, the optimal cooling rate was greatly influenced by the cryoprotectant. When the cells were treated with a very permanent agent, the cells could rapidly restore osmotic balance and are thus able to tolerate faster cooling [[30]]. In order to limit potential toxicity of cryoprotective agents, such as DMSO and glycerol, it has been suggested that mixtures of two or more agents with lesser individual concentrations might be used [[31]]. Although limited in availability and application, the present experiments, together with published information, permit some generalizations concerning the further development of cryopreservation methods for vascular and bone tissues. First, it is likely that the successful cryopreservation of those tissues requires freezing rates around or faster than −1.0°C/min, the lowest rate employed in this study (Figs. 4B and 5). Second, our results confirm the view that the addition of a cryoprotectant is indispensable for successful cryopreservation. Because of the tradeoff between cryoprotection and toxicity with most permeating cryoprotectants, further experiments are required with various kinds and dosages of permeating as well as nonpermeating cryoprotectants. Moreover, future studies must also describe the possibility that tissues could be cryopreserved by rapid cooling without cryoprotectant, as shown in Apis mellifera [[32]].

The optimum values determined for the two factors examined in this study are only preliminary determinations; significant improvements in the cell viability of cryopreserved tissues may be achieved by examining the same parameters in further details. One point that deserves attention is the loss of viability observed with time after thawing. This phenomenon can be only partly attributed to cryoprotectant toxicity since it was observed also in cells frozen without DMSO. One possible cause could be “volume effects,” or cryoinjuries due to large and sudden changes in cell volume, which are particularly common after thawing [[25]]. Cryopreserved cells are generally hypertonic due to the addition of cryoprotectant and/or dehydration caused by ice formation in the extracellular medium. The cells therefore tend to swell upon thawing, stretching and damaging the cell membrane [[25]]. In relation to this fact, Leveroni Calvi and Maisse did not observe any significant decrease in viability with time after thawing, which could be attributed to the use of a step-wise dilution method for cryoprotectant removal [[33]]. Thus, the removal of cryoprotectant swiftly and with minor cell volume changes after thawing is an important consideration, as probably are the composition of the culture medium and the determination of optimal freezing rate.

Compared with cells in suspension, the freezing of tissues introduces additional factors, such as response to freezing rate and tolerance against solution effects injury, which may influence the survival of cells. In conclusion, a significant difference between cellular viabilities in the HSVs frozen using the freezing rates determined by the direct and indirect thermophysical calculations would have been expected because the freezing rate was applied to the vessels on a large scale. It might be suggested that this program will be helpful in easily finding the ideal freezing rate. However, there was no difference in cellular viabilities of the TEBs, which postulated to result from the small volume of the freezing material, the scaffolds containing cellular component.