The publishers would like to make readers aware that the Appendix for Microcirculation, 16(3), April, 213–219 appeared online at: http://www.informaworld.com/openurl?genre=article&issn=1073-9688&volume=16&issue=3&spage=213 and is also shown below:
Glycocalyx volume measurements: a critical review of tracer dilution methods for its measurement
CHARLES C. MICHEL AND FITZ-ROY E. CURRY
APPENDIX
Estimation of the maximum width of the entrances between the plasma and the water filled spaces within the ECL available to a spherical macromolecule. The Stokes Einstein radii (aES) of dextran molecules can be calculated from their diffusion coefficients in aqueous solutions and have been widely used (See for example [9–12]). For D40, aES has a value of 4.9 nm. The maximum diameter of the entrance from the plasma into the ECL that is available to a neutral molecule of this size can be estimated from the known molecular properties of serum albumin, a negatively charged macromolecule, which is almost completely excluded from the ECL [20]. This is possible because in addition to steric exclusion, which affects both charged and uncharged molecules, the effects of a charged matrix in excluding a molecule of the same charge is determined by the Debye length. In aqueous solutions of the ionic strength of mammalian plasma, the Debye length has a value of 1.0 nm. (for discussion of this approach see [6]). For a negatively charged albumin molecule to be excluded from entering a negatively charged matrix, the portals of the matrix can be no more than 4 nm larger than the diameter of the albumin molecule (which is 7.1 nm). The 4 nm is made up of 2 nm linked to effects of the net negative charge on each side of the albumin molecule and a further 2 nm associated with the negative charge on each side of the entrance to the matrix. This means that the opening is no more than 7.1 + 4 = 11.1 nm. This phenomenon is illustrated in general terms in .
Appendix Figure A1. Diagram to illustrate steric plus electrostatic charge exclusion in a matrix. Radius of solute molecules (=a; radius of matrix molecules = r; D is the Debye length (the range of electrostatic influence) and this is ~1.0 nm in solutions the ionic strength of plasma. Figure A1A shows a neutral solute molecule (grey) adjacent to a charged matrix molecule of radius r (solid black). The centre of the neutral solute molecule is excluded from a region of solution of radius r + a (heavy broken line black distance a surrounding the matrix molecule but with no effect of the electrostatic exclusion zone a distance D (=1nm) surrounding the matrix (inner broken line). Figure A1B shows the case where negatively charged solutes (light hatched) are excluded by both steric and electrostatic charge (similar charge density on both solute and matrix). The center of the charged solute is excluded from a region of solution of radius r + a+2D (dot and dash line). The space available to 2 negatively charged solute molecules (ds) between matrix molecules that are a distance d apart when the matrix molecules also carry a negative charge is ds=d − 2(r + a+2D) whereas the space available to water and small solutes (a close to zero) = d − 2r.

Since D40 has a molecular diameter of 4.9×2 = 9.8 nm, the center of a D40 molecule is excluded from over 88% of the entrance region. Water molecules by contrast (diameter 3 nm) are able to occupy 97% of the entrance region. Thus the concentration of D40 within the matrix must be considerably less than its concentration in the plasma.
In these calculations we have used the Stokes Einstein radii as molecular radii for serum albumin and D40. The Stokes Einstein radius of a molecule is the radius of a sphere that faces the same friction resistance to diffusion through an aqueous solution as the molecule. Studies of rotational diffusion coefficients of serum albumin suggested that it was ellipsoidal rather than spherical with axes of 14.4×4.4×3.2 nm [7] i.e. its Stokes Einstein diameter is approximately half long as its major axis. Models based on its chemical [3] and crystallographic structure suggest that it is more spherical in shape [4]. More recently Sugio et al [19] have indicated that human serum albumin is roughly heart shaped with dimensions of 8×8×3 nm. From this it seems reasonable to take the Stokes Einstein diameter of 7.1 nm.
Estimation of λ for a series of possible matrix structures. If a molecule can enter the matrix, the value of λ is determined by the dimensions of the molecule and the spacing between the component matrix molecules of the ECL. We have explored what λ might be for simple hypothetical structures based on the ECL being a matrix of cylindrical molecules or cylindrical chain molecules linking larger globular molecules (see ).
Appendix Figure A2. Four examples of possible structures for which λ has been calculated. Figs A2A and A2C represent the glycocalyx as a series of cylindrical molecular chains, which arise from trans-membrane proteins in the luminal endothelial cell membrane. In figures A2B and A2D the cylindrical chains link globular proteins (represented by spheres). In Figure 1A and 1B the chains are based on a square array, the diagonal of which is 11.2 nm (note the cylinders are further apart in A2C because the diagonal is measured between the spheres). In Figures A2C and A2D the chains arise from equilateral triangles of side length 11.2 nm. Calculations suggest that highest values of the partition coefficient (λ) between plasma and the fluid within the glycocalyx occur with variants of Figure A2D when λ may have a value as high as 0.4 and there is no cross linking. Cross-linking between the chains (shown as solid connecting lines) reduces λ to less than 0.05. For Figures A1A and A1C all values for λ are less than 0.05.
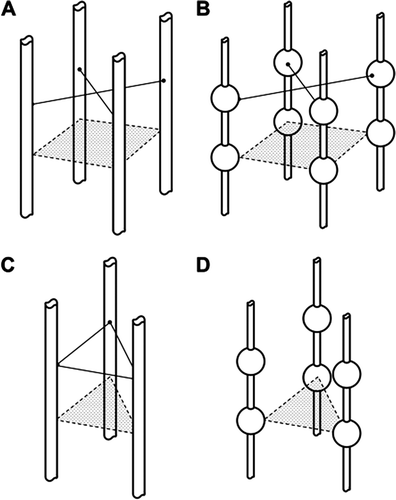
Four representative structures are shown below. For all structures composed of cylindrical molecules separated by 11.2 nm. λ for a molecule of diameter 9.8 nm has a value of 0.05 or less. If the entrances to the water filled spaces within the ECL are guarded by large globular molecules set on relatively small diameter (e.g. 1 nm) cylindrical molecules, λ may rise to 0.1 or more. Further increases in λ can be achieved theoretically by increasing the ratio of the diameters of the gatekeeper globular molecules to those of the cylindrical chains and increasing the length of the latter. Structures such as these are unlikely to be stable as the chains lengthen, unless there is some cross-linking between the cylindrical chains. The cross-links, however, increase the degree of exclusion of a probe molecule and consequently lower the value of λ. The most likely structures would appear to have λ values of no more 0.05 for molecule with a Stokes Einstein radius of 4.9 nm.