Nonlinear model of liquid chromatography considering finite rates of adsorption-desorption kinetics and core-shell adsorbents

Abstract

A nonlinear general rate model is numerically approximated to simulate fixed-bed chromatographic columns packed with core-shell particles. The model incorporates explicitly the effect of finite rates of adsorption and desorption at the adsorption sites, typically assumed to be very fast compared to the rates of the various transport processes. Using core-shell particles as a stationary phase can have advantages over applying a fully-porous stationary phase, such as higher efficiencies and better resolution of the sample components. A high resolution finite volume scheme is extended and applied to approximate the model equations. Ranges of the kinetic parameters in which limited rates of the intrinsic adsorption and desorption steps needs to be taken into account are estimated. A few case studies of predicting the elution of single-component and two-component mixtures are considered to evaluate the effects of adsorption and desorption rate constants, core-radius fraction, axial-dispersion coefficient, film mass transfer, and intraparticle diffusion on the elution profiles. Furthermore, it is demonstrated that optimum values of the inert core radius can be obtained by evaluating a typical criterion for process performance.

Graphical Abstract

Keywords:

• Liquid chromatography
• general rate model
• core-shell particles
• slow rates of sorption kinetics
• numerical solution technique

Introduction

A key information required to quantify nonlinear preparative chromatography concerns adsorption equilibria, which determine the mean elution times.^[1] A second key information is related to process kinetics. This field is more complex because numerous different mechanisms can contribute and decide about the widths and shapes of the elution profiles.

Various mathematical models have been considered in the literature for simulating liquid chromatographic processes including kinetic effects. The models applied differ in the levels of complexities considered. The models which are most frequently used by liquid chromatographic community include the equilibrium dispersive model (EDM), the lumped kinetic model (LKM), and the general rate model (GRM).^[1–3] The GRM is considered as the most complete model. It takes into account the axial dispersion and all mass-transfer kinetics like external mass transfer of adsorbate from the bulk phase to the external surface of the adsorbent, diffusion transport through the pores of the adsorbent, and finite rates of the adsorption-desorption kinetics at the active sites.^{[1, 2]}

The LKM can be extracted from the GRM by assuming that particles are homogeneous and the partial differential equation describing intra particular mass transport across the particle radii is modified accordingly. The intraparticle mobile and stationary phase concentrations are replaced by average concentrations, and the intra particle diffusion term is replaced with a kinetic expression. The kinetic expression describes mass transfer in the bulk liquid phase and intraparticle mobile phase via an overall mass transfer coefficient which is related to the external and internal mass transfer coefficients. The EDM is the simplest model that takes axial dispersion and mass transfer kinetics into account. In the EDM, the mobile and stationary phases are assumed constantly in equilibrium, i.e. mass transfer kinetic and the kinetics of adsorption and desorption are very fast. The contribution of these kinetics are lumped together in an apparent dispersion coefficient which is related to the axial dispersion and mass transfer kinetics.

The fact that finite rates of adsorption and desorption steps at the active sites of the stationary phases can be rate limiting is only captured in the GRM model. The general possibility of this kinetic mechanism was first discussed by Giddings^[4] on the basis of stochastic theory. It was discussed that Gaussian-type elution peaks form when the exchange of solute molecules between the mobile and stationary phases is very fast. In contrast, if adsorption and desorption rates of solute molecules are slow, a significant portion of the injected solute molecules eluted without being captured by these sites and causing the formation of tails. Later on only a few other researchers have investigated this effect,^{[1, 5, 6]} which is typically ignored.

In recent years chromatographic column are frequently packed with core beads (also known as core-shell particles) instead of using fully porous particles.^[7–9] Due to the application of thin porous layers coated on solid impenetrable cores, there are shorter intraparticle diffusion pathways causing the elution of narrower peaks.^[8–12] Numerous theoretical studies are available describing analytical chromatography using core-shell particles.

Kaczmarski and Guiochon have used a lumped particle model to simulate chromatographic columns packed with core-shell particles of thin porous layers and have assumed a single averaged value of the concentration inside the porous layer.^[13] A general rate model (GRM) of fully porous particles was used to analyze the performance of thin-layered core-shell particles. A study on inert core size optimization for linear chromatography has been done by Li et al.^[14] A nonlinear quasi-stationary GRM for core-shell particles has been numerically investigated by Gu et al.^[15] Core-shell particles have also been used for chiral.^[16] Lambert et al. have analyzed the mass transfer properties of insulin by considering both core-shell and fully-porous particles as packing materials.^[17] Monolithic and fused core HPLC columns were compared for fast chromatographic analysis of fat-soluble vitamins.^[18] Ibrahim et al. have compared core-shell and totally porous particle stationary phases for fast and green LC determination of five hepatitis-C antiviral drugs.^[19] Theoretical aspects and technical properties of the columns packed with core-shell particles are described deeply in serval reviews.^[20–23]

In our recent article, we have numerically investigated elution profiles using core-shell particles under overloaded nonlinear conditions using a reduced GRM considering infinitely fast rates of adsorption and desorption, i.e. permanently established adsorption equilibria.^[24] The current article extends now these theoretical investigations to a GRM explicitly considering slow adsorption-desorption rates. The model equations incorporate core-shell adsorbents of variable layer thicknesses as packing materials. For such a nonlinear model, no analytical solutions can be derived and numerical solution techniques are required for predicting dynamics inside the chromatographic column. In this article, a semi-discrete flux-limiting high resolution finite volume scheme (HR-FVS) is extended and applied to solve the current model equations.^{[24, 25]} A second order nonlinearly stable explicit Runge-Kutta method is applied to solve the resulting system of ordinary differential equations (ODEs). To demonstrate the effect of selected parameters, results of a number of case studies are presented. In particular, consequence of limited rates of adsorption-desorption processes are illustrated.

The structure of this article is as follows. The considered nonlinear GRM for core-breads including finite adsorption and desorption rates is described in Section 2. The suggested numerical scheme is ntroduced in Section 3. Quantitative criteria suitable to evaluate the performance of nonlinear preparative chromatography are presented in Section 4. Results of numerical case studies are given in Section 5. Lastly, conclusions are drawn in Section 6.

Mathematical model

The GRM of liquid chromatography is regarded as the most comprehensive and accurate model. The mass balance of GRM consist of two sets of coupled equations for the mobile phase, one is for the bulk-fluid that travels within the column bed carrying the components (where the concentrations of sample components are assumed as function of time and axial-coordinate of the column) and the other one is for the liquid stored inside the porous particles (where the solute concentrations are functions of time, axial-coordinate and particle radii). An adiabatic and isothermal adsorption column packed with inert core particles is considered. Each core-shell particle has three storage regions, i.e. the inert core (impermeable), the pores, and the inner surface. At time zero, a step change in the concentration of an adsorbate is introduced into a flowing stream. The adsorption column is subjected to axial dispersion, pore diffusion, external mass transfer resistance, surface diffusion and finite rates of adsorption-desorption kinetics. It is assumed that solid concentration changes due to mass transport in the pores only. It is further assumed that cored beads have uniform particle size R_p and core size $R_{\text{core}}$. The inert core cannot be penetrated and there is only diffusion (no convection) in the porous shell.

The mass balances for the bulk-phase are expressed as [1, 2](1) $$\frac{\partial c_{b,i}}{\partial t}+u\frac{\partial c_{b,i}}{\partial z}=D_{b,i}\frac{{\partial }^2{c}_{b,i}}{\partial z^2}-\frac{3}{R_P}{F}_b{k}_{\text{ext},i}(c_{b,i}-{c_{p,i}|}_{r=R_p}),\hspace{1em}i=1,2,\dots ,N_c.$$(1)

Here, $t z$, r denote the time, axial and particle radii coordinates, respectively. For each ith-component of the sample, $c_{b,i}=c_{b,i}(t,z)$ represents the solute concentration in the bulk phase, u is interstitial velocity, $D_{b,i}$ denotes the axial dispersion, $F_b=(1-{ϵ}_b)/{ϵ}_b$ is the phase ratio with bulk porosity ϵ_b, $k_{\text{ext},i}$ is the effective external mass transfer coefficient, $c_{p,i}=c_{p,i}(t,z,r)$ is the solute concentration in the particle pores, and N_c is the number of components in the mixture.

The model equation representing the change of solute concentration in the particle pores is given as^{[1, 2]}(2) $${ϵ}_p\frac{\partial c_{p,i}}{\partial t}+(1-{ϵ}_p)\frac{\partial q_{p,i}}{\partial t}={ϵ}_p{D}_{p,i}\left[\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2\left[\frac{\partial c_{p,i}}{\partial r}\right]\right)\right],\hspace{1em}i=1,2,\dots ,N_c,$$(2) where $q_{p,i}=q_{p,i}(t,z,r)$ is the solid-phase concentration, $D_{p,i}$ is the pore diffusivity, and ϵ_p is the internal porosity. In the current study, in contrast to previous study,^[24] the rates of nonlinear adsorption-desorption kinetics are assumed finite. The ordinary differential equation below describes the amount of ith component which is adsorbed on the stationary phase:^{[1, 2]}(3) $$\frac{\partial q_{p,i}}{\partial t}=k_{a,i}\left(q_m-\sum _{j=1}^{Nc}{q}_{p,j}\right)c_{p,i}-k_{d,i}{q}_{p,i}.$$(3)

Here, q_m denotes the adsorption saturation capacity which is assumed same for for all components and $k_{a,i}$ and $k_{d,i}$ represent the adsorption and desorption rates constants for ith component of the mixture. Adsorption and desorption are important interface mass-transfer processes. The description of such processes need information on the equilibrium achieved between phases and the rate on which equilibrium is approached. In any case these processes may be affected by physicochemical properties of the solid and liquid phases. Study of such kinetics of the adsorbent is useful as they provide information about its efficiency and mechanisms of adsorption. Equation (3)(3) $$\frac{\partial q_{p,i}}{\partial t}=k_{a,i}\left(q_m-\sum _{j=1}^{Nc}{q}_{p,j}\right)c_{p,i}-k_{d,i}{q}_{p,i}.$$(3) is a simplified adsorption-desorption kinetic expression. In most of the studies, it is assumed that a permanent adsorption equilibrium is established, i.e. adsorption-desorption rates are sufficiently high.^{[1, 24]} Then, the left-hand side of Equation (3)(3) $$\frac{\partial q_{p,i}}{\partial t}=k_{a,i}\left(q_m-\sum _{j=1}^{Nc}{q}_{p,j}\right)c_{p,i}-k_{d,i}{q}_{p,i}.$$(3) can be set equal to zero which reduces Equation (3)(3) $$\frac{\partial q_{p,i}}{\partial t}=k_{a,i}\left(q_m-\sum _{j=1}^{Nc}{q}_{p,j}\right)c_{p,i}-k_{d,i}{q}_{p,i}.$$(3) to the common multi-component Langmuir isotherm if the saturation capacities are the same for all the components, i.e.^{[1, 2]}(4) $$q_{p,i}=q_m\frac{b_i{c}_{p,i}}{1+\sum _{j=1}^{Nc}{b}_j{c}_{p,j}}\hspace{1em}\text{with} b_i=\frac{k_{a,i}}{k_{d,i}}.$$(4)

Here, b_i quantifies the extent of nonlinearity coefficient. In this limiting case, the current GRM reduces to the one presented in previous article [24].

For simplification of expressions, the following non-dimensional quantities are considered for a column of length L containing particles of radii R_p:(5a) $$\tau =\frac{ut}{L},\hspace{1em}x=\frac{z}{L},\hspace{1em}\rho =\frac{r}{R_P},\hspace{1em}{K}_{a,i}=\frac{L{q}_m{k}_{a,i}}{u},$$(5a) (5b) $$P{e}_{b,i}=\frac{Lu}{D_{b,i}},\hspace{1em}B{i}_{p,i}=\frac{k_{\text{ext},i}{R}_p}{{ϵ}_{p,i}{D}_{p,i}},\hspace{1em}{\eta }_{p,i}=\frac{{ϵ}_p{D}_{p,i}L}{u{R}_p^2},\hspace{1em}{\xi }_{p,i}=3B{i}_{p,i}{\eta }_{p,i}{F}_b,$$(5b) where τ, $x\in [0,1]$ and $\rho \in [0,1]$ are the dimensionless time, space and particle radii coordinates, respectively. Further, $K_{a,i}$ is the dimensionless adsorption rate constant which of key interest in this paper, $P{e}_{b,i}$ is the Pectlet number based on column length, $B{i}_{p,i}$ represents modified Biot number, and ${\eta }_{p,i}$ describes the ratio of space time and intraparticle diffusion time.

By introducing the dimensionless variables of Equations (5a)(5a) $$\tau =\frac{ut}{L},\hspace{1em}x=\frac{z}{L},\hspace{1em}\rho =\frac{r}{R_P},\hspace{1em}{K}_{a,i}=\frac{L{q}_m{k}_{a,i}}{u},$$(5a) and (5b)(5b) $$P{e}_{b,i}=\frac{Lu}{D_{b,i}},\hspace{1em}B{i}_{p,i}=\frac{k_{\text{ext},i}{R}_p}{{ϵ}_{p,i}{D}_{p,i}},\hspace{1em}{\eta }_{p,i}=\frac{{ϵ}_p{D}_{p,i}L}{u{R}_p^2},\hspace{1em}{\xi }_{p,i}=3B{i}_{p,i}{\eta }_{p,i}{F}_b,$$(5b) in the model Equations (1)–(3), we obtain(6) $$\frac{\partial c_{b,i}}{\partial \tau }+\frac{\partial c_{b,i}}{\partial x}=\frac{1}{P{e}_{b,i}}\frac{{\partial }^2{c}_{b,i}}{\partial x^2}-{\xi }_{p,i}\left(c_{b,i}-c_{p,i}{|}_{\rho =1}\right),\hspace{1em}i=1,2,\dots ,N_c,$$(6) (7) $${ϵ}_p\frac{\partial c_{p,i}}{\partial \tau }+(1-{ϵ}_p)\frac{\partial q_{p,i}}{\partial \tau }={\eta }_{p,i}\left[\frac{1}{{\rho }^2}\frac{\partial }{\partial \rho }\left({\rho }^2\frac{\partial c_{p,i}}{\partial \rho }\right)\right],$$(7) (8) $$\frac{\partial q_{p,i}}{\partial \tau }=K_{a,i}\left(c_{p,i}-c_{p,i}\sum _{j=1}^{Nc}\frac{q_{p,j}}{q_m}-\frac{q_{p,i}}{q_m{b}_i}\right).$$(8)

Considering a regenerated column, the Equations (6)–(8) are subjected to the following initial and boundary conditions (BCs)(9a) $$c_{b,i}(0,x)=0,\hspace{1em}{c}_{p,i}(0,x,\rho )=0,\hspace{1em}{q}_{p,i}(0,x,\rho )=0,\hspace{1em}\forall x,\rho \in [0,1],$$(9a) (9b) $$c_{b_i}(\tau ,0)-\frac{1}{P{e}_{b,i}}{\frac{\partial c_{b_i}(\tau ,x)}{\partial x}|}_{x=0}=\{\begin{array}{c}{c}_i{,}_{\text{inj}},\hspace{1em}0\le \tau \le {\tau }_{\text{inj}},\hfill \\ \hspace{1em}0,\hspace{1em}\hspace{1em}\tau >{\tau }_{\text{inj}},\hfill \end{array},\hspace{1em}{\frac{\partial c_{b,i}(\tau ,x)}{\partial x}|}_{x=1}=0,$$(9b) (9c) $$\begin{array}{c}\\ {\frac{\partial c_{p,i}}{\partial \rho }|}_{\rho =0}=0,\hspace{1em}{\frac{\partial c_{p,i}}{\partial \rho }|}_{\rho =1}=B{i}_{p,i}(c_{b,i}-c_{p,i}{|}_{\rho =1}).\end{array}$$(9c)

Here, $c_{i,\text{inj}}$ represents the injected concentration of the ith-component of the sample.

For fully-porous particles, the range of ρ is from 0 to 1, while for cored particles its range is from ${\rho }_{\text{core}}=R_{\text{core}}/R_p$ to 1. Thus, for fully-porous beads ${\rho }_{\text{core}}=0$, while ${\rho }_{\text{core}}\ne 0$ for cored beads.

Numerical scheme

Numerous schemes are available in the literature for the approximation of chromatographic models.^{[1, 2, 25]} In this article, a semi-discrete high resolution finite volume scheme (HR-FVS) is applied to approximate the current GRM incorporating core-shell particles and finite rates of adsorption-desorption kinetics.^{[24, 25]} A second-order TVD-RK method is used for solving the resulting ODEs system.^[25] A complete derivation of the proposed numerical scheme is presented in Appendix A of this article.

Critical performance criteria

Optimization of preparative chromatography requires suitable performance criteria. Here, we propose a performance criteria by which the quality of a product can be enhanced.^{[24, 26, 27]} Consider a mixture of two components (N_c = 2) in which component 1 is less retained as compared to the component 2, i.e. $a_1<a_2$.

Assume that τ₁ is the dimensionless time during which the fraction of first component exceeds certain threshold, i.e. $c_{b_1}\ge \widehat{ϵ}{c}_{1,\text{inj}}$, where we take $\widehat{ϵ}={10}^{-5}$. Further, let τ₂ be the time duration during which fraction of component 2 drops below certain specified threshold, i.e. $c_{b_2}\le \widehat{ϵ}{c}_{2,\text{inj}}$.

The common performance attributes used in this work are cycle time, purity, productivity and yield. Here, cycle time, productivity and yield are used as performance functions, while purity is used as a constraint.

Cycle time

The cycle time ${\tau }_{\text{cyc}}$ is defined as the time lapse between two successive injections:(10) $${\tau }_{\text{cyc}}={\tau }_2-{\tau }_1.$$(10)

Purity

The time during which fractionation of component 1 stops is referred to as cut time. The following express is used in our calculations to find the cut time ${\tau }_{\text{cut}}$ of component 1:(11) $$\text{Pur}=\frac{\underset{{\tau }_1}{\overset{{\tau }_{\text{cut}}}{\int }}{c}_{b_1}(\tau ,x=1)d\tau }{\underset{{\tau }_1}{\overset{{\tau }_{\text{cut}}}{\int }}[c_{b_1}(\tau ,x=1)+c_{b_2}(\tau ,x=1)]d\tau }.$$(11)

The required purity, which is based on the peak area, was set equal to 99%.

Productivity

A reduced-productivity $\text{Pr}$ is the desired amount of a compound produced per time-cycle. In the case of component 1, it can be expressed as(12) $$\text{Pr}=\frac{\underset{{\tau }_1}{\overset{{\tau }_{\text{cut}}}{\int }}{c}_{b_1}(\tau ,x=1)d\tau }{{\tau }_{\text{cyc}}}.$$(12)

One can multiply volumetric flow rate with this $\text{YPr}$ to transform it to a dimensional form.

Yield

Yield of a desired component describes the ratio of amount in purified form and amount injected at the column inlet. In the case of component 1, it can be expressed as(13) $$\mathrm{Y}=\frac{\underset{{\tau }_1}{\overset{{\tau }_{\text{cut}}}{\int }}{c}_{b_1}(\tau ,x=1)d\tau }{\underset{{\tau }_1}{\overset{{\tau }_2}{\int }}{c}_{b_1}(\tau ,x=1)d\tau } .$$(13)

Numerical case studies

A few numerical case studies of single-component (N_c = 1) and two-component (N_c = 2) mixtures are carried to analyze the effects of adsorption rate $K_{a,i}$, core-radius fraction ${\rho }_{\text{core}}$, axial dispersion $P{e}_{b,i}$, external diffusion (Bi_p) and internal diffusion (η_p) on the elution profiles. All parameters of numerical test problem are listed in Table 1. Their values are chosen from the ranges of parameters typically used in high pressure liquid chromatography applications.

Table 1. Standard model parameters used in the numerical solutions.

Figure Nr.	Component Nr.	Peb	$B{i}_{p,i}$	${\eta }_{p,i}$	ϵb	ϵp	$q_m [g/l]$	bi	$c_{i,\text{inj}} [g/l]$
1, 2 & 3	1	1500	50	2.0	0.4	0.5	10	1.0	1.0
4 & 5	1	1500	50	2.0	0.4	0.5	20	0.5	1.0
	2	1500	50	2.0			20	1.25	1.0

Single-component elution profiles

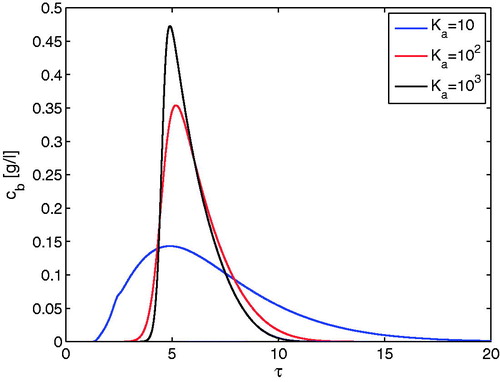
Figure 1 shows the effect of the dimensionless adsorption rate constant K_a on the outlet concentration profiles for a fixed core radius fraction of 0.8. For illustration, at first the elution of just one component is considered. The three kinetic effects related to axial dispersion (Pe_b), external diffusion (Bi_p) and internal diffusion (η_p) are fixed according to typical values given in Table 1. It can be observed that a relative slow rate of adsorption corresponding to K_a = 10 causes an additional band broadening. As the value of k_a increases, the concentration profile becomes sharper and less broadened. For $K_a\ge {10}^3$ the effect becomes negligible and the GRM predictions converge into the results of a simplified GRM considering just the aforementioned three limiting effects. This limiting dimensionless rate constant corresponds to the rate constant for the desorption step of $k_d=100 s^{-1}$. 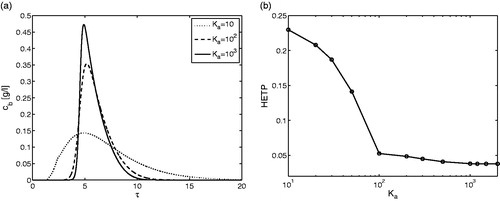This magnitude confirms the general belief that the intrinsic step of settling down and escaping of molecules on active surfaces is taking place very rapidly. Unfortunately, there are no reliable estimates for these rate constants in the literature. The border values for the related rate constants identified here by numerical simulation indicate that a detailed modelling of the adsorption and desorption steps is frequently indeed not required. However, the mathematical model applied here provides a quantitative tool to identify this border, which will shift for other constellations of Pe_b, Bi_p and η_p. In Figure 1 we have also demonstrated the effect of K_a on the conventionally used HETP-curve indicating the remaining band broadening effect due to the other three effects when K_ais sufficiently large.^[1]

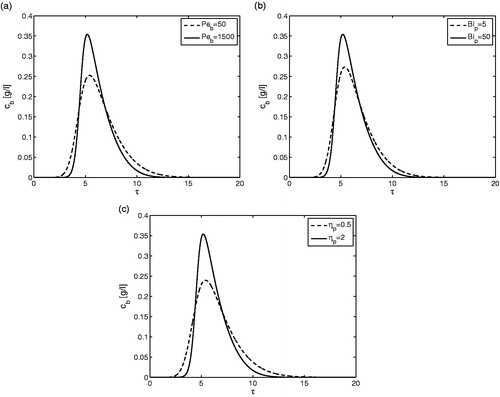
Figure 1. Single-component elution. Effect of dimensionless adsorption rate constant K_a on the outlet concentration profiles for ${\rho }_{\text{core}}=0.8$. Here, the dimensionless HETP is obtained by taking ratio of the second central moment and square of the first moment. All other parameters are given in Table 1.

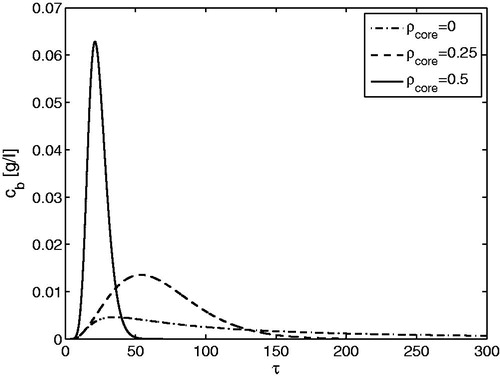
Figure 2 displays again for a single solute the effect of core-radius fraction ${\rho }_{\text{core}}$ on the elution curves. On increasing the value of ${\rho }_{\text{core}}$ from 0.0 to 0.5, the retention times decrease, whereas the peaks become sharper. These two trends continue for larger values of ${\rho }_{\text{core}}$. The results are given for K_a = 100, thus containing still an impact of the limited rates of adsorption and desorption. For all core radius fractions, a further increase in the value of K_a will lead to converging results and to the possibility to simplify the GRM. Now, the border values for K_a will also depend on ${\rho }_{\text{core}}$.

Figure 2. Single-component elution. Effect of ${\rho }_{\text{core}}$ on the outlet concentration profiles for $K_a={10}^2$. All other parameters are given in Table 1.

Figure 3 shows another time for single component elution and ${\rho }_{\text{core}}=0.8$ the effects of the three other dimensionless kinetic parameters on the outlet concentration profiles for a fixed value of K_a = 100. As the value of Pe_b increases (here from 50 to 1500), and keeping Bi_p and η_p at their reference values, the known effect is illustrated that peak broadening decreases (Figure 3(a)). Similarly, Figure 3(b) depicts, as also can be expected, that as Bi_p increases from 5 to 50 the band broadening of elution profile reduces. Finally, a similar well-known trend is exemplified in Figure 3(c), where the internal diffusion parameters captured by η_p is increased from 0.5 to 2. Smaller or larger values of K_a would alter the magnitude of these trends.

Figure 3. Single-component elution, plot (a) shows the effect of Pe_b, plot (b) shows the effect of Bi_p and plot (c) shows the effect of η_p for fixed $K_a={10}^2$ and ${\rho }_{\text{core}}=0.8$. All other parameters are given in Table 1.

Two-component elution profile

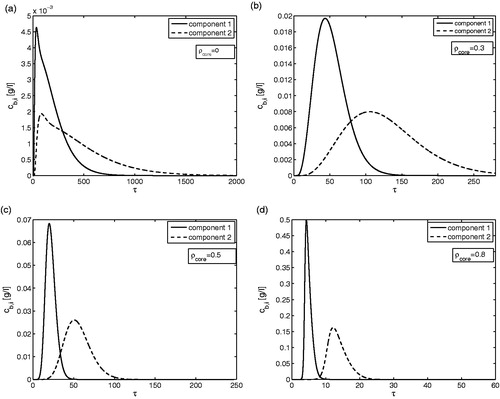
Figure 4 shows the predicted elution profiles of two-components present in a binary mixture for four different values of ${\rho }_{\text{core}}$. The already discussed effects of ${\rho }_{\text{core}}$ on the retention times and band widths of the elution profiles are obvious, now for both components. The results are still influenced by the finite rates of the adsorption and desorption steps because of the chosen values for $K_{a,i}$ for the two components (i.e. 100 and 250). For the case considered, the fully porous particles are not able to separate the two-components (Figure 4(a)). Figure 4(b) (${\rho }_{\text{core}}=0.3$) depicts an already better resolution, which further impoves for ${\rho }_{\text{core}}=0.5$ in Figure 4(c). At ${\rho }_{\text{core}}=0.8$ (Figure 4(d)) the two components are almost base-line separated. The results shown in Figure 4 are further evaluated in terms of the performance criteria introduced.

Figure 4. Two-component elution. Effect of ${\rho }_{\text{core}}$ on the outlet concentration profiles for fixed values of $K_{a,1}={10}^2$ and $K_{a,2}=250$. All other parameters are given in Table 1.

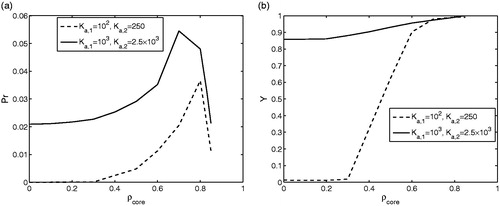
Figure 5 presents the predicted productivities Pr (Equation (12)(12) $$\text{Pr}=\frac{\underset{{\tau }_1}{\overset{{\tau }_{\text{cut}}}{\int }}{c}_{b_1}(\tau ,x=1)d\tau }{{\tau }_{\text{cyc}}}.$$(12) , Figure 5(a)) and yields Y (Equation (13)(13) $$\mathrm{Y}=\frac{\underset{{\tau }_1}{\overset{{\tau }_{\text{cut}}}{\int }}{c}_{b_1}(\tau ,x=1)d\tau }{\underset{{\tau }_1}{\overset{{\tau }_2}{\int }}{c}_{b_1}(\tau ,x=1)d\tau } .$$(13) , Figure 5(b)) as functions of ${\rho }_{\text{core}}$. To determine these criteria the cycle and cut times had to be calculated specifiying the purity requirements. The figure shows the results over ${\rho }_{\text{core}}$ for two sets of K_a, differing by a factor of 10. The larger values correspond to negligible limitations by finite adsorption and desorption rates. This case is obviously the best and leads to the highest performance. An interesting results is the fact that for smaller rate constants of these steps a shift to larger values of ${\rho }_{\text{core}}$ is advisable. It should be mentioned that the results descriebd are valid for given nonlinearity parameters b_i and injection concentration $c_{i,\text{inj}}$. Changing these parameters will of course change the shape of the elution profiles and the proportions of the contributions of different kinetic effects, which is seen as outside the scope of this paper.

Figure 5. Two-component elution. Plots of productivity $\text{Pr}$ and yield Y as functions of ${\rho }_{\text{core}}$. All other parameters are given in Table 1.

Conclusion

A nonlinear General rate Model (GRM) for fixed-beds packed with core-bead particles was investigated numerically. The model considered explicitly finite rates of the adsorption and desorption steps at the active sites of the stationary phase. A high resolution finite volume scheme was extended to solve the nonlinear model equations incorporating core-shell particles. This tool allows quantifying the effect of limited rates of adsorption and desorption on the shape of elution profiles for both fully porous and core-shell particles and allows identifying minimal rates required to neglect this effect and to further simplify the model. The model developed and the solution strategy derived are seen useful for predicting optimal layer thicknesses for the core-shell particles.

Appendix A: Numerical schemes

Here, a complete derivations of the proposed numerical scheme is presented. In the case of fully-porous particles, ρ ranges from 0 to 1, while for cored particles it ranges from ${\rho }_{\text{core}}=R_{\text{core}}/R_p$ to 1. Thus, ρ-axis can be replaced by a new variable $0\le \gamma \le 1$ such that(A-1) $$\gamma =\frac{\rho -{\rho }_{\text{core}}}{1-{\rho }_{\text{core}}}.$$(A-1)

Using this transformation, Equations (6)–(9c) can be re-written in term of new variable γ as(A-2) $$\frac{\partial c_{b,i}}{\partial \tau }+\frac{\partial c_{b,i}}{\partial x}=\frac{1}{P{e}_{b,i}}\frac{{\partial }^2{c}_{b,i}}{\partial x^2}-{\xi }_{p,i}\left(c_{b,i}-c_{p,i}{|}_{\gamma =1}\right),\hspace{1em}i=1,2,\dots ,N_c.$$(A-2) (A-3) $${ϵ}_p\frac{\partial c_{p,i}}{\partial \tau }+(1-{ϵ}_p)\frac{\partial q_{p,i}}{\partial \tau }=\frac{{\eta }_{p,i}}{{(1-{\rho }_{\text{core}})}^2}\left[\frac{{\partial }^2{c}_{p,i}}{\partial {\gamma }^2}+\frac{2}{\gamma +{\rho }_{\text{core}}/(1-{\rho }_{\text{core}})}\frac{\partial c_{p,i}}{\partial \gamma }\right],$$(A-3) (A-4) $$\frac{\partial q_{p,i}}{\partial \tau }=K_{a,i}\left(c_{p,i}-c_{p,i}\sum _{j=1}^{Nc}\frac{q_{p,j}}{q_m}-\frac{q_{p,i}}{q_m{b}_i}\right).$$(A-4)

Similarly, the transformation in Equation (A-1) can be used to change variable ρ to γ in the initial and boundary conditions given by Equations (9a)–(9c).

In compact form, the above system of dimensionless equations can be expressed as (A-2)-(A-4):(A-5) $$\frac{\partial {\mathbf{c}}_b}{\partial \tau }+\frac{\partial {\mathbf{c}}_b}{\partial x}=P{e}^{-1}\frac{{\partial }^2{\mathbf{c}}_b}{\partial x^2}-\xi ({\mathbf{c}}_b-{\mathbf{c}}_p{|}_{r=1}),$$(A-5) (A-6) $${ϵ}_p\frac{\partial {\mathbf{c}}_p}{\partial \tau }+(1-{ϵ}_p)\frac{\partial {\mathbf{q}}_p}{\partial \tau }=\frac{\eta }{{(1-{\rho }_{\text{core}})}^2}\left[\frac{{\partial }^2{\mathbf{c}}_p}{\partial {\gamma }^2}+\frac{2}{\gamma +{\rho }_{\text{core}}/(1-{\rho }_{\text{core}})}\frac{\partial {\mathbf{c}}_p}{\partial \gamma }\right],$$(A-6) (A-7) $$\frac{\partial {\mathbf{q}}_p}{\partial \tau }=K\left({\mathbf{c}}_p-{\mathbf{c}}_p\sum _{j=1}^{Nc}\frac{q_{p,j}}{q_m}-q_m^{-1}{B}^{-1}{\mathbf{q}}_p\right),$$(A-7) where ${\mathbf{c}}_b={(c_{b,1},c_{b,2},\dots ,c_{b,N_c})}^T,{\mathbf{c}}_p={(c_{p,1},c_{p,2},\dots ,c_{p,N_c})}^T,{\mathbf{q}}_p\in {(q_{p,1},q_{p,2},\dots ,q_{p,N_c})}^T$, and for $\alpha \in \{P{e}^{-1},\xi ,\eta ,K,B^{-1}\}$ and ${\alpha }_i=\in \{P{e}_{b,i}^{-1},{\xi }_{p,i},{\eta }_{p,i},K_{d,i},b_i^{-1}\}$, we have(A-8) $$\alpha =\left(\begin{array}{cccccc}{\alpha }_1& 0& 0& 0& \cdots & 0\\ 0& {\alpha }_2& 0& 0& \cdots & 0\\ 0& 0& {\alpha }_3& 0& \cdots & 0\\ ⋮& ⋮& ⋮& \ddots & & ⋮\\ 0& 0& 0& 0& \cdots & {\alpha }_{N_c}\end{array}\right).$$(A-8)

In order to apply the scheme, the first step is to discretize the computational domain. Let N_x and $N_{\gamma }$ are the number of discretization points along the x and γ-coordinates. The computational domain is taken as $[0,1]\times [0,1]$ which is covered by cells ${\Omega }_{lm}\equiv \left[x_{l-\frac{1}{2}},x_{l+\frac{1}{2}}\right]\times \left[{\gamma }_{m-\frac{1}{2}},{\gamma }_{m+\frac{1}{2}}\right]$ for $1\le l\le N_x$ and $1\le m\le N_{\gamma }$. The characteristic coordinates in the cell Ω_lm are denoted by $(x_l,{\gamma }_m)$. Here(A-9) $$(x_{1/2},x_{1/2})=(0,0), x_l=\frac{x_{l-1/2}+x_{l+1/2}}{2}, {\gamma }_m=\frac{{\gamma }_{m-1/2}+{\gamma }_{m+1/2}}{2},$$(A-9) and for the uniform mesh(A-10) $$\Delta x=x_{l+1/2}-x_{l-1/2} ,\hspace{1em}\Delta \gamma ={\gamma }_{m+1/2}-{\gamma }_{m-1/2} .$$(A-10)

Then, for $I_l:=\left[x_{l-\frac{1}{2}},x_{l+\frac{1}{2}}\right]$ and ${\Omega }_{lm}:=\left[x_{l-\frac{1}{2}},x_{l+\frac{1}{2}}\right]\times \left[{\gamma }_{m-\frac{1}{2}},{\gamma }_{m+\frac{1}{2}}\right]$, the cell averaged values ${\mathbf{c}}_{b,l}(t)$ and ${\mathbf{c}}_{p,l,m}(t)$ at any time t are given as(A-11) $${\mathbf{c}}_{b,l}:=\frac{1}{\Delta x_l}{\int }_{I_l}{\mathbf{c}}_b(t,x) dx,\hspace{1em}{\mathbf{c}}_{p,l,m}:={\mathbf{c}}_{p,l,m}\left(t\right)=\frac{1}{\Delta x_l\Delta {\gamma }_m}{\int }_{{\Omega }_{lm}}{\mathbf{c}}_p(t,x,\gamma ) d\gamma dx,$$(A-11) (A-12) $${\mathbf{q}}_{p,l,m}:={\mathbf{q}}_{p,l,m}\left(t\right)=\frac{1}{\Delta x_l\Delta {\gamma }_m}{\int }_{{\Omega }_{lm}}{\mathbf{q}}_p(t,x,\gamma ) d\gamma dx.$$(A-12)

By integrating Equation (A-5) on interval I_l and using Equation (A-11), we obtain(A-13) $$\frac{d{\mathbf{c}}_{b,l}}{d\tau }=-\frac{({\mathbf{c}}_{b,l+1/2}-{\mathbf{c}}_{b,l-1/2})}{\Delta x}+\frac{1}{P{e}_b\Delta x}\left[{\left(\frac{\partial {\mathbf{c}}_b}{\partial x}\right)}_{l+1/2}-{\left(\frac{\partial {\mathbf{c}}_b}{\partial x}\right)}_{l-1/2}\right]-\xi ({\mathbf{c}}_{b,l}-{\mathbf{c}}_{p,l,N_{\gamma }}),$$(A-13) where $l=1,2,\dots ,N_x$ and the differential terms can be approximated as(A-14) $${\left(\frac{\partial {\mathbf{c}}_b}{\partial x}\right)}_{l\pm 1/2}=\pm \frac{({\mathbf{c}}_{b,l\pm 1}-{\mathbf{c}}_{b,l})}{\Delta x} .$$(A-14)

Integration of Equation (A-6)(A-6) $${ϵ}_p\frac{\partial {\mathbf{c}}_p}{\partial \tau }+(1-{ϵ}_p)\frac{\partial {\mathbf{q}}_p}{\partial \tau }=\frac{\eta }{{(1-{\rho }_{\text{core}})}^2}\left[\frac{{\partial }^2{\mathbf{c}}_p}{\partial {\gamma }^2}+\frac{2}{\gamma +{\rho }_{\text{core}}/(1-{\rho }_{\text{core}})}\frac{\partial {\mathbf{c}}_p}{\partial \gamma }\right],$$(A-6) over the interval Ω_lm gives(A-15) $$\frac{d{\mathbf{c}}_{p,l,m}}{d\tau }=\frac{\eta }{{ϵ}_p{(1-{\rho }_{\text{core}})}^2\Delta \gamma }\left[{\left(\frac{\partial {\mathbf{c}}_b}{\partial \gamma }\right)}_{l,m+1/2}-{\left(\frac{\partial {\mathbf{c}}_b}{\partial \gamma }\right)}_{l,m-1/2}+\frac{2({\mathbf{c}}_{p,l,m+1/2}-{\mathbf{c}}_{p,l,m-1/2})}{{\gamma }_{m+1/2}+{\rho }_{\text{core}}/(1-{\rho }_{\text{core}})}\right]$$(A-15) (A-16) $$-\frac{(1-{ϵ}_p)}{{ϵ}_p}\frac{d{q}_{p,l,m}}{d\tau },$$(A-16) where(A-17) $${\left(\frac{\partial {\mathbf{c}}_p}{\partial x}\right)}_{l,m\pm 1/2}=\pm \frac{({\mathbf{c}}_{p,l,m\pm 1}-{\mathbf{c}}_{p,l,m})}{\Delta \gamma } .$$(A-17)

Finally, integrating Equation (A-7)(A-7) $$\frac{\partial {\mathbf{q}}_p}{\partial \tau }=K\left({\mathbf{c}}_p-{\mathbf{c}}_p\sum _{j=1}^{Nc}\frac{q_{p,j}}{q_m}-q_m^{-1}{B}^{-1}{\mathbf{q}}_p\right),$$(A-7) over interval Ω_lm gives(A-18) $$\frac{d{\mathbf{q}}_{p,l,m}}{d\tau }=K\left({\mathbf{c}}_{p,l,m}-{\mathbf{c}}_p\sum _{j=1}^{Nc}\frac{{\left(q_{p,j}\right)}_{l,m}}{q_m}-q_m^{-1}{B}^{-1}{\mathbf{q}}_{p,l,m}\right).$$(A-18)

Furthermore, concentrations approximation in Equations (A-13) and (A-15) is needed at the cells interfaces $x_{l\pm 1/2}$ and ${\gamma }_{m\pm 1/2}$. Numerous ways are present for their approximation. We are presenting here the first and second order approximations. Due to the positivity of velocity u and $\frac{2\eta }{{ϵ}_p\Delta \gamma [{\gamma }_{m+1/2}{(1-{\rho }_{\text{core}})}^2+{\rho }_{\text{core}}(1-{\rho }_{\text{core}})]}$, the contractions vectors at the interfaces of cell, c_b and c_p, are approximated as follows.

First order approximation of cell interface concentrations

Here, the backward difference formula is applied for the approximation of concentrations at the cell interfaces:(A-19) $${\mathbf{c}}_{b,l+\frac{1}{2}}={\mathbf{c}}_{b,l},{\mathbf{c}}_{b,l-\frac{1}{2}}={\mathbf{c}}_{b,l-1},{\mathbf{c}}_{p,l,m+\frac{1}{2}}={\mathbf{c}}_{p,l,m},{\mathbf{c}}_{p,l,m-\frac{1}{2}}={\mathbf{c}}_{p,l,m-1} .$$(A-19)

With the use of aforementioned approximations, a first order accurate numerical scheme is obtained in the axial coordinates.

Second order approximation of cell interface concentrations

Here, the cell interface concentrations are calculated as:(A-20) $${\mathbf{c}}_{b,l+\frac{1}{2}}={\mathbf{c}}_{b,l}+\frac{1}{2}\phi \left({\mu }_{l+\frac{1}{2}}\right)({\mathbf{c}}_{b,l}-{\mathbf{c}}_{b,l-1}),\hspace{1em}{\mu }_{l+\frac{1}{2}}=\frac{{\mathbf{c}}_{b,l+1}-{\mathbf{c}}_{b,l}+\zeta }{{\mathbf{c}}_{b,l}-{\mathbf{c}}_{b,l-1}+\zeta },$$(A-20) (A-21) $${\mathbf{c}}_{p,l,m+\frac{1}{2}}={\mathbf{c}}_{p,l,m}+\frac{1}{2}\psi \left({\nu }_{l,m+\frac{1}{2}}\right)({\mathbf{c}}_{p,l,m}-{\mathbf{c}}_{p,l,m-1}),\hspace{1em}{\nu }_{l+\frac{1}{2}}=\frac{{\mathbf{c}}_{p,l,m+1}-{\mathbf{c}}_{p,l,m}+\zeta }{{\mathbf{c}}_{p,l,m}-{\mathbf{c}}_{p,l,m-1}+\zeta },$$(A-21) where $\zeta ={10}^{-10}$ is used to avoid division by zero. The flux limiting functions ψ and $\phi$ are given as [25](A-22) $$\phi \left({\mu }_{l+\frac{1}{2}}\right)=\max \left(0,\min \left(2{\mu }_{l+\frac{1}{2}},\min \left(\frac{1}{3}+\frac{2}{3}{\mu }_{l+\frac{1}{2}},2\right)\right)\right),$$(A-22) (A-23) $$\psi \left({\nu }_{l,m+\frac{1}{2}}\right)=\max \left(0,\min \left(2{\nu }_{l,m+\frac{1}{2}},\min \left(\frac{1}{3}+\frac{2}{3}{\nu }_{l,m+\frac{1}{2}},2\right)\right)\right).$$(A-23)

The scheme given by Equations (A-20)-(A-23) can not be used at the boundary intervals. Therefore, backward approximations are applied on the boundary intervals. For computing fluxes at interior intervals, Equations (A-20)-(A-23) are used. It is to be noted that this first order approximation at the boundary cells does not reduces the overall accuracy of this scheme.

To guarantee the same accuracy in time coordinate, a second order accurate TVD-RK method is applied for solving Equations (A-20)-(A-23). Let us denote the right-hand side of Equations (A-20) and (A-21) by $({\mathbf{c}}_b,{\mathbf{c}}_p{|}_{\gamma =1}),\mathcal{M}({\mathbf{c}}_p)$ and $\mathcal{N}({\mathbf{q}}_p)$. A second order TVD-RK scheme updates c_b and ${\mathbf{c}}_p$ through the following two stages [28](A-24a) $${\mathbf{c}}_b^{\left(1\right)}={\mathbf{c}}_b^n+\Delta t\ell ({\mathbf{c}}_b^n,{\mathbf{c}}_p^n{|}_{\gamma =1}),\hspace{1em}{\mathbf{c}}_p^{\left(1\right)}={\mathbf{c}}_p^n+\Delta t\mathcal{M}\left({\mathbf{c}}_p^n\right),\hspace{1em}{\mathbf{q}}_p^{\left(1\right)}={\mathbf{q}}_p^n+\Delta t\mathcal{N}\left({\mathbf{q}}_p^n\right),$$(A-24a) (A-24b) $${\mathbf{c}}_b^{n+1}=\frac{1}{2}\left[{\mathbf{c}}_b^n+{\mathbf{c}}_b^{\left(1\right)}+\Delta t \ell ({\mathbf{c}}_b^{\left(1\right)},{\mathbf{c}}_p^{\left(1\right)}{|}_{\gamma =1})\right],\hspace{1em}{\mathbf{c}}_p^{n+1}=\frac{1}{2}\left[{\mathbf{c}}_p^n+{\mathbf{c}}_p^{\left(1\right)}+\Delta t \mathcal{M}\left({\mathbf{c}}_p^{\left(1\right)}\right)\right],$$(A-24b) (A-24c) $${\mathbf{q}}_p^{n+1}=\frac{1}{2}\left[{\mathbf{q}}_p^n+{\mathbf{q}}_p^{\left(1\right)}+\Delta t \mathcal{N}\left({\mathbf{q}}_p^{\left(1\right)}\right)\right].$$(A-24c) where ${\mathbf{c}}_b^n,{\mathbf{c}}_p^n$ and ${\mathbf{q}}_p^n$ represent solutions at previous time step, tⁿ, and ${\mathbf{c}}_b^{n+1}$, ${\mathbf{c}}_p^{n+1}$ and ${\mathbf{q}}_p^{n+1}$ are updated one calculated at the next time step $t^{n+1}$. Also, $\Delta t$ is time step which is evaluated using the following CFL condition(A-25) $$\Delta t\le 0.5\min \left(\Delta x,\max \left(P{e}_{b,k}\right)\Delta x^2,\frac{\Delta {\gamma }^2{ϵ}_p{(1-{\rho }_{\text{core}})}^2}{{\eta }_{p,k}},\frac{\Delta \gamma {ϵ}_p{\gamma }_{m+1/2}{(1-{\rho }_{\text{core}})}^2+{\rho }_{\text{core}}(1-{\rho }_{\text{core}})}{2\left({\eta }_{p,k}\right)}\right).$$(A-25)

The above-mentioned numerical algorithm was implemented in C programming language.