?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.
?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.Abstract
A nonlinear general rate model (GRM) of liquid chromatography is formulated to analyze the influence of temperature variations on the dynamics of multi-component mixtures in a thermally insulated liquid chromatographic reactor. The mathematical model is formed by a system of nonlinear convection–diffusion reaction partial differential equations (PDEs) coupled with nonlinear algebraic equations for reactions and isotherms. The model equations are solved numerically by applying a semi-discrete high-resolution finite volume scheme (HR-FVS). Several numerical case studies are conducted for two different types of reactions to demonstrate the influence of heat transfer on the retention time, separation, and reaction. It was found that the enthalpies of adsorption and reaction significantly influence the reactor performance. The ratio of density time heat capacity of solid and liquid phases significantly influences the magnitude and velocity of concentration and thermal waves. The results obtained could be very helpful for further developments in non-isothermal reactive chromatography and provide a deeper insight into the sensitivity of chromatographic reactor operating under non-isothermal conditions.
GRAPHICAL ABSTRACT
Introduction
High-performance liquid chromatography is a selective separation technique which is based on differences in the distribution of chemical species between the phases of the separation column. The technique is mainly used for the separation of components from complex mixtures, such as fine chemicals, pharmaceutical, food additives, and biological products. In recent years, reactive chromatography has gained ample interest in chemical engineering research. Chromatographic reactor is a multi-functional unit in which chemical reaction and chromatographic separation lead to an integrated process that improves the conversion of reactants and purity of products. In chemical engineering, the reactive chromatography is available as an invaluable laboratory tool and as an industrial unit for multiple reasons.[Citation1] First, continuous removal of at least one of the reaction products for an equilibrium limited reactions shift the equilibrium in a direction that reduces by-product formation and increases conversion. Second, when a catalyst is used as packing material in the column, it stays inside the column and its removal from the product stream is not required. Third, complex mixtures can be separated with great precision using reactive chromatography, such as separation of proteins mixture or production of biodiesel. In reactive chromatography, it is often easier to meet the purity requirements of the products as compared to other separation methods. Thus, reactive chromatography can be utilized to obtain delicate products and harsh process conditions can be easily avoided.
A reaction inside the chromatographic reactor can be catalyzed homogeneously or heterogeneously. In the homogeneously catalyzed reaction, a catalyst for the reaction is included in the mobile phase. Thus, removal of catalyst from the product is needed at the end of the process. On the other hand, in the heterogeneously catalyzed reaction, the stationary phase is used simultaneously as a catalyst for the reactant and as an adsorbent for the separation of mixture components. Reactive chromatography can be applied to several classes of reactions. Some typical applications include esterification by ion-exchange resins[Citation2–7] or by immobilized enzymes,[Citation8] transesterifications,[Citation9,Citation10] hydrogenation,[Citation11] and sugar involving reactions.[Citation12,Citation13]
Elution order of components and the type of reaction has a strong influence on the reactive chromatography. Mostly equilibrium limited reaction of the form and
are extensively investigated in the literature for isothermal case.[Citation14–19] The elution order constraint is important to gain high purity products. In consecutive or parallel reactions, the formation of by-products leads to a reduction in product purities.[Citation20] To understand the basic concept of chromatographic batch reactors, consider a single chromatographic column in which an equilibrium limited reversible reaction of the form
takes place. In such a reaction process, the reactant A is injected as a rectangular pulse into the chromatographic column constituting an adsorbent of lower affinity toward the reactant A and the product C and high affinity toward the product B. The reactant A reacts with the surface of catalyst to form the product B and C. Both product species will move at different velocities through the reactor, with B stays behind the reaction front as being retained strongly than A and C. Pure fractions of products could be collected separately on the basis of their elution time. Such separation facilitates the reversible reaction to go beyond the thermodynamic equilibrium by continuously separating the products from the reaction zone. Therefore, high purity product could be withdrawn from these systems due to their separation from the reactants.[Citation21–23]
Thermal effects such as heat generated by chemical reaction, heat of adsorption, and mixing are mostly overlooked in the analysis of liquid chromatographic reactors. The available experimental, theoretical, and numerical investigation in the literature is limited to isothermal conditions. A few contributions regarding thermal effects in liquid chromatography are also available in the literature.[Citation24–29] However, thermal effects have been discussed extensively for gas chromatography.[Citation30–34] Some authors have discussed the effects of temperature on the constant equilibrium under constant inlet pressure.
Mathematical modeling is widely used as an important tool for studying the chromatographic process. In this regard, a number of mathematical models with different complexity have been developed in the literature, which provides detailed information about the mass transfer and partitioning process inside the chromatographic column. These models include the equilibrium dispersive model (EDM), the non-equilibrium lumped kinetic model (LKM), and the general rate model (GRM).[Citation35–38] Analytical solutions are possible under linear adsorption conditions only. In the case of non-isothermal reactive chromatography, we have to linearize the adsorption isotherm and reaction term for solving the model equations analytically.[Citation19] Thus, the same nonlinear and non-isothermal reaction behavior presented in this article cannot be accommodated in the analytical framework. The analytical results presented for linearized isotherms and reactions can only be used to simulate chromatography processes considering small volumes of the injected or diluted samples. Such solutions are only valid and meaningful for small values of the enthalpy of adsorption and they give over-predicted solutions for larger values of the enthalpy of adsorption.
The aim of this work is to demonstrate the significant influence of thermal effects on separation and conversion and to quantify the magnitude of thermal effects on the performance of non-isothermal chromatographic reactor. A three-component non-isothermal GRM of reactive liquid chromatography with nonlinear heterogeneous reaction term is considered along with nonlinear adsorption conditions to simulate the process of chromatographic reactor. The reactive non-isothermal GRM can be described by a coupled system of nonlinear convection-diffusion reaction-type partial differential equations (PDEs) for mass and energy balances coupled with algebraic equations describing the adsorption isotherms and reaction. The high-resolution finite volume scheme (HR-FVS) of Koren is recommended to solve the model equations. Several test problems of practical applicability are considered to explain the coupling between the concentration and temperature profiles in the chromatographic reactor. The significant effect of thermal gradient on separation and conversion is demonstrated and the influence of key parameters is analyzed. It is observed that analogous to gas chromatography, density time heat capacity ratio of solid to liquid phase has a significant influence on the reactor performance. The current nonlinear model is more general and flexible for the simulation of reactive liquid chromatography process considering a variety of samples.
This article is further arranged in the following manner. In Section 2, a three-component GRM is formulated for non-isothermal liquid chromatographic reactor. In Section 3, a semi-discrete HR-FVS is derived and implemented for solving the model equations. Section 4 presents basic formulation and procedure to check the consistency of the results. Section 5 presents some numerical case studies. Finally, conclusions are drawn in Section 6.
Non-isothermal GRM of reactive chromatography
The GRM of column chromatography incorporates several sorption and transport processes. Molecules in the mobile phase are transported between the chromatographic beads by convection and are dispersed due to eddies and other inhomogeneities of flow. The film mass transfer equilibrates concentration gradient between the particle bulk phase and the stagnant film around the particle surface. The molecules are then diffused in the pores of the particles (mobile phase) and, hence, adsorbed selectively at their inner surface. Many properties of sorption dynamics and equilibria play a major role to separate the individual components from a complex mixture.
In the derivation of the model equations, it is assumed that column is insulated thermally and is packed homogeneously, the mobile phase is incompressible, the volumetric flow rate is constant and the solid phase is acting as a catalyst for heterogeneous reaction, the effect of temperature variation is negligible on the physical properties (e.g. viscosity, density, and heat capacity) and transport coefficients (e.g. axial dispersion and heat-conductivity), and the axial dispersion and the heat-conductivity coefficients are independent of the flow rate.
The governing mass balance equations for the bulk-fluid phase are expressed as
(1)
(1)
where Nc represents the number of components in the mixture introduced at the column inlet,
represents the solute concentration of the ith component in the bulk-fluid phase, u is the interstitial velocity,
denotes the axial dispersion coefficient, the phase ratio
represents the interstitial bulk volume over the total bead volume,
is the bulk porosity,
is the effective mass transfer coefficient, Rp is the radius of spherical particles, the factor
denotes the surface to volume ratio of spherical particles,
is the i-th component solute concentration in the particle pores, and
represents the concentration differences between the extra particular mobile phase in the external film and the intra particular mobile phase at the surface of the particle.
The corresponding differential mass balance for the sorbent particle pores, assuming diffusion and sorption of components within the sorbent pores and reaction in the stationary phase, is expressed as
(2)
(2)
where
is the local equilibrium concentration of solute in the stationary phase for i-th component,
is the effective internal pore diffusivity,
denotes the heterogeneous reaction rate in the solid phase and νi are the corresponding stoichiometric coefficients of i-th component. In general, the stoichiometric coefficient νi is negative for reactants and positive for products.
The corresponding energy balance for an adiabatic chromatographic reactor is given as
(3)
(3)
In the above equations, Tb is temperature of the bulk fluid, Tp is fluid temperature inside the particle pores, represents effective axial heat conductivity coefficient, ρL is density per unit volume in the liquid phase,
is heat capacity for liquid phase and
is effective heat transfer coefficient quantifying the rate of heat exchange between mobile and stationary phases.
An energy balance law for the radial temperature profile inside particles pores is expressed as
(4)
(4)
here
represents the enthalpy of adsorption of j-th component,
is the enthalpy of reaction,
is the heterogeneous reaction rate,
denotes the internal heat diffusivity coefficient. Moreover,
(5)
(5)
where ρS is the density per unit volume of solid phase and
is the corresponding heat capacity. The considered density and heat capacity ρL, ρS,
and
are not depending on temperature.
Consider a simple case of non-reactive, non-dispersive, and equilibrium chromatography, i.e.
and all dispersion and reaction terms are zero. Then, the speeds of concentration profiles
and of the thermal wave uT inside the column can be approximated from EquationEquations (1)–(4) as[Citation29]
(6)
(6)
It is clear from EquationEquation (6)(6)
(6) that the speed
is depending on the respective local gradients of adsorption isotherms and uT is influenced by the ratio of density times heat capacity. For less adsorbed components or for smaller gradients of isotherms
and for a larger ratio of
the speeds
of concentration fronts are higher than the speed uT of thermal wave.
The equilibrium adsorption isotherms are assumed to be nonlinear in terms of the concentrations and temperature and are described by van’t Hoff type relation using the enthalpy of adsorption
(7)
(7)
where
denotes the Henry’s constant and
represents the nonlinearity coefficient of the ith component at the reference temperature, Rg is the gas constant, and
represents the reference temperature. The chemical reaction in the chromatographic reactor could occur either in the liquid phase (i.e., homogenous reaction) or in the particle phase (i.e., heterogeneous reaction) or in both phases. Heterogeneously catalyzed reaction is usually considered for esterification where the same ion exchange resin acts as a catalyst for the reaction and as an absorbent for the separation. In this study, we consider only the heterogeneous (solid phase) reaction. Based on the laws of conservation, the reaction rate of three components model reaction (
) is given as
(8)
(8)
here
represent the heterogeneous forward reaction rate constant and
represent reaction equilibrium constant, respectively. The Arrhenius equation uses activation energy
to describe the temperature effect on the chemical reaction rate
as an exponential function of absolute temperature:
(9)
(9)
To simplify the notations and reduce the number of parameters appearing in the model equations, the following dimensionless quantities are introduced:
(10)
(10)
here L denotes the column length, while
and PeT is the peclet numbers,
and BT is the Biot numbers for mass and energy, while
ηT,
and ξT are the dimensionless constants. After using the above dimensionless parameters in the mass and energy balances (c.f. EquationEquations (1)–(4)), we obtain
(11)
(11)
(12)
(12)
(13)
(13)
(14)
(14)
where
Equations (c.f. EquationEquations (11)–(14)) are solved using the appropriate initial and boundary conditions (BCs).
The initial conditions are given as
(15)
(15)
(16)
(16)
here
and
represent the initial temperature in the bulk and particle phase of the column, respectively.
BCs are required at the column inlet and the column outlet, at the center of the particles and for the stagnant film. In this study, the following Robin type BCs, also known as Danckwert BCs,[Citation39] are considered at the column inlet. These BCs are based on the flux conversation which are expressed as
(17a)
(17a)
(17b)
(17b)
here
is concentration and
is temperature of the injected sample. In this work, we have taken
and
the same. At the column outlet (x = 1), the zero Neumann BCs are utilized:
(17c)
(17c)
For EquationEquations (12)(12)
(12) and Equation(14)
(14)
(14) , radial BCs at r = 0 and r = 1 are expressed as
(17d)
(17d)
(17e)
(17e)
This completes the derivation of non-isothermal GRM for chromatographic reactors. In the next section, the suggested semi-discrete HR-FVS is applied to solve the model equations.
Numerical scheme
Various numerical procedures have been introduced in the literature for approximating the model equations for chromatographic models.[Citation37,Citation38,Citation40–42] In this article, a semi-discrete high resolution flux-limiting finite volume method of Koren is applied to solve current non-isothermal GRM.[Citation41,Citation42] A second-order TVD-RK method is used for solving the resulting ODEs system.[Citation41,Citation42] The order of accuracy of this scheme has been verified analytically and numerically in one of our previous articles.[Citation42] It was found that this scheme is second-to-third order accurate. Moreover, the scheme has capability to resolve sharp fronts and peaks in the solutions accurately. In this section, a complete derivation of the proposed numerical scheme is presented for a three-component reaction.
In compact form, the above system of equations (c.f. EquationEquations (11)–(14)) can be rewritten as
(18)
(18)
(19)
(19)
where
(20)
(20)
The model EquationEquations (18)(18)
(18) and Equation(19)
(19)
(19) ) constitute a system of nonlinear PDEs. These equations are discretized first in the spatial domain by using finite volume scheme. Domain discretization will result in a system of ordinary differential equations which is also nonlinear.
Domain discretization
Let Nx and Nr are the numbers of discretization points along the x and r-coordinates. The computational domain is taken as which is covered by cells
for
and
The characteristic coordinate points in the cell Ωlm are represented by
Here,
(21)
(21)
and for the uniform mesh
(22)
(22)
Since
(23)
(23)
Therefore, for and
the averaged values of the cell
and
expressed at any time τ, are given as
(24)
(24)
(25)
(25)
By integrating EquationEquation (18)(18)
(18) over the interval Il and utilizing EquationEquations (24)
(24)
(24) and Equation(25)
(25)
(25) , we obtain
(26)
(26)
where
and the differential term of the axial diffusion part is approximated as
(27)
(27)
Integration of EquationEquation (19)(19)
(19) over the interval Ωlm gives
(28)
(28)
where
(29)
(29)
Moreover, approximated values are required at the cell interfaces and
for EquationEquations (26)
(26)
(26) and Equation(28)
(28)
(28) . Various methods can be used to approximate them. We are presenting here the first and second-order approximations together with the TVD-RK scheme, used to get a second-order accuracy in time.[Citation42]
First order scheme
Here, the concentration vector and cp are approximated at the interfaces of the cell by applying backward difference formula:
(30)
(30)
(31)
(31)
A first-order accurate numerical scheme is obtained in the axial- coordinates by using the aforementioned approximations given by EquationEquations (30)(30)
(30) and Equation(31)
(31)
(31) .
Second-order scheme
Here, the cell interface concentrations are calculated in the following manner to get a second-order accurate scheme
(32)
(32)
(33)
(33)
A flux-limiting high-resolution scheme is produced by EquationEquations (32)(32)
(32) and Equation(33)
(33)
(33) . Here,
is used to avoid division by zero. The flux limiting functions
and
are used to preserve the local monotonicity (positivity) of the numerical scheme.[Citation42] They are defined as
(34)
(34)
(35)
(35)
The high-resolution scheme is given by EquationEquations (32)(32)
(32) and Equation(33)
(33)
(33) cannot be applied at the boundary intervals. Therefore, the first order backward approximations are applied to the boundary intervals. The fluxes at all other interior interval are computed by using EquationEquations (32)
(32)
(32) and Equation(33)
(33)
(33) . It is to be noted that this first-order scheme at the boundary cells does not reduce the overall accuracy of this method.[Citation42]
To reassure the same second-order accuracy in the time coordinate, a second-order accurate TVD-RK scheme is used for solving EquationEquations (32)–(35). Denoting the right-hand-side of EquationEquations (32)(32)
(32) and Equation(33)
(33)
(33) by
and
a second-order TVD RK scheme updates
and cp through the following two stages:
(36)
(36)
(37)
(37)
where
and
denote the solutions at the previous time step τn and
are updated solutions at the next time step
Moreover,
represents the time step which is calculated under the following Courant-Friedrichs-Lewy (CFL) condition:
(38)
(38)
The aforementioned numerical algorithm was programmed in C language with 100 × 50 grid points. An Intel processor of core-i5 laptop computer Intel(R) Core(TM) with a random access memory (RAM) size of 4096 MB was used to execute the program.
Performance consistency criteria
Optimization of performance for non-isothermal reactive chromatographic processes requires suitable performance criteria. Here, we propose the following integral consistency tests for mass and energy balance equations to check the accuracy of the numerical scheme and the formulated model equations. In this section, these tests are performed to analyze the conservation of mass and energy balances for three-component nonlinear reactive model considering the reaction of type,
Identity of integrated extents of reaction
A general approach for solving a system with multiple reactions is to calculate the extent to which reactions proceeds. It can be applicable whenever we know: (i) the complete composition of either the inlet or the existing stream from a reactor and (ii) the one constraint (conservation, selectivity, second composition, equilibrium constant, and etc.) for each reaction. Every chemical reaction adheres to the law of conservation, as mass cannot be created or destroyed during a chemical reaction. Thus, the total amount of concentration injected at the column inlet remains conserved during a chemical reaction. Conservation constraint is required to see the extent at which the reactants are converted into products during a reversible reaction, as for such reactions, reactants never attain a complete conversion. A change in the mole numbers ni of reactants and products participating in a chemical reaction depends on the stoichiometry of the reaction. For the considered chemical reaction A B + C, the integrated extent of reaction ξ is defined by the following relation:
(39)
(39)
here ξ denotes the total changes occurred in the number of moles due to the chemical reaction and
quantifies the number of moles injected into the column. Here,
represents the injected volume at the inlet of the column and
is the time of injection. For the considered test problems, concentrations of the products
and
at the column inlet are taken to be zero.
The mole numbers of reactant and products at the column outlet can be calculated by using the following integral formula:
(40)
(40)
here
represents the volumetric flow rate. In this work, the trapezoidal rule is used to approximate the above integral numerically. Moreover, simulations are considered for a longer time in each case study in order to bring back the system in its initial equilibrium state (time
).
The three values of ξk obtained from EquationEquation (39)(39)
(39) can be utilized to calculate the standard deviation as follows:
(41)
(41)
In the above expression, the average of three ξi for is represented by
This standard deviation tends to zero, if the mass balances respect reaction stoichiometry.
Integrated energy balance considering extent of reaction
Energy balance is a useful quantity for analyzing the performance of non-isothermal reactors because the temperature of a chemical reactor is determined by the energy balance for the reactor. Here, the computation of energy balance is performed by comparing the enthalpies entering () and leaving (
) the system. These enthalpies are defined as
(42)
(42)
where
for
Moreover, there will be no overall sorption effect in the case of a complete adsorption and desorption cycle (for sufficiently long
). On the basis of reaction’s effect quantified by heat of reaction
and the extent of reaction ξ, we can derive the following balanced equation, e.g. EquationEquation (41)
(41)
(41) :
(43)
(43)
To achieve the accurate numerical simulation, the aforementioned EquationEquation (43)(43)
(43) is required to be fulfilled as proof. Let the right-hand-side of EquationEquation (43)
(43)
(43) , which represents the error in numerical simulation is denoted as
There are several sources of numerical errors which should be taken into account, such as round off errors, discretization errors, errors in the numerical integrations of the outlet profiles, and etc. Due to these errors, the value
might not be exactly zero, i.e.
(44)
(44)
Thus, to achieve better fulfillment of the joint mass and energy balances, the value of should be as small as possible. Due to the accumulation of all possible errors in this more critical consistency check one could expect large errors in
as compared to errors in ξ. A relative percentage error in this energy can be defined as
(45)
(45)
Numerical case studies
In this section, some test problems are considered to figure out the effects of different parameters that influence separation and conversion in non-isothermal reactive liquid chromatography. The considered case studies also explain coupling between elution profiles of concentration and temperature in the non-isothermal chromatographic reactor. The axial dispersion is assumed to be the same for all components. Moreover, the values of some kinetic parameters, such as effective mass transfer coefficient
effective internal pore diffusivity
effective heat conductivity coefficient
effective heat transfer coefficient
and the enthalpy of adsorption
are assumed to be the same for all components. However, the current model equations and the proposed numerical solution technique allow different values for these quantities with respect to components. All the parameters used in these test problems are listed in which are in accordance with ranges of parameters typically encountered in HPLC applications. The parameters used in the test problems are similar to those presented in.[Citation26,Citation28]
Table 1. Parameters used in the test problems.
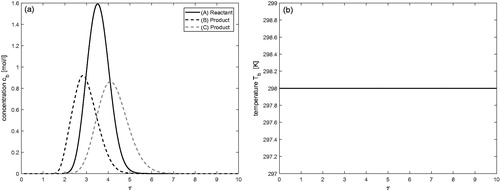
Isothermal case (
 )
)
demonstrates the isothermal behavior of the process for the considered reversible reaction In this case, the reactant A is injected as a pulse using Danckwerts BCs. Here,
thus, no variations in the temperature profile could be expected, i.e., it remains constant. The result indicates that reactant A is continuously converting into products B and C during its propagation through the column. At the same time, the separation between the components A, B, and C is also visible due to their different affinities with the solid bed. This case study can be taken as a reference to inspect non-isothermal behavior.
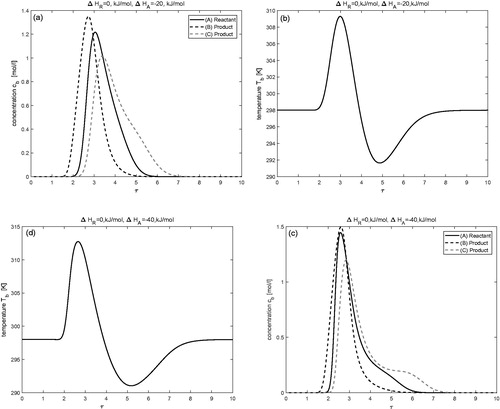
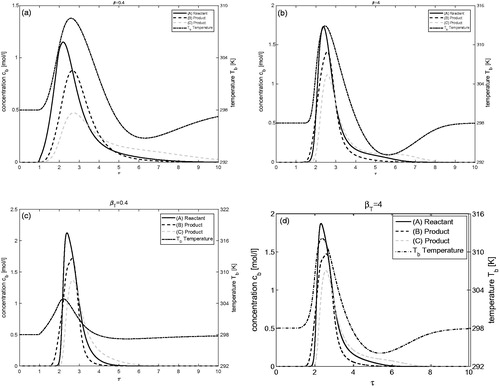
Effects of enthalpy of reaction (
 )
)
The influence of enthalpy of reaction on concentration and temperature profiles is investigated in this test problem while keeping the enthalpy of adsorption as
The results are displayed in for two different values of
and
Now increasing the value of exothermic reaction has a visible effect on concentration and temperature profiles. Significant rise in the temperature profile can be observed for
and
It can also be observed that an increase in the magnitude of heat of reaction
enhances the conversion of reactant A into products B and C. For
the rate of conversion is
which improves further to
for
The same trend can also be seen in .
Figure 2. Effect of enthalpy of reaction: (a,b) is for and
(c,d) is for
and
Moreover,
for j = 1, 2, 3.
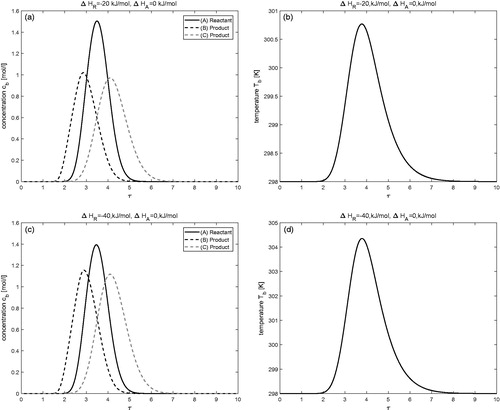
Table 2. Here,
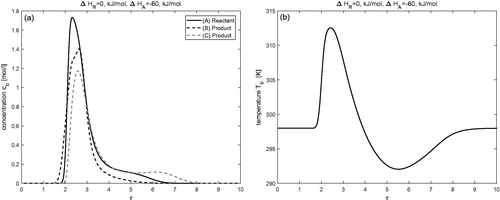
Effects of enthalpy of adsorption (
 )
)
In and , the effects of enthalpy of adsorption are analyzed, while the enthalpy of reaction is kept as
The results are obtained by considering three different values of enthalpy of adsorption, i.e.
(c.f ) and
in (c.f ). The separation of products from reactant in the chromatographic reactor is affected by differences in the adsorption ability of components and by temperature through the individual enthalpies of adsorption,
and reveal completely different behavior of concentration and temperature profiles in comparison to those obtained in the previously considered cases. Moreover, it can be observed from quantitative data presented in that an increase in the magnitude of
leads to a significant reduction in conversion and separation. The conversion rate is 41(%), when
is
and reduces to 35%, when
is
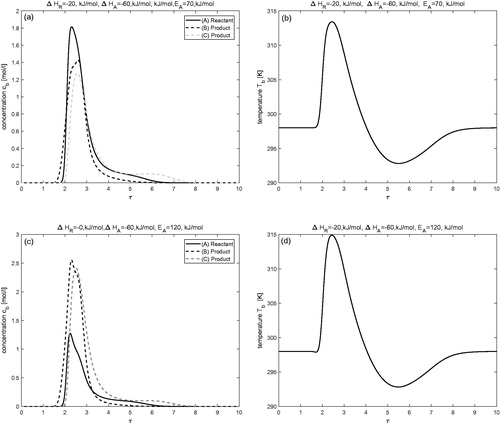
Joint effects of enthalpies of reaction and adsorption (
 )
)
In this test problem, combine effects of enthalpies of adsorption and reaction are evaluated to completely investigate the behavior of non-isothermal chromatographic reactors. The enthalpy of adsorption and the enthalpy of reaction
are considered to be the same for all components. The results are shown in . Comparison of and affirmed that concentration and temperature profiles follow similar trends. As reactant A is eluted in the middle of products, the reaction yields more amount of pure products. In one can observe a noticeable decrease in the peak height of reactant A and a significant rise in the peak heights of products B and C. Further, it can be observed from the simulated results shown in that larger values of activation energy, i.e.
and
enhance the reaction rate. Resultantly, more amount of reactant is converted into products. The rate of conversion increases up to 47 (%) and 56 (%) for the parameters considered. The collective errors in the integral mass and energy balances, denoted by EH (c.f. EquationEquation (45)
(45)
(45) ), is less than 1(%) in all the test problems. The corresponding quantitative values given in demonstrate the precision of numerical solutions.
Effects of the model parameters η, ηT, β, and βT
In this subsection, the effects of the intraparticle diffusion coefficients for mass and energy (η and ηT) and mass transfer coefficients for mass and energy (β and βT) are investigated. gives the results showing the effects of η and ηT. It is important to mention that for the cases where the value of η is altered, the value of ηT remains the same as given in and vice-versa. The plots show that small values of η (or ηT) give broadened profiles of low peak heights for both the concentration and temperature. Very similar results are witnessed in when the value of β (or βT) is reduced.
Effects of the density times heat capacity ratio of solid to liquid phases (
 )
)
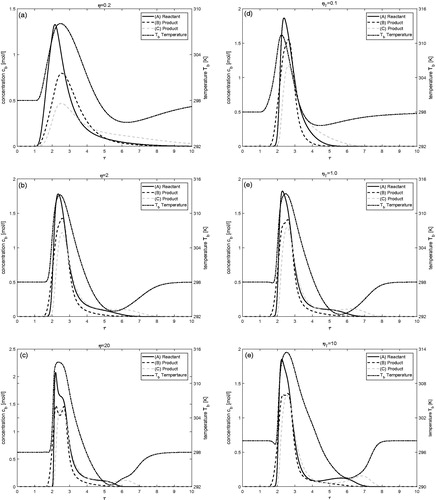
In this problem, the effects of varying density time heat capacity ratio are investigated under the influence of both enthalpies of adsorption and reaction. Retention times and the speed of concentration and temperature profiles inside the reactor are described by this ratio. The results are shown in . For
obtained by taking
and
see , the adsorption related to positive peak of thermal wave is moving slightly faster than concentration pulses and the desorption related negative peak is coupled with concentration pulses. For
obtained by taking
and
(), the mean retention times for concentration and temperature profiles are the same and, thus, travel with the same velocity. The figure depicts the coupling between the predicted profiles. For
obtained by taking
and
see (), the adsorption related peak of temperature is coupled with concentration profiles while the desorption related peak elutes later from the reactor. It can also be observed that more reactant is converted into product for the case
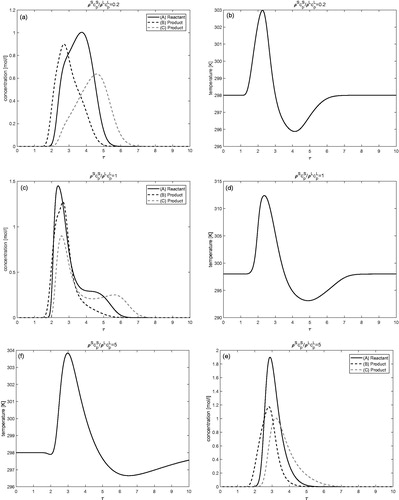
Isotherm nonlinearities with respect to concentration
and show the results of numerical calculations for fully nonlinear isotherm given by EquationEquation (7)(7)
(7) with
for j = 1, 2, and 3 and
respectively. The remaining parameters are exactly the same as given in . and Citation10a,b give the results for isothermal condition, while and Citation10c,d display the results for non-isothermal condition. A typical Langmuir behavior can be recognized from the right peak tailings of the concentration profiles. Due to non-linearity in the isotherm and in the reaction term, less amount of reactant is converted into the products. The conversion of reactant into the product is improved in the non-isothermal case as compared to the isothermal case. It can also be observed that conversion of reactant decreases further as the values of nonlinearity coefficient
increase. Moreover, in the non-isothermal case, significant deviation in the temperature profile could be seen from the reference temperature of 298 K. It should be finally mentioned that the numerical method applied is capable to easily handle other types of non-linearities.
Figure 9. Fully nonlinear isotherm (c.f. EquationEquations (7)(7)
(7) and Equation(8)
(8)
(8) ): Results of numerical calculations for isothermal and non-isothermal conditions. Here,
and
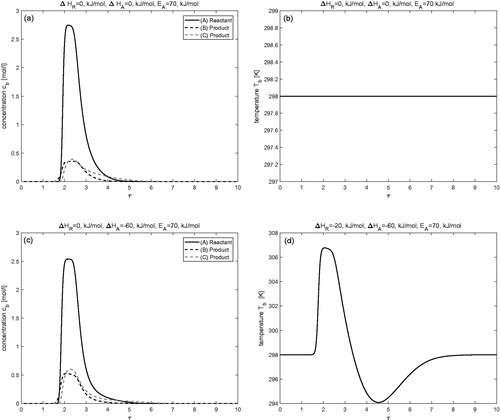
Figure 10. Fully nonlinear isotherm (c.f. EquationEquation (7)(7)
(7) and Equation(8)
(8)
(8) ): Results of numerical calculations for isothermal and non-isothermal conditions. Here,
and
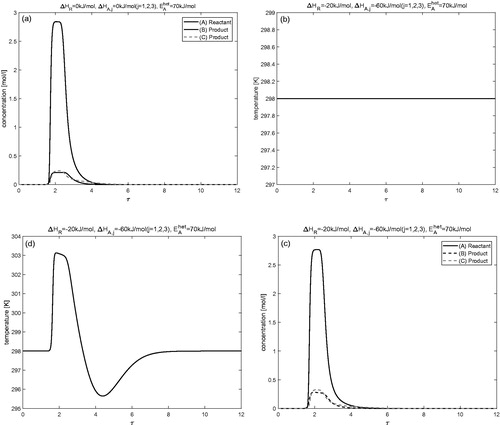
Conclusion
A multi-component non-isothermal GRM of nonlinear reactive chromatography was formulated and numerically approximated. The mass and energy balances describing non-isothermal reactive processes form a system of convection-diffusion reaction PDEs coupled with an algebraic equation for adsorption isotherms and reaction. An HR-FVS was implemented to numerically approximate the model equations. Several case studies of three-component reactions were considered and analyzed to demonstrate the influence of different parameters on the process performance, such as rate of reaction, retention time, injected volume of reactant, adsorption enthalpies, density time heat capacity ratio of solid to liquid phases, and etc. Consistency tests related to mass and energy conservation were carried out to verify accuracy of the suggested numerical algorithm. It was observed that non-isothermal reactors are more useful to achieve a high conversion rate as compared to isothermal reactors. The computed results are very useful tools for understanding the transport mechanisms in non-isothermal reactors to scale up physiochemical parameters that affect the reactor performance and to optimize experimental conditions.
References
- Rodrigues, A. E.; Pereira, C. S. M.; Santos, C. S. M. The Chromatographic Reactors. Chem. Eng. Technol. 2012, 35, 1171–1183.
- Kawase, M.; Suzuki, T. B.; Inoue, K.; Yoshimoto, K.; Hashimoto, K. Increased Esterification Conversion by Application of the Simulated Moving Bed Reactor. Chem. Eng. Sci. 1996, 51, 2971–2981.
- Kawase, M.; Inoue, Y.; Araki, T.; Hashimoto, K. The Simulated-Moving-Bed Reactor for Production of Bisphenol. Catal. Today. 1999, 48, 199–209.
- Mazzotti, M.; Kruglov, A.; Neri, B.; Gelosa, D.; Morbidelli, M. A Continuous Chromatographic Reactor: SMBR. Chem. Eng. Sci. 1996, 51, 1827–1836.
- Mazzotti, M.; Neri, B.; Gelosa, D.; Kruglov, A.; Morbidelli, M. Kinetics of Liquid-Phase Esterification Catalyzed by Acidic Resins. Ind. Eng. Chem. Res. 1997, 36, 3–10.
- Mazzotti, M.; Neri, B.; Gelosa, D.; Morbidelli, M. Dynamics of a Chromatographic Reactor: Esterification Catalyzed by Acidic Resins. Ind. Eng. Chem. Res. 1997, 36, 3163–3172.
- Mai, P. T.; Vu, T. D.; Mai, K. X.; Seidel-Morgenstern, A. Analysis of Heterogeneously Catalyzed Ester Hydrolysis Performed in a Chromatographic Reactor and in a Reaction Calorimeter. Ind. Eng. Chem. Res. 2004, 43, 4691–47026.
- Carta, G. Exact Analytical Solution of a Mathematical Model for Chromatographic Operations. Chem. Eng. Sci. 1988, 43, 2877–2883.
- Mensah, P.; Carta, G. Adsorptive Control of Water in Esterification with Immobilized Enzymes. Continuous Operation in a Periodic Countercurrent Reactor. Biotechnol. Bioeng. 1999, 66, 137–146.
- Fricke, J.; Meurer, M.; Dreisörner, J.; Schmidt-Traub, H. Effect of Process Parameters on the Performance of a Simulated Moving Bed Chromatographic Reactor. Chem. Eng. Sci. 1999, 54, 1487–1492.
- Fricke, J.; Schmidt-Traub, H.; Kawase, M. Chromatographic Reactor–Ullmann’s Encyclopedia of Industrial Chemistry; Wiley-VCH Verlag: Weinheim, Germany, 2005.
- Hashimoto, K.; Adachi, S.; Noujima, H.; Ueda, Y. A New Process Combining Adsorption and Enzyme Reaction for Producing Higher-Fructose Syrup. Biotechnol. Bioeng. 1983, 25, 2371–2393.
- Howard, A.; Carta, G.; Byers, C. Separation of Sugars by Continuous Annular Chromatography. Ind. Eng. Chem. Res. 1988, 27, 1873–1882.
- Takeuchi, K.; Uraguchi, Y. Basic Design of Chromatographic Moving Bed Reactors for Product Refining. J. Chem. Eng. Jpn. 1976, 9, 246–248.
- Takeuchi, K.; Uraguchi, Y. Separation Conditions of the Reactant and the Product with a Chromatographic Moving Bed Reactor. J. Chem. Eng. Jpn. 1976, 9, 164–166.
- Takeuchi, K.; Miyauchi, T.; Uraguchi, Y. Computational Studies of a Chromatographic Moving Bed Reactor for Consecutive and Reversible Reactions. J. Chem. Eng. Jpn. 1978, 11, 216–220.
- Qamar, S.; Bibi, S.; Khan, F. U.; Shah, M.; Javeed, S.; Seidel-Morgenstern, A. Irreversible and Reversible Reactions in a Liquid Chromatographic Column: Analytical Solutions and Moment Analysis. Ind. Eng. Chem. Res. 2014, 53, 2461–2472.
- Qamar, S.; Perveen, S.; Seidel-Morgenstern, A. Numerical Approximation of a Two-Dimensional Nonlinear and Nonequilibrium Model of Reactive Chromatography. Ind. Eng. Chem. Res. 2016, 55, 9003–9014.
- Qamar, S.; Sattar, F. A.; Seidel-Morgenstern, A. Seidel-Morgenstern, A. Theoretical Investigation of Thermal Effects in Non-Isothermal Non-Equilibrium Reactive Liquid Chromatography. Chem. Eng. Res. Design 2016, 115, 145–159.
- Michel, M.; Schmidt‐Traub, H.; Ditz, R.; Schulte, M.; Kinkel, J.; Stark, W.; Küpper, M.; Vorbrodt, M. Development of an Integrated Process for Electrochemical Reaction and Chromatographic SMB-Separation. J. Appl. Electrochem. 2003, 33, 939–949.
- Ganetsos, G.; Barker, P. E. Preparative and Production Scale Chromatography; Marcel Dekker, Inc.: New York, NY, 1993; Vol. 61; pp 375–523.
- Sardin, M.; Schweich, D.; Barker, P.E. (Eds.). Preparative Fixed-Bed Chromatographic Reactor, Preparative and Production Scale Chromatography; Marcel Dekker Inc.: New York, 1993; pp 477–522.
- Borren, T.; Fricke, J.; Schmidt-Traub, H. (Eds.). Chromatographic Reactors in Preparative Chromatography of Fine Chemicals and Pharmaceutical Agents; Wiley-VCH Verlag: Weinheim, Germany, 2005; pp 371–395.
- Brandt, A.; Mann, G.; Arlt, W. Temperature Gradients in Preparative Highperformance Liquid Chromatography Columns. J. Chromatogr. A. 1997, 769, 109–117.
- Sainio, T. Ion-exchange Resins as Stationary Phase in Reactive Chromatography. Acta Universitatis Lappeenrantaensis 218, Dissertation. Lappeenranta University of Technology, 2005.
- Sainio, T.; Kaspereit, M.; Kienle, A.; Seidel-Morgenstern, A. Thermal Effects in Reactive Liquid Chromatography. Chem. Eng. Sci. 2007, 62, 5674–5681.
- Sainio, T.; Zhang, L.; Seidel-Morgenstern, A. Adiabatic Operation of Chromatographic Fixed-Bed Reactors. Chem. Eng. J. 2011, 168, 861–871.
- Vu, T. D.; Seidel-Morgenstern, A. Quantifying Temperature and Flow Rate Effects on the Performance of a Fixed-Bed Chromatographic Reactor. J. Chromatogr. A. 2011, 1218, 8097–8109.
- Javeed, S.; Qamar, S.; Seidel-Morgenstern, A.; Warnecke, G. Parametric Study of Thermal Effects in Reactive Liquid Chromatography. Chem. Eng. J. 2012, 191, 426–440.
- Kruglov, A. Methanol Synthesis in a Simulatedcountercurrent Moving-Bed Adsorptive Catalytic Reactor. Chem. Eng. Sci. 1994, 49, 4699–4716.
- Yongsunthon, I.; Alpay, E. Design of Periodic Adsorptivereactors for the Optimal Integration of Reaction, Separationand Heat Exchange. Chem. Eng. Sci. 1999, 54, 2647–2657.
- Xiu, G.; Li, P.; Rodrigues, A. E. Sorption-Enhanced Reactionprocess with Reactive Regeneration. Chem. Eng. Sci. 2002, 57, 3893–3908.
- Glöckler, B.; Dieter, H.; Eigenberger, G.; NieKen, U. Efficientreheating of a Reverse-Flow Reformer-an Experimental Study. Chem. Eng. Sci. 2007, 62, 5638–5643.
- Eigenberger, G.; Kolios, G.; NieKen, U. Efficient Reheating of a Reverse-Flow Reformer-an Experimental Study. Chem. Eng. Sci. 2007, 62, 4825–4841.
- Ruthven, D. M. Principles of Adsorption and Adsorption Processes; Wiley-Interscience: New York, NY, 1984.
- Guiochon, G. Preparative Liquid Chromatography. J. Chromatogr. A. 2002, 965, 129–161.
- Guiochon, G.; Lin, B. Modeling for Preparative Chromatography; Academic Press: Cambridge, MA, 2003.
- Guiochon, G.; Felinger, A.; Shirazi, D. G.; Katti, A. M. Fundamentals of Preparative and Nonlinear Chromatography, 2nd ed.; ELsevier Academic Press: New York, NY, 2006.
- Danckwerts, P. V. Continuous Flow System Distribution of Residence Times. J. Chem. Eng. Sci. 1953, 2, 1–13.
- Lieres, E. V.; Andersson, J. A Fast and Accurate Solver for the General Rate Model of Column Liquid Chromatography. J. Comput. Chem. Eng. 2010, 34, 1180–1191.
- Koren, B. A Robust Upwind Discretization Method for Advection, Diffusion and Source Terms. In Numerical Methods for Advection-Diffusion Problems, Volume 45 of Notes on Numerical Fluid Mechanics; Vreugdenhil, C. B., Koren, B., Eds.; Chapter 5; Vieweg Verlag: Braunschweig, Germany, 1993; pp. 117.
- Javeed, S.; Qamar, S.; Seidel-Morgenstern, A.; Warnecke, G. Efficient and Accurate Numerical Simulation of Nonlinear Chromatographic Processes. J. Comput. Chem. Eng. 2011, 35, 2294–2305.