Rise and Shock: Optimal Defibrillator Placement in a High-rise Building

Abstract

Objective: Out-of-hospital cardiac arrests (OHCA) in high-rise buildings experience lower survival and longer delays until paramedic arrival. Use of publicly accessible automated external defibrillators (AED) can improve survival, but “vertical” placement has not been studied. We aim to determine whether elevator-based or lobby-based AED placement results in shorter vertical distance travelled (“response distance”) to OHCAs in a high-rise building. Methods: We developed a model of a single-elevator, n-floor high-rise building. We calculated and compared the average distance from AED to floor of arrest for the two AED locations. We modeled OHCA occurrences using floor-specific Poisson processes, the risk of OHCA on the ground floor (λ₁) and the risk on any above-ground floor (λ). The elevator was modeled with an override function enabling direct travel to the target floor. The elevator location upon override was modeled as a discrete uniform random variable. Calculations used the laws of probability. Results: Elevator-based AED placement had shorter average response distance if the number of floors (n) in the building exceeded three quarters of the ratio of ground-floor OHCA risk to above-ground floor risk (λ₁/λ) plus one half (n ≥ 3λ₁/4λ + 0.5). Otherwise, a lobby-based AED had shorter average response distance. If OHCA risk on each floor was equal, an elevator-based AED had shorter average response distance. Conclusions: Elevator-based AEDs travel less vertical distance to OHCAs in tall buildings or those with uniform vertical risk, while lobby-based AEDs travel less vertical distance in buildings with substantial lobby, underground, and nearby street-level traffic and OHCA risk.

Key words::

• resuscitation
• cardiac arrest
• public access defibrillator
• automated external defibrillator
• high-rise building

Introduction

Since survival from out-of-hospital cardiac arrest (OHCA) is extremely time sensitive,^1–3 there is significant interest in determining high risk locations for cardiac arrest^4–11 and optimizing public access automated external defibrillator (AED) placement and accessibility.^12–16 However, most studies have limited their analysis to two-dimensional geography, with minimal attention paid to AED placement and OHCA risk in the third (vertical) dimension.

It is well-known that patients in high-rise buildings experience delays in emergency response,^17–19 and “vertically challenged” locations such as high-rise and condominium buildings have a survival disadvantage from OHCA.²⁰ Moreover, rapid worldwide urbanization and densification will likely make the vertical height issue an increasingly central challenge in emergency OHCA response. Currently, over 50% of the world's population lives in urban areas and this number is projected to be 66% by 2050.²¹ In Toronto, Canada, the number of households living in high-rise apartments grew by over 13%, while the overall number of households increased by only 7%. Furthermore, over the past 15 years, almost 70% of all new households in Toronto were in high-rise apartments.²²

Unfortunately, current guidelines^23,24 lack specific recommendations regarding vertical AED placement. Elevators, which should be core to the discussion of vertical placement, only receive mention in passing when describing AED program implementation. For example, the American Heart Association suggests placing AEDs “in visible and accessible locations” such as “near elevators.”²⁵ The U.S. Department of Health and Human Services notes that buildings with elevators “present unique challenges to lay responders and rescuers.”²⁶ Additionally, there are no formal studies regarding optimal AED placement in high-rise buildings, though locations such as the elevator lobby or inside an elevator have been proposed as possible solutions.²⁰ The paucity of analysis is likely a major contributor to the lack of specific guidelines for vertical placement.

This paper provides a novel analysis on optimal AED placement in the vertical dimension to address the gap in the literature and help shape future discussion on this topic. Using a mathematical model, we aim to 1) determine the average and maximum response distance (vertical distance between AED and floor of cardiac arrest) implications of placing an AED in an elevator versus in the elevator lobby on the ground floor, and 2) determine how a building's height and vertical OHCA risk profile influence when an elevator-based AED or lobby-based AED will be preferred.

Methods

Model

We developed a mathematical model of a high-rise building with n floors, a single elevator, and a single AED. OHCA occurrences were modeled using independent Poisson processes on each floor, with floor i having rate of occurrence λ_i. We denoted the rate of OHCA occurrence on the ground floor as λ₁ and assumed all above-ground floors had the same rate denoted λ (λ = λ₂ = … = λ_n). We call an arrest that occurs above the ground floor an at-height arrest and an arrest on the ground floor an at-grade arrest. We compared two possible locations where the AED, assumed to be registered with and known to the 9-1-1 operator, can be placed: the elevator and the elevator lobby.

The process of getting an in-building AED to the patient side depends on how response is operationalized, which involves several factors. First, we assumed the high-rise building had a staffed security desk on the ground floor and when a 9-1-1 call originates from the building, the dispatcher not only dispatches paramedics but also calls the security desk. Second, we assumed there is a second lay responder who can retrieve an AED while the primary lay responder stays with the patient. Third, we assumed the elevator has an override that the guard can use to take control of the elevator no matter where it is and send it to any floor. Elevator override would take effect after the completion of any existing operation such as door closing following passenger loading. Fourth, the floor the elevator is on when the override occurs is modeled as a discrete uniform random variable (U) that takes values between 1 and n. We also did a sensitivity analysis using a second model for the location of the elevator at override: a discrete random variable (X) that takes values between 1 and n according to the probability distribution induced by the floor-level OHCA risk (i.e., probability of λ_i / (λ₁ + λ₂ + … + λ_n) for floor i). We assume the entire response process is completed for any given OHCA, and the AED is returned to its original position, before the next OHCA occurs.

The time from 9-1-1 call to AED arrival at the floor of the arrest was defined as the AED arrival time (T), which can be divided into three intervals: 9-1-1 call to security notification, security notification to elevator override, and elevator override to arrival at target floor with the AED. Of these three time intervals, only the last one, the override-to-arrival time (T_OA), depends on the AED location. Furthermore, we assumed the elevator moves at a constant speed, which means that the only difference between the two locations is the override-to-arrival distance (D_OA). Thus, for each location we calculated the average and maximum values of D_OA. In the Supplemental Appendix, we extend the calculations of average D_OA to average AED arrival time.

Analysis

Computing Average Response Distance

For each AED location, we first determined the override-to-arrival distance to a cardiac arrest on floor i. To compute the average D_OA, we then calculated the expected value over all floors according to the equation , where E(D_OA|i) is the expected override-to-arrival distance conditioned on the arrest occurring on floor i, and p_i is the probability the arrest occurs on floor i.

For an elevator-based AED, D_OA is the distance between the location of the elevator at the time of override, modeled using U, and the floor of the arrest. The number of floors between floor i and the position of the elevator at override is equal to the absolute value of the difference between the two: |U − i|. Thus, for a cardiac arrest on floor i, E(D^elev_OA|i) = E(|U − i|).

For a lobby-based AED and an at-height arrest, upon override the elevator must travel down to the ground floor to pick up the AED and then back up to floor of the arrest. The number of floors between the elevator location at override and the ground floor is U − 1 and the number of floors between floor i and the ground floor is i − 1. Thus, for i ⩾ 2, E(D^lobby_OA|i) = E((U − 1) + (i − 1)). For an at-grade arrest, the vertical travel distance is zero since the AED is already in the lobby. Therefore, E(D^lobby_OA|i) = 0 if i = 1.

The sensitivity analysis proceeds using the same steps, except with the random variable X, and its corresponding probability distribution, used in place of U.

Computing Maximum Response Distance

To compute the maximum D_OA, denoted max (D_OA), we determined the combination of elevator and arrest locations that maximizes the elevator distance travelled for the two possible AED locations.^{Figure 1}

Determining the Optimal AED Location

Once we derived the final algebraic expressions for E(D^elev_OA) and E(D^lobby_OA), we compared them for different values of n, λ₁, and λ to determine which AED location had a shorter average response distance. We conducted a similar comparison of max (D^elev_OA) and max (D^lobby_OA).

Computing and Comparing Variance in Response Distance

Finally, we compare the variances in response distance for the two locations, in the situation where the average response distances are the same. Since the average response distances are assumed equal, the comparison of variance simplifies to a comparison of the second moments, denoted E((D^elev_OA)²) and E((D^lobby_OA)²), i.e., the expected value of the override-to-arrival distance squared.

Results

Average Response Distance

By comparing the equations for E(D^elev_OA) and E(D^lobby_OA) (see Supplemental Appendix), an elevator-based AED has a shorter average response distance than a lobby-based AED if and only if: (1)

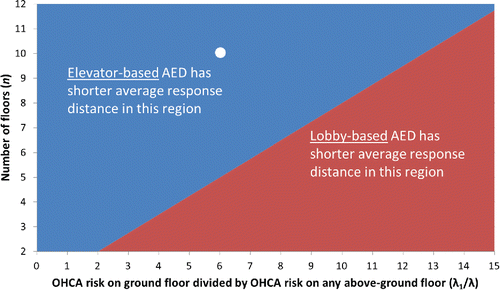
Recall that λ₁ is the rate of OHCA occurrences on the ground floor and λ is the rate on any above ground-floor. Expression (1(1) ) can be visualized in Figure 1. Combinations of the parameters that result in an elevator-based AED being optimal lie above the diagonal; combinations below the diagonal correspond to a lobby-based AED being optimal. An equivalent interpretation of expression (1) is that the optimality of an elevator-based versus lobby-based AED depends on the ratio.

Figure 1. Combinations of ground floor risk (λ₁), above-ground floor risk (λ), and number of floors (n) where an elevator-based AED (above diagonal) or lobby-based AED (below diagonal) has shorter average response distance. For example, white dot: In 10-floor building (n = 10 on y-axis) with six times the OHCA risk on the ground vs. above-ground floor (λ₁/λ = 6 on x-axis), an elevator-based AED is optimal.

(2)

If the ratio is less than 1, then the elevator-based AED is optimal, whereas if the ratio is greater than 1, a lobby-based AED is optimal.

Maximum Response Distance

For an elevator-based AED, travel distance is maximized when the arrest is on the top floor and the elevator is on the bottom floor, or vice versa. Thus, max (D^elev_OA) = n − 1. For a lobby-based AED, travel distance is maximized when both the arrest and the elevator are on the top floor, requiring the elevator to travel the length of the building twice to pick up and deliver the AED. Therefore, max (D^lobby_OA) = 2(n − 1). Thus, an elevator-based AED will always have shorter maximum response distance.

Sensitivity Analysis

By comparing the revised expressions for E(D^elev_OA) and E(D^lobby_OA) (see Supplemental Appendix), the conditions for when an elevator-based AED or lobby-based AED has shorter average response distance when elevator override location is modeled using X are exactly the same as when elevator override location is modeled using U. Namely, expressions (1(1) ) and (2(2) ) exactly characterize when an elevator-based or lobby-based AED is optimal.

Variance in Response Distance

By comparing the expressions for E((D^elev_OA)²) and E((D^lobby_OA)²) (see Supplemental Appendix), it is clear that an elevator-based AED always has less variance in its response distance compared to a lobby-based AED, when the average response distances are equal.

Discussion

In this study, we mathematically analyzed the problem of optimal AED placement in the vertical dimension. The analysis requires careful consideration of how AED response in a high-rise building may be operationalized, which is then modeled accordingly. The result is a simple inequality that prescribes when an elevator-based AED is expected to travel less distance than a lobby-based AED, and depends solely on the height of the building and the relative risk of arrest on the ground floor to an above-ground floor.

Main Findings

The main result characterizes the trade-off inherent in the location decision: an elevator-based AED can make a one-way trip and potentially reach upper floors more quickly, but a lobby-based AED will be accessible more quickly for at-grade arrests. The ratio given in expression (2(2) ) reinforces this intuitive trade-off: if the building is sufficiently tall (large n), then an elevator-based AED will respond more quickly on average. However, if the OHCA risk on the ground floor is sufficiently high (large λ₁ relative to λ), then a lobby-based AED will be optimal. Practically speaking, a tall building with a fairly uniform vertical risk profile will likely benefit more from an elevator-based AED. However, a high-rise that has a lot of ground floor and street level traffic, and perhaps a connection to an underground pedestrian network or shopping area, may benefit more from a lobby-based AED.

Expression (1(1) ), like expression (2(2) ), characterizes the optimal decision: if the number of floors is at least 0.5 plus three quarters of the relative risk of cardiac arrest on the ground floor to an above-ground floor, then an elevator-based AED will have shorter average response. For example, suppose the likelihood of an arrest on the ground floor is three times that on an above-ground floor, then expression (1(1) ) says a building with at least three floors will be better off with an elevator-based AED. If the risk is 10 times greater on the ground floor, then expression (1(1) ) implies a building needs to be at least eight floors high for an elevator-based AED to be optimal. An elevator-based AED is always optimal if the vertical risk profile is uniform (i.e., if λ₁ = λ). Only if there is sufficiently high risk on the ground floor, relative to an above ground floor, will a lobby-based AED be optimal. In terms of maximum response distance, an elevator-based AED will always be preferred, though the likelihood of such a worst-case scenario occurring is low.

We also examined the variance in response distance for the two AED locations. We found that if the average response distances were equal, the variance in response distance was always smaller for an elevator-based AED. This result suggests that an elevator-based AED should still be preferred if the average response distances are the same. Furthermore, given how quickly the difference in variance between the lobby-based and elevator-based AED grows as a function of n (quadratically; thus, the difference in standard deviations grows linearly in n), it may be that an elevator-based AED could be preferred even when its average response distance is larger than a lobby-based AED. For example, a building might have a certain vertical risk profile and height such that the average response distance of an elevator-based AED is only slightly larger than a lobby-based AED, but its variance is smaller by a large margin (e.g., if the building is tall, it would have large n). In this case, the smaller variance might be preferred since the tail of the response time distribution would be shorter.

Survival from OHCA decreases up to 10% for every minute of delay in treatment.² Lower survival and response delays are well-documented challenges in high-rise situations.^17–20 Having an AED in a high-rise building has the potential to improve survival by enabling bystanders to reduce the delay to defibrillation. However, poor placement may eliminate any advantage of AED pre-positioning in the building, which is why rigorous analysis of the location decision is critical, especially in a limited resource setting with only one AED.

Our analysis identified important factors that influence the location decision, including the building's vertical risk profile, elevator operations, and the presence of supporting responders or security staff. For example, only a building with sophisticated elevator control systems may be able to capitalize on the potential of an elevator-based AED. Furthermore, the benefit of a one-way elevator trip can only be realized if there is a second lay responder who can meet the AED at the elevator while the other responder is performing CPR. If an elevator-based AED needs to travel down to the lobby to pick up a second responder like the security guard before going back up to the floor of the arrest, then there is essentially no benefit over a lobby-based AED.

Overall, the mathematical expression derived in this paper should be seen as a starting point regarding analysis of vertical AED placement and guideline development, rather than a definitive solution. There are other relevant factors to consider when it comes to AED placement beyond response time. For example, security, visibility, and ease of access for nearby arrests that happen outside the building might tip the scale in favour of a lobby-based AED even for a very tall building.

Assumptions and Limitations

Since this problem had not been studied before, we made several assumptions to facilitate a tractable analysis. However, we believe these assumptions do not compromise the core insights that arise from our analysis. Every major assumption from the methods section is discussed in the following paragraphs.

Although we assumed a single elevator, tall buildings may have several. With many elevators but only a single AED, the analysis of response distance is the same for an elevator-based AED (unless there are specific elevator holding patterns; e.g., some elevators hold at certain floors in high-rise buildings when idle). However, a lobby-based AED will become more attractive since there will typically be an elevator closer to the ground floor than in the single-elevator case. A tall building may also have multiple AEDs. If AEDs were placed in both the lobby and elevators, or every few floors throughout the building, a location analysis is less critical. However, not all high-rise buildings would have the resources to invest in multiple AEDs.

Regarding the Poisson process assumption, previous research offers support for modeling cardiac arrest occurrences this way.²⁷ Further study is required to determine whether different floors have different rates of OHCA occurrence and are independent. We do believe it is plausible that the rate of at-grade arrests would be higher than the rate of arrests on a given above-ground floor due to the extra traffic flow or commercial activity in a building lobby, the proximity of potential arrests outside the building, and potential connections to underground areas. By assuming that each OHCA finishes before the next one occurs, we ensure that the AED is in its original location when each OHCA occurs. This assumption is reasonable since the rate of occurrences is fairly low (e.g., less than 10 a day in Toronto with a population of about 2.8M spread over more than 600 km²), suggesting a low likelihood of two occurring in the same building in close succession.

Not all high-rise buildings will have a security desk, and even if there is a security desk in the lobby, the guard may not be contacted by 9-1-1 or be unavailable when the 9-1-1 dispatcher calls the desk. In these cases, we believe our main insight still holds. If the risk of at-height OHCA is dominant, then an elevator will still be the best location for an AED since an at-height lay responder can get an AED more quickly by simply calling the elevator manually. However, if there is only a single lay responder, an elevator-based AED may provide no additional benefit over a lobby-based AED for at-height arrests since the lay responder will not be able to leave the patient side to meet the elevator.

Regarding elevator override, if the override function does not allow the elevator to be sent directly to the target floor, but instead requires it to go to the ground floor first (akin to the universal elevator key override that fire fighters have), then there is essentially no difference between an elevator-based and lobby-based AED. Technology exists to conduct elevator override in the manner assumed in this paper,²⁸ although it is not widespread. Also, by assuming elevator override takes place once the current operation is completed (e.g., doors closed after passenger loading/unloading, or reaching the next closest floor when ascending/descending), we do not need to assume the elevator has any extra features when dealing with passengers; it simply needs to operate like normal until override begins. Lastly, modeling the elevator location upon override as a discrete uniform random variable may not be appropriate if an elevator holding pattern is implemented during idle times. However, our sensitivity analysis shows that our results are unchanged when elevator location at override is assumed to match the vertical OHCA risk profile, which may be a reasonable approximation to overall traffic flow.

Future Directions

There are many directions for future research. A key unknown is the risk of cardiac arrest as a function of the floor of a high-rise building, which may vary due to differences in traffic flow, demographics of the inhabitants, and presence of different types of businesses/activities on each floor. Cardiac arrest incidence has been observed to be higher on lower-numbered floors than higher-numbered floors,²⁰ but this result may simply reflect the fact that there are more buildings with lower-numbered floors. Thus, the exact distribution of floors in all buildings city-wide is needed to determine the correct denominator and estimate floor-based risk. With estimates of the relative risk of cardiac arrest on the ground floor compared to above-ground floors, a height cut-off could be determined to prescribe the optimal AED location for different types of buildings using our model. In the absence of cardiac arrest data, one could examine the type and amount of traffic flow on each floor, and the types of activities that take place or businesses that reside on each floor. Additionally, an in-depth analysis using computer simulation could generate the entire response time distribution (not just the average or maximum) for a building with a complex vertical risk profile, multiple elevators, elevator holding strategies, and additional AED locations.

Conclusion

This paper provides a novel analysis of optimal AED placement in a high-rise building. Our results suggest that cardiac arrests in a tall building may experience faster response from an AED-based elevator, whereas a building with much higher risk on the ground floor compared to any above-ground floor would be better off with a lobby-based AED. Overall, survival from cardiac arrest in a high-rise building may be improved with intelligent AED deployment and operationalization of an internal emergency response process.