Comparison of six particle size distribution models on the goodness-of-fit to particulate matter sampled from animal buildings

Abstract

Lognormal distribution is often used as a default model for regression analysis of particle size distribution (PSD) data; however, its goodness-of-fit to particle matter (PM) sampled from animal buildings and its comparison to other PSD models have not been well examined. This study aimed to evaluate and to compare the goodness-of-fit of six PSD models to total suspended particulate matter (TSP) samples collected from 15 animal buildings. Four particle size analyzers were used for PSD measurement. The models' goodness-of-fit was evaluated based on adjusted R ², Akaike's information criterion (AIC), and mean squared error (MSE) values. Results showed that the models' approximation of measured PSDs differed with particle size analyzer. The lognormal distribution model offered overall good approximations to measured PSD data, but was inferior to the gamma and Weibull distribution models when applied to PSD data derived from the Horiba and Malvern analyzers. Single-variable models including the exponential, Khrgian-Mazin, and Chen's empirical models provided relatively poor approximations and, thus, were not recommended for future investigations. A further examination on model-predicted PSD parameters revealed that even the best-fit model of the six could significantly misestimate mean diameter, median diameter, and variance. However, compared with other models, the best-fit model still offered the relatively best estimates of mean and median diameters, whereas the best predicted variances were given by the gamma distribution model.

Implications

Particulate matter from animal buildings contains a large portion of coarse particles and, thus, has different particle size distribution (PSD) than ambient aerosols. The findings suggest a default use of the prevalent lognormal distribution model can lead to significant misestimates of PSD parameters such as mean diameter, median diameter, and variance. Other models, such as the gamma and Weibull distribution models, may be considered as alternative options. Because of a complexity in the shape of measured PSD profiles, the goodness-of-fit for each of the different PSD models must be compared before selecting one for data regression, parameter estimation, and reporting.

Introduction

Particle matter (PM) emitted from animal buildings often contains toxic, allergenic, and pathogenic components (Kirkhorn and Garry, 2000; Schenker et al., 1998), leading to its association with public health issues such as occupational allergy and swine influenza (Heederik et al., 2007). As one of the most important physical characteristics, particle size is closely related to the environmental and health effects of PM (Zhang, 2005). Small particles can penetrate deeply into the respiratory tract and travel a relatively long distance in the atmosphere (Wilson et al., 2002). A comprehensive investigation of particle size distribution (PSD) of PM from animal buildings is, therefore, of great importance.

A PSD can be derived by fractioning particles into a number of size ranges. Numerous particle size analyzers are currently available and can be mostly classified into several categories by their detecting principle: sedimentation, image analysis, electrical and optical sensing zones, and light diffraction (Miller and Lines, 1988). Because of the differences in detection principles and experimental protocols, different particle size analyzers may produce significantly different PSD profiles from identical PM samples (Etzler and Sanderson, 1995). Many previous studies on PM from animal buildings used only one or two particle size analyzers and most often different analyzers were used by different research groups (Chen et al., 1995; Donham et al., 1986; Heber et al., 1988; Jerez et al., 2011; Maghirang et al., 1997; Redwine et al., 2002). As a result, the derived PSD profiles and parameters, such as volume median diameter (VMD) and geometric standard deviation (GSD), were barely comparable between different studies. There is a need to characterize and to compare PSD profiles measured by different particle size analyzers.

A number of mathematical models have been developed for parameterization of measured PSD profiles that may consist of tens to hundreds of size ranges depending on the instrumental resolution. These models can greatly simplify discussions on size-dependent PM properties, for example, optical and radioactive properties, and provide an inherent mechanism for researchers to share large data sets by reporting the PSD model and just one or two model variables. For example, the most frequently used lognormal distribution model allows a large data set to be easily reported and reconstructed in terms of two variables, the volume median diameter (VMD) and geometric standard deviation (GSD). Other commonly used PSD models include but are not limited to the normal distribution model, the gamma distribution model, the Nukiyama-Tanasawa (Nukiyama and Tanasawa 1939)/modified gamma distribution (Liu and Liu, 1994) model, the Weibull distribution (Weibull, 1951)/Rosin-Rammler (Rosin and Rammler 1933) model, the power law/Junge model (Junge, 1963), the exponential model, the Khrgian-Mazin model (Mazin and Khrgian, 1989), and the Chen's empirical model (Chen et al., 1995). Although the lognormal distribution model is often used by default, better goodness-of-fit may often be achieved by other PSD models (Chen et al., 1995). According to Knutson and Lioy (1989), the PSD data measured by cascade impactors exhibited a significant departure from lognormality and they concluded that the lognormal distribution model can be misused if applied to such data sets.

A proper selection of PSD models is vitally important because different models can predict very different results, for example, on the mass (or number or surface) fraction of particles in a certain size range (e.g., PM with an aerodynamic diameter ≤2.5 μm [PM_2.5] and respirable particles), and these results are often critical for properly assessing the public health and environmental consequences of PM inside or released from animal buildings. Selecting an adequate PSD model requires a systematic examination of the goodness-of-fit for different models, and the best-fit model is highly dependent on the data set being parameterized, which may differ with particle size analyzer. Previously the ability to compare the goodness-of-fit for many PSD models for PM from animal buildings was constrained by the availability of reliable PSD data. A recent effort on PSD measurements has made this examination possible (Lee, 2009; Lee et al., 2008).

In this study, total suspended particulate matter (TSP) samples were collected from multiple animal buildings in different seasons and their size distributions were determined using four different particle size analyzers. A total of 217 PSD profiles were subjected to regression analysis. The research objectives were to evaluate the goodness-of-fit for six different PSD models to the measured PSD profiles, to compare the PSD parameters predicted by these models, and to identify the best applicable model for each particle size analyzer.

Materials and Methods

A total of 15 animal buildings were selected for PSD measurements, including five building types: swine farrowing, swine gestation, swine finishing, laying hens, and tom turkey, with three buildings for each type. Each building was visited three times in different seasons (hot: summer; mild: spring and fall; cold: winter). Four particle size analyzers were selected for PSD analysis (Table 1). The DSP (Aerosizer DSP Model 3223; TSI Inc., St. Paul, MN) offers a capability of in-field, real-time measurement, whereas the Horiba (Horiba LA-300 particle sizer; Horiba Group, Edison, NJ), Coulter (Coulter Multisizer Model 3; Beckman Counter Inc., Fullerton, CA), and Malvern (Malvern Multisizer 2000; Malvern Instruments Ltd., Worcestershire, UK) are all filter-based methods, that is, PM samples must be collected on filters prior to PSD analysis. In field, PSD measurement and PM sample collection were conducted upstream of exhaust fans with spacing typically of 0.3–0.6 m from the fan face. The DSP analyzer was placed on a folding table with its sampling inlet facing upward, approximately 1.3 m from the floor. DSP measurements were performed twice a day, one in the morning and the other in the afternoon. For each measurement, at least 10 replicates were monitored, from which an average PSD profile was derived for subsequent data analysis. For filter-based methods, PM samples were collected on 37-mm Teflon filters (Zefluor PTFE member filter, P/N P5RJ037; Pall Corporation, Ann Arbor, MI) using isokinetic TSP samplers developed at the University of Illinois (Jerez et al., 2006). The installation height of TSP samplers were typically 1.2–1.4 m, depending on the height of the selected exhaust fan. Particle-laden filter samples were stored in 50-mm Petri dishes at 4 ºC in a refrigerator and then extracted with chemical solutions of NaPMP (sodium polymetaphosphate)/water for Horiba, LiCl (lithium chloride)/methanol for Coulter, and pure ethanol for Malvern. The extracts (particle suspensions) were then subjected to PSD test. All selected particle size analyzers were calibrated with mono-dispersed particle size standards and the PSD data presented here had been corrected with obtained calibration curves. A detailed description regarding field sampling and PSD analysis procedures can be found in the publication from Lee (2009).

Table 1. Summary of particle size analyzers selected in this study

Instrument	Horiba	DSP	Coulter	Malvern
Number of profiles	83 ^†	44 ^‡	45	45
Detection principle	Mie scattering	Time of flight	Electrical impedance	Mie scattering
Diameter type ^#	EVD	AD	EVD	EVD
Detection range (μm)	0.1–600	0.3–700	0.4–1200	0.02–2000
Number of channels	64	100	300	100
Notes: ^†Extra PSD profiles were obtained from tests on spare samples.
^‡One data set was lost due to a failure in analyzer operation.
^#EVD = equivalent volume diameter; AD = aerodynamic diameter.

Six PSD models were selected for regression analysis: lognormal distribution, Weibull distribution, gamma distribution, exponential, Khrgian-Mazin, and Chen's empirical model (Table 2). The Nukiyama-Tanasawa model (1939) (eq 1) was not selected because the Weibull distribution, gamma distribution, exponential, and Khrgian-Mazin models are all its special cases (Paloposki, 1991). The Nukiyama-Tanasawa model undoubtedly offers superior goodness-of-fit. However, it contains more independent variables and is, thus, incomparable to its daughter models.

Table 2. Particle size distribution models that were examined

PSD Model (Zhang, 2005)	Probability Density Function ^†	Independent Variables
Lognormal	, x > 0	VMD,σg (GSD)
Weibull ^‡	, x > 0.	λ, k
Gamma ^‡	, x > 0	a, b
Exponential	, x > 0	a, b
Khrgian-Mazin	, x > 0	a, b
Chen's empirical	, x > 0	a, b
Notes: ^† v(x) and n(x) represent the probability density function for volume- and for number-based particle size distributions, respectively. VMD, σ g , λ, k, a, and b are independent variables/fit parameters of the examined models.
^‡The Weibull and gamma distribution functions were cited from the publication by Zhang (Zhang, 2005) but rewritten into their most known mathematical forms by referring to a book authored by Devore and Berk (Devore and Berk, 2007).

(1)

where x refers to the diameter of particles, n(x) is the probability density function of the number distribution, and a, b, p, and q are independent variables in the Nukiyama-Tanasawa model.

For evaluation of the goodness-of-fit, three statistics were calculated: adjusted R ², Akaike's information criterion (AIC), and mean squared error (MSE).

(2)

(3)

(4)

where RSS is the residual sum of squares, N is the number of PSD channels, P is the number of independent variables in a PSD model, and TSS is the total sum of squares. The adjusted R ² is widely used as a goodness-of-fit measure in statistical software programs (e.g., MATLAB, SPSS, and GraphPad) and scientific publications (Bah et al., 2009; Chen et al., 1995); however, its applicability to nonlinear regression has been argued for decades (Spiess and Neumeyer, 2010). The AIC and MSE could more adequately measure the goodness-of-fit for nonlinear modeling and have been suggested for use in addition to R ² (Spiess and Neumeyer, 2010; Wallach and Goffinet, 1989). In principle, a given PSD model will achieve a better goodness-of-fit compared with other models, if it has a higher adjusted R ², a lower AIC, and a lower MSE for a single data set.

Because all PSD data sets examined in this study were given in the form of volume-based distribution, particle number–based probability density functions in Table 2 must be transformed into volume-based ones prior to regression analysis. This conversion can be done with eq 5 (Paloposki, 1991).

(5)

Meanwhile, it should be noted that n(x) is normalized (eq 6), that is:

(6)

The raw PSD data given by the investigated particle size analyzers consist of three columns: particle size, volume frequency in the nearest size range, and cumulative volume fraction. To conduct nonlinear regression on these data, a model-predicted cumulative volume fraction function, V(x), was calculated (eq 7).

(7)

Accordingly, the PSD models selected for examination were transformed as follows.

Lognormal:

(8)

Weibull:

(9)

Gamma:

(10)

So,

(11)

(12)

Let , then,

(13)

(14)

Basically, if a number-based PSD follows the gamma distribution, then its corresponding volume-based PSD will also follow the gamma distribution, and vice versa. The only difference is in independent variable a, but a convenient conversion is available.

Exponential:

(15)

So,

(16)

(17)

(18)

Khrgian-Mazin:

(19)

So,

(20)

(21)

(22)

Chen's empirical:

(23)

So,

(24)

(25)

(26)

It can be seen that after transformation, the exponential, Khrgian-Mazin, and Chen's empirical models actually contain only a single independent variable, whereas the lognormal, Weibull, and gamma distribution models have two independent variables.

The model-predicted volume frequency of particles with size ranging from x ₁ to x ₂ was calculated with eq 27.

(27)

With both predicted and measured volume frequency data, an ordinary least squares (OLS) nonlinear regression was performed using a function of “nlinfit” in MATLAB 7.0 (Math Works, Inc., Natick, MA) based on the Gauss-Newton algorithm. A MATLAB program was developed to process a large number of PSD profiles in a single run, with functions including data reading, calibration (with the calibration curves derived from mono-dispersed particle size standards), model fitting, and calculation of the goodness-of-fit measures (i.e., adjusted R ², AIC, and MSE). The initial values of model variables, which are required for nonlinear regression, were estimated from preliminary examination of several typical PSD profiles. A trial-and-error process was still occasionally needed for finding the appropriate initial values to allow the nonlinear regression to converge.

PSD models with good approximations to measured data were selected for calculating model-predicted mean diameter (μ), median diameter (VMD), and variance (σ²). We also calculated these parameters directly from measured PSD data with eqs 28–30 and referred to them as measured PSD parameters.

(28)

where f_i refers to the frequency of particles in a size range with mean size of d_i and N is the number of size ranges (detection channels).

(29)

where D ₅₀ is the size corresponding to 50% cumulative particle volume fraction.

(30)

Ordinary and repeated-measures one-way analyses of variance (ANOVAs) were used for multiple comparisons of unpaired and paired data, respectively. Specifically in this study, unpaired data were from comparisons between different particle size analyzers, whereas paired data were mostly from comparisons between different PSD models. A Tukey's post hoc test was conducted when a significant difference was identified by one-way ANOVA; an exception was for comparing measured PSD parameters to those predicted by multiple PSD models—in this case, a Dunnett's post hoc test was performed because the measured parameters were taken as controls. All ANOVA tests were performed in GraphPad Prism 5.0 (Graph Pad Software, Inc., La Jolla, CA) with a significance level of α = 0.05 selected.

Results and Discussion

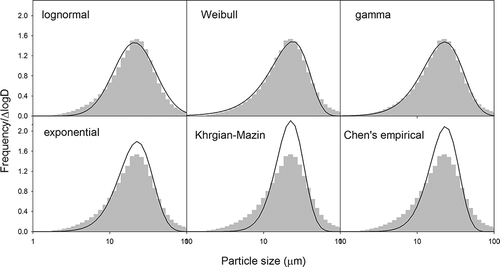
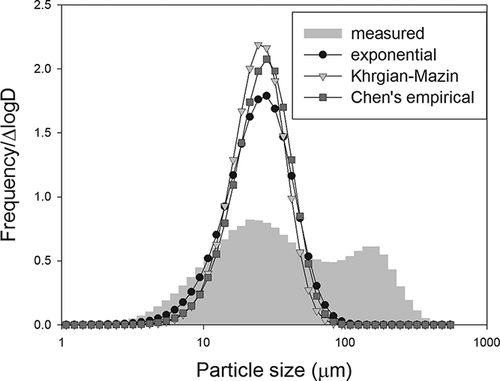
The PSD curves predicted by different models have similar geometry; however, differences may still exist (Figure 1). For example, the lognormal distribution model generates a symmetric peak on a semilogarithmic plot, whereas the Weibull distribution model produces a left-skewed peak. The goodness-of-fit of a PSD model is greatly dependent on the geometry of measured PSD profiles, which in reality is determined by not only the “true” size distribution of PM samples but also the detection principle and experimental protocol of the particle size analyzer being used.

Figure 1. Geometry of particle size distribution (PSD) curves predicted by different models. An example—Gray bar: a measured PSD profile by Horiba; solid line: the predicted PSD curve.

As expected, the goodness-of-fit of PSD models was found to differ with particle size analyzer (Figures 2 and 3). For the Horiba and Malvern, better approximations were obtained with the lognormal, Weibull, and gamma distribution models, with adjusted R ² values mostly greater than 0.9. Among the exponential, Chen's empirical, and Khrgian-Mazin models, the exponential model performed slightly better; however, all three produced relatively poor approximations, with adjusted R ² values typically less than 0.9 (Figure 2). The same ranking of model-fit was indicated by the AIC (Figure 3) and MSE values (data not shown). For the DSP, the worst fit was found with the exponential model. Even for models with relatively poor approximations (exponential, Khrgian-Mazin, and Chen's empirical), the adjusted R ² values were mostly greater than 0.8, better than those in the Horiba and Malvern cases. For the Coulter, no PSD models provided excellent approximations as the mean adjusted R ² values were all smaller than 0.9. The lognormal and gamma distribution models provided the relatively best fits, followed by the exponential model, whereas a poor approximation was found with the Weibull distribution, Khrgian-Mazin, and Chen's empirical models.

Figure 2. Box plots of adjusted R ² values calculated from six different particle size distribution (PSD) models: L = lognormal, W = Weibull, G = Gamma, E = exponential, K = Khrgian-Mazin, and C = Chen's empirical models. PSD data from all five types of animal buildings were combined for comparison.

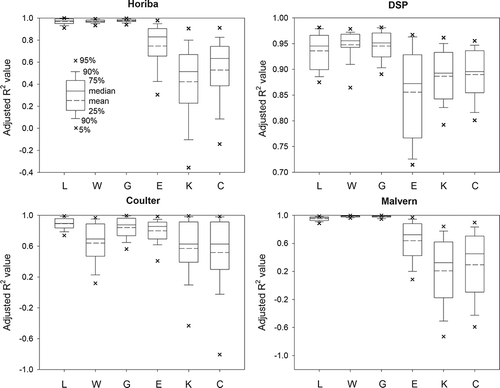
Figure 3. Box plots of Akaike's information criterion (AIC) values derived from six different particle size distribution (PSD) models: L = lognormal, W = Weibull, G = Gamma, E = exponential, K = Khrgian-Mazin, and C = Chen's empirical models. PSD data from all five types of animal buildings were combined for comparison.

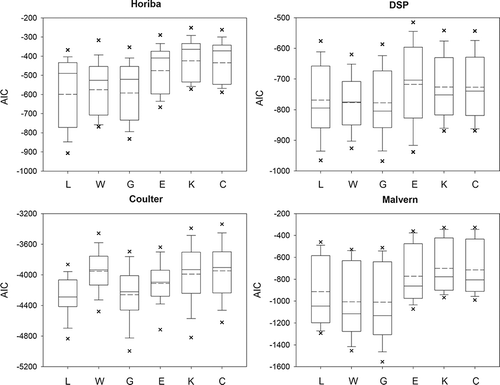
The significant effect of PSD models on adjusted R ² values was affirmed by the repeated-measures one-way ANOVA results (P < 0.001). Following that, a Tukey's test was used for pairwise comparisons of the mean adjusted R ² values generated by different PSD models (Table 3). Results showed that the gamma and lognormal distribution models offered the overall best fits, followed by the Weibull distribution model. Comparatively, single-variable models, including the exponential, Khrgian-Mazin, and Chen's empirical models, produced relatively poor fits to measured PSD data. The same results were obtained from the Tukey's test on AIC and MSE values.

Table 3. Summary of adjusted R ² values produced by different particle size distribution models (average ± standard deviation) ^{† ‡}

Model	Horiba	DSP	Coulter	Malvern
Lognormal	0.968 ± 0.028^a	0.936 ± 0.036^a	0.891 ± 0.076^a	0.951 ± 0.032^a
Weibull	0.968 ± 0.023^a	0.948 ± 0.032^a	0.640 ± 0.271^b	0.985 ± 0.011^a
Exponential	0.747 ± 0.251^b	0.856 ± 0.087^c	0.799 ± 0.170^a	0.638 ± 0.274^b
Khrgian-Mazin	0.423 ± 0.393^d	0.887 ± 0.059^b	0.568 ± 0.410^bc	0.210 ± 0.483^c
Chen's empirical	0.528 ± 0.336^c	0.890 ± 0.052^b	0.517 ± 0.481^c	0.293 ± 0.476^c
Gamma	0.975 ± 0.025^a	0.945 ± 0.030^a	0.840 ± 0.139^a	0.982 ± 0.017^a
Notes: ^†Best-fit models were highlighted in gray.
^‡Within the same column, R ^2 values labeled with same letter were not significantly different (Tukey's test, α = 0.05).

Nearly 70% of measured PSD profiles in this study had only one major peak. For describing the geometry of a peak, at least three basic characteristics need to be addressed: peak position, height, and width. Because in many cases the measured PSD data have been normalized by instruments, for example, with number or volume frequencies presented in the form of percentage, the height and width of a PSD peak are interdependent. A “good” PSD model, therefore, should theoretically have at least two independent variables. However, the exponential, Khrgian-Mazin, and Chen's empirical models have only one independent variable that to a larger extent relates to the peak position but to a lower extent pertains to the peak height and width (Figure 4). Because the peak height and width are relatively constant and less adjustable in these three models, the approximated PSD profiles can be very different from the measured profiles, leading to low adjusted R ² values even less than zero in some extreme PSD cases (Figure 5). Considering such a limitation, these single-variable PSD models are not recommended for modeling the size distribution of PM from animal buildings in future research. Instead, the gamma, lognormal, and Weibull distribution models are recommended. This is not only because these two-variable models provide superior goodness-of-fit but also for the reason that they deliver well-defined mathematical forms to PSD parameters such as mean, median, mode, variance, skewness, and kurtosis (Table 4) so that further discussions on size-dependent PM properties can be greatly simplified.

Table 4. Properties of the lognormal, Weibull, and gamma distribution models ^†

	Lognormal	Weibull	Gamma
Mean
Median			No simple form
Mode
Variance
Skewness
Kurtosis
Note: ^†Relevant equations were compiled from multiple textbooks and double-checked by the authors.

Figure 4. Particle size distribution (PSD) curves predicted by single-variable models with different variable values.

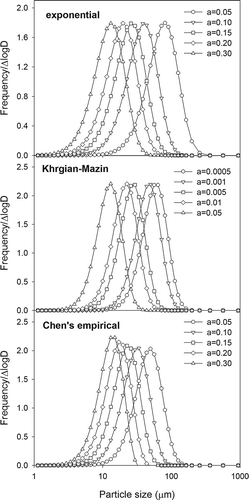
Figure 5. Comparison of a measured particle size distribution (PSD) to its corresponding regression curves generated by the exponential (R ² = −0.537), Khrgian-Mazin (R ² = −1.318), and Chen's empirical models (R ² = −1.063). It is important to note that the presented PSD presented an extreme case and was not typical.

It should be noted that both the exponential and Khrgian-Mazin models are actually special cases of the gamma distribution model that can also be presented as n(x)= N ₀  x ^a e^−bx (Liu and Liu, 1994). This explains why the gamma distribution model always offered better fits than the exponential and Khrgian-Mazin models.

As mentioned previously, the goodness-of-fit of a PSD model is greatly dependent on the geometry of measured PSD profiles, which is affected by the detection principle of selected particle size analyzers. Both the Horiba and Malvern are based on Mie scattering principles. The good and poorly fitting PSD models as well as their order of superiority were found to be similar for those two analyzers (Table 3). From observation, both analyzers tended to produce PSD profiles with a left-skewed major peak. This geometry is better described by the Weibull and gamma distribution models (Figure 1), which accordingly offered superior goodness-of-fit. Noticeably, a slight difference in modeling results still existed between these two analyzers (Tables 3 and 5), probably in part because of their differences in settings of detection channels (size ranges), solvents used for particle extraction, sample dispersion and delivering systems, and data processing algorithms. These minor factors could also affect the geometry of measured PSDs. The DSP measures the aerodynamic size distribution of particles by determining their inertias in high-velocity airflow. It utilizes a time-of-flight detection principle, which is significantly different than those adopted by the Horiba, Malvern, and Coulter. The Coulter measures the equivalent volume diameter of particles by tracking a particle-induced, size-specific change in electrical impendence in a liquid suspension. Thus, it is not surprising to find that the good and poorly fitting PSD models for the Coulter were different than those for the DSP as well as the Horiba and Malvern.

Table 5. Best-fit particle size distribution models varying with particle size analyzer and animal building type

Animal	Building Type	Horiba	DSP	Coulter	Malvern
Swine	Farrowing	Gamma	Weibull	Lognormal	Gamma
	Gestation	Gamma	Weibull	Lognormal	Weibull
	Finishing	Gamma	Gamma	Lognormal	Gamma
Poultry	Laying hen	Lognormal	Lognormal	Gamma	Weibull
	Tom turkey	Weibull	Gamma	Lognormal	Weibull

Chen et al. (1995) compared four PSD models (lognormal, Weibull, power law, and Chen's empirical) with a total of 25 swine building PM samples and reported that the Chen's empirical model they proposed produced the best fit. However, their PSD data were of number-based distribution and therefore had substantially different distribution profiles than the volume-based distribution data used in this study. Moreover, an aerodynamic particle counter (APC) was used in their study. The use of a different particle size analyzer and different PSD data sets could be a reason why different conclusions were drawn from their study.

Which PSD model should be trusted for parameter estimation? The model with the best goodness-of-fit would be an apparently logical choice. However, the “best-fit models” suggested by the adjusted R ², AIC, and MSE can occasionally be slightly different. For simplicity, we selected the adjusted R ² value as a single criterion to provide a quantitative ranking of different PSD models because of a wide recognition of this goodness-of-fit measure. Thus, the PSD model with the highest average R ² value would be recommended as the best-fit model for estimating the PSD parameters.

The best-fit PSD model was found to vary with particle size analyzer as well as animal building type as shown in Table 5. This is understandable because many building configuration–related factors, such as ventilation rate and animal density, may affect PM formation, suspension, and transport in animal buildings and ultimately influence the size and shape of PM. To further assess the influence of particle size analyzer and animal building type, an ordinal logistic generalized linear model (done with SPSS 17.0; SPSS, Chicago, IL) was built with animal building type and particle size analyzer as the predictors and the best-fit model for each measured PSD as the response variable. Results showed that particle size analyzer significantly (P = 0.024) affected the selected best-fit model, whereas animal building type did not have a significant effect (P = 0.077). Thus, for simplicity, the following analysis would be conducted on the data combined from all buildings.

Since the lognormal, Weibull, and gamma distribution models generated relatively good fits for measured PSD profiles, we further examined and compared regression coefficients and PSD parameters predicted by these three models (Table 6). Results showed that the model-predicted mean and median diameters were all greater than 10 μm, which indicates that PM from animal buildings contains a great portion of large particles. Similar findings were reported from previous investigations (Donham et al., 1986; Heber et al., 1988; Jerez et al., 2011; Maghirang et al., 1997; Redwine et al., 2002). The ordinary one-way ANOVA/Tukey's test revealed that for each PSD model, significant differences in mean and median diameters were present between the Horiba and Malvern (or DSP or Coulter) and between the Malvern and Coulter. Among these four analyzers, the Horiba produced the largest mean and median diameters, followed by the Malvern, whereas the smallest mean and median diameters were produced from the Coulter. The Horiba and Malvern, both relying on Mie scattering, produced significantly larger variances (wider peaks) than the DSP and Coulter.

Table 6. Regression coefficients and key parameters of lognormal, Weibull, and gamma distribution models (average ± standard deviation)

Model	Parameter	Horiba	DSP	Coulter	Malvern
Lognormal	VMD	26.1 ± 11.5	17.0 ± 2.2	13.5 ± 2.0	18.8 ± 6.5
	GSD (σg)	2.14 ± 0.37	1.51 ± 0.15	1.74 ± 0.14	2.21 ± 0.28
	Mean	30.2 ± 16.8	17.7 ± 2.3	14.4 ± 2.0	21.4 ± 6.7
	Median	26.1 ± 11.5	17.0 ± 2.2	13.5 ± 2.0	18.8 ± 6.5
	Variance	650.7 ± 2512.6	26.4 ± 16.9	29.4 ± 10.7	139.5 ± 67.0
Weibull	λ	31.2 ± 16.1	18.6 ± 2.5	16.3 ± 1.9	22.4 ± 6.8
	k	1.49 ± 0.26	2.90 ± 0.70	2.43 ± 0.23	1.44 ± 0.21
	Mean	28.9 ± 17.2	16.6 ± 2.2	14.5 ± 1.7	20.4 ± 5.8
	Median	23.8 ± 10.5	16.2 ± 2.0	14.0 ± 1.6	17.4 ± 5.8
	Variance	907.8 ± 2979.0	47.1 ± 28.9	41.8 ± 12.9	214.4 ± 91.2
Gamma	a	2.12 ± 0.67	7.29 ± 3.22	4.30 ± 0.97	1.93 ± 0.54
	b	18.1 ± 22.3	2.99 ± 1.52	3.58 ± 0.81	11.3 ± 2.5
	Mean	30.1 ± 16.7	17.6 ± 2.3	14.8 ± 1.9	21.3 ± 6.4
	Median ^†	24.4 ± 10.4	16.7 ± 2.1	13.6 ± 1.8	17.7 ± 6.0
	Variance	897.4 ± 2727.7	54.5 ± 33.3	53.6 ± 17.4	248.4 ± 113.1
Directly from PSD	Mean	32.2 ± 16.4	17.1 ± 3.0	14.1 ± 1.8	20.2 ± 5.0
	Median	24.7 ± 10.1	16.4 ± 2.3	12.9 ± 2.0	17.3 ± 5.4
	Variance	1056.6 ± 2112.9	55.3 ± 40.1	55.7 ± 13.0	231.4 ± 84.6
Note: ^†The median diameter of gamma distribution is calculated with a function of gammainv in MS EXCEL.

The repeated-measures one-way ANOVA/Tukey's test was performed to compare the mean diameters, median diameters, and variances predicted by the lognormal, Weibull, and gamma distribution models. Results showed that for the Horiba, Malvern, and DSP, the lognormal distribution model predicted significantly larger median diameters and significantly lower variances (narrower peaks) than the Weibull and gamma distribution models, whereas the mean diameters predicted by the Weibull distribution model were significantly smaller than those by the lognormal and gamma distribution models. However, different results were obtained for the Coulter: the lognormal distribution model predicted the lowest mean and median diameters and also the smallest variances, whereas the Weibull distribution model predicted significantly lower variances but significantly larger median diameters than the gamma distribution model. A possible explanation is that the Coulter employs a unique detection principle (i.e., electrical impedance) and, thus, may produce PSD profiles with distinctly different geometry than other three analyzers. From observation, the Coulter tended to produce a noisy and strongly distorted PSD peak, which is rarely seen on PSD profiles measured by other analyzers. It is noteworthy that the Weibull distribution model, although with two independent variables, was a very poor fit with PSD data from the Coulter (Table 3) and, thus, should not be applied to Coulter data for parameter estimation in practice.

However, the best-fit PSD model did not necessarily offer accurate estimates of PSD parameters. The repeated-measures one-way ANOVA/Dunnett's test results (Table 7) revealed that the measured mean diameters, median diameters, and variances were, in most cases, significantly different from those predicted by the lognormal, Weibull, and gamma distribution models. An exception is for PSD data from the Malvern, the Weibull distribution also the best-fit model offered fairly good estimates with no significant difference than measured PSD parameters. It is noteworthy that although a significant difference could exist between model-predicted and measured PSD parameters, the best-fit PSD model selected based on the adjusted R ² still offered the overall best prediction for mean and median diameters, but not for variances. The overall best predictions of variances, however, were made by the gamma distribution model, with no significant difference than measured ones for all selected particle size analyzers.

Table 7. Comparison of model-predicted to measured mean diameters, median diameters, and variances ^†

		Horiba		DSP		Coulter		Malvern
Model ^‡	Parameter	R.E. (%) ^#	P < 0.05?	R.E. (%)	P < 0.05?	R.E. (%)	P < 0.05?	R.E. (%)	P < 0.05?
L–M	Mean	−6.1 ± 8.8	Yes	4.1 ± 7.1	Yes	2.1 ± 2.8	Yes	4.4 ± 8.0	Yes
	Median	4.9 ± 4.4	Yes	3.7 ± 2.6	Yes	4.4 ± 1.8	Yes	7.6 ± 4.3	Yes
	Variance	−61.2 ± 17.6	Yes	−48.1 ± 13.4	Yes	−48.1 ± 9.1	Yes	−39.3 ± 16.3	Yes
W–M	Mean	−10.9 ± 7.5	Yes	−2.4 ± 6.4	Yes	3.1 ± 5.5	Yes	0.2 ± 5.4	No
	Median	−4.0 ± 3.1	Yes	−1.1 ± 2.8	Yes	9.3 ± 7.0	Yes	0.0 ± 2.8	No
	Variance	−38.2 ± 21.2	No	−7.2 ± 18.5	Yes	−25.5 ± 9.4	Yes	−6.1 ± 20.1	No
G–M	Mean	−6.4 ± 8.0	Yes	3.8 ± 6.8	Yes	5.0 ± 3.8	Yes	4.5 ± 6.4	Yes
	Median	−1.5 ± 3.2	Yes	1.5 ± 2.7	Yes	5.7 ± 4.1	Yes	1.6 ± 3.2	Yes
	Variance	−30.2 ± 21.4	No	8.1 ± 24.8	No	−4.9 ± 12.3	No	7.9 ± 24.4	No
Notes: ^†Best-fit models were highlighted in gray.
^‡M = measured; L = lognormal; W = Weibull; and G = gamma. L–M refers to a comparison of the lognormal distribution model–predicted parameters to the measured values. The difference is significant when the P value is smaller than 0.05.
^#R.E. refers to the relative error in comparison to measured parameters.

It was also found that if we stick with the lognormal distribution model, the resulting PSD parameters would poorly represent data from the Horiba, DSP, and Malvern analyzers. Specifically in this study, the lognormal distribution model overall overestimated median diameters by 6.3% ± 2.3% but underestimated variances by 42.6% ± 7.2% compared with the best-fit models for those three analyzers.

By combining model comparison results in Tables 3 and 7, we suggest using the gamma distribution model for processing PSD data from the Horiba, the Weibull distribution model for the DSP and the Malvern, and the lognormal distribution model for the Coulter data. However, it should be recognized that the recommended PSD models may not be readily applicable to future investigations on PM from animal buildings where the animal species, building type, PM sampler, and sampling point are different. Nevertheless, a key point raised from in this study is that the goodness-of-fit of a PSD model must be evaluated and compared with that of other models before using it for estimating PSD parameters. A default use of the lognormal distribution model can be inappropriate without any evaluation of the goodness-of-fit as determined by the adjusted R ², AIC, or MSE values; other PSD models, such as the gamma and Weibull distribution models, may deliver better approximations to measured data and, thus, be considered as alternative modeling options.

It is also important to note that the uncertainties associated with PSD measurements may influence the PSD modeling results. For the DSP, the sampling efficiency of the up-facing sampling inlet, the deposition of large particles, the dilution ratio, and the misread of “phantom” particles by the sensing unit could all affect the geometry of measured PSDs. For filter-based methods such as the Horiba, Coulter, and Malvern, the low sampling efficiency of particle samplers, the gas/particle partitioning, the deformation of particles on filters, the deposition, dissolution, and agglomeration of particles in liquid media, the wrongly selected refractive index, and the improper setting of detection modes could all cause errors and/or bias to PSD test results. Extraordinary efforts should be made to develop and validate a standard test protocol for PSD measurements based upon a consideration of potential uncertainty sources, and to strictly follow the test protocol in every experiment to provide solid and reliable data for PSD modeling.

Conclusion

Six PSD models were evaluated for their ability to approximate 217 measured PSD profiles from PM samples collected at 15 animal buildings. The best-fit models were found to differ with particle size analyzer and, to a less degree, with animal building type. The gamma and lognormal distribution models offered the overall best fits, followed by the Weibull distribution model. Single-variable models, including the exponential, Khrgian-Mazin, and Chen's empirical models, produced relatively poor fits, and, thus, are not recommended for future research on PM from animal buildings. PSD parameters including mean diameter, median diameter, and variance predicted by different models could be significantly different from one another and also different from those calculated directly from individual PSD profiles. The best-fit model, selected based on the highest adjusted R ² values, offered better estimates of mean and media diameter, whereas the gamma distribution model provided the least error in predicted variances. Based on our preliminary results, this study suggests that the gamma distribution model is overall best for the Horiba PSD data, the Weibull distribution model is overall best for the Malvern and DSP data, and the lognormal distribution model is overall best for the Coulter data. This study also illustrates the importance of evaluating and comparing the goodness-of-fit in terms of R ², AIC, and MSE values for PSD models before applying them to PSD parameter estimation. A default use of the prevalent lognormal distribution model, instead, could lead to substantial errors in estimates of PSD parameters.

Acknowledgments

This work was supported by USDA NRI competitive grants (Award No. 2006‐35112‐16671 and 2007‐55112‐17851). The authors thank to Dr. William B. Faulkner, Mr. Dustin Dean, Dr. Bryan W. Shaw, and Dr. Gary L. Riskowski at the Texas A&M University for helping on Coulter and Malvern PSD measurements, and to Dr. Richard S. Gates at the University of Illinois for discussions on data analysis.