A coupled factorial-analysis-based interval programming approach and its application to air quality management

Abstract

In this study, a coupled factorial-analysis-based interval programming (CFA-IP) approach is developed through incorporating factorial analysis within an interval-parameter linear programming framework. CFA-IP can tackle uncertainties presented as intervals that exist in the objective function and the left- and right-hand sides of constraints, as well as robustly reflect interval information in the solutions for the objective-function value and decision variables. Moreover, CFA-IP has the advantage of investigating the potential interactions among input parameters and their influences on lower- and upper-bound solutions, which is meaningful for supporting an in-depth analysis of uncertainty. A regional air quality management problem is studied to demonstrate applicability of the proposed CFA-IP approach. The results indicate that useful solutions have been generated for planning the air quality management practices. They can help decision makers identify desired pollution mitigation strategies with minimized total cost and maximized environmental efficiency, as well as screen out dominant parameters and explore the valuable information that may be veiled beneath their interrelationships.

Implications:

The CFA-IP approach can not only tackle uncertainties presented as intervals that exist in the objective function and the left- and right-hand sides of constraints, but also investigate their interactive effects on model outputs, which is meaningful for supporting an in-depth analysis of uncertainty. Thus CFA-IP would be applicable to air quality management problems under uncertainty. The results obtained from CFA-IP can help decision makers identify desired pollution mitigation strategies, as well as investigate the potential interactions among factors and analyze their consequent effects on modeling results.

Introduction

In recent years, regional air pollution continues to pose a significant threat to human health worldwide. The World Health Organization (WHO) states that approximately 2 million premature deaths each year can be directly attributed to the effects of air pollution. More than half of this disease burden is borne by people in developing countries (WHO, 2005). Therefore, control measures need to be taken to mitigate air pollution. However, an air pollution control system involves many components, such as pollutant emission standards, pollutant treatment efficiencies of different control techniques, and environmental loading capacities; these components may be associated with uncertainties. Advanced optimization methods are thus desired for supporting air quality management and pollution control planning under uncertainty.

Over the past decades, a number of inexact optimization methods have been developed for dealing with uncertainties in air quality control systems (An and Eheart, 2007; Cao et al., 2011; Ellis et al., 1985, 1986; Li et al., 2006; Lu et al., 2010a; Qin et al., 2010). Among them, the interval linear programming (ILP) approach proposed by Huang et al. (1992) is effective and efficient in tackling uncertainties for the following reasons: (1) ILP does not require distributional information for input parameters, which can be difficult to specify in practical applications; (2) ILP problems can be solved through a two-step method (TSM) with low computational requirements; and (3) ILP incorporates interval numbers into the optimization process and generates interval solutions, which reflects inherent system uncertainties and is convenient for decision makers to interpret and adjust decision schemes according to practical situations.

Accordingly, a number of ILP methods were proposed for dealing with uncertainties in environmental management systems (Huang, 1998; Li and Huang, 2010; Lu et al., 2010b; Luo et al., 2005; Qin et al., 2007; Wang et al., 2012; Wang and Huang, 2011). Nevertheless, the main limitation of ILP is its solution method that TSM may result in a potential violation of the best-case constraints when decision variables vary within the generated decision space. Recently, Fan and Huang (2012) developed a robust two-step method (RTSM) to solve the ILP problems, which improved upon TSM through incorporating additional constraints into solution procedures. Such a method can guarantee no violation of the best-case constraints when decision variables fluctuate within the solution space obtained through RTSM. However, all of these ILP methods can hardly reveal the effects of uncertainties on system performance, even though they are capable of tackling uncertainties that exist in the objective function and constraints. In fact, input parameters interact with each other; they have different effects on model outputs. Thus, the joint effects of parameters should not be neglected or underestimated in practical applications.

Previously, factorial analysis was widely used to reveal the potential interrelationships among a variety of uncertain parameters and their impacts on system performance. Maqsood et al. (2003) conducted a set of 2⁴ factorial experiments for quantitatively analyzing the individual and combined effects of four uncertain input parameters on modeling outputs; for each factorial experiment, a 100-run Monte Carlo simulation was undertaken through a multiphase compositional simulator. Lin et al. (2008) proposed a simulation-aided two-level factorial analysis approach for characterizing the interactive effects of composting factors on composting processes; findings could be useful in guiding the composting-process operation and developing associated control strategies in different composting stages, because the factors had various effects on the composting process in different stages. Qin et al. (2008) developed a factorial-design-based stochastic modeling system (FSMS) to investigate the impacts of uncertainties associated with hydrocarbon-contamination transport in subsurface. Mabilia et al. (2010) performed an experimental test according to a fractional factorial design with replicated central point, which identified the best configuration for a formaldehyde passive sampler by statistically evaluating the significance of effects of the concerned factors and their interactions. Onsekizoglu et al. (2010) used a two-level factorial experimental design for evaluating the effects of temperature difference between the feed and permeate side of the membrane, concentration of the osmotic agent, and flow rate. Zhou and Huang (2011) proposed a factorial two-stage stochastic programming (FTSP) approach for supporting water resources management under uncertainty; a fractional factorial design was conducted to identify the individual and joint effects of nine uncertain parameters on net system benefit. Previous studies mainly focused on the investigation of effects of factors, but barely incorporated uncertainties into the modeling process. It is thus desired to tackle uncertainties and investigate their effects in a systematic manner.

The objective of this study is to develop a coupled factorial-analysis-based interval programming (CFA-IP) approach through incorporating factorial analysis within an interval-parameter linear programming framework. CFA-IP can not only deal with uncertainties presented as intervals that exist in the objective function and the left- and right-hand sides of constraints, but also investigate their potential effects on model outputs. Then the proposed CFA-IP approach will be applied to a regional air quality management problem for demonstrating its applicability. Results will help decision makers identify desired pollution mitigation strategies and conduct an in-depth analysis of uncertainty.

Methodology

Interval-parameter linear programming

According to Huang (1998), an interval-parameter linear programming (ILP) model can be defined as follows:

(1a)

subject to

(1b)

(1c)

where , , , , and R denotes a set of interval numbers; , , , and . An interval number is defined as a range with known lower and upper bounds (Huang, 1996): , where and are the lower and upper bounds of , respectively.

To solve model (1), RTSM can be adopted to convert the ILP problem into two submodels that correspond to the lower and upper bounds of the objective-function value (Fan and Huang, 2012). Because the objective function is to be minimized, the submodel corresponding to can be first formulated as follows (assume that > 0 and > 0):

(2a)

subject to

(2b)

(2c)

(2d)

where ≥ 0 (j = 1, 2, …, k) and ≤ 0 (j = k + 1, k + 2, …, n); solutions of (j = 1, 2, …, k) and (j = k + 1, k + 2, …, n) can be obtained through solving submodel (2). Based on the solutions of submodel (2), the submodel corresponding to can be formulated as follows (assume that > 0 and > 0):

(3a)

subject to

(3b)

(3d)

(3e)

(3f)

(3g)

where ≥ 0 (j = 1, 2, …, l_{i 1}; j = l_{i 2} + 1, l_{i 2} + 2, …, n) and ≤ 0 ( j = l_{i 1} + 1, l_{i 1} + 2, …, l_{i 2}), where l_{i 1} ≤ k, and l_{i 2} ≥ k. Thus, solutions of ( j = 1, 2, …, k) and ( j = k +1, k + 2, …, n) can be generated through submodel (3). By combining the solutions from two submodels, the final solutions for model (1) can be obtained as follows:

ILP is effective in tacking uncertainties presented as intervals that exist in the objective function and the left- and right-hand sides of constraints. In practical applications, importance of parameters is different in the decision-making process. Variations of several parameters may bring about a significant difference in model response, whereas some others may have no effect at all. It is thus necessary to investigate their effects on model outputs. Conventional sensitivity analysis can be performed to examine the effects of changes in a single parameter over its range with the other parameters held constant. Such a one-parameter-at-a-time strategy only reveals the single effects of parameters, but fails to reflect any possible interaction among parameters. In fact, joint effects exist among many parameters and they may have a considerable influence on model outputs. Moreover, valuable information may be veiled beneath the interrelationships among parameters and their consequent effects. Therefore, it is desired to investigate the interactive effects of parameters and then explore their hidden information.

Factorial analysis

Factorial analysis, a multivariate inference method, can thus be introduced to reveal the potential interrelationships among a variety of uncertain parameters and their impacts on system performance (Box et al., 1978). The most important case of factorial analysis is the 2 ^k factorial design, which consists of k factors, with each at two levels. The statistical model for a complete 2 ^k design would include 2 ^k  − 1 effects that comprise k main effects, two-factor interactions, three-factor interactions, … , and one k-factor interaction (Montgomery, 2001). The treatment combinations for a 2 ^k factorial design can be written in standard order (or Yates’ order) by introducing one at a time, with each new factor being successively combined with those that precede it (Box et al., 1978). For example, the standard order for a 2⁴ design is (1), a, b, ab, c, ac, bc, abc, d, ad, bd, abd, cd, acd, bcd, and abcd, where (1) denotes all factors at their low levels, ab denotes factors A and B at their high levels and factors C and D at their low levels, and abc denotes factors A, B, and C at their high levels and factor D at its low level. This reveals that the high level of a factor is represented by the corresponding lowercase letter and the low level of a factor is denoted by the absence of the corresponding letter in the treatment combination. To estimate an effect or to compute the sum of squares for an effect, the contrast associated with that effect needs to be determined by expanding the right-hand side of

(4)

where “1” needs to be replaced by (1) when expanding eq (4). The sign in each set of parentheses is negative if the factor is included in the effect and positive if the factor is not included. Once the contrasts for the effects are determined, the effects and the sum of squares can be estimated according to

(5)

and

(6)

where is the single or joint effects of factors; is the sum of squares for the effects; and n denotes the number of replicates.

A 2 ^k factorial design requires 2 × 2 × ··· × 2 = 2 ^k runs. As the number of factors in a 2 ^k factorial design increases, the number of runs required for a complete design increases exponentially, resulting in a great computational burden. In fact, most systems are dominated by the main effects and low-order interactions, and most high-order interactions are negligible (Montgomery, 2001). Therefore, fractional factorial design can be introduced to expose the information on the main effects and low-order interactions by running only a fraction of the runs of the full factorial design. A 2 ^k fractional factorial design containing runs is called a fractional factorial design, which requires the selection of p independent generators based on a criterion that the best possible alias relationships can be obtained (Montgomery, 2001). In other words, care should be taken to ensure that the effects of potential interest are not aliased with each other when choosing the generators. The alias structure can be obtained by multiplying each effect column by the defining relation that consists of the initially chosen p generators and their − p − 1 generalized interactions (Box et al., 1978; Montgomery, 2001). For example, consider a fractional factorial design, where C = AB and I = ABC are used as design generator and defining relation, respectively. Then the aliases can be obtained by multiplying A, B, and C by I = ABC, that is, A × I = A × ABC = A ² BC, B × I = B × ABC = AB² C, and C × I = C × ABC = ABC ². The aliases of A, B, and C are generated as A = BC, B = AC, and C = AB, because the square of any column is the identity I. In fact, it is impossible to differentiate the effects between A and BC, B and AC, and C and AB. Such a design would be of resolution III. The concept of design resolution is a useful way to catalog fractional factorial designs according to their alias patterns. Designs of resolutions III, IV, and V are particular important and their definitions are given as follows (Montgomery, 2001):

	Definition 1. Resolution III designs have no main effect aliased  with any other main effect, but main effects are aliased with two-factor interactions and two-factor interactions may be aliased with each other.
	Definition 2. Resolution IV designs have no main effect aliased  with any other main effect or with any two-factor interaction, but two-factor interactions are aliased with each other.
	Definition 3. Resolution V designs have no main effect or two-  factor interaction aliased with any other main effect or two-factor interaction, but two-factor interactions are aliased with three-factor interactions.

In the fractional factorial design, the effects and the sum of squares can be estimated according to the following equations (Montgomery, 2001):

(7)

and

(8)

where is the ith effect; Contrast _i associated with the ith effect is calculated using the plus and minus signs in column i of Yates’ order table; is the sum of squares for the ith effect.

Coupled factorial-analysis-based interval programming

To tackle uncertainties presented as intervals and explore their effects on model outputs, factorial analysis can be incorporated within the interval-parameter linear programming framework. This leads to a coupled factorial-analysis-based interval programming (CFA-IP) model as follows:

(9 \textrm a)

subject to

(9 \textrm b)

(9 \textrm c)

(9 \textrm d)

where , , and are interval parameters; and are the concerned factors expressed as intervals with known lower and upper bounds corresponding to the low and high levels in factorial analysis; r is the number of constraints with interval parameters; t is the number of constraints involving the factors of interest; and m is the total number of constraints.

Model (9) can be solved in two phases: (1) the aforementioned RTSM can be adopted to convert the ILP problem into two submodels that correspond to the lower and upper bounds of the objective-function value; and (2) factorial analysis can then be performed to investigate the effects of the concerned factors for each of two submodels. The detailed solution processes for the CFA-IP model can be described as follows:

	Step 1: Formulate the CFA-IP model.
	Step 2: Transform the CFA-IP model into two submodels, where the upper-bound submodel corresponding to is first desired because the objective is to minimize .
	Step 3: Obtain a set of solutions through solving the submodel.
	Step 4: Formulate and solve the lower-bound submodel corresponding to based on the solutions from submodel.
	Step 5: Integrate the solutions from two submodels, the ultimate solutions for the CFA-IP model can be obtained: and .
	Step 6: Choose several uncertain parameters as the factors of interest.
	Step 7: Conduct factorial analysis associated with the concerned factors for each of the two submodels.
	Step 8: Identify the effects of factors for and submodels, respectively.
	Step 9: Stop.

Application to Air Quality Management

Statement of problems

Air pollution involves a series of events related to sources, atmosphere, and receptors, such as pollutant emission, pollutant transport, and dilution in the atmosphere, as well as adverse effects on human, materials, and environment (Flagan and Seinfeld, 1988). Over the past decade, air pollution control has been an issue of substantial concern due to the increasing deterioration of ambient air quality that has caused harmful effects on human health, property (e.g., animals, vegetation, materials), and visibility (Li et al., 2010). An air pollution control system is associated with a number of factors, such as properties of pollutants, locations of sources and receptors, meteorological conditions, and control measures. Generally, an air pollution control problem can be characterized by one or several sources that generate harmful effects on receptors, whereas various pollution control techniques can be installed by different sources for controlling air pollutant emissions. Because it is economically infeasible or technically impossible to design processes with zero emission of air pollutants, local authorities and decision makers always seek to control the emissions to meet the environmental standards and meanwhile minimize the total cost of control measures (Liu et al., 2003). Therefore, it is desired to identify the cost-effective air pollution control strategies while satisfying the environmental standards.

In the air pollution control system, uncertainties exist in a variety of system components, such as air pollutant emission standards, efficiencies of different pollution control techniques, and environmental loading capacities. They may be given as interval values instead of deterministic values. For example, the sulfur dioxide (SO₂)-emission standard for power plant can be specified within the range from 39.2 to 44.2 tonnes per day; the SO₂-treatment efficiency of the oxidation packed absorption (OPA) technique can fluctuate between 78% and 88% due to different operating conditions (e.g., temperature and SO₂ concentration); the SO₂-loading capacity for agricultural zone can be regulated within the range from 27.2 to 31.2 μg/m³. Uncertainty is inherent in future-oriented planning efforts; it stems from a variety of sources, including inadequate information and imperfect knowledge of the values of parameters associated with pollution mitigation processes, as well as from the variability of natural processes. It is thus desired to develop advanced optimization methods for supporting air pollution control planning under uncertainty. Moreover, system components are not independent of each other; instead, they interact in various ways and have different effects on system performance. Decision makers may want to focus on the significant interactions and ignore those unimportant ones, which is an efficient and effective strategy in the decision-making process. Therefore, the proposed CFA-IP approach is appropriate for not only tackling uncertainties presented as interval numbers in the decision-making process, but also exploring their effects on system performance.

Overview of the study system

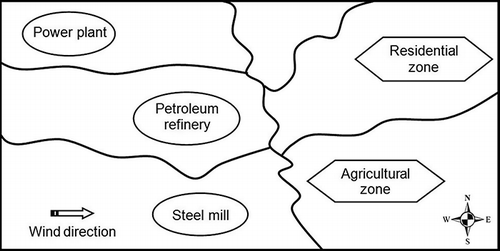
In the study system, SO₂ is the air pollutant of potential concern. According to the air pollutant emissions data for the year 2009 in Canada (Environment Canada, 2011), industrial sources emitted 64% of the total SO₂ emissions (approximately 1.4 million tonnes). The largest proportion of SO₂ emissions came from fuel for electricity, accounting for 29% of total emissions; the second largest proportion was from petroleum refinery, representing 27% of total emissions. One power plant, one petroleum refinery, and one steel mill are thus considered as the major SO₂ emission sources. Two receptors, including one agricultural zone and one residential zone, are adversely affected by the emitted SO₂ from the three sources (Figure 1). The planning horizon is 15 yr (with three 5-yr periods). From a long-term planning point of view, economic development within the region will cause an increased demand for fossil fuels, resulting in continuous increase in SO₂ generations at each source. However, the environmental quality must be controlled to satisfy the air pollution regulations. Table 1 shows the SO₂-generation rates, as well as the uncertain SO₂-emission allowances and SO₂-loading levels expressed as intervals over the planning horizon. To meet the environmental requirements, each emission source has to install various control measures to mitigate the SO₂ emissions. Tables 2 and 3 show the types of SO₂-emission control techniques installed by different sources, as well as their treatment efficiencies presented as intervals and operating costs. The control technique of alkali absorption (AA) has the highest SO₂-removal efficiency associated with a considerable operating cost, whereas limestone wet scrubbing (LWS) has the lowest treatment efficiency related to a reasonable operating cost. It is thus desired to identify the cost-effective pollution control strategies. In this study system, the representative costs and technical data were investigated from governmental reports and other related literatures (Environment Canada, 2011; Flagan and Seinfeld, 1988; Li et al., 2010; Liu et al., 2003).

Table 1. Technical data

Technical Data	Period 1	Period 2	Period 3
SO2-generation rates, Sik (tonne/day)
Power plant	[141.5, 151.5]	[164.5, 174.5]	[199.0, 209.0]
Petroleum refinery	[38.0, 48.0]	[40.3, 50.3]	[42.6, 52.6]
Steel mill	[7.9, 8.5]	[8.2, 8.8]	[8.5, 9.1]
SO2-emission standards, eik (tonne/day)
Power plant	[39.2, 44.2]	[37.7, 42.7]	[36.2, 41.2]
Petroleum refinery	[8.0, 8.6]	[7.5, 8.1]	[7.1, 7.6]
Steel mill	[2.2, 2.5]	[1.7, 2.0]	[1.2, 1.5]
SO2-loading capacities, apk (μg/m^3)
Agricultural zone	[27.2, 31.2]	[25.9, 29.9]	[23.8, 27.8]
Residential zone	[55.0, 65.0]	[46.0, 56.0]	[37.0, 47.0]

Table 2. SO₂-emission control techniques installed by different sources

Source	Control Technique
Power plant	OPA, AA, LWS, SC
Petroleum refinery	OPA, AA, SC
Steel mill	OPA, AA, SC
Notes: OPA = oxidation packed absorption; AA = alkali absorption; LWS = limestone wet scrubbing; SC = spray chamber.

Table 3. SO₂-treatment efficiencies and operating costs of different pollution control techniques

Technique	Efficiency (%)	Period	Operating Cost ($/tonne)
OPA	[78, 88]	k = 1	[40.0, 54.0]
		k = 2	[48.0, 60.0]
		k = 3	[54.2, 70.2]
AA	[89, 99]	k = 1	[60.0, 70.0]
		k = 2	[66.5, 76.5]
		k = 3	[73.6, 83.6]
LWS	[67, 77]	k = 1	[27.0, 37.0]
		k = 2	[31.8, 41.8]
		k = 3	[37.3, 47.3]
SC	[84, 94]	k = 1	[50.0, 60.0]
		k = 2	[58.3, 68.3]
		k = 3	[67.7, 77.7]

Figure 1. The study system.

The Gaussian dispersion model can be used to predict the SO₂ concentrations at each receptor zone under different meteorological conditions. The ground-level concentration at each arbitrary downwind location (x, y) can be estimated as follows (De Nevers, 2000; Haith, 1982):

(10)

where H represents average effective stack height (m); Q denotes pollutant emission rate (mg/sec); is mean wind velocity (m/sec); and and are the dispersion coefficients that respectively represent standard deviations of the plume at y and z directions (m); they depend on wind speed, solar heating, and local turbulence. In this study, and are the functions of both meteorological conditions and downwind distances, and their values can be estimated through the Pasquill-Gifford curves (Pasquill, 1961; Turner, 1970). Table 4 provides the effective stack heights of different sources. Thus, a transfer factor that represents the contributions of unit pollutant emission rate at each emission source to the ground-level concentration at location (x, y) can be estimated by

Table 4. Effective stack heights of different sources

Source	Effective Stack Height (m)
Power plant	282
Petroleum refinery	140
Steel mill	130

(11)

where t_ip represent the contribution of each source (i) to the ground concentration in each receptor zone (p).

Modeling formulation

The problem under consideration focuses on the mitigation of SO₂ emissions from multiple sources through different control measures. The objective is to minimize total operating cost for SO₂ abatement over a planning horizon while satisfying the environmental standards. The decision variables, denoted as , represent the amount of SO₂ generated from source i and allocated to control measure j during period k. The constraints mainly include SO₂-emission standards and SO₂-loading capacities. Thus, we have

(12a)

subject to

(12b)

[Constraints of SO₂ generation]

(12c)

[Constraints of emission standard]

(12d)

[Constraints of environmental loading capacity]

(12e)

[Non-negativity constraints] where i is the name of SO₂ emission source; j is the type of SO₂ control measure; k is the planning period; p is the name of receptor zone; is the length of period k (day); is the operating cost of control measure j during period k ($/tonne); is the amount of SO₂ generated from source i and allocated to control measure j during period k (tonne/day); is the amount of SO₂ generated from source i during period k (tonne/day); is the efficiency of control measure j, which is considered as the concerned factor; is the SO₂-emission standard for source i during period k (tonne/day), which is considered as the concerned factor; t_ip is the transfer factor from emission source i to receptor zone p; and is the SO₂-loading capacity of receptor zone p during period k (μg/m³).

Result analysis

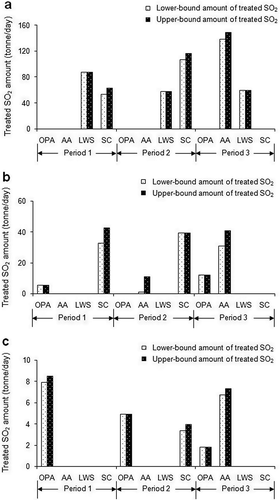
Table 5 shows the solutions obtained from the CFA-IP model. It is indicated most of non-zero decision variables and the objective-function value are expressed as intervals. These interval solutions reflect potential system-condition variations caused by uncertain input parameters and their interactions. The results indicate that the objective-function value would be $[62.10, 82.34] × 10⁶, which provides two extreme values of system cost. The system cost would correspondingly change between $62.10 and $82.34 × 10⁶ through adjusting the values of continuous variables within their lower and upper bounds.

Table 5. Solutions obtained from the CFA-IP model

Source i	Period k	Control Measure j	Treated SO2 Amounts (tonne/day)
Power plant	1	OPA	0
		AA	0
		LWS	88.00
		SC	[53.50, 63.50]
	2	OPA	0
		AA	0
		LWS	57.53
		SC	[106.97, 116.97]
	3	OPA	0
		AA	[138.95, 148.95]
		LWS	60.05
		SC	0
Petroleum refinery	1	OPA	5.33
		AA	0
		LWS	0
		SC	[32.67, 42.67]
	2	OPA	0
		AA	[0.96, 10.96]
		LWS	0
		SC	39.34
	3	OPA	11.95
		AA	[30.65, 40.65]
		LWS	0
		SC	0
Steel mill	1	OPA	[7.90, 8.50]
		AA	0
		LWS	0
		SC	0
	2	OPA	4.87
		AA	0
		LWS	0
		SC	[3.33, 3.93]
	3	OPA	1.81
		AA	[6.69, 7.29]
		LWS	0
		SC	0
Total operating cost ($10^6) [62.10, 82.34]

Figure 2 presents the schemes for mitigating the SO₂ emissions from power plant, petroleum refinery, and steel mill, respectively. For power plant, techniques of limestone wet scrubbing (LWS) and spray chamber (SC) would be adopted for SO₂ abatement during periods 1 and 2. During period 3, however, SC would be replaced by alkali absorption (AA) with a higher efficiency to satisfy the stricter environmental standards; meanwhile, an amount of 60.05 tonne/day would still be treated by LWS due to its lower operating cost. In comparison, the total amounts of SO₂ emission from petroleum refinery would be much lower than those from power plant. For petroleum refinery, a majority of SO₂ emission would be treated by SC, whereas a small amount of 5.33 tonne/day would be allocated to oxidation packed absorption (OPA) during period 1. AA would have to be used for treating an amount of [0.96, 10.96] tonne/day due to the increased strictness on the SO₂ emission and ambient air quality standards during period 2. During period 3, the amount of SO₂ emission treated by AA would become as high as [30.65, 40.65] tonne/day; meanwhile, SC would be replaced by OPA with a lower operating cost. In terms of SO₂ emissions, the total amounts from steel mill would be lowest in comparison with those from power plant and petroleum refinery. For steel mill, OPA would be the only SO₂-abatement measure during period 1, because it has a relatively low treatment cost. SC and AA would have to be adopted during periods 2 and 3, respectively, due to the increasingly stringent environmental standards over the planning horizon. In general, LWS and OPA should be adopted for treating as many as possible amounts of SO₂ emissions from different sources due to their relatively low operating costs. However, when SO₂-generation rates increase and environmental standards become stricter, techniques with high efficiency would be favored. Therefore, AA with the highest efficiency would have to be adopted frequently to satisfy the strictest emission and ambient air quality standards during period 3. Because technique with a higher efficiency is associated with a higher operating cost, a tradeoff exists between removal rate and system cost.

Figure 2. SO₂-abatement schemes for (a) power plant, (b) petroleum refinery, and (c) steel mill.

The proposed CFA-IP approach is capable not only of dealing with uncertainties presented as intervals, but also of exploring their effects on model outputs. In model (12), 13 input parameters (expressed as intervals) related to SO₂-emission standards and efficiencies of SO₂-emission control techniques were considered as the factors of interest, including , , , , , , , , , , , , and . To conduct factorial analysis, they were denoted as A, B, C, D, E, F, G, H, J, K, L, M, and N, respectively. According to CFA-IP, a fractional factorial design of resolution V was performed for two submodels that correspond to the upper- and lower-bound solutions, respectively. Thus, 256 runs were carried out for conducting factorial analysis for each of the two submodels. Such a fractional factorial design of resolution V can expose the information on the main effects and two-factor interactions by running only a fraction of the runs of the full factorial design.

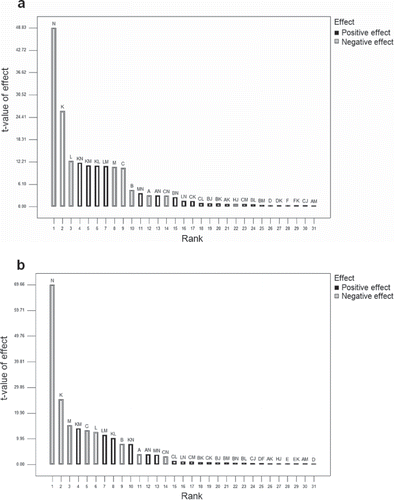
Table 6 provides the effects of significant factors and their interactions for the lower and upper bounds of system cost. It is indicated that seven significant factors, including A, B, C, K, L, M, and N, are identified through the fractional factorial analysis. These factors, which respectively represent the SO₂-emission standards for power plant during periods 1, 2, and 3, as well as the SO₂-treatment efficiencies of the OPA, AA, SC, and LWS techniques, have different main and interactive effects on the lower and upper bounds of system cost. For example, factor N denoting the SO₂-treatment efficiency of LWS has a negative effect of −6.09 and contributes 56.71% to the lower-bound system cost, whereas it has a negative effect of −7.42 and contributes 70.94% to the upper-bound system cost. Factor BN denoting the interaction between SO₂-emission standard for power plant during period 2 and SO₂-treatment efficiency of LWS has a significant influence on the lower bound of system cost, but no effect on its upper bound.

Table 6. Effects of significant factors and their interactions for lower and upper bounds of system cost

	Lower-Bound Solution			Upper-Bound Solution
Factor	Standardized Effects	Sum of Squares	% Contribution	Standardized Effects	Sum of Squares	% Contribution
A: Power plant ESp1	−0.37	8.97	0.21	−0.42	11.17	0.22
B: Power plant ESp2	−0.56	20.25	0.48	−0.85	45.96	0.92
C: Power plant ESp3	−1.31	110.05	2.63	−1.41	126.81	2.55
K: OPA efficiency	−3.25	677.98	16.19	−2.69	464.11	9.33
L: AA efficiency	−1.55	154.18	3.68	−1.34	114.59	2.30
M: SC efficiency	−1.35	117.16	2.80	−1.62	168.10	3.38
N: LWS efficiency	−6.09	2375.25	56.71	−7.42	3527.18	70.94
AN	0.37	8.97	0.21	0.42	11.17	0.22
BN	0.31	6.34	0.15	—	—	—
CN	−0.37	8.75	0.21	−0.34	7.21	0.15
KL	1.39	123.61	2.95	1.09	76.05	1.53
KM	1.40	125.09	2.99	1.49	141.86	2.85
KN	1.49	142.79	3.41	0.84	45.42	0.91
LM	1.38	121.89	2.91	1.22	95.24	1.92
MN	0.45	13.00	0.31	0.40	10.16	0.20
Notes: ESp1, ESp2, and ESp3 are the abbreviations for emission standards during periods 1, 2, and 3, respectively.

Figure 3 shows two Pareto charts of effects for the lower and upper bounds of system cost, in which factor effects are ranked in descending order according to their significant levels. The Pareto charts reveal that the most significant effect is the main (negative) effect of factor N, which implies that the SO₂-treatment efficiency of LWS has the largest influence on both the lower and upper bounds of system cost. This is because the technique of LWS is only available to power plant, which is the largest source of SO₂ emissions; moreover, LWS would be adopted for treating as many as possible amounts of SO₂ emission from power plant due to its relatively low operating cost. Any change in this factor would bring about a considerable variation in system cost. Furthermore, the first three significant factors (i.e., N, K, and L for lower-bound system cost and N, K, and M for upper-bound system cost) are all related to the SO₂-treatment efficiencies of different techniques, which implies that the efficiencies of control techniques play an important role in system performance. The fourth most significant effects that emerge respectively from Figure 3a and b are the interactive (positive) effects of factors KN and KM, which discloses that the SO₂-treatment efficiencies of OPA and LWS have the most significant joint effect on the lower-bound system cost, whereas the interactive effect of the SO₂-treatment efficiencies of OPA and SC appears to be remarkable among all the joint effects for the upper-bound system cost.

Figure 3. Pareto charts of effects for (a) lower-bound system cost and (b) upper-bound system cost.

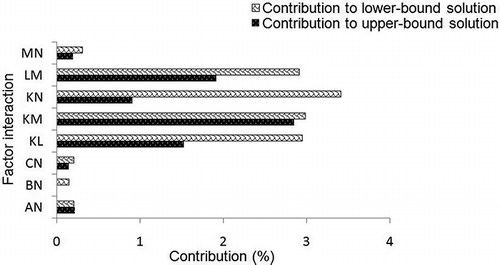
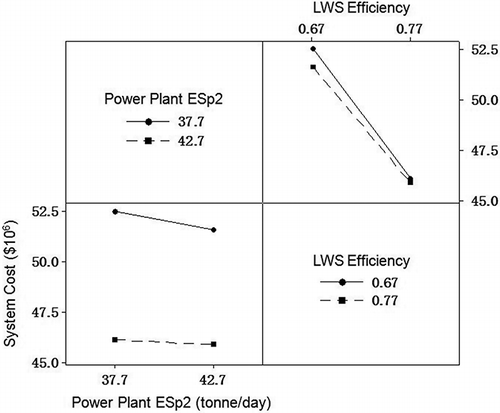
Figure 4 presents the contributions of factor interactions to the lower- and upper-bound system costs. It is indicated that factor interactions contribute differently to the lower and upper bounds of system cost. For example, factor KN has the largest contribution of 3.41% to the lower bound, but a relatively small contribution of 0.91% to the upper bound; meanwhile, factor KM with a contribution of 2.85% becomes the greatest contributor to the upper-bound system cost. Moreover, factor BN contributes 0.15% to the lower bound of system cost, but has no contribution to its upper bound. When factor BN varies, however, at least one bound of system cost would be changed. Accordingly, system cost would be changed. Thus, factor BN has a considerable effect on model response. Figure 5 shows the interaction plot for power plant ESp2 (emission standard during period 2) and LWS efficiency (i.e., factor BN). This plot indicates that when the SO₂-treatment efficiency of LWS is at its low level, the lower-bound system cost would be reduced from $52.52 to 51.64 × 10⁶ if the SO₂-emission standard for power plant during period 2 varies from 37.7 to 42.7 tonne/day; when the SO₂-treatment efficiency of LWS is at its high level, a variation from 37.7 to 42.7 tonne/day in the SO₂-emission standard for power plant during period 2 would result in a decrease from 46.11 to 45.87 × 10⁶ in the lower-bound system cost. Thus, the lowest system cost would be obtained when the SO₂-treatment efficiency of LWS and the SO₂-emission standard for power plant during period 2 are at their high levels.

Figure 4. Contributions of factor interactions to lower and upper bounds of system cost.

Figure 5. Interaction plot for power plant ESp2 and LWS efficiency.

Discussion

In the air pollution control system, uncertainties exist in many system components; they may be given as intervals instead of deterministic values. Such a problem cannot be addressed through conventional optimization methods. Therefore, interval-parameter linear programming (ILP) has the advantage of dealing with uncertainties presented as intervals, enhancing the robustness of optimization efforts. In practical applications, importance of uncertainty in model inputs is different in the decision-making process. Variations of several parameters may bring about an apparent difference in model response, whereas some others may have no effect at all. It is thus indispensable to investigate the effects of uncertainties.

Conventional sensitivity analysis can be carried out to describe how much model output values are affected by changes in model input values. It examines the effects of changes in a single input parameter over its range, assuming no changes in all the other parameters. Such a one-parameter-at-a-time strategy only investigates the single effects of parameters, but fails to consider any possible interaction between parameters, which may result in misleading conclusions. In comparison, factorial analysis is a more efficient strategy, in which parameters are varied together instead of one at a time. Such a multivariate inference method is capable of revealing the potential interactions among parameters and their influences on modeling results, as well as of exploring the valuable information that may be hidden beneath their interrelationships. Thus, the proposed CFA-IP approach, which incorporates factorial analysis within the interval-parameter linear programming framework, is an efficient way in not only tacking uncertainties presented as intervals but also exploring their effects on the lower- and upper-bound solutions, which plays an important role in the decision-making process.

Nevertheless, when there are too many parameters that need to be investigated in large-scale problems, estimating their effects through CFA-IP would be extremely challenging. It is therefore expected that decision makers can first identify relatively important parameters based on their experience and historical data for facilitating further factorial analysis.

Conclusion

In this study, a coupled factorial-analysis-based interval programming (CFA-IP) approach has been developed through incorporating factorial analysis within an interval-parameter linear programming framework. CFA-IP can handle uncertainties presented as intervals that exist in the objective function and the left- and right-hand sides of constraints. Based on a robust two-step method (RTSM), interval information can also be robustly reflected in the solutions for the objective-function value and decision variables. Moreover, CFA-IP is capable of investigating the potential interactions among parameters and their influences on model outputs, which is meaningful for supporting an in-depth analysis of uncertainty.

A regional air pollution control problem has been studied to demonstrate applicability of the proposed CFA-IP approach. Results of the case study indicate that useful solutions have been generated for planning the regional air quality management practices. They can help decision makers identify desired pollution mitigation strategies with minimized total cost and maximized environmental efficiency. Through a thorough analysis of factors, several parameters and their interactions have significant influences on the lower and upper bounds of system cost. The findings can help decision makers identify dominant parameters and obtain valuable information that may be veiled beneath their interrelationships.

This study focuses on the investigation of input parameters that exist in the left- and right-hand sides of constraints; however, coefficients in the objective function such as the operating costs of different control measures may be also sensitive to model outputs. Future studies would thus be undertaken to explore the effects of coefficients in the objective function using CFA-IP. Moreover, CFA-IP can tackle uncertainties presented as intervals; however, it has difficulties in dealing with uncertainties expressed in other formats, such as fuzzy sets and probability distributions. Therefore, CFA-IP would be integrated with various inexact optimization techniques such as fuzzy and stochastic programming to enhance its capacities in tackling uncertainties presented in multiple formats.

Acknowledgment

This research was supported by the Program for Innovative Research Team (IRT1127), the Natural Science and Engineering Research Council of Canada, and the MOE Key Project Program (311013). The authors would like to express thanks to the editor and the anonymous reviewers for their constructive comments and suggestions.