A reanalysis of fine particulate matter air pollution versus life expectancy in the United States

Abstract

A reduction in population exposure to fine particulate matter air pollution (PM2.5) has been associated with improvements in life expectancy. This article presents a reanalysis of this relationship and comments on the results from a study on the reduction of ambient air PM_2.5 concentrations versus life expectancy in metropolitan areas of the United States. The results of the reanalysis show that the statistical significance of the correlation is lost after removing one of the metropolitan areas from the regression analysis, suggesting that the results may not be suitable for a meaningful and reliable inference.

Implications:

The observed loss of statistical significance in the correlation between the reduction of ambient air PM_2.5 concentrations and life expectancy in metropolitan areas of the United States, after removing one of the metropolitan areas from the regression analysis, may raise concern for the policymakers in decisions regarding further reductions in permitted levels of air pollution emissions.

Introduction

In their study on fine particulate matter air pollution (PM_2.5) and life expectancy in the United States for the late 1970s and early 1980s and the late 1990s and early 2000s, Pope et al. (2009) found that “a decrease of 10 μg per cubic meter in the concentration of fine particulate matter was associated with an estimated increase in mean (±SE) life expectancy of 0.61 ± 0.20 year (P = 0.004)” and concluded that “a reduction in exposure to ambient fine-particulate air pollution contributed to significant and measurable improvements in life expectancy in the United States.” However, a visual analysis of Figure 4 presented on page 382 of their article indicates that data-point number 46 (Topeka, Kansas) is a potentially influential statistical outlier when the 51 metropolitan areas only are considered. Although the 211-county data show statistically significant association between the reduction in PM_2.5 and the change in life expectancy, it is important to take into consideration that epidemiological data obtained for the 51 densely populated large metropolitan areas are expected to be more reliable than the data for the smaller county areas within the same regions. Hence, if the assumption of a causal nonthreshold relationship between fine particulate matter air pollution and population mortality is correct (Pope and Dockery, 2006; Schwartz et al., 2008), the statistical significance of the correlation between the reduction in PM_2.5 and population-weighted life expectancy in the 51 largest U.S. metropolitan areas should not be affected by the removal of a single data point. Unfortunately, it appears that the statistical significance of the correlation is lost after removing Topeka, Kansas, from the regression analysis.

Discussion

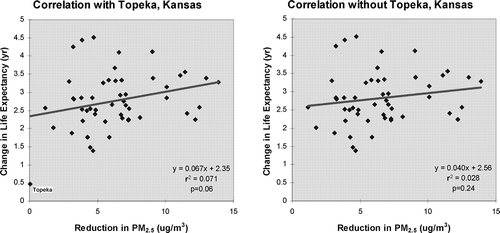
The interactive graphics data of the article by Pope et al. (2009) are used to recalculate the correlation between the reduction in PM_2.5 and the change in life expectancy in the 51 metropolitan areas. Although the authors have acknowledged in the article that “the data set used for the interactive graphic was redacted to make the presentation manageable,” a reanalysis on the basis of the interactive graphics data shows a similar slope value for a 10-μg/m³ decrease in the concentration of fine particulate matter (i.e., ∼0.62 years per 10 μg/m³; r ² = 0.061; p = 0.08). However, removing data point number 46 (Topeka, Kansas), as an observed potentially influential statistical outlier, yields weak and not statistically significant correlation (i.e., ∼0.35 years per 10 μg/m³; r ² = 0.022; p = 0.31) between the studied variables (Table 1).

Table 1. Linear Regression Reanalyses of Change in Life Expectancy vs. Reduction in PM_{2. 5} Concentration in 51 Metropolitan Areas of the United States

	Model with Topeka, Kansas^‡			Model without Topeka, Kansas^‡
Data	Y-axis intercept	Reduction in PM2.5 (μg/m^3)	r ^2	Y-axis intercept	Reduction in PM2.5 (μg/m^3)	r ^2
Pope et al. (2009)—Redacted interactive graphics data	2.41 ± 0.25	0.062 ± 0.035	0.061	2.62 ± 0.24	0.035 ± 0.034	0.022
	(p < 0.001)	(p = 0.08)		(p < 0.001)	(p = 0.31)
Pope et al. (2009)—Complete data	2.35 ± 0.25	0.067 ± 0.035	0.071	2.56 ± 0.24	0.040 ± 0.034	0.028
	(p < 0.001)	(p = 0.06)		(p < 0.001)	(p = 0.24)
Note: ^‡Plus-minus values are regression coefficients and standard errors (i.e., ±SE); r ^2 is coefficient of determination.

Similar and statistically not significant results are obtained on the basis of the complete data kindly provided by the authors for the 211 counties from the 51 metropolitan areas as described in the study by Pope et al. (2009). The change in life expectancy and reduction in PM_2.5 data for the 51 metropolitan areas are mean values from the corresponding county-level data. It should be noted that some metropolitan areas, such as Topeka, Kansas, are represented by only one county where the metropolitan-level and the county-level data values are the same. This second reanalysis shows the slopes with and without Topeka, Kansas, of 0.67 per 10 μg/m³ (r ² = 0.071; p = 0.06) and 0.40 per 10 μg/m³ (r ² = 0.028; p = 0.24), respectively (Table 1 and Figure 1).

Figure 1. Change in life expectancy vs. reduction in PM_2.5 concentration with and without Topeka, Kansas as an influential outlier. Data from Pope et al. (2009).

Statistical outliers and potentially influential data points are not discussed by the authors, and the results from the correlation/regression analyses are used to obtain a slope for estimating directly an increase in mean life expectancy following a 10-μg/m³ decrease in the concentration of fine airborne particulate matter. Although lack of statistical significance in the observed correlation warrants a statement of limitations and a discussion of uncertainties in the conclusions, a slope of 0.61 years per 10-μg/m³ reduction in PM_2.5 could be applied directly to predict improvements in life expectancy only if the coefficient of correlation (r) between the studied variables is close to 1. However, even if the observed correlation using the complete county-level data is statistically significant at α = 0.05 (p < 0.05), as presented in the article by Pope et al. (2009), a coefficient of determination (r ²) of 0.05 indicates in statistical terms that only approximately 5% (not close to 100%) of the total variation in the dependent variable (Y; change in life expectancy) could be explained, or accounted for, by the variation in the independent variable (X; reduction in PM_2.5 (μg/m³)). This means that other variables, not accounted for, may contribute up to 95% to the observed change.

Regression diagnostics should be implemented and discussed when regression models are used in epidemiology (Greenland, 2005). Isolated data points located in or close to any of the four corners of the regression graph should be considered and tested as potentially influential outliers. Stevens (1984) discusses outliers and influential data points in regression analysis and diagnostics for their identification. The author provides guidelines for interpretation of the diagnostics, indicates that not all identified outliers will necessarily be influential in affecting the regression coefficients, and concludes that “Because the results of a regression analysis may be seriously affected by just 1 or 2 errant data points, it is crucial for the researcher to isolate such points” (Stevens, 1984). In a paper on graphical models for causation, Freedman (2004) suggests that regressions should not be used for inferring causal relationships from a data set in situations where a substantial prior knowledge about the mechanisms that generated the data is absent.

In addition, Krause et al. (2005) suggest that “for a proper model assessment the gradient b should always be discussed together with r² ” (emphasis added) and that “by weighting r² under- or overpredictions are quantified together with the dynamics which results in a more comprehensive reflection of model results.” Hence, in case of a weak correlation between air pollution and life expectancy (e.g., r ² ∼ 0.05) the slope (b) should be adjusted using the coefficient of determination (r ²) to obtain a weighted coefficient of determination (wr ²). Therefore, provided that the correlation is statistically significant and free of influential outliers, the slope of 0.67 per 10 μg/m³ on the basis of 51 metropolitan areas with Topeka, Kansas, should be adjusted to account only for the suspected PM_2.5 attributable change in life expectancy (i.e., 0.67 × 0.071 = 0.048 years or 17.4 days). If the calculations are based on the data excluding Topeka, Kansas, the r ² adjusted slope yields a statistically not significant improvement in life expectancy of approximately 0.01 years or 4 days (i.e., 0.40 × 0.028 = 0.01 years per 10-μg/m³ reduction in airborne PM_2.5 concentration).

In their recent paper on validity of observational studies in accountability analyses, Pope et al. (2012) provide a comparative relationship between air pollution and life expectancy using the 51 metropolitan areas with and without an arbitrary control for the covariate changes in socioeconomic, demographic, and smoking variables. However, there is no discussion regarding the presence of an influential statistical outlier in the original data set (i.e., Topeka, Kansas). The authors have acknowledged that “given that the study had to rely on only available socioeconomic and demographic data, given that the study had to rely on proxy and/or incomplete cigarette smoking data, and given that there are other determinates of life expectancy that may have changed in correlation with changes in air pollution, this analysis cannot fully eliminate the potential of some residual confounding” (Pope et al., 2012). Other potentially significant confounding factors, such as climate, seasonal variation in air temperature, and disease outbreaks, are not considered. For example, a study by Krstić (2011) shows that elderly population mortality from circulatory and respiratory causes in Metro Vancouver, British Columbia, is associated with the variation in apparent temperature, while the association with air pollution appears to be weak and negative.

Under conditions of limited covariate data availability, as appears to be the case in the study by Pope et al. (2009; 2012), a partial control for the selected covariates in a multivariate regression analysis model may lead to unpredictable distortions in the observed relationships between the studied variables and potentially misleading inferences. This may be the case particularly when the physiological mechanism is not clear and an original association between fine particulate matter air pollution and life expectancy is evidently not statistically significant at the metropolitan level without the Topeka, Kansas, data.

In reassessing the human health benefits from cleaner air, Cox (2012) questions the significance of the positive association between PM_2.5 and mortality rates, suggesting that the projected increase in life expectancy and overall public health benefits gained from the proposed further reductions in permitted levels of air pollution emissions in the United States by the year 2020 are probably overestimated. The author indicates in a discrete uncertainty analysis, with probability greater than 90% under plausible alternative assumptions, that the costs of the Clean Air Act Amendment (CAAA) exceed its benefits (Cox, 2012).

Conclusion

The results of the presented reanalysis on the basis of the data from Pope et al. (2009) show that the statistical significance of the association between the reduction in PM_2.5 and the change in life expectancy in the United States is lost after removing one of the metropolitan areas from the regression analysis. Hence, the observed weak and statistically not significant correlation between the studied variables does not appear to provide the basis for a meaningful and reliable inference regarding potential public health benefits from air pollution emission reductions, which may raise concern for policymakers in decisions regarding further reductions in permitted levels of air pollution emissions.

Acknowledgment

The author thanks Dr. Arden Pope and colleagues for kindly providing the complete data used in their study on fine particulate matter air pollution (PM_2.5) and life expectancy in the United States. This work would not be possible without an enthusiastic support and encouragement from the author's wife, Dušica Krstić (Pejović), to continue to pursue scientific research.

Notes

This article was originally published in the Journal of the Air & Waste Management Association, 62(9): 989–991. doi:10.1080/10962247.2012.697445.