Freight shipment modal split and its environmental impacts: An exploratory study

Abstract

Freight transportation activities are responsible for a large share of air pollution and greenhouse gas emissions in the United States. Various freight transportation modes have significantly different impacts on air quality and environmental sustainability, and this highlights the need for a better understanding of interregional freight shipment mode choices. This paper develops a binomial logit market share model to predict interregional freight modal share between truck and rail as a function of freight and shipment characteristics. This model can be used to estimate the impacts of various factors, such as oil price, on shippers’ mode choice decisions. A set of multiyear freight and geographical information databases was integrated to construct regression models for typical freight commodities. The atmospheric impact levels incurred by different freight modal choice decisions are analyzed to provide insights on the relationship among freight modal split, oil price change, and air quality.

Implications:

Freight transportation has become a major source of energy consumption and air pollution, and emissions rates vary significantly across different modes. Understanding freight shipment mode choice under various economic and engineering factors will help assess the environmental impacts of freight shipment systems at the national level. This paper develops a binomial logit model for two dominating modes (truck and rail) and shows how this model is incorporated into an environmental impact analysis. The framework will be useful to policy makers to assess the impacts of freight movements on air quality and public health and to mitigate those adverse impacts.

Introduction

With rapid global industrialization and the ever-increasing demand for freight movements, freight transportation has become a major source of air pollution. According to ICF Consulting (2005), most freight transportation modes such as trucks, locomotives, and ships are powered by diesel engines, which are significant emission sources of national nitrogen oxides (NO_X), particulate matter (PM), as well as greenhouse gases such as carbon dioxide (CO₂). For example, NO_X and PM_2.5 emissions from freight trucks and trains respectively constitute about 32 and 21% of the total NO_X and PM_2.5 emissions from the U.S. transportation sector (Bickford, 2012). In the case of greenhouse gas emissions, freight transportation contributes about 25% of the total emissions from all transportation sources in the U.S. (ICF Consulting, 2005). Emissions from freight transportation operations usually vary significantly across different modes. For example, the U.S. Environmental Protection Agency (2008) reported that for each ton-mile of freight shipment, truck, rail, waterborne craft, and aircraft respectively produce 0.297, 0.0252, 0.048, and 1.527 kg of CO₂ emission; 0.0035, 0.002, 0.0041, and 0.0417 g of CH₄ emission; and 0.0027, 0.0006, 0.0014, and 0.0479 g of N₂O emission. In addition, the Natural Resources Defense Council (2012) shows that truck, rail, water, and air transportation modes respectively generate 92, 13, 25, and 119 mg of PM₁₀ emissions for each ton-mile of freight movement. Therefore, even to transport the same amount of freight for the same origin–destination (O/D) pair, different shipment modes can result in different emissions, which in turn affect air quality and human health. As of today, the truck mode carries the largest percentage of the total national freight movements in the U.S., and this percentage becomes even more prominent in the case of freight shipments within large states (Chin et al., 1998). However, compared to trains, trucks exhibit significantly lower fuel efficiency and higher emission levels. In order to understand the environmental impact from freight systems, therefore, we need to investigate modal choice for freight shipment demand.

Overall, shippers’ freight modal choice decisions are influenced by many factors, such as strength of regional economy, infrastructure capacity, and shipping distance (or time). The dramatic surge in oil price during the past decade has become a critical issue in the U.S. freight transportation market, because the fuel cost comprises more than 50% of the total operating cost for the transportation industry (Transportation Economics and Management Systems, 2008). Because the sensitivity of transport operating costs to changes in oil prices varies significantly across shipment modes, oil prices have become an important factor in freight mode choices. Unfortunately, previous studies have largely ignored the effect of oil prices on freight modal choice decisions, and few have tried to connect oil prices to freight transportation emissions. Most of the existing work focused on theoretical model developments; for example, interregional commodity flow analysis in an input–output framework, freight demand modal choice based on shipper's profit maximization, and route selection in multimodal transportation networks. The empirical implementation of freight modal split models was also quite rare (possibly due to a lack of data). Although more multiyear freight data have become available in recent years, few efforts have been made to clarify the relationship among various economic factors, freight transportation modal choice, and freight transportation emissions.

This paper aims to fill these gaps by constructing an aggregated binomial logit market share model that estimates modal split between truck and rail (the two major freight shipment modes in the U.S.) for 10 groups of typical commodities. In this model, we explicitly incorporated various economic and engineering factors as explanatory variables in the utility function in order to quantify their effect on freight transport mode choices. Such explanatory variables include oil price, shipping distance, and freight value per unit weight for each type of commodities. Quantitative models were obtained using empirical freight transportation demand data between origins and destinations (e.g., freight analysis zones), and the models were validated using extra empirical data. We used 4 years of available data that can be found in the public domain. This paper also provides discussions on freight transportation demand data statistics, interpretations of the parameter estimations, insights on their effects on freight mode choice, and environmental impact assessments.

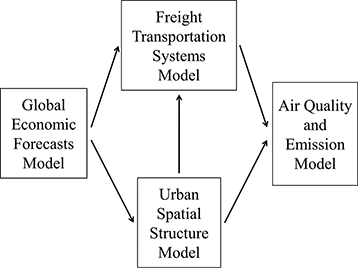
This study is a part of a collaborative research project that aims to develop an integrated modeling framework to estimate future emissions from freight transportation systems at global, regional, and urban levels based on future economic growth scenarios, projections of urban spatial structure, and vehicle emission characteristics. The four main tasks of this project are illustrated in Figure 1.

Figure 1. Framework of an integrated freight emission project.

Global economic forecasts are used to generate global and interregional freight transportation demand under different future economic growth scenarios. An urban spatial structure model predicts future distribution of employment and population within major metropolitan areas. Given the projected economic growth and interregional freight demand, the freight transportation systems model forecasts freight movements by freight analysis zones (and by mode; e.g., truck and rail) and loads them onto the respective transportation networks. The required freight transportation and delivery activities at national and regional levels will be used as the basis to estimate global, regional, and urban air quality. As such, the work presented in this paper is part of the efforts on freight transportation model development.

The remainder of this paper is organized as follows: the following section reviews the related literature. A simple freight transportation modal split model is presented next. Then we describe the empirical data source and the data cleaning procedure. The next section presents estimation results, model validations, and an illustrative example. Finally, concluding remarks and discussions on related future work are provided.

Literature Review

Early attention has been given to interregional freight transportation and commodity flows. Isard (1951, 1960) and Moses (1955) considered interregional commodity flow analysis in terms of an input–output method, and Leontief and Strout (1963) suggested a gravity-type model formulation. Wilson (1970a, 1970b) presented several methods for analyzing a system of interregional commodity flows, including a Newtonian gravity model, an input–output framework, an entropy maximizing method, and a hybrid gravity and input–output modeling approach. Kim et al. (1983) proposed an interregional commodity flow input–output model and provided empirical applications. Rho et al. (1989) used small- and large-scale networks to compare solution techniques for the interregional commodity flow model in Wilson (1970a, 1970b). Despite these early efforts, the development and application of interregional commodity shipment models have been far less advanced compared to their counterparts on the urban passenger side, probably due to the lack of freight transportation flow data (Ham et al., 2005). Only a few studies related to implementation and application of the analytical models can be found since the comprehensive commodity flow survey data from the U.S. Bureau of the Census became available in the 1990s (Ham et al., 2002, 2005).

There have been some studies related to freight demand modal choice modeling. Allen (1977) and Daugherty (1979) proposed microeconomic freight transport demand models to show that optimal total flow and mode choice can be obtained via shippers’ profit maximization. Winston (1981) developed a freight transportation mode choice model based on utility maximization of individual decision makers. Winston (1983) compared the aggregate and disaggregate freight transportation demand models, and Gray (1982) reviewed three types of freight modal choice models, including economic positivist, technological positivist, and perceptual approaches. Abdelwahab and Sargious (1991) and Holguín-Veras (2002) proposed joint discrete–continuous decision processes on shipment size and freight transportation mode choices. In their models, the decisions on shipment size take continuous values and those on mode choice are discrete. Windisch et al. (2010) presented a transportation chain and shipment size choice model in which the shipment size is categorized into 18 discrete levels. Multinomial logit models (and different variants) have been widely applied to freight shipment mode choice (Golias and Yannis, 1998; Catalani, 2001; Arunotayanun and Polak, 2011). Nam (1997) developed a set of logit mode choice models for shipments of six freight commodity types in South Korea. Shinghal and Fowkes (2002) examined determinants of freight shipment mode choice in India. This study used stated preference empirical survey data in 1998 and analyzed mode choice attributes including service frequency, reliability, service time, and cost. Jiang et al. (1999) developed a nested multinomial logit modal choice model using a large-scale, national freight demand survey database in France in 1988. The study concluded that French shippers tend to show the highest likelihood of selecting public road transportation if the shipping distance is approximately 700 km, whereas that of choosing rail transportation peaks around 1,300 km. A similar trend was also shown in the U.S.; Bryan et al. (2007) reported that trucks have been appealing for local and regional freight shipments in urban areas, whereas rail and intermodal are competitive for interregional traffic shipments spanning several hundred miles or more.

Freight transportation models have also been implemented in decision support software. For instance, Winebrake et al. (2008) presented a geospatial intermodal freight transportation model developed in a geographic information system platform. It finds the path with the least delivery time, least cost, or least emissions in an intermodal freight transportation network for a given O/D pair so that tradeoffs between the different criteria can be evaluated. The geospatial intermodal freight transportation model was applied in Comer et al. (2010) to investigate the use of marine vessels instead of heavy-duty trucks in the U.S. Great Lakes regions. Cohen et al. (2008) presented five freight transportation forecasting models (i.e., the direct facility flow factoring method, the O/D factoring method, the truck model, the four-step commodity model, and the economic activity model), each of which contains a subset of six basic model components (i.e., direct factoring, trip generation, trip distribution, mode split, traffic assignment, and economic/land use modeling). This report also provided several examples of model implementation by state agencies. For instance, the State of Florida adopted the four-step commodity model and used the TRANSEARCH database (Cambridge Systematics, Inc., 2002).

These previous studies provided useful insights into how freight transportation modal choice decisions are influenced by various factors. However, these studies have not explicitly considered the effect of oil price changes, which have taken a large share in freight transportation operation costs across all modes. In addition, the high energy efficiency has become the key factor for choosing the transportation mode (Transportation Economics and Management Systems, 2008). Therefore, we aim to incorporate oil price as an independent variable in our mode choice model so that this model will be useful for decision makers to evaluate the effects of future oil prices on freight delivery modal choice decisions. Furthermore, it will play an important role in estimating the impact of consequent modal choice decisions on air quality and climate change.

Freight Transportation Mode Choice Modeling

In this work, we focus on developing a freight modal split model within a four-step freight demand modeling framework that is similar to the urban passenger travel demand forecasting model (Cohen et al., 2008). Assuming that a set of O/D freight demand data is given, we develop a macroscopic logit market share model for mode choice decisions as a function of a set of explanatory variables (e.g., oil price, freight value, shipment distance, etc.) because our databases only contain aggregated annual freight shipment observations at the freight zone level. Our study focuses on two dominating freight modes, truck and rail, in a binomial logit model framework.

In this model, the annual market share of truck shipments (in terms of tonnage) between any O/D pair is a dependent variable (whose value is between 0 and 1). Due to data availability, we consider three different explanatory variables for each commodity type: commodity value per ton ($/ton, denoted by VALUE), the average truck shipment distance (mile, denoted by DIST), and crude oil price ($/barrel, denoted by OILPRC). The average rail shipment distance is not included in the set of explanatory variables because the truck shipment distance and the rail shipment distance for the same O/D pair are highly correlated (i.e., the correlation between those two variables exceeded 0.95). We have also examined possible collinearity among all other explanatory variables but none was found significant (i.e., the correlations between VALUE and DIST, VALUE and OILPRC, and DIST and OILPRC were all less than 0.05). There might be additional factors affecting freight transportation mode choice. However, the independent variables used in this study are reasonably comprehensive. They include not only the majority of the most frequently used independent variables in this context (Gray, 1982) but also those in the recent study for the State of Florida (Cambridge Systematics, Inc., 2002). In this analysis, the truck shipment distance for each O/D pair was measured in the U.S. highway network. Crude oil price was selected as a proxy to represent a single oil price index because the crude oil price is a dominating factor in determining diesel fuel price (U.S. Energy Information Administration, 2008). It shall be noted that although trucks and trains both use diesel oil as fuel, the unit diesel prices for trucks and railroads are different; even for the same railroad company, diesel price varies significantly across fueling locations (Nourbakhsh and Ouyang, 2010). Here, we assume that the mode choices in a given year are affected by the average oil prices in the past years (considering that the influence to shippers may be lagged). After careful deliberation and trials, we found that the mode choice decisions in a given year (e.g., 2007) are mainly affected by the average oil price in the immediate previous year (e.g., 2006).

As such, we assume that the utility functions for truck () for commodity type , can be defined as follows:

1

In eq 1, we include an interaction term because the utility of using trucks for freight movement will be affected by truck shipment cost, which is directly captured by this interaction term (i.e., average shipping distance times fuel cost rate).

We define as the market share of truck mode for commodity type n. This percentage can be constructed as follows (Gruca and Sudharshan, 1991):

2

Because we have only two modes, truck and rail, the market share of rail mode can be determined as for commodity type n once the truck shipment share is obtained. Then, the binomial logit model can be transformed into the form of eq 3 as follows (Pindyck and Rubinfeld, 1998):

3

This equation takes a generalized linear form with three explanatory variables. The intercept and the coefficients and can be estimated via linear regression for each commodity type.

Freight Transportation Data

To construct the freight transportation demand model, we collected data sets from the Freight Analysis Framework data versions 2 and 3 (FAF² and FAF³) from the Federal Highway Administration, U.S. Department of Transportation (2011), Commodity Flow Survey (CFS) data from Research and Innovative Technology Administration, U.S. Department of Transportation (2011), and the crude oil price information from Economagic, LLC (1996).

Data sources and processing procedures

In order to develop the above-mentioned model, we had to merge data from multiple sources into one useable data set. The FAF² and FAF³ record commodity shipment flows and related freight transportation activities between the U.S. geographical regions in years 2002 and 2007. The CFS data sets provide freight transportation activities in years 1993 and 1997, such as the volume and value of different types of commodities shipped between various origins and destinations by different modes. FAF², FAF³, and 1997 CFS use the Standard Classification of Transported Goods and the 1993 CFS adopted the Standard Transportation Commodity Code to define commodity types. Average shipment distances of truck and rail modes are extracted from the CFS data sets to estimate freight demand and emissions. Because our research aims to address the impact of oil prices on freight shipment mode choices, we incorporate the West Texas Intermediate (WTI) crude oil price from Economagic, LLC (1996) as a proxy of oil price. In our study, average oil prices in years 1992, 1996, 2001, and 2006 were obtained because the mode choice decisions (i.e., in years 1993, 1997, 2002, and 2007) will be affected by the average oil prices in the immediate previous years. WTI crude oil was selected among the three major crude oil benchmarks (i.e., WTI, Brent Blend, and Dubai) because WTI is used as a primary benchmark not only in the U.S. but also in the international market (Wikipedia Contributors, 2012).

When we processed the data, each of the four data sets (FAF² for year 2002, FAF³ for year 2007, 1993 CFS, and 1997 CFS) were combined with distance data based on origin, destination, and mode. Figure 2 shows the maps of the freight analysis zones in the FAF³ database and the national transportation analysis regions in the 1993 CFS database. Freight analysis zones in the FAF² are largely the same as those in FAF³, whereas the 1997 CFS defines zones along state boundaries. We only used the data related to truck and rail modes, and different kinds of products (originally defined in the data sets) were grouped into 10 types of commodities based on physical and economical similarity. All monetary values in the original data sets were adjusted according to inflation rates to the values of year 2007 (U.S. Bureau of Labor Statistics, 2013). The yearly averaged WTI crude oil price remained rather stable, at $30.43 per barrel in 1992, $27.47 per barrel in 1996, and $28.48 per barrel in 2001, until a sharp increase to $64.38 per barrel occurred in 2006 (all constant 2007 dollars). Finally, information from these four sources was joined into one data set that had 69,477 observations in total, and each observation corresponded to a year, a commodity type, and a shipment O/D pair. The data set also contained information on commodity value per unit weight, truck and rail shipment distances, WTI crude oil price, and observed truck and rail shipment shares.

Figure 2. Maps of freight zones (adapted from Federal Highway Administration, U.S. Department of Transportation [2011] and Research and Innovative Technology Administration, U.S. Department of Transportation [2011]): (a) FAF³ analysis zones and (b) national transportation analysis regions (1993 CFS).

Freight transportation demand data statistics

Table 1 shows the definition of commodity groups, the number of data observations, and the total tonnage shipped by trucks and rail for each type of commodity in the 4 years of interest. From column (d) we see that the truck mode serves a broad spectrum of commodities, and commodity type 3 (i.e., stones, nonmetallic minerals, and metallic ores), type 7 (i.e., base metal and machinery), type 4 (i.e., coal and petroleum products), and type 1 (i.e., agriculture products and fish) show the highest percentage share in shipment tonnage. However, it can be noticed from column (e) that the railroad mode serves a very concentrated market; for example, commodity type 4 (i.e., coal and petroleum products) occupies a dominant share (i.e., more than 50%) of the total rail shipment tonnage.

Table 1. Data statistics by mode and commodity type (4 years total)

(a) Commodity type	(b) Commodity description	(c) Number of observations	(d) Truck		(e) Rail
			tons (thousands)	%	tons (thousands)	%
1	Agricultural products and fish	5,704	4,585,159	12.63	530,930	9.52
2	Grain, alcohol, and tobacco products	8,202	2,485,347	6.84	158,335	2.84
3	Stones, nonmetallic minerals, and metallic ores	5,630	7,830,644	21.56	550,560	9.87
4	Coal and petroleum products	4,657	5,339,089	14.70	2,999,961	53.76
5	Basic chemicals, chemical and pharmaceutical products	8,824	1,928,319	5.31	585,510	10.49
6	Logs, wood products, and textile and leather	9,102	3,197,305	8.80	261,422	4.69
7	Base metal and machinery	9,053	6,377,410	17.56	291,342	5.22
8	Electronic, motorized vehicles, and precision instruments	7,651	597,028	1.64	51,440	0.92
9	Furniture, mixed freight, and miscellaneous manufactured products	7,561	3,326,713	9.16	145,849	2.61
10	Commodity unknown	3,093	649,901	1.79	4,428	0.08
	Total	69,477	36,316,916	100.00	5,579,778	100.00

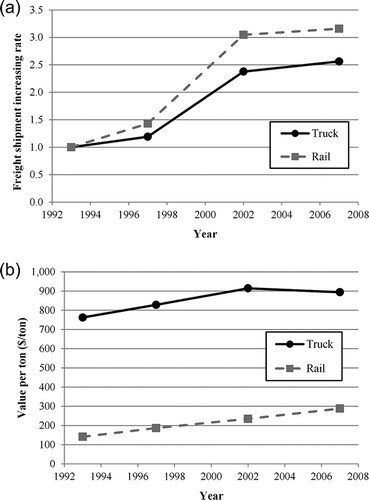
Figure 3a shows that though the total annual freight tonnage increases steadily for both modes from 1993 to 2007, the increase was larger for railroads. Figure 3b compares the freight value per ton shipped by trucks and rail. It can be seen that the truck mode consistently carries much more valuable goods on average.

Figure 3. Total tonnage and freight value per ton in 4 years: (a) total freight tonnage increasing rate and (b) freight value per ton.

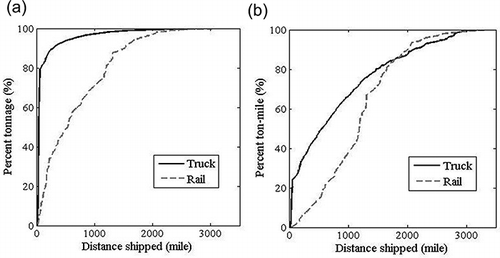
Figure 4 shows the cumulative percentage of 4-year total tons and ton-miles shipped by truck and rail (for all commodities). Truck and rail shipments display very different distributions across distances; for example, Figure 4a shows that over 90% of truck tonnage was shipped for less than 300 miles, but more than 40% of railroad tonnage was shipped to a destination more than 700 miles away. A similar trend is also shown in Figure 4b, which shows that over 50% of truck ton-miles was transported within 550 miles; however, more than 50% of railroad ton-miles involved trips of more than 1,200 miles. This suggests a strong relationship between shipment distance and mode choice.

Figure 4. Cumulative percentage of (a) total tons and (b) ton-miles shipped.

Estimation, Validation, and Application

Estimation results

Statistical software package R (R Foundation for Statistical Computing, Vienna, Austria, version 2.15.2) was used in this analysis to estimate the intercept and coefficients in eq 3. We divided the database into two sets for each commodity type: two thirds of the observations were included in a training data set to estimate the model, and the remaining data were assigned to a test data set to validate the suggested model. The estimation results for each commodity type, based on the training data set, are included in Table 2. The sample size for estimation and the goodness of fit are also shown.

Table 2. Estimation results and goodness of fit

			Type 1	Type 2	Type 3	Type 4	Type 5	Type 6	Type 7	Type 8	Type 9	Type 10
(a) Estimation results	Intercept	Estimate	1.902E+00	1.163E+00	3.116E+00	−1.025E+00	4.035E−01	2.570E+00	3.305E+00	1.654E+00	3.131E+00	1.000E+00
		z-Statistic	18,886.00	4,133.00	43,384.00	−12,938.00	3,623.00	22,229.00	27,944.00	4,071.00	19,169.00	712.30
		Pr(>|z|)	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001
	Value per ton	Estimate	2.379E−03	1.913E−03	1.100E−03	1.199E−02	7.781E−04	4.285E−04	1.627E−04	1.580E−04	2.977E−04	4.413E−03
		z-Statistic	8,939.00	7,237.00	1,414.00	29,956.00	10,033.00	4,201.00	1,880.00	2,672.00	2,053.00	2,833.20
		Pr(>|z|)	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001
	Average truck distance × WTI crude oil price	Estimate	−4.681E−05	−2.748E−05	−6.435E−05	−5.718E−05	−1.812E−05	−3.392E−05	−2.858E−05	−1.547E−05	−2.059E−05	−3.941E−05
		z-Statistic	−16,435.00	−8,868.00	−11,929.00	−17,077.00	−8,360.00	−10,774.00	−8,523.00	−3,534.00	−4,569.00	−1,153.80
		Pr(>|z|)	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001
(b) Number of data used			3,803	5,468	3,753	3,105	5,883	6,068	6,036	5,101	5,041	2,062
(c) Pseudo	McFadden		0.305	0.316	0.171	0.665	0.256	0.241	0.121	0.127	0.044	0.332
R ^2	Nagelkerke		0.348	0.344	0.187	0.764	0.300	0.262	0.129	0.143	0.047	0.338

Table 2 shows that all types of commodities except type 4 had positive intercepts, implying that everything else being equal, truck was more likely to be chosen. In the case of commodity type 4 (i.e., coal and petroleum products), the intercept had a negative sign, which indicates that rail is by default a preferred mode for shipping these kinds of products. This trend was also shown in the previous data statistics analysis; that is, coal and petroleum are the dominant cargo for the U.S. railroad industry. The coefficients of value per ton were positive for all commodity types, indicating that trucks tend to ship higher value goods than rail. Finally, the coefficients of average truck distance × WTI crude oil price were negative across all commodity types, which implies that as the crude oil price or the average truck distance increases, the utility of truck shipment decreases. In other words, the rail mode will be advantageous with high oil prices or for long-distance freight shipments. To test whether any of the estimated intercepts and coefficients was statistically different from zero, z-statistics and their p-values are also included in row (a) of Table 2. The absolute values of the z-statistics were very large for all cases, and all p-values were less than 0.001. Hence, we can conclude that all estimates of the model coefficients were statistically significant for all types of commodities.

Table 2 also shows two pseudo R ² measures (i.e., indicating the goodness of fit of the logit model) in row (c). McFadden and Nagelkerke pseudo R ² (Menard, 2001; Faraway, 2006), the most commonly used tests, generated very close measures. In case of commodities types 1, 2, 4, 5, and 10, the current models showed more than 30% higher maximal likelihood over the intercept-only models.

Model implementation and validation

To test how accurately the estimated model predicts reality, model validation was conducted using reserved data in the original database (i.e., test data set). The data structure of the test data set was exactly the same as that of the training data set; thus, we could obtain truck and rail shipment share predictions for each commodity and O/D pair and compare them with the observed shares.

Column (a) of Table 3 represents the size of the test data set for each commodity type used to validate the proposed model. They included approximately one third of the total observations. Columns (b) and (c) of Table 3 respectively show the observed and predicted total truck shipment shares for each commodity type, summed across all O/D pairs in the test data set. It can be seen from column (d) that the estimated model yielded very close predictions of the total modal shares, probably benefiting from the law of large numbers.

Table 3. Comparison between observed and predicted total truck shares and paired comparison

	(a) Number of data used	Total truck shipment share (%)			Paired comparison (α = 0.05)
		(b) Observed	(c) Predicted	(d) = |(b) − (c)|	(e) p-Value	(f) Test result
Type 1	1,901	89.306	89.997	0.691	0.6490	Do not reject H0
Type 2	2,734	94.147	94.245	0.097	0.8436	Do not reject H0
Type 3	1,877	92.013	94.410	2.397	0.3013	Do not reject H0
Type 4	1,552	68.086	69.409	1.322	0.4658	Do not reject H0
Type 5	2,941	77.928	77.328	0.600	0.6329	Do not reject H0
Type 6	3,034	92.568	92.274	0.294	0.7060	Do not reject H0
Type 7	3,017	94.879	96.077	1.198	0.5125	Do not reject H0
Type 8	2,550	92.403	91.158	1.246	0.3011	Do not reject H0
Type 9	2,520	94.223	96.442	2.219	0.2052	Do not reject H0
Type 10	1,031	99.363	99.497	0.134	0.6305	Do not reject H0

To verify whether there was any statistical difference between the groups of observed and predicted truck shipment shares, pairwise t tests were conducted as show in columns (e) and (f) of Table 3. In this analysis, comparison of the matched O/D pairs for each commodity type was adopted to improve precision and reduce variability. The sample sizes for the tests are shown in column (a) of Table 3. The null hypothesis (H₀) was that there is no obvious difference between truck shipment predictions and observations, and the alternative hypothesis (H₁) was that there is a significant difference between them. Column (f) of Table 3 shows that we do not reject the null hypothesis at the 0.05 level of significance for all types of commodities. Thus, we can conclude that there is no significant difference between the predicted truck shipment shares obtained from our proposed models and the observed truck shipment shares for all commodity types.

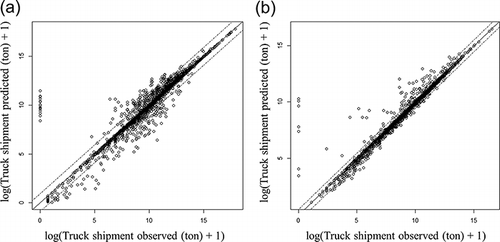
Figure 5 visually illustrates how the observed truck shipment shares (x-axis) are consistent with the model predictions (y-axis) for each data record in the test data set. Due to space limitations, only commodity types 6 and 8 were selected for illustration. Figures for all other commodity types are included in Figure A1 in the Appendix. Each dot in Figure A1 corresponds to an observation in the test data sets.

Figure 5. Observed and predicted truck shipment shares for (a) type 6 and (b) type 8 commodities.

Figure A1. Observed and predicted truck shipment shares for all commodity types: (a) commodity type 1, (b) commodity type 2, (c) commodity type 3, (d) commodity type 4, (e) commodity type 5, (f) commodity type 6, (g) commodity type 7, (h) commodity type 8, (i) commodity type 9, and (j) commodity type 10.

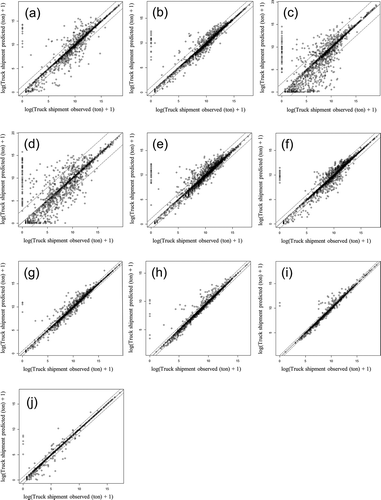
Note that Figure 5 plots the logarithm of (truck shipment tonnages + 1) because we have data records whose observed truck share is zero. The dotted lines located on both sides of the 45° solid line represent one standard deviation from the mean. Both figures show that the predictions from the models are generally well matched with the observed values, although those for commodities types 3 and 4 in Figure A1 show more outliers.

Emission estimation

The estimated modal split model can be used to estimate the effect of oil price change on freight shipment modal choices and the environmental impact. WTI crude oil price is frequently more than $100 per barrel nowadays and freight shipment market for the railroad mode has been expanding rapidly. A freight train is reported to move a ton of freight 436 miles on one gallon of fuel, which is three or more times as fuel-efficient as most trucks (Association of American Railroads, 2008). Moreover, freight trucks have been reported to be a dominant source of freight transportation emissions in many studies (ICF Consulting, 2005), and it is well known that rail produces less emissions and greenhouse gases than trucks in terms of ton-mile units (Bryan et al., 2007). Thus, improvement of air quality can be expected by shifting freight transportation demand from truck to rail, which is induced by high oil prices.

To illustrate this, we picked an arbitrary data record in the test data set that describes the freight movement of commodity type 5 (i.e., basic chemicals, chemical and pharmaceutical products) from Texas to Colorado. In this record, the freight value per unit weight is $1,600.70/ton, and the average shipping distances for truck and rail are 1,005 and 1,332 miles, respectively. Given all of the information for the explanatory variables above as well as the crude oil price, we can forecast the annual freight shipment share ratios for both modes. Then, by applying appropriate emission factors that relate the amount of emission production with freight transportation activity for each mode, we can estimate the total emission and greenhouse gas inventory. In the following analysis, we adopt CO₂, CH₄, and N₂O emission rates from the U.S. Environmental Protection Agency (2008) and PM₁₀ emission rate from the Natural Resources Defense Council (2012), such that each ton-mile of truck and rail shipments respectively generates 0.2970 and 0.0252 kg of CO₂, 0.0035 and 0.0020 g of CH₄, 0.0027 and 0.0006 g of N₂O, and 0.092 and 0.013 g of PM₁₀. Because the total annual freight shipment demand is given as 328,000 tons in the data, we can obtain a truck and rail demand split prediction and the various emission estimations for a range of oil prices, as shown in Table 4.

Table 4. Modal split and emission estimations under different WTI crude oil prices

(a) WTI crude oil price ($/barrel)	(b) Truck share prediction (%)	(c) Rail share prediction (%)	(d) Truck CO2 emission (ton)	(e) Rail CO2 emission (ton)	(f) Total CO2 emission (ton)	(g) Truck CH4 emission (kg)	(h) Rail CH4 emission (kg)	(i) Total CH4 emission (kg)	(j) Truck N2O emission (kg)	(k) Rail N2O emission (kg)	(l) Total N2O emission (kg)	(m) Truck PM10 emission (kg)	(n) Rail PM10 emission (kg)	(o) Total PM10 emission (kg)
50	68	32	66,247	3,560	69,807	781	283	1,063	602	85	687	20,521	1,836	22,358
60	64	36	62,228	4,012	66,240	733	318	1,052	566	96	661	19,276	2,070	21,346
70	59	41	58,006	4,487	62,493	684	356	1,040	527	107	634	17,968	2,315	20,283
80	55	45	53,640	4,978	58,618	632	395	1,027	488	119	606	16,616	2,568	19,184
90	50	50	49,198	5,477	54,675	580	435	1,014	447	130	578	15,240	2,826	18,065
100	46	54	44,751	5,977	50,728	527	474	1,002	407	142	549	13,862	3,084	16,946
110	41	59	40,373	6,470	46,842	476	513	989	367	154	521	12,506	3,338	15,844
120	37	63	36,132	6,947	43,078	426	551	977	328	165	494	11,192	3,584	14,776
130	33	67	32,088	7,401	39,489	378	587	966	292	176	468	9,940	3,818	13,758
140	29	71	28,289	7,828	36,118	333	621	955	257	186	444	8,763	4,039	12,802
150	25	75	24,771	8,224	32,995	292	653	945	225	196	421	7,673	4,243	11,916
160	22	78	21,555	8,586	30,141	254	681	935	196	204	400	6,677	4,429	11,106
170	19	81	18,650	8,912	27,563	220	707	927	170	212	382	5,777	4,598	10,375
180	16	84	16,054	9,204	25,259	189	731	920	146	219	365	4,973	4,748	9,721
190	14	86	13,757	9,463	23,220	162	751	913	125	225	350	4,261	4,882	9,143
200	12	88	11,741	9,689	21,431	138	769	907	107	231	337	3,637	4,999	8,636

From columns (a)–(o) in Table 4 we can conclude that as the WTI crude oil price varies from $50 to $200 per barrel, the total truck shipment share and the truck emissions considered in this analysis decrease. In addition, the total CO₂, CH₄, N₂O, and PM₁₀ emissions from both modes decrease, despite the increase in rail freight share and the following emissions. The national emission estimation can be further estimated by aggregating such emission calculations across all O/D pairs and all commodity types.

Conclusion and Future Study

Demand for freight transportation has been persistently increasing for several decades as a result of economic growth and globalization. However, at the same time, emissions from different freight transportation modes have contributed to a large share of air pollution and caused significant concerns regarding air quality and public health. Meanwhile, energy shortage and oil price surges during the past decade have affected freight transportation systems significantly. Hence, the motivation of this research is to draw connections among freight transportation demand modal choice, various economic factors (e.g., oil prices), and the air quality and climate impacts.

In this study, a macroscopic binomial logit market share model is proposed to study freight transportation modal choices between the dominating truck and rail modes. In our model, the mode choice decision between truck and rail, for each of 10 commodity types, is assumed to be a function of not only freight and shipment characteristics (such as freight value and average shipping distance) but also crude oil price. Four years of data on freight transportation activities and characteristics were obtained from the FAF² and FAF³ data sets and 2 years of CFS data to support the model development. Model validation results show that the developed models are effective in predicting the freight modal shares. Generally, it is shown that trucks tend to be chosen to handle higher value products for shorter distances. In addition, probably due to the oil price surge, the freight tonnage increase for railroads was much larger than that for trucks during the study period from 1993 to 2007. Interpretations of the coefficient estimations are used to draw insights on the effect of oil price change on freight transportation modal choice decisions and their environmental impacts.

In future studies, we would like to consider network assignment of estimated truck and rail annual freight shipment demand for each O/D pair because the mode choice as well as the route choice in freight deliveries can significantly affect regional and urban air quality and human health. Moreover, it could be possible to update the models once additional freight transportation demand data become available, which will be useful to estimate environmental impact from freight transportation systems precisely for various future freight shipment demands. Lastly, it will also be interesting to see whether the current railroad capacity can handle the growth of future demand.

Funding

The authors are part of an interdisciplinary research group supported by the U.S. Environmental Protection Agency (Project # R834280 “Global-to-Urban Models for Minimizing Air Quality and Climate Impacts of Freight Choice”). Members of the group also include Christopher Barkan, Tami Bond, Bumsoo Lee, Sungwon Lee, Steven J. Smith, and Fang Yan.

Acknowledgment

The authors thank the two anonymous reviewers for their helpful comments.

Appendix