Health benefits of air pollution abatement policy: Role of the shape of the concentration–response function

Abstract

There is strong evidence that fine particulate matter (aerodynamic diameter <2.5 μm; PM_2.5) air pollution contributes to increased risk of disease and death. Estimates of the burden of disease attributable to PM_2.5 pollution and benefits of reducing pollution are dependent upon the shape of the concentration response (C-R) functions. Recent evidence suggests that the C-R function between PM_2.5 air pollution and mortality risk may be supralinear across wide ranges of exposure. Such results imply that incremental pollution abatement efforts may yield greater benefits in relatively clean areas than in highly polluted areas. The role of the shape of the C-R function in evaluating and understanding the costs and health benefits of air pollution abatement policy is explored. There remain uncertainties regarding the shape of the C-R function, and additional efforts to more fully understand the C-R relationships between PM_2.5 and adverse health effects are needed to allow for more informed and effective air pollution abatement policies. Current evidence, however, suggests that there are benefits both from reducing air pollution in the more polluted areas and from continuing to reduce air pollution in cleaner areas.

Implications: Estimates of the benefits of reducing PM_2.5 air pollution are highly dependent upon the shape of the PM_2.5-mortality concentration-response (C-R) function. Recent evidence indicates that this C-R function may be supralinear across wide ranges of exposure, suggesting that incremental pollution abatement efforts may yield greater benefits in relatively clean areas than in highly polluted areas. This paper explores the role of the shape of the C-R function in evaluating and understanding the costs and health benefits of PM_2.5 air pollution abatement.

Introduction

There is a large and growing literature that provides compelling evidence that air pollution contributes substantially to adverse health effects (U.S. Environmental Protection Agency [EPA], 2009; Pope and Dockery, 2006; Brook et al., 2010). The Global Burden of Disease 2010 collaboration estimated that the number of deaths attributable to ambient particulate matter air pollution, PM_2.5 (particulate matter with an aerodynamic diameter <2.5 μm), and household air pollution from solid fuels were approximately 3.2 and 3.5 million in 2010, respectively (Lim et al., 2012). These estimates, especially in global regions with the highest concentrations of ambient PM_2.5, were dependent upon assumptions regarding the shape of the concentration-response (C-R) functions. Although current evidence suggests that the C-R function between PM_2.5 air pollution and mortality risk is approximately linear for a relatively narrow range at low levels of pollution (Dockery et al., 1993; Pope et al., 2002; Miller et al., 2007; Crouse et al., 2012), recent research suggests that the C-R function is likely to be supralinear (concave) for wide ranges that include very high levels of exposure (Pope et al., 2009, 2011; Burnett et al., 2014). Even for lower concentrations observed in North America, the possibility of supralinearity has been suggested (Krewski et al., 2009; Crouse et al., 2012). Such results appear to imply that a given incremental reduction in concentrations will yield greater benefits in relatively clean areas than in the most highly polluted areas (Goodkind et al., 2014). Such findings may seem counterintuitive and even ethically unappealing because they appear inconsistent with a reasonable public policy objective to clean up the most polluted areas and protect populations most at risk. The objective of this paper is to explore the role of the shape of the C-R function in evaluating and understanding the costs and health benefits of air pollution abatement policy.

Traditional Conceptual Framework

A traditional economic theoretic framework to evaluate pollution abatement policy is illustrated in Figure 1. The horizontal axis of this figure represents levels of pollution. Going from left to right indicates greater levels of pollution. Levels of pollution at the extreme far right of the axis are levels that would occur with no restrictions on pollution and no effort devoted to pollution abatement. Moving along the horizontal axis from right to left indicates pollution abatement or reduced pollution. At any given time and place, it is presumed that there will be some maximum level of pollution where there are no benefits to polluters from additional polluting. An unregulated polluting sector may be expected to pollute at this level, avoiding entirely any expenditure on abatement. It is also presumed that high pollution levels continue to occur even though, at least initially, pollution abatement would likely have relatively low cost. That is, the marginal (or incremental) cost of pollution abatement is low for the inexpensive and effective abatement strategies that will be adopted initially. However, further incremental efforts to abate air pollution results in ever-rising marginal abatement costs. Figure 1 presents a marginal cost of pollution abatement curve that illustrates that the marginal (or incremental) costs of pollution abatement rise as the air gets cleaner and it becomes increasingly difficult to obtain more pollution abatement and cleaner air.

Figure 1. Traditional conceptual framework for economic analysis of marginal costs versus marginal benefits.

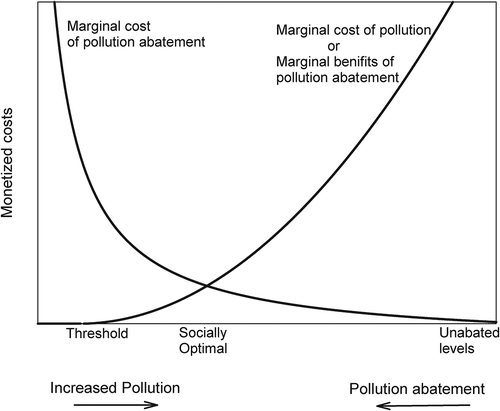
Figure 1 also presents a traditional conceptualization of a marginal benefit of abatement curve. This curve represents the marginal (or incremental) benefits of additional air pollution abatement and is based on two key assumptions: (1) there is a threshold level of emissions below which pollution poses zero threat to human health; and (2) the marginal (or incremental) harm to health is more severe as pollution levels rise. This second assumption is fairly standard in the economics/policy literature and means that marginal abatement benefits fall as pollution levels fall. The marginal benefit of abatement curve also represents the marginal cost or marginal health damage of additional emissions, because the avoided costs of pollution are the benefits of pollution abatement. The marginal cost of pollution as illustrated in Figure 1, therefore, represents underlying assumptions that the largest marginal improvements in health come from pollution abatement at the highest levels of pollution. Put another way, the first unit of abatement is the most beneficial.

Figure 1 also helps illustrate various air pollution abatement policies. One possible approach would be a policy of laissez faire (let it be or do nothing). This policy might be welcomed by polluters who don’t want to face costs of controlling their pollution, but in many cases it is far from optimal from society’s perspective. Classic externality theory (and many real-world observations) suggests that this approach would result in excessive air pollution. If there is free unrestricted access to use the ambient air as a place to emit pollutants, polluters have little or no incentive to control their pollution and will engage in polluting activities as long as there are positive marginal returns to these activities. Because the costs of pollution abatement are largely borne by polluters, but the benefits of pollution abatement (avoided health costs) are dispersed more broadly across society, there are few incentives to abate air pollution. A second policy approach is to restrict air pollution levels at or below the threshold level where there are no or minimal health effects. The U.S. Clean Air Act implicitly assumes threshold levels for some pollutants (so-called criteria pollutants) and requires that national ambient air quality standards be set that “are requisite to protect the public health” with “an adequate margin of safety” (Clean Air Act Section 109(b)(1) [or 42 U.S.C. 7409]). There are two obvious difficulties with this policy approach. First, there may be no clearly identifiable threshold. Second, reducing air pollution to some very low threshold level may result in excessively high marginal costs of pollution abatement.

Economists define a socially optimal policy as one that maximizes total net benefits (i.e., total benefits minus total costs). As illustrated in Figure 1, more pollution abatement contributes to higher social welfare as long as the marginal costs of pollution abatement are less than the marginal benefits of abatement. The socially optimal level of air pollution occurs where the marginal benefits of abatement and the marginal cost of abatement are equal. We do not discuss alternative policy tools to reach this optimal level of pollution (e.g., regulations, emission taxes, or tradable pollution permits) in detail. The traditional framework illustrated in Figure 1 is appealing because it provides, at least conceptually, an approach to identifying socially optimal levels of pollution and suggests cleaning up the most polluted areas, which would provide protection to those who are most at risk.

How Research Informs Marginal Benefit Analysis

Over the last few decades, research on the health effects of air pollution has provided much additional information regarding the marginal costs of air pollution i.e. the marginal benefits of pollution abatement. It suggests that the assumptions embedded in Figure 1 may not be fully valid. Figure 2a

Figure 2. Stylized analysis of pollution abatement for linear and supralinear C-R functions.

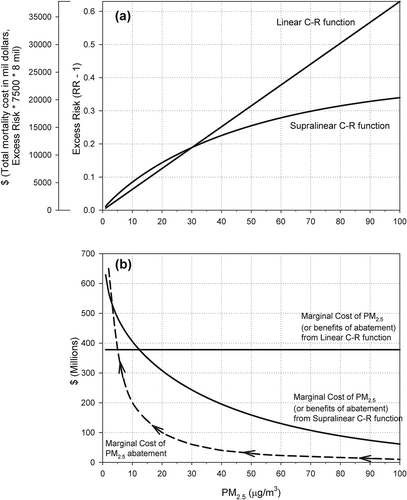
provides an illustration of two alternative C-R functions, one linear and the other supralinear. Figure 2b shows the corresponding marginal benefit of abatement curves (solid) as well as an illustrative marginal cost curve (dashed). These marginal benefit curves are more empirically based on recent research results. A key issue and important issue illustrated in Figure 2b is that the marginal benefits associated with a supralinear C-R function are increasing with increased abatement. The marginal benefits due to initial abatement activities are quite small, whereas the marginal benefits due to the last unit of abatement, taking concentrations down to the cleanest practicable level, are quite high. Because C-R functions and cost structures are not known with certainty and because they are also different across settings and times, Figure 2 remains stylistic and is used only for more realistic illustration. There remains some uncertainty regarding the health effects of air pollution, but the relationships depicted in Figure 2 illustrate at least four general fundamental research findings that are relevant to a contemporary exploration of the health benefits of air pollution abatement policy.

First, fine particulate matter air pollution (particles with an aerodynamic diameter <2.5 µm, PM_2.5) is strongly and consistently associated with adverse health effects (EPA, 2009; Pope and Dockery, 2006; Brook et al., 2010). The horizontal axes in Figure 2 indicate PM_2.5 concentrations (in units of µg/m³) ranging from 0 to 100. Multiple cities in China, India, and elsewhere have average concentrations of PM_2.5 that are approximately equal to or even exceed 100 µg/m³ (Chen et al., 2012; Brauer et al., 2012).

Second, in terms of health costs, the most dominant health effect is the increased risk of all-cause and/or cardiovascular mortality associated with long-term chronic exposure to PM_2.5 (Dockery et al., 1993; Pope et al., 2002; Miller et al., 2007; Krewski et al., 2009; Brook et al., 2010; Crouse et al., 2012). Studies of the health costs of air pollution suggest that approximately 90% of the total health costs are associated with increased mortality (EPA, 2011).

Third, although there remains some uncertainty regarding the shape of the C-R function, at ranges of pollution levels common to the United States, Canada, and Western Europe (generally PM_2.5 concentrations between 5 and 30 µg/m³), the estimated PM_2.5-mortality C-R functions tend to be near linear with no discernible thresholds for PM_2.5 exposures (Dockery et al., 1993; Pope et al., 2002; Crouse et al., 2012), suggesting that the marginal benefit of reductions in PM_2.5 concentrations is constant or flat in these areas. In Figure 2a, the linear C-R function reflects this assumed linearity and projects it out throughout the full range of exposure. A recent meta-analytic review of the association between long-term exposure to PM_2.5 and all-cause mortality provided an overall pooled estimate of approximately 6% excess risk of all-cause mortality per 10 µg/m³ increase in PM_2.5 (Hoek et al., 2013). The C-R functions illustrated in Figure 2a approximately reflect this pooled estimate for PM_2.5 concentrations below 30 µg/m³. The excess risk (ER) for the linear C-R function is calculated as

(1)

Fourth, there is some evidence, even in the U.S. and Canadian studies, of a supralinear C-R function where the marginal (or incremental) effects of exposure actually decline with increased exposure (Krewski et al., 2009; Crouse et al., 2012). Recent analyses that integrate information from studies of PM_2.5 ambient air pollution, secondhand cigarette smoke exposure, and active cigarette smoking provide further evidence that the exposure-response function is not linear throughout the range of potential exposures (Pope et al., 2009, 2011; Burnett et al., 2014), but that it flattens out when exposure is extended to very high levels. The excess risk for the assumed supralinear C-R function illustrated in Figure 2 is calculated as

(2)

This function is based on the functional form of the integrated risk function that was used for estimating the global burden of disease attributable to PM_2.5 (Burnett et al., 2014; Lim et al., 2012), but it is modified for illustrative purposes and appears to be approximately consistent with estimates of all-cause mortality in the United States (Krewski et al., 2009).

Stylized Analysis of Pollution Abatement

Figure 2 now allows us to illustrate a stylized analysis of pollution abatement that is reasonably consistent with the available air pollution research. We can also rescale (monetize) the ER from the C-R function in Figure 2a to approximately reflect the costs of excess mortality in a given population. Larger populations have more affected persons and, therefore, larger human health costs of pollution. The rescaling in Figure 2 assumes a population of one million people. We assume a baseline morality rate, with no pollution exposure, of 7500/million (although the baseline mortality rates can differ significantly across populations depending on age/health profiles and other competing risk factors). We also assign a value of a statistical life (VSL) equal to $8 million. VSL represents the sum of what individuals would pay for reductions in their risk of dying that sum to saving one statistical life. VSL estimates are, therefore, dependent on incomes, preferences regarding risk trade-offs, and related factors. For example, if a policy reduced the risk of death over the coming year by 1 in 10,000 for each of 10,000 people, one statistical life would be saved. If people were willing to pay, on average, $800 for a 1 in 10,000 risk reduction, the VSL would be $8 million, a value consistent with recent labor market estimates of the VSL in the United States (Kniesner et al., 2014). This value is also comparable to VSL estimates used in a cost-benefit analysis conducted by the EPA (EPA, 2011).

The marginal cost of PM_2.5 curves in Figure 2b are the first derivatives (or slopes) of the C-R functions in Figure 2a scaled to reflect monetized costs of excess morality. The marginal cost of PM_2.5 from the linear C-R function is clearly constant throughout the range of exposure, whereas the marginal cost of PM_2.5 from the supralinear C-R function declines with increasing levels of exposure.

In the situation with constant or even declining marginal (or incremental) costs of pollution, does pollution abatement make sense, especially in highly polluted areas? It depends upon the marginal costs of pollution abatement relative to the marginal costs of pollution (the marginal benefits of reducing pollution). For example, in Figure 2b, the dashed line represents a possible marginal cost of abatement curve, where the marginal cost of abatement is low initially but rises as the air gets cleaner. Although the marginal benefit of PM_2.5 also rises as the air becomes cleaner, at high levels of pollution the marginal benefit of reducing pollution exceeds the marginal cost, implying that it is efficient to reduce pollution. The socially optimal level of pollution abatement is not reached until the marginal cost of abatement exceeds the marginal benefits of abatement (i.e., the avoided marginal costs of pollution). In Figure 2b, this occurs at about 5 µg/m³ of PM_2.5, assuming the linear C-R function, and even less for the supralinear. Of course, it could turn out that pollution abatement is extremely expensive, so that the marginal cost of abatement curve shifts upward in the figure. If this is the case, marginal costs of pollution abatement may always exceed the marginal benefits and the optimal policy would be no abatement at all, but rather to accept the relatively less expensive health costs of air pollution.

More complicated situations can also arise. One example, not essential to this analysis, is a marginal benefit curve that slopes upward and is also steeper than marginal abatement costs, which can cause either zero abatement or maximal abatement to be optimal from society’s perspective. This possibility can be of special interest when there is significant uncertainty in the cost of abatement.

Implications of a Supralinear C-R Function for Optimal Pollution Abatement in the United States

What are the implications of a supralinear C-R function for optimal pollution abatement? In a recent study using data from the United States, Goodkind et al. (2014) evaluated three air pollution abatement policies, comparing their performance when either a linear or a supralinear C-R function is the correct specification of the pollution-health relationship. Their analysis is based upon a synthetic model of a rectangular geographic region. In each of 600 25 km × 25 km spatial grid cells, population approximates the latest Census Bureau data for a section of the U.S. Midwest. Each cell contains a single source of primary PM_2.5, whose emissions disperse spatially according to a Gaussian plume model. The cost of abatement takes the usual shape, resembling that found in Figure 1.

The first of three abatement policies considered selects the socially optimal abatement level for each source—optimal in the sense that the combination leads to the maximum possible aggregate net benefits. The second is a uniform maximum concentration standard, resembling the National Ambient Air Quality Standards (NAAQS) but set so as to achieve the greatest possible net benefits among all uniform standards. The third is an emission tax paid by sources for each ton of pollution they emit.

The analysis of these policies is based upon a simulation exercise in which abatement for each source is set according to the policy rule in question. In each of 1000 runs, two elements of the model are randomized: the initial distribution of emissions across space and the parameters in the source-specific abatement cost functions. The two C-R functions are taken from table 11 in Krewski et al. (2009), which resemble the functional forms given in eqs 1 and 2 and depicted in Figure 2a.

In comparing the socially optimal policy to the uniform standard, Goodkind et al. (2014) find that for both C-R specifications, the optimal policy leads to lower emissions, lower resulting pollution concentrations, and greater net social benefits than the uniform standard. Under either policy, emissions and concentrations are lower and net benefits higher if the supralinear C-R function is correct than if the linear C-R function is correct. If the true health relationship is supralinear, then society should strive for much cleaner air.

In comparing the socially optimal policy to the emission tax, the same general comparative results are obtained. Once again, the optimal policy leads to lower emissions and concentrations and higher net social benefits than the alternative tax policy. And again, under either policy, the supralinear C-R function, if correct, leads to lower emissions, pollution concentrations, and higher net social benefits than if the linear function is correct.

These results suggest that understanding the curvature of the C-R function might be of critical importance in the formulation of clean-air policy. In particular, if the relationship between pollution and human health is supralinear, then the benefits to aggressive abatement in the United States could be much larger than otherwise thought.

A final set of findings provides a useful glimpse into the question of fairness or environmental justice. If the C-R function is linear, then reducing concentration by 1 µg/m³ provides the same marginal health benefit everywhere. There is no intrinsic tension between cleaning the dirtiest places and achieving the greatest health gains for the greatest number. If, on the other hand, the C-R function is supralinear, then one must worry that a socially optimal policy will make the cleanest places cleaner, whereas those in dirty places see little improvement. As indicated by Figure 2a, the greatest incremental health gains are achieved where the air is already relatively clean.

The results of Goodkind et al. suggest that, in the United States, this concern may not be as great as expected, and the reason is found in the spatial nature of pollution and its dispersion across the landscape. Indeed, Gini coefficients (Marshall et al., 2014), indicating the degree of exposure inequality, differ very little for the various policy approaches. In all cases, inequality is reduced significantly relative to the initial situation, before the policy is imposed. The difference in Ginis for the two C-R functions is also quite small. This surprising result appears to be due to the way in which the large reductions called for in clean places under the supralinear C-R function led to large reductions in neighboring places. In short, because PM_2.5 disperses widely, cleaning the cleanest places means also cleaning dirty places.

Implications of a Supralinear C-R Function for Air Pollution Control Policies in India and China

Are the results obtained by Goodkind et al. (2014) likely to hold in countries such as India and China where pollution levels are much higher than in the United States? The slope of the supralinear C-R function, evaluated at the annual average PM_2.5 standard in the United States (12 µg/m³), is actually slightly larger than the slope of the linear function in eq 1. It is at the air pollution levels observed in India and China that the slope of the C-R function may become much flatter, implying a smaller reduction in excess mortality for each µg/m³ reduction in PM_2.5. A flatter C-R function does not, however, necessarily imply that the marginal benefits of a pollution control project will be lower in India or China than in the United States—or that the benefits of a project will fall short of the costs. We illustrate this by considering recent studies of the benefits and costs of installing flue-gas desulfurization units (scrubbers) on coal-fired power plants in India and China to reduce sulfur dioxide emissions and the associated PM_2.5.

The lives saved by installing a scrubber at a power plant are the product of the change in ambient PM_2.5 concentrations, the size of the exposed population, the baseline death rate in the exposed population, and the change in excess risk (the slope of the C-R function). The marginal benefits of the project are the product of lives saved times the VSL.

(3a)

(3b)

Holding the slope of the C-R function fixed, implementing the policy in a densely populated area will increase the marginal benefits of the policy. The value of these benefits will also be higher the more people are willing to pay to reduce risk of death (i.e., the higher the VSL), which should increase with income. Whether marginal benefits exceed the marginal costs also depends, of course, on the cost of installing and operating the scrubber. Given economies of scale, the marginal cost of reducing emissions is likely to be lower at larger power plants.

A recent study of the costs and benefits of retrofitting coal-fired power plants in India with flue-gas desulfurization units (Malik, 2013) suggests that this policy does pass the benefit-cost test, especially in densely populated areas. Retrofitting 72 coal-fired power plants with scrubbers would save lives at an average cost of 6 million Rs. (approximately $100,000) per life saved. The cost per life saved varies greatly across plants, from 1.56 million Rs. to 31.5 million Rs. depending on the size of the exposed population and the size of the plant. At the 30 largest plants, which account for two-thirds of the sulfur emissions generated, the cost per life saved varies from 1.56 to 14.7 million Rs. Bhattacharya et al. (2007) report a preferred VSL estimate of 1.3 million Rs. (2006 Rs.) based on a stated preference study of Delhi residents. Madheswaran’s (2007) estimate of the VSL based on a compensating wage study of workers in Calcutta and Mumbai is approximately 15 million Rs. Shanmugam (2001) reports a much higher value (56 million Rs.) using data from 1990. Although published estimates of the VSL for India vary widely, studies suggest that retrofitting scrubbers indeed passes the benefit-cost test, in spite of the higher average PM_2.5 levels in India.

Partridge and Gamkhar (2010, 2012) examine the benefits and costs of installing a scrubber on a 1200-MW coal-fired power plant in each of 29 locations in China, which span the six regions of the Chinese electricity grid (Central, North, Eastern, Northeast, Northwest, and South). The health benefits of the scrubber are valued using a VSL for China of 1.3 million 2007 RMB (about $171,000 USD at market exchange rates), based on contingent valuation studies conducted in China. The authors also calculated the value of reductions in chronic bronchitis and hospital admissions, based on Aunan and Pan (2004); however, over 95% of the benefits were attributed to premature mortality. Results for the 29 plants are grouped by grid region. Benefits per MWhr of electricity generated are highest for plants in the Central, East, and North regions of China, which are also the most populous regions of the country. These benefits exceed the estimated cost per MWhr of scrubbing in the most populous region (the Central region), implying that scrubbers pass the benefit-cost test in that region. They are, however, less than half the cost of scrubbing in the least densely populated regions (the Northwest, Northeast, and South).

These examples suggest that even if a supralinear C-R function is correct, this does not necessarily imply that pollution abatement policies will fail to have health benefits greater than the costs in countries with exceptionally high pollution levels. The slope of the C-R function describes the percentage reduction in baseline deaths associated with a reduction in air pollution. Marginal benefits also depend on the size of the exposed population, baseline death rates, and the value attached to mortality risk reductions. This implies that considerable benefits could accrue from improving air quality in low- and middle-income countries such as China and India where population-weighted air pollution exposure has increased over the past 20 years and where, over that same interval, mortality from noncommunicable diseases affected by air pollution is increasing in their large and aging populations.

Conclusion

The traditional understanding of environmental policy, reflected in the language of the U.S. Clean Air Act, holds that the marginal health benefits associated with abatement become smaller as the air becomes cleaner. Recent research results, which suggest that the C-R function for PM_2.5 may in fact be supralinear at levels of air pollution prevalent in low- and middle-income countries such as China and India, suggest that the traditional understanding of policy may be incorrect. A supralinear C-R function, if correct, would imply that the percentage reduction in mortality per unit of abatement would be lower at the higher air pollution levels currently found in India and China than in the United States. This implies then that considerable improvements in air quality will be required to achieve substantial reductions disease burden. However, the marginal benefits associated with pollution control policies depend also upon the size of the exposed population, baseline death rates, and the value attached to reductions in mortality risks. Therefore, even incremental improvements could confer important public health benefits. This is the view embodied in the World Health Organization’s (WHO) world air quality guidelines, which include interim targets in addition to the much lower air quality guideline itself (WHO, 2006).

The current epidemiologic evidence does not provide strong support for nonlinearity over the range of ambient air pollution in the world’s cleanest places, e.g., the United States and Western Europe, although the shape of the mortality exposure-response for PM_2.5 at low levels is subject to some uncertainty. If future research were to strengthen the evidence in support supralinearity at low levels of pollution, tighter standards, at which the high marginal health benefits associated with achieving substantially lower concentrations are experienced, might be justified.

The estimation of benefits of pollution abatement is further complicated by the broad spatial dispersion of PM_2.5, its precursors, and related pollutants. Substantial air pollution abatement efforts focused on reducing pollution in highly polluted areas can result in significant improvements in air quality in other areas with relatively clean air. The supralinear C-R function suggests that there may be relatively high collateral benefits as a result of reduced dispersed pollution to other cleaner areas.

Given the toll imposed on human health by particulate pollution around the world, these questions are of great significance. At this point, there would appear to be benefits both from reducing air pollution in the most polluted places and continuing to reduce air pollution in the cleanest places as well, the uncertainties regarding the shape of the exposure-response relations notwithstanding. There is also a clear and compelling need for a more thorough understanding of the shape of the C-R function over the entire global range. This can come only with additional research, especially new, large epidemiologic studies with sufficient statistical power and precision to better characterize the shape of the exposure-response relations at the high and low ends of the global exposure distribution. Reducing the uncertainties in the current understanding of the C-R relationships between PM_2.5 and adverse health effects would allow more informed environmental policy decisions and warrants devoting further energy and resources to addressing these questions.

Acknowledgment

The views expressed in this article do not represent those of the Health Effects Institute or its sponsors.

Additional information

Notes on contributors

C. Arden Pope

C. Arden Pope III is the Mary Lou Fulton Professor of Economics at Brigham Young University at Provo, UT, USA.

Maureen Cropper

Maureen Cropper is a distinguished university professor and chair of the Department of Economics at the University of Maryland in College Park, MD, USA, and is a senior fellow at Resources for the Future.

Jay Coggins

Jay Coggins is an associate professor in the Department of Applied Economics at the University of Minnesota in St. Paul, MN, USA.

Aaron Cohen

Aaron Cohen is a principle scientist at the Health Effects Institute in Boston, MA, USA.